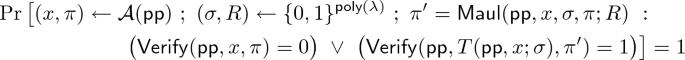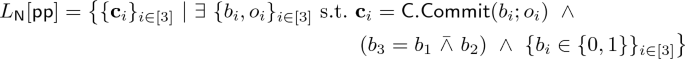Fully Homomorphic NIZK and NIWI Proofs

Abstract

In this work, we define and construct fully homomorphic non-interactive zero knowledge (FH-NIZK) and non-interactive witness-indistinguishable (FH-NIWI) proof systems.

     We focus on the NP complete language L, where, for a boolean circuit C and a bit b, the pair $(C,b)\in L$ if there exists an input $\mathbf {w}$ such that $C(\mathbf {w})=b$. For this language, we call a non-interactive proof system fully homomorphic if, given instances $(C_i,b_i)\in L$ along with their proofs $\varPi _i$, for $i\in \{1,\ldots ,k\}$, and given any circuit $D:\{0,1\}^k\rightarrow \{0,1\}$, one can efficiently compute a proof $\varPi$ for $(C^*,b)\in L$, where $C^*(\mathbf {w}^{(1)},\ldots ,\mathbf {w}^{(k)})=D(C_1(\mathbf {w}^{(1)}),\ldots ,C_k(\mathbf {w}^{(k)}))$ and $D(b_1,\ldots ,b_k)=b$. The key security property is unlinkability: the resulting proof $\varPi$ is indistinguishable from a fresh proof of the same statement.

     Our first result, under the Decision Linear Assumption (DLIN), is an FH-NIZK proof system for L in the common random string model. Our more surprising second result (under a new decisional assumption on groups with bilinear maps) is an FH-NIWI proof system that requires no setup.

A full version of this paper appears on ePrint [4].

1 Introduction

Homomorphism is a desirable feature that enhances the capabilities of many cryptographic systems. Most notably, the concept of fully homomorphic encryption [13, 18, 25] has revolutionized the area of cryptography. Other primitives such as homomorphic signatures [10, 20] and homomorphic secret sharing [12] have also found useful cryptographic applications [11, 22]. In this work, we study homomorphism in the context of non-interactive proof systems. Our goal is to design homomorphic proof systems with secrecy guarantees; specifically, we focus on the most common secrecy guarantees studied in the literature, namely zero-knowledge [9] and witness indistinguishability [6, 17].

Our Work: Fully-Homomorphic NIZK and NIWI Proofs. We introduce the notion of fully-homomorphic non-interactive zero-knowledge (FH-NIZK) and witness-indistinguishable (FH-NIWI) proof systems. In the simplest setting, this proof system allows for combining proofs for the instances A and B into a proof for the instance $A \wedge B$. In the more general setting, this proof system allows for combining proofs for multiple instances $A_1,\ldots ,A_n$ using a function f into a single proof for $f(A_1,\ldots ,A_n)$.

A naïve attempt to combine proofs for the instances $(A_1,\ldots ,A_n)$ using a function f is to simply output the concatenation of the individual proofs on each of the instances $A_1,\ldots ,A_n$ together with the function f. However, this combined proof does not resemble an honestly generated proof for the instance $f(A_1,\ldots ,A_n)$. Our goal is to combine proofs in a way that is indistinguishable from an honestly generated proof for the instance $f(A_1,\ldots ,A_n)$. We call this property unlinkability.

There are several reasons why unlinkability is an interesting feature: Firstly, it is often desirable to hide the fact that a proof was obtained by combining multiple proofs. Unlinkability also preserves the privacy of the underlying proof; namely, it ensures that homomorphic evaluation of multiple NIZK (resp., NIWI) proofs still results in a NIZK (resp., NIWI) proof. Moreover, it guarantees that the homomorphic evaluation can be multi-hop, meaning that the proofs can be evaluated upon multiple times. We describe the homomorphic evaluation procedure and unlinkability property below.

We define the notion of a fully-homomorphic proof system for the NP-complete language $L_\mathcal {U}$ which consists of instances (C, b), where C is a boolean circuit with single-bit output and b is a bit, such that there exists a witness $\mathbf {w}$ (a vector of bits) for which $C(\mathbf {w})=b$. A non-interactive proof system for proving membership in this language consists of the algorithms $\mathsf {Prove}$ and $\mathsf {Verify}$. A fully homomorphic proof system additionally has the algorithm $\mathsf {Eval}$ defined as follows:

Homomorphic Evaluation $(\mathsf {Eval})$: On input k instances $\{z_i = (C_i,b_i)\}_{i \in [k]}$ accompanied with proofs $\{\varPi _i\}_{i \in [k]}$ for the statements $\{z_i \in L_\mathcal {U}\}_{i \in [k]}$, and a circuit $D: \{0,1\}^k \rightarrow \{0,1\}$, $\mathsf {Eval}$ outputs a proof $\varPi ^*$ for the statement $z^*= (C^*,D(b_1,\ldots ,b_k)) \in L_\mathcal {U}$, where $C^*$ is defined to be the circuit that on input $(\mathbf {w}_1,\ldots ,\mathbf {w}_k)$ outputs $D(C_1(\mathbf {w}_1),\ldots ,C_k(\mathbf {w}_k))$.

We define unlinkability as follows: A proof $\varPi ^*$ output by $\mathsf {Eval}$ on input $\{z_i \in L_\mathcal {U}\}_{i \in [k]}$ accompanied with proofs $\{\varPi _i\}_{i \in [k]}$, where $\varPi _i$ is output by $\mathsf {Prove}$ on input $z_i$ and a valid witness $\mathbf {w}_i$, should be indistinguishable from the output of $\mathsf {Prove}$ on input the instance $(C^*,D(b_1,\ldots ,b_k))$ and witness $(\mathbf {w}_1,\ldots ,\mathbf {w}_k)$. As mentioned above, unlinkability guarantees that the evaluation property preserves zero-knowledge (ZK) or witness-indistinguishability (WI) of an evaluated proof, depending on whether the fresh proof is ZK or WI respectively. We refer the reader to Fig. 1 for an illustrative description of unlinkability, and refer the reader to Sect. 4 for our definition of fully homomorphic proofs.

Our Results. We construct both a NIZK and a NIWI fully homomorphic proof system.

Fig. 1.

Unlinkability property of Fully Homomorphic Proofs: Let $\varPi ^*$ be the output of $\mathsf {Eval}$ on input $\{ (C_i, b_i) \in L_\mathcal {U}\}_{i \in [k]}$ accompanied with proofs $\{\varPi _i\}_{i \in [k]}$, where $\varPi _i$ is output by $\mathsf {Prove}$ on input $(C_i, b_i)$ and a valid witness $\mathbf {w}_i$. Let $C^*$ be the circuit that on input $(\mathbf {w}_1,\ldots ,\mathbf {w}_k)$, outputs $D(C_1(\mathbf {w}_1),\ldots ,C_k(\mathbf {w}_k))$ and let $\varPi _F$ be an honestly generated proof for the instance $(C^*, b^*) \in L_\mathcal {U}$. We require that $\varPi ^*$ is computationally indistinguishable from $\varPi _F$.

Theorem 1 (Informal)

Assuming Decisional Linear Assumption (DLIN), there exists a fully-homomorphic non-interactive zero-knowledge proof system in the common random string model.

We describe the construction of FH-NIZK in the technical sections and defer the proof to the full version [4].

For constructing FH NIWI proofs, we rely on a new decisional assumption on groups with bilinear maps called DLIN with leakage, defined in Fig. 2.

A proof of security of the assumption in the bilinear generic model is provided in the full version of the paper [4].

Theorem 2 (Informal)

Assuming DLIN with Leakage, there exists a fully-homomorphic non-interactive witness-indistinguishable proof system in the plain model (i.e. without setup).

We describe the construction of FH-NIWI in the technical sections and defer the proof to the full version [4].

Related Works. Most relevant to our work is the work on malleable proof systems [14, 16], who studied unary transformations, i.e., when $\mathsf {Eval}$ receives a single instance-proof pair and outputs a mauled instance along with the corresponding proof. The work of [14] studied malleable proof systems for specific relations, and [16] studied malleability for general relations albeit under knowledge assumptions. Moreover, these works consider NIZK proof systems and thus require trusted setup. We note that [14] satisfies a stronger proof of knowledge property (called controlled-malleable simulation-sound extractability) that we don’t achieve in this work.

The notion of malleability, although seemingly limited due to its unary nature, has found many applications, such as verifiable shuffles [14], delegatable anonymous credentials [7, 15] and leakage-resilient proof systems [5]. Re-randomizability [7], a special case of malleability, has also been studied in the literature. Following [14, 16], Ananth et al. [3] construct privately malleable NIZK proof systems, and the works of [1, 2] study homomorphic proof systems for specific relations.

Fig. 2.

Description of the DLIN with leakage, with respect to a group ${\mathbb G}$ of prime order p with a bilinear map $e: {\mathbb G}\times {\mathbb G}\rightarrow {\mathbb G}_T$. We refer to this as DLIN with leakage assumption since the first row in both the distributions are indistinguishable assuming DLIN, and the second and third rows can be viewed as leakage.

It is important to stress that all the prior works, even in the case of unary transformations studied in the context of malleable proofs [14, 16], assume trusted setup. Thus, in the context of WI proof systems, our results are especially surprising since it allows for combining proofs that were created completely independently, with no shared setup.

We now describe some applications of fully-homomorphic proofs.

Private Incremental Proofs. Incremental proofs, introduced by Valiant [26], allow for merging many computationally sound proofs [23] into one proof which is as short and easily verifiable as the original proofs. Incremental proofs have been applied in several contexts such as proof-carrying data [8] and cryptographic image authentication mechanisms [24]. It is useful in two types of settings: one where the computation dynamically evolves over a period of time, hence a proof of correctness of the entire computation cannot be computed all at once, and the other where different entities wish to compute a proof for the correctness of computation in a distributed setting.

The focus of prior works on incremental proofs was on succinctness whereas the focus of our work is on privacy. While our work does not achieve succinctness, as we will see later achieving privacy alone turns out to be quite challenging (especially, in the context of fully-homomorphic NIWIs). We hope that our tools can be combined with succinct incremental proofs to yield incremental proofs that enjoy both succinctness and privacy guarantees.

Commit-and-Compute Paradigm. Another application of fully-homomorphic proofs is the commit-and-compute paradigm. At a high level, the commit-and-compute paradigm allows a prover to commit to its sensitive data, and later on, prove statements about the committed data. Proofs from different provers can then be combined to infer arbitrary statements about the committed data. We give below an example that illustrates the applicability of this paradigm.

Verifiable Data Analysis. Consulting firms often collect data from different research groups, perform analysis on the joint dataset and then share the analyzed results with different organizations. For instance, there are firms that collect medical data from different research groups and share the analysis on the medical data to pharmaceutical companies. This raises concerns about trusting the research groups and the consulting firms to not lie about their conclusions. We can tackle this concern by using fully homomorphic NIZK or NIWI proofs. The research groups can publish their (committed) data along with a proof that it was collected from valid sources, without revealing the identity of the sources. The consulting firms can then perform analysis on the joint data sets and homomorphically compute a proof that the analysis was performed correctly. Moreover, the homomorphically computed proof will also hide the identities of the research groups involved in sharing the data to the firms.

Commit-and-compute paradigm is formalized by defining the NP language $L_\mathsf {COM}$, a modification of $L_\mathcal {U}$ so that the instance includes a vector of commitments along with (C, b). The language $L_\mathsf {COM}$ is defined as follows:

$$L_\mathsf {COM}= \left\{ (C, (\mathsf {com}_1,\ldots ,\mathsf {com}_n), b)~\Big |~\exists \{w_i,r_i\} \text { s.t. }\ \begin{matrix} C(w_1,\ldots ,w_n)=b \text {, and} \\ \{\mathsf {com}_i = \mathsf {Commit}(w_i,r_i)\} \end{matrix} \right\} $$

The evaluation is defined similarly to that of homomorphic $\mathsf {Eval}$ for $L_\mathcal {U}$. We define and instantiate the commit-and-compute paradigm using fully-homomorphic proofs in the full version [4].

Roadmap. In Sect. 2, we give an overview of our techniques. In Sect. 3, we describe some notation and definitions. In Sect. 4, we present our definition of fully homomorphic NIZK and NIWI proof systems. In Sect. 5, we define and instantiate the building blocks for our constructions, and describe our DLIN with Leakage assumption (in Sect. 5.3). In Sect. 6, we construct fully homomorphic NIZK proofs for $\mathsf {NP}$ from DLIN. In Sect. 7, we describe our main result of fully homomorphic NIWI proofs from the DLIN with Leakage assumption. We refer the reader to the full version of the paper [4] for a detailed description of the constructions.

2 Technical Overview

Let us start with some intuition. Suppose we want to generate a proof for the satisfiability of $C_1 \wedge C_2$ for some circuits $C_1, C_2$. Given a proof $\varPi _1$ for the satisfiability of $C_1$ and a proof $\varPi _2$ for the satisfiability of $C_2$, clearly $\varPi = (\varPi _1, \varPi _2)$ is a proof for the satisfiability of $C_1 \wedge C_2$. However, such a proof does not satisfy unlinkability. Moreover, the structure of the proof $\varPi = (\varPi _1, \varPi _2)$ may be different from that of a fresh proof computed for the satisfiability of $C_1 \wedge C_2$.

To achieve homomorphism and unlinkability, a natural candidate is a proof system that works gate-by-gate as follows: Commit to all the wire values of the circuit and prove that each gate is consistent with the committed values. Such a proof structure is a good candidate because structurally, a proof of the composed instance $C_1 \wedge C_2$ will be similar to a fresh proof.

Indeed the beautiful work of Groth, Ostrovsky and Sahai [21] (henceforth referred to as GOS) has this proof structure and it is the starting point for our FH NIZK construction as well as our FH NIWI construction. GOS constructed NIZK and NIWI proofs under the decisional linear (DLIN) assumption. First in Sect. 2.1, we describe our FH NIZK construction which builds on the GOS NIZK. Then in Sect. 2.2, we describe our FH NIWI construction which contains the bulk of the technical difficulty in this work.

2.1 Overview: Fully Homomorphic NIZK

Recall that an $L_\mathcal {U}$ instance is of the form $(C,\mathsf {out})$ where $C:\{0,1\}^t \rightarrow \{0,1\}$ and $\mathsf {out}\in \{0,1\}$. Let $\mathbf {w} = (w_1,\dots , w_t)$ be a witness such that $C(\mathbf {w}) = \mathsf {out}$. Let us first recall the GOS NIZK proof for $L_\mathcal {U}$.

GOS NIZK. The GOS NIZK proof system is associated with a commitment scheme with public parameters (as we elaborate on later). The $\mathsf {CRS}$ consists of the parameters $\mathsf {pp}$ for the commitment scheme. The prover on input $(C,\mathsf {out})$ along with witness $\mathbf {w}$ does the following:

• 1. Let $w_1,\dots ,w_n$ be the values induced by witness $\mathbf {w} = (w_1,\dots , w_t)$ on all the wires of the circuit C. Commit to all the wire values with respect to $\mathsf {pp}$, except the output wire. For every $i \in [n-1]$, denote by $\mathbf {c}_i$ the commitment to wire value $w_i$. Denote by $\mathbf {c}_n = w_n$.

• 2. For each $i \in [n]$, prove that the commitment $\mathbf {c}_i$ is a commitment to a boolean value. We refer to such proofs by Bit Proofs.

• 3. For each gate in C, prove that the commitments to the input and the output wires of the gate are consistent with the gate functionality. We refer to such proofs by Gate Proofs.

In their construction, GOS use a commitment scheme which has two indistinguishable modes of public parameters: perfectly binding and perfectly hiding. Loosely speaking, the perfectly binding mode is used to argue perfect soundness, and the perfectly hiding mode is used to argue zero-knowledge. In addition, they require the commitment scheme to be additively homomorphic and the additive homomorphism is used in the Gate Proofs.

GOS constructed NIWI proof systems for Bit Proofs and Gate Proofs, and proved that this is sufficient for their NIZK construction. Both Bit and Gate Proofs are computed using the openings of the commitments as the witness. Our FH NIZK construction follows a similar template (our NIZK construction is identical to the GOS NIZK) but in order to achieve unlinkability, we need additional properties from the commitment scheme as well as from the Bit Proofs and Gate Proofs, as we explain below.

Homomorphic Evaluation. Homomorphic evaluation works as follows: On input k instances $\{z_i = (C_i,b_i)\}_{i \in [k]}$ along with proofs $\{\varPi _i\}_{i \in [k]}$ where each $\varPi _i$ is a proof that $z_i \in L_\mathcal {U}$, and a circuit D, we want to output a proof that $(C^*, b^*) \in L_\mathcal {U}$ where $C^*$ is the composed circuit and $b^* = D(b_1,\dots , b_k)$. First, compute a fresh proof for the circuit D with witness $(b_1,\dots , b_k)$. Note that the fresh proof for $(D,b^*)$ together with the proofs $\{\varPi _i\}_{i \in [k]}$, forms a verifying proof with respect to $(C^*, b^*)$. This follows from the fact that in each proof $\varPi _i$, the output wire $b_i$ is given in the clear. However this combined proof is distinguishable from a fresh proof (given the individual proofs $\{\varPi _i\}_{i \in [k]}$). Thus, to achieve unlinkability, we randomize this entire proof.

Randomizing the NIZK Proof. A proof system is said to be randomizable [7] if given a proof $\varPi$ for an instance x, it is possible to randomize the proof $\varPi$ to obtain a proof $\varPi '$ for x, such that $\varPi '$ is indistinguishable from a fresh proof for x. Randomizability of a proof system is sufficient for achieving unlinkability in our construction, as explained above.

At a high level, we randomize the proof $\varPi$ as follows: Randomize all the commitments in the proof, and then “update” the existing proofs to be with respect to the randomized commitments. Thus, given the original Bit Proofs and Gate Proofs, we need to be able to “maul” them to be with respect to the new randomized commitments in such a way that the updated proofs are distributed as fresh Bit Proofs and Gate Proofs. We refer to such proofs as malleable proofs.

Ingredients for Our FH NIZK. In summary, for constructing FH NIZK, we use a commitment scheme $(\mathsf {C.}\mathsf {Setup}, \mathsf {C.}\mathsf {Commit}, \mathsf {C.}\mathsf {Rand})$ from GOS, which is also randomizable. We also need malleable proof systems for Bit proofs and for Gate proofs. (we define the corresponding proof systems $(\mathsf {Bit}.\mathsf {Prove}, \mathsf {Bit}.\mathsf {Verify}, \mathsf {Bit}.\mathsf {Maul})$ and $(\mathsf {N}.\mathsf {Prove}, \mathsf {N}.\mathsf {Verify},\mathsf {N}.\mathsf {Maul})$ in Sect. 3).

As shown in GOS, both Bit Proofs and Gate Proofs can be reduced to proofs of linearity with respect to the $\mathsf {NP}$ language $L_\mathsf {Lin}$. The language $L_{\mathsf {Lin}}$ is parameterized by three random group elements (f, h, g) in some underlying group ${\mathbb G}$ of prime order (which has a bilinear map), and whose instances consists of pairs (A, B), where $A=(f^{a_1},h^{a_2},g^{a_3})$ and $B=(f^{b_1},h^{b_2},g^{b_3})$, such that $a_1+a_2 =a_3$ or $b_1+b_2 =b_3$¹.

GOS constructed a NIWI proof for $L_\mathsf {Lin}$. Recall that for our purposes, we need malleable proof systems for Bit Proofs and Gate Proofs, and as a result we need the underlying NIWI proof for $L_\mathsf {Lin}$ to be malleable with respect to randomization. Namely given a pair $(\mathbf {A}, \mathbf {B}) \in L_\mathsf {Lin}$ with a NIWI proof $\varPi$, it should be possible to maul the proof $\varPi$ for $(\mathbf {A}, \mathbf {B})$ into a proof $\varPi '$ for a randomization $(\mathbf {A}', \mathbf {B}')$ of $(\mathbf {A}, \mathbf {B})$. We show that the GOS proof for $L_\mathsf {Lin}$ has the desired malleability property, and we refer the reader to Sect. 3 for the definition of a malleable proof system.

2.2 Overview: Fully Homomorphic NIWI

We now focus on our construction of a FH NIWI proof system for $L_\mathcal {U}$. As we will see, this is a significantly harder task compared to the FH NIZK, since NIWI is constructed in the plain model without a CRS.

The GOS NIWI Construction. We will first describe the GOS NIWI proof system. Recall that in the GOS NIZK construction, the $\mathsf {CRS}$ consists of the parameters $\mathsf {pp}$ of the commitment scheme. In a NIWI construction, there is no $\mathsf {CRS}$. In the GOS NIWI, the prover chooses two parameters $(\mathsf {pp}^0, \mathsf {pp}^1)$ such that it is possible to publicly verify that one of them is binding. The NIWI proof for $(C, \mathsf {out}) \in L_\mathcal {U}$ is of the form $(\mathsf {pp}^0, \varPi ^0, \mathsf {pp}^1, \varPi ^1)$ where $\varPi ^b$ is the NIZK proof with respect to $\mathsf {pp}^b$ for each $b \in \{0,1\}$.

Towards Homomorphic Evaluation and Unlinkability. It is not clear how to use the GOS NIWI construction to construct an FH NIWI. In particular, achieving unlinkability here is significantly harder. Intuitively, the difficulty stems from the fact that even though the GOS NIWI appears to be gate-by-gate, there is an over-arching pair of parameters associated with the entire proof, and this pair is different for different proofs.

In more detail, a fresh GOS NIWI proof as described above has two parameters $(\mathsf {pp}^0, \mathsf {pp}^1)$ associated with it. Thus, if we use an approach similar to the FH NIZK construction for composing proofs, namely if we prove that $(D(C_1,\dots , C_k), b^*) \in L_\mathcal {U}$, given k instances $\{z_i = (C_i,b_i)\}_{i \in [k]}$ along with corresponding proofs $\{\varPi _i\}_{i \in [k]}$, where $b^* = D(b_1,\dots ,b_k)$, then the resulting composed proof will have 2k parameters associated with it. It is unclear how to randomize such a composed proof to look like a fresh proof which has only two parameters associated with it.

In order to achieve unlinkability in our construction, we diverge from the GOS construction. Rather than choosing a pair of parameters per proof, we choose a fresh pair of parameters $(\mathsf {pp}_j^0, \mathsf {pp}_j^1)$ for each gate of the circuit. As in the GOS construction, the honest prover chooses one of them to be binding and the other hiding such that one can publicly verify that indeed one of the parameters is binding. Recall that in the GOS NIWI construction, the prover committed to each wire value with respect to two parameters $(\mathsf {pp}^0, \mathsf {pp}^1)$. Now that we are choosing fresh parameters per gate, the question is which parameters do we use to commit to a wire value?

We associate four parameters $\mathsf {pp}_i^0, \mathsf {pp}_i^1, \mathsf {pp}_j^0, \mathsf {pp}_j^1$ with an internal wire between the $i^{th}$ and the $j^{th}$ gate in the circuit. In our construction, we commit to the wire value with respect to all of these parameters and thus, have four commitments $\mathbf {c}_i^0, \mathbf {c}_i^1, \mathbf {c}_j^0,\mathbf {c}_j^1$ per wire. We compute Bit Proofs with respect to each of the four commitments, and compute Gate Proofs for every gate with respect to both parameters associated with that gate.

Ensuring Soundness. Recall that the GOS NIWI consists of two independent NIZK proofs $\varPi ^0, \varPi ^1$ with respect to parameters $\mathsf {pp}^0, \mathsf {pp}^1$ respectively. Thus, the commitments, Bit Proofs and Gate Proofs with respect to both the parameters are independent of each other, and $\varPi ^0, \varPi ^1$ are verified separately. This is not the case in our setting.

Our proof contains a pair of parameters per gate, and has four commitments per wire. Thus, we need to prove that the multiple commitments per wire commit to the same value. In particular for soundness, it is sufficient to prove that among the four commitments per wire, the two commitments corresponding to the two binding parameters commit to the same value.

However the verifier does not know which of the four parameters $\mathsf {pp}_i^0, \mathsf {pp}_i^1, \mathsf {pp}_j^0,$ $\mathsf {pp}_j^1$ are binding. All we are guaranteed is that for every gate j, one of $(\mathsf {pp}_j^0, \mathsf {pp}_j^1)$ is binding. So in our construction, we give four pairwise proofs that each commitment with respect to gate i commits to the same value as each commitment with respect to gate j. Namely, for all $b_1,b_2 \in \{0,1\}$, the commitments $(\mathbf {c}_i^{b_1}, \mathbf {c}_j^{b_2})$ with respect to $\mathsf {pp}_i^{b_1},\mathsf {pp}_j^{b_2}$ commit to the same value. This ensures consistency with respect to the two binding commitments across gates i, j. This, along with the Bit and Gate proofs will ensure that there is a consistent boolean assignment $w_1,\dots ,w_n$ induced by the witness $\mathbf {w}$ across all the wires of the circuit, such that $C(\mathbf {w}) = \mathsf {out}$.

We emphasize that we do not provide consistency proofs between the two commitments $(\mathbf {c}_i^0, \mathbf {c}_i^1)$ for a gate i, and in fact this is crucial for achieving witness indistinguishability, as we explain later. Towards constructing such pairwise proofs, we define the language $L_\mathsf {TC}$² which consists of instances of the form $(\mathbf {c}_i, \mathbf {c}_j, \mathsf {pp}_i, \mathsf {pp}_j)$ where commitment $\mathbf {c}_i$ with respect to parameters $\mathsf {pp}_i$ and $\mathbf {c}_j$ with respect to $\mathsf {pp}_j$ commit to the same bit.

Arguing Witness Indistinguishability. The main challenge is to prove that the final construction is witness indistinguishable even given the additional $L_\mathsf {TC}$ proofs for instances of the form $(\mathbf {c}_i, \mathbf {c}_j, \mathsf {pp}_i, \mathsf {pp}_j)$. We note that even if the proof system for $L_\mathsf {TC}$ satisfies WI, we do not know how to argue that the final construction is WI. Intuitively, the issue is that an $L_\mathsf {TC}$ statement may have a unique witness, in which case WI offers no secrecy. As we explain below, we need our $L_\mathsf {TC}$ proof system to have a secrecy guarantee of the flavor of strong NIWI (with respect to specific distributions).

To argue WI of our final FH NIWI construction, we prove that a proof $\varPi _0$ for $(C,\mathsf {out}) \in L_\mathcal {U}$ with respect to witness $\mathsf {wit}_0$ is indistinguishable from a proof $\varPi _1$ with respect to witness $\mathsf {wit}_1$. Let us zoom in on a wire k between gates i, j whose value changes from 0 (for $\mathsf {wit}_0$) to 1 (for $\mathsf {wit}_1$). Both $\varPi _0, \varPi _1$ will contain four commitments to the wire k with respect to parameters $\mathsf {pp}_i^0, \mathsf {pp}_i^1, \mathsf {pp}_j^0, \mathsf {pp}_j^1$, along with the four $L_\mathsf {TC}$ proofs (see Fig. 3).

Denote by $\mathsf {PP}= (\mathsf {pp}_i^0, \mathsf {pp}_i^1, \mathsf {pp}_j^0, \mathsf {pp}_j^1)$. Denote by $\mathsf {W}(b)$ the four commitments to bit b on wire k, that is $\mathsf {W}(b) = (\mathbf {c}_i^0, \mathbf {c}_i^1, \mathbf {c}_j^0,\mathbf {c}_j^1)$ where all the four commitments are to the bit b. Denote by $\mathsf {\mathbf {\Pi }}(b)= (\pi ^{00}, \pi ^{01}, \pi ^{10}, \pi ^{11})$ where for all $b_1,b_2 \in \{0,1\}$, $\pi ^{b_1 b_2}$ is a proof for $(\mathbf {c}_i^{b_1}, \mathbf {c}_j^{b_2}, \mathsf {pp}_i^{b_1},\mathsf {pp}_j^{b_2}) \in L_\mathsf {TC}$.

Fig. 3.

Zooming in on wire k of circuit C with parameters $\mathsf {PP}= (\mathsf {pp}_i^0, \mathsf {pp}_i^1, \mathsf {pp}_j^0, \mathsf {pp}_j^1)$, commitments $\mathsf {W}= (\mathbf {c}_i^0, \mathbf {c}_i^1, \mathbf {c}_j^0,\mathbf {c}_j^1)$ and $L_\mathsf {TC}$ proofs $\mathsf {\mathbf {\Pi }}= (\pi ^{00}, \pi ^{01}, \pi ^{10}, \pi ^{11})$.

To prove WI of the final construction, in particular the following should hold:

$$\begin{aligned} \big (\mathsf {PP}, \mathsf {W}(0),\mathsf {\mathbf {\Pi }}(0) \big ) \approx \big (\mathsf {PP}, \mathsf {W}(1),\mathsf {\mathbf {\Pi }}(1) \big ) \end{aligned}$$

(1)

This indistinguishability requirement already implies a strong NIWI for $L_\mathsf {TC}$, with respect to distributions $\mathcal {D}_0$ and $\mathcal {D}_1$, where $\mathcal {D}_b$ samples $L_\mathsf {TC}$ instances $(\mathbf {c}_i, \mathbf {c}_j, \mathsf {pp}_i, \mathsf {pp}_j)$ such that $\mathbf {c}_i, \mathbf {c}_j$ commit to the bit b.

For our analysis, Eq. (1) is insufficient since we need Eq. (1) to hold even given the rest of the proof for $(C,\mathsf {out})\in L_\mathcal {U}$. In other words, we need Eq. (1) to hold given some auxiliary information $\mathsf {aux}$, where given $\mathsf {aux}$ it should be possible to efficiently compute the rest of the proof from it. One possible $\mathsf {aux}$ is the openings of all the four commitments so that it is then possible to compute Bit and Gate Proofs for the rest of the proof. But if we give the openings with respect to 0 and 1 respectively, then the two distributions in Eq. (1) are clearly distinguishable.

So the question is, what $\mathsf {aux}$ can we give? Our key insight is that we can give equivocated openings for the commitments with respect to the two hiding parameters and honest openings with respect to the binding parameters, so that in both the distributions in Eq. (1), two of the openings are to 0 and two of them are to 1. Without loss of generality, we think of $\mathsf {pp}_i^0, \mathsf {pp}_j^0$ as the binding parameters and $\mathsf {pp}_i^1, \mathsf {pp}_j^1$ as the hiding parameters. We strengthen the requirement in Eq. (1) as follows:

$$\begin{aligned} \big (\mathsf {PP}(0), \mathsf {W}(0), \mathsf {\mathbf {\Pi }}(0), \mathsf {O}(0)) \approx (\mathsf {PP}(1), \mathsf {W}(1), \mathsf {\mathbf {\Pi }}(1), \mathsf {O}(1) \big ) \end{aligned}$$

(2)

where $\mathsf {PP}(b) = (\mathsf {pp}_i^b, \mathsf {pp}_i^{1-b}, \mathsf {pp}_j^b, \mathsf {pp}_j^{1-b})$, and $\mathsf {W}(b), \mathsf {\mathbf {\Pi }}(b)$ are as before, and where in both the distributions, $\mathsf {O}(b)$ contains openings for the commitments $\mathsf {W}(b)$ to (0, 1, 0, 1) respectively. This is the case since in the left-hand-side parameters $\mathsf {PP}(0)$, the second and fourth parameters are hiding, and we equivocate $\mathbf {c}_i^1, \mathbf {c}_j^1$ to open to 1, whereas in the right-hand-side parameters $\mathsf {PP}(1)$, the first and third parameters are hiding, and we equivocate $\mathbf {c}_i^1, \mathbf {c}_j^1$ to open to 0. Note that the $L_\mathsf {TC}$ proofs in $\mathsf {\mathbf {\Pi }}(b)$ are still computed using the (honest) openings to b.

This is still not sufficient for our WI analysis. In order to argue WI of the final construction, we need to invoke Eq. (2) for every wire k in the circuit for which the value of $\mathsf {wit}_0$ on wire k is different from value of $\mathsf {wit}_1$ on wire k. These invocations are not completely independent since two different wires may be associated with the same gate, and in particular the two wires may be associated with an overlapping set of parameters. Thus, we need to further strengthen Eq. (2) to as follows:

$$\begin{aligned}&\big (\mathsf {PP}(0), \mathsf {W}(0), \mathsf {\mathbf {\Pi }}(0), \mathsf {O}(0), \mathsf {W}(1), \mathsf {\mathbf {\Pi }}(1),\mathsf {O}(1) \big ) \approx \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \,\, \big (\mathsf {PP}(1), \mathsf {W}(1), \mathsf {\mathbf {\Pi }}(1), \mathsf {O}(1), \mathsf {W}(0), \mathsf {\mathbf {\Pi }}(0), \mathsf {O}(0) \big ) \end{aligned}$$

(3)

where $\mathsf {PP}(b), \mathsf {W}(b), \mathsf {\mathbf {\Pi }}(b)$ and $\mathsf {O}(b)$ are as described above. We note that in the left-hand-side, $\mathsf {W}(1)$ are four commitments to 1 with respect to $\mathsf {PP}(0)$, $\mathsf {\mathbf {\Pi }}(1)$ are the corresponding $L_\mathsf {TC}$ proofs computed using the honest openings to 1, and $\mathsf {O}(1)$ are the openings to (1, 0, 1, 0) respectively. Similarly, in the right-hand-side, $\mathsf {W}(0)$ are four commitments to 0 with respect to $\mathsf {PP}(1)$, $\mathsf {\mathbf {\Pi }}(0)$ are the corresponding $L_\mathsf {TC}$ proofs, and again $\mathsf {O}(0)$ are the openings to (1, 0, 1, 0) respectively. We refer to the property from Eq. (3) as Strong Secrecy of $L_\mathsf {TC}$. The Strong Secrecy requirement of $L_\mathsf {TC}$ as in Eq. (3) is sufficient for our WI analysis. Before explaining our WI analysis, we describe the ingredients for our FH NIWI Construction.

Recall that our NIWI proof for $(C,\mathsf {out}) \in L_\mathcal {U}$ is computed as follows: Choose a fresh pair of parameters per gate, commit to all the wire values with respect to all the associated parameters (2 commitments per input wire, 4 commitments per connecting wire), compute Bit Proofs (one per commitment), compute Gate Proofs (two per gate) and compute $L_\mathsf {TC}$ proofs (four per connecting wire). In order to randomize our NIWI proof, we randomize all the parameters, correspondingly update the commitments and update the proofs to be with respect to the randomized parameters and commitments. Specifically, we need the following ingredients for our final FH NIWI Construction.

Ingredients for our FH NIWI.

• A Commitment Scheme as required in the FH NIZK construction, but with the additional feature that allows for randomizing the parameters and updating the commitments to be with respect to the randomized parameters, so that the randomized parameters and commitments are distributed like fresh commitments.

• Bit Proofs and Gate Proofs as required in the FH NIZK construction, but with the following (modified) malleability property: Given a proof for commitments with respect to some $\mathsf {pp}$, it is possible to efficiently randomize the parameters, correspondingly update the commitments and update the proofs to be with respect to the new parameters and commitments, such that they are all distributed like fresh ones. As in the FH NIZK, we require the Bit and Gate Proofs to satisfy WI.

• A proof system for $L_\mathsf {TC}$ with the same malleability property as Bit and Gate Proofs, and with the Strong Secrecy property as described in Eq. (3).

We show that the GOS commitment scheme $(\mathsf {C.}\mathsf {Setup}, \mathsf {C.}\mathsf {Commit}, \mathsf {C.}\mathsf {Rand})$ satisfies the additional feature that we require. The malleability of Bit Proofs and Gate Proofs can be reduced to the malleability of the $\mathsf {NP}$ language $L_\mathsf {Lin}$ described previously (similar to the FH NIZK construction). We then describe the corresponding proof systems $(\mathsf {Bit}.\mathsf {Prove}, \mathsf {Bit}.\mathsf {Verify}, \mathsf {Bit}.\mathsf {GenMaul})$ and $(\mathsf {N}.\mathsf {Prove}, \mathsf {N}.\mathsf {Verify}, \mathsf {N}.\mathsf {GenMaul})$.

Jumping ahead, we construct the proof system for $L_\mathsf {TC}$ also using the proof system for $L_\mathsf {Lin}$, and the malleability of $L_\mathsf {TC}$ follows from the malleability of $L_\mathsf {Lin}$. We then argue that the Strong Secrecy follows from our new DLIN with Leakage assumption.

WI Analysis. To explain our WI analysis, we describe an algorithm $\mathsf {ProofGen}$ that on input a sample from the left-hand-side distribution in Eq. (3), generates an entire proof $\varPi$ for $(C,\mathsf {out}) \in L_\mathcal {U}$ which is indistinguishable from an honest proof generated using $\mathsf {wit}_0$, and on input a sample from the right-hand-side distribution, $\mathsf {ProofGen}$ generates a proof $\varPi$ which is indistinguishable from an honest proof generated using $\mathsf {wit}_1$.

$\mathsf {ProofGen}$ Algorithm. Without loss of generality, we assume that every circuit is layered; that is, all the gates of the circuit can be arranged in t layers so that for all $i \in [t]$, all the output wires of gates from layer i are input wires to gates in layer $i+1$. Fix any two witnesses $\mathsf {wit}_0$ and $\mathsf {wit}_1$ for $(C,\mathsf {out}) \in L_\mathcal {U}$.

On input $\big (\mathsf {PP}(b), \mathsf {W}(b), \mathsf {\mathbf {\Pi }}(b), \mathsf {O}(b), \mathsf {W}(1-b), \mathsf {\mathbf {\Pi }}(1-b), \mathsf {O}(1-b) \big )$, $\mathsf {ProofGen}$ does the following:

• 1. Recall that $\mathsf {PP}(b) = (\mathsf {pp}_i^b, \mathsf {pp}_i^{1-b}, \mathsf {pp}_j^b, \mathsf {pp}_j^{1-b})$. Assign parameters $(\mathsf {pp}_i^b, \mathsf {pp}_i^{1-b})$ to all the odd layer gates of the circuit and $(\mathsf {pp}_j^b, \mathsf {pp}_j^{1-b})$ to all the even layer gates of the circuit. We will refer to $\{ \mathsf {pp}_i^b, \mathsf {pp}_j^b \}$ as the Left Parameters and $\{ \mathsf {pp}_i^{1-b}, \mathsf {pp}_j^{1-b} \}$ as the Right Parameters.

• 2. For all the input wires of the circuit C, commit to $\mathsf {wit}_0$ with respect to $\mathsf {pp}_i^b$ (Left Parameter) and commit to $\mathsf {wit}_1$ with respect to $\mathsf {pp}_i^{1-b}$ (Right Parameter).

• 3. For every wire k, produce the 4 commitments and 4 $L_\mathsf {TC}$ proofs for the wire as follows: Denote by $w_{k,0}$ the value induced by $\mathsf {wit}_0$ on wire k, and denote by $w_{k,1}$ the value induced by $\mathsf {wit}_1$ on wire k in the circuit.

  • If $w_{k,0} = w_{k,1}$ then compute the commitments and $L_\mathsf {TC}$ proofs honestly.

  • If $w_{k,0} = 0$ and $w_{k,1} = 1$ then use $\mathsf {W}(b)$ as the commitments and $\mathsf {\mathbf {\Pi }}(b)$ as the $L_\mathsf {TC}$ proofs.

  • If $w_{k,0} = 1$ and $w_{k,1} = 0$ then use $\mathsf {W}(1-b)$ as the commitments and $\mathsf {\mathbf {\Pi }}(1-b)$ as the $L_\mathsf {TC}$ proofs.

• 4. Compute the Bit Proofs and Gate Proofs honestly: We have the openings for all the commitments to the input bits (from Step 2). We also have the openings for the commitments to every non-input wire k, namely $\mathsf {O}(b)$ for $\mathsf {W}(b)$ when $w_{k,0} = 0$ and $w_{k,1} = 1$, or $\mathsf {O}(1-b)$ for $\mathsf {W}(1-b)$ when $w_{k,0} = 1$ and $w_{k,1} = 0$, or since we generated the commitments honestly when $w_{k,0} = w_{k,1}$. Note that the openings with respect to the Left Parameters always correspond to $\mathsf {wit}_0$ and the openings with respect to the Right Parameters always correspond to $\mathsf {wit}_1$.

  • Bit Proofs can be computed honestly since all the openings are to 0 or 1.

  • Gate Proofs can be computed honestly since all the openings with respect to the Left Parameters are consistent with $\mathsf {wit}_0$ and all the openings with respect to the Right Parameters are consistent with $\mathsf {wit}_1$.

• 5. Randomize the entire proof as follows:

  • For every gate, randomize the pair of parameters for that gate.

  • Update all the commitments (2 commitments per input wire, 4 commitments per connecting wire) to be with respect to the randomized parameters.

  • Maul all the Bit Proofs (one per commitment), all the Gate Proofs (two per gate) and all the $L_\mathsf {TC}$ proofs (four for every connecting wire) to be with respect to the updated parameters and commitments.

  Finally output this randomized proof.

So far, we described the $\mathsf {ProofGen}$ algorithm that given a sample from the distributions in Eq. (3), generates an entire proof for $(C, \mathsf {out}) \in L_\mathcal {U}$. Let $\varPi _\mathsf {Gen}^0$ be a proof output by $\mathsf {ProofGen}$ on input a sample from the left-hand-side of Eq. (3) and let $\varPi _\mathsf {Gen}^1$ be a proof output by $\mathsf {ProofGen}$ on input a sample from the right-hand-side of Eq. (3).

From Eq. (3), it follows that $\varPi _\mathsf {Gen}^0 \approx \varPi _\mathsf {Gen}^1$. All that remains is to argue that $\varPi _0 \approx \varPi _\mathsf {Gen}^0$ and $\varPi _1 \approx \varPi _\mathsf {Gen}^1$, where $\varPi _b$ is an honestly computed proof for $(C, \mathsf {out}) \in L_\mathcal {U}$ using witness $\mathsf {wit}_b$. Note that $\varPi _0$ and $\varPi _\mathsf {Gen}^0$ are identical except that $\varPi _\mathsf {Gen}^0$ uses equivocated openings to $\mathsf {wit}_1$ on the Right Parameters to compute the Bit and Gate Proofs. Hence, $\varPi _0 \approx \varPi _\mathsf {Gen}^0$ follows from WI of the Bit and Gate Proofs, and in addition follows by the randomizability of the commitment scheme and the malleability of the underlying proofs. By a similar argument, $\varPi _1 \approx \varPi _\mathsf {Gen}^1$. Thus, WI of the final construction follows form the Strong Secrecy of $L_\mathsf {TC}$.

Constructing the $\varvec{L_\mathsf {TC}}$ Proof System. We construct a proof system for $L_\mathsf {TC}$ with the following properties:

• 1. Strong Secrecy: As defined in Eq. (3).

• 2. Malleability: Given a proof $\pi$ for $(\mathbf {c}_1, \mathbf {c}_2, \mathsf {pp}_1, \mathsf {pp}_2)\in L_\mathsf {TC}$, one can efficiently randomize the parameters to obtain $\mathsf {pp}_1', \mathsf {pp}_2'$, update the commitments to obtain $\mathbf {c}_1', \mathbf {c}_2'$ which are with respect to $\mathsf {pp}_1', \mathsf {pp}_2'$, and then maul $\pi$ to a proof $\pi '$ for $(\mathbf {c}_1', \mathbf {c}_2', \mathsf {pp}_1', \mathsf {pp}_2') \in L_\mathsf {TC}$ such that $(\mathbf {c}_1', \mathbf {c}_2', \mathsf {pp}_1', \mathsf {pp}_2')$ looks like a fresh instance and $\pi '$ is distributed like a fresh proof.

• 3. Soundness: We require that soundness holds for all instances $(\mathbf {c}_1, \mathbf {c}_2, \mathsf {pp}_1, \mathsf {pp}_2)$ where both $\mathsf {pp}_1,\mathsf {pp}_2$ are binding. As noted above, this is sufficient for the soundness of the final construction.

We construct such a proof system using the malleable NIWI proof system for $L_\mathsf {Lin}$ described before. Recall that $L_\mathsf {Lin}$ is a parameterized language with parameters $\mathsf {pp}= (f,h,g)$ where f, h, g are generators of a group ${\mathbb G}$, and it consists of a pair of tuples $(\mathbf {A},\mathbf {B})$ such that one of them is of the form $(f^{a_1}, h^{a_2}, g^{a_3})$ where $a_3 = a_1 + a_2$.

We reduce proving that $(\mathbf {c}_1, \mathbf {c}_2, \mathsf {pp}_1, \mathsf {pp}_2)\in L_\mathsf {TC}$ to proving that $(\mathbf {A},\mathbf {B})\in L_\mathsf {Lin}$ for some $(\mathbf {A},\mathbf {B})$. However, we only know how to do this reduction for $L_\mathsf {TC}$ instances $(\mathbf {c}_1, \mathbf {c}_2, \mathsf {pp}_1, \mathsf {pp}_2)$ for which $\mathsf {pp}_1 = \mathsf {pp}_2$. Therefore, we consider an $\mathsf {NP}$-relation for $L_\mathsf {TC}$ with an additional witness which lets us convert an instance $(\mathbf {c}_1, \mathbf {c}_2, \mathsf {pp}_1, \mathsf {pp}_2)$ into an instance $(\mathbf {c}_*, \mathbf {c}_2, \mathsf {pp}_2, \mathsf {pp}_2)$. The additional witness for $(\mathbf {c}_1, \mathbf {c}_2, \mathsf {pp}_1, \mathsf {pp}_2)$ is a hard-to-compute function of the parameters $\mathsf {pp}_1, \mathsf {pp}_2$, and we refer to it as an “intermediate parameter” $\mathsf {pp}_*$ of $\mathsf {pp}_1, \mathsf {pp}_2$. Using the intermediate parameter $\mathsf {pp}_*$ we can convert the commitment $\mathbf {c}_1$ with respect to $\mathsf {pp}_1$ into a commitment $\mathbf {c}_*$ with respect to $\mathsf {pp}_2$.

More specifically in our proof, $\mathsf {pp}_*$ helps in converting the commitment $\mathbf {c}_1$ with respect to parameters $\mathsf {pp}_1$, into a commitment $\mathbf {c}_{*}$ (to the same value) with respect to $\mathsf {pp}_2$. Then, we can reduce the instance $(\mathbf {c}_*, \mathbf {c}_2, \mathsf {pp}_2, \mathsf {pp}_2) \in L_\mathsf {TC}$ to a pair of tuples $(\mathbf {A}, \mathbf {B}) \in L_\mathsf {Lin}$. The soundness and malleability of the $L_\mathsf {TC}$ proof system follows from the corresponding properties of $L_\mathsf {Lin}$ proof system. We refer to the full version [4] for a detailed description of the construction.

Strong Secrecy from DLIN with Leakage. All that remains is to show that the strong secrecy of $L_\mathsf {TC}$ follows from our new assumption of DLIN with Leakage. We first prove that Strong Secrecy of $L_\mathsf {TC}$ follows from the fact that the NIWI for $L_{\mathsf {Lin}}$ is strong WI with respect to the following distributions $\mathcal{D}_0$ and $\mathcal{D}_1$.

• $\mathcal{D}_0$ generates $(\mathbf {A},\mathbf {B})$ where $\mathbf {A}=(f^{a_1},h^{a_2},g^{a_3})$ for random $a_1,a_2,a_3$ such that $a_1+a_2 =a_3$, and $\mathbf {B}=(f^{a_1},h^{a_2},g^{a_3+1})$.

• $\mathcal{D}_1$ generates $(\mathbf {A},\mathbf {B})$ where $\mathbf {A}=(f^{a_1},h^{a_2},g^{a_3-1})$ for random $a_1,a_2,a_3$ such that $a_1+a_2 =a_3$, and $\mathbf {B}=(f^{a_1},h^{a_2},g^{a_3})$.

We then prove that the proof system for $L_\mathsf {Lin}$ is strong WI with respect to $\mathcal{D}_0$ and $\mathcal{D}_1$ under DLIN with Leakage assumption. We refer to full version [4] for a detailed description of the reduction.

3 Preliminaries

We denote the security parameter by $\lambda$. We use PPT to denote that an algorithm is probabilistic polynomial time. We denote by $y \leftarrow A(x)$ if y is the output of a single execution of A on input x. We denote by $y = A(x; r)$ to explicitly mention the randomness used in the execution. We denote $y \in A(x)$ if there exists randomness r such that $y = A(x; r)$.

We use [n] to represent the set $\{1,\dots ,n\}$. Vectors are denoted by $\mathbf {a}$ where $\mathbf {a} = (a_1,\dots , a_n)$ and $a_i$ is the i th element of $\mathbf {a}$. $|\mathbf {a}|$ denotes the size of $\mathbf {a}$. $\mathbf {a} \circ \mathbf {b}$ denotes concatenation of the vectors $\mathbf {a}, \mathbf {b}$. $\{\mathcal {X}\}_{\lambda \in {\mathbb N}} \approx _c \{ \mathcal {Y}\}_{\lambda \in {\mathbb N}}$ will denote that distributions $\{\mathcal {X}\}_{\lambda \in {\mathbb N}}$ and $\{Y\}_{\lambda \in {\mathbb N}}$ are computationally indistinguishable.

3.1 Definition of Proof Systems

Definition 1

(Non-interactive Zero-knowledge Proofs [9]). Let $L \in \mathsf {NP}$ and let $R_L$ be the corresponding $\mathsf {NP}$ relation. A triplet of PPT algorithms $(\mathsf {Setup}, \mathsf {Prove}, \mathsf {Verify})$ is called a non interactive zero knowledge (NIZK) proof system for L if it satisfies:

• Perfect Completeness: For all security parameters $\lambda \in {\mathbb N}$ and for all $~(x,w) \in R_L$,

  $$ \Pr [\mathsf {CRS}\leftarrow \mathsf {Setup}(1^{\lambda });~\pi \leftarrow \mathsf {Prove}(\mathsf {CRS},x,w) : \mathsf {Verify}(\mathsf {CRS}, x, \pi ) = 1 ] = 1$$

• Adaptive Soundness: For any all-powerful prover $P^*$, there exists a negligible function $\mu$ such that for all $\lambda$,

  $$ \Pr [\mathsf {CRS}\leftarrow \mathsf {Setup}(1^{\lambda });~(x, \pi ) = P^*(\mathsf {CRS}): \mathsf {Verify}(\mathsf {CRS}, x, \pi ) = 1~\wedge ~x \notin L] \le \mu (\lambda ) $$

  When this probability is 0, we say it is perfectly sound.

• Adaptive Zero Knowledge: There exists a PPT simulator $S = (S_1,S_2)$ where $S_1(1^{\lambda })$ outputs $(\mathsf {CRS}_S, \tau )$ and $S_2(\mathsf {CRS}_S, \tau , x)$ outputs $\pi _s$ such that for all non-uniform PPT adversaries $\mathcal {A}$,

  $$\{ \mathsf {CRS}\leftarrow \mathsf {Setup}(1^{\lambda })~:~\mathcal {A}^{\mathcal {O}_1(\mathsf {CRS}, \cdot , \cdot )} (\mathsf {CRS}) \} \approx _c$$
  $$ \{ (\mathsf {CRS}_S, \tau ) {\leftarrow } S_1(1^{\lambda })~:~\mathcal {A}^{\mathcal {O}_2(\mathsf {CRS}_S, \tau , \cdot , \cdot )} (\mathsf {CRS}_S) \}$$

  where $\mathcal {O}_1,\mathcal {O}_2$ on input (x, w) first check that $(x,w) \in R_L$, else output $\bot$. Otherwise $\mathcal {O}_1$ outputs $\mathsf {Prove}(\mathsf {CRS},x,w)$ and $\mathcal {O}_2$ outputs $S_2(\mathsf {CRS}_S, \tau , x)$.

Definition 2

(Non interactive Witness Indistinguishable Proofs [6, 17]). A pair of PPT algorithms $(\mathsf {Prove}, \mathsf {Verify})$ is called a non interactive witness indistinguishable (NIWI) proof for an $\mathsf {NP}$ language L with $\mathsf {NP}$ relation $R_L$ if it satisfies:

• Completeness: For all security parameters $\lambda$ and for all $(x,w) \in R_L$,

  $$ \Pr [\pi \leftarrow \mathsf {Prove}(1^\lambda ,x,w)~:~\mathsf {Verify}(1^\lambda , x, \pi ) = 1 ] = 1$$

• Soundness: For any all-powerful prover $P^*$, if $P^*(1^\lambda )= (x, \pi )$ and $x \notin L$, then $\mathsf {Verify}(1^\lambda , x, \pi ) = 0$.

• Witness Indistinguishability: For all non-uniform PPT adversaries $\mathcal {A}$, there exists a negligible function $\nu$ such that for every $\lambda \in {\mathbb N}$, probability that $b' = b$ in the following game is at most $1/2+ \nu (\lambda )$:

  • 1. $(\mathsf {state}, x, w_0, w_1) \leftarrow \mathcal {A}(1^\lambda )$.

  • 2. Choose $b \overset{\$}{\leftarrow } \{0,1\}$. If $R_L(x, w_0) \ne 1$ or $R_L(x, w_1) \ne 1$ then output $\bot$. Else, if $b = 0$ then $\pi \leftarrow \mathsf {Prove}(1^\lambda , x, w_0)$, and if $b =1$ then $\pi \leftarrow \mathsf {Prove}(1^\lambda , x, w_1)$.

  • 3. $b' \leftarrow \mathcal {A}(\mathsf {state}, \pi )$.

We say that a pair of PPT algorithms $( \mathsf {Prove}, \mathsf {Verify})$ is called a non interactive proof system for an $\mathsf {NP}$ language L if it satisfies completeness and adaptive soundness.

For our purposes, we will be using NIWI proofs with respect to parameterized languages of the form $L[\mathsf {pp}]$ where $\mathsf {pp}$ denotes some global parameters.

Definition 3

(Non interactive Witness Indistinguishability proofs for Parameterized Languages). Let $\mathsf {Setup}$ be a PPT algorithm that takes as input the security parameter and outputs a set of parameters $\mathsf {pp}$. A pair of PPT algorithms $(\mathsf {Prove}, \mathsf {Verify})$ is called a NIWI proof for a parameterized $\mathsf {NP}$ language $L[\mathsf {pp}]$, with $\mathsf {NP}$ relation $R_L[\mathsf {pp}]$ if it satisfies:

• Completeness: For all security parameters $\lambda$, for all $\mathsf {pp}\in \mathsf {Setup}(1^\lambda )$ and for all $(x,w) \in R_L[\mathsf {pp}]$, $\Pr [\pi \leftarrow \mathsf {Prove}(\mathsf {pp},x,w)~:~ \mathsf {Verify}(\mathsf {pp}, x, \pi ) = 1] = 1$.

• Adaptive Soundness: For any all-powerful prover $P^*$, there exists a negligible function $\mu$ such that for all $\lambda$,

  $$ \Pr [ \mathsf {pp}\leftarrow \mathsf {Setup}(1^\lambda )~:~(x, \pi ) \leftarrow P^*(\mathsf {pp})~:~ \mathsf {Verify}(\mathsf {pp}, x, \pi ) = 1~\wedge ~x \notin L ] \le \mu (\lambda )$$

• Witness Indistinguishability: For all non-uniform PPT adversaries $\mathcal {A}$, there exists a negligible function $\nu$ such that for every $\lambda \in {\mathbb N}$, probability that $b' = b$ in the following game is at most $1/2+ \nu (\lambda )$:

  • 1. $\mathsf {pp}\leftarrow \mathsf {Setup}(1^\lambda )$.

  • 2. $(\mathsf {state}, x, w_0, w_1) \leftarrow \mathcal {A}(\mathsf {pp})$.

  • 3. Choose $b \overset{\$}{\leftarrow } \{0,1\}$. If $R_L[\mathsf {pp}](x, w_0) \ne 1$ or $R_L[\mathsf {pp}](x, w_1) \ne 1$ then output $\bot$. Else if $b = 0$ then $\pi \leftarrow \mathsf {Prove}(\mathsf {pp}, x, w_0)$, else if $b =1$ then $\pi \leftarrow \mathsf {Prove}(\mathsf {pp}, x, w_1)$. Send $\pi$ to $\mathcal {A}$.

  • 4. $b' \leftarrow \mathcal {A}(\mathsf {state}, \pi )$.

Definition 4

(Randomizable NIZK and NIWI Proofs [7]). A NIZK proof system for an $\mathsf {NP}$ language L with $\mathsf {NP}$ relation $R_L$ with algorithms $(\mathsf {Setup}, \mathsf {Prove}, \mathsf {Verify})$ is said to be a randomizable proof system if there exists a PPT algorithm $\mathsf {Rand}$ which on input a $\mathsf {CRS}$, an instance x and a proof $\pi$, outputs a “randomized” proof $\pi '$ for x such that for all non-uniform PPT adversaries $\mathcal {A}$, there exists a negligible function $\nu$ such that for every $\lambda \in {\mathbb N}$, the probability that $b' = b$ in the following game is at most $1/2+ \nu (\lambda )$:

• 1. $\mathsf {CRS}\leftarrow \mathsf {Setup}(1^{\lambda })$.

• 2. $(\mathsf {state}, x, w, \pi ) \leftarrow \mathcal {A}(\mathsf {CRS})$.

• 3. Choose $b \overset{\$}{\leftarrow } \{0,1\}$. If $\mathsf {Verify}(\mathsf {CRS}, x, \pi ) \ne 1$ or $R_L(x, w) \ne 1$ then output $\bot$.

• 4. Else if $b = 0$ then $\pi ' \leftarrow \mathsf {Prove}(\mathsf {CRS}, x, w)$, else if $b =1$ then $\pi ' \leftarrow \mathsf {Rand}(\mathsf {CRS}, x, \pi )$.

• 5. $b' \leftarrow \mathcal {A}(\mathsf {state}, \pi ')$.

More generally, a (WI) proof system $(\mathsf {Prove}, \mathsf {Verify})$ is said to be randomizable if there exists a PPT algorithm $\mathsf {Rand}$ with the same description and properties as above and where $\mathsf {CRS}= 1^\lambda$.

Definition 5

(Malleable NIWI Proofs for Parameterized Languages [14]). Let $(\mathsf {Prove},\mathsf {Verify})$ be a NIWI proof system for a parameterized $\mathsf {NP}$ language $L[\mathsf {pp}]$ with $\mathsf {NP}$ relation $R_L[\mathsf {pp}]$ where $\mathsf {pp}\leftarrow \mathsf {Setup}(1^\lambda )$ (as per Definition 3). Let $T = (T_(C, b), T_\mathsf {wit})$ be a pair PPT transformations such that for every $(x,w) \in R_L$ and for every randomness $\sigma \in \{0,1\}^{\mathsf {poly}(\lambda )}$, $\big (T_(C, b)(\mathsf {pp}, x; \sigma ), T_\mathsf {wit}(\mathsf {pp}, x, w, \sigma ) \big ) \in R_L$.

Such a proof system is said to be malleable with respect to T, if there exists a randomized PPT algorithm $\mathsf {Maul}$ which on input parameters $\mathsf {pp}$, an instance x, randomness $\sigma$ and proof $\pi$, outputs a “mauled” proof $\pi '$ for $T(\mathsf {pp}, x; \sigma )$ such that the following properties hold:

• Malleability. For all non-uniform PPT $\mathcal {A}$, for all $\mathsf {pp}\in \mathsf {Setup}(1^\lambda )$, for all $\lambda \in {\mathbb N}$,

  

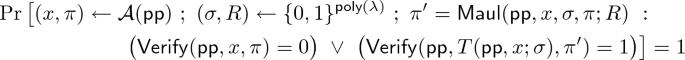
• Perfect Randomizability. There exists a poly-time function $f_T$ such that for all $\mathsf {pp}\in \mathsf {Setup}(1^\lambda )$ and every $(x,w) \in R_L[\mathsf {pp}]$, for every $R,\sigma \in \{0,1\}^{\mathsf {poly}(\lambda )}$,

  $$ \mathsf {Maul}(\mathsf {pp}, x, \sigma , \mathsf {Prove}(\mathsf {pp}, x, w ; R) ; R') =$$
  $$ \mathsf {Prove}(\mathsf {pp}, T_(C, b)(\mathsf {pp}, x; \sigma ), T_\mathsf {wit}(\mathsf {pp}, x,w, \sigma ) ; S)$$

  where $S = f_T( \mathsf {pp}, w, R, R', \sigma )$. Moreover, if $R', \sigma$ are uniform, then $f_T(w,R, R', \sigma )$ is uniformly distributed.

Definition 6

(Strong Non-interactive Witness Indistinguishability [19]). Let $\mathsf {Setup}$ be a PPT algorithm that takes as input the security parameter and outputs a set of parameters $\mathsf {pp}$. Let $\mathcal {D}_0 = \{ \mathcal {D}_{0, \lambda } \}_{\lambda \in {\mathbb N}}, \mathcal {D}_1 = \{ \mathcal {D}_{1, \lambda } \}_{\lambda \in {\mathbb N}}$ be distribution ensembles in the support of $R_L[\mathsf {pp}] \cap \{0,1\}^\lambda$ such that for every $b\in \{0,1\}$, $(x_b,w_b) \leftarrow \mathcal {D}_b$ such that $(x_b,w_b) \in R_L[\mathsf {pp}]$.

A NIWI proof system $( \mathsf {Prove}, \mathsf {Verify})$ for a parameterized $\mathsf {NP}$ language $L[\mathsf {pp}]$ is a strong non interactive witness indistinguishable (Strong NIWI) proof with respect to distributions $\mathcal {D}_0 ,\mathcal {D}_1$, if the following holds:

$$ \text { If } \{ \mathsf {pp}, x_0 \} \approx \{ \mathsf {pp}, x_1 \} \text { then } E_0 \approx E_1$$

where $E_b(1^\lambda )$ does the following: Sample $(x_b, w_b) \leftarrow \mathcal {D}_b(\mathsf {pp})$ and compute $\pi _b \leftarrow \mathsf {Prove}( \mathsf {pp}, x_b, w_b)$. Output $( \mathsf {pp}, x_b, \pi _b)$.

3.2 Bilinear Maps

We will be working with abelian groups ${\mathbb G},{\mathbb G}_T$ of prime order p equipped with a symmetric bilinear map $e : {\mathbb G}\times {\mathbb G}\mapsto {\mathbb G}_T$. We let $\mathcal {G}$ be a deterministic polynomial time algorithm that takes as input the security parameter $1^\lambda$ and outputs $(p, {\mathbb G}, {\mathbb G}_T,e,g_p)$ such that p is a prime, ${\mathbb G}, {\mathbb G}_T$ are descriptions of groups of order p, $g_p$ is a fixed generator of ${\mathbb G}$ and $e : {\mathbb G}\times {\mathbb G}\mapsto {\mathbb G}_T$ is a bilinear map with the following properties:

• (Non-degenerate). For any generator g of ${\mathbb G}$, $g_T = e(g,g)$ has order p in ${\mathbb G}_T$

• (Bilinear). For all $a,b \in {\mathbb G}$, for all $x,y \in \mathbb {Z}_p$, $e(a^x, b^y) = e(a,b)^{xy}$

We require that the group operations and the bilinear operations are computable in polynomial time with respect to security parameter.

Assumption 1

(Decisional Linear Assumption). We say that the Decisional Linear (DLIN) Assumption holds for a bilinear group generator $\mathcal {G}$ if the following distributions are computationally indistinguishable:

$$\{ (p, {\mathbb G}, {\mathbb G}_T, e, g) \leftarrow \mathcal {G}(1^\lambda )~;~(x,y) \overset{\$}{\leftarrow } \mathbb {Z}_p^*~:~(r,s) \overset{\$}{\leftarrow } \mathbb {Z}_p~:~$$

$$ (p, {\mathbb G}, {\mathbb G}_T, e, g, g^x, g^y, g^{xr}, g^{ys}, g^{r+s}) \} \text { and } $$

$$ \{ (p, {\mathbb G}, {\mathbb G}_T, e, g) \leftarrow \mathcal {G}(1^\lambda )~;~(x,y) \overset{\$}{\leftarrow } \mathbb {Z}_p^*~:~ (r,s,d) \overset{\$}{\leftarrow } \mathbb {Z}_p~:~$$

$$(p, {\mathbb G}, {\mathbb G}_T, e, g, g^x, g^y, g^{xr}, g^{ys}, g^d) \}$$

4 Fully Homomorphic Proofs: Definition

In this section we define fully homomorphic NIZK and NIWI proofs for the $\mathsf {NP}$-complete language $L_\mathcal{{U}}$ consisting of instances of the form (C, b) where $C: \{0,1\}^k \rightarrow \{0,1\}$ is a boolean circuit and $b \in \{0,1\}$. Formally, $L_\mathcal{{U}}$ is defined as:

$$ L_\mathcal{{U}}= \{ (C,b) ~|~\exists ~\mathbf {w} \text { such that }C(\mathbf {w}) = b \} $$

Let $R_\mathcal{{U}}$ be the corresponding $\mathsf {NP}$-relation. We first define the notion of composing multiple instances of $L_\mathcal{{U}}$ to get a new instance in $L_\mathcal{{U}}$:

Composing $L_\mathcal{{U}}$ Instances: On input k instances $\{ (C_i, b_i)\}_{i=1}^k$ where $C_i: \{0,1\}^{t_i} \rightarrow \{0,1\}$ and $C': \{0,1\}^k \rightarrow \{0,1\}$,

$$\mathsf {Compose}(\{ (C_i, b_i)\}_{i=1}^k, C') = (C,b) $$

where $C: \{0,1\}^T \rightarrow \{0,1\}$ and $T = \sum _{i=1}^k t_i$ and for all $(\mathbf {w_1},\ldots ,\mathbf {w_k}) \in \{0,1\}^{t_1} \times \dots \times \{0,1\}^{t_k}$,

$$C(\mathbf {w_1},\ldots ,\mathbf {w_k})=C'\big (C_1(\mathbf {w_1}),\ldots ,C_k(\mathbf {w_k}) \big )~\wedge ~b = C'(b_1,\dots ,b_k).$$

4.1 Definition: Fully Homomorphic NIZK and NIWI Proofs

We now define fully homomorphic NIZK and NIWI proofs for the language $L_\mathcal{{U}}$ defined above.

Definition 7

(Fully Homomorphic NIZK Proofs). A randomizable NIZK proof system $(\mathsf {Setup}, \mathsf {Prove}, \mathsf {Verify}, \mathsf {Rand})$ is a fully homomorphic proof system if there exists a PPT algorithm $\mathsf {Eval}$ with the following input-output behavior:

$((C,b), \varPi ) \leftarrow \mathsf {Eval}(\mathsf {CRS}, \{ (C_i,b_i),\varPi _i\}_{i=1}^k ,C')$: The $\mathsf {Eval}$ algorithm takes as input the $\mathsf {CRS}$, k instances $\{ (C_i,b_i)\}_{i=1}^k$ along with their proofs $\{ \varPi _i\}_{i=1}^k$, and a circuit $C':\{0,1\}^k \rightarrow \{0,1\}$. It outputs the composed instance $(C,b)=\mathsf {Compose}(\{ (C_i, b_i)\}_{i=1}^k,C')$ and a corresponding proof $\varPi$ such that the following properties hold:

Completeness of Eval: We require that evaluating on valid proofs (proofs that verify), should result in a proof that verifies. More concretely, we require that for all non-uniform PPT $\mathcal {A}$ and for all $\lambda \in {\mathbb N}$,

$$ \Pr \left[ \begin{array}{c} \mathsf {CRS}\leftarrow \mathsf {Setup}(1^{\lambda })~;~(\{ (C_i, b_i,\varPi _i)\}_{i=1}^k, C') \leftarrow \mathcal {A}(\mathsf {CRS})~;\\ \ \\ ((C,b), \varPi ) \leftarrow \mathsf {Eval}( \mathsf {CRS}, \{ (C_i,b_i),\varPi _i\}_{i=1}^k, C') ~:~\\ \ \\ \big (\mathsf {Valid}(C') = 0 \big )~\vee ~\big (\exists ~i \in [k] \text { s.t.} \mathsf {Verify}(\mathsf {CRS}, (C_i,b_i), \varPi _i) = 0 \big )~\vee ~\\ \ \\ \big ((\mathsf {Verify}(\mathsf {CRS}, (C,b), \varPi )\,=\,1)~\wedge ~(C,b)\,=\,\mathsf {Compose}(\{ (C_i,b_i)\}_{i=1}^k, C') \big ) \end{array} \right] = 1 $$

where $\mathsf {Valid}(C') = 1$ if and only if $C': \{0,1\}^k \rightarrow \{0,1\}$.

Unlinkability: We require that a proof for $(C,b) \in L_\mathcal {U}$ obtained by $\mathsf {Eval}$ should be indistinguishable from a fresh proof for the same instance. Namely, for any non-uniform PPT adversary $\mathcal {A}$, there exists a negligible function $\nu$ such that for every $\lambda$ the probability that $\mathsf {bit}= \mathsf {bit}'$ in the following game is at most $1/2 + \nu (\lambda )$:

• 1. $\mathsf {CRS}\leftarrow \mathsf {Setup}(1^{\lambda })$.

• 2. $(\mathsf {state}, \{((C_i ,b_i), \mathbf {w}_i, \varPi _i)\}_{i=1}^k, C') \leftarrow \mathcal {A}(\mathsf {CRS})$

• 3. Choose $\mathsf {bit}\overset{\$}{\leftarrow } \{0,1\}$. If for any $i \in [k]$, $\mathsf {Verify}(\mathsf {CRS}, (C_i, b_i), \varPi _i) \ne 1$ or $((C_i,b_i), \mathbf {w}_i) \notin R_\mathcal{{U}}$, output $\bot$.

• 4. Else if $\mathsf {bit}= 0$ then $((C,b), \varPi ) \leftarrow \mathsf {Eval}(\mathsf {CRS}, \{ (C_i,b_i) ,\varPi _i\}_{i=1}^k, C')$. Else if $\mathsf {bit}=1$ then compute $(C,b) = \mathsf {Compose}(\{ (C_i,b_i)\}_{i=1}^k, C')$ and

  $\varPi \leftarrow \mathsf {Prove}(\mathsf {CRS}, (C,b),\mathbf {w})$ where $\mathbf {w} = \mathbf {w}_1 \circ \dots \circ \mathbf {w}_k$. Send $(C,b,\varPi )$ to $\mathcal {A}$.

• 5. $\mathsf {bit}' \leftarrow \mathcal {A}(\mathsf {state}, (C,b,\varPi ))$.

Definition 8

(Fully Homomorphic NIWI Proofs). A randomizable NIWI proof system $(\mathsf {Prove},\mathsf {Verify}, \mathsf {Rand})$ is a fully homomorphic NIWI proof system if there exists a PPT algorithm $\mathsf {Eval}$ with the same description and properties as in Definition 7 and where $\mathsf {CRS}= 1^\lambda$.

5 Building Blocks for Fully Homomorphic Proofs

In this section we describe the building blocks for our fully homomorphic (FH) NIZK and NIWI constructions. In Sect. 5.1, we define a commitment scheme with additional properties, which we will use in our FH NIZK and NIWI constructions, and we then instantiate it from DLIN.

In Sect. 5.2, we describe a NIWI proof system for the $\mathsf {NP}$ language $L_\mathsf {Lin}$ (defined in Definition 10) based on DLIN. This proof system is the main ingredient in constructing FH NIZK and FH NIWI proofs.

For our FH NIWI construction, we need the NIWI proof for $L_\mathsf {Lin}$ to have additional properties of malleability and strong WI with respect to specific distributions. We prove that the proof system is malleable and we prove that strong WI holds under a new assumption on bilinear groups: DLIN with Leakage. We describe the corresponding bilinear assumption in Sect. 5.3.

5.1 Randomizable Commitment Scheme

Definition 9

(Randomizable Commitment Scheme). A Randomizable commitment scheme for message space $\mathcal {M}$ consists of PPT algorithms ${\mathsf {COM}} = (\mathsf {C.}\mathsf {Setup}, \mathsf {C.}\mathsf {Commit}, \mathsf {C.}\mathsf {Rand})$ with the following descriptions and properties:

• $\mathsf {pp}\leftarrow \mathsf {C.}\mathsf {Setup}(1^{\lambda })$: On input the security parameter, the setup algorithm outputs public parameters $\mathsf {pp}$.

• $\mathsf {com}= \mathsf {C.}\mathsf {Commit}(\mathsf {pp}, b ; o)$: Using the public parameters $\mathsf {pp}$, the commit algorithm produces commitment $\mathsf {com}$ to message $b \in \{0,1\}$ using randomness $o \leftarrow \{0,1\}^{p(\lambda )}$ for some polynomial p. We will refer to o as “opening” for the commitment $\mathsf {com}$.

• $\mathsf {com}' = \mathsf {C.}\mathsf {Rand}(\mathsf {pp}, \mathsf {com}; o')$: On input parameters $\mathsf {pp}$, commitment $\mathsf {com}$, randomness $o'$, $\mathsf {C.}\mathsf {Rand}$ outputs a randomized commitment $\mathsf {com}'$ to same value.

We require the following properties from the commitment scheme:

• Perfectly Binding: For all $(m_0,m_1) \in \mathcal {M}$ such that $m_0 \ne m_1$ and for all $o_0,o_1 \in \{0,1\}^{\mathsf {poly}(\lambda )}$

  $$\Pr [ \mathsf {pp}\leftarrow \mathsf {C.}\mathsf {Setup}(1^{\lambda }) ~:~ \mathsf {C.}\mathsf {Commit}(\mathsf {pp}, m_0 ; o_0) = \mathsf {C.}\mathsf {Commit}(\mathsf {pp}, m_1 ; o_1) ] = 0 $$

• Computationally Hiding: Let $\mathsf {pp}\leftarrow \mathsf {C.}\mathsf {Setup}(1^{\lambda })$. For all $(m_0,m_1) \in \mathcal {M}$ and $o_0, o_1 \leftarrow \{0,1\}^{\mathsf {poly}(\lambda )}$, $\big ( \mathsf {C.}\mathsf {Commit}(\mathsf {pp}, m_0; o_0) \big ) \approx _c \big ( \mathsf {C.}\mathsf {Commit}(\mathsf {pp}, m_1; o_1) \big )$

• Perfect Randomizability: Let $\mathsf {pp}\leftarrow \mathsf {C.}\mathsf {Setup}(1^{\lambda })$. There exists an efficient function $f_\mathsf {com}$ such that for any randomness $o$, the following holds:

  • For every $o' \in \{0,1\}^{\mathsf {poly}(\lambda )}$, $\mathsf {C.}\mathsf {Rand}(\mathsf {pp}, \mathsf {C.}\mathsf {Commit}(\mathsf {pp}, m ; o) ; o')= \mathsf {C.}\mathsf {Commit}(\mathsf {pp}, m ; s)$ where $s = f_\mathsf {com}(o,o')$.

  • If $o'$ is chosen uniformly at random, then $f_\mathsf {com}(o,o')$ is uniformly distributed.

We now describe additional properties that we require from our commitment scheme for our FH NIZK construction:

• Additive Homomorphism: We require that if $\mathbf {c}_1$ and $\mathbf {c}_2$ are commitments to $m_1$ and $m_2$ respectively, then there exists an efficient function $f_\mathsf {add}$ such that $\mathbf {c}= f_\mathsf {add}(\mathbf {c}_1, \mathbf {c}_2)$ is a commitment to $(m_1 + m_2)$.

• Perfect Equivocation: There exists a PPT algorithm $\mathsf {C.}\mathsf {Setup}'$ and a polynomial time algorithm $\mathsf {C.}\mathsf {Equivocate}$ such that

  • $\mathsf {C.}\mathsf {Setup}'$ on input the security parameter, outputs $\mathsf {pp}',$ such that

    $$\{ \mathsf {pp}\leftarrow \mathsf {C.}\mathsf {Setup}(1^{\lambda })~:~\mathsf {pp}\} \approx _c \{ \mathsf {pp}' \leftarrow \mathsf {C.}\mathsf {Setup}'(1^{\lambda })~:~\mathsf {pp}' \}. $$

  • Fix any $r_\mathsf {pp}\in \{0,1\}^{\mathsf {poly}(\lambda )}$, any $m, m' \in \mathcal {M}$ and any randomness $o\in \{0,1\}^{\mathsf {poly}(\lambda )}$. Let $\mathsf {pp}' = \mathsf {C.}\mathsf {Setup}'(1^{\lambda }; r_\mathsf {pp})$ and $\mathbf {c}= \mathsf {C.}\mathsf {Commit}(\mathsf {pp}',m ; o)$. Algorithm $\mathsf {C.}\mathsf {Equivocate}$ on input $(\mathsf {pp}', r_\mathsf {pp}, \mathbf {c}, o, m')$ outputs $o'$ such that $\mathbf {c}= \mathsf {C.}\mathsf {Commit}(\mathsf {pp}', m'; o')$. Also, for truly random $o$, $(\mathbf {c}, o')$ is distributed identically to $(\mathbf {c}'', o'')$ where $o''$ is chosen at random and $\mathbf {c}'' = \mathsf {C.}\mathsf {Commit}(\mathsf {pp}',m'; o'')$.

  Note that the parameters output by $\mathsf {C.}\mathsf {Setup}(1^\lambda )$ are binding and the parameters output by $\mathsf {C.}\mathsf {Setup}'(1^\lambda )$ are hiding.

We will denote a randomizable commitment which is also additively homomorphic (aH) and equivocable (E) as described above, by a $\mathsf {RaHE}$-commitment scheme.

Remark 1

We will denote by $\mathbf 1$ and $\mathbf 0$ the canonical commitments to 1, 0 respectively, namely the commitments computed with randomness $o= 0$. Given such a commitment it is possible to verify, that the commitment is indeed to 0 or 1.

Additional Functionalities for FH NIWI. In our FH NIWI construction, we use a $\mathsf {RaHE}$-commitment scheme which has additional functionalities $(\mathsf {OutParam}, \mathsf {ValidParam},\mathsf {RParam}, \mathsf {ChangeCom})$ with properties described below:

• Outputting hiding parameters: The deterministic algorithm $\mathsf {OutParam}$ takes as input parameters $\mathsf {pp}^0$ and outputs $\mathsf {pp}^1$ such that for all $r_\mathsf {pp}$, if $\mathsf {pp}^0 = \mathsf {C.}\mathsf {Setup}(1^\lambda ; r_\mathsf {pp})$, then $\mathsf {pp}^1 = \mathsf {C.}\mathsf {Setup}'(1^\lambda ; r_\mathsf {pp})$.

• Verifying if two parameters are valid: The algorithm $\mathsf {ValidParam}$ is an efficient predicate that outputs 1 if $\mathsf {pp}^0 \in \mathsf {C.}\mathsf {Setup}(1^\lambda )$ and $\mathsf {pp}^1 = \mathsf {OutParam}(\mathsf {pp}^0)$. It outputs 0 if both parameters are hiding, namely if $\mathsf {pp}^0, \mathsf {pp}^1 \in \mathsf {C.}\mathsf {Setup}'(1^\lambda )$.

• Randomization of parameters: The $\mathsf {RParam}$ algorithm takes as input parameters $\mathsf {pp}$, randomness $r_\mathsf {pp}'$, and outputs new parameters $\mathsf {pp}'$ such that for all $r_\mathsf {pp}$ and for $\mathsf {pp}= \mathsf {C.}\mathsf {Setup}(1^\lambda ; r_\mathsf {pp})$, the following properties hold:

  • There exists an efficient function $f_\mathsf {pp}$: $f_\mathsf {pp}(r_\mathsf {pp}, r_\mathsf {pp}')= \sigma$ and $\mathsf {pp}' = \mathsf {RParam}(\mathsf {pp}; r_\mathsf {pp}') = \mathsf {C.}\mathsf {Setup}(1^\lambda ; \sigma )$.

  • $\mathsf {RParam}(\mathsf {OutParam}(\mathsf {pp}); r_\mathsf {pp}') = \mathsf {OutParam}(\mathsf {RParam}(\mathsf {pp}; r_\mathsf {pp}'))$.

• Transformation of commitments with respect to new parameters: The $\mathsf {ChangeCom}$ algorithm takes in parameters $\mathsf {pp}$, randomness $r_\mathsf {pp}'$, commitment $\mathbf {c}$, and outputs commitment $\mathbf {c}'$ to the same value, with respect to the parameters $\mathsf {pp}' = \mathsf {RParam}(\mathsf {pp}; r_\mathsf {pp}')$.

Proposition 1

Assuming DLIN, there exists an additively homomorphic randomizable commitment scheme as per Definition 9.

5.2 Proofs of Linearity

In this section we describe the main ingredient for our fully homomorphic proofs, which is a NIWI proof system with additional properties for the parameterized language $L_\mathsf {Lin}[\mathsf {pp}]$.

Definition 10

(Linear Tuples). Let $(p, {\mathbb G}, {\mathbb G}_T, e, g_p) = \mathcal {G}(1^\lambda )$ and let f, h, g be any three generators of ${\mathbb G}$. A tuple $\mathbf {A}= (f^{a_1}, h^{a_2}, g^{a_3})$ is said to be linear with respect to (f, h, g) if $a_1 + a_2 = a_3$.

Before describing the parameterized language $L_\mathsf {Lin}[\mathsf {pp}]$, we describe the corresponding setup algorithm for the parameters of the language, given by $\mathsf {Lin}.\mathsf {Setup}$.

$\mathsf {Lin}.\mathsf {Setup}(1^\lambda )$: Compute $\mathcal {G}(1^\lambda ) = (p, {\mathbb G}, {\mathbb G}_T, e, g_p)$. Choose at random $x,y,z \leftarrow \mathbb {Z}_p^*$. Compute $f = g_p^x, h = g_p^y, g = g_p^z$. Output $\mathsf {pp}= [p, {\mathbb G}, {\mathbb G}_T, e, g_p, f,h,g ]$.

We abuse notation and let $\mathsf {pp}$ denote the output of $\mathsf {Lin}.\mathsf {Setup}$ as well as the output of $\mathsf {C.}\mathsf {Setup}$. Note that $\mathsf {pp}\leftarrow \mathsf {Lin}.\mathsf {Setup}(1^\lambda )$ is a subset of $\mathsf {pp}\leftarrow \mathsf {C.}\mathsf {Setup}(1^\lambda )$.

We now define the language $L_\mathsf {Lin}[\mathsf {pp}]$ where $\mathsf {pp}\leftarrow \mathsf {Lin}.\mathsf {Setup}(1^\lambda )$. $L_\mathsf {Lin}[\mathsf {pp}]$ is the language consisting of a pair of tuples such that one of them is linear. It is defined as follows:

NIWI Proof from GOS. We first describe the NIWI proof $(\mathsf {Lin}.\mathsf {Prove}, \mathsf {Lin}.$$\mathsf {Verify})$ for $L_\mathsf {Lin}[\mathsf {pp}]$ from GOS [21]:

• $\mathsf {Lin}.\mathsf {Prove}(\mathsf {pp}, (A_1, A_2, A_3), (B_1, B_2, B_3), (a_1, a_2, a_3) )$: Without loss of generality, let $(a_1, a_2, a_3)$ be such that $(A_1,A_2,A_3) = (f^{a_1}, h^{a_2}, g^{a_3})$ and $a_1 + a_2 = a_3$. Choose $t \overset{\$}{\leftarrow } \mathbb {Z}_p^*$ and output proof $\varPi$ which consists of the following matrix:

  $$\begin{aligned} \begin{bmatrix} \pi _{11}= B_1^{a_1} &{} \pi _{12}= B_2^{a_1}h^{-t} &{} \pi _{13}= B_3^{a_1}g^{-t}\\ \pi _{21}= B_1^{a_2}f^{t}&{} \pi _{22}= B_2^{a_2} &{} \pi _{23}= B_3^{a_2}g^{t} \\ \end{bmatrix} \end{aligned}$$

• $\mathsf {Lin}.\mathsf {Verify}(\mathsf {pp}, (A_1, A_2, A_3), (B_1, B_2, B_3), \varPi )$:

  • Compute $\pi _{31} = \pi _{11} \pi _{21}$ and $\pi _{32} =\pi _{12} \pi _{22}$ and $\pi _{33} = \pi _{13} \pi _{23}$.

  • Check $e(A_1, B_1) = e(f, \pi _{11})$, $e(A_2, B_2) = e(h, \pi _{22})$, $e(A_3, B_3) = e(g, \pi _{33})$.

  • Finally check $e(A_1, B_2)e(A_2, B_1) = e(f, \pi _{12})e(h, \pi _{21})$, $e(A_2, B_3)e(A_3, B_2) = e(h, \pi _{23})e(g, \pi _{32})$ and $e(A_1, B_3)e(A_3, B_1) = e(f, \pi _{13})e(g, \pi _{31})$.

Proposition 2

([21]). Assuming DLIN, the proof system described above is a perfectly sound witness indistinguishable proof system for the language $L_\mathsf {Lin}[\mathsf {pp}]$ (as per Definition 3).

Remark 2

If $\varPi = [\pi _{11},\dots , \pi _{33}]$ is a valid proof for $((A_1, A_2, A_3),$$(B_1, B_2, B_3)) \in L_\mathsf {Lin}[\mathsf {pp}]$, then $\varPi ^{-1} = [\pi _{11}^{-1},\dots , \pi _{33}^{-1}]$ is a valid proof for $((A_1^{-1}, A_2^{-1}, A_3^{-1}), (B_1, B_2, B_3)) \in L_\mathsf {Lin}[\mathsf {pp}]$ and for $((A_1, A_2, A_3),$$(B_1^{-1}, B_2^{-1}, B_3^{-1})) \in L_\mathsf {Lin}[\mathsf {pp}]$.

GOS [21] provided a NIWI proof for $L_\mathsf {Lin}[\mathsf {pp}]$ as described above. In our work, we need the NIWI proof system to satisfy two additional properties: The first is malleability with respect to randomization, namely given a tuple $(\mathbf {A}, \mathbf {B}) \in L_\mathsf {Lin}[\mathsf {pp}]$ with NIWI proof $\varPi$, it is possible to randomize $(\mathbf {A}, \mathbf {B})$ to a new tuple $(\mathbf {A}', \mathbf {B}') \in L_\mathsf {Lin}[\mathsf {pp}]$ and maul the proof $\varPi$ to be proof $\varPi '$ with respect to $(\mathbf {A}', \mathbf {B}')$.

As a second property, we require that the proof system satisfies strong witness indistinguishability with respect to specific distributions (which we describe later in the section).

Malleable Proofs for $\varvec{L_\mathsf {Lin}}{} \mathbf{.}$ We now show that $(\mathsf {Lin}.\mathsf {Prove}, \mathsf {Lin}.\mathsf {Verify})$ is malleable with respect to the transformation $\mathsf {Lin}.\mathsf {T}= (\mathsf {Lin}.\mathsf {Transform}, \mathsf {Lin}.\mathsf {WitTrans})$ defined as follows:

$$\mathsf {Lin}.\mathsf {Transform}(\mathsf {pp}, \mathbf {A},\mathbf {B}; (\mathbf{r},\mathbf{s})) \triangleq \big ((A_1f^{r_1}, A_2h^{r_2}, A_3g^{r_1+r_2}), (B_1f^{s_1}, B_2h^{s_2}, B_3g^{s_1 + s_2}) \big )$$

where $\mathsf {pp}= [p, {\mathbb G}, {\mathbb G}_T, e, g_p, f,h,g ]$, $\mathbf {A}= (A_1, A_2, A_3)$ and $\mathbf {B}= (B_1, B_2, B_3)$.

Mauled proof for $\mathsf {Lin}.\mathsf {Transform}(\mathsf {pp}, \mathbf {A},\mathbf {B}, (r_1, r_2, s_1, s_2))= (A_1f^{r_1}, A_2h^{r_2},$$A_3g^{r_3}), (B_1f^{s_1}, B_2h^{s_2}, B_3g^{s_3})$ is given by $\mathsf {Lin}.\mathsf {Maul}(\mathsf {pp}, (\mathbf {A}, \mathbf {B}), (r_1, r_2, s_1, s_2), \varPi )$: Choose $t\leftarrow \mathbb {Z}_p^*$, and output a proof $\varPi '$ consisting of the following matrix:

$$\begin{aligned} \begin{bmatrix} \pi _{11}'= \pi _{11}A_1^{s_1}B_1^{r_1}f^{r_1s_1} &{} \pi _{12}'= \pi _{12}A_2^{s_1}B_2^{r_1}h^{r_1s_2-t} &{} \pi _{13}'= \pi _{13}A_3^{s_1}B_3^{r_1}g^{r_1s_3 - t} \\ \pi _{21}'= \pi _{21}A_1^{s_2}B_1^{r_2}f^{r_2s_1+t} &{} \pi _{22}'= \pi _{22}A_2^{s_2}B_2^{r_2}h^{r_2s_2} &{} \pi _{23}'= \pi _{23}A_3^{s_2}B_3^{r_2}g^{r_2s_3+t} \\ \end{bmatrix}\end{aligned}$$

Proposition 3

Assuming DLIN, the proof system $(\mathsf {Lin}.\mathsf {Prove}, \mathsf {Lin}.\mathsf {Verify},$$\mathsf {Lin}.\mathsf {Maul})$ is a malleable NIWI for $L_\mathsf {Lin}[\mathsf {pp}]$ as per Definition 5, with respect to transformation $\mathsf {Lin}.\mathsf {T}= (\mathsf {Lin}.\mathsf {Transform}, \mathsf {Lin}.\mathsf {WitTrans})$.

Remark 3

We denote by $\mathsf {Lin}.\mathsf {Transform}(\mathsf {pp}, (\mathbf {A}, \mathbf {B}),(r_1, r_2))$ the transformation given by $\mathsf {Lin}.\mathsf {Transform}(\mathsf {pp}, (\mathbf {A}, \mathbf {B}), (r_1, r_2,r_1,r_2))$.

Strong NIWI for $\varvec{L_\mathsf {Lin}}$. For our FH NIWI construction, we require that the NIWI proofs for $(\mathbf {A}, \mathbf {B}) \in L_\mathsf {Lin}[\mathsf {pp}]$ satisfy strong witness indistinguishability with respect to distributions $\mathcal {D}_0(\mathsf {pp}), \mathcal {D}_1(\mathsf {pp})$ for $\mathsf {pp}\leftarrow \mathsf {Lin}.\mathsf {Setup}(1^\lambda )$. For every $b\in \{0,1\}$, distribution $\mathcal {D}_b(\mathsf {pp})$ is defined as follows:

Parse $\mathsf {pp}= [p, {\mathbb G}, {\mathbb G}_T,e,g_p,f,h,g]$. Choose $a_1, a_2 \leftarrow \mathbb {Z}_p^*$, let $a_3 = a_1 + a_2$. Let $\mathbf {A}_b = (f^{a_1}, h^{a_2}, g^{a_3 - b})$ and let $\mathbf {B}_b = (f^{a_1}, h^{a_2}, g^{a_3 - b+ 1})$. Output $(\mathbf {A}_b, \mathbf {B}_b)$.

Recall that $(\mathsf {Lin}.\mathsf {Prove}, \mathsf {Lin}.\mathsf {Verify}, \mathsf {Lin}.\mathsf {Maul})$ is said to be strong NIWI with respect to distributions $\mathcal {D}_0(\mathsf {pp}), \mathcal {D}_1(\mathsf {pp})$ (as per Definition 6), if the following holds:

$$ \{ \mathsf {pp}, (\mathbf {A}_0, \mathbf {B}_0), \pi _0 \} \approx \{ \mathsf {pp}, (\mathbf {A}_1, \mathbf {B}_1), \pi _1 \}$$

where $(\mathbf {A}_b, \mathbf {B}_b) \leftarrow \mathcal {D}_b(\mathsf {pp})$ and where $\pi _b \leftarrow \mathsf {Lin}.\mathsf {Prove}(\mathsf {pp}, \mathbf {A}_b, \mathbf {B}_b, (a_1, a_2, a_3) )$.

5.3 Assumption: DLIN with Leakage

In this subsection, we state our new assumption on bilinear maps: DLIN with Leakage.

Let $\mathsf {pp}\leftarrow \mathsf {Lin}.\mathsf {Setup}(1^\lambda )$ and parse $\mathsf {pp}= [p, {\mathbb G}, {\mathbb G}_T, e, f,h,g ]$. DLIN with Leakage states that $\mathcal {D}_0'(1^\lambda ) \approx _c \mathcal {D}_1'(1^\lambda )$ where $\mathcal {D}_b'(1^\lambda )$ is as follows:

• $\mathcal {D}_0'(1^\lambda ):$ Choose $R, S,t \leftarrow \mathbb {Z}_p^*$ and output $\mathsf {pp}$ along with the following matrix:

  $$\begin{aligned} \begin{bmatrix} f^{R} &{} h^{S} &{} g^{R+S} \\ f^{R^2} &{} h^{ RS - t} &{} g^{R(R+S+1) - t} \\ f^{RS+t} &{} h^{ S^2} &{} g^{S(R+S+1) + t} \\ \end{bmatrix} \end{aligned}$$

• $\mathcal {D}_1'(1^\lambda ):$ Choose $R, S,t \leftarrow \mathbb {Z}_p^*$ and output $\mathsf {pp}$ along with the following matrix:

  $$\begin{aligned} \begin{bmatrix} f^{R} &{} h^{S} &{} g^{R+S-1} \\ f^{R^2} &{} h^{ RS - t} &{} g^{R(R+S-1) - t} \\ f^{RS+t} &{} h^{ S^2} &{} g^{S(R+S-1) + t} \\ \end{bmatrix} \end{aligned}$$

Proposition 4

The DLIN with Leakage assumption is secure in the generic group model.

Proposition 5

Assuming DLIN with Leakage, $(\mathsf {Lin}.\mathsf {Prove}, \mathsf {Lin}.\mathsf {Verify})$ is strong NIWI for $L_\mathsf {Lin}[\mathsf {pp}]$ with respect to $\mathcal {D}_0, \mathcal {D}_1$ (as described in Sect. 5.2).

6 Fully Homomorphic NIZK Proofs

We use the following ingredients for our FH NIZK construction:

• Randomizable commitment scheme as per Definition 9, which is additively homomorphic and equivocable, denoted by

  $$(\mathsf {C.}\mathsf {Setup}, \mathsf {C.}\mathsf {Commit}, \mathsf {C.}\mathsf {Rand})$$

• Malleable NIWI proof system for $L_\mathsf {com}[\mathsf {pp}]$ with respect to transformation $\mathsf {Bit}.\mathsf {Transform}$, denoted by

  $$ ( \mathsf {Bit}.\mathsf {Prove}, \mathsf {Bit}.\mathsf {Verify}, \mathsf {Bit}.\mathsf {Maul}) \text { where }$$
  $$ L_\mathsf {com}[\mathsf {pp}] = \{ \mathbf {c}~|~\exists ~(b, o) \text { s.t. } \mathbf {c}= \mathsf {C.}\mathsf {Commit}(\mathsf {pp}, b; o)~\wedge ~b \in \{0,1\}\} $$

  for $\mathsf {pp}\leftarrow \mathsf {C.}\mathsf {Setup}(1^\lambda )$, and transformation $\mathsf {Bit}.\mathsf {T} = (\mathsf {Bit}.\mathsf {Transform},$$\mathsf {Bit}.\mathsf {WitTrans})$ is given by $\mathsf {Bit}.\mathsf {Transform}(\mathsf {pp}, \mathbf {c}, o') = \mathsf {C.}\mathsf {Rand}(\mathsf {pp}, \mathbf {c}; o')$ and $\mathsf {Bit}.\mathsf {WitTrans}(\mathsf {pp}, \mathbf {c}, (b, o),o') = f_\mathsf {com}(\mathsf {pp},o, o')$ where $o'$ is fresh randomness.

• Malleable NIWI proof system for $L_\mathsf {N}[\mathsf {pp}]$ with respect to transformation $\mathsf {N}.\mathsf {Transform}$, denoted by

  $$(\mathsf {N}.\mathsf {Prove}, \mathsf {N}.\mathsf {Verify}, \mathsf {N}.\mathsf {Maul}) \text { where }$$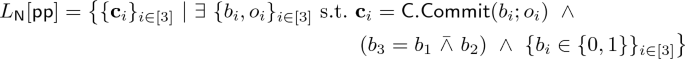

  

  for $\mathsf {pp}\leftarrow \mathsf {C.}\mathsf {Setup}(1^\lambda )$, and the transformation: $\mathsf {N}.\mathsf {T} = (\mathsf {N}.\mathsf {Transform},$$\mathsf {N}.\mathsf {WitTrans})$ is given by $\mathsf {N}.\mathsf {Transform}(\mathsf {pp}, \{ \mathbf {c}_i \}_{i \in [3] } , \{ o_i' \}_{i \in [3] } ) = \{ \mathbf {c}_i' \}_{i \in [3] }$ and $\mathsf {N}.\mathsf {WitTrans}(\mathsf {pp}, \{ \mathbf {c}_i, b_i,o_i, o_i' \}_{i \in [3] }) = f_\mathsf {com}( \mathsf {pp}, o,o')$ where $\mathbf {c}_i' = \mathsf {C.}\mathsf {Rand}(\mathsf {pp}, \mathbf {c}_i, o_i')$ for fresh randomness $(o_1',o_2',o_3')$ and where $o= o_1 + o_2 + 2o_3 - 2$ and $o' = o_1' + o_2' + 2o_3' -2$.

We now describe our construction:

Theorem 3

Assuming DLIN, the construction as described above is a fully homomorphic NIZK proof system for $L_\mathcal{{U}}$ as per Definition 7.

We refer the reader to the full version [4] for a proof of Theorem 3.

7 Fully Homomorphic NIWI Proofs

Our first ingredient for FH NIWI is $(\mathsf {C.}\mathsf {Setup}, \mathsf {C.}\mathsf {Commit}, \mathsf {C.}\mathsf {Rand})$, a $\mathsf {RaHE}$-commitment scheme with the additional functionalities $(\mathsf {OutParam}, \mathsf {ValidParam},$$\mathsf {RParam}, \mathsf {ChangeCom}, \mathsf {ValidInter}, \mathsf {InterParam})$ as defined in Sect. 5.1.

Our second ingredient is a malleable proof system $(\mathsf {TC}.\mathsf {Prove}, \mathsf {TC}.\mathsf {Verify},$$\mathsf {TC}.\mathsf {Maul})$ for the language $L_\mathsf {TC}$ defined as follows:

$$\begin{aligned} L_\mathsf {TC}=&\Big \{ (\mathbf {c}_1, \mathbf {c}_2, \mathsf {pp}_1, \mathsf {pp}_2 )~|~\exists ~(b,\mathsf {pp}_*, o_1, o_2) \text { s.t. }\\&\quad \{ \mathbf {c}_i = \mathsf {C.}\mathsf {Commit}(\mathsf {pp}_i, b; o_i) \}_{i \in [2]}~\wedge ~ \big ( \mathsf {ValidInter}(\mathsf {pp}_1, \mathsf {pp}_2, \mathsf {pp}_*) = 1 \big ) \Big \} \end{aligned}$$

Recall that $\mathsf {pp}_*$ is the intermediate parameter between $\mathsf {pp}_1, \mathsf {pp}_2$. It is a hard-to-compute function of the parameters which we require as an additional witness for the language.

The malleability is with respect to the transformation $\mathsf {TC}.\mathsf {T} = (\mathsf {TC}.\mathsf {Transform}, \mathsf {TC}.\mathsf {WitTrans})$. $\mathsf {TC}.\mathsf {Transform}$ takes as input an instance $(\mathbf {c}_1, \mathbf {c}_2, \mathsf {pp}_1, \mathsf {pp}_2)$, randomness $(r_\mathsf {pp}^1, r_\mathsf {pp}^2, o_1, o_2)$ and outputs transformed instance $(\mathbf {c}_1', \mathbf {c}_2', \mathsf {pp}_1', \mathsf {pp}_2')$.

In detail, $\mathsf {TC}.\mathsf {Transform}$ on input $(\mathbf {c}_1, \mathbf {c}_2, \mathsf {pp}_1, \mathsf {pp}_2)$, does the following:

• Randomize the parameters as follows: For all $i \in [2]$, compute $\mathsf {pp}_i' = \mathsf {RParam}(\mathsf {pp}_i; r_\mathsf {pp}^i)$.

• Change the commitment $\mathbf {c}_i$ to be with respect to the new parameters $\mathsf {pp}_i'$, by computing $z_i = \mathsf {ChangeCom}(\mathsf {pp}_i, \mathbf {c}_i; r_\mathsf {pp}^i)$ for all $i \in [2]$.

• Randomize the commitments as follows: For all $i \in [2]$, compute $\mathbf {c}_i' = \mathsf {C.}\mathsf {Rand}(\mathsf {pp}_i', z_i; o_i)$. Output $(\mathbf {c}_1', \mathbf {c}_2', \mathsf {pp}_1', \mathsf {pp}_2')$.

Correspondingly,

$$\mathsf {TC}.\mathsf {WitTrans}\big ((\mathbf {c}_1, \mathbf {c}_2, \mathsf {pp}_1, \mathsf {pp}_2), (b,\mathsf {pp}_*, o_1, o_2), (r_\mathsf {pp}^1, r_\mathsf {pp}^2, o_1', o_2') \big ) = (b, \widehat{\mathsf {pp}}, r_1, r_2)$$

where $\widehat{\mathsf {pp}} = \mathsf {InterParam}(\mathsf {pp}_1, \mathsf {pp}_2, r_\mathsf {pp}^1)$ and where for every $i \in [2]$, $r_i = f_\mathsf {com}(o_i, o_i')$. Recall that $\mathsf {InterParam}$ and $f_\mathsf {com}$ are as per the definition of the $\mathsf {RaHE}$-commitment scheme described in Sect. 5.1.

Let us look at the soundness and secrecy requirements from this proof system. We weaken the soundness requirement of our NIWI proof system and require a stronger secrecy property from the proof system. We now describe both of these properties:

• 1. Weak Soundness: Rather than requiring soundness to hold for every $(\mathbf {c}_1, \mathbf {c}_2, \mathsf {pp}_1, \mathsf {pp}_2) \in L_\mathsf {TC}$, we only require soundness to hold for all instances for which $\mathsf {pp}_1, \mathsf {pp}_2 \in \mathsf {C.}\mathsf {Setup}(1^\lambda )$ (when both parameters are binding). Note that our construction for NIWI proof of $L_\mathsf {TC}$ achieves standard soundness, however for the FH NIWI construction it suffices for the proof system to have weak soundness.

• 2. Strong Secrecy: We require that the distributions $\mathcal {D}_\mathsf {Bind}$ and $\mathcal {D}_\mathsf {Hide}$ (described below) are computationally indistinguishable.

  • $\mathcal {D}_\mathsf {Bind}(1^\lambda ):$ Choose $r_\mathsf {pp}$ at random and compute $\mathsf {pp}= \mathsf {C.}\mathsf {Setup}(1^\lambda ; r_\mathsf {pp})$. Compute $\mathsf {pp}' = \mathsf {OutParam}(\mathsf {pp})$. For every $d \in \{0,1\}$, do the following:

    • Choose $o_d, o_d''$ at random and compute $\mathbf {c}_d = \mathsf {C.}\mathsf {Commit}(\mathsf {pp}, d~; o_d)$, $\mathbf {c}_d' = \mathsf {C.}\mathsf {Commit}(\mathsf {pp}', d; o_d'')$.

    • Compute $\varPi _\mathsf {TC}^d \leftarrow \mathsf {TC}.\mathsf {Prove}((\mathbf {c}_d, \mathbf {c}_d', \mathsf {pp}, \mathsf {pp}'), (d, \mathsf {pp}, o_d, o_d''))$.³

    • Compute $o_d' = \mathsf {C.}\mathsf {Equivocate}(\mathsf {pp}', r_\mathsf {pp}, \mathbf {c}_d', o_d'', 1-d)$.

    Output $\big (\mathsf {pp}, \mathsf {pp}', \mathbf {c}_0, \mathbf {c}_0', \mathbf {c}_1, \mathbf {c}_1', o_0, o_0', o_1, o_1', \varPi _\mathsf {TC}^0, \varPi _\mathsf {TC}^1 \big )$.

  • $\mathcal {D}_ \mathsf {Hide}(1^\lambda ):$ Choose $r_\mathsf {pp}$ at random and compute $\mathsf {pp}= \mathsf {C.}\mathsf {Setup}'(1^\lambda ; r_\mathsf {pp})$. Compute $\mathsf {pp}' = \mathsf {OutParam}(\mathsf {pp})$. For every $d \in \{0,1\}$, do the following:

    • Choose $o_d', o_d''$ at random. Compute $\mathbf {c}_d = \mathsf {C.}\mathsf {Commit}(\mathsf {pp}, 1- d~; o_d'')$ and compute $\mathbf {c}_d' = \mathsf {C.}\mathsf {Commit}(\mathsf {pp}', 1-d; o_d')$.

    • Compute $\varPi _\mathsf {TC}^d \leftarrow \mathsf {TC}.\mathsf {Prove}((\mathbf {c}_d, \mathbf {c}_d', \mathsf {pp}, \mathsf {pp}'), (1-d, \mathsf {pp}, o_d'', o_d'))$.

    • Compute $o_d = \mathsf {C.}\mathsf {Equivocate}(\mathsf {pp}, r_\mathsf {pp}, \mathbf {c}_d, o_d'', d)$.

    Output $\big (\mathsf {pp}, \mathsf {pp}', \mathbf {c}_0 ,\mathbf {c}_0', \mathbf {c}_1, \mathbf {c}_1', o_0, o_0', o_1, o_1', \varPi _\mathsf {TC}^0, \varPi _\mathsf {TC}^1 \big )$.

Recall that

$$ L_\mathcal{{U}}= \{ (C, \mathsf {out})~|~\exists ~\mathbf {w} \text { such that }C(\mathbf {w}) = \mathsf {out}\}. $$

We will use the following ingredients in our FH NIWI construction:

• A $\mathsf {RaHE}$-commitment scheme $(\mathsf {C.}\mathsf {Setup}, \mathsf {C.}\mathsf {Commit}, \mathsf {C.}\mathsf {Rand})$ with the additional functionalities $(\mathsf {OutParam}, \mathsf {ValidParam}, \mathsf {RParam}, \mathsf {ChangeCom},$$\mathsf {ValidInter}, \mathsf {InterParam})$ as defined in Sect. 5.1.

• Malleable proof system for $L_\mathsf {TC}$ with weak soundness and strong secrecy, with respect to the transformation $\mathsf {TC}.\mathsf {T} = (\mathsf {TC}.\mathsf {Transform}, \mathsf {TC}.\mathsf {WitTrans})$ as described before, denoted by $(\mathsf {TC}.\mathsf {Prove}, \mathsf {TC}.\mathsf {Verify}, \mathsf {TC}.\mathsf {Maul}).$

• Malleable NIWI proof system for $L_\mathsf {com}[\mathsf {pp}]$ with respect to the transformation $\mathsf {Bit}.\mathsf {GenT} = (\mathsf {Bit}.\mathsf {GenTrans}, \mathsf {Bit}.\mathsf {GWitTrans})$.

• Malleable NIWI proof system for $L_\mathsf {N}[\mathsf {pp}]$ with respect to the transformation $\mathsf {N}.\mathsf {GenT} = (\mathsf {N}.\mathsf {GenTrans},\mathsf {N}.\mathsf {GWitTrans})$.

Theorem 4

Assuming the existence of the ingredients as described above, the following construction $\Pi _{\mathsf {FHNIWI}}$ is a Fully Homomorphic NIWI proof system as per Definition 8.

We instantiate the first, third and fourth ingredients from DLIN and instantiate the second ingredient from DLIN with Leakage. This gives the following corollary:

Corollary 1

Assuming DLIN with Leakage, the following construction $\Pi _{\mathsf {FHNIWI}}$ is a Fully Homomorphic NIWI proof system as per Definition 8.

We refer the reader to the full version [4] for a proof of Theorem 4 and instantiation of ingredients.