Eighteenth Century Land Surveying as a Context for Learning Similar Triangles and Measurement

Abstract

In our study, we investigated the value and applicability of the history of mathematics as a didactical tool for teaching mathematics. Recent literature has disclosed conceptual, cultural, and motivational arguments for including historical mathematical texts and methods in the mathematics curriculum. We explored how these theoretical assumptions worked out when designing historically-based instructional material and when using this material for teaching. The focus was on teaching measurement skills and the application of similar triangles to eight- and ninth-grade students. The profession of the Dutch land surveyor in the 18th century served as a historical context. Analyses of the data indicated that several aspects of this historical context were helpful for teaching these subjects. The practical activities along the 18th century lines appeared to have a positive effect on the students’ motivation and on their conceptual understanding. The ninth-graders reacted more positively to the historically inspired text than the eighth-graders. The integration of historical elements, especially the need to read the old language, was generally not applauded, nor did we observe a positive cognitive effect. Even so, the practical activities inspired by the context appeared significantly effective and were judged positively by the students.

13.1 Introduction

Interest in the application of the history of mathematics as a didactical tool can already be seen in the early 20th century, for example in the work of Otto Toeplitz (1927). The new element in the current chapter is the research aspect. Not only do we present a geometry text at secondary school level that is based on historical problems and methods, we also survey how this text was used and evaluated by a large number of students. The survey was part of a project called ‘Reinvention of geometry’, and followed on the project Reinvention of Early Algebra (Van Maanen, 2002). Both names reveal the connection with the educational philosophy of Freudenthal (1973). In his view, the mathematics teacher should guide his or her students to re-invent mathematics (Freudenthal wrote re-invention with a hyphen). This approach to mathematics education also criticised the antididactic inversion, the phenomenon that in general mathematics is taught in reversed order: not the problem that led to a certain theorem is presented first, but in teaching one starts with proving the theorem and only then comes the problem, as an example or an exercise for the students.

Although Freudenthal was very interested in the history of mathematics, a discipline in which he had great expertise, he doubted whether the reinvention process should follow the historical line. We will argue in favour of the historical line for the reinvention of geometry. The student text will also make it clear that historical reinvention fits seamlessly in realistic mathematics education. We use the profession of the Dutch surveyor in the 18th century as a historical context for teaching measurement skills and the application of triangles. From a cultural perspective, this context is relevant for Dutch students. The profession of surveying was already developed in the Netherlands in the 17th century. The growing need for surveyors arose from the expansion of the nation, from designing maps, from the construction of buildings and fortifications. Since then, surveying served as an educational context and the first surveying books in Dutch were published.

13.2 Surveying and the Teaching and Learning of Measurement by Using Similar Triangles

Measurement is generally done by comparing the object that has to be measured against an instrument. One determines the size of a book by keeping it next to a graded ruler and by reading off the lengths of its three dimensions. The focus of this study is on teaching the mathematics needed when it is impossible or unpractical to compare the object to be measured. For example, think of the situation depicted in Fig. 13.1, where one wants to measure the width of a river. Nowadays it is common in such situations to use electronic tools, either based on optics or on satellite signals (GPS). More attractive for discussion in mathematical education, since more transparent and well accessible at the theoretical level, is the classical method of applying similar triangles.

Fig. 13.1

An 18th century application of similar triangles for measuring the width of a river (Morgenster, 1744, figure 246)

Until GPS fundamentally changed surveying, the mathematical tool used in these cases was the combination of triangulation and trigonometry with the theory of similar triangles. Much simplified, the surveyor divides the surface to be measured in a net of triangles. One side of one triangle is then measured accurately in the classical tactile manner (this segment is the base line), and after that only angles are measured. All other lengths are calculated with trigonometric methods, especially the sine rule.

In our study, trigonometry was not yet in the curriculum of the classes that we wanted to observe, so the students worked with similar triangles and with direct proportionality of two pairs of homologous sides. More generally, we intended to explore the appeal and power of land measurement as an authentic practice, which stimulates students to learn (in our case) the theory of similar triangles. And since the current surveying techniques go beyond the scope of students in eighth and ninth grade, we proposed to the students in our experiment to imagine that they were 18th century apprentice surveyors.

This sets the scene: land measurement as an authentic practice in which the students work with similar triangles, and the historical setting which keeps the mathematics within the reach of the students.

13.3 History of Mathematics as a Context for Mathematics Education

Our study is inspired by the movement in the United Kingdom and France which proposed to teach mathematical subjects in relation with their historical development and, if possible, with the help of original problems and sources. The idea was strongly promoted in the 1990s in France by Evelyne Barbin, who coordinated joint work on the history and teaching of mathematics between teachers and academics within the French IREMs (Instituts de Récherche pour l’Enseignement des Mathématiques), institutes for the research on the teaching of mathematics. In England, this idea was propagated by John Fauvel, who edited a collection of IREM papers (Fauvel, 1990) and published a special issue of the journal For the Learning of Mathematics on history in mathematics education (Fauvel, 1991). Fauvel was the driving force behind a series of seminal HIMED (History In Mathematics EDucation) conferences, which started in Leicester in 1990. The idea was fostered by developers and researchers within the International Study Group into the Relations Between History and Pedagogy of Mathematics (also known as HPM), an affiliated study group of ICMI. The key survey of the developments by the end of the 20th century is published in the report History In Mathematics Education of the respective ICMI Study (Fauvel & Van Maanen, 2000). In the decade 2001–2010, educational research in the HIMED domain grew more important. Good historical information about mathematical development and suggestions about how this could be used in teaching was still current. But more than before, studies were done to find out in a more structured and less anecdotal manner how teaching went with resources in which historical elements were integrated. Our research, which was part of the broader PhD project Reinvention of Geometry, belongs to this stream of classroom studies. Teaching similar triangles in a context in which students acted as 17th century surveyors was part of the project, discussed in Gulikers (2003). The report of the complete study appeared in Van Gulik-Gulikers (2005). More recent studies in the same vein are Glaubitz (2011) and several articles by Jankvist, especially Jankvist (2011), with a firm theoretical digestion of his earlier work.

The arguments that are mentioned in the 20th century literature on this subject were analysed by Gulikers and Blom (2001) and can be subdivided into conceptual, (multi-)cultural and motivational arguments. From a conceptual point of view, knowledge of the history of mathematics can result in an enrichment of the didactic repertoire of the teacher and in a more conscious use of the teaching methods involved. Students develop a better understanding by familiarising themselves with the way in which mathematical concepts developed. From a cultural perspective mathematics is an activity in which solutions are sought and found for problems from daily practice. During this process overlaps with other disciplines become visible. In this respect, it is not unimportant that a major part of the origin of mathematics is rooted in non-western cultures. This may enhance mutual respect and tolerance in multi-cultural classes. Using historical formulations of a problem in the curriculum can have a positive effect upon the motivation of students, because the historical source material sometimes contains amazing examples that enliven the lessons and challenge the students.

13.4 Research Questions

13.4.1 Role of History for Motivation

An argument in favour of using the history of mathematics as an educational tool that some designers and researchers put forward is that it motivates students. The unusual problems and the practical orientation of historical resources may serve to create a vivid lesson climate, and break through the common chalk-and-talk lessons. History appeals to different fields of interest and to different skills of the students, and this may enhance their motivation to do mathematics. At least, so it is claimed. This claim is precisely our main question: To what extent is this claim confirmed when we propose to students an ordinary mathematical textbook chapter in ‘historical disguise’? This disguise implies that we replaced the usual exercises about similarity by historical methods and problems from the practice of a surveyor.

To answer this question, we compared the motivation observed in the students before the experimental history-based lessons, with that observed after the experiment. We also tried to find out whether changes in motivation are caused by the historical elements, by the practical character of the exercises and the actual execution of measurements, or more in general by the change in the layout of the lessons.

13.4.2 Influence on the Learning Process

A surplus of motivation may have the effect that students understand mathematics better. Since it is difficult to observe how history affects a student, we chose to investigate what students think about their mathematical ability: Did the history make mathematics more accessible to the students, or did they experience more difficulties because of the historical elements? Our expectation was that history would make the content more concrete and that students would therefore find the mathematics easier to understand.

13.4.3 Students’ View on the Role of Mathematics in Society

Another, different argument in favour of integrating history is that it enables students to see and almost feel some important applications of history in society. Students often ask, “Why do we have to do mathematics?” Our lesson design includes a series of applications that relate to an important period in Dutch history, when measuring and similar triangles were tools in the hands of builders and architects, the ‘Golden Age’, in which many Dutch cities were first built or grew larger, in which ports and fortifications were constructed. Also, students can identify with a mathematical practitioner, since no measurement exists without someone who performs that measurement.

13.4.4 Two Questions in the Margin: Is History Essential, and What Is the Role of Old Language?

Although not crucial when the focus is on measurement, two marginal questions that arise naturally within the design of our study still deserve attention. The first concerns causality: If we notice that motivation improved within the experimental history-based lessons, can we be sure that this happened as a result of the history, or is it just the difference in outlook which appeals to the students?

A closely related question is about the authenticity of the historical resources. Written Dutch of the 17th and 18th centuries closely resembles current written Dutch, but especially the fonts used for printing books do cause reading difficulties. This raises the question of how students react to these difficulties, and how they judge the extra energy needed to decipher the texts.

13.5 Method

13.5.1 Background

The idea that measurement, and more particularly surveying of land, can be taught in a historical context and with historical resources, was tested in a design experiment in two cycles. In both cycles the topic of calculations in connection with similar triangles was taught using student texts that were based on an 18th century course for surveyors. The authentic practice of surveying played an important role in the developed teaching material.

The first cycle of the experiment was piloted in five classes in the course year 2001–2002. In 2002–2003 a revised version of the material was tested. In this chapter, we report about this second cycle. The design for this cycle differed in some respects from the design used in the first cycle. A new introduction about calculations based on similar triangles was added to better connect the historical problems with the mathematical knowledge that the students had at hand. Also, the revised teaching material gave better support to the students with respect to tasks which required understanding 18th century Dutch. The Dutch language has not changed dramatically since 1750, but not everything is immediately obvious either.

13.5.2 Participants and Data Collection

The second cycle of the experiment was carried out at 16 schools in various regions of the Netherlands. All in all, almost 1100 students from 46 classes (24 eighth-grade classes and 22 ninth-grade classes) taught by 32 teachers participated. Data were collected through:

• questionnaires for both students and teachers, administered before and after the experimental lessons

• classroom observations of 19 lessons at 9 schools

• evaluations of the students’ work, including worksheets and posters.

Due to organisational problems, far less than 1100 students filled in both questionnaires. Only the questionnaires of students who participated both before and after the experimental lessons were analysed.

13.5.3 Teaching Material

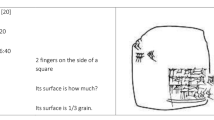
The mathematical subject addressed by the teaching material was the application of similar triangles in the determination of distances and lengths. The material replaced the chapter on similarity from two Dutch mathematics textbooks (Moderne Wiskunde¹ and Getal en Ruimte²). The historically oriented assignments contained an introduction on calculating with similarity. Similarity was applied in 17th century land surveying to calculate the height of buildings and the width of rivers. The students were taken back a few centuries and were asked to put themselves in the position of the surveyor. They first did a historical theoretical assignment on the basis of old mathematical texts and bits of historical background information (Fig. 13.2). This was followed by a practical assignment (see below) and finally they made a poster.

Fig. 13.2

Historical theoretical assignment, text for students (^aAs Morgenster did not use italics to indicate line segments, we will not use italics when literally translating his text)

The text for the students was in Dutch, but one of the schools had a bilingual programme and taught mathematics in English, therefore here an English translation was used. Figure 13.2 displays the English version of the experimental text as it was used by the students. The text was written so that it fully replaced the textbook chapter on similar triangles. In this way, the participating schools did not ‘lose time’, and the results of experimental classes could be compared to those of classes that used the textbook.

The practical assignment is a regular element in Dutch education, during which the students, often in couples or small groups, work on a more complex, practical problem which requires good mastery of the subject taught, as well as other knowledge and skills. In this case the students carried out measurements in pairs with the aim to calculate, with the help of the principle of similarity, the height of a building or the width of a ditch. The students could choose from the various methods they had seen in the teaching material. Following the choice of the method they had to design a solution strategy: planning how to do the measurements, followed by how to incorporate all the findings in a poster.

Teachers were supported by a short teacher manual which gave suggestions for the distribution of the material over the lessons, and for didactical arrangements. This teacher guide also contained advice about certain exercises, a scheme for evaluating the practical assignment and the worked-out exercises. Next to this, there was information about the historical background, which included an overview of the history of surveying in the Netherlands. The teacher guide also contained advice and materials for multidisciplinary activities together with the Dutch language teachers.

13.6 Findings

13.6.1 An Observation: Two Students as Surveyor

In this section, we describe our findings gathered from observing two students when they were engaged in a so-called ‘practical exercise’, which included the preparations, the practical measurements and the calculations afterwards. The school where the observation took place was a bilingual Dutch school (Maartenscollege, Haren), which teaches mathematics in English. Before the students started on the actual measurements, they had to design a solution strategy (“plan van aanpak”), in which they showed the methods they intended to use and calculated the expected results (Fig. 13.3). The practical exercise was independent student work, about which the students reported on a poster. When Stefan and Marco started this exercise, they had already worked on the booklet with application problems about similar triangles in the context of surveying. So they already knew several classical methods. In the exercise they were asked to measure the height of the school gym. Their solution strategy was based on two methods, taught in the booklet:

• Using a mirror which is placed on the ground.

• Looking over the top of a stick.

The first method is based on the work (Fig. 13.5) of the Dutch reckonmaster Cardinael (1620). See also Fig. 13.3. See for the second method and the elaboration on the poster Figs. 13.4 and 13.9.

13.6.1.1 Solution Strategy

Stefan and Marco used the two methods mentioned above to measure the height of the gym of the school. Figure 13.3 shows their worksheet describing Method 1. They first designed a solution strategy using fictitious numbers. Method 1 is the mirror method, illustrated in Cardinael (Fig. 13.5). However, in the following observation it will become clear that they did not quite grasp the strength of this method, which is based on the assumption that one cannot know the distance between the mirror and the object to be measured.

Fig. 13.3

Work by Stefan and Marco, Method 1

Fig. 13.4

Work by Stefan and Marco, Method 2

Fig. 13.5

Cardinael’s diagram measuring a height

Their text on the worksheet reads as follows:

• 1. We choose a length from the Maartens College building

  [Below the drawing is written:] chosen length e.g., 10 m

• 2. Place a mirror at ∠C

• 3. Position yourself at such a distance from the mirror that [looking into the mirror] you can see ∠A.

  [The drawing indicates that Stefan, drawn as a standing figure EF with length x and called ‘me’, looks into the mirror. On the left side of the drawing is written:] Marco looks over Stefan’s head and sees point A.

  [The calculation then reads:]

• 4. x = 170 cm [BA follows from the equal proportions EF : AB = EC : BC represented in the table, EC is supposed to be y, for example 3, and BC was chosen to be x, for example 10; the cross product produces for BA is] (1.7 × 10) ÷ 3 = 5.67.

Figure 13.4 shows the worksheet of Stefan and Marco describing Method 2. Here they work in a similar manner: ED is now a ‘stick’ (or Marco can serve as a stick; see below); Stefan looks over the stick and sees $\angle C$. Again, the lengths AD, DE and EB are fictitious (2, 3, and 10 respectively). Subsequently, Stefan and Marco collect all tools that they need for the actual measurements. They borrow a tape-measure from their teacher. At the physics lab, they acquire a mirror and the porters help them with a broom, which they will use as a stick.

13.6.1.2 The Actual Measurement

Before we continue the observations of our two surveyors, it is worthwhile studying Cardinael’s diagram (Fig. 13.5) in its own right.

The method proposed by Cardinael does not involve the length BC. The only lengths that are to be measured are CD, DE and DF (the mirror is at C, the stick is at D, so over its top E one sees the top of the tower A in the mirror, and F is the point on the ground from which one sees A and E in one line). If triangle CDE is then reflected in DE, the angles ∠ACB and ∠EGD are equal, since they are both equal to ∠ECD. Therefore, lines AC and EG are parallel and therefore triangles ACF and EGF are similar. So, AB : CF = ED : GF, and in this proportionality AB is the only unknown. That, however, was too advanced for Stefan and Marco (they might have worked like this, but our observation shows that they did not).

Another way of solving this problem, provided one can measure the distance between the foot of the tower and the mirror, is as follows. Stand where you can see the top of the tower in the mirror, which will be at point D. Measure the height of your eyes from the ground (DE), the distance between you and the mirror (CD) and the distance of the mirror from the tower (BC). It is this second method that Stefan and Marco use, placing the mirror at a point C (Fig. 13.6). First, they set a fixed distance for the distance BC, in their case the distance between the mirror and the wall of the gym. They take BC = 10 m. Stefan searches from where on the extension of BC he sees the edge of the gym’s roof in the mirror (Fig. 13.6). Marco measures Stefan’s height (1.64 m) and the distance from Stefan’s feet to the mirror (1.67 m) and concludes: “Now we have all measures and we can start our calculations.” Stefan makes a note of the measures, and they decide to continue the calculations inside.

Fig. 13.6

Stefan sees the edge of the roof in mirror C; Marco measures Stefan’s distance from C

For the second method, where they use only a stick, Marco tries to find a point on the ground from which he can see the edge of the roof and the top of Stefan’s head in one line (Fig. 13.7). Next, Stefan measures his distance to Marco (4.12 m), and comments: “The measures are not nice, but [that is not really a problem, because] we can use a calculator.” Then, Marco, speaking to Stefan: “We do not even use the broom, since you are the stick.”

Fig. 13.7

Marco tries to find a point from where he can see the roof and the top of Stefan’s head in one line

13.6.1.3 The Calculations and the Poster

While Stefan is still engaged in drawing, Marco also elaborates on the method with the stick (Fig. 13.8). For the height of the roof he finds 6.29 m ($\frac{ 1 5. 7 9 \times 1. 6 4}{4.12}$, in which 15.79 comes from (15.79 = 10 + 1.67 + 4.12). Marco says: “That is a very big difference between both methods.” He reconsiders his own work and continues: “Both methods look alright, but there is quite a difference; 9 m seems rather high to me.” In the meantime, a classmate asks whether Stefan and Marco have calculated the height in two ways.

Fig. 13.8

Marco and Stefan at work with their data

“Yes”, Stefan says, “but we have two different answers.” The classmate says: “How is that possible?” Stefan answers: “That is what we are trying to find out.” Then, Marco proposes to make a scale drawing of the situation for the stick method (Fig. 13.8). First, he draws the distance from the gym to the point on the ground, and then he inserts the ‘stick’ in the right position. With the help of the ray from the eye, he then draws the edge of the gym roof. Then he inserts the mirror in the drawing, in the right place.

Then, it is time to measure in the drawing. Marco determines the height of the gym, taking the scale into account. He says: “The method with the stick seems to have given the right answer: 6 m seems logical for the gym.” Afterwards, the boys proceed to find out what went wrong with the mirror method. Marco suggests measuring the two angles at C (incidence and reflection) in the drawing. If these angles are not equal in the drawing, the boys must have made a mistake in their measurements. They inspect the angles in the drawing and find them to be unequal. Marco says to Stefan: “So, you did the sighting incorrectly.” Stefan answers: “Or you were wrong when you measured the distances.” The end of lesson signal ends this collaboration, which lasted a double lesson (100 min). Stefan and Marco decide that they want to redo the measurements at a later moment.

Stefan and Marco reported about this practical exercise in a poster. They clearly had first repeated the measurements. In the poster they illustrated the methods used with drawings. With the new figures they presented their final calculations (Fig. 13.9) and their conclusions (Fig. 13.10). They found different results for the two methods. The stick method led to 6,8 m. With the mirror method their calculations for the height of the building resulted in 6,697 m.

Fig. 13.9

Part of the poster with report on the stick method

Fig. 13.10

The part of the poster with conclusions

With respect to the technical execution of the performed measurements, two comments can be made, which also throw some light on the deviations between the final results. First, in Fig. 13.6, Stefan looks into the mirror at C. In this case, not Stefan’s length (1,64 m) should be used in the subsequent calculations, but the height of Stefan’s eye. This will be about 10 cm less than his length, which will lead to a more accurate result in Fig. 13.8, where the calculation is carried out.

Second, in Fig. 13.7, Marco sights the roof and “the top of Stefan’s head in one line” (at least, that is what the two are thinking). But the ray from Marco’s eye to the roof is tangent to the side of Stefan’s head and not to its top. In this case they should not calculate with Stefan’s length but with a larger number, which depends on Stefan’s length, the radius of his skull and the slope of the ray from Marco’s eye to the roof. Both problems do not arise if a pointed stick is used instead of the human body.

13.6.1.4 Provisional Conclusions Based on the Observations of the Two Students

Apparently, the exercise had a number of features which only come up when students actually carry out the measurements. The well-known but not often experienced fact that people make errors when measuring, is revealed here thanks to the two methods. Quite probably the method with the mirror is less precise than the stick method, although a deeper analysis is necessary to clarify this matter. The decision to make a scale drawing is also very interesting. There is nice intuitive reasoning here. If in reality the angles are equal (they should be equal because of the reflection law), then they must also be equal in a scale drawing. Finally, the attention that the students pay to the (probably unexpected) problem of finding different heights for the same object, their honesty and eagerness in dealing with this problem and the decision to redo the measurements gives insight into how scientific ethics develop in young students. The problems inherent with measurement prompted them, and they took up the challenge.

13.6.2 Findings from All Students Involved in the Data Set

Next to doing observations on a micro-level, we investigated the judgements of the students about the historical and practical aspects of the teaching material. Table 13.1 gives an overview of our findings based on the pre- and post-questionnaires, on interviews with students and teachers, on classroom observations and on evaluations of written material produced by students (exercises and posters). Only the questionnaire data of the students who filled in the questionnaire both before and after the experimental lessons were included in the analysis. The results are marked positive (+) when there is significant positive statistical evidence, indecisive (±) when there is both positive and negative evidence and negative (–) when there is significant counterevidence. In the remaining part of this section these results are further elaborated.

Table 13.1 Judgement of students on historical and practical aspects

13.6.2.1 Students’ Motivation

Working with the text for students in which elements from the history of mathematics were integrated, had a negative effect on the motivation to learn mathematics. Judgements by students were rendered on a scale from 0 (“history is not useful, not agreeable, …”) to 1 (“history is interesting, nice, useful, …”). The difference in motivation between before and after working with the experimental text was found to be significant (p < 0.01) (Table 13.2).

Table 13.2 Motivation to learn mathematics before and after working with the experimental text

There were also significant differences between subgroups. This was the case between those students who find mathematics easy and those who find mathematics difficult (see Table 13.3). Students who in the pre-questionnaire indicated finding mathematics easy, were less motivated to learn mathematics after working with the experimental text. For those who found mathematics difficult beforehand, nothing had changed in their motivation after working with the text.

Table 13.3 Motivation to learn mathematics before and after working with the experimental text by students who indicated finding mathematics easy and students who indicated finding mathematics difficult

Another relevant difference is that between those students who preferred to do problems with bare numbers, and those who reported to like problems that they have to derive from a story (see Table 13.4). The motivation of the first group had decreased after working through the text, while for the second group the change was not significant.

Table 13.4 Motivation to learn mathematics before and after working with the text for students who prefer bare number problems and for the students who prefer context problems

One explanation for the negative effect on the motivation of the students is that the students appeared to encounter many difficulties with the historical sources presented in the old Dutch language. They were not acquainted with it, and they experienced reading and interpreting these texts as too complicated and time-consuming. Some students remarked that working with these sources “has nothing to do with mathematics”. They reported that it had “no use” for them and they also called it “a waste of time”. This reaction was not unanimous, though, since other students said that they found it interesting to learn something about the old language. These students considered it a challenge to derive the mathematics from the historical source material.

Another important reason why the motivation of students was not stimulated by the integration of history is that it made the tasks much more complex than they were used to. Working with this material requires other competences, and, as some students said, they do not like that. It makes mathematics less attractive for them. Much also depends on the insight and support of the teacher.

Although the quantitative data were not that positive, classroom observations made by the first author and interviews with students and teachers enabled us also to signal some encouraging effects (though these positive reactions did not dominate). During the observations and the interviews, it came to the fore that the variation in activities was considered as positive; especially the change in perspective. History gives an unexpected turn to mathematics and it makes the lessons livelier. Both teachers and students appreciated learning about how mathematics was applied in the past, for example, the methods to measure the height of a building. And the interviewed students were especially enthusiastic about applying these methods themselves in reality.

In particular, the concluding practical assignment was valued positively. An open question at the end of the lesson series revealed that three quarters of the students liked the practical assignment. Most students found that the practical assignment brought interesting variation and also a challenge, namely, they themselves could make a practical application of the theory that they had studied in the preceding lessons. In doing so, they saw that what they had learned in the text about 17th century surveying “really worked”. Students liked that they were allowed to go outside during their mathematics lesson, which is “different from an ordinary lesson in the classroom”. Also, the cooperation with fellow students in measuring the height of a building was welcomed. Students were thrilled that, “without modern tools”, but “with simple materials”, they were able to do the necessary measurements themselves.

Students who did not fully understand the mathematical explanation in the experimental text did not like the practical assignment, because they had no clear clue how they should do the measurements. Some students found the step from the theoretical explanation of plane geometry in their regular textbook to the practical task of measuring in space difficult. Some of them also preferred to do “just abstract mathematics”. They called the practical assignment superfluous, because they “know for certain that they will never apply these measuring methods”.

13.6.2.2 Influence on the Learning Process

Working with the historically-oriented experimental text did not change the view of students about how well they were able to do their mathematical work (the feasibility). Some students found the exercises easier because the information about the ancient ways to measure made the text less abstract. They commented that they learned much from carrying out the applications. They memorised better what they had to learn, because it fired their imagination. Thanks to the practical assignment—they said—they sooner noticed mistakes that they had made in earlier, formal exercises, since now they “had to really think about the matter”. This put a check on their acquired knowledge.

Teachers said that they noticed that students remembered with more ease how calculations on similar triangles had to be performed. They expected that the students in the experimental group would have a better command of the concept of similarity in a later school year than the students who did the regular chapter from the textbook. Our study did not extend so far that we can confirm or reject this claim. It would certainly be interesting to investigate the effect of such experimental text on memorisation and retention.

Clearly, other students had problems due to the historical elements. One third of the students indicated that the historical practical assignment was one of the most difficult elements of the experimental text. Problems arose from the old language, and also because the mathematics was not as straightforward as it is presented in the textbook. Many students needed to get acquainted with more complex and more extended exercises. They were used to questions subdivided into sub-questions, and often directly related to the mathematical theory and to examples that were just discussed. Now, they had to figure out a strategy themselves, and that was difficult for them. Students who had previously worked on unusual exercises, in projects and small research tasks, were better equipped for these practical exercises.

We found a remarkable significant difference in the judgement about feasibility between two subsets of the students, that is between the students who had answered in the pre-questionnaire that they found mathematics easy and those who had answered that mathematics was difficult for them. In both groups there were many changes in judgement (see Table 13.5). The subset that at first found mathematics easy shifted towards difficult, and in the other group there was a shift from difficult in the pre-questionnaire to easy in the post-questionnaire.

Table 13.5 Students’ judgement about the feasibility of mathematics before and after working with the experimental text for students who at first found mathematics easy and who at first found mathematics difficult

There was also a noticeable difference in shift between the eighth-grade and ninth-grade students who worked with the experimental text (see Table 13.6). For the eighth-graders, the idea that mathematics is feasible shifted significantly to less feasible. For the ninth-graders there was no significant shift.

Table 13.6 Eighth- and ninth-grade students’ judgement about the feasibility of mathematics before and after working with the experimental text

The posters and reports about the practical assignments revealed that in most cases the students mastered the calculations based on the concept of similarity quite well. This does not hold to the same extent for the historical exercises in the theoretical part of the experimental text. In several lessons, the first author observed that for the practical assignment, in which calculations with similar triangles were the basic ingredient, students first returned to the theoretical sections with the mathematical explanations and retried the unsuccessful calculations. Those students who were again unable to do the calculations, also failed on the practical assignment.

13.6.2.3 Students’ Views on the Role of Mathematics in Society

The importance and usefulness of mathematics is, unexpectedly, noticed less by the students after having worked through the experimental text (see Table 13.7).

Table 13.7 Students’ judgement about the usefulness of mathematics before and after working with the experimental text

For an explanation of this finding, one could argue that students already knew about the importance and usefulness of mathematics before they started to work with the experimental text. The historical context would then not add anything to their view. Moreover, the problems with the old language might even have distracted them from their views and beliefs about mathematics.

However, in the open questions of the post-questionnaire, students answered that the experimental text sheds light on the societal role of mathematics. They noted that they saw how mathematics was applied in the 17th century, especially in the measurements done by the surveyor. This raised enthusiasm, since they now saw what they could do with their mathematical knowledge. Whether or not the historical presentation helped, is still disputed. Some students appreciated the elementary character of the tools, while others said that there was no need to work with these old instruments, since current measuring equipment would let you determine location and height much easier.

13.6.2.4 Students’ Opinions About the Integration of History

Table 13.8 summarises what students thought about the integration of history in the experimental text.

Table 13.8 Students’ opinions about the integration of history

In the open questions in the post-questionnaire 37% of the students indicated that in their view history made the mathematics lessons more attractive. It was important for them to see where mathematics comes from, and “how people worked in the past”. This was useful if they wanted to apply mathematics themselves. They also appreciated the experimental approach as a welcome interruption of the usual “throwing around figures” and boring problems “without a story”.

Some students emphasised that the experimental text attracted them because they liked the two disciplines, mathematics as well as history, and they said that they liked the combination. Others valued that they now knew more about the development of mathematics, but for them it had rather been “just mathematics” and not “that old Dutch”.

When students were asked what they found least attractive about the experimental text, 20% of the students pointed at the exercises with a historical character. Moreover, 30% counted these exercises among the most difficult elements in the experimental text. They reacted by saying “all these stories are difficult” and “are not really about mathematics”. Just as some students were in favour of both mathematics and history, there were students who disliked both disciplines. For them the experimental text was doubly unpleasant. A common objection was that the two disciplines should be treated separately. Students who had this objection found that when history is integrated within a mathematical text, “it is not about mathematics anymore”. Also, the focus on the past was rejected by some students. They would rather hear about current developments and were of the opinion that “mathematics should rather be directed towards the future”.

As expected, regarding the students’ opinions about the integration of history several differences were found between different groups of students. The students who liked to derive a problem from a story were more positive about the historical elements than those who preferred to do problems with bare numbers (see Table 13.9).

Table 13.9 Appreciation of the historical elements in the experimental text by students who prefer bare number problems and by students who prefer context problems

As is shown in Table 13.10, differences were found between the eighth- and ninth-grade students with respect to motivation, perceived feasibility, usefulness of mathematics and the attractiveness of history-based mathematics lessons. The ninth-graders were more positive than the eighth-grade students about their motivation and the perceived feasibility of mathematics. For their opinion about the usefulness of mathematics some difference was found between the eighth- and ninth-grade students, but this difference was not significant. The open question about the attractiveness of mathematics lessons in which history was integrated was answered more positively by the ninth-grade students.

Table 13.10 Eighth- and ninth-grade students’ opinions about their motivation, perceived feasibility and usefulness of mathematics, and attractiveness of history-based mathematics lessons

As expected, there was also a significant difference between the students who studied the experimental text in lessons in which the Dutch language teachers and mathematics teachers worked together, and the students who studied the text only in the mathematics lessons. The first group recognised the usefulness of mathematics significantly more clearly (see Table 13.11).

Table 13.11 Students’ opinions about usefulness of mathematics for students who had joint lessons in Dutch language and mathematics and students who did not have joint lessons

13.6.3 Judgements and Views of the Teachers

A first finding was that experience helps in teaching history-based mathematics lessons. This was clearly concluded by teachers who participated in both cycles of the experiment. They reported that they could deal with the material more easily in the second cycle. The experimental text and the supporting teacher material were designed so that all teachers could work with it, including those who had no prior experience with the integration of historical elements in mathematics lessons. Of the teachers who were not involved in the first cycle, many did not have experience with this. When they were asked in advance what the integration of historical elements meant for them, it appeared to be restricted to giving information about a great name or an important year as a bit of background for a new subject. Despite the fact that they had less experience with using historical material, the overall reaction of the teachers was that they were stimulated by this material. It increased their motivation for mathematics.

Since the commitment and approach of the teachers are important for the execution of such uncommon lessons, it is important to note that all the 32 teachers who taught the experimental text in the second cycle did so on a voluntary basis and that their overall reactions were positive. To illustrate this, we quote here a number of comments by one of the teachers, who sharply analysed some of the central issues discussed in our chapter. According to this teacher,

[t]he benefit of the project must be found in the integration of your textbook and a part of the history of mathematics. The textbook chapter on similarity can be used straightaway as an introduction to its practical application. That is your main benefit. You do not lose time, whereas you acquire a definite additional advantage.

Another remark was that the experimental text helped to answer questions about the usefulness of mathematics.

Students often come up with the remark that they do not understand what purpose is served by mathematics. In what way is it enjoyable and what can you use it for? As a teacher, you have of course some examples at your disposal to clarify things a little bit. In the textbook, there are certain contexts that may help you. But still, how do you visualise that mathematics has a certain relevance?

Also, the teacher emphasised that not only students can profit from the practical assignment, the teacher does so as well.

Especially the practical assignment appeared to be a challenge. Leaving the classroom and then finding an object in the vicinity of the school that you have to measure. Making your personal choice from the methods that have been discussed. You are bound to notice large differences in the ways students try to come with a solution. An excellent opportunity to see what skills are being used. Accompanying several groups gives you the possibility to observe the thought process.

Furthermore, the teacher discussed the problem of working with texts in older Dutch.

Students must get used to this kind of ‘old language’. However, if you help them along they will usually manage. It gives you the opportunity to have a useful talk about mathematics. In any case, for a part of the students it is a challenge. Students help each other and together they are trying to find a translation for the text. It is a good thing to see them working and trying to solve a problem. Especially working together under the supervision of the teacher gives an extra dimension to the work. Reading, reading again, drawing up a sketch, adding the missing data and classifying them.

13.7 Conclusions and Discussion

Earlier, we already drew some provisional conclusions based on the observations of the two students. Based on the larger group of students and teachers involved, we can conclude now that the domain of measurement is important in mathematics education for several reasons:

• it engages students in practical activities

• it often requires cooperation in order to produce good results

• the measuring errors provoke valuable discussion between students; it could also be taken as the starting point for statistical considerations

• the use of tools, and the discussion about what tools to choose in relation with their possibilities and precision, is a welcome aspect; the discussion needs not to be provoked, since now that the world has GPS, students rightly question why one still needs all these triangles and calculations

• it is an area well within reach of the students, in which they themselves can apply formal mathematical theory.

The analysis of the pre- and post-questionnaires showed that students appreciate practical measurement activities and surveying. Students produced their own results, independently from the teacher. The results mean something, and in doing the measurements and the resulting calculations students could identify themselves with a mathematical practitioner: the surveyor.

Furthermore, in addition to what is said already, particularly in Table 13.1, about our findings on the role of history in teaching mathematics we would like to add here that we observed that quite some students have a view on mathematics that leads them to a quick rejection of the experimental text. For them mathematics is doing short problems according to a clear example, and preferably with the least amount of text possible. When they start working on a problem, they expect that the solution strategy is at hand as soon as they have read the problem. For these students, the experimental text was ‘wrong’ in a number of respects: it required reading, it required time-consuming practical work, and the strategies were not immediately clear. Moreover, the methods were outdated and produced results that can be obtained much quicker and with greater precision. Indeed, they do have a point. However, there is also a point to the wide range of possibilities that the historical aspects offer, namely to connect mathematics teaching to culture, to language, to appreciating the centuries when the Netherlands were an economical power. There is a point in learning to solve complex problems, in learning to do practical work and learning to cooperate. Another finding is that we could identify particular subgroups of students that responded more positively to the history in the experimental text: those who were taught mathematics and the old language jointly, as well as those who already liked to solve ‘word problems’. Also, the ninth-grade students were more positively than eight-graders. Therefore, we may conclude that history is not essential, but that for some students it is beneficial.

The concept of similarity and the applications of similar triangles is a topic that can adequately be taught (and learned!) in the context of practical problems. Measurement is a crucial part of this approach. Integration of historical elements is possible, but probably one will obtain the same or maybe better results without history. The topic is suitable for inviting a visiting practitioner for a guest lesson.

A major reason for students to dislike the experimental text was that it was too complicated and long for them, and that they did not immediately understand the problem or see the solution strategy. This reaction of the students is maybe influenced by the structure of the textbooks. In secondary education, textbooks are meant for students to work on independently, i.e., without the help and sometimes also without the presence of a teacher. The consequence is that tasks that require fundamental thinking, broader exploration and endurance, are skipped or split into a number of small, easy-to-digest parts. Hence, it is no surprise that students noticed the difference between the more complex tasks in the experimental text and the usual problems from the textbook, and that some of them answered that for that reason they disliked the experimental text.

The responses of 32 teachers who volunteered to teach similar triangles in the second cycle of the experiment were stimulating. It might well be that in some schools the teachers learned more from the experiment than their students. The comments of the teacher quoted earlier, showed which aspects of the text were welcomed as they are.

In this study we have not studied how the approach and attitude of the teacher influenced the results and views of the students. This is one important question that remains open for later research. In addition, there were many more questions that came up during our study that need to be answered before we can fully benefit from history as a didactical tool for teaching mathematics. Further research is necessary in several directions, including issues such as

• the age of the students (would this type of text be more suitable for older students, maybe for student teachers?)

• the value of such a text for the teacher (would it be a useful resource for professional development, for a lesson study?)

• the influence of the approach and attitude of the teacher

• the possibly avoidable problems with the old language (Is it possible to maintain the historical character without direct access to the sources?)

• the aspect of memory and retention (what is the effect of a text like the one studied here in the longer term and does it lead to better retention of the concepts and methods?).

Although the work on using the history of mathematics as a didactical tool for teaching mathematics is not yet finished, and many important questions require more research, it is remarkable that, since we carried out our research and reported about it, the history of mathematics has become in many teacher education institutions a standard feature in the education of teachers. In most of the institutions which teach the history of mathematics, designing lessons in which history of mathematics plays a major part, has become one of the assignments.