Abstract
This paper investigates parallel random sampling from a potentially-unending data stream whose elements are revealed in a series of element sequences (minibatches). While sampling from a stream was extensively studied sequentially, not much has been explored in the parallel context, with prior parallel random-sampling algorithms focusing on the static batch model. We present parallel algorithms for minibatch-stream sampling in two settings: (1) sliding window, which draws samples from a prespecified number of most-recently observed elements, and (2) infinite window, which draws samples from all the elements received. Our algorithms are computationally and memory efficient: their work matches the fastest sequential counterpart, their parallel depth is small (polylogarithmic), and their memory usage matches the best known.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Consider a model of data processing where data is revealed to the processor in a series of element sequences (minibatches) of varying sizes. A minibatch must be processed soon after it arrives. However, the data is too large for all the minibatches to be stored within memory, though the current minibatch is available in memory until it is processed.
Such a minibatch streaming model is a generalization of the traditional data stream model, where data arrives as a sequence of elements. If each minibatch is of size 1, our model reduces to the streaming model. Use of minibatches is common. For instance, in a data stream warehousing system [13], data is collected for a specified period (such as an hour) into a minibatch and then ingested while statistics and properties need to be maintained continuously. Minibatches may be relatively large, potentially of the order of Gigabytes or more, and could leverage parallelism (e.g., a distributed memory cluster or a shared-memory multicore machine) to achieve the desired throughput. Furthermore, this model matches the needs of modern “big data” stream processing systems such as Apache Spark Streaming [22], where newly-arrived data is stored as a distributed data set (an “RDD” in Spark) that is processed in parallel. Queries are posed on all the data received up to the most recent minibatch.
This paper investigates the foundational aggregation task of random sampling in the minibatch streaming model. Algorithms in this model observe a (possibly infinite) sequence of minibatches \(B_1,B_2,\ldots , B_t, \ldots \). We consider the following variants of random sampling, all of which are well studied in the context of sequential streaming algorithms. In the infinite window model, a random sample is chosen from all the minibatches seen so far. Thus, after observing \(B_t\), a random sample is drawn from \(\cup _{i=1}^t B_i\). In the sliding window model with window size w, the sample after observing \(B_t\) is chosen from the w most-recent elements. Typically, the window size w is much larger than a minibatch size.Footnote 1 In this work, the window size w is provided at query time, but an upper bound W on w is known beforehand.
We focus on optimizing the work and parallel depth of our algorithms. This is a point of departure from the traditional streaming algorithms literature, which has mostly focused on optimizing the memory consumed. Like in previous work, we consider memory to be a scarce resource and design for scenarios where the size of the stream is very large—and the stream, or even a sliding window of the stream, does not fit in memory. But in addition to memory efficiency, this work strives for parallel computational efficiency.
Our Contributions. We present parallel random-sampling algorithms for the minibatch streaming model, in both infinite-window and sliding-window settings. These algorithms can use the power of shared-memory parallelism to speedup the processing of a new minibatch as well as a query for random samples.
\(\rhd \) Efficient Parallel Algorithms. Our algorithms are provably efficient in parallel processing. We analyze them in the work-depth model, showing (1) they are work-efficient, i.e., total work across all processors is of the same order as an efficient sequential algorithm, and (2) their parallel depth is logarithmic in the target sample size, which implies that they can use processors nearly linear in the input size while not substantially increasing the total work performed. In the infinite-window case, the algorithm is work-optimal since the total work across all processors matches a lower bound on work, which we prove in this paper, up to constant factors. Interestingly, for all our algorithms, the work of the parallel algorithm is sublinear in the size of the minibatch.
\(\rhd \) Small Memory. While the emphasis of this work is on improving processing time and throughput, our algorithms retain the property of having a small memory footprint, matching the best sequential algorithms from prior work.
Designing such parallel algorithms requires overcoming several challenges. Sliding-window sampling is typically implemented with Priority Sampling [1, 3], whose work performed (per minibatch) is linear in the size of the minibatch. Parallelizing it reduces depth but does not reduce work. Generating skip offsets, à la Algorithm Z [20] (reservoir sampling), can significantly reduce work but offers no parallelism. Prior algorithms, such as in [20], seem inherently sequential, since the next location to sample from is derived as a function of the previously chosen location. This work introduces a new technique called \(\textsf {R}^3\) sampling, which combines reversed reservoir sampling with rejection sampling. \(\textsf {R}^3\) sampling is a new perspective on Priority Sampling that mimics the sampling distribution of Priority Sampling but is simpler and has less computational dependency, making it amendable to parallelization. To enable parallelism, we draw samples simultaneously from different areas of the stream using a close approximation of the distribution. This leads to slight oversampling, which is later corrected by rejection sampling. We show that all these steps can be implemented in parallel. In addition, we develop a data layout that permits convenient update and fast queries. As far as we know, this is the first efficient parallelization of the popular reservoir-sampling-style algorithms.
Related Work. Reservoir sampling (attributed to Waterman) was known since the 1960s. There has been much follow-up work, including methods for speeding up reservoir sampling by “skipping past elements” [20], weighted reservoir sampling [9], and sampling over a sliding window [1, 3, 10, 21].
The difference between the distributed streams model [5,6,7, 11] considered earlier, and the parallel stream model considered here is that in the distributed streams model, the focus is on minimizing the communication between processors while in our model, processors can coordinate using shared memory, and the focus is on work-efficiency of the parallel algorithm. Prior work on shared-memory parallel streaming has considered frequency counting [8, 19] and aggregates on graph streams [17], but to our knowledge, there is none so far on random sampling. Prior work on warehousing of sample data [4] has considered methods for sampling under minibatch arrival, where disjoint partitions of new data are handled in parallel. Our work also considers how to sample from a single partition in parallel, and can be used in conjunction with a method such as [4].
2 Preliminaries and Notation
A stream \(\mathcal {S}\) is a potentially infinite sequence of minibatches \(B_1 B_2,\ldots \), where each minibatch consists of one or more elements. Let \(\mathcal {S}_t\) denote the stream so far until time t, consisting of all elements in minibatches \(B_1,B_2,\ldots ,B_{t}\). Let \(n_i = |B_i|\) and \(N_t = \sum _{i=1}^t n_i\), so \(N_t\) is the size of \(\mathcal {S}_t\). The size of a minibatch is not known until the minibatch is received, and the minibatch is received as an array in memory. A stream segment is a finite sequence of consecutive elements of a stream. For example, a minibatch is a stream segment. A window of size w is the stream segment consisting of the w most recent elements.
A sample of size s drawn without replacement from a set B with at least s elements is defined as a random set whose distribution matches S, the result of the following process. (1) Initialize S to empty. (2) Repeat s times: draw a uniform random element e from B, add e to S and delete e from B. A sample of size s drawn with replacement from a non-empty set B is defined as a random set whose distribution matches T, the result of the following process. (1) Initialize T to empty. (2) Repeat s times: draw a uniform random element e from B, add e to T and do not delete e from B.
Let [n] denote the set \(\{1, \dots , n\}\). For sequence \(X = \langle x_1, x_2, \dots , x_{|X|} \rangle \), the i-th element is denoted by \(X_i\) or X[i]. For convenience, negative index \(-i\), written \(X[-i]\) or \(X_{-i}\), refers to the i-th index from the right end—i.e., \(X[|X| - i + 1]\). Following common array slicing notation, let \(X[a\texttt {:}]\) be the subsequence of X starting from index a onward. An event happens with high probability (whp) if it happens with probability at least \(1 - n^{-c}\) for some constant \(c \ge 1\). Let
 (a, b), \(a \le b\), be a function that returns an element from \(\{a, a+1, \dots , b\}\) chosen uniformly at random. For \(0 < p \le 1\),
(a, b), \(a \le b\), be a function that returns an element from \(\{a, a+1, \dots , b\}\) chosen uniformly at random. For \(0 < p \le 1\),
 (p)\(\;\in \{\textsf { H}, \textsf { T}\}\) returns heads (H) with probability p and tails (T) with probability \(1-p\). For \(m \le n\), an m-permutation of a set S, \(|S| = n\), is an ordering of m distinct elements from S.
(p)\(\;\in \{\textsf { H}, \textsf { T}\}\) returns heads (H) with probability p and tails (T) with probability \(1-p\). For \(m \le n\), an m-permutation of a set S, \(|S| = n\), is an ordering of m distinct elements from S.
We analyze algorithms in the work-depth model assuming concurrent reads and arbitrary-winner concurrent writes. The work of an algorithm is the total operation count, and depth (also called parallel time or span) is the length of the longest chain of dependencies within that algorithm. The gold standard in this model is for an algorithm to perform the same amount of work as the best sequential counterpart (work-efficient) and to have polylogarithmic depth. This setting has been fertile ground for research and experimentation on parallel algorithms. Moreover, results in this model are readily portable to other related models, e.g., exclusive read and exclusive write, with a modest increase in cost (see, e.g., [2]).
We measure the space complexity of our algorithms in terms of the number of elements stored. Our space bounds do not represent bit complexity. Often, the space used by the algorithm is a random variable, so we present bounds on the expected space complexity.
3 Parallel Sampling from a Sliding Window
This section presents parallel algorithms for sampling without replacement from a sliding window (SWOR-Sliwin). Specifically, for target sample size s and maximum window size W, SWOR-Sliwin is to maintain a data structure \(\mathcal {R}\) supporting two operations: (i)
 \((B_i)\) incorporates a minibatch \(B_i\) of new elements arriving at time i into \(\mathcal {R}{}\) and (ii) For parameters \(q \le s\) and \(w \le W\),
\((B_i)\) incorporates a minibatch \(B_i\) of new elements arriving at time i into \(\mathcal {R}{}\) and (ii) For parameters \(q \le s\) and \(w \le W\),
 (q, w) when posed at time i returns a random sample of q elements chosen uniformly without replacement from the w most recent elements in \(\mathcal {S}_i\).
(q, w) when posed at time i returns a random sample of q elements chosen uniformly without replacement from the w most recent elements in \(\mathcal {S}_i\).
In our implementation,
 (q, w) does something stronger and returns a q-permutation (not only a set) chosen uniformly at random from the w newest elements from \(\mathcal {R}\)—this can be used to generate a sample of any size j from 1 till q by only considering the first j elements of the permutation.
(q, w) does something stronger and returns a q-permutation (not only a set) chosen uniformly at random from the w newest elements from \(\mathcal {R}\)—this can be used to generate a sample of any size j from 1 till q by only considering the first j elements of the permutation.
One popular approach to sampling from a sliding window in the sequential setting [1, 3] is the Priority Sampling algorithm: Assign a random priority to each stream element, and in response to
 , return the s elements with the smallest priorities among the latest w arrivals. To reduce the space consumption to be sublinear in the window size, the idea is to store only those elements that can potentially be included in the set of s smallest priorities for any window size w. A stream element e can be discarded if there are s or more elements with a smaller priority than e that are more recent than e. Doing so systematically leads to an expected space bound of \(O(s + s\log (W/s))\) [1]Footnote 2.
, return the s elements with the smallest priorities among the latest w arrivals. To reduce the space consumption to be sublinear in the window size, the idea is to store only those elements that can potentially be included in the set of s smallest priorities for any window size w. A stream element e can be discarded if there are s or more elements with a smaller priority than e that are more recent than e. Doing so systematically leads to an expected space bound of \(O(s + s\log (W/s))\) [1]Footnote 2.
As stated, this approach expends work linear in the stream length to examine/assign priorities, but ends up choosing only a small fraction of the elements examined. This motivates the question: How can one determine which elements to choose, ideally in parallel, without expending linear work to generate or look at random priorities? We assume \(W \gg n_i \ge s\), where \(n_i\) is the size of minibatch i. The main result of this section is as follows:
Theorem 1
There is a data structure for SWOR-Sliwin that uses \(O(s + s\log (W/s))\) expected space and supports the following operations:
-
(i)
 (B) for a new minibatch B uses \(O(s + s\log (\tfrac{W}{s}))\) work and \(O(\log W)\) parallel depth; and
(B) for a new minibatch B uses \(O(s + s\log (\tfrac{W}{s}))\) work and \(O(\log W)\) parallel depth; and -
(ii)
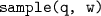 for sample size \(q \le s\) and window size \(w \le W\) uses O(q) work and \(O(\log W)\) parallel depth.
for sample size \(q \le s\) and window size \(w \le W\) uses O(q) work and \(O(\log W)\) parallel depth.
Note that the work of the data structure for inserting a new minibatch is only logarithmic in the maximum window size W and independent of the size of the minibatch. To prove this theorem, we introduce \(\textsf {R}^3\) sampling, which brings together reversed reservoir sampling and rejection sampling. We begin by describing reversed reservoir sampling, a new perspective on priority sampling that offers more parallelism opportunities. After that, we show how to implement this sampling process efficiently in parallel with the help of rejection sampling.
3.1 Simple Reversed Reservoir Algorithm
We now describe reversed reservoir (RR) sampling, which mimics the behavior of priority sampling but provides more independence and more parallelism opportunities. This process will be refined and expanded in subsequent sections. After observing sequence X, Simple-RR (Algorithm 1) yields uniform sampling without replacement of up to s elements for any suffix of X.
We say the i-th most-recent element has age i; this position/element will be called age i when the context is clear. The algorithm examines the input sequence X in reverse, \(X_{-1}, X_{-2}, \dots \), and stores selected elements in a data structure A, recording the age of an element in X as well as a slot (from [s]) into which the element is mapped. Multiple elements may be mapped to the same slot. The slot numbers are used to generate a permutation. The probability of selecting an age-i element into A decreases as i increases.
For maximum sample size \(s > 0\) and integer \(i > 0\), define \( p_{-i}^{(s)} = \min \left( 1, \frac{s}{i} \right) \), which is exactly the probability age-i element is retained in standard priority sampling when drawing s samples.

Let A denote the result of Simple-RR. Using this, sampling s elements without replacement from any suffix of X is pretty straightforward. Define
where \( \nu _A(\ell ) = \mathop {\mathrm {arg\,max}}\nolimits _{k \ge 1} \{ (k, \ell ) \in A \}\) isFootnote 3 the oldest element assigned to slot \(\ell \). Given A, we can derive \(A_{i}\) for any \(i \le |X|\) by considering the appropriate subset of A. We have that \(\chi (A_i)\) is an s-permutation of the i most recent elements of X. This is stated in the following lemma:
Lemma 1
If R is any s-permutation of \(X[-i\,\texttt {:}]\), then 
Proof
We proceed by induction on i. The base case of \(i = s\) is easy to verify since \(\pi \) is a random permutation of [s] and \(\chi (A_s)\) is a permutation of \(X[-s:]\) according to \(\pi \). For the inductive step, assume that the relationship holds for any R that is an s-permutation of \(X[-i:]\). Now let \(R'\) be an s-permutation of \(X[-(i+1):]\). Let \(x_{-(i+1)}\) denote \(X[-(i+1):]\). Consider two cases:
Case I: \(x_{-(i+1)}\) appears in \(R'\), say at \(R'_\ell \). For \(R' = \chi (A_{i+1})\), it must be the case that \(x_{-(i+1)}\) was chosen and was assigned to slot \(\ell \). Furthermore, \(\chi (A_i)\) must be identical to \(R'\) except in position \(\ell \), where it could have been any of the \(i - (s - 1)\) choices. This occurs w.p. \((i - [s-1])\cdot \frac{(i - s)!}{i!} \cdot p_{-(i+1)}^{(s)}\cdot \frac{1}{s} = \frac{(i+1-s)!}{(i+1)!}\).
Case II: \(x_{-(i+1)}\) does not appear in \(R'\). Therefore, \(R'\) must be an s-permutation of \(X[-i:]\) and \(x_{-(i+1)}\) was not sampled. This happens with probability \( \textstyle \frac{(i-s)!}{i!} \cdot (1 - p_{-(i+1)}) = \frac{(i+1 -s)!}{(i+1)!} \).
In either case, this gives the desired probability. \(\square \)
Note that the space taken by this algorithm (the size of \(A_{|X|}\)) is \(O(s + s \log (|X|/s))\), which is optimal [10]. The steps are easily parallelizable but still need O(|X|) work, which can be much larger than the \((s+s\log (|X|/s))\) bound on the number of elements the algorithm must sample. We improve on this next.
3.2 Improved Single-Element Sampler
This section addresses the special case of \(s = 1\). Our key ingredient is the ability to compute the next index that will be sampled, without touching the elements that are not sampled.
Let \(X_{-i}\) be an element just sampled. We can now define a random variable \(\textsc {Skip}(i)\) that indicates how many elements past \(X_{-i}\) will be skipped over before selecting index \(-(i + \textsc {Skip}(i))\) according to the distribution given by Simple-RR. Conveniently, this random variable can be efficiently generated in O(1) time using the inverse transformation method [15] because its cumulative distribution function (CDF) has a simple, efficiently-solvable form:  . This leads to the following improved algorithm:
. This leads to the following improved algorithm:

This improvement significantly reduces the number of iterations:
Lemma 2
Let  be the number of times the while-loop in the Fast-Single-RR algorithm is executed on input X with \(n = |X|\). Then,
be the number of times the while-loop in the Fast-Single-RR algorithm is executed on input X with \(n = |X|\). Then,  . Also, for \(m \ge n\) and \(c \ge 4\),
. Also, for \(m \ge n\) and \(c \ge 4\), 
Proof
Let \(Z_i\) be an indicator variable for whether \(x_{-i}\) contributes to an iteration of the while-loop. Hence,  , where \(Z = \sum _{i=2}^{|X|} Z_i\). But
, where \(Z = \sum _{i=2}^{|X|} Z_i\). But
 , so
, so  . This proves the expectation bound. The concentration bound follows from a Chernoff bound. \(\square \)
. This proves the expectation bound. The concentration bound follows from a Chernoff bound. \(\square \)
Immediately, this means that if \(A = { {\textsc {Fast}\text {-}{\textsc {Single}\text {-}{\textsc {RR}}}}}(X)\) is kept as a simple sequence (e.g., an array), the running time—as well as the length of A—will be \(O(1 + \log (|X|))\) in expectation. Moreover, \({ {\textsc {Fast}\text {-}{\textsc {Single}\text {-}{\textsc {RR}}}}}(X)\) produces the same distribution as Simple-RR with \(s = 1\), only more efficiently computed.
3.3 Improved Multiple-Element Sampler
In the general case of reversed reservoir sampling, generating skip offsets from the distribution for \(s > 1\) turns out to be significantly more involved than for \(s = 1\). While this is still possible, e.g., using a variant of Vitter’s Algorithm Z [20], prior algorithms appear inherently sequential.
This section describes a new parallel algorithm that builds on Fast-Single-RR. In broad strokes, it first “oversamples” using a simpler distribution and subsequently, “downsamples” to correct the sampling probability. To create parallelism, we logically divide the stream segment into s “tracks” of roughly the same size and have the single-element algorithm work on each track in parallel.
Track View. Define \({\textsc {Create}}\text {-}{\textsc {View}} (X, k)\) to return a view corresponding to track k on X: if \(Y = {\textsc {Create}}\text {-}{\textsc {View}} (X, k)\), then \(Y_{-i}\) is \(X[-\alpha _s^{(k)}(i)]\), where \(\alpha _s^{(k)}(i) = i\cdot {}s + k\). That is, track k contains, in reverse order, indices \(-(s+k), -(2s+k), -(3s+k), \dots \). Importantly, these views never have to be materialized.
Algorithm 3 combines the ideas developed so far. We now argue that Fast-RR yields the same distribution as Simple-RR:

Lemma 3
Let A be a return result of \({ {\textsc {Fast}}\text {-}{\textsc {RR}}}(X, s)\). Then, for \(j=1,\dots , |X|\) and \(\ell \in [s]\), 
Proof
For \(j \le s\), age j is paired with a slot \(\ell \) drawn from a random permutation of [s], so
 . For \(j > s\), write j as \(j = s\cdot i + \tau \), so age j appears as age i in view
. For \(j > s\), write j as \(j = s\cdot i + \tau \), so age j appears as age i in view  . Now age j appears in A if both of these events happen: (1) age i was chosen into \(T_\tau \) and (2) the coin turned up heads so it was retained in \(T'_\tau \). These two independent events happen together with probability \( p^{(1)}_{-i} \cdot \frac{i\cdot s}{\alpha _s^{(\tau )}(i)} = \frac{1}{i}\cdot \frac{i\cdot s}{s\cdot i + \tau } = \frac{s}{j} = p^{(s)}_{-j}\). Once age j is chosen, it goes to slot \(\ell \) with probability 1 / s. Hence,
. Now age j appears in A if both of these events happen: (1) age i was chosen into \(T_\tau \) and (2) the coin turned up heads so it was retained in \(T'_\tau \). These two independent events happen together with probability \( p^{(1)}_{-i} \cdot \frac{i\cdot s}{\alpha _s^{(\tau )}(i)} = \frac{1}{i}\cdot \frac{i\cdot s}{s\cdot i + \tau } = \frac{s}{j} = p^{(s)}_{-j}\). Once age j is chosen, it goes to slot \(\ell \) with probability 1 / s. Hence,
 . \(\square \)
. \(\square \)
3.4 Storing and Retrieving Reserved Samples
How Should We Store the Sampled Elements? An important design goal is for samples of any size \(q \le s\) to be generated without first generating s samples. To this end, observe that restricting \(\chi (A)\) to its first \(q \le s\) coordinates yields a q-permutation over the input. This motivates a data structure that stores the contents of different slots separately.
Denote by \(\mathcal {R}(A)\), or simply \(\mathcal {R}\) in clear context, the binned-sample data structure for storing reserved samples A. The samples are organized by their slot numbers \((\mathcal {R}_i)_{i=1}^s\), with \(\mathcal {R}_i\) storing slot i’s samples. Within each slot, samples are binned by their ages. In particular, each \(\mathcal {R}_i\) contains \(\lceil \log _2(\lceil |X|/s \rceil ) \rceil + 1\) bins, numbered \(0, 1, 2, \dots , \lceil \log _2(\lceil |X|/s \rceil ) \rceil \)—with bin k storing ages j in the range \(2^{k-1} < \lceil j/s \rceil \le 2^k\). Below, bin t of slot i will be denoted by \(\mathcal {R}_i[t]\).
Additional information is kept in each bin for fast queries: every bin k stores \(\phi (k)\), defined to be the age of the oldest element in bin k and all younger bins for the same slot number.
Below is an example. Use \(s = 3\) and \(|X| = 16\). Let the result from Fast-RR be \(A = \{(1, 2), (2, 3), (3, 1), (7, 1), (10, 3), (11, 3), (14, 2)\}\). Then, \(\mathcal {R}\) keeps the following bins, together with \(\phi \) values:

From this construction, the following claims can be made:
Lemma 4
-
(i)
The expected size of the bin \(\mathcal {R}_i[t]\) is
 .
. -
(ii)
The size of slot \(\mathcal {R}_i\) is expected \(O(1 + \log (|X|/s))\). Furthermore, for \(c \ge 4\),
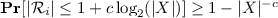 .
.
Proof
Bin t of \(\mathcal {R}_i\) is responsible for elements wit age j in the range \(2^{t-1} < \lceil j/s \rceil \le 2^t\), for a total of \(s(2^t - 2^{t-1}) = s\cdot 2^{t-1}\) indices. Among them, the age that has the highest probability of being sampled is \((s2^{t-1} + 1)\), which is sampled into slot i with probability \(\frac{1}{s}\cdot \frac{s}{s2^{t-1} + 1} \le \frac{1}{s\cdot 2^{t-1}}\). Therefore, 
Moreover, let  , so \(|\mathcal {R}_i| = \sum _{t=1}^{|X|} Y_t\). Since
, so \(|\mathcal {R}_i| = \sum _{t=1}^{|X|} Y_t\). Since  , we have
, we have

which proves the expectation bound. Because \(Y_t\)’s are independent, using an argument similar to the proof of Lemma 2, we have the probability bound. \(\square \)
Data Structuring Operations. Algorithm 4 shows algorithms for constructing a binned-sample data structure and answering queries. To Construct a binned-sample data structure, the algorithm first arranges the entries into groups by slot number, using a parallel semisorting algorithm, which reorders an input sequence of keys so that like sorting, equal keys are arranged contiguously, but unlike sorting, different keys are not necessarily in sorted order. Parallel semisorting of n elements can be achieved using O(n) expected work and space, and \(O(\log n)\) depth [12]. The algorithm then, in parallel, processes each slot, putting every entry into the right bin. Moreover, it computes a \(\min \)-prefix, yielding \(\phi (\cdot )\) for all bins. There is not much computation within a slot, so we do it sequentially but the different slots are done in parallel. To answer a Sample query, the algorithm computes, for each slot i, the oldest age within \(X[-w\texttt {:}]\) that was assigned to slot i. This can be found quickly by figuring out the bin k where w should be. Once this is known, it simply has to look at \(\phi \) of bin \(k - 1\) and go through the entries in bin k. This means a query touches at most two bins per slot.

Cost Analysis. We now analyze Fast-RR, Construct, and Sample for their work and parallel depth. More concretely:
Lemma 5
-
(i)
By storing \(T_0, T_i\)’s, and \(T'_i\)’s as simple arrays, Fast-RR(X, s) runs in expected \(O(s + s\log \tfrac{|X|}{s})\) work and \(O(\log |X|)\) parallel depth.
-
(ii)
Construct(A, n, s) runs in \(O(s + s\log \tfrac{n}{s})\) work and \(O(\log n)\) parallel depth.
-
(iii)
Sample \((\mathcal {R}, q, t)\) runs in O(q) work and \(O(\log n)\) parallel depth, where n is the length of X on which \(\mathcal {R}\) was built.
For detailed analysis, see the full paper [18]. In brief, generating the initial length-s permutation in parallel takes O(s) work and \(O(\log s)\) depth [14]. The dominant cost stems from running s parallel instances of Fast-Single-RR, which takes \(O(1 + \log (|X|/s))\) work and depth each by Lemma 2. Furthermore, aside from the cost of semisorting, the cost of Construct follows from Lemma 4(i)–(ii) and standard analysis. Finally, the cost of Sample follows from Lemma 4, together with the fact that each query looks at q slots and only 2 bins per slot.
3.5 Handling Minibatch Arrival
This section describes how to incorporate a minibatch into our data structure to maintain a sliding window of size W. Assume that the minibatch size is \(n_i \le W\). If not, we can only consider its W most recent elements. When a minibatch arrives, retired sampled elements must be removed and the remaining sampled elements are “downsampled” to maintain the correct distribution.
Remember that the number of selected elements is \(O(s + s\log (W/s))\) in expectation, so we have enough budget in the work bound to make a pass over them to filter out retired elements. Instead of revisiting every element of the window, we apply the process below to the selected elements to maintain the correct distribution. Notice that an element at age i was sampled into slot \(\ell \) with probability \(\frac{1}{s}p^{(s)}_{-i}\). A new minibatch will cause this element to shift to age j, \(j > i\), in the window. At age j, an element is sampled into slot \(\ell \) with probability \(\frac{1}{s}p^{(s)}_{-j}\). To correct for this, we flip a coin that turns up heads with probability \({p^{(s)}_{-j}}/{p^{(s)}_{-i}} \le 1\) and retain this sample only if the coin comes up heads.
Therefore,
 \((B_i)\), \(|B_i| = n_i\) handles a minibatch arrival as follows:
\((B_i)\), \(|B_i| = n_i\) handles a minibatch arrival as follows:
-
Step i:
Discard and downsample elements in \(\mathcal {R}\); the index shifts by \(n_i\).
-
Step ii:
Apply Fast-RR on \(B_i\), truncated to the last W elements if \(n_i > W\).
-
Step iii:
Run Construct on the result of Fast-RR with a modification where it appends to an existing \(\mathcal {R}\) as opposed to creating a new structure.
Overall, this leads to the following cost bound for
 :
:
Lemma 6
 takes \(O(s + s\log (W/s))\) work and \(O(\log W)\) depth.
takes \(O(s + s\log (W/s))\) work and \(O(\log W)\) depth.
4 Parallel Sampling from an Infinite Window
This section addresses sampling without replacement from an infinite window, consisting of all elements seen so far in the stream. This is formulated as the SWOR-Infwin task: For each time \(i = 1, \ldots , t\), maintain a random sample of size \(\min \{s, N_i\}\) chosen uniformly without replacement from \(\mathcal {S}_i\). We present a work-efficient algorithm for SWOR-Infwin and further show it to be work optimal, up to constant factors.
For \(p,q \in [r]\), let \(\mathcal {H}(p,q,r)\) be the hypergeometric random variable, which can take an integer value from 0 to \(\min \{p,q\}\). Suppose there are q balls of type 1 and \((r-q)\) balls of type 2 in an urn. Then, \(\mathcal {H}(p,q,r)\) is the number of balls of type 1 drawn in p trials, where in each trial, a ball is drawn at random from the urn without replacement. It is known that  .
.
Work Lower Bound. We first show a lower bound on the work of any algorithm for SWOR-Infwin, sequential or parallel, by considering the expected change in the sample output after a new minibatch is received.
Lemma 7
Any algorithm that solves SWOR-Infwin must have expected work at least \(\varOmega \left( t + \sum _{i=1}^t \min \{n_i, \frac{sn_i}{N_i}\}\right) \) over minibatches \(B_1 \ldots B_t\).
Proof
First consider the number of elements that are sampled from each minibatch. If \(N_i \le s\), then the entire minibatch is sampled, resulting in a work of \(\varOmega (n_i)\). Otherwise, the number of elements sampled from the new minibatch \(B_i\) is \(\mathcal {H}(s, n_i, N_i)\). The expectation is  , which is a lower bound on the expected cost of processing the minibatch. Next, note that any algorithm must pay \(\varOmega (1)\) for examining minibatch \(B_i\), since in our model the size of the minibatch is not known in advance. If an algorithm does not examine a minibatch, then the size of the minibatch may be as large as \(\varOmega (N_i)\), causing \(\varOmega (1)\) elements to be sampled from it. The algorithm needs to pay at least \(\varOmega (t)\) over t minibatches. Hence, the total expected work of any algorithm for SWOR-Infwin after t steps must be \(\varOmega \left( t + \sum _{i=1}^t \min \{n_i, \frac{sn_i}{N_i}\}\right) \). \(\square \)
, which is a lower bound on the expected cost of processing the minibatch. Next, note that any algorithm must pay \(\varOmega (1)\) for examining minibatch \(B_i\), since in our model the size of the minibatch is not known in advance. If an algorithm does not examine a minibatch, then the size of the minibatch may be as large as \(\varOmega (N_i)\), causing \(\varOmega (1)\) elements to be sampled from it. The algorithm needs to pay at least \(\varOmega (t)\) over t minibatches. Hence, the total expected work of any algorithm for SWOR-Infwin after t steps must be \(\varOmega \left( t + \sum _{i=1}^t \min \{n_i, \frac{sn_i}{N_i}\}\right) \). \(\square \)
Parallel Algorithm for SWOR-Infwin. Our solution is presented in Algorithm 5. The main idea is as follows: When a minibatch \(B_i\) arrives, generate a random variable \(\kappa \) according to the hypergeometric distribution to determine how many of the s samples will be chosen from \(B_i\), as opposed to prior minibatches. Then, choose a random sample of size \(\kappa \) without replacement from \(B_i\) and update the sample S accordingly. We leverage Sanders et al. [16]’s recent algorithm for parallel sampling without replacement (from static data), restated below in the work-depth model:
Observation 2
([16]). There is a parallel algorithm to draw s elements at random without replacement from N elements using O(s) work and \(O(\log s)\) depth.
Our algorithm uses static parallel sampling without replacement in two places: once to sample new elements from the new minibatch, and then again to update the current sample. In more detail, when a minibatch arrives, the algorithm (i) chooses \(\kappa \), the number of elements to be sampled from \(B_i\), in O(1) time; (ii) samples \(\kappa \) elements without replacement from \(B_i\) in parallel; and (iii) replaces \(\kappa \) randomly chosen elements in S with the new samples using a two-step process, by first choosing the locations in S to be replaced, followed by writing the new samples to the chosen locations. Details appear in Algorithm 5.

Theorem 3
Algorithm 5 is a work-efficient algorithm for SWOR-Infwin. The total work to process t minibatches \(B_1,\ldots ,B_t\) is \(O\left( t + \sum _{i=1}^t \min \{n_i, \frac{sn_i}{N_i}\} \right) \) and the parallel depth of the algorithm for processing a single minibatch is \(O(\log s)\). This work is optimal up to constant factors, given the lower bound from Lemma 7.
Proof
When a new minibatch \(B_i\) arrives, for the case \(N_i \le s\), copying \(n_i\) elements from \(B_i\) to S can be done in parallel in \(O(n_i)\) work and O(1) depth, by organizing array S so that the empty locations in the array are all contiguous, so that the destination for writing an element can be computed in O(1) time.
For the case \(N_i > s\), random variable \(\kappa \) can be generated in O(1) work. The next two steps of sampling \(\kappa \) elements from \(B_i\) and from \(\{1,\ldots ,n\}\) can each be done using \(O(\kappa )\) work and \(O(\log \kappa )\) depth, using Observation 2. The final for loop of copying data can be performed in \(O(\kappa )\) work and O(1) depth. Hence, the expected total work for processing \(B_i\) is \(1 + \min \{n_i, \frac{sn_i}{N_i}\}\), and the depth is \(O(\log \kappa )\). Summing over all t minibatches, we get our result. Since \(\kappa \le s\), the parallel depth is \(O(\log s)\). \(\square \)
5 Parallel Sampling with Replacement
We now consider parallel algorithms for SWR-Infwin, sampling with replacement. A simple solution, which uses O(s) work per minibatch and has O(1) parallel depth, is to run s independent parallel copies of a single element stream sampler, which is clearly correct. When minibatch \(B_i\) is received, each single element sampler decides whether or not to replace its sample, with probability \(n_i/N_i\), which can be done in O(1) time. We show that it is possible to do better than this by noting that when \(n_i/N_i\) is small, a single element sampler is unlikely to change its sample, and hence the operation of all the samplers can be efficiently simulated using less work. The main results are below (proof omitted):
Theorem 4
There is a parallel algorithm for SWR-Infwin such that for a target sample size s, the total work to process minibatches \(B_1, \dots , B_t\) is \(O(t + \sum _{i=1}^t s n_i/N_i)\), and the depth for processing any one minibatch \(B_i\) is \(O(\log s)\). This work is optimal, up to constant factors.
This work bound is optimal, since the expected number of elements in the sample that change due to a new minibatch is \(s n_i/N_i\).
6 Conclusion
We presented low-depth, work-efficient parallel algorithms for the fundamental data streaming problem of streaming sampling. Both the sliding-window and infinite-window cases were addressed. Interesting directions for future work include the parallelization of other types of streaming sampling problems, such as weighted sampling and stratified sampling.
Notes
- 1.
One could also consider a window to be the w most recent minibatches, and similar techniques are expected to work.
- 2.
The original algorithm stores the largest priorities but is equivalent to our view.
- 3.
Because \(|X| \ge s\), the function \(\nu \) is always defined.
References
Babcock, B., Datar, M., Motwani, R.: Sampling from a moving window over streaming data. In: Proceedings of the Annual ACM-SIAM Symposium on Discrete algorithms (SODA), pp. 633–634 (2002)
Blelloch, G.E., Maggs, B.M.: Chapter 10: parallel algorithms. In: The Computer Science and Engineering Handbook, 2nd edn. Chapman and Hall/CRC (2004)
Braverman, V., Ostrovsky, R., Zaniolo, C.: Optimal sampling from sliding windows. In: Proceedings of the ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems (PODS), pp. 147–156 (2009)
Brown, P.G., Haas, P.J.: Techniques for warehousing of sample data. In: Proceedings of the International Conference on Data Engineering (ICDE), p. 6 (2006)
Chung, Y., Tirthapura, S., Woodruff, D.P.: A simple message-optimal algorithm for random sampling from a distributed stream. IEEE Trans. Knowl. Data Eng. (TKDE) 28(6), 1356–1368 (2016)
Cormode, G.: The continuous distributed monitoring model. SIGMOD Rec. 42(1), 5–14 (2013)
Cormode, G., Muthukrishnan, S., Yi, K., Zhang, Q.: Continuous sampling from distributed streams. J. ACM 59(2), 10:1–10:25 (2012)
Das, S., Antony, S., Agrawal, D., El Abbadi, A.: Thread cooperation in multicore architectures for frequency counting over multiple data streams. Proc. VLDB Endow. (PVLDB) 2(1), 217–228 (2009)
Efraimidis, P.S., Spirakis, P.G.: Weighted random sampling with a reservoir. Inf. Process. Lett. 97(5), 181–185 (2006)
Gemulla, R., Lehner, W.: Sampling time-based sliding windows in bounded space. In: Proceedings of the International Conference on Management of Data (SIGMOD), pp. 379–392 (2008)
Gibbons, P., Tirthapura, S.: Estimating simple functions on the union of data streams. In: Proceedings of the ACM Symposium on Parallelism in Algorithms and Architectures (SPAA), pp. 281–291 (2001)
Gu, Y., Shun, J., Sun, Y., Blelloch, G.E.: A top-down parallel semisort. In: Proceedings of the ACM Symposium on Parallelism in Algorithms and Architectures (SPAA), pp. 24–34 (2015)
Johnson, T., Shkapenyuk, V.: Data stream warehousing in tidalrace. In: Proceedingsof the Conference on Innovative Data Systems Research (CIDR) (2015)
Reif, J.H.: An optimal parallel algorithm for integer sorting. In: Proceedings of the IEEE Annual Symposium on Foundations of Computer Science (FOCS), pp. 496–504 (1985)
Ross, S.M.: Introduction to Probability Models, 10th edn. Academic Press, Cambridge (2009)
Sanders, P., Lamm, S., Hübschle-Schneider, L., Schrade, E., Dachsbacher, C.: Efficient parallel random sampling - vectorized, cache-efficient, and online. ACM Trans. Math. Softw. 44(3), 29:1–29:14 (2018)
Tangwongsan, K., Pavan, A., Tirthapura, S.: Parallel triangle counting in massive streaming graphs. In: Proceedings of the ACM International Conference on Information and Knowledge Management (CIKM), pp. 781–786 (2013)
Tangwongsan, K., Tirthapura, S.: Parallel streaming random sampling. arXiv:1906.04120 [cs.DS], https://arxiv.org/abs/1906.04120, June 2019
Tangwongsan, K., Tirthapura, S., Wu, K.: Parallel streaming frequency-based aggregates. In: Proceedings of the ACM Symposium on Parallelism in Algorithms and Architectures (SPAA), pp. 236–245 (2014)
Vitter, J.S.: Random sampling with a reservoir. ACM Trans. Math. Softw. 11(1), 37–57 (1985)
Xu, B., Tirthapura, S., Busch, C.: Sketching asynchronous data streams over sliding windows. Distrib. Comput. 20(5), 359–374 (2008)
Zaharia, M., Das, T., Li, H., Hunter, T., Shenker, S., Stoica, I.: Discretized streams: fault-tolerant streaming computation at scale. In: Proceedings of the ACM Symposium on Operating Systems Principles (SOSP), pp. 423–438 (2013)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Tangwongsan, K., Tirthapura, S. (2019). Parallel Streaming Random Sampling. In: Yahyapour, R. (eds) Euro-Par 2019: Parallel Processing. Euro-Par 2019. Lecture Notes in Computer Science(), vol 11725. Springer, Cham. https://doi.org/10.1007/978-3-030-29400-7_32
Download citation
DOI: https://doi.org/10.1007/978-3-030-29400-7_32
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29399-4
Online ISBN: 978-3-030-29400-7
eBook Packages: Computer ScienceComputer Science (R0)





 (B) for a new minibatch B uses
(B) for a new minibatch B uses 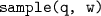 for sample size
for sample size  .
.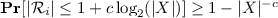 .
.