Abstract
We formalize the theory of quantum Hoare logic (QHL) [TOPLAS 33(6),19], an extension of Hoare logic for reasoning about quantum programs. In particular, we formalize the syntax and semantics of quantum programs in Isabelle/HOL, write down the rules of quantum Hoare logic, and verify the soundness and completeness of the deduction system for partial correctness of quantum programs. As preliminary work, we formalize some necessary mathematical background in linear algebra, and define tensor products of vectors and matrices on quantum variables. As an application, we verify the correctness of Grover’s search algorithm. To our best knowledge, this is the first time a Hoare logic for quantum programs is formalized in an interactive theorem prover, and used to verify the correctness of a nontrivial quantum algorithm.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Due to the rapid progress of quantum technology in the recent years, it is predicted that practical quantum computers can be built within 10–15 years. Especially during the last 3 years, breakthroughs have been made in quantum hardware. Programmable superconductor quantum computers and trapped ion quantum computers have been built in universities and companies [1, 3, 4, 6, 23].
In another direction, intensive research on quantum programming has been conducted in the last decade [16, 45, 51, 53], as surveyed in [27, 52]. In particular, several quantum programming languages have been defined and their compilers have been implemented, including Quipper [31], Scaffold [35], QWire [47], Microsoft’s LIQUi [25] and Q# [57], IBM’s OpenQASM [22], Google’s Cirq [30], ProjectQ [56], Chisel-Q [40], Quil [55] and \(Q\left| SI \right\rangle \) [39]. These research allow quantum programs to first run on an ideal simulator for testing, and then on physical devices [5]. For instance, many small quantum algorithms and protocols have already been programmed and run on IBM’s simulators and quantum computers [1, 2].
[25] and Q# [57], IBM’s OpenQASM [22], Google’s Cirq [30], ProjectQ [56], Chisel-Q [40], Quil [55] and \(Q\left| SI \right\rangle \) [39]. These research allow quantum programs to first run on an ideal simulator for testing, and then on physical devices [5]. For instance, many small quantum algorithms and protocols have already been programmed and run on IBM’s simulators and quantum computers [1, 2].
Clearly, simulators can only be used for testing. It shows the correctness of the program on one or a few inputs, not its correctness under all possible inputs. Various theories and tools have been developed to formally reason about quantum programs for all inputs on a fixed number of qubits. Equivalence checking [7, 8], termination analysis [38], reachability analysis [64], and invariant generation [62] can be used to verify the correctness or termination of quantum programs. Unfortunately, the size of quantum programs on which these tools are applicable is quite limited. This is because all of these tools still perform calculations over the entire state space, which for quantum algorithms has size exponential in the number of qubits. For instance, even on the best supercomputers today, simulation of a quantum program is restricted to about 50–60 qubits. Most model-checking algorithms, which need to perform calculations on operators over the state space, are restricted to 25–30 qubits with the current computing resources.
Deductive program verification presents a way to solve this state space explosion problem. In deductive verification, we do not attempt to execute the program or explore its state space. Rather, we define the semantics of the program using precise mathematical language, and use mathematical reasoning to prove the correctness of the program. These proofs are checked on a computer (for example, in proof assistants such as Coq [15] or Isabelle [44]) to ensure a very high level of confidence.
To apply deductive reasoning to quantum programs, it is necessary to first define a precise semantics and proof system. There has already been a lot of work along these lines [9, 20, 21, 61]. A recent result in this direction is quantum Hoare logic (QHL) [61]. It extends to sequential quantum programs the Floyd-Hoare-Naur inductive assertion method for reasoning about correctness of classical programs. QHL is proved to be (relatively) complete for both partial correctness and total correctness of quantum programs.
In this paper, we formalize the theory of quantum Hoare logic in Isabelle/HOL, and use it to verify a non-trivial quantum algorithm – Grover’s search algorithmFootnote 1. In more detail, the contributions of this paper are as follows.
-
1.
We formally prove the main results of quantum Hoare logic in Isabelle/HOL. That is, we write down the syntax and semantics of quantum programs, specify the basic Hoare triples, and prove the soundness and completeness of the resulting deduction system (for partial correctness of quantum programs). To our best knowledge, this is the first formalization of a Hoare logic for quantum programs in an interactive theorem prover.
-
2.
As an application of the above formalization, we verify the correctness of Grover’s search algorithm. In particular, we prove that the algorithm always succeeds on the (infinite) class of inputs where the expected probability of success is 1.
-
3.
As preparation for the above, we extend Isabelle/HOL’s library for linear algebra. Based on existing work [13, 58], we formalize many further results in linear algebra for complex matrices, in particular positivity and the Löwner order. Another significant part of our work is to define the tensor product of vectors and matrices, in a way that can be used to extend and combine operations on quantum variables in a consistent way. Finally, we implement algorithms to automatically prove identities in linear algebra to ease the formalization process.
The organization of the rest of the paper is as follows. Section 2 gives a brief introduction to quantum Hoare logic. Section 3 describes in detail our formalization of QHL in Isabelle/HOL. Section 4 describes the application to Grover’s algorithm. Section 5 discusses automation techniques, and gives some idea about the cost of the formalization. Section 6 reviews some related work. Finally, we conclude in Sect. 7 with a discussion of future directions of work.
We expect theorem proving techniques will play a crucial role in formal reasoning about quantum computing, as they did for classical computing, and we hope this paper will be one of the first steps in its development.
2 Quantum Hoare Logic
In this section, we briefly recall the basic concepts and results of quantum Hoare logic (QHL). We only introduce the proof system for partial correctness, since the one for total correctness is not formalized in our work. In addition, we make two simplifications compared to the original work: we consider only variables with finite dimension, and we remove the initialization operation. The complete version of QHL can be found in [61].
In QHL, the number of quantum variables is pre-set before each run of the program. Each quantum variable \(q_i\) has dimension \(d_i\). The (pure) state of the quantum variable takes value in a complex vector space of dimension \(d_i\). The overall (pure) state takes value in the tensor product of the vector spaces for the variables, which has dimension \(d = \prod d_i\). The mixed state for variable \(q_i\) (resp. overall) is given by a \(d_i\times d_i\) (resp. \(d\times d\)) matrix satisfying certain conditions (making them partial density operators). The notation \(\overline{q}\) is used to denote some finite sequence of distinct quantum variables (called a quantum register). We denote the vector space corresponding to \(\overline{q}\) by \(\mathcal {H}_{\overline{q}}\).
The syntax of quantum programs is given by the following grammar:
where
-
In \(\overline{q}:=U\overline{q}\), U is a unitary operator on \(\mathcal {H}_{\overline{q}}\), i.e., \(U^{\dag }U=UU^{\dag }=\mathbb {I}\), where \(U^{\dag }\) is the conjugate transpose of U.
-
In \(\mathbf{measure}\ M[\overline{q}]:\overline{S}\), \(M=\{M_m\}\) is a quantum measurement on \(\mathcal {H}_{\overline{q}}\), and \(\overline{S}=\{S_m\}\) gives quantum programs that will be executed after each possible outcome of the measurement;
-
In \(\mathbf{while}\ M[\overline{q}]=1\ \mathbf{do}\ S\), \(M=\{M_0,M_1\}\) is a yes-no measurement on \(\overline{q}\).
Quantum programs can be regarded as quantum extensions of classical while programs. The skip statement does nothing, which is the same as in the classical case. The unitary transformation changes the state of \(\overline{q}\) according to U. It is the counterpart to the assignment operation in classical programming languages. The sequential composition is similar to its classical counterpart. The measurement statement is the quantum generalisation of the classical case statement \(\mathbf{if}\ (\Box m\cdot b_m\rightarrow S_m)\ \mathbf{fi}\). The loop statement is a quantum generalisation of the classical loop while b do S.
Formally, the denotational semantics for quantum programs is defined as a super-operator \(\llbracket S\rrbracket (\cdot )\), assigning to each quantum program S a mapping between partial density operators. As usual, the denotational semantics is defined by induction on the structure of the quantum program:
-
1.
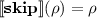 .
. -
2.
 .
. -
3.
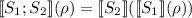 .
. -
4.
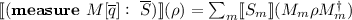 .
. -
5.
 , where \(\bigvee \) stands for the least upper bound of partial density operators according to the Löwner partial order \(\sqsubseteq \).
, where \(\bigvee \) stands for the least upper bound of partial density operators according to the Löwner partial order \(\sqsubseteq \).
The correctness of a quantum program S is expressed by a quantum extension of the Hoare triple \(\{P\}S\{Q\}\), where the precondition P and the postcondition Q are matrices satisfying certain conditions for quantum predicates [24]. The semantics for partial correctness is defined as follows:
for all partial density operators \(\rho \). Here \({\text {tr}}\) is the trace of a matrix. The semantics for total correctness is defined similarly:
We note that they become the same when the quantum program S is terminating, i.e. \({\text {tr}}(\llbracket S\rrbracket (\rho ))={\text {tr}}(\rho )\) for all partial density operators \(\rho \).
The proof system \(\textit{qPD}\) for partial correctness of quantum programs is given in Fig. 1. The soundness and (relative) completeness of \(\textit{qPD}\) is proved in [61]:
Theorem 1
The proof system \(\textit{qPD}\) is sound and (relative) complete for partial correctness of quantum programs.
3 Formalization in Isabelle/HOL
In this section, we describe the formalization of quantum Hoare logic in Isabelle/HOL. Isabelle/HOL [44] is an interactive theorem prover based on higher-order logic. It provides a flexible language in which one can state and prove theorems in all areas of mathematics and computer science. The proofs are checked by the Isabelle kernel according to the rules of higher-order logic, providing a very high level of confidence in the proofs. A standard application of Isabelle/HOL is the formalization of program semantics and Hoare logic. See [43] for a description of the general technique, applied to a very simple classical programming language.
3.1 Preliminaries in Linear Algebra
Our work is based on the linear algebra library developed by Thiemann and Yamada in the AFP entry [58]. We also use some results on the construction of tensor products in another AFP entry by Bentkamp [13].
In these libraries, the type
 of vectors with entries in type
of vectors with entries in type
 is defined as pairs (n, f), where n is a natural number, and f is a function from natural numbers to
is defined as pairs (n, f), where n is a natural number, and f is a function from natural numbers to
 , such that f(i) is undefined when \(i\ge n\). Likewise, the type
, such that f(i) is undefined when \(i\ge n\). Likewise, the type
 of matrices is defined as triples (nr, nc, f), where nr and nc are natural numbers, and f is a function from pairs of natural numbers to
of matrices is defined as triples (nr, nc, f), where nr and nc are natural numbers, and f is a function from pairs of natural numbers to
 , such that f(i, j) is undefined when \(i\ge nr\) or \(j\ge nc\). The terms
, such that f(i, j) is undefined when \(i\ge nr\) or \(j\ge nc\). The terms
 (resp.
(resp.
 ) represent the set of vectors of length n (resp. matrices of dimension \(m\times n\)). In our work, we focus almost exclusively on the case where
) represent the set of vectors of length n (resp. matrices of dimension \(m\times n\)). In our work, we focus almost exclusively on the case where
 is the complex numbers. For this case, existing libraries already define concepts such as the adjoint of a matrix, and the (complex) inner product between two vectors. We further define concepts such as Hermitian and unitary matrices, and prove their basic properties.
is the complex numbers. For this case, existing libraries already define concepts such as the adjoint of a matrix, and the (complex) inner product between two vectors. We further define concepts such as Hermitian and unitary matrices, and prove their basic properties.
A key result in linear algebra that is necessary for our work is the Schur decomposition theorem. It states that any complex \(n\times n\) matrix A can be written in the form \(QUQ^{-1}\), where Q is unitary and U is upper triangular. In particular, if A is normal (that is, if \(AA^{\dag }=A^{\dag }A\)), then A is diagonalizable. A version of the Schur decomposition theorem is formalized in [58], showing that any matrix is similar to an upper-triangular matrix U. However, it does not show that Q can be made unitary. We complete the proof of the full theorem, following the outline of the previous proof.
Next, we define the key concept of positive semi-definite matrices (called positive matrices from now on for simplicity). An \(n\times n\) matrix A is positive if \(v^{\dag }Av\ge 0\) for any vector v. We formalize the basic theory of positive matrices, in particular showing that any positive matrix is Hermitian.
Density operators and partial density operators are then defined as follows:

Next, the Löwner partial order is defined as a partial order on the type
 as follows:
as follows:

A key result that we formalize states that under the Löwner partial order, any non-decreasing sequence of partial density operators has a least upper bound, which is the pointwise limit of the operators when written as \(n\times n\) matrices. This is used to define the infinite sum of matrices, necessary for the semantics of the while loop.
3.2 Syntax and Semantics of Quantum Programs
We now begin with the definition of syntax and semantics of quantum programs. First, we describe how to model states of a quantum program. Recall that each quantum program operates on a fixed set of quantum variables \(q_i\), where each \(q_i\) has dimension \(d_i\). These information can be recorded in a locale [33] as follows:

The total dimension d is given by (here
 denotes the product of a list of natural numbers).
denotes the product of a list of natural numbers).

The (mixed) state of the system is given by a partial density operator with dimension \(d\times d\). Hence, we declare


Next, we define the concept of quantum programs. They are declared as an inductively-defined datatype in Isabelle/HOL, following the grammar given in Sect. 2.

At this stage, we assume that all matrices involved operate on the global state (that is, all of the quantum variables). We will define commands that operate on a subset of quantum variables later. Measurement is defined over any finite number of matrices. Here
 is a measurement with n options,
is a measurement with n options,
 for \(i < n\) are the measurement matrices, and
for \(i < n\) are the measurement matrices, and
 is the command to be executed when the measurement yields result i. Likewise, the first argument to
is the command to be executed when the measurement yields result i. Likewise, the first argument to
 gives measurement matrices, where only the first two values are used.
gives measurement matrices, where only the first two values are used.
Next, we define well-formedness and denotation of quantum programs. The predicate
 expresses the well-formedness condition. For a quantum program to be well-formed, all matrices involved should have the right dimension, the argument to
expresses the well-formedness condition. For a quantum program to be well-formed, all matrices involved should have the right dimension, the argument to
 should be unitary, and the measurements for
should be unitary, and the measurements for
 and
and
 should satisfy the condition \(\sum _i M_i^{\dag }M_i=\mathbb {I}_n\). Denotation is written as
should satisfy the condition \(\sum _i M_i^{\dag }M_i=\mathbb {I}_n\). Denotation is written as
 , defined as in Sect. 2. Both
, defined as in Sect. 2. Both
 and
and
 is defined by induction over the structure of the program. The details are omitted here.
is defined by induction over the structure of the program. The details are omitted here.
3.3 Hoare Triples
In this section, we define the concept of Hoare triples, and state what needs to be proved for soundness and completeness of the deduction system. First, the concept of quantum predicates is defined as follows:

With this, we can give the semantic definition of Hoare triples for partial and total correctness. These definitions are intended for the case where P and Q are quantum predicates, and S is a well-formed program. They define what Hoare triples are valid.


Next, we define what Hoare triples are provable in the \(\textit{qPD}\) system. A Hoare triple for partial correctness is provable (written as
 ) if it can be derived by combining the rules in Fig. 1. This condition can be defined in Isabelle/HOL as an inductive predicate. The definition largely parallels the formulae shown in the figure.
) if it can be derived by combining the rules in Fig. 1. This condition can be defined in Isabelle/HOL as an inductive predicate. The definition largely parallels the formulae shown in the figure.
With these definitions, we can state and prove soundness and completeness of the Hoare rules for partial correctness. Note that the statement for completeness is very simple, seemingly without needing to state “relative to the theory of the field of complex numbers”. This is because we are taking a shallow embedding for predicates, hence any valid statement on complex numbers, in particular positivity of matrices, is in principle available for use in the deduction system (for example, in the assumption to the order rule).


The soundness of the Hoare rules is proved by induction on the predicate \(\vdash _p\), showing that each rule is sound with respect to \(\models _p\). Completeness is proved using the concept of weakest-preconditions, following [61].
3.4 Partial States and Tensor Products
So far in our development, all quantum operations act on the entire global state. However, for the actual applications, we are more interested in operations that act on only a few of the quantum variables. For this, we need to define an extension operator, that takes a matrix on the quantum state for a subset of the variables, and extend it to a matrix on all of the variables. More generally, we need to define tensor products on vectors and matrices defined over disjoint sets of variables. These need to satisfy various consistency properties, in particular commutativity and associativity of the tensor product. Note that directly using the Kronecker product is not enough, as the matrix to be extended may act on any (possibly non-adjacent) subset of variables, and we need to distinguish between all possible cases.
Before presenting the definition, we first review some preliminaries. We make use of existing work in [13], in particular their encode and decode operations, and emulate their definitions of
 and
and
 (used in [13] to convert between tensors represented as a list and matrices). Given a list of dimensions \(d_i\), the encode and decode operations (named
(used in [13] to convert between tensors represented as a list and matrices). Given a list of dimensions \(d_i\), the encode and decode operations (named
 and
and
 ) produce a correspondence between lists of indices \(a_i\) satisfying \(a_i<d_i\) for each \(i<n\), and a natural number less than \(\prod _i d_i\). This works in a way similar to finding the binary representation of a number (in which case all “dimensions” are 2). List operation
) produce a correspondence between lists of indices \(a_i\) satisfying \(a_i<d_i\) for each \(i<n\), and a natural number less than \(\prod _i d_i\). This works in a way similar to finding the binary representation of a number (in which case all “dimensions” are 2). List operation
 constructs the subsequence of
constructs the subsequence of
 containing only the elements at indices in the set
containing only the elements at indices in the set
 .
.
The locale
 extends
extends
 , adding
, adding
 for a subset of quantum variables. Our goal is to define the tensor product of two vectors or matrices over
for a subset of quantum variables. Our goal is to define the tensor product of two vectors or matrices over
 and its complement
and its complement
 , respectively.
, respectively.

First,
 and
and
 are dimensions of variables
are dimensions of variables
 and
and
 :
:

The operation
 (resp.
(resp.
 ) provides the map from the product of
) provides the map from the product of
 to the product of
to the product of
 (resp.
(resp.
 ).
).

With this, tensor products on vectors and matrices are defined as follows (here
 is the product of
is the product of
 ).
).


We prove the basic properties of
 and
and
 , including that they behave correctly with respect to identity, multiplication, adjoint, and trace.
, including that they behave correctly with respect to identity, multiplication, adjoint, and trace.
Extension of matrices is a special case of the tensor product, where the matrix on
 is the identity (here
is the identity (here
 is the product of
is the product of
 ).
).

With
 , we can define “partial” versions of quantum program commands
, we can define “partial” versions of quantum program commands
 ,
,
 and
and
 . They take a set of variables \(\overline{q}\) as an extra parameter, and all matrices involved act on the vector space associated to \(\overline{q}\). These commands are named
. They take a set of variables \(\overline{q}\) as an extra parameter, and all matrices involved act on the vector space associated to \(\overline{q}\). These commands are named
 ,
,
 and
and
 . They are usually used in place of the global commands in actual applications.
. They are usually used in place of the global commands in actual applications.
More generally, we can define the tensor product of vectors and matrices on any two subsets of quantum variables. For this, we define another locale:

To make use of
 to define tensor product in this more general setting, we need to find the relative position of variables
to define tensor product in this more general setting, we need to find the relative position of variables
 within
within
 . This is done using
. This is done using
 , which counts the position of
, which counts the position of
 within
within
 .
.

Finally, the more general tensor products are defined as follows (note since we are now outside the
 locale, we must use qualified names for
locale, we must use qualified names for
 and
and
 , and supply extra arguments for variables in the locale. Here
, and supply extra arguments for variables in the locale. Here
 is the total list of dimensions).
is the total list of dimensions).


The partial extension
 is defined in a similar way as before.
is defined in a similar way as before.

The definitions
 and
and
 satisfy several key consistency properties. In particular, they satisfy associativity of tensor product. For matrices, this is expressed as follows:
satisfy several key consistency properties. In particular, they satisfy associativity of tensor product. For matrices, this is expressed as follows:

Together, these constructions and consistency properties provide a framework in which one can reason about arbitrary tensor product of vectors and matrices, defined on mutually disjoint sets of quantum variables.
3.5 Case Study: Products of Hadamard Matrices
In this section, we illustrate the above framework for tensor product of matrices with an application, to be used in the verification of Grover’s algorithm in the next section.
In many quantum algorithms, we need to deal with the tensor product of an arbitrary number of Hadamard matrices. The Hadamard matrix (denoted
 in Isabelle) is given by:
in Isabelle) is given by:
For example, in Grover’s algorithm, we need to apply the Hadamard transform on each of the first n quantum variables, given by
 . A single Hadamard transform on the i’th quantum variable, extended to a matrix acting on the first n quantum variables, is defined as follows:
. A single Hadamard transform on the i’th quantum variable, extended to a matrix acting on the first n quantum variables, is defined as follows:

The effect of consecutively applying the Hadamard transform on each of the first n quantum variables is equivalent to multiplying the quantum state by
 , where
, where
 is defined as follows.
is defined as follows.

Crucially, this matrix product of extensions of Hadamard matrices must equal the tensor product of Hadamard matrices. That is, with
 defined as
defined as

we have the theorem

The proof of this result is by induction, requiring the use of associativity of tensor product stated above.
4 Verification of Grover’s Algorithm
In this section, we describe our application of the above framework to the verification of Grover’s quantum search algorithm [32]. Quantum search algorithms [18, 32] concern searching an unordered database for an item satisfying some given property. This property is usually specified by an oracle. In a database of N items, where M items satisfy the property, finding an item with the property requires on average O(N / M) calls to the oracle for classical computers. Grover’s algorithm reduces this complexity to \(O(\sqrt{N/M})\).
The basic idea of Grover’s algorithm is rotation. The algorithm starts from an initial state/vector. At every step, it rotates towards the target state/vector for a small angle. As summarised in [18, 19, 42], it can be mathematically described by the following equation [42, Eq. (6.12)]:
where G represents the operator at each step, \(\left| \psi _0 \right\rangle \) is the initial state, \(\theta =2\arccos {\sqrt{(N-M)/N}}\), \(\left| \alpha \right\rangle \) is the bad state (for items not satisfying the property), and \(\left| \beta \right\rangle \) is the good state (for items satisfying the property). Thus when \(\theta \) is very small, i.e., \(M\ll N\), it costs \(O(\sqrt{{N/M}})\) rounds to reach a target state.
Originally, Grover’s algorithm only resolves the case \(M=1\) [32]. It is immediately generalized to the case of known M with the same idea and the case of unknown M with some modifications [18]. After that, the idea is generalized to all invertible quantum processes [19].
The paper [61] uses Grover’s algorithm as the main example illustrating quantum Hoare logic. We largely follow its approach in this paper. See also [42, Chapter 6] for a general introduction.
First, we setup a locale for the inputs to the search problem.

Here n is the number of qubits used to represent the items. That is, we assume \(N=2^n\) items in total. The oracle is represented by the function f, where only its values on inputs less than \(2^n\) are used. The number of items satisfying the property is given by
 .
.
Next, we setup a locale for Grover’s algorithm.

As in [61], we assume \(R=\pi /2\theta - 1/2\) is an integer. This implies that the quantum algorithm succeeds with probability 1. This condition holds, for example, for all N, M where \(N=4M\). Since we did not formalize quantum states with infinite dimension, we replace the loop counter, which is infinite dimensional in [61], with a variable of dimension \(K > R\). We also remove the control variable for the oracle used in [61]. Overall, our quantum state consists of n variables of dimension 2 for representing the items, and one variable of dimension K for the loop counter.
We now present the quantum program to be verified. First, the operation that performs the Hadamard transform on each of the first n variables is defined by induction as follows.

Here
 denotes the tensor product of a matrix on the first n variables (of dimension \(2^n\times 2^n\)) and a matrix on the loop variable (of dimension \(K\times K\)). Executing this program is equivalent to multiplying the quantum state corresponding to the first n variables by \(H^{\otimes n}\), as shown in Sect. 3.5.
denotes the tensor product of a matrix on the first n variables (of dimension \(2^n\times 2^n\)) and a matrix on the loop variable (of dimension \(K\times K\)). Executing this program is equivalent to multiplying the quantum state corresponding to the first n variables by \(H^{\otimes n}\), as shown in Sect. 3.5.
The body of the loop is given by:

where each of the three matrices
 ,
,
 and
and
 can be defined directly.
can be defined directly.

Finally, the Grover’s algorithm is as follows. Since we do not have initialization, we skip initialization to zero at the beginning and instead assume that the state begins in the zero state in the precondition.

where the measurements for the while loop and at the end of the algorithm are:

We can now state the final correctness result. Let
 be the outer product \(vv^{\dag }\), and
be the outer product \(vv^{\dag }\), and
 be \(|k\rangle \langle k|\), where \(|k\rangle \) is the k’th basis vector on the vector space corresponding to the loop variable. Let
be \(|k\rangle \langle k|\), where \(|k\rangle \) is the k’th basis vector on the vector space corresponding to the loop variable. Let
 and
and
 be given as follows:
be given as follows:

Then, the (partial) correctness of Grover’s algorithm is specified by the following Hoare triple.

We now briefly outline the proof strategy. Following the definition of
 , the proof of the above Hoare triple is divided into three main parts, for the initialization by Hadamard matrices, for the while loop, and for the measurement at the end.
, the proof of the above Hoare triple is divided into three main parts, for the initialization by Hadamard matrices, for the while loop, and for the measurement at the end.
In each part, assertions are first inserted around commands according to the Hoare rules to form smaller Hoare triples. In particular, the precondition of the while loop part is exactly the invariant of the loop. Moreover, it has to be shown that these assertions satisfy the conditions for being quantum predicates, which involve computing their dimension, showing positiveness, and being bounded by the identity matrix under the Löwner order. Then, these Hoare triples are derived using our deduction system. Before combining them together, we have to show that the postcondition of each command is equal to the precondition of the later one. After that, the three main Hoare triples can be obtained by combining these smaller ones.
After the derivation of the three Hoare triples above, we prove the Löwner order between the postcondition of each triple and the precondition of the following triple. Afterwards, the triples can be combined into the Hoare triple below:

Finally, the (partial) correctness of Grover’s algorithm follows from the soundness of our deduction system.
5 Discussion
Compared to classical programs, reasoning about quantum programs is more difficult in every respect. Instead of discrete mathematics in the classical case, even the simplest reasoning about quantum programs involves complex numbers, unitary and positivity properties of matrices, and the tensor product. Hence, it is to be expected that formal verification of quantum Hoare logic and quantum algorithms will take much more effort. In this section, we describe some of the automation that we built to simplify the manual proof, and give some statistics concerning the amount of effort involved in the formalization.
5.1 Automatic Proof of Identities in Linear Algebra
During the formalization process, we make extensive use of ring properties of matrices. These include commutativity and associativity of addition, associativity of multiplication, and distributivity. Compared to the usual case of numbers, applying these rules for matrices is more difficult in Isabelle/HOL, since they involve extra conditions on dimensions of matrices. For example, the rule for commutativity of addition of matrices is stated as:

These extra conditions make the rules difficult to apply for standard Isabelle automation. For our work, we implemented our own tactic handling these rules. In addition to the ring properties, we also frequently need to use the cyclic property of trace (e.g. \({\text {tr}}(ABC)={\text {tr}}(BCA)\)), as well as the properties of adjoint (\((AB)^{\dag }=B^{\dag }A^{\dag }\) and \(A^{\dag \dag }=A\)). For simplicity, we restrict to identities involving only \(n\times n\) matrices, where n is a parameter given to the tactic.
The tactic is designed to prove equality between two expressions. It works by computing the normal form of the expressions – using ring identities and identities for the adjoint to fully expand the expression into polynomial form. To handle the trace, the expression \({\text {tr}}(A_1\cdots A_n)\) is normalized to put the \(A_i\) that is the largest according to Isabelle’s internal term order last. All dimension assumptions are collected and reduced (for example, the assumption
 is reduced to
is reduced to
 ).
).
Overall, the resulting tactic is used 80 times in our proofs. Below, we list some of the more complicated equations resolved by the tactic. The tactic reduces the goal to dimensional constraints on the atomic matrices (e.g.
 and
and
 in the first case).
in the first case).
5.2 Statistics
Overall, the formalization consists of about 11,500 lines of Isabelle theories. An old version of the proof is developed on and off for two years. The current version is re-developed, using some ideas from the old version. The development of the new version took about 5 person months. Detailed breakdown of number of lines for different parts of the proof is given in the following table.
Description | Files | Number of lines |
|---|---|---|
Preliminaries |
| 4197 |
Semantics |
| 1110 |
Hoare logic |
| 1417 |
Tensor product |
| 1664 |
Grover’s algorithm |
| 3184 |
Total | 11572 |
In particular, with the verification framework in place, the proof of correctness for Grover’s search algorithm takes just over 3000 lines. While this shows that it is realistic to use the current framework to verify more complicated algorithms such as Shor’s algorithm, it is clear that more automation is needed to enable verification on a larger scale.
6 Related Work
The closest work to our research is Robert Rand’s implementation of \(\mathcal {Q}\)wire in Coq [49, 50]. \(\mathcal {Q}\)wire [47] is a language for describing quantum circuits. In this model, quantum algorithms are implemented by connecting together quantum gates, each with a fixed number of bit/qubit inputs and outputs. How the gates are connected is determined by a classical host language, allowing classical control of quantum computation. The work [49] defines the semantics of \(\mathcal {Q}\)wire in Coq, and uses it to verify quantum teleportation, Deutsch’s algorithm, and an example on multiple coin flips to illustrate applicability to a family of circuits. In this framework, program verification proceeds directly from the semantics, without defining a Hoare logic. As in our work, it is necessary to solve the problem of how to define extensions of an operation on a few qubits to the global state. The approach taken in [49] is to use the usual Kronecker product, augmented either by the use of swaps between qubits, or by inserting identity matrices at strategic positions in the Kronecker product.
There are two main differences between [49] and our work. First, quantum algorithms are expressed using quantum circuits in [49], while we use quantum programs with while loops. Models based on quantum circuits have the advantage of being concrete, and indeed most of the earlier quantum algorithms can be expressed directly in terms of circuits. However, several new quantum algorithms can be more properly expressed by while loops, e.g. quantum walks with absorbing boundaries, quantum Bernoulli factory (for random number generation), HHL for systems of linear equations and qPCA (Principal Component Analysis). Second, we formalized a Hoare logic while [49] uses denotational semantics directly. As in verification of classical programs, Hoare logic encapsulates standard forms of argument for dealing with each program construct. Moreover, the rules for QHL is in weakest-precondition form, allowing the possibility of automated verification condition generation after specifying the loop invariants (although this is not used in the present paper).
Besides Rand’s work, quite a few verification tools have been developed for quantum communication protocols. For example, Nagarajan and Gay [41] modeled the BB84 protocol [12] and verified its correctness. Ardeshir-Larijani et al. [7, 8] presented a tool for verification of quantum protocols through equivalence checking. Existing tools, such as PRISM [37] and Coq, are employed to develop verification tools for quantum protocols [17, 29]. Furthermore, an automatic tool called Quantum Model-Checker (QMC) is developed [28, 46].
Recently, several specific techniques have been proposed to algorithmically check properties of quantum programs. In [63], the Sharir-Pnueli-Hart method for verifying probabilistic programs [54] has been generalised to quantum programs by exploiting the Schrödinger-Heisenberg duality between quantum states and observables. Termination analysis of nondeterministic and concurrent quantum programs [38] was carried out based on reachability analysis [64]. Invariants can be generated at some steps in quantum programs for debugging and verification of correctness [62]. But up to now no tools are available that implements these techniques. Another Hoare-style logic for quantum programs was proposed in [36], but without (relative) completeness.
Interactive theorem proving has made significant progress in the formal verification of classical programs and systems. Here, we focus on listing some tools designed for special kinds of systems. EasyCrypt [10, 11] is an interactive framework for verifying the security of cryptographic constructs in the computational model. It is developed based on a probabilistic relational Hoare logic to support machine-checked construction and verification of game-based proofs. Recently, verification of hybrid systems via interactive theorem proving has also been studied. KeYmaera X [26] is a theorem prover implementing differential dynamic logic (\(d\mathcal {L}\)) [48], for the verification of hybrid programs. In [60], a prover has been implemented in Isabelle/HOL for reasoning about hybrid processes described using hybrid CSP [34].
Our work is based on existing formalization of matrices and tensors in Isabelle/HOL. In [59] (with corresponding AFP entry [58]), Thiemann et al. developed the matrix library that we use here. In [14] (with corresponding AFP entry [13]), Bentkamp et al. developed tensor analysis based on the above work, in an effort to formalize an expressivity result of deep learning algorithms.
7 Conclusion
We formalized quantum Hoare logic in Isabelle/HOL, and verified the soundness and completeness of the deduction system for partial correctness. Using this deduction system, we verified the correctness of Grover’s search algorithm. This is, to our best knowledge, the first formalization of a Hoare logic for quantum programs in an interactive theorem prover.
This work is intended to be the first step of a larger project to construct a framework under which one can efficiently verify the correctness of complex quantum programs and systems. In this paper, our focus is on formalizing the mathematical machinery to specify the semantics of quantum programs, and prove the correctness of quantum Hoare logic. To verify more complicated programs efficiently, better automation is needed at every stage of the proof. We have already begun with some automation for proving identities in linear algebra. In the future, we plan to add to it automation facility for handling matrix computations, tensor products, positivity of matrices, etc., all linked together by a verification condition generator.
Another direction of future work is to formalize various extensions of quantum Hoare logic, to deal with classical control, recursion, concurrency, etc., with the eventual goal of being able to verify not only sequential programs, but also concurrent programs and communication systems.
Notes
- 1.
Available online at https://www.isa-afp.org/entries/QHLProver.html.
References
IBM Q devices and simulators. https://www.research.ibm.com/ibm-q/technology/devices/
IBM Q experience community. https://quantumexperience.ng.bluemix.net/qx/community?channel=papers&category=ibm
A preview of Bristlecone, Google’s new quantum processor. https://ai.googleblog.com/2018/03/a-preview-of-bristlecone-googles-new.html
Qiskit Aer. https://qiskit.org/aer, https://medium.com/qiskit/qiskit-aer-d09d0fac7759
Unsupervised machine learning on Rigetti 19Q with Forest 1.2. https://medium.com/rigetti/unsupervised-machine-learning-on-rigetti-19q-with-forest-1-2-39021339699
Ardeshir-Larijani, E., Gay, S.J., Nagarajan, R.: Equivalence checking of quantum protocols. In: Piterman, N., Smolka, S.A. (eds.) TACAS 2013. LNCS, vol. 7795, pp. 478–492. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36742-7_33
Ardeshir-Larijani, E., Gay, S.J., Nagarajan, R.: Verification of concurrent quantum protocols by equivalence checking. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014. LNCS, vol. 8413, pp. 500–514. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54862-8_42
Baltag, A., Smets, S.: LQP: the dynamic logic of quantum information. Math. Struct. Comput. Sci. 16(3), 491–525 (2006)
Barthe, G., Dupressoir, F., Grégoire, B., Kunz, C., Schmidt, B., Strub, P.-Y.: EasyCrypt: a tutorial. In: Aldini, A., Lopez, J., Martinelli, F. (eds.) FOSAD 2012-2013. LNCS, vol. 8604, pp. 146–166. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10082-1_6
Barthe, G., Grégoire, B., Heraud, S., Béguelin, S.Z.: Computer-aided security proofs for the working cryptographer. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 71–90. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_5
Bennett, C.H., Brassard, G.: Quantum cryptography: public key distribution and coin tossing. In: International Conference on Computers, Systems and Signal Processing, pp. 175–179. IEEE (1984)
Bentkamp, A.: Expressiveness of deep learning. Archive of Formal Proofs, Formal proof development, November 2016. http://isa-afp.org/entries/Deep_Learning.html
Bentkamp, A., Blanchette, J.C., Klakow, D.: A formal proof of the expressiveness of deep learning. In: Interactive Theorem Proving - 8th International Conference, ITP 2017, Brasília, Brazil, September 26–29, 2017, Proceedings, pp. 46–64 (2017). https://dblp.org/rec/bib/conf/itp/BentkampBK17
Bertot, Y., Castran, P.: Interactive Theorem Proving and Program Development: Coq’Art The Calculus of Inductive Constructions, 1st edn. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-662-07964-5
Bettelli, S., Calarco, T., Serafini, L.: Toward an architecture for quantum programming. Eur. Phys. J. D 25, 181–200 (2003)
Boender, J., Kammüller, F., Nagarajan, R.: Formalization of quantum protocols using Coq. In: QPL 2015 (2015)
Boyer, M., Brassard, G., Høyer, P., Tapp, A.: Tight bounds on quantum searching. Fortschr. der Phys. Prog. Phys. 46(4–5), 493–505 (1998)
Brassard, G., Hoyer, P., Mosca, M., Tapp, A.: Quantum amplitude amplification and estimation. Contemp. Math. 305, 53–74 (2002)
Brunet, O., Jorrand, P.: Dynamic quantum logic for quantum programs. Int. J. Quantum Inf. 2, 45–54 (2004)
Chadha, R., Mateus, P., Sernadas, A.: Reasoning about imperative quantum programs. Electron. Notes Theoret. Comput. Sci. 158, 19–39 (2006)
Cross, A.W., Bishop, L.S., Smolin, J.A., Gambetta, J.M.: Open quantum assembly language. arXiv preprint arXiv:1707.03429 (2017)
Debnath, S., Linke, N.M., Figgatt, C., Landsman, K.A., Wright, K., Monroe, C.: Demonstration of a small programmable quantum computer with atomic qubits. Nature 536(7614), 63–66 (2016)
D’Hondt, E., Panangaden, P.: Quantum weakest preconditions. Math. Struct. Comput. Sci. 16, 429–451 (2006)
Wecker, D., Svore, K.: Liqui\(|\rangle \): a software design architecture and domain-specific language for quantum computing. (http://research.microsoft.com/en-us/projects/liquid/)
Fulton, N., Mitsch, S., Quesel, J.-D., Völp, M., Platzer, A.: KeYmaera X: an axiomatic tactical theorem prover for hybrid systems. In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 527–538. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_36
Gay, S.: Quantum programming languages: survey and bibliography. Math. Struct. Comput. Sci. 16, 581–600 (2006)
Gay, S.J., Nagarajan, R., Papanikolaou, N.: QMC: a model checker for quantum systems. In: Gupta, A., Malik, S. (eds.) CAV 2008. LNCS, vol. 5123, pp. 543–547. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70545-1_51
Gay, S.J., Nagarajan, R., Papanikolaou, N.: Probabilistic model-checking of quantum protocols. In: DCM Proceedings of International Workshop on Developments in Computational Models, p. 504007. IEEE (2005). https://arxiv.org/abs/quant-ph/0504007
Google AI Quantum team. https://github.com/quantumlib/Cirq
Green, A.S., Lumsdaine, P.L., Ross, N.J., Selinger, P., Valiron, B.: Quipper: a scalable quantum programming language. In: Proceedings of the 34th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2013, pp. 333–342. ACM, New York (2013)
Grover, L.K.: A fast quantum mechanical algorithm for database search. In: Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing, STOC 1996, pp. 212–219. ACM, New York (1996)
Haftmann, F., Wenzel, M.: Local theory specifications in isabelle/isar. In: Berardi, S., Damiani, F., de’Liguoro, U. (eds.) TYPES 2008. LNCS, vol. 5497, pp. 153–168. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02444-3_10
He, J.: From CSP to hybrid systems. In: A Classical Mind, Essays in Honour of C.A.R. Hoare, pp. 171–189. Prentice Hall International (UK) Ltd. (1994)
JavadiAbhari, A., et al.: ScaffCC: scalable compilation and analysis of quantum programs. In: Parallel Computing, vol. 45, pp. 3–17 (2015)
Kakutani, Y.: A logic for formal verification of quantum programs. In: Datta, A. (ed.) ASIAN 2009. LNCS, vol. 5913, pp. 79–93. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10622-4_7
Kwiatkowska, M., Norman, G., Parker, P.: Probabilistic symbolic model-checking with PRISM: a hybrid approach. Int. J. Softw. Tools Technol. Transf. 6, 128–142 (2004)
Li, Y., Yu, N., Ying, M.: Termination of nondeterministic quantum programs. Acta Informatica 51, 1–24 (2014)
Liu, S., et al.: \(Q|SI\rangle \): a quantum programming environment. In: Jones, C., Wang, J., Zhan, N. (eds.) Symposium on Real-Time and Hybrid Systems. LNCS, vol. 11180, pp. 133–164. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-01461-2_8
Liu, X., Kubiatowicz, J.: Chisel-Q: designing quantum circuits with a scala embedded language. In: 2013 IEEE 31st International Conference on Computer Design (ICCD), pp. 427–434. IEEE (2013)
Nagarajan, R., Gay, S.: Formal verification of quantum protocols (2002). arXiv: quant-ph/0203086
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information: 10th Anniversary Edition, 10th edn. Cambridge University Press, New York (2011)
Nipkow, T., Klein, G.: Concrete Semantics: With Isabelle/HOL. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10542-0
Nipkow, T., Wenzel, M., Paulson, L.C. (eds.): Isabelle/HOL: A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
Ömer, B.: Structured quantum programming. Ph.D. thesis, Technical University of Vienna (2003)
Papanikolaou, N.: Model checking quantum protocols. Ph.D. thesis, Department of Computer Science, University of Warwick (2008)
Paykin, J., Rand, R., Zdancewic, S.: QWIRE: a core language for quantum circuits. In: Proceedings of 44th ACM Symposium on Principles of Programming Languages (POPL), pp. 846–858 (2017)
Platzer, A.: A complete uniform substitution calculus for differential dynamic logic. J. Autom. Reas. 59(2), 219–265 (2017)
Rand, R.: Formally verified quantum programming. Ph.D. thesis, University of Pennsylvania (2018)
Robert Rand, J.P., Zdancewic, S.: QWIRE practice: formal verification of quantum circuits in coq. In: Quantum Physics and Logic (2017)
Sanders, J.W., Zuliani, P.: Quantum programming. In: Backhouse, R., Oliveira, J.N. (eds.) MPC 2000. LNCS, vol. 1837, pp. 80–99. Springer, Heidelberg (2000). https://doi.org/10.1007/10722010_6
Selinger, P.: A brief survey of quantum programming languages. In: Kameyama, Y., Stuckey, P.J. (eds.) FLOPS 2004. LNCS, vol. 2998, pp. 1–6. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24754-8_1
Selinger, P.: Towards a quantum programming language. Math. Struct. Comput. Sci. 14(4), 527–586 (2004)
Sharir, M., Pnueli, A., Hart, S.: Verification of probabilistic programs. SIAM J. Comput. 13, 292–314 (1984)
Smith, R.S., Curtis, M.J., Zeng, W.J.: A practical quantum instruction set architecture. arXiv preprint arXiv:1608.03355 (2016)
Steiger, D.S., Häner, T., Troyer, M.: ProjectQ: an open source software framework for quantum computing. Quantum 2, 49 (2018)
Svore, K., et al.: Q#: enabling scalable quantum computing and development with a high-level DSL. In: Proceedings of the Real World Domain Specific Languages Workshop 2018, pp. 7:1–7:10 (2018)
Thiemann, R., Yamada, A.: Matrices, Jordan normal forms, and spectral radius theory. Archive of Formal Proofs, Formal proof development, August 2015. http://isa-afp.org/entries/Jordan_Normal_Form.html
Thiemann, R., Yamada, A.: Formalizing Jordan normal forms in Isabelle/HOL. In: Proceedings of the 5th ACM SIGPLAN Conference on Certified Programs and Proofs, CPP 2016, pp. 88–99. ACM, New York (2016)
Wang, S., Zhan, N., Zou, L.: An improved HHL prover: an interactive theorem prover for hybrid systems. In: Butler, M., Conchon, S., Zaïdi, F. (eds.) ICFEM 2015. LNCS, vol. 9407, pp. 382–399. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-25423-4_25
Ying, M.: Floyd-Hoare logic for quantum programs. ACM Trans. Programm. Lang. Syst. 33(6), 19:1–19:49 (2011)
Ying, M., Ying, S., Wu, X.: Invariants of quantum programs: characterisations and generation. In: Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages, POPL 2017, pp. 818–832 (2017)
Ying, M., Yu, N., Feng, Y., Duan, R.: Verification of quantum programs. Sci. Comput. Programm. 78, 1679–1700 (2013)
Ying, S., Feng, Y., Yu, N., Ying, M.: Reachability probabilities of quantum Markov chains. In: D’Argenio, P.R., Melgratti, H. (eds.) CONCUR 2013. LNCS, vol. 8052, pp. 334–348. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40184-8_24
Acknowledgements
This research is supported through grants by NSFC under grant No. 61625206, 61732001. Bohua Zhan is supported by CAS Pioneer Hundred Talents Program under grant No. Y9RC585036. Yangjia Li is supported by NSFC grant No. 61872342.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Liu, J. et al. (2019). Formal Verification of Quantum Algorithms Using Quantum Hoare Logic. In: Dillig, I., Tasiran, S. (eds) Computer Aided Verification. CAV 2019. Lecture Notes in Computer Science(), vol 11562. Springer, Cham. https://doi.org/10.1007/978-3-030-25543-5_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-25543-5_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25542-8
Online ISBN: 978-3-030-25543-5
eBook Packages: Computer ScienceComputer Science (R0)






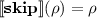 .
. .
.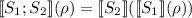 .
.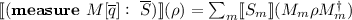 .
. , where
, where 



