Abstract
Quasi-Newton methods are popular gradient-based optimization methods that can achieve rapid convergence using only first-order derivatives. However, the choice of the initial Hessian matrix upon which quasi-Newton updates are applied is an important factor that can significantly affect the performance of the method. This fact is especially true for limited-memory variants, which are widely used for large-scale problems where only a small number of updates are applied in order to minimize the memory footprint. In this paper, we introduce both a scalar and a sparse diagonal Hessian initialization framework, and we investigate its effect on the restricted Broyden-class of quasi-Newton methods. Our implementation in PETSc/TAO allows us to switch between different Broyden class methods and Hessian initializations at runtime, enabling us to quickly perform parameter studies and identify the best choices. The results indicate that a sparse Hessian initialization based on the diagonalization of the BFGS formula significantly improves the base BFGS methods and that other parameter combinations in the Broyden class may offer competitive performance.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Quasi-Newton methods are a variation of Newton’s method where the Jacobian or the Hessian is approximated using the secant condition. Since their inception in the late-1950s by Davidon [10, 11] and Fletcher and Powell [19], quasi-Newton methods have been widely used in solving nonlinear systems of equations, especially in optimization applications. For a comprehensive review of these methods, see Dennis and Moré [15] and Nocedal and Wright [32].
Our interest in quasi-Newton methods is motivated by the computational cost and difficulty in calculating exact Hessians for large-scale or partial differential equation (PDE)-constrained optimization problems. In particular, for reduced-space methods for PDE-constrained problems where the PDE constraint is eliminated via the implicit function theorem, constructing exact second-order information at each iteration requires as many adjoint solutions as the number of optimization variables [33]. Computing Hessian-vector products without computing the Hessian itself can be computationally cheaper [3, 24, 28], but the matrix-free nature of this approach poses additional difficulties in preconditioning the systems [13, 14].
Limited-memory quasi-Newton methods circumvent these issues by directly constructing approximations to the inverse Hessian using only first-order information; however, they also typically exhibit slower convergence than truncated-Newton methods [27]. Our goal is to investigate the so-called restricted Broyden class of quasi-Newton methods and develop new strategies to accelerate their convergence in order to minimize the number of function and gradient evaluations.
For a given bound-constrained optimization problem,
with \(f: \mathbb {R}^{n} \rightarrow \mathbb {R}\) as the objective function and \(g_k = \nabla f(x_k)\) as its gradient at the \(\text {k}^\text {th}\) iteration, Broyden’s method [4] constructs the approximate Hessian with the update formula,
where \(s_k = x_{k+1} - x_k\), \(y_k = g_{k+1} - g_k\),
and \(\phi \) is a scalar parameter. In the active-set approach, the inverse of this approximate Hessian is applied to the negative gradient and a projected line search is performed along the resulting step direction. The process repeats until the projected gradient norm is reduced below a prescribed tolerance or an iteration limit is reached. Many methods are available for estimating the index set of active variables [2, 7, 26, 31]; however, our focus in the present work is the quasi-Newton approximation.
Methods in the Broyden class are defined by the different scalar values of the parameter \(\phi \). The restricted Broyden class, in particular, limits the choice of \(\phi \) to the range [0, 1], which guarantees that the updates are symmetric positive-definite provided that \(s_k^T y_k > 0\). The most well-known methods of this type are the Broyden-Fletcher-Goldfarb-Shanno (BFGS) [5, 18, 22, 34] and Davidon-Fletcher-Powell (DFP) [11] methods, which are recovered with \(\phi =0\) and \(\phi =1\), respectively. The restricted Broyden-class formulation in (2) can also be rewritten as a convex combination of the BFGS and DFP methods, such that
The limited-memory variant of the restricted Broyden update takes the form
where \(B_0\) is an initial Hessian, \(m = \{\max (0, k-M+1) \ldots k\}\) is the index set for the sequence of quasi-Newton updates, and M is the maximum number of updates to be applied to the initial Hessian (i.e.: the “memory” size). Since Newton-type optimization algorithms seek to apply the inverse of the Hessian matrix to the gradient, the Sherman-Morrison-Woodbury formula [25] is utilized to update an approximation to the inverse of the Hessian matrix directly, such that
where
and
In practice, the limited-memory formula is often implemented in a matrix-free fashion where only M of the \((s_k, y_k)\) vector pairs are stored and the action of the approximate Hessian – the product between the approximate inverse of the Hessian and a given vector – is defined by multiplying (5) with a vector. With this approach, the \(H_m\) terms inside the summation recurse into their own quasi-Newton formulas and are implemented with nested loops. Some special cases, such as the BFGS formula, can be unrolled into two independent loops that minimize the number of operations [8]. For a more comprehensive look at this approach, we refer the reader to [17].
In this paper, we investigate a framework for constructing scalar or sparse diagonal choices for the initial Hessian \(B_0\) in (4). Our software implementation of (5) including the sparse Hessian initialization is available as part of PETSc/TAO Version 3.10 [1, 12]. We leverage PETSc extensibility to explore values of \(\phi \) and other parameters associated with the initial Hessian at runtime to study the convergence and performance of our approach on the complete set of 119 bound-constrained CUTEst test problems [23].
2 Hessian Initialization
The choice of a good initial Hessian \(H_0\) in limited-memory quasi-Newton methods is critically important to the quality of the Hessian approximation. It has been well documented that the scaling of the approximate Hessian depends on this choice and dramatically affects convergence [21, 29]. Our goal is to develop a modular framework that can generate effective initializations that preserve the symmetric positive-definite property of the restricted Broyden class methods and are easily invertible as part of efficient matrix-free applications of limited-memory quasi-Newton formulas (e.g., two-loop L-BFGS inversion [8]). To that end, we construct our initial Hessians in scalar and sparse diagonal forms, the latter of which is based on the restricted Broyden-class formula.
The first step is to address the starting point \(x_0\) when there is no accumulated information with which to construct either scalar or diagonal initializations. It is common for the matrix at iteration 0 to be set to a multiple \(B_0 = \rho _0 I\) of the identity that promotes acceptance of the unit-step length by the line search; however, no good general strategy exists for choosing a suitable value for \(\rho _0\). Gilbert and Lemaréchal [20] proposed \(\rho _0 = 2\varDelta /||g_0||_2^2\), where \(\varDelta \) is a user-supplied parameter that represents the expected decrease in f(x) at the first iteration. We use

which has proven to be an effective choice across our numerical experiments and eliminates a user-defined parameter from the algorithm. This choice also appears to be related to more recent investigations into scaled gradient descent steps with an a priori estimation of the local minimum [9], with \(f(x^*) = 0\) where \(x^*\) is the minimizer. Both the scalar and sparse diagonal \(B_0\) constructions we introduce below leverage this initial scalar choice.
2.1 Scalar Formulation
Scalar Hessian initializations restrict the estimate to a positive scalar multiple of the identity matrix, such that \(B_0 = \rho _k I\) during iteration k. For BFGS matrices, a common and well-understood choice has been
which is an approximation to an eigenvalue of \(\nabla ^2 f(x_k)\) [32].
Our scalar construction begins with the recognition that (7) is the positive solution to the scalar minimization problem

which is also a least-squares solution to the secant equation \(B_0^{-1}y_k = s_k\) with \(B_0=\rho I\) [6]. We then introduce a new parameter \(\alpha \in [0, 1]\) such that \(B_0=\rho ^{2\alpha -1}I\) and we solve the modified least-squares problem,

After constructing the optimality conditions and solving for \(\rho \), we arrive at the following values:
-
1.
If \(\alpha = 0\), then
$$\begin{aligned} \rho _k = \frac{y_k^T s_k}{s_k^T s_k} \end{aligned}$$ -
2.
If
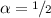 , then $$\begin{aligned}\rho _k = \sqrt{\frac{y_k^T y_k}{s_k^T s_k}} \end{aligned}$$
, then $$\begin{aligned}\rho _k = \sqrt{\frac{y_k^T y_k}{s_k^T s_k}} \end{aligned}$$ -
3.
If \(\alpha = 1\), then
$$\begin{aligned} \rho _k = \frac{y_k^T y_k}{y_k^T s_k} \end{aligned}$$Note: this value corresponds to the commonly used eigenvalue estimate in (7).
-
4.
Otherwise, \(\rho _k\) is the positive root of the quadratic equation,
$$\begin{aligned} \alpha (y_k^T y_k)\rho ^2 - (2\alpha -1)(y_k^Ts_k)\rho + (\alpha -1)(s_k^Ts_k) = 0. \end{aligned}$$
Since \(s_k^T s_k\) and \(y_k^T y_k\) cannot be negative and are zero only for a zero step length, the scalar Hessian approximation preserves symmetric positive
 definiteness for any \((s_k, y_k)\) update that satisfies the Wolfe conditions.
definiteness for any \((s_k, y_k)\) update that satisfies the Wolfe conditions.
2.2 Sparse Diagonal Formulation
The sparse diagonal formulation constructs an initial Hessian as a diagonal matrix, \(B_0 = \text {diag}(b_k)\), at iteration k defined by and stored as the vector of diagonal entries \(b_k\). Specifically, we construct this diagonal vector using the full-memory restricted Broyden formula in (2), such that
This expression is the expanded version of the convex combination notation in (3), where \((1-\theta )\) and \(\theta \) correspond to the BFGS and DFP components, respectively. Since we compute only diagonal entries, all matrix-vector products have been replaced by Hadamard products with the previous diagonal. As in Broyden’s method, \(\theta =0\) corresponds to a pure BFGS formulation, while \(\theta =1\) recovers DFP.
This initialization is a full-memory approach; the diagonal entries of \(B_0\) are explicitly stored in \(b_k\) and updated with every accepted new iterate. Consequently, \(B_0\) contains information from all iterates traversed in the optimization instead of only the last M iterates stored for the limited-memory formula, but without the large memory cost of storing dense matrices.
Gilbert and Lemaréchal have explored a similar initial Hessian using diagonalizations of the BFGS formula only [20] and reported the need to rescale the diagonal to account for the inability to rapidly modify it in large steps. To that end, we redefine the initial Hessian as \(B_0 = \sigma _k^{2\alpha -1}\text {diag}(b_k)\) and compute the rescaling factor \(\sigma _k\) by seeking the least-squares solution to the secant equation, \(B_0^{-1}y_k = s_k\), such that

Note that the expression inside the \(l_2\)-norm is equivalent to the secant equation in residual form, restructured so that the solution can be more easily expressed in the form of quadratic roots. The solution yields the following values:
-
1.
If \(\alpha = 0\), then
$$\begin{aligned} \sigma _k = \frac{y_k^T s_k}{s_k^T (b_k \circ s_k)}. \end{aligned}$$ -
2.
If
 , then $$\begin{aligned} \sigma _k = \sqrt{\frac{y_k^T (b_k^{-1} \circ y_k)}{s_k^T (b_k \circ s_k)}}. \end{aligned}$$
, then $$\begin{aligned} \sigma _k = \sqrt{\frac{y_k^T (b_k^{-1} \circ y_k)}{s_k^T (b_k \circ s_k)}}. \end{aligned}$$ -
3.
If \(\alpha = 1\), then
$$\begin{aligned} \sigma _k = \frac{y_k^T (b_k^{-1} \circ y_k)}{y_k^T s_k}. \end{aligned}$$ -
4.
Otherwise, \(\sigma _k\) is the positive root of the quadratic equation,
$$\begin{aligned} \alpha \left[ y_k^T (b_k^{-1} \circ y_k)\right] \sigma ^2 - (2\alpha -1)(y_k^T s_k)\sigma + (\alpha -1)\left[ s_k^T(b_k \circ s_k)\right] = 0. \end{aligned}$$
As with the scalar initialization, the sparse diagonal \(B_0\) remains positive definite for any \((s_k, y_k)\) pair that satisfies the Wolfe conditions. Nonetheless, we have encountered cases where numerical problems surface in finite precision arithmetic. Therefore, we safeguard all the methods by checking whether the denominators are equal to zero and setting their value to a small constant, \(10^{-8}\), if so.
3 Numerical Studies
We now investigate the numerical performance of our proposed scalar and sparse Hessian initializations and study the parameter space of the user-controlled scalar factors to determine useful recommendations. Our quasi-Newton implementation in PETSc/TAO utilizes an active-set estimation based on the work of Bertsekas [2] and is discussed in further detail in the TAO manual [12]. The step direction is globalized via a projected Moré-Thuente line search [30], which is capable of taking step lengths greater than 1.
Our numerical experiments are based on 119 bound-constrained problems from the CUTEst test set [23], covering a diverse range of problems from 2 to \(10^5\) variables. In all cases presented in this section, we set the quasi-Newton memory size to \(M=5\) updates, limit the maximum number of iterations to 1, 000, and require convergence to an absolute tolerance of \(||g^*||_2 \le 10^{-6}\).
Performance profiles are constructed by using the methodology proposed by Dolan and Moré [16]. For a given CUTEst problem \(p \in \mathcal {P}\) and solver configuration \(c \in \mathcal {C}\), we define a cost measure
and normalize it by the best configuration for each problem, such that
Performance of each configuration is then given by
which describes the probability for configuration \(c \in \mathcal {C}\) to have a cost ratio \(r_{p,c}\) that is within a factor of \(\pi \in \mathbb {R}^{}\) of the best configuration.
We begin our analysis with a sweep through the \(\phi \) parameter space in the restricted Broyden updates in Fig. 1. For this study we turn off all Hessian initialization (i.e., \(H_0 = I\)) and investigate only the relative performances of the raw Broyden-class methods. Note that \(\phi =0\) and \(\phi =1\) are included, which correspond to the BFGS and DFP methods, respectively. The results indicate that \(\phi \) values in range (0, 0.5] produce Hessian approximations that outperform BFGS, with \(\phi =0.5\) yielding the best performance.
For the next study, we used the L-BFGS method as the basis for analyzing the effects of different \(H_0\) initialization methods. We start with the scalar \(H_0\) in Fig. 2a and investigate the effect of the \(\alpha \) parameter. Here, setting \(\alpha =1.0\) recovers the widely used  factor that approximates an eigenvalue of \(\nabla ^2 f(x_k)^{-1}\). As expected, this choice yields the best scaled Hessian approximation and the lowest number of function evaluations on most problems. Surprisingly, however, the results indicate that \(\alpha =0.75\) remains competitive in cost, while converging on two additional test problems.
factor that approximates an eigenvalue of \(\nabla ^2 f(x_k)^{-1}\). As expected, this choice yields the best scaled Hessian approximation and the lowest number of function evaluations on most problems. Surprisingly, however, the results indicate that \(\alpha =0.75\) remains competitive in cost, while converging on two additional test problems.
Figure 2b shows the relative performances of the sparse diagonal \(H_0\) initialization. For this study, we fix the rescaling parameter to \(\alpha =1.0\). We investigate the effect of the rescaling parameter below. Not surprisingly, the results indicate that \(\theta =0.0\), which corresponds to a “full-memory” BFGS diagonal, produce the best convergence improvement for L-BFGS updates.
Fixing \(\theta =0.0\) as the best case for the sparse diagonal \(H_0\), we now perform a parameter sweep through the rescaling term in Fig. 2c. The results indicate that \(\alpha =1.0\) produces the most well-scaled initialization for the sparse diagonal case. Additional experiments not shown have failed to recover a better diagonal initialization at different \(\alpha \) and \(\theta \) combinations.
In Fig. 2d, we compare the best-case configurations for both \(H_0\) initialization types to the raw L-BFGS results. The sparse diagonal initialization enables L-BFGS to solve over \(90\%\) of the bound-constrained CUTEst test set in under 1, 000 iterations and accelerates convergence on all problems, offering a significant improvement over both the scalar and identity initialization methods. Statistics for a subset of the problems from this plot are available in Table 1.
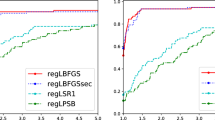
We also explore additional \(H_0\) parameters to accelerate convergence of DFP and the best Broyden method at \(\phi =0.5\). Figure 3a and b show the parameter study for the scalar initialization in the Broyden and DFP methods, respectively. The best case for DFP at \(\alpha =0\) yields a scalar \(H_0\) that is the dual of the best scalar term for BFGS (i.e.: interchanging roles for \(s_k\) and \(y_k\)). This mimics the duality between the DFP and BFGS formulas themselves. Additionally, the best case for Broyden’s method matches the \(\alpha \) parameter to the convex combination term of \(\phi =0.5\). This observation suggests that the best scalar initialization parameter, \(\alpha \), for any member of the Broyden-class method may be the same as the convex combination term \(\phi \) that defines the method.
In Fig. 4, we compare these scalar \(H_0\) terms with one another and against the best BFGS initializations above. Results show that selecting the correct scalar \(H_0\) for each method significantly improves all quasi-Newton methods tested and makes the \(\phi =0.5\) Broyden method competitive with BFGS in the number of problems solved. Our observations indicate that a more comprehensive parameter study may reveal other Broyden-class methods with different convex combination and Hessian initialization terms that offer competitive or better performance than BFGS on some problems. Preliminary numerical experiments we have conducted suggest that the DFP method does not benefit from a diagonal Hessian initialization; however, we aim to utilize our flexible quasi-Newton framework to explore the diagonal \(H_0\) with other Broyden-class methods in the near future.
4 Conclusions
We have introduced a flexible framework for constructing both scalar and sparse diagonal, positive-definite Hessian initializations for limited-memory quasi-Newton methods based on the restricted Broyden-class updates. Our implementation in PETSc/TAO allows us to rapidly change parameters and shift between different members of the Broyden-class methods and select the form for the Hessian initializations at runtime.
Our numerical experiments indicate that intermediate values of \(\phi \) in the Broyden-class outperform the base BFGS formula for a significant subset of the bound-constrained CUTEst problems. We also compare different scalar initializations for different quasi-Newton methods; the results suggest that the best possible \(\alpha \) parameter in our \(H_0\) formulation tracks with the convex combination parameter \(\phi \) that defines members of the Broyden-class.
We demonstrate that the diagonal Hessian initialization successfully accelerates BFGS convergence at minimal additional memory and algebra cost compared with scalar initializations. Our preliminary experience testing similar initializations with DFP and other Broyden-class methods suggests that other parameter values may reveal alternative quasi-Newton methods that are competitive with BFGS on large-scale optimization problems. We hope to leverage our flexible Broyden-class quasi-Newton algorithm to further investigate these possibilities in the future.
References
Balay, S., et al.: PETSc users manual. Technical report ANL-95/11 - Revision 3.10, Argonne National Laboratory (2018). http://www.mcs.anl.gov/petsc
Bertsekas, D.P.: Projected Newton methods for optimization problems with simple constraints. SIAM J. Control Optim. 20(2), 221–246 (1982)
Biros, G., Ghattas, O.: Parallel Lagrange-Newton-Krylov-Schur methods for PDE-constrained optimization. Part i: The Krylov-Schur solver. SIAM J. Sci. Comput. 27(2), 687–713 (2005)
Broyden, C.G.: A class of methods for solving nonlinear simultaneous equations. Math. Comput. 19(92), 577–593 (1965)
Broyden, C.G.: The convergence of a class of double-rank minimization algorithms 1. General considerations. IMA J. Appl. Math. 6(1), 76–90 (1970)
Burke, J.V., Wiegmann, A., Xu, L.: Limited memory BFGS updating in a trust-region framework. Technical report, Department of Mathematics, University of Washington (2008)
Byrd, R.H., Lu, P., Nocedal, J., Zhu, C.: A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 16(5), 1190–1208 (1995)
Byrd, R.H., Nocedal, J., Schnabel, R.B.: Representations of Quasi-Newton matrices and their use in limited memory methods. Math. Program. 63(1–3), 129–156 (1994)
D’Alves, C.: A Scaled Gradient Descent Method for Unconstrained Optimization Problems With A Priori Estimation of the Minimum Value. Ph.D. thesis (2017)
Davidon, W.C.: Variable metric method for minimization, argonne natl. Technical report No. ANL-5990, Argonne National Laboratory (1959)
Davidon, W.C.: Variable metric method for minimization. SIAM J. Optim. 1(1), 1–17 (1991)
Dener, A., et al.: Tao users manual. Technical report ANL/MCS-TM-322 - Revision 3.10, Argonne National Laboratory (2018). http://www.mcs.anl.gov/petsc
Dener, A., Hicken, J.E.: Matrix-free algorithm for the optimization of multidisciplinary systems. Struct. Multidiscip. Optim. 56(6), 1429–1446 (2017)
Dener, A., Hicken, J.E., Kenway, G.K., Martins, J.: Enabling modular aerostructural optimization: individual discipline feasible without the Jacobians. In: 2018 Multidisciplinary Analysis and Optimization Conference, p. 3570 (2018)
Dennis Jr., J.E., Moré, J.J.: Quasi-Newton methods, motivation and theory. SIAM Rev. 19(1), 46–89 (1977)
Dolan, E.D., Moré, J.J.: Benchmarking optimization software with performance profiles. Math. Program. 91(2), 201–213 (2002)
Erway, J.B., Marcia, R.F.: On solving large-scale limited-memory quasi-Newton equations. Linear Algebr. Appl. 515, 196–225 (2017)
Fletcher, R.: A new approach to variable metric algorithms. Comput. J. 13(3), 317–322 (1970)
Fletcher, R., Powell, M.J.: A rapidly convergent descent method for minimization. Comput. J. 6(2), 163–168 (1963)
Gilbert, J.C., Lemaréchal, C.: Some numerical experiments with variable-storage quasi-Newton algorithms. Math. Program. 45(1–3), 407–435 (1989)
Gill, P.E., Leonard, M.W.: Reduced-hessian quasi-Newton methods for unconstrained optimization. SIAM J. Optim. 12(1), 209–237 (2001)
Goldfarb, D.: A family of variable-metric methods derived by variational means. Math. Comput. 24(109), 23–26 (1970)
Gould, N.I., Orban, D., Toint, P.L.: CUTEst: a constrained and unconstrained testing environment with safe threads for mathematical optimization. Comput. Optim. Appl. 60(3), 545–557 (2015)
Haber, E., Ascher, U.M.: Preconditioned all-at-once methods for large, sparse parameter estimation problems. Inverse Probl. 17(6), 1847 (2001)
Hager, W.W.: Updating the inverse of a matrix. SIAM Rev. 31(2), 221–239 (1989)
Hager, W.W., Zhang, H.: A new active set algorithm for box constrained optimization. SIAM J. Optim. 17(2), 526–557 (2006)
Hicken, J., Alonso, J.: Comparison of reduced-and full-space algorithms for PDE-constrained optimization. In: 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, p. 1043 (2013)
Hinze, M., Pinnau, R.: Second-order approach to optimal semiconductor design. J. Optim. Theory Appl. 133(2), 179–199 (2007)
Liu, D.C., Nocedal, J.: On the limited memory BFGS method for large scale optimization. Math. Program. 45(1–3), 503–528 (1989)
Moré, J.J., Thuente, D.J.: Line search algorithms with guaranteed sufficient decrease. ACM Trans. Math. Softw. (TOMS) 20(3), 286–307 (1994)
Moré, J.J., Toraldo, G.: On the solution of large quadratic programming problems with bound constraints. SIAM J. Optim. 1(1), 93–113 (1991)
Nocedal, J., Wright, S.J.: Numerical Optimization, 2nd edn. Springer, New York (2006). https://doi.org/10.1007/978-0-387-40065-5
Papadimitriou, D., Giannakoglou, K.: Direct, adjoint and mixed approaches for the computation of Hessian in airfoil design problems. Int. J. Numer. Methods Fluids 56(10), 1929–1943 (2008)
Shanno, D.F.: Conditioning of quasi-Newton methods for function minimization. Math. Comput. 24(111), 647–656 (1970)
Acknowledgments
This work was supported by the Exascale Computing Project (17-SC-20-SC), a collaborative effort of two U.S. Department of Energy organizations (Office of Science and the National Nuclear Security Administration) responsible for the planning and preparation of a capable exascale ecosystem, including software, applications, hardware, advanced system engineering, and early testbed platforms, in support of the nation’s exascale computing imperative.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 The U.S. government retains certain licensing rights. This is a U.S. government work and certain licensing rights apply
About this paper
Cite this paper
Dener, A., Munson, T. (2019). Accelerating Limited-Memory Quasi-Newton Convergence for Large-Scale Optimization. In: Rodrigues, J.M.F., et al. Computational Science – ICCS 2019. ICCS 2019. Lecture Notes in Computer Science(), vol 11538. Springer, Cham. https://doi.org/10.1007/978-3-030-22744-9_39
Download citation
DOI: https://doi.org/10.1007/978-3-030-22744-9_39
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-22743-2
Online ISBN: 978-3-030-22744-9
eBook Packages: Computer ScienceComputer Science (R0)




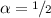 , then
, then  , then
, then 


