Keywords

1 Introduction

Ellipses are planar closed curves described by five independent geometric parameters (or six algebraic coefficients, defined up to a scaling factor). They are ubiquitous in images, especially those representing human environments, and they help in describing a scene. Ellipse extraction in images is a particular case of template matching, generally solved either by area- or feature-based approaches.

This paper investigates specific feature-based approaches, where the chosen features are the edge points (or contour points) extracted from the image and their associated image gradients. This is a meaningful combination as, if most of an ellipse is visible in the image, we expect edge points to be localizable on the ellipse border and the image gradient at these edge points to be directed along the normal to the ellipse contour (and then also orthogonal to the tangent to the ellipse). Therefore, edge points with their associated gradients are possible evidences of the presence of an ellipse in the image.

Formally, ellipse matching comprises two interdependent parts: detection (selection of the ellipse in the image) and fitting (estimation of the parameters). Ellipse fitting algorithms (such as in [1]) estimate the parameters of an unknown ellipse from a set of points originating from this ellipse reasonably well, but they are not robust to outliers. So, in practical applications, we first need to select or detect the points belonging to an ellipse before being able to fit it.

There exist two main approaches for ellipse detection: RANSAC-like methods (see [1], Chap. 4) and Hough Transform (HT) algorithms (see [2, 3]). Both approaches may even be intermixed in applications, but this paper will only consider the case of HT. So, we focus on a specific contour-based ellipse matching method named Elliptic Hough Transform (EHT), where the contour is represented by a list of edge points extracted from the image.

In HT, the unknown template (ellipse) is represented by a point in its parameter space (five-dimensional, or 5D, space for ellipses), and all the evidences of the presence of the template in the image (edge points) vote for some subset of this parameter space. For instance, an edge point and its associated gradient impose two constraints to the unknown ellipse (passing by the point and touching the line orthogonal to the gradient at this point). Accordingly, these two evidences reduce the compatible ellipse parameter set to a three-dimensional (3D) space (5D parameter space minus two constraints). We say that these two evidences votes for the compatible 3D parameter subset. Then, in the parameter space, we accumulate the votes of all the evidences (edge points and gradients) extracted from the image. At the end of the accumulation process, the algorithm chooses (extracts) the ellipse that has accumulated the largest number of votes.

EHT methods first aim at detecting the presence of any number of elliptic structures in an image and, incidentally, at computing an approximation of their geometric parameters or algebraic coefficients. They are not intended to provide a precise value for the parameters or coefficients, which is the role of a subsequent ellipse fitting algorithm.

In the literature, authors use different types of evidences for EHT. In this paper, the evidences are pairs of edge points with their associated gradients, and we impose no conditions on the gradients. In the following, the availability of associated gradients is assumed implicitly. A pair of edge point thus represents four evidences and imposes four constraints on the compatible ellipses (passing by two points and touching two lines). Therefore, a pair of edge points votes for a one-dimensional (1D) ellipse parameter subset.

In EHT, we would need to accumulate the votes in a 5D space, which is complicated in practice. So, authors separate the problem in two steps. In [4], Tsuji et al. presented an EHT algorithm based on pairs of edge points with parallel gradients, which uses a kind of 2D histogram for computing the center of the ellipse. Likewise, Yuen et al. [5] were the first to use pairs of edge points with arbitrary gradients. They accumulate lines in the 2D Hough space of the ellipse centers and then accumulate planes in the 3D Hough space of the remaining normalized algebraic coefficients. Other authors (see [6, 7]) use the same first step but resort to specific geometric parameters for the three remaining parameters, which they determine in two steps rather than one.

It is interesting to note that two articles, more specifically [8] and [9], presented, independently and without explicitly naming it, the pencil of bi-tangent conics as the right mathematical framework for analyzing the family of ellipses built on two edge points. In fact, Yoo et al. [8] use the framework only for the first part of the EHT algorithm. Besides, Benett et al. [9] noticed that the framework enables to compute, as a first step, any pair or triplet of parameters (not only the center) and to easily incorporate any prior geometrical constraints. None of these works consider the framework for the second step of the EHT.

A key point of the EHT is the choice of the set of (algebraic or geometric) parameters used for the accumulation process. In the following, we show that the usual method of center accumulation is well described within the framework of the dual equation. We also show that the set of parameters of the direct equation of the framework, introduced in [10] for fitting applications (see [11, 12]), has never been used explicitly in the accumulation process of the EHT. This direct form accumulates a pair of parameters, which are equivalent to the eccentricity and orientation of the ellipse.

2 Problem Statement

In this section, we introduce the main notation and equations. In the following, a specific point, named \(\mathrm {P}_{}^{}\), is represented by the 2D vector of its Cartesian coordinates \({\varvec{\bar{P}}_{\varvec{}}^{}}=\left( \begin{array}{cc} {{X_{P}^{}}}&{{Y_{P}^{}}}\end{array}\right) ^{T}\) and/or by the 3D vector of its homogeneous coordinates \({\varvec{P}_{\varvec{}}^{}}=\left( \begin{array}{ccc} {{x_{P}^{}}}&{{y_{P}^{}}}&{{z_{P}^{}}}\end{array}\right) ^{T}\) or \({\varvec{P}_{\varvec{}}^{}}=\left( \begin{array}{ccc} {{X_{P}^{}}}&{{Y_{P}^{}}}&1\end{array}\right) ^{T}\). Likewise, an unknown point is represented by its Cartesian coordinate \({\varvec{\bar{X}}_{\varvec{}}^{}}=\left( \begin{array}{cc} {X_{}^{}}&{Y_{}^{}}\end{array}\right) ^{T}\) and also by its homogeneous coordinates \({\varvec{X}_{\varvec{}}^{}}=\left( \begin{array}{ccc} {x_{}^{}}&{y_{}^{}}&{z_{}^{}}\end{array}\right) ^{T}\) or \({\varvec{X}_{\varvec{}}^{}}=\left( \begin{array}{ccc} {X_{}^{}}&{Y_{}^{}}&1\end{array}\right) ^{T}\). A line, named \(\mathrm {l}_{}^{}\), then satisfies an equation of type \({\varvec{l}_{\varvec{}}^{T}}{{\varvec{X}_{\varvec{}}^{}}}=0\), where \({\varvec{l}_{\varvec{}}^{}}=\left( \begin{array}{ccc} {{u_{l}^{}}}&{{v_{l}^{}}}&{{w_{l}^{}}}\end{array}\right) ^{T}\) is the 3D vector of the homogeneous coefficients of its equation. Also, an unknown line satisfies an equation \({\varvec{u}_{\varvec{}}^{T}}{{\varvec{X}_{\varvec{}}^{}}}=0\), where \({\varvec{u}_{\varvec{}}^{}}=\left( \begin{array}{ccc} {u_{}^{}}&{v_{}^{}}&{w_{}^{}}\end{array}\right) ^{T}\). Most of the time, we use the homogeneous coordinates of the projective plane \(\mathbb {P}^{2}=P^{2}\left( \mathbb {R}\right) \) and, for the sake of conciseness, we often identify the geometric elements with their representation.

2.1 Ellipses and Conics

Geometric Parameters of Ellipses. Geometrically speaking, an ellipse is commonly defined by (the Cartesian coordinates of) its center \(\left( {C_{}},{C_{}^{\prime }}\right) \), its half-axes \(\left( {r_{}},{r_{}^{\prime }}\right) \), and its orientation \({\theta _{}}\). In the following, we will also use the eccentricity \({e_{}}\), defined as \({e_{}}^{2}=1-\nicefrac {{r_{}^{\prime }}^{2}}{{r_{}}^{2}}\).

Point (Direct) Equation. An ellipse may be defined algebraically as a special kind of conics, which is a second degree algebraic curve. A conic \(\mathcal {C}\) is any curve whose point coordinates satisfy the following equation

$$\begin{aligned} \mathcal {C}:\,{a_{}}{X_{}^{}}^{2}+2{b_{}^{\prime \prime }}{X_{}^{}}{Y_{}^{}}+{a_{}^{\prime }}{Y_{}^{}}^{2}+2{b_{}^{\prime }}{X_{}^{}}+2{b_{}}{Y_{}^{}}+{a_{}^{\prime \prime }}={\varvec{X}_{\varvec{}}^{T}}{{\mathtt {F}_{\mathtt {}}^{}}}{\varvec{X}_{\varvec{}}^{}}=0\,\text{, } \end{aligned}$$
(1)

where the symmetric matrix \({{\mathtt {F}_{\mathtt {}}^{}}}\) is easily obtained by identification of the two members of Eq. (1).

The conic is also fully determined by the vector of its six homogeneous coefficients \({{\varvec{f}_{\varvec{}}^{}}}=\left( {a_{}},{b_{}^{\prime \prime }},{a_{}^{\prime }},{b_{}^{\prime }},{b_{}},{a_{}^{\prime \prime }}\right) ^{T}\), defined up to a scaling factor. This vector belongs to the projective space of the conic coefficient vectors \({{\varvec{f}_{\varvec{}}^{}}}\in \mathbb {P}^{5}=P^{5}\left( \mathbb {R}\right) \). In the following, we use the operator flatten that operates on the symmetric matrix \({{\mathtt {F}_{\mathtt {}}^{}}}\) and returns the vector \({{\varvec{f}_{\varvec{}}^{}}}\); so we write \({{\varvec{f}_{\varvec{}}^{}}}=\text {flatten}\left( {{\mathtt {F}_{\mathtt {}}^{}}}\right) \).

We later show (see Eq. (8)) that, when the conic is an ellipse, we always have \({a_{}}+{a_{}^{\prime }}\ne 0\), and we may also use the following alternative form (introduced in [10]) for the algebraic equation of an ellipse:

$$\begin{aligned} \left( {X_{}^{2}}+{Y_{}^{2}}\right) -{d_{}}\left( {X_{}^{2}}-{Y_{}^{2}}\right) -2{d_{}^{\prime }}{X_{}^{}}{Y_{}^{}}-2{c_{}}{X_{}^{}}-2{c_{}^{\prime }}{Y_{}^{}}-{c_{}^{\prime \prime }}=0\,\text{, } \end{aligned}$$
(2)

where the five direct coefficients \({\varvec{\bar{f}}_{\varvec{}}^{}}=\left( {d_{}},{d_{}^{\prime }},{c_{}},{c_{}^{\prime }},{c_{}^{\prime \prime }}\right) \) are related to the homogeneous direct coefficients in Eq. (1) and to the geometric parameters by

$$\begin{aligned} \begin{array}{ccc} \left\{ \begin{array}{ccccl} {d_{}} &{} = &{} \frac{{a_{}^{\prime }}-{a_{}}}{{a_{}}+{a_{}^{\prime }}} &{} = &{} \frac{{e_{}}^{2}\cos 2{\theta _{}}}{2-{e_{}}^{2}}\\ {d_{}^{\prime }} &{} = &{} \frac{-2{b_{}^{\prime \prime }}}{{a_{}}+{a_{}^{\prime }}} &{} = &{} \frac{{e_{}}^{2}\sin 2{\theta _{}}}{2-{e_{}}^{2}} \end{array}\right. &{} \,\text{, }&{} \left\{ \begin{array}{ccccl} {c_{}} &{} = &{} \frac{-2{b_{}^{\prime }}}{{a_{}}+{a_{}^{\prime }}} &{} = &{} {\scriptstyle \left( 1-{d_{}}\right) {C_{}}-{d_{}^{\prime }}{C_{}^{\prime }}}\\ {c_{}^{\prime }} &{} = &{} \frac{-2{b_{}}}{{a_{}}+{a_{}^{\prime }}} &{} = &{} {\scriptstyle -{d_{}^{\prime }}{C_{}}+\left( 1+{d_{}}\right) {C_{}^{\prime }}}\\ {c_{}^{\prime \prime }} &{} = &{} \frac{-2{a_{}^{\prime \prime }}}{{a_{}}+{a_{}^{\prime }}} &{} = &{} \frac{2{r_{}}^{2}{r_{}^{\prime }}^{2}}{{r_{}}^{2}+{r_{}^{\prime }}^{2}}{\scriptstyle -{c_{}}{C_{}}-{c_{}^{\prime }}{C_{}^{\prime }}}\,\text{. }\end{array}\right. \end{array} \end{aligned}$$
(3)

The notation \({\varvec{\bar{f}}_{\varvec{}}^{}}\) for the 5D vector and \({{\varvec{f}_{\varvec{}}^{}}}\) for the 6D homogeneous vector is similar to the notation \({\varvec{\bar{P}}_{\varvec{}}^{}}\) for the 2D Cartesian coordinates and \({\varvec{P}_{\varvec{}}^{}}\) for the 3D homogeneous coordinates. In some way, the vectors \({{\varvec{f}_{\varvec{}}^{}}}\) and \({\varvec{\bar{f}}_{\varvec{}}^{}}\) may be respectively considered as the projective and Cartesian direct coordinates of an ellipse.

Tangential (Dual) Equation. A line \({\varvec{u}_{\varvec{}}^{T}}{{\varvec{X}_{\varvec{}}^{}}}=0\) is a tangent to the conic described by Eq. (1) if and only if its triplet of coefficients \({\varvec{u}_{\varvec{}}^{}}\) satisfies the dual equation (also called tangential equation) of the conic

$$\begin{aligned} \mathcal {C^{\mathrm {*}}}:\,{A_{}}{u_{}^{}}^{2}+2{B_{}^{\prime \prime }}{u_{}^{}}{v_{}^{}}+{A_{}^{\prime }}{v_{}^{}}^{2}+2{B_{}^{\prime }}{u_{}^{}}{w_{}^{}}+2{B_{}}{v_{}^{}}{w_{}^{}}+{A_{}^{\prime \prime }}{w_{}^{}}^{2}={\varvec{u}_{\varvec{}}^{T}}{{\mathtt {F}_{\mathtt {}}^{*}}}{\varvec{u}_{\varvec{}}^{}}=0\,\text{, } \end{aligned}$$
(4)

where \({{\mathtt {F}_{\mathtt {}}^{*}}}\) is the matrix of the cofactors of \({{\mathtt {F}_{\mathtt {}}^{}}}\). We can also represent the dual conic by the vector of its six homogeneous coefficients \({{\varvec{F}_{\varvec{}}^{}}}=\left( {A_{}},{B_{}^{\prime \prime }},{A_{}^{\prime }},{B_{}^{\prime }},{B_{}},{A_{}^{\prime \prime }}\right) ^{T}=\text {flatten}\left( {{\mathtt {F}_{\mathtt {}}^{*}}}\right) \).

For an ellipse, \({A_{}^{\prime \prime }}={a_{}}{a_{}^{\prime }}-{b_{}^{\prime \prime }}^{2}\ne 0\) and we also have an alternative form for the dual equation:

$$\begin{aligned} {D_{}^{\prime \prime }}\left( {u_{}^{2}}+{v_{}^{2}}\right) +2{D_{}^{\prime }}{u_{}^{}}{v_{}^{}}-{D_{}}\left( {u_{}^{2}}-{v_{}^{2}}\right) +2{C_{}}{u_{}^{}}{w_{}^{}}+2{C_{}^{\prime }}{v_{}^{}}{w_{}^{}}+{w_{}^{2}}=0\,\text{, } \end{aligned}$$
(5)

where the 5 dual coefficients \({\varvec{\bar{F}}_{\varvec{}}^{}}=\left( {C_{}},{C_{}^{\prime }},{D_{}},{D_{}^{\prime }},{D_{}^{\prime \prime }}\right) \) are related to the dual homogeneous coefficients of Eq. (4) and to the geometric parameters by

$$\begin{aligned} \begin{array}{ccc} \left\{ \begin{array}{ccc} {C_{}} &{} = &{} \frac{{B_{}^{\prime }}}{{A_{}^{\prime \prime }}}\\ {C_{}^{\prime }} &{} = &{} \frac{{B_{}}}{{A_{}^{\prime \prime }}} \end{array}\right. &{} \,\text{, }&{} \left\{ \begin{array}{ccccl} {D_{}} &{} = &{} \frac{{A_{}^{\prime }}-{A_{}}}{2{A_{}^{\prime \prime }}} &{} = &{} {\scriptstyle \frac{1}{2}\left( {C_{}}^{2}-{C_{}^{\prime }}^{2}\right) +\frac{1}{2}\left( {r_{}}^{2}-{r_{}^{\prime }}^{2}\right) \cos 2{\theta _{}}}\\ {D_{}^{\prime }} &{} = &{} \frac{{B_{}^{\prime \prime }}}{{A_{}^{\prime \prime }}} &{} = &{} {\scriptstyle {C_{}}{C_{}^{\prime }}-\frac{1}{2}\left( {r_{}}^{2}-{r_{}^{\prime }}^{2}\right) \sin 2{\theta _{}}}\\ {D_{}^{\prime \prime }} &{} = &{} \frac{{A_{}}+{A_{}^{\prime }}}{2{A_{}^{\prime \prime }}} &{} = &{} {\scriptstyle \frac{1}{2}\left( {C_{}}^{2}+{C_{}^{\prime }}^{2}-{r_{}}^{2}-{r_{}^{\prime }}^{2}\right) }. \end{array}\right. \end{array} \end{aligned}$$
(6)

We highlight the fact that the two coefficients \(\left( {C_{}},{C_{}^{\prime }}\right) \) in Eq. (6) effectively represents the Cartesian coordinates of the ellipse center and thus have the same notation. The vectors \({{\varvec{F}_{\varvec{}}^{}}}\) and \({\varvec{\bar{F}}_{\varvec{}}^{}}\) may be respectively considered as the projective and Cartesian dual coordinates of an ellipse.

Type of a Conic. It is known that a conic is an ellipse if and only if

$$\begin{aligned} {A_{}^{\prime \prime }}={a_{}}{a_{}^{\prime }}-{b_{}^{\prime \prime }}^{2}>0\quad \text{ or }\quad 0\le {e_{}}<1\,\text{. } \end{aligned}$$
(7)

This condition implies that \({a_{}}{a_{}^{\prime }}>{b_{}^{\prime \prime }}^{2}\ge 0\). Subsequently, \({a_{}}\) and \({a_{}^{\prime }}\) must have the same sign and may not be null. As a consequence, we have the following relations:

$$\begin{aligned} \mathrm {sign}\left( {a_{}}\right) =\mathrm {sign}\left( {a_{}^{\prime }}\right) =\mathrm {sign}\left( {a_{}}+{a_{}^{\prime }}\right) \quad \text{ and }\quad {a_{}}+{a_{}^{\prime }}\ne 0\,\text{. } \end{aligned}$$
(8)

With the notation \({\varDelta _{}}=\det {{\mathtt {F}_{\mathtt {}}^{}}}\), an ellipse is a real ellipse if, in addition,

$$\begin{aligned} {a_{}}{\varDelta _{}}<0\Longleftrightarrow \left( {a_{}}+{a_{}^{\prime }}\right) {\varDelta _{}}<0\,\text{. } \end{aligned}$$
(9)
Fig. 1.
figure 1

The edge points \(\mathrm {P}_{}^{}\), \(\mathrm {Q}_{}^{}\), and their associated gradients \(\overrightarrow{\mathrm {G}}_{}^{}\), \(\overrightarrow{\mathrm {H}}_{}^{}\) are evidences of the presence of an ellipse in the image.

Full size image

2.2 The Triangle of Edge Points and Associated Gradients

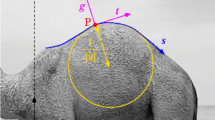
We now consider two edge points \(\mathrm {P}_{}^{}\) and \(\mathrm {Q}_{}^{}\) and their associated gradients \(\overrightarrow{\mathrm {G}}_{}^{}\) and \(\overrightarrow{\mathrm {H}}_{}^{}\); this configuration is illustrated in Fig. 1.

The mid-point of \(\mathrm {P}_{}^{}\) and \(\mathrm {Q}_{}^{}\) is represented by \({\varvec{M}_{\varvec{}}^{}}=\frac{1}{2}\left( {\varvec{P}_{\varvec{}}^{}}+{\varvec{Q}_{\varvec{}}^{}}\right) \) and their difference by \({\varvec{K}_{\varvec{}}^{}}={\varvec{Q}_{\varvec{}}^{}}-{\varvec{P}_{\varvec{}}^{}}\). The line \(\mathrm {o}_{}^{}\) (with \({\varvec{o}_{\varvec{}}^{}}={\varvec{P}_{\varvec{}}^{}}\wedge {\varvec{Q}_{\varvec{}}^{}}\), where \(\wedge \) is the cross-product), joining the points \({\varvec{P}_{\varvec{}}^{}}\) and \({\varvec{Q}_{\varvec{}}^{}}\), is a chord secant to the unknown ellipse.

The vectors \(\overrightarrow{\mathrm {G}}_{}^{}\) and \(\overrightarrow{\mathrm {H}}_{}^{}\) are the image gradients at the points \(\mathrm {P}_{}^{}\) and \(\mathrm {Q}_{}^{}\), they are represented by the directions (points at infinity) \({\varvec{G}_{\varvec{}}^{}}=\left( \begin{array}{ccc} {{X_{G}^{}}}&{{Y_{G}^{}}}&0\end{array}\right) ^{T}\) and \({\varvec{H}_{\varvec{}}^{}}=\left( \begin{array}{ccc} {{X_{H}^{}}}&{{Y_{H}^{}}}&0\end{array}\right) ^{T}\). We also introduce the dot products \({{\lambda _{G}}}={\varvec{G}_{\varvec{}}^{}}\cdot {\varvec{K}_{\varvec{}}^{}}\) and \({{\lambda _{H}}}={\varvec{H}_{\varvec{}}^{}}\cdot {\varvec{K}_{\varvec{}}^{}}\); we later show that they cannot be null in the practical situations of interest.

The line \(\mathrm {q}_{}^{}\), defined by \({\varvec{q}_{\varvec{}}^{}}=\frac{1}{{{\lambda _{G}}}}{\varvec{P}_{\varvec{}}^{}}\wedge \left( {\varvec{G}_{\varvec{}}^{}}\wedge {\varvec{e}_{\varvec{z}}^{}}\right) \) with \({\varvec{e}_{\varvec{z}}^{}}=\left( \begin{array}{ccc} 0&0&1\end{array}\right) ^{T}\), passing by \(\mathrm {P}_{}^{}\) and orthogonal to \(\overrightarrow{\mathrm {G}}_{}^{}\), is tangent to the unknown ellipse. Likewise, the line \(\mathrm {p}_{}^{}\) (with \({\varvec{p}_{\varvec{}}^{}}=\frac{1}{{{\lambda _{H}}}}{{\left( {\varvec{H}_{\varvec{}}^{}}\wedge {\varvec{e}_{\varvec{z}}^{}}\right) }}\wedge {\varvec{Q}_{\varvec{}}^{}}\)) passing by \(\mathrm {Q}_{}^{}\) and orthogonal to \(\overrightarrow{\mathrm {H}}_{}^{}\), is tangent to the unknown ellipse. In the expression of \({\varvec{p}_{\varvec{}}^{}}\) and \({\varvec{q}_{\varvec{}}^{}}\), we choose the arbitrary scaling factors \({{\lambda _{G}}}\) and \({{\lambda _{H}}}\) to simplify the expression of some of the following equations. The intersection point \(\mathrm {O}_{}^{}\) of the two lines \(\mathrm {q}_{}^{}\) and \(\mathrm {p}_{}^{}\) is represented by \({\varvec{O}_{\varvec{}}^{}}={\varvec{p}_{\varvec{}}^{}}\wedge {\varvec{q}_{\varvec{}}^{}}\).

We consider the triangle \(\triangle \mathrm {O}_{}^{}\mathrm {P}_{}^{}\mathrm {Q}_{}^{}\) defined by the edge points \(\mathrm {P}_{}^{}\), \(\mathrm {Q}_{}^{}\), and the intersection point \(\mathrm {O}_{}^{}\). The sides of this triangle are thus the lines \(\mathrm {o}_{}^{}\), \(\mathrm {q}_{}^{}\), and \(\mathrm {p}_{}^{}\). The matrix of the triangle vertices is named \({\mathtt {V}_{\mathtt {}}^{}}\). Thanks to the choice of the scaling factors \({{\lambda _{G}}}\) and \({{\lambda _{H}}}\), it can be shown that the matrix \({\mathtt {S}_{\mathtt {}}^{}}={\mathtt {V}_{\mathtt {}}^{*}}\) of the cofactors of \({\mathtt {V}_{\mathtt {}}^{}}\) is also the matrix of the coefficients of the side lines of the triangle. Therefore, we have

$$\begin{aligned} {\mathtt {V}_{\mathtt {}}^{}}=\left( \begin{array}{ccc} {\varvec{O}_{\varvec{}}^{}}&{\varvec{P}_{\varvec{}}^{}}&{\varvec{Q}_{\varvec{}}^{}}\end{array}\right) \quad \text{ and }\quad {\mathtt {V}_{\mathtt {}}^{*}}={\mathtt {S}_{\mathtt {}}^{}}=\left( \begin{array}{ccc} {\varvec{o}_{\varvec{}}^{}}&{\varvec{p}_{\varvec{}}^{}}&{\varvec{q}_{\varvec{}}^{}}\end{array}\right) \,\text{, } \end{aligned}$$
(10)

with \(\det {\mathtt {S}_{\mathtt {}}^{}}=\det {\mathtt {V}_{\mathtt {}}^{}}=1\), \({\mathtt {V}_{\mathtt {}}^{-1}}={\mathtt {S}_{\mathtt {}}^{T}}\), and \({\mathtt {S}_{\mathtt {}}^{-1}}={\mathtt {V}_{\mathtt {}}^{T}}\).

Conditions on the Edge Points. From Fig. 1, we see that it is only possible to build an ellipse from a pair of edge points \(\mathrm {P}_{}^{}\) and \(\mathrm {Q}_{}^{}\) if they are distinct, if their gradients \(\overrightarrow{\mathrm {G}}_{}^{}\) and \(\overrightarrow{\mathrm {H}}_{}^{}\) are not null and if the edge point \(\mathrm {Q}_{}^{}\) (resp. \(\mathrm {P}_{}^{}\)) do not belongs to \(\mathrm {q}_{}^{}\) (resp. \(\mathrm {p}_{}^{}\)). So, in practice, we have to discard the pairs of edge points that do not verify the corresponding conditions given hereafter:

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{K}_{\varvec{}}^{}}\ne {\varvec{0}_{\varvec{}}^{}}\,\text{, }\;{\varvec{G}_{\varvec{}}^{}}\ne {\varvec{0}_{\varvec{}}^{}}\,\text{, }\;{\varvec{H}_{\varvec{}}^{}}\ne {\varvec{0}_{\varvec{}}^{}}\\ {{\lambda _{G}}}={\varvec{G}_{\varvec{}}^{}}\cdot {\varvec{K}_{\varvec{}}^{}}\ne 0\,\text{, }\;{{\lambda _{H}}}={\varvec{H}_{\varvec{}}^{}}\cdot {\varvec{K}_{\varvec{}}^{}}\ne 0\,\text{. }\end{array}\right. \end{aligned}$$
(11)

2.3 Pencil of Bi-Tangent Conics

The unknown ellipse belongs to the family of conics passing through the two points \(\mathrm {P}_{}^{}\) and \(\mathrm {Q}_{}^{}\), and tangent to the lines \(\mathrm {q}_{}^{}\) and \(\mathrm {p}_{}^{}\). Mathematically speaking, this family is the pencil of conic bi-tangent to the lines \(\mathrm {q}_{}^{}\) and \(\mathrm {p}_{}^{}\) at their respective intersection points (\(\mathrm {P}_{}^{}\) and \(\mathrm {Q}_{}^{}\)) with the line \(\mathrm {o}_{}^{}\).

The general equation of a conic \(\mathcal {C}_{k}\) belonging to this pencil is

$$\begin{aligned} \mathcal {C}_{k}:\,\left( {\varvec{p}_{\varvec{}}^{T}}{\varvec{X}_{\varvec{}}^{}}\right) \left( {\varvec{q}_{\varvec{}}^{T}}{\varvec{X}_{\varvec{}}^{}}\right) -\frac{k}{2}\left( {\varvec{o}_{\varvec{}}^{T}}{\varvec{X}_{\varvec{}}^{}}\right) ^{2}=0\,\text{, } \end{aligned}$$
(12)

where \(k\) is any real number, which is the index of the conic \(\mathcal {C}_{k}\) in the pencil.

As said before, a conic is fully described by five parameters. As all the conics in the pencil have to verify four constraints (to pass through two given points and to touch two given lines), we obtain an equation for a conic in the pencil that only depends on one parameter, namely the index \(k\). The notion of index of the conic is an essential component of our approach in Sect. 3.

Point (Direct) Equation of the Pencil. From Eq. (12), we compute the matrix of a conic in the pencil \({{\mathtt {F}_{\mathtt {k}}^{}}}={\varvec{p}_{\varvec{}}^{}}{\varvec{q}_{\varvec{}}^{T}}+{\varvec{q}_{\varvec{}}^{}}{\varvec{p}_{\varvec{}}^{T}}-k{\varvec{o}_{\varvec{}}^{}}{\varvec{o}_{\varvec{}}^{T}}\) and also \({{\mathtt {F}_{\mathtt {k}}^{}}}={\mathtt {S}_{\mathtt {}}^{}}\left( \begin{array}{ccc} -k{\varvec{e}_{\varvec{x}}^{}}&{\varvec{e}_{\varvec{z}}^{}}&{\varvec{e}_{\varvec{y}}^{}}\end{array}\right) {\mathtt {S}_{\mathtt {}}^{T}}\), where \({\mathtt {S}_{\mathtt {}}^{}}\) is the matrix defined in Eq. (10). By identification with Eq. (1), we obtain the corresponding vector of direct homogeneous coefficients \({{\varvec{f}_{\varvec{k}}^{}}}={{\varvec{f}_{\varvec{pq}}^{}}}-k{{\varvec{f}_{\varvec{oo}}^{}}}\), where \({{\varvec{f}_{\varvec{pq}}^{}}}=\text {flatten}\left( {\varvec{p}_{\varvec{}}^{}}{\varvec{q}_{\varvec{}}^{T}}+{\varvec{q}_{\varvec{}}^{}}{\varvec{p}_{\varvec{}}^{T}}\right) \) and \({{\varvec{f}_{\varvec{oo}}^{}}}=\text {flatten}\left( {\varvec{o}_{\varvec{}}^{}}{\varvec{o}_{\varvec{}}^{T}}\right) \).

If we take \(\alpha _{pq}={{{u_{p}^{}}}}{{{u_{q}^{}}}}+{{{v_{p}^{}}}}{{{v_{q}^{}}}}\) and \(\alpha _{oo}={{{u_{o}^{2}}}}+{{{v_{o}^{2}}}}\), we obtain the direct Cartesian coefficients of the ellipses in the pencil, where \({\varvec{\bar{f}}_{\varvec{pq}}^{}}\) and \({\varvec{\bar{f}}_{\varvec{oo}}^{}}\) may easily be computed from Eq. (3),

$$\begin{aligned} {\varvec{\bar{f}}_{\varvec{k}}^{}}=\xi _{k}{\varvec{\bar{f}}_{\varvec{pq}}^{}}-\left( 1+\alpha _{pq}\xi _{k}\right) {\varvec{\bar{f}}_{\varvec{oo}}^{}}\,\text{, }\text { with }\xi _{k}=\dfrac{{\scriptstyle 2}}{{\scriptstyle -2\alpha _{pq}+k\alpha _{oo}}}\,\text{. } \end{aligned}$$
(13)

Tangential (Dual) Equation of a Conic in the Pencil. Likewise, the dual or tangential equation is determined by the matrix of the cofactors of the matrix of the conic and may be expressed (when the conic is not degenerated) in two ways \({{\mathtt {F}_{\mathtt {k}}^{*}}}={\mathtt {V}_{\mathtt {}}^{}}\left( \begin{array}{ccc} -{\varvec{e}_{\varvec{x}}^{}}&k{\varvec{e}_{\varvec{z}}^{}}&k{\varvec{e}_{\varvec{y}}^{}}\end{array}\right) {\mathtt {V}_{\mathtt {}}^{T}}\) and \({{\mathtt {F}_{\mathtt {k}}^{*}}}=-{\varvec{O}_{\varvec{}}^{}}{\varvec{O}_{\varvec{}}^{T}}+k\left[ {\varvec{P}_{\varvec{}}^{}}{\varvec{Q}_{\varvec{}}^{T}}+{\varvec{Q}_{\varvec{}}^{}}{\varvec{P}_{\varvec{}}^{T}}\right] \). By identification with Eq. (4), we obtain the corresponding vector of dual homogeneous coefficients \({{\varvec{F}_{\varvec{k}}^{}}}=-{{\varvec{F}_{\varvec{OO}}^{}}}+k{{\varvec{F}_{\varvec{PQ}}^{}}}\), where \({{\varvec{F}_{\varvec{PQ}}^{}}}=\text {flatten}\left( {\varvec{P}_{\varvec{}}^{}}{\varvec{Q}_{\varvec{}}^{T}}+{\varvec{Q}_{\varvec{}}^{}}{\varvec{P}_{\varvec{}}^{T}}\right) \) and \({{\varvec{F}_{\varvec{OO}}^{}}}=\text {flatten}\left( {\varvec{O}_{\varvec{}}^{}}{\varvec{O}_{\varvec{}}^{T}}\right) \).

Finally, we obtain the dual Cartesian coefficients of the ellipses in the pencil, where \({\varvec{\bar{F}}_{\varvec{PQ}}^{}}\) and \({\varvec{\bar{F}}_{\varvec{OO}}^{}}\) may easily be computed from Eq. (6),

$$\begin{aligned} {\varvec{\bar{F}}_{\varvec{k}}^{}}=\left( 1+\varXi _{k}{{{z_{O}^{}}}}^{2}\right) {\varvec{\bar{F}}_{\varvec{PQ}}^{}}-\varXi _{k}{\varvec{\bar{F}}_{\varvec{OO}}^{}}\,\text{, }\text { with }\varXi _{k}=\dfrac{{\scriptstyle 1}}{{\scriptstyle 2k-{{{z_{O}^{2}}}}}}\,\text{. } \end{aligned}$$
(14)

Type of a Conic in the Pencil. Because we are looking for a real ellipse, based on Eqs. (7) and (9), we should have \(2k>{{{z_{O}^{}}}}^{2}\Leftrightarrow \varXi _{k}>0\) and \(k>2\frac{\alpha _{pq}}{\alpha _{oo}}\Leftrightarrow \xi _{k}>0\), and it is possible to prove that the second condition is always verified when the first one is true.

3 An Algorithm for Obtaining the Matching Ellipse

3.1 Parameters of an Ellipse Built upon Two Edge Points and Their Gradients

We may identify the set of all the conics in the plane with the projective space \(\mathbb {P}^{5}=P^{5}\left( \mathbb {R}\right) \) of their algebraic coefficients. The subset of the (algebraic coefficients of the) conics compatible with four evidences (a pair of edge points, plus their gradients) is a pencil of bi-tangent conics. From Eq. (12), we derive that such a pencil of conics is represented by a line in \(\mathbb {P}^{5}\).

Unfortunately, the scale and the domain of the algebraic coefficients are not easy to determine because these coefficients are only defined up to a scaling factor. So, it would be more appropriate to accumulate them in the space of the geometric parameters. But, in such a space, the pencil of conics is represented by a much more complicated curve, which is intractable.

Possible solution consist to use Eq. (13) in the 5D space of the parameters \(\left( {d_{}},{d_{}^{\prime }},{c_{}},{c_{}^{\prime }},{c_{}^{\prime \prime }}\right) \) or Eq. (14) in the dual 5D space of the parameters \(\left( {C_{}},{C_{}^{\prime }},{D_{}},{D_{}^{\prime }},{D_{}^{\prime \prime }}\right) \). In both spaces, the pencil of bi-tangent conics is again a line and the domain of variation of the parameters is easy to determine from a practical perspective. Indeed, these parameters may be easily expressed in terms of the geometric parameters of the ellipse.

3.2 A General Algorithm

The general principles and steps of a typical algorithm for the computation of the Elliptic Hough Transform (EHT) are:

  1. 1.

    We define a 5D discrete accumulator corresponding to the 5D space of the parameters \(\left( {d_{}},{d_{}^{\prime }},{c_{}},{c_{}^{\prime }},{c_{}^{\prime \prime }}\right) \) or \(\left( {C_{}},{C_{}^{\prime }},{D_{}},{D_{}^{\prime }},{D_{}^{\prime \prime }}\right) \). In this accumulator, each cell is indexed by a 5D vector whose components are the quantized values of the corresponding parameters. All cells are initialized to 0.

  2. 2.

    For all pairs of edge points which verify the conditions mentioned in (11), we draw the line corresponding to the pencil of bi-tangent conics in the 5D accumulator.

  3. 3.

    When all the evidences has been processed and the corresponding lines drawn, we look for the peak (maximum) values in the accumulator.

  4. 4.

    If the value of this peak, which represents the number of votes for a vector of parameters, is not large enough, then the process stops with no ellipse detected nor matched.

  5. 5.

    To a contrary, an ellipse is detected if a peak is validated and we look back for all the evidences that voted for this peak. These evidences are then removed from the initial list of evidences and we repeat the process from the beginning until no ellipses are detected anymore.

Obviously, managing a 5D accumulator may be very time and memory consuming in practice. Fortunately, solutions exist to reduce the dimension of the accumulator.

3.3 First Step: Reduce the Problem Dimension

Projection of the Dual Parameters to \(\left( {C_{}},{C_{}^{\prime }}\right) \). In the literature, without always explicitly noting it, authors reduce the dimension of the problem by considering a projection (of the process explained in the previous section) to a lower dimension space. For example, some geometric observations lead to the solution chosen by all authors that consists in accumulating the line \(\mathrm {l}_{}^{}\) joining the mid-point \(\mathrm {M}_{}^{}\) of the edge points \(\mathrm {P}_{}^{}\) and \(\mathrm {Q}_{}^{}\) from one side, and the intersection point \(\mathrm {O}_{}^{}\) of the two tangents \(\mathrm {q}_{}^{}\) and \(\mathrm {p}_{}^{}\) from the other side (see Fig. 1). This line is always a diameter of the unknown ellipse and passes through the ellipse center. The accumulation of this line in a plane, whose dimensions are similar to those of the image, highlights the possible ellipse centers.

In the framework of the pencil of bi-tangent conics, this method is equivalent to the projection of the line representing the pencil in the 5D space to a line in the 2D space. Figure 2 illustrates the process for the dual approach; the blue line in the 5D space (represented in 3D in the figure) represents the locus of the parameters \(\left( {C_{}},{C_{}^{\prime }},{D_{}},{D_{}^{\prime }},{D_{}^{\prime \prime }}\right) \) of the conics in the pencil defined by a specific pair of edge points, and the blue line in the plane \(\left( {C_{}},{C_{}^{\prime }}\right) \) represents its projection.

From Eq. (14), we see that a degenerate case occurs when the gradients are parallel. In this situation, the 5D line is exactly orthogonal to the \(\left( {C_{}},{C_{}^{\prime }}\right) \) plane and its projection reduces to a point. This means that, when the gradients are parallel, the position of the ellipse center is known perfectly.

Projection of the Direct Parameters to \(\left( {d_{}},{d_{}^{\prime }}\right) \). However, there are other possibilities to reduce the dimensions of the problem. For instance, we could also project the line in the 5D space \(\left( {d_{}},{d_{}^{\prime }},{c_{}},{c_{}^{\prime }},{c_{}^{\prime \prime }}\right) \) into a line in the 2D space \(\left( {d_{}},{d_{}^{\prime }}\right) \). Indeed, from Eq. (3), we know that these \(\left( {d_{}},{d_{}^{\prime }}\right) \) parameters are equivalent to the eccentricity \({e_{}}\) (aspect ratio) and orientation \({\theta _{}}\) of the ellipse. An interesting property of these parameters is that they are always comprised within the unit circle of their plane. The domain of the accumulator is then well defined and bounded. Also, based on Eq. (13), it is possible to demonstrate that, in the case of this new projection, there is no degenerated case, and that the 5D line is never exactly orthogonal to the \(\left( {d_{}},{d_{}^{\prime }}\right) \) plane.

Accumulation in 2D. Regardless of the chosen (direct or dual) 2D projection, the first step of the algorithm is to iterate on all pairs of edge points which verify the conditions expressed in Eq. (11), and to draw a line in the corresponding plane (2D accumulator). In Fig. 2, the gray lines in the plane \(\left( {C_{}},{C_{}^{\prime }}\right) \) are instances, in the dual framework, of these 2D lines (diameters \(\mathrm {O}_{}^{}\mathrm {M}_{}^{}\)) for several pairs of edge points.

When the accumulation or voting process is complete, we look for the maximum value (or the most prominent cluster). If this value (or the sum of the cluster values) is not large enough, we stop the process with no ellipse detected. Otherwise, the position (a 2D index) of this peak (or cluster center) is chosen as the estimated value \(\left( {\varDelta _{}},{\varDelta _{}^{\prime }}\right) \) of the two ellipse parameters (the big red point in Fig. 2).

Edge Points Selection. In the dual framework, when the detected center is close, in the 2D space \(\left( {C_{}},{C_{}^{\prime }}\right) \), to a line (diameter \(\mathrm {O}_{}^{}\mathrm {M}_{}^{}\)) related to a given pair of edge points, we consider that this pair of edge points has voted for the detected center and we select this pair for the second step of the algorithm. In Fig. 2, the blue line of the plane \(\left( {C_{}},{C_{}^{\prime }}\right) \) is a 2D line which is related to a specific pair of edge points. It passes near the detected center and is then selected as having voted for this center.

3.4 Second Step: Back-Projection

State of the Art Methods. In the literature, authors switch to other methods or algorithms to find the remaining parameters. Most of the time, they use the information about the center location to obtain the equation of the centered ellipse. Then, all the edge points (and their gradients) that previously voted for the detected center are used to provide two conditions on the three remaining parameters. So, by a similar process of line accumulation in a three dimension space, they obtain an estimate of the remaining parameters.

Our Proposed Algorithm. In the framework of the pencil of bi-tangent conics, the three remaining parameters can advantageously be computed by back-projecting the points obtained during the 2D accumulation process onto the line in the full 5D space.

Fig. 2.
figure 2

Back-projection of the estimated center \(\left( {\varDelta _{}},{\varDelta _{}^{\prime }}\right) \) into a 3D space (illustration of the back-projection into a 5D space). (Color figure online)

Full size image

Index of the Closest Ellipse. In Fig. 2, the detected center \(\left( {\varDelta _{}},{\varDelta _{}^{\prime }}\right) \) (big red point) is orthogonally projected onto the 2D line (blue line in the \(\left( {C_{}},{C_{}^{\prime }}\right) \) plane) relating to a specific pair of edge points. As a point of the line, this orthogonal projection should be of the form \(\left( {C_{\kappa }},{C_{\kappa }^{\prime }}\right) \) (given by the two first equations in (12) and (14)), where \(\kappa \) is a specific value for the index \(k\). In the following, \(\kappa \) will be named the index of the closest conic in the pencil defined by this specific pair of edge points.

Likewise, for the direct approach, the same reasoning holds for finding the index of the couple of parameters that is the closest to the estimated values in the \(\left( {d_{}},{d_{}^{\prime }}\right) \) plane.

However, there is a major difference between the two approaches. In the dual approach, when the gradients are parallel, the 5D line is orthogonal to the plane \(\left( {C_{}},{C_{}^{\prime }}\right) \). So, in this situation, it is not possible to derive the value of \(\kappa \) from the estimated center and, for this step, we must discard the pairs of edge points whose gradients are parallel. In the direct approach, there is no such situation; the 5D line is never orthogonal to the plane \(\left( {d_{}},{d_{}^{\prime }}\right) \) and all pairs of edge points may be used for the back-projection step.

The Three Remaining Parameters. In order to compute the three remaining ellipse parameters \(\left( {D_{}},{D_{}^{\prime }},{D_{}^{\prime \prime }}\right) \), we use, in Eq. (14), this index \(\kappa \) of the closest ellipse whose the parameters \(\left( {C_{\kappa }},{C_{\kappa }^{\prime }}\right) \) are the closest to the estimated center \(\left( {\varDelta _{}},{\varDelta _{}^{\prime }}\right) \). This means that a pair of edge points, which voted for a detected center, also provides (or votes for) one 3D vector of the remaining parameters. In Fig. 2, a point \(\left( {C_{\kappa }},{C_{\kappa }^{\prime }}\right) \) on the 2D line corresponds to one 5D point \(\left( {C_{\kappa }},{C_{\kappa }^{\prime }},{D_{\kappa }},{D_{\kappa }^{\prime }},{D_{\kappa }^{\prime \prime }}\right) \).

The last step consists to iterate on all the pairs of edge points supporting the estimated center and to fill a 3D histogram (or three 1D histograms) with the provided vectors of the remaining parameters. If the peak of (or the most prominent cluster in) the histogram is not large enough, no ellipse is detected nor matched. Otherwise, the 3D vector of indices of the peak (or cluster center) is chosen as the estimated value for the three remaining parameters.

Likewise, the same reasoning also holds in the direct approach for finding the three remaining parameters \(\left( {c_{}},{c_{}^{\prime }},{c_{}^{\prime \prime }}\right) \).

Finally, we remove from the list of pairs of edge points those supporting the chosen vector of remaining parameters, and we start the whole process again until no ellipses are detected anymore.

4 Results

To illustrate the feasibility of the methods introduced in this paper, we present some preliminary comparative results between our dual algorithm and the State-of-the-Art (abbreviated SoA in the following) algorithm outlined in Sect. 3.4. Both algorithms have been implemented with the same list of edge points, the same center detection first step, the same accumulator cell size and without any post-processing. Obviously, in a practical set-up, both algorithms could benefit from additional processing step, but we are interested here in the bare properties of the methods.

We built a custom dataset with 100 synthetic images (of size 450 by 600 pixels) containing one random black ellipse on a white background (see on the left of Fig. 3) and we added salt-and-pepper noise and a randomly (Gaussian) textured image.

For comparing the SoA and dual algorithms, we computed the Hausdorff distance between the detected and the true ellipse for each test image; these statistics are given in Table 1. We also provided the numbers of detected ellipses whose Hausdorff distance to the true ellipse are respectively less than 2, 5, 10 and 15 pixels (Table 2).

Table 1. Statistics of the Hausdorff distance between the detected and true ellipse.
Full size table
Table 2. Number of detected ellipses whose Hausdorff distance to the true ellipse is less than the threshold given in the first column.
Full size table

In this experiment, we observe that the dual approach provides a better estimate (in terms of Hausdorff distance) of the ellipse than our implementation of the SoA approach. In addition, if we consider that an ellipse is not (correctly) detected when its Hausdorff distance to the true ellipse is larger than 10, from the Table 2, we see that, in our experiment, \(1\%\) (resp. \(15\%\)) of the ellipse were not detected by the dual (resp. SoA) approach.

Figure 3 shows a typical example of one test image (left) with the true ellipse delineated in red. The background of the middle and the right images represents the same edge points (in white) extracted from the left image. In the middle (resp. right) image, the green curve is the detected ellipse and the red points are the selected edge points, both by our implementation of the SoA (resp. dual) algorithm. The selected edge points (in red) are chosen as being closer than 10 pixels to the ellipse detected and may be used as the input of an additional ellipse fitting step, if necessary. On this example, the Hausdorff distance between the detected and the true ellipse is 11.8 for the SoA algorithm and 3.4 for the dual approach. This illustration, for the SoA algorithm, how a poor precision for the ellipse parameter estimation negatively impacts on the capacity of the algorithm to correctly extract the edge points belonging to an ellipse.

Fig. 3.
figure 3

A sample test image (left), the results of the SoA algorithm (middle), and of our method (right). The detected ellipse is drawn in green and the selected edge points are drawn in red. (Color figure online)

Full size image

5 Conclusions

In this paper, we show that the concept of pencil of bi-tangent conics, either in its direct or dual form, is an adequate framework to discuss the theoretical aspects of the EHT based on pairs of edge points and their associated gradients. The usual process of splitting the full 5D problems into two (or three sometimes) steps of reduced dimension is well modeled by the notion of projection of the problem to a 2D sub-space followed by a back-projection of the results into the full 5D space.

The algebraic coherence allows us to unify both parts of the EHT into a single framework, highlights the eligibility conditions of the pairs of edge points (to be possible evidences of the presence of an ellipse), and is capable to manage special cases for the pairs of edges points or their gradients.

The dual form of the framework copies the first step of the state-of-the-art methods that consists in finding the ellipse center, but it innovates for finding the remaining parameters. Our preliminary results suggest that our new approach could have a better accuracy in the estimation of the ellipse parameters.

The direct form of the framework is, as far as we now, a new approach to reduce the dimension and solve the problem. This direct approach first looks for a couple of ellipse parameters similar to the eccentricity and the orientation. Theoretically, both approaches have benefits and drawbacks; the choice between them will be a matter of practical considerations.

In the future, we expect that the use of direct and dual equations of the pencil of bi-tangent conics for the EHT will pave the way for new approaches.