An Out of Sample Version of the EM Algorithm for Imputing Missing Values in Classification

Abstract

Finding real-world applications whose records contain missing values is not uncommon. As many data analysis algorithms are not designed to work with missing data, a frequent approach is to remove all variables associated with such records from the analysis. A much better alternative is to employ data imputation techniques to estimate the missing values using statistical relationships among the variables.

The Expectation Maximization (EM) algorithm is a classic method to deal with missing data, but is not designed to work in typical Machine Learning settings that have training set and testing set.

In this work we present an extension of the EM algorithm that can deal with this problem. We test the algorithm with ADNI (Alzheimer’s Disease Neuroimaging Initiative) data set, where about 80% of the sample has missing values.

Our extension of EM achieved higher accuracy and robustness in the classification performance. It was evaluated using three different classifiers and showed a significant improvement with regard to similar approaches proposed in the literature.

This work was supported by the Fondecyt Grant 1170123 and in part by Fondecyt Grant FB0821.

1 Introduction

Nowadays, data are generated from several distinct sources: sensor networks, opinion polls about political and socio-economical topic, medical diagnosis, social networks, recommendation systems, etc. Many of these real-world applications suffer from a common drawback, missing or unknown data (incomplete feature vector). This problem makes it very difficult to mine them using Machine Learning (ML) methods that can work only with complete data. The missing data problem can be handled in two ways. Firstly, all samples having a missing record are removed before any analysis takes place. This is a reasonable approach when the percentage of removed samples is low so that a possible bias in the study can be discarded. Secondly, the missing values can be estimated from the incomplete measured data. This approach is known as imputation [6] and is recommended when the adopted data analysis techniques are not designed to work with missing entries as is the case of almost all ML techniques.

The Alzheimer’s Disease Neuroimaging Initiative¹ (ADNI) is a well-known example of a missing data problem [5, 11]. Most of the research related to the ADNI database is made with the purpose of contributing to the development of biomarkers for the early detection (diagnostic) and tracking (prognostic) of Alzheimer Disease (AD). The features belonging to this dataset are derived from longitudinal clinical, medical images (PET, MRI, fMRI), genetic, and biochemical data from patients with Alzheimer disease (AD), mild cognitive impairment (MCI), and healthy controls (HC).

Pattern analysis in ADNI is strongly hampered by missing data, i.e. patients with incomplete records, cases where the different data modalities are partially or fully absent due to several reasons: high measurement cost, equipment failure, unsatisfactory data quality, patients missing appointments or dropping out of the study, and unwillingness to undergo invasive procedures. About 80% of the ADNI patients have missing records. Thus, resorting to missing data imputation becomes mandatory in order to find useful patterns of clinical significance.

Among the most prominent approaches used for data imputation, it can be found the well-known and widely used Expectation-Maximization (EM) algorithm. On its classic form, the EM algorithm is an iterative and general method to estimate the parameters $\theta$ of a probability distribution by means of likelihood maximization. The method, proposed by Dempster [1], can be summarized in the E-Step and the M-Step. The E-Step computes a function for the expectation of the log-likelihood function using the current estimate of the parameters. Then, the M-Step computes the new values of the parameters maximizing the expected.

Many subsequent improvements based on the original EM algorithm idea can be found in the literature. Consider the work of Schneider [8] in which a new step of imputation is added based on a regression framework.

Existing approaches for imputation of missing data rely on the necessity of the whole incomplete data matrix and do not allow to evaluate new samples once the model is trained. This characteristic makes some existing methods for imputation, including Schneider method, not suitable for most Machine Learning algorithms. In this context, some authors [3, 10] call to the methods can be evaluate new samples: Out-of-Sample version.

This work presents an out-of-sample extension for applying the EM algorithm in missing data problems. The idea behind the proposed method is to introduce a new version of the EM algorithm to impute missing data in ADNI and then using the imputed data to improve the classification of subjects.

The Paper is Organized as Follow: In Sect. 2 we provide further background on the reguralized EM (regEM, Schneider proposal) and EM Out-of-Sample (regEM-oos) version (proposal of this work). Section 3 details the experimental settings on which we tested the different classification problems with regEM and regEM-oos, discussing our findings. Final remarks and future work are examined in Sect. 4.

2 Proposal

This section introduces the proposed approach for feature imputation. Let us begin by introducing the notation used through this work. A data matrix $X_{n\times d}$ can be represented by $\mathbf {X}=[\mathbf {x}_{1},\mathbf {x}_{2},\dots ,\mathbf {x}_{j},\dots ,\mathbf {x}_{d}]$, where d is the total number of variables (or features) and n is the total number of examples (or subjects). When $\mathbf {X}$ has missing data, X is represented by concatenating two submatrices, i.e. $\mathbf {X}=[\mathbf {X}_{o},\mathbf {X}_{m}]$, where $\mathbf {X}_{o}$ is the matrix of fully observed features and $\mathbf {X}_{m}$ is the matrix that encompasses features with missing values.

Our proposal leverages the EM algorithm and the approach proposed by Schneider [8] for missing data imputation. This method will be summarized as follows. The algorithm iterates between three steps, the E-Step, the M-step and the imputation step. In the E-step, the expected of the log-likelihood function is computed using the current estimate of the log-likelihood parameters. During the M-step, new estimates of the log-likelihood function parameters are obtained using the previous log-likelihood estimates obtained during the E-step. Formally, the E-Step and M-Step can be expressed as:

where $\theta _{t}$ is the vector of parameters in the iteration t and $l(\cdot )$ is the log-likelihood function.

The imputation step is made by using a linear regression model that connects the variables with missing values and the variables without missing values:

$$\begin{aligned} x_{m} = \mu _{m} + (x_{o} - \mu _{o})\beta + e \end{aligned}$$

(1)

where $x_{o} \in \mathbb {R}^{1\times p_{o}}$ is the sub-vector of $p_{o}$ variables with observable data, $x_{m} \in \mathbb {R}^{1\times p_{m}}$ is the sub-vector of $p_{m}$ variables with missing values, $\mu _{o} \in \mathbb {R}^{1\times p_{o}}$ is the sub-vector with the mean of the variables with observable data and $\mu _{m} \in \mathbb {R}^{1\times p_{m}}$ is the sub-vector with the mean of the variables with missing values. $\beta \in \mathbb {R}^{p_{o}\times p_{m}}$ is the coefficients regression matrix and $e \in \mathbb {R}^{1\times p_{m}}$ is a random vector with mean 0 (zero) and an unknown covariance matrix $C \in \mathbb {R}^{p_{m}\times p_{m}}$.

$\widehat{\beta } = \widehat{\varSigma }^{-1}_{oo}\widehat{\varSigma }_{om}$, where $\widehat{\varSigma }_{oo}$ is the covariance matrix estimated from variables with observable values and $\widehat{\varSigma }_{om}$ is the covariance matrix estimated from variables with missing and observable values.

In the Schneider’s approach [8], the inverse of the covariance matrix of the observed data, $\widehat{\varSigma }_{oo}^{-1}$, is iteratively estimated according to the expression:

$$\begin{aligned} \widehat{\varSigma }_{oo}^{-1} \longleftarrow (\widehat{\varSigma }_{oo} + h^{2}\widehat{D})^{-1} \end{aligned}$$

(2)

where $\widehat{D} = Diag(\widehat{\varSigma }_{oo})$ is the diagonal matrix consisting of the diagonal elements of the covariance matrix $\widehat{\varSigma }_{oo}$ and h is a regularization parameter. That is, the ill-conditioned inverse $\widehat{\varSigma }_{oo}^{-1}$ is replaced with the inverse of the matrix that results from the covariance matrix $\widehat{\varSigma }_{oo}^{-1}$ when the diagonal elements are amplified.

This version of the EM algorithm (regEM) is used in several works [7, 9], where the datasets have missing values and it is necessary to perform the classification task. In this context, the typical way to use this algorithm is to apply it to the training set and then, separately, to use it in the testing set. This way of using it, we consider that it is not correct, since every algorithm that works with a training set, must create a model, which will be later applied to the testing set. This methodology is always performed with the classification algorithms (ANN, SVM, etc.) and should also be applied with pre-processing algorithms, such as dimensionality reduction techniques, and missing values imputation algorithms.

In addition to the above mentioned remarks, our approach solves the problem that arises when the testing set arrives one data point at a time (very typical in real situations), since the original proposal can not construct the imputation model, since it is based on a regression model.

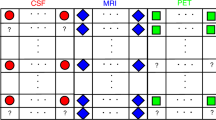
We will call this new version: regEM-Out of Sample (regEM-oos). regEM-oos can be applied in scenarios where both the training set and the testing set have missing values. Once used in the training set, the algorithm creates a general model that consists of as many regression models as missing patterns exist in the training set. These regression models are based on the Eq. 1, therefore in addition to using the matrix $\beta$, the vector of mean $\mu$ must be used. An example of this procedure, with three information sources $S_{i}$ and three missing values patterns is shown in Fig. 1.

Fig. 1.

Each missing values (MV) pattern in the training set has a regression model. Then, these regression models are used to impute the missing values in the testing set.

Although it is very rare, it may occur that a new MV pattern appears in the testing set. This means that this MV pattern does not have a regression model and therefore the imputation can not be made directly. To solve this, it is necessary to return to the training set and build a model for this new pattern. With the training set already imputed, we proceed to generate the new pattern found in the testing set, but in a synthetic way. With this, an imputation model of the new pattern found is obtained to make future imputations in the testing set.

3 Experimental Results

With the purpose of illustrating how well our approach performs, we consider three baseline ADNI modalities: cerebrospinal fluid (CSF), magnetic resonance imaging (MRI) and positron emission tomography (PET). The modalities were preprocessed according to [4], with 43 out of 819 subjects excluded for not passing the quality control. The CSF source contains three variables that measure the levels of some proteins and amino acids that are crucially involved in AD. The MRI source provides volumetric features of 83 brain anatomical regions. The PET source (with FDG radiotracer) provides the average brain function, in terms of the rate of cerebral glucose metabolism, within the 83 anatomical regions. Hence, each subject consists of 169 features. Table 1 shows details of the data distribution.

Table 1. Details of the data. First column shows the amount of examples for each class. The other columns show the amount of examples with MV per modalities. Individuals with MCI can be divided into two groups: those who remained in a stable condition (s-MCI) and those who later progressed to AD (p-MCI).

We consider three experiments: AD/HC with 395 subjects and MCI/HC with 591 subjects and pMCI/sMCI with 381 subjects. In each experiment we used 75% of the data to train three classifiers, a K-Nearest Neighbors (K-NN), a $\nu$-Support Vector Machine ($\nu$-SVM) and a Random Forest (RF) models, evaluated over 100 runs to avoid bias. The remaining 25% of the data was used for testing. We employed the implementations found in the scikit-learn library². The number K and $metric\_distance$ for K-NN, $\nu$ and $\sigma$ for $\nu$-SVM and the number of trees and number of features for RF were determined using 5-fold CV.

We performed a normalization process before of the classification step following the Out-of-sample strategy. Considering we want the features had an interval [0, 1], the testing set was normalized with:

$$\begin{aligned} X_{norm}^{te} = \frac{X_{raw}^{te} - X_{min}^{tr}}{X_{max}^{tr} - X_{min}^{tr}} \end{aligned}$$

(3)

where $X_{min}^{tr}$ and $X_{max}^{tr}$ are the minimum and maximum from the training set respectively, and $X_{raw}^{te}$ is the original values from the testing set.

For completeness, we include the results when the classifiers are trained solely with the reduced set of subjects having complete records and thus no imputation is needed. The number of subjects in this case is 72 for AD/HC, 110 for MCI/HC and 75 for pMCI/sMCI and is represented with none in the tables.

Tables 2, 3 and 4 show the classification results for the experiments based on ROC analysis [2].

Table 2. AD/HC multi-modality classification accuracy (acc.), area under the curve (AUC), sensitivity (sens.), specificity (spec.), and F-measure (F). Results are expressed as mean (standard deviation).

Table 3. MCI/HC multi-modality classification accuracy (acc.), area under the curve (AUC), sensitivity (sens.), specificity (spec.), and F-measure (F). Results are expressed as mean (standard deviation).

Table 4. pMCI/sMCI multi-modality classification accuracy (acc.), area under the curve (AUC), sensitivity (sens.), specificity (spec.), and F-measure (F). Results are expressed as mean (standard deviation).

It can be noted that the classification improves when the full data set is used, imputing the missing values. This clearly provides more information to discriminate among the different diagnostic groups.

These experiments suggest that regEM-oos have the best performance in AD/HC, MCI/HC and pMCI/sMCI considering that when the difference is small, a lower standard deviation is preferred.

The classifiers present similar performances in each experiment, but a remarkable point is that their robustness (low variance) is increased in cases in which imputation is performed. Additionally, regEM-oos has the least variance in almost all experiments.

Regarding to execution time, an important feature of regEM-oos is that is faster than the regEM approach in about 27%. This is because regEM creates a new model for the testing set and regEM-oos use the model created from the training set. Obviously, while the testing set is larger, the time saving would become more significant.

4 Conclusions and Future Work

We have seen how imputation techniques allow using additional information, that in absence of accurate imputation methods would be discarded. In our experiments we have showed that using our imputation method we can achieve more accurate results in the task of determining the diagnostic groups to which ADNI’s subjects belong.

Our results showed that training classifiers with imputed data is better than constructing a predictive model with a reduced number of subjects with complete records. This is supported in part by the fact that the imputation techniques increase both performance metrics and robustness of the classifiers.

It is necessary to use the Out-of-sample version of the algorithms when we are working in classification problems. Creating a model with the training set, and then using it in the testing set is one of the most relevant principles in Machine Learning. This issue is not typically taken into account within the imputation and dimensionality reduction literature.

In this work we presented a straightforward Out-of-sample version of regEM (regEM-oos) that improves the performance of the original algorithm, considering execution time and metrics based on ROC analysis.

Future work includes studying the performance of regEM-oos with other data sets and from the theoretical point of view. Furthermore, there is an interest in analyzing the relationship between the imputation and classification accuracies.

An interesting approach would be to consider the information of the labels from the training set to create a model for each class. With an ad-hoc model for each class we believe that the imputation and classification will be better, but the problem that must be addressed is how to decide which model should be used when new testing data becomes available.