1 Introduction

This paper discusses the construction of stochastic forecasts of human mortality and fertility rates and their use in making stochastic forecasts of pension funds. The method of mortality analysis was developed by Lee and Carter (1992), henceforth called the LC method. Lee and Tuljapurkar (1994) combined the LC method with a related fertility forecast to make stochastic population forecasts for the US. Tuljapurkar and Lee (1999) and Lee and Tuljapurkar (2000) combined these population forecasts with a number of other forecasts to generate stochastic forecasts of the US Social Security system.

My goal is to explain the distinctive features, strengths, and shortcomings of the stochastic method rather than to explain the method. I begin with a discussion of stochastic forecasts and their differences from scenario forecasts. Then I discuss mortality forecasts using Swedish mortality data, including a new forecast for Sweden. I go on to consider briefly how population forecasts are made and their use in modeling pension systems.

2 Stochastic Forecasts

A population forecast made in year T aims to predict population P(t) for later years, where P includes numbers and composition. The information on which the forecast is based includes the history of the population and of environmental factors (economic, social, etc.). Every forecast maps history into a prediction. Scenario forecasts rely on a subjective mapping made by an expert, whereas stochastic forecasts attempt to make an explicit model of the historical dynamics and project this dynamic into the future. Stochastic forecasts may rely partly on a subjective mapping as well. What are the pros and cons of the two approaches?

When historical data contain a strong “signal” that describes the dynamics of a process, it is essential to use the signal as a predictive mechanism. Equally, it is important to include information that is not contained in the signal – this residual information is an important element of uncertainty that should be reflected in the forecast. The LC method shows that there is such a signal in mortality history. When there is no strong signal in the historical data, a subjective prediction may be unavoidable. Fertility history tends to reveal relatively little predictive signal. Even here, uncertainty ought to be included because history does tell us about uncertainty, and we can estimate the variability around a subjective prediction.

The use of history to assess uncertainty certainly does make assumptions about persistence in the dynamic processes that drive the variables we study. This does not imply that we assume an absence of surprises or discontinuities in the future. Rather it assumes that all shocks pass through a complex filter (social, economic, and so on) into demographic behavior, and that future shocks will play out in the same statistical fashion as past shocks. I would not abandon this assumption without some demonstration that the filtering mechanisms have changed – witness for example the stock market bubble in the US markets in 1999–2000 and its subsequent decline. It may be useful to think about extreme scenarios that restructure aspects of how the world works – one example is the possibility that genomics may change the nature of both conception and mortality in fundamental ways – but I regard the exploration of such scenarios as educational rather than predictive.

I argue strongly for the systematic prediction of uncertainty in the form of probability distributions. This position does not argue against using subjective analysis where unavoidable. One way of doing a sound subjectively based analysis is to follow the work of Keilman (1997, 1998) and Alho and Spencer (1997) and use a historical analysis of errors in past subjective forecasts to generate error distributions and project them. The practice of using “high-low” scenarios should be avoided. Uncertainty accumulates, and must be assessed in that light. In my view, the best that a scenario can do is suggest extreme values that may apply at a given time point in the future – for example, demographers are often reluctant to believe that total fertility rate (TFR) will wander far from 2 over any long interval, so the scenario bounds are usually an acceptable window around 2, such as 1.5–2.2. Now this may be plausible as a period interval in the future but in fact tells us nothing useful about the dynamic consequences of TFR variation over the course of a projection horizon.

Uncertainty, when projected in a probabilistic manner, provides essential information that is as valuable as the central location of the forecast. To start with, probabilities tell us how rapidly the precision of the forecast degrades as we go out into the future. It can also be the case that our ability to predict different aspects of population may differ, and probability intervals tell us about this directly. Probabilities also make it possible to use risk metrics to evaluate policy: these are widely used in insurance, finance, and other applications, and surely deserve a bigger place in population-related planning and analysis.

3 Mortality Forecasts

The LC method seeks a dominant temporal “signal” in historical mortality data in the form of the simplest model that captures trend and variation in death rates, and seeks it by a singular-value decomposition applied to the logarithms log m(x, t) of central death rates. For each age x subtract the sample average a(x) of the logarithm, and obtain the decomposition

$$ \log\;\mathrm{m}\left(\mathrm{x},\mathrm{t}\right)-\mathrm{a}\left(\mathrm{x}\right)={\sum}_{\mathrm{i}}{\mathrm{s}}_{\mathrm{i}}\;{\mathrm{u}}_{\mathrm{i}}\left(\mathrm{x}\right)\;{\mathrm{v}}_{\mathrm{i}}\left(\mathrm{t}\right). $$

On the right side above are the real singular values s1 ≥ s2 … ≥ 0. The ratio of \( {\mathrm{s}}_1^2 \) to the sum of squares of all singular values is the proportion of the total temporal variance in the transformed death rates that is explained by just the first term in the singular-value decomposition.

In all the industrialized countries that we have examined, the first singular value explains well over 90% of the mortality variation. Therefore we have a dominant temporal pattern, and we write

$$ \log\;\mathrm{m}\left(\mathrm{x},\mathrm{t}\right)=\mathrm{a}\left(\mathrm{x}\right)+\mathrm{b}\left(\mathrm{x}\right)\;\mathrm{k}\left(\mathrm{t}\right)+\mathrm{E}\left(\mathrm{x},\mathrm{t}\right). $$

The single factor k(t) corresponds to the dominant first singular value and captures most of the change in mortality. The far smaller variability from other singular values is E(x, t).

The dominant time-factor k(t) displays interesting patterns. Tuljapurkar et al. (2000) analyzed mortality data in this way for the G 7 countries over the period from approximately 1955–1995. They found that the first singular value in the decomposition explained over 93% of the variation, and that the estimated k(t) in all cases showed a surprisingly steady linear decline in k(t). The mortality data for Sweden from 1861 to 1999 constitute one of the longest accurate series, and a similar analysis in this case reveals two regimes of change in k(t). The estimated k(t) for Sweden is shown in Fig. 12.1. There is steady decline from 1861 to about 1910 and after 1920 there is again steady decline but at a much faster rate. Note that the approximately linear long-term declines are accompanied by quite significant short-term fluctuations. It is possible that we can interpret period-specific fluctuations in terms of particular effects (e.g., changes in particular causes of death) but it is difficult to project these forward. For example, the change in the pattern in the early 1900s is consistent with our views of the epidemiological transition, but we do not know if the future will hold such a qualitative shift. Within the twentieth century we take the approach of using the dominant linearity coupled with superimposed stochastic variation.

Fig. 12.1
figure 1

Lee Carter k(t) Sweden 1861 to 1999

Full size image

Mortality decline at any particular age x is proportional to the signal k(t) but its actual magnitude is scaled by the response profile value b(x). Figure 12.2 shows the b(x) profiles computed for Swedish data using 50 year spans preceding the dates 1925, 1945, 1965, and 1985. Note that there is a definite time evolution, in which the age schedules rotate (around an age in the range 40–50) and translate so that their weight shifts to later ages as time goes by. This shifting corresponds to the known sequence of historical mortality decline starting with declines initially at the youngest ages and then in later ages over time. An intriguing possibility is that temporal changes in the b(x) schedules may be described by a combination of a scaling and translation – a sort of nonlinear mapping over time. An important matter for future work is to explore the time evolution of the b(x), even though it appears (see below) that one can make useful forecasts over reasonable time spans of several decades by relying on a base span of several decades to estimate a relevant b(x).

Fig. 12.2
figure 2

b(x) Response factors Sweden

Full size image

What accounts for the regular long-term decline in mortality that is observed over any period of a few decades? It is reasonable to assume that mortality decline in this century has resulted from a sustained application of resources and knowledge to public health and mortality reduction. Let us assume, as appears to be the case, that societies allocate attention and resources to mortality reduction in proportion to observed levels of mortality at different ages (e.g., immunization programs against childhood disease, efforts to reduce cardiovascular disease at middle age). Such allocation would produce an exponential (proportional) change in mortality, though not necessarily at a constant rate over time. Over time, the rate of proportional decline depends on a balance between the level of resources focused on mortality reduction, and their marginal effectiveness. Historically, the level of resources has increased over time but their marginal effectiveness has decreased over time (because, for example, we are confronted with ever more complex causes of mortality that require substantial resources or new knowledge). The observation of linearly declining k(t) – roughly constant long-run exponential rates of decline – implies that increasing level and decreasing effectiveness have balanced each other over long times. It is of course possible that the linear pattern of decline we report has some other basis. For the future, we expect a continued increase in resources spent on mortality reduction, and a growing complexity of causes of death. The balance between these could certainly shift if there were departures from history – for example, if new knowledge is discovered and translated into mortality reductions at an unprecedented rate. But this century has witnessed an amazing series of discoveries that have altered medicine and public health, and there is no compelling reason why the future should be qualitatively different. Therefore, I expect a continuation of the long-run historical pattern of mortality decline.

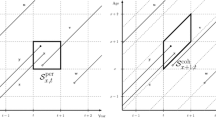
The LC method uses the long-term linear decline in k(t) to forecast mortality. A naive forecast based on the long-run trend is not sensible because the short-term variation will accumulate over time, so it is essential to employ a stochastic forecast. In LC, the stochastic term E(t) is modeled as a stationary noise term, and this procedure leads to forecasts for Sweden as shown in Fig. 12.3, for life expectancy at birth, e00, and in Fig. 12.4 for life expectancy at age 65, e65. In both cases we use a 50-year span of historical data prior to a launch date of 1999. The intervals shown are 95% prediction intervals for each forecast year. Notice that there are separate forecasts for each sex, as well as a combined-sex forecast. The joint analysis of the two sexes in an LC framework has not been fully resolved, although Li et al. (2004) suggest one method for doing this.

Fig. 12.3
figure 3

e0 Stochastic forecast Sweden launch 1999

Full size image
Fig. 12.4
figure 4

e65 Stochastic forecast Sweden, launch data 1999

Full size image

Some previous comments on the LC method have asserted that it is simply equivalent to a linear extrapolation in the log scale of the individual rates at each age, but it is not. For one thing, the extrapolations would include elements of the E(t) terms in each age, and these may be larger at some ages than at others. For another, I take the stochastic variation seriously as an integral part of the forecast, and the realized long run trend can be rather different depending on where in the prediction interval one ends up. Without this variability, the forecasts would not be terribly useful over long horizons.

To illustrate the robustness of the LC method, Lee and Miller (2001) have analyzed the performance of the method using internal validation. A more extensive analysis for Sweden echoes their finding that the method is surprisingly robust. To illustrate, I use different base periods to forecast e0 in 1999. I first select a starting base year, say 1875, and then a launch year which is chosen from the set 1935, 1945, …, 1995; this gives a total of seven forecasts starting in 1875. We expect that a forecast for 1999 using the 1875–1935 base period would be much less accurate than a forecast which uses the 1875–1995 base period. The object of the exercise is to see whether the projection intervals for e0 in 1999 will decrease in some systematic way as we include more recent (relative to 1999) history and whether they speak to the accuracy of the method. Figure 12.5 plots the projection intervals obtained in this way, using each of three starting years (1875, 1900, or 1925) and the seven launch years indicated above, so for each starting year we have an upper and lower prediction “fan” for e0 in 1999. The figure shows that as we use more recent histories, we close in on the true 1999 value of e0 of 79.4 years – the 95% prediction interval brackets the true value most of the time which is impressive especially when compared with the historical performance of scenario forecasts. From a practical point of view, the prediction interval width is under 7 years for launch dates from 1960 to 1980 and any of the starting base years. This means that we may expect a reasonable performance from LC forecasts for as far as 40 years into the future.

Fig. 12.5
figure 5

Forecasts that use data going back to 1875, 1900, 1925

Full size image

4 From Population to Pension Systems and Policy

For a population forecast we must supplement mortality forecasts with similar forecasts for fertility and if necessary for immigration. These elements can then be combined in the usual cohort-component procedure to generate stochastic population forecasts. Fertility forecasts pose special challenges because there does not seem to be a strong temporal pattern to fertility dynamics. Lee and Tuljapurkar (1994) use time series models for fertility to make stochastic forecasts for the US. Their simple models have been considerably extended by Keilman and Pham (2004) who suggest several ways of modeling and constraining the volatility of fertility forecasts.

How can stochastic forecasts be used in analyzing pension policy? At a purely demographic level, it is well known that the old-age dependency ratio is the key variable that underlies pension costs. As the old-age dependency ratio for a population increases, the more retirees-per-worker there are in the population, which implies greater stress on a pay-as-you-go pension system which relies on today’s workers to pay the benefits of today’s retirees. An interesting insight into the demographic impact of aging on the dependency ratio can be created by asking the following question. Suppose that the age at which people retire is, e.g., 65. If this “normal retirement age” age cutoff could be changed arbitrarily, how high would we have to raise it in order to keep the dependency ratio constant? If we have a population trajectory forecast, then we can simply compute in each year the retirement age, say R(t), at which the old-age dependency ratio would be the same ratio as in the launch year. When we have stochastic forecasts, there is, in each forecast year t, a set of random values R(t); in our analysis we look for the integer value of R(t) that comes closest to yielding the target dependency ratio. Figure 12.6 shows the results of computing these stochastic R(t) for the US population. What is plotted is actually three percentiles of the distribution of R(t) in each year, the median value, and the upper and lower values in a 95% projection interval. The plots show some long steps because the dependency ratio distribution changes fairly slowly over time. The smooth line shows the average value of R(t) for each forecast year, which is surprisingly close to the median. Observe, for example, that there is a 50% chance that the “normal retirement age” would have to be raised to 74 by 2060 in order to keep the dependency ratio constant at its 1997 value. There is only a 2½% chance that the “normal retirement age” of 69 years would suffice. Given that current US Social Security policy is only intended to raise the “normal retirement age” to 67 years, and that even the most draconian proposals would only raise it to 69 years, we conclude that changes in the “normal retirement age” are very unlikely to hold the dependency ratio constant. Anderson et al. (2001) present similar results for the G7 countries. In Tuljapurkar and Lee (1999) there are additional examples of how stochastic forecasts can be combined with objective functions to analyze fiscal questions.

Fig. 12.6
figure 6

Normal retirement age to maintain US old-age dependency ratio, 1997-2072

Full size image

To go beyond this type of analysis we need a full model of the structure of a pension system which may be “fully funded” or “pay-as-you-go” or some mixture. Many systems, in order to operate with a margin of security, are modified versions of pay-as-you-go systems that include a reserve fund. In the United States the OASDI (Old Age Survivors and Disability Insurance, or Social Security) Trust Fund, the holdings of the system are federal securities, and the “fund” consists of federally-held debt. A fund balance earns interest, is subject to withdrawals in the form of benefit payments, and receives deposits in the form of worker contributions (usually in the form of tax payments). Lee and Tuljapurkar (2000) discuss such models for the US Social Security system and also for other fiscal questions. The dynamics of such models proceed by a straightforward accounting method. Starting with a launch year (initial year) balance, we forecast contributions and benefit payments for each subsequent year, as well as interest earned. This procedure yields a trajectory of fund balance over time. Future contributions depend both on how many workers contribute how much to the system. Future benefit payments depend on how many beneficiaries receive how much in the future. Our population forecasts do not directly yield a breakdown in terms of workers and retirees. Therefore, we estimate and forecast per-capita averages by age and sex, for both contributions and benefits. We combine these age and sex-specific “profiles” with age and sex-specific population forecasts to obtain total inflows and outflows for each forecast year.

Contribution profiles evolve over time according to two factors. First, increases in contributions depend in turn on increases in the real wage. We forecast real wage increases stochastically (as described below), and contributions increase in proportion to wages. Second, changes in the labor force participation rates also affect contributions; we forecast labor force participation rates deterministically. Benefit profiles evolve over time in response to several factors. In our model of the U.S. Social Security system, we disaggregate benefits into disability benefits and retirement benefits. Retirement benefit levels reflect past changes in real wages because they depend on a worker’s lifetime wages. Also, legislated or proposed changes in the Normal Retirement Age (the age at which beneficiaries become eligible to collect 100% of their benefits) will reduce benefits at the old NRA.

Demographic variables are obviously not the only source of uncertainty facing fiscal planners; there are sizable economic uncertainties as well. Taxes and future benefits usually depend on wage increases (economic productivity) and funds can accumulate interest or investment returns on tax surpluses. Our models combine uncertainty in productivity and investment returns by converting productivity to real 1999 dollars, subtracting out increases in the CPI. We then model productivity rates and investment returns stochastically.

There is substantial correlation between interest rates on government bonds and returns to equities, so it is important to model these two variables jointly. For our historical interest rate series we use the actual, effective real interest rate earned by the trust fund, and for historical stock market returns we use the real returns on the overall stock market as a proxy. These two series are modeled jointly as a vector auto-regressive process.

Our stochastic model allows us to simulate many (1000 or more, usually) trajectories of all variables and obtain time trajectories of the fund balance from which we estimate probabilities and other statistical measures of the system’s dynamics. This method may be used to explore the probability that particular policy outcomes are achieved, for example, that the “fund” stays above a zero balance for a specified period of years, or that the level of borrowing by the fund does not exceed some specified threshold.