Learning Soft-Consistent Correlation Filters for RGB-T Object Tracking

Abstract

To track objects efficiently and effectively in adverse illumination conditions even in dark environment, this paper presents a novel soft-consistent correlation filters (SCCF) using RGB and thermal infrared (RGB-T) data for visual tracking. The proposed SCCF uses soft consistency to take both collaboration and heterogeneity into account for joint learning of the correlation filters of RGB and thermal spectra, while the computational time is reduced significantly by employing the Fast Fourier Transform (FFT). Moreover, a novel weighted fusion mechanism is proposed to compute the final response map in the detection phase. Extensive experiments on the benchmark dataset show that the proposed approach performs favorably against state-of-the-art methods, while runs at 50 frames per second.

1 Introduction

Visual tracking is an active research area in the computer vision community, since it is an essential and significant task in various applications, such as visual surveillance, robotics, human-computer interaction, and self-driving systems, to name a few [8, 21, 22]. Despite of many breakthroughs recently [16, 23, 29], the visual tracking mainly relies on traditional RGB sensors and tracks target objects in case of cluttered background and low visibility at night and in bad weather, and is thus still regarded as a challenging problem.

The adoption of thermal infrared sensors has provided new opportunities to advance the state-of-the-art trackers by handle the aforementioned challenges [13, 15, 17,18,19,20, 26]. However, how to perform efficient and effective fusion of different modalities for boosting tracking performance is an open issue.

In recent years, many methods [13, 18,19,20, 26] have been proposed to fuse different spectra for improving tracking performance. Some trackers [13, 20, 26] focus on the sparse representation in Bayesian filtering framework because of its capability of suppressing noises and errors. Some trackers [13, 19] introduce spectral weights to fuse RGB and thermal information. Despite all these significant progress, these methods [13, 19] still have some limitations. These methods only consider the collaboration of different source data. However, different spectra are usually heterogeneous (e.g., RGB and thermal), and thus direct fusion that only employs the collaboration might be ineffective. On the other hand, the method [13] based on collaborative sparse representation in Bayesian filtering framework is time-consuming. However, most applications demand real-time tracking.

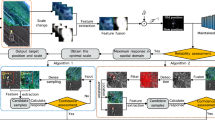
To deal with these issues, we present a novel multi-spectral approach based on correlation filters [10] to perform efficient object tracking. Specifically, we propose a novel scheme to deploy the inter-spectral information by imposing soft consistency in the correlation filters. Our method take both the collaboration and the heterogeneity of different spectral information into account for more effective fusion. For the collaboration, we observe that the learned filters should select similar circular shifts such that they have similar motion. While for the heterogeneity, we intend to allow filters have sparse different elements to each other. Moreover, we design a novel mechanism to fuse RGB and thermal information for robust visual tracking. We calculate the spectral weights according to the response map in the detection phase, and the final response map is obtained by weighted fusion of each spectral response map.

We validate the effectiveness and efficiency of the proposed method on the benchmark dataset, i.e., GTOT [13], and the results show that our approach achieves big superiority in terms of accuracy and comparable performance in terms of efficiency.

To summarize, the main contributions of this work are three-fold.

• A novel soft-consistent correlation filters for RGB-T object tracking is proposed. In order to take both collaboration and the heterogeneity of RGB and thermal spectra into account, the correlation filters of multi-spectral are learned jointly by imposing soft consistency. And the computational time is reduced significantly by employing the Fast Fourier Transform (FFT).

• A spectral fusion mechanism is designed. The spectral weights are obtained according to the response map in the detection phase, and the final response map is obtained by weighted fusion of different spectra.

• It performs favorably against a number of state-of-the-art trackers with the running speed over 50 frames per second. To facilitate further studies, our source code will be made available to the public.

2 Related Work

We review the related work to us from two research streams, i.e., RGB-T object tracking and Correlation filter tracking.

2.1 RGB-T Object Tracking

RGB-T object tracking has drawn a lot of attentions in the computer vision community with the popularity of thermal infrared sensors [3, 13, 14, 18,19,20, 26]. Cvejic et al. [3] investigate the impact of pixel-level fusion of videos from RGB-T surveillance cameras, and accomplish their tracker by means of a particle filter with the fusion of a color cue and the structural similarity measure. Wu et al. [26] and Liu and Sun [20] directly employ the sparse representation to calculate the likelihood score using reconstruction residues or coefficients in Bayesian filtering framework. They ignore modality reliabilities in fusion, which may limit the tracking performance when facing malfunction or occasional perturbation of individual sources. Li et al. [13] and Li et al. [19] introduce modality weights to handle this problem, and propose sparse representation based algorithms to fuse RGB and thermal information. Different from these methods, we take both collaboration and the heterogeneity of RGB and thermal spectrums into account by imposing soft consistency in the correlation filter tracking framework to perform efficient and effective multispectral tracking.

2.2 Correlation Filter Tracking

Correlation filters have achieved great breakthroughs in visual tracking due to its accuracy and computational efficiency [1, 4,5,6,7, 10, 11, 29]. Bolme et al. [1] first introduce correlation filters into visual tracking, named MOSSE, and achieve hundreds of frames per second, and high tracking accuracy. Recently, many researchers further improve MOSSE from different aspects. For example, Henriques et al. [10, 11] extend MOSSE to non-linear one with kernel trick, and incorporate multiple channel features efficiently by summing all channels in kernel space. To handle scale variations, Danelljan et al. [4] learn correlation filters for translation and scale estimation separately by using a scale pyramid representation. Dong et al. [7] propose a sparse correlation filter for combining the robustness of sparse representation and the efficiency of correlation filter. Zhang et al. [29] integrate multiple parts and multiple features into a unified correlation particle filter framework to perform effective object tracking.

3 Proposed SCCF Tracker

In this section, we first present the technical details of the proposed algorithm and then describe the optimization process of the model.

3.1 SCCF Formulation

For a typical correlation filter, many negative samples are used to improve the discriminability of the track-by-detector scheme. In this work, denote $\mathbf{x}_k$ as the feature vector of ${M \times N \times D}$ of k-th spectrum, where M, N, and D indicates the width, height, and the number of channels, respectively. We consider all the circular shifts of $\mathbf{x}_k$ along the M and N dimensions as training samples of k-th spectrum. Each shifted sample $\mathbf{x}^k_{m,n}$, $(m,n) \in \{0,1,...,M-1\} {\times } \{0,1,...,N-1\}$, has a Gaussian function label $y(m,n) = e^{-\frac{(m-M/2)^2+(n-N/2)^2}{2\sigma ^2}}$, where $\sigma$ is the kernel width. Let $\mathbf{X}_k = [\mathbf{x}_{0,0},...,\mathbf{x}_{m,n},...\mathbf{x}_{M-1,N-1}]^\mathrm{T}$ denote all training samples of the k-th spectrum ${(k = 1,...,K)}$. The purpose is to find the optimal correlation filters $\mathbf{w}_k$ for K different spectra,

$$\begin{aligned} \begin{aligned} \min _{\mathbf{w}_k}\sum _{k=1}^K \frac{1}{2}||{\mathbf{X}_k\mathbf{w}_k}-\mathbf{y}||^2_2+\lambda _1||\mathbf{w}_k||_2^2, \end{aligned} \end{aligned}$$

(1)

where $\lambda _1$ is a regularization parameter. The objective function (1) can equivalently be expressed in its dual form,

$$\begin{aligned} \begin{aligned} \min _{\mathbf{z}_k}\sum _{k=1}^K \frac{1}{4\lambda _1}{} \mathbf{z}_k^\mathrm {T} \mathbf{G}_k\mathbf{z}_k + \frac{1}{4}{} \mathbf{z}_k^\mathrm {T}{} \mathbf{z}_k - \mathbf{z}_k^\mathrm {T}{} \mathbf{y}. \end{aligned} \end{aligned}$$

(2)

Here, the vector $\mathbf{z}_k$ contains $M {\times } N$ dual optimization variables $\mathbf{z}^k_{m,n}$, and $\mathbf{G}_k = \mathbf{X}_k\mathbf{X}_k^\mathrm{T}$. The two solutions are related by $\mathbf{w}_k = \frac{\mathbf{X}_k^\mathrm {T}{} \mathbf{z}_k}{2\lambda _1}$. The discriminative training samples $\mathbf{x}^k_{m,n}$ are selected by the learned $\mathbf{z}^k_{m,n}$ to distinguish the target object from the background. Obviously, the training samples $\mathbf{x}^k_{m,n}$, $(m,n) \in \{0,1,...,M-1\} {\times } \{0,1,...,N-1\}$ are the all possible circular shifts, which denote the possible locations of the target object.

Most of existing works only consider the collaboration of different source data [13, 19]. However, different spectra are usually heterogeneous (e.g., RGB and thermal), and thus direct fusion that only employs the collaboration might be ineffective. Therefore, in this paper, we propose a novel scheme to take both the collaboration and the heterogeneity of different spectral information into account for more effective fusion. For the collaboration, we observe that the learned $\{\mathbf{z}_k\}$ should select similar circular shifts such that they have similar motion. While for the heterogeneity, we intend to allow $\{\mathbf{z}_k\}$ have sparse different elements to each other. Taking the above considerations together, we propose a soft-consistent constraint on $\{\mathbf{z}_k\}$ that makes them consistent while allowing the sparse inconsistency exists, and formulated as a $l_1$-optimization based sparse learning problem. Finally, we obtain the soft-consistent correlation filter(SCCF) for multi-spectral tracking as

$$\begin{aligned} \begin{aligned} \min _{\mathbf{z}_k}\sum _{k=1}^K \frac{1}{4\lambda _1}{} \mathbf{z}_k^\mathrm {T}{} \mathbf{G}_k\mathbf{z}_k + \frac{1}{4}{} \mathbf{z}_k^\mathrm {T}{} \mathbf{z}_k - \mathbf{z}_k^\mathrm {T}{} \mathbf{y} + \lambda _2\sum _{k=2}^{K}||\mathbf{z}_k - \mathbf{z}_{k-1}||_1, \end{aligned} \end{aligned}$$

(3)

where $\lambda _1$ and $\lambda _2$ are regularization parameters.

3.2 Optimization Algorithm

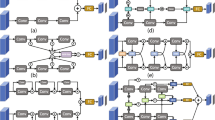
In this section, we present algorithmic details on how to efficiently solve the optimization problem (3). Two auxiliary variables $\mathbf{P}$ and $\mathbf{q}_k$ are introduced to make Eq. (3) separable:

$$\begin{aligned} \begin{aligned}&\min _{\mathbf{z}_k,\mathbf{P},\mathbf{q}_k}\sum _{k=1}^K \frac{1}{4\lambda _1}{} \mathbf{q}_k^\mathrm {T}{} \mathbf{G}_k\mathbf{q}_k + \frac{1}{4}{} \mathbf{q}_k^\mathrm {T}{} \mathbf{q}_k - \mathbf{q}_k^\mathrm {T}{} \mathbf{y} + \lambda _2||\mathbf{P}||_1\\&~~~~~~~~~~~s.t.\mathbf{P} = \mathbf{C}{} \mathbf{Z}, \mathbf{z}_k = \mathbf{q}_k, \end{aligned} \end{aligned}$$

(4)

where $\mathbf{Z} = [\mathbf{z}_1;\mathbf{z}_2;...;\mathbf{z}_K]$, $\mathbf{C}$ is the consistency matrix, which is defined as: $\mathbf{C} = \begin{bmatrix} -\mathbf{I}^1&\mathbf{I}^2\\&-\mathbf{I}^2&\mathbf{I}^3\\&...&...\\&&-\mathbf{I}^{K-1}&\mathbf{I}^{K} \end{bmatrix}$. $\mathbf{I}$ is the identity matrix.

We use the fast first-order Alternating Direction Method of Multipliers (ADMM) to efficiently solve the optimization problem (4). By introducing augmented Lagrange multipliers to incorporate the equality constraints into the objective function, we obtain a Lagrangian function that can be optimized through a sequence of simple closed form update operations in (5).

$$\begin{aligned} \begin{aligned}&\min _{\mathbf{z}_k,\mathbf{P},\mathbf{q}_k}\sum _{k=1}^K \frac{1}{4\lambda _1}{} \mathbf{q}_k^\mathrm {T}{} \mathbf{G}_k\mathbf{q}_k + \frac{1}{4}{} \mathbf{q}_k^\mathrm {T}{} \mathbf{q}_k - \mathbf{q}_k^\mathrm {T}{} \mathbf{y} + \langle \mathbf{Y}_{2,k},\mathbf{q}_k-\mathbf{z}_k\rangle + \frac{\mu }{2}||\mathbf{q}_k-\mathbf{z}_k||^2_2\\&~~~~~~~~~+ \lambda _2||\mathbf{P}||_1 + \langle \mathbf{Y}_1,\mathbf{P}-\mathbf{CZ}\rangle + \frac{\mu }{2}||\mathbf{P}-\mathbf{CZ}||^2_F \\&=\sum _{k=1}^K \frac{1}{4\lambda _1}{} \mathbf{q}_k^\mathrm {T}{} \mathbf{G}_k\mathbf{q}_k + \frac{1}{4}{} \mathbf{q}_k^\mathrm {T}{} \mathbf{q}_k - \mathbf{q}_k^\mathrm {T}{} \mathbf{y} + \frac{\mu }{2}||\mathbf{q}_k-\mathbf{z}_k+\frac{\mathbf{Y}_{2,k}}{\mu }||^2_2 -\frac{1}{2\mu }||\mathbf{Y}_{2,k}||^2_2\\&~~~~~~~~~+ \lambda _2||\mathbf{P}||_1 + \frac{\mu }{2}||\mathbf{P}-\mathbf{CZ}+\frac{\mathbf{Y}_1}{\mu }||^2_F-\frac{1}{2\mu }||\mathbf{Y}_1||^2_F \end{aligned} \end{aligned}$$

(5)

Here, $\langle \mathbf{A},\mathbf{B}\rangle$ = Tr$(\mathbf{A}^\mathrm {T}{} \mathbf{B})$ denotes the matrix inner product. $\mathbf{Y}_1$ and $\mathbf{Y}_{2,k}$ are Lagrangian multipliers. We then alternatively update one variable by minimizing (5) with fixing other variables. Besides the Lagrangian multipliers, there are three variables, including $\mathbf{q}_k$, $\mathbf{Z}$ and $\mathbf{P}$, to solve. The solutions of the subproblems are as follows:

q-subproblem. Given fixed $\mathbf{P}$ and $\mathbf{Z}$, $\mathbf{q}_k$ is updated by solving the optimization problem (6) with the solution (7)

$$\begin{aligned} \begin{aligned}&\min _{\mathbf{q}_k}\sum _{k=1}^K \frac{1}{4\lambda _1}{} \mathbf{q}_k^\mathrm {T}{} \mathbf{G}_k\mathbf{q}_k + \frac{1}{4}{} \mathbf{q}_k^\mathrm {T}{} \mathbf{q}_k - \mathbf{q}_k^\mathrm {T}{} \mathbf{y} + \frac{\mu }{2}||\mathbf{q}_k-\mathbf{z}_k+\frac{\mathbf{Y}_{2,k}}{\mu }||^2_2, \end{aligned} \end{aligned}$$

(6)

$$\begin{aligned} \begin{aligned}&\mathbf{q}_k = (\frac{1}{2\lambda _1}{} \mathbf{G}_k + \frac{1}{2}{} \mathbf{I} + \mu \mathbf{I})^{-1}(\mathbf{y} + \mu \mathbf{z}_k - \mathbf{Y}_{2,k}). \end{aligned} \end{aligned}$$

(7)

Here, $\mathbf{G}_k = \mathbf{X}_k\mathbf{X}_k^\mathrm{T}$. $\mathbf{I}$ is an identity matrix. Note that, all circulant matrices are made diagonal by the Discrete Fourier Transform (DFT), regardless of the generating vector. If $\mathbf{X}_k$ is a circulant matrix, it can be expressed with its base sample $\mathbf{x}_k$ as

$$\begin{aligned} \begin{aligned}&\mathbf{X}_k = { {F}} diag(\mathbf{\hat{x}}_k) {{F}}^\mathrm {H}, \end{aligned} \end{aligned}$$

(8)

where $\mathbf{\hat{x}}_k$ denotes the DFT of the generating vector, $\mathbf{\hat{x}}_k = {\mathcal {F}}(\mathbf{x}_k)$, and F is a constant matrix that does not depend on $\mathbf{x}_k$. The constant matrix F is known as the DFT matrix. $\mathbf{X}_k^\mathrm{H}$ is the Hermitian transpose, i.e., $\mathbf{X}_k^\mathrm {H} = (\mathbf{X}_k^*)^\mathrm{T}$, and ${\mathbf{X}_k^*}$ is the complex-conjugate of $\mathbf{X}_k$. For real numbers, $\mathbf{X}_k^\mathrm{H}$ = $\mathbf{X}_k^\mathrm{T}$. It (Eq. (7)) can be calculated very efficiently in the Fourier domain by considering the circulant structure property of $\mathbf{X}_k$,

$$\begin{aligned} \begin{aligned}&\mathbf{q}_k = {\mathcal {F}}^{-1}[\frac{2\lambda _1(\mathbf{\hat{y}} + \mu \mathbf{\hat{z}}_k - \mathbf{\hat{Y}}_{2,k})}{{\mathbf{\hat{x}}_k^*}\odot {\mathbf{\hat{x}}_k} + \lambda _1 + 2\lambda _1\mu }]. \end{aligned} \end{aligned}$$

(9)

Here, ${\mathcal {F}}^{-1}$ denotes the inverse DFT, while $\odot$ as well as the fraction denote the element-wise product and division, respectively. The $\mathbf{x}_k$ is the base sample of circulant matrix $\mathbf{X}_k$.

P-subproblem. Given fixed $\mathbf{Z}$ and $\mathbf{q}_k$, Eq. (5) can be rewritten as

$$\begin{aligned} \begin{aligned}&\min _{\mathbf{P}}\lambda _2||\mathbf{P}||_1 + \frac{\mu }{2}||\mathbf{P}-\mathbf{CZ}+\frac{\mathbf{Y}_1}{\mu }||^2_F. \end{aligned} \end{aligned}$$

(10)

According to (Lin et al. 2009), an efficient closed-form solution can be computed by the soft-thresholding (or shrinkage) method:

$$\begin{aligned} \begin{aligned}&\mathbf{P} = S_{\frac{\lambda _2}{\mu }}(\mathbf{CZ} - \frac{\mathbf{Y}_{1}}{\mu }), \end{aligned} \end{aligned}$$

(11)

where the definition of ${S_\lambda }(a)$ is ${S_\lambda }(a)$ = sign(a)max$(0,|a|-\lambda )$.

Z-subproblem. Given fixed $\mathbf{q}_k$ and $\mathbf{P}$, Eq. (5) can be rewritten as

$$\begin{aligned} \begin{aligned}&\min _{\mathbf{Z}}\frac{\mu }{2}(||\mathbf{P}-\mathbf{CZ}+\frac{\mathbf{Y}_1}{\mu }||^2_F+||\mathbf{Q}-\mathbf{Z}+\frac{\mathbf{Y}_2}{\mu }||^2_F). \end{aligned} \end{aligned}$$

(12)

Fig. 1.

Pipeline of the proposed spectral fusion mechanism. The spectral weights are obtained according to the response map in the detection phase, and the final response map is obtained by weighted fusion of different spectra response maps.

where $\mathbf{Q} = [\mathbf{q}_1;\mathbf{q}_2;...;\mathbf{q}_K]$. The solution of Eq. (12) is:

$$\begin{aligned} \begin{aligned}&\mathbf{Z} = (\mu \mathbf{C}^\mathrm {T}{} \mathbf{C}+\mu \mathbf{I})^{-1}(\mu \mathbf{C}^\mathrm {T}{} \mathbf{P} + \mathbf{C}^\mathrm {T}{} \mathbf{Y}_1 + \mu \mathbf{Q} + \mathbf{Y}_2) \end{aligned} \end{aligned}$$

(13)

Since each subproblem of Eq. (4) is convex, we can guarantee that the limit point by our algorithm satisfies the Nash equilibrium conditions [27]. And the main steps of the optimization procedure are summarized in Algorithm 1.

3.3 Tracking

Target Position Estimation. After solving this optimization problem, we obtain the correlation filter $\mathbf{z}_k$ for each type of spectrum. Given an image patch in the next frame, the feature vector on the k-th spectrum is denoted by $\mathbf{s}_k$ and of size $M \times N \times D$. We first transform it to the Fourier domain $\mathbf{\hat{s}}_k$ = ${\mathcal {F}}(\mathbf{s}_k)$, and then the k-th correlation response map is computed by

$$\begin{aligned} \begin{aligned}&\mathbf{R}_k = \mathcal {F}^{-1}(\mathbf{\hat{s}}_k\odot \mathbf{\hat{x}}_k^*\odot \mathbf{\hat{z}}_k). \end{aligned} \end{aligned}$$

(14)

Some existed trackers [13] learn spectral weights in a single unified algorithm. Actually, this may increase the complexity of the proposed model. In this work, we use a novel criterion called average peak-to-correlation energy (APCE) measure, as proposed in [25], to calculate the priori influence factor. The definition of APCE is

$$\begin{aligned} \begin{aligned} APCE = \frac{|R_{max} - R_{min}|^2}{mean(\sum _{m,n}(R_{m,n} - R_{min})^2)}, \end{aligned} \end{aligned}$$

(15)

where ${R_{max}}$, ${R_{min}}$ and ${R_{m,n}}$ denote the maximum,minimum and the m-th row n-th column entry of the response map $\mathbf{R}$, respectively. APCE indicates the degree of fluctuation of the response maps. For sharper peaks and fewer noise, i.e., the target apparently appearing in the detection region, APCE will become larger and the response map will become smooth except for only one sharp peak. Otherwise, APCE will significantly decrease if the response map is multi-peaks. Based on the nature of the APCE, we design a new method to calculate the weights of different spectra as follow:

$$\begin{aligned} \begin{aligned} \alpha _k = \frac{APCE_k}{\sum _{k=1}^{K}APCE_k}, \end{aligned} \end{aligned}$$

(16)

where $APCE_k$ denotes the value of APCE of the k-th spectrum. As illustrated in Fig. 1, the weight of reliable spectrum is larger than unreliable spectrum because the APCE of reliable spectrum is much larger than unreliable spectrum. Then the final correlation response map is computed by

$$\begin{aligned} \begin{aligned}&\mathbf{R} = \sum _{k=1}^{K}\alpha _k\mathbf{R}_k. \end{aligned} \end{aligned}$$

(17)

The target location then can be estimated by searching for the position of maximum value of the correlation response map $\mathbf{R}$ of size $M$ $\times$ $N$.

Model Update. Similar to other CF trackers [10, 23, 24, 29]. To improve our robustness to pose, scale and illumination changes, we adopt an incremental strategy, which only uses new samples $\mathbf{x}_k$ in the current frame to update models as shown in (18), where t is the frame index and $\eta$ is a learning rate parameter.

$$\begin{aligned} \begin{aligned}&\mathcal {F}(\mathbf{x}{_k^t}) = (1-\eta )\mathcal {F}(\mathbf{x}{_k^{t-1}}) + \eta \mathcal {F}(\mathbf{x}{_k^t}),\\&\mathcal {F}(\mathbf{z}{_k^t}) = (1-\eta )\mathcal {F}(\mathbf{z}{_k^{t-1}}) + \eta \mathcal {F}(\mathbf{z}{_k^t}). \end{aligned} \end{aligned}$$

(18)

4 Experiments

In this section, we present extensive experimental evaluations on the proposed soft-consistent correlation filters (SCCF) tracker. We first introduce the experimental setups, and then extensive experiments are conducted to evaluate the SCCF tracker against plenty of state-of-the-art trackers on GTOT benchmark.

4.1 Experimental Setups

Implementation Details. We set the regularization parameters of (3) to $\lambda _1$ = 0.038 and $\lambda _2$ = 0.012, and use a kernel width of 0.1 for generating the Gaussian function labels. Their learning rate $\eta$ in (18) is set to 0.025. To remove the boundary discontinuities, the extracted feature are weighted by a cosine window. In addition, we utilize an adaptive multi-scale strategy to adapt to the scale variations. We implement our tracker in MATLAB on an Intel I7-6700K 4.00 GHz CPU with 32 GB RAM. Furthermore, all the parameter settings are available in the source code to be released for accessible reproducible research.

Fig. 2.

The evaluation results on public GTOT benchmark. The representative score of PR/SR is presented in the legend.

Dataset. Our algorithm is evaluated on a large visual tracking benchmark dataset: GTOT [13]. GTOT includes 50 aligned RGB-T video pairs with about 12 K frames in total. They are annotated with ground truth bounding boxes and various visual attributes.

Fig. 3.

Attribute-based evaluation on 50 sequences. We also put the overall performance here (the first one) for comparison convenience facing a single challenge and their combination.

Evaluation Protocol. All trackers are evaluated according to widely used metrics, precision rate (PR) and success rate (SR), as defined in GTOT [13]. PR is the percentage of frames whose output location is within the given threshold distance of ground truth. SR is the ratio of the number of successful frames whose overlap is larger than a threshold. By changing the threshold, the SR plot can be obtained, and we employ the area under curve of SR plot to define the representative SR.

4.2 Performance Evaluation

We evaluate our SCCF algorithm with 10 trackers on GTOT, including CSR [13], SGT [19], Struck [9], SCM [30], CN [6], STC [28], KCF [10], L1-PF [26], JSR [20] and TLD [12].

Quantitative Evaluation. As shown in Fig. 2, we report the PR/SR score for each tracker in the figure legend. Among all the trackers, our SCCF method occupies the best one in terms of SR. Compared with CSR, SCCF achieves about $6.5\%$ improvement with SR. Furthermore, compared with SGT, SCCF achieves much better performance with about $5.3\%$ improvement. Although SGT tracker performs the best against the other trackers in PR score, its model is more complex than ours. Moreover, the proposed tracker performs at about 50 FPS (frames per second) which is much faster than SGT (about 5 FPS).

Attribute-Based Evaluation. We further analyze the robustness of the proposed tracker performance in various scenes (e.g., thermal crossover, low illumination, fast motion) annotated in the benchmark. Our tracker performs well against other methods in most tracking challenges as shown in Fig. 3. In particular, SCCF outperforms other methods by a huge margin in handling low illumination and thermal crossover, which can be attributed to the use of soft consistency. However, our method does not perform as well in the presence of occlusion and deformation, as SCCF does not adopt a delayed update strategy [2, 25] in order to reduce the computational load.

More qualitative results are given in Fig. 4.

Fig. 4.

Sample results of our method against other tracking methods, including L1-PF, CSR, Struck, and CN.

5 Conclusion

In this paper, we propose a novel learning soft-consistent correlation filters for RGB-T object tracking. The proposed tracking algorithm can effectively exploit collaboration and heterogeneity among different spectra to learn their correlation filters jointly. Moreover, we design a novel mechanism to fuse RGB and thermal information for robust visual tracking. Experimental results compared with several state-of-the-art methods on visual tracking benchmark demonstrate the effectiveness and robustness of the proposed algorithm. In the future, we will investigate the performance of multi-channel features (such as HOG) and design a new algorithm based on this work to calculate the correlation filters and spectral weights simultaneously.