Keywords

1 Introduction

Multi-label classification (MLC) solves the problem of assigning multiple labels to a single input instance, which has been seen in a variety of applications in the fields of machine learning, computer vision, data mining, and bio-informatics [2, 9, 28].

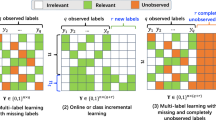
Like most classification algorithms, one typically needs a large number of data with ground truth labels, so that the associated MLC model can be learned with satisfactory performance. However, for the task of MLC, collecting fully annotated data would take extensive efforts and costs. How to alleviate the above limitation for designing effective MLC models becomes a challenging yet practical task. To be more specific, it would be desirable to train MLC models using training data with only partial labels, or even some training data with empty label sets observed. Thus, learning MLC models under the above settings can be formalized as a weakly-supervised setting. The differences between weakly-supervised MLC and related MLC settings are summarized in Table 1. The goal of this paper is to present an effective weakly-supervised MLC (WS-MLC) model by advancing deep learning techniques.

A number of MLC approaches which utilize partially labeled data exist (i.e., some training data are only with partial ground truth label information observed) [13, 31, 32, 35]. As a representative work, [31] handles missing labels by imposing a label smoothness regularization during the learning of their model. However, this type of approaches cannot easily leverage rich information from unlabeled training data, which might not be desirable in practical scenarios in which a majority of collected training data are totally unlabeled.

To address the above challenging (semi-supervised) MLC problems, graph-based [37] approaches are proposed [5, 14, 18, 20, 33]. While they exhibit impressive abilities in handling unlabeled data, take label propagation based algorithms [5, 18, 20] for example, they only work under the transductive setting but not the inductive setting. That is, prediction can only be made for the presented unlabeled data but not for future test inputs. Another family of manifold regularization based algorithms [14, 33], while applicable for inductive settings, are highly sensitive to graph structures and the associated distance measurements.

Deep generative models, on the other hand, have recently been widely applied to solving semi-supervised learning tasks [16, 24]. Take [16] as an example, it described a deep generative model for single-label data, and applied variational inference for semi-supervised learning via observing both labeled and unlabeled data. Nevertheless, despite the compelling probabilistic interpretation of observed data, existing works mainly apply deep generative models for single label learning tasks. While generative approaches for MLC have been investigated in literature [13, 23, 29], existing solutions typically require training data to be fully or at least partially labeled. In other words, they cannot be easily extended to solving semi-supervised MLC or even WS-MLC tasks.

Table 1. Different settings for multi-label classification.
Full size table

In this paper, we tackle the challenging WS-MLC, which includes both semi-supervised MLC and MLC with missing labels as special cases as illustrated in Table 1. We achieve so by advancing novel deep generative models [16, 17]. Inspired by [8, 21, 22, 30], we approach WS-MLC by viewing MLC as a sequential prediction problem. We propose a deep sequential generative model to describe the multi-label data for WS-MLC with a unified probabilistic framework. In our proposed model, we present a deep sequential classification model for both prediction and approximation of posterior inference, and derive efficient learning algorithms with variational inference for addressing WS-MLC with promising performances.

The contributions of this paper are highlighted as follows:

  • To the best of our knowledge, we are the first to advance deep generative models to tackle WS-MLC problems.

  • We propose a probabilistic framework which integrates sequential prediction and generation processes with an efficient optimization procedure, so that information from unlabeled data or data with partially missing labels can be exploited.

  • Our framework results in interpretable MLC models in weakly-supervised settings, and performs favorably against recent MLC approaches on multiple datasets.

2 Related Works

Multi-label classification (MLC) is among active research topics and benefits a variety of real-world applications [2, 7, 9]. Earlier studies of MLC algorithms typically utilize linear models as the building block [22, 26, 28]. Binary relevance [28], as a well-known example, trains a set of independent linear classifiers for each label.

In recent years, approaches based on deep neural networks (DNN)  [10, 21, 30, 34] attract the attention of researchers in related fields. For example, [30] proposes to learn a linear embedding function, with label correlations modeled with a chain structure by recurrent neural networks (RNN). [21] further investigates different exploitation of RNN to perform MLC. On the other hand, [34] proposes to learn nonlinear embedding via deep canonical correlation analysis, while it decodes outputs labels with co-occurrence information preserved. Nevertheless, despite the success in applying DNN for MLC, training DNNs typically requires a large amount of labeled data, whose annotation process generally requires extensive manual efforts.

Weakly-supervised MLC (WS-MLC) is a practical setup that aims to learn MLC models from the dataset containing fully-labeled plus partially-labeled and/or unlabeled training data. As noted above, WS setting is particularly appealing regarding MLC tasks, as the cost to fullying annotate multi-label data is generally much more expensive than that for single-label data. MLC algorithms designed for dealing with partially-labeled data (or data with missing labels) exist [31, 32, 35]. For example, [32] formulates the problem of MLC with partially-labeled data as a convex quadratic optimization problems. [31] handles the missing labels by imposing a label smoothness regularization. Unfortunately, both [32] and [31] work only under transductive setting, i.e., the data to be predicted need to be presented during learning. While inductive MLC algorithms with missing labels are available [35], their incapability of exploiting information unlabeled data still makes them less desirable for practical scenarios.

Semi-supervised MLC algorithms which leverage information from both fully-labeled and unlabeled data have also been studied [5, 14, 18, 20, 33]. The majority of such methods focus on graph-based techniques to utilize the unlabeled data. Several graph-based algorithms consider label propagation techniques [5, 18, 20]. [18] is a representative example which designs a dynamic propagation procedures that explicitly considers the label correlation based on k-nearest-neighbors graph. Other graph-based algorithms exploit the information of unlabeled data by manifold regularization [14, 33]. For example, [14] imposes manifold regularization during the learning of MLC models by enforcing similar predictions for both labeled and unlabeled data that is also similar in feature space. Nevertheless, most label propagation based algorithms also require a transductive setting, limiting their applicability to real-wolrd scenarios. Manifold regularization based approaches are mainly inductive. However, the performance of these approaches critically depends on the predefined graph structures. Moreover, all the above semi-supervised MLC algorithms fail to generalize to handle data with partially observed labels.

We note that, generative leaning algorithms for semi-supervised single-label classification can be found in recent literature [1, 16]. Focusing on the task of MLC, several generative approaches have also been investigated [13, 23]. For example, [23] focuses on the mining of multi-labeled text data, where the data generative process is formulated based on Latent Dirichlet Analysis. Nevertheless, the above algorithms are not designed to handle tarining data with missing labels or unlabeled training data, and thus cannot be easily extended to WS-MLC. In the next section, we will introduce our proposed deep generative model for WS-MLC.

Fig. 1.
figure 1

Architectures of (a) encoder \({\varvec{\phi }}\) and (b) decoder \({\varvec{\theta }}\) in our DSGM. The former sequentially encodes the input data and their labels into each stochastic variable \(\mathbf {z}_{\varvec{\phi }}^k\), and predicts the following label \(\hat{y}_k\) of the k-th label conditioned on \(\mathbf {x}\) and \(y_1,\cdots ,y_{k-1}\). The latter decodes \(\mathbf {z}\) to \(\mathbf {x}\) by sequentially incorporating each label \(y_k\) into stochastic variables \(\mathbf {z}_{\varvec{\theta }}^k\). Note that we take three labels \(y_1\), \(y_2\) and \(y_3\) for illustration purposes.

Full size image

3 Our Proposed Method

3.1 Problem Formulation

In multi-label classification (MLC), we denote \(\mathbf {x} \in \mathbb {R}^d\) as an instance with \(\mathbf {y} \in \{0,1\}^K\) as the corresponding label vector (i.e., \(\mathbf {y}[k] = 1\) if the instance is associated with the k-th label (out of K labels), otherwise \(\mathbf {y}[k] = 0\)). For weakly-supervised MLC (WS-MLC), we observe a training dataset \(\mathcal {D} = \mathcal {D}_\ell \cup \mathcal {D}_o \cup \mathcal {D}_u\), where \(\mathcal {D}_\ell = \{(\mathbf {x}_i, \mathbf {y}_i)\}_{i=1}^{N_\ell }\) denotes fully-labeled \(N_\ell \) instances, \(\mathcal {D}_o = \{(\mathbf {x}_j, \mathbf {y}_j^{\mathbf {o}})\}_{j=1}^{N_o}\) is the partially-labeled dataset with \(N_o\) instances, and \(\mathcal {D}_u = \{\tilde{\mathbf {x}}_m\}_{m=1}^{N_u}\) is the unlabeled one with \(N_u\) instances. We use \(\mathbf {y}^{\mathbf {o}}\) to indicates the partially labeled vector (see detailed settings in experiments). For the sake of simplicity, we omit the subscripts i, j and m if possible in the remaining of this paper. And, we use the term “weakly-labeled” when referring to a subset of training data that is either partially-labeled or unlabeled.

Now, given a training set \(\mathcal {D}\), the goal of WS-MLC is to learn a classification model so that the multi-label vector \(\hat{\mathbf {y}}\) of an unseen instance \(\hat{\mathbf {x}}\) can be predicted. In WS-MLC, the size of fully-labeled dataset is typically much smaller than that of weakly-labeled dataset. Therefore, an effective WS-MLC algorithm to exploit the information from both \(\mathcal {D}_o\) and \(\mathcal {D}_u\) would be desirable, so that improved MLC performance can be expected.

3.2 Deep Sequential Generative Models for WS-MLC

Inspired by recent advances in deep generative models (particularly those for semi-supervised learning [16, 17]) and the use of sequential learning models for MLC [8, 21, 22, 30], we propose a novel Deep Sequential Generative Model (DSGM) to tackle the challenging problem of WS-MLC. As illustrated in Fig. 1, our DGSM can be viewed as an extension of conditional variational autoencoder (CVAE) [25] with sequential layers of stochastic variables \(\{\mathbf {z}_{\varvec{\phi }}^k\}_{k=1}^K\) and \(\{\mathbf {z}_{\varvec{\theta }}^k\}_{k=1}^K\) decided by each label \(y_k\). In particular, our DGSM consists of sequential generative models which aims at describing the generation of multi-label data, followed by a deep classification model for MLC. This classification stage would jointly perform classifcation and approximated posterior inference, and the derivation of the learning objective based on variational inference (VI), so that multi-label prediction in such a weakly-supervised learning setting can be achieved. It is worth pointing out that, from the encoder-decoder perspective, Fig. 1a and b illustrates the framework of our classification and generative models, respectively. In the following subsections, we will detail the functionality and design for the above models.

Fig. 2.
figure 2

Illustration of our sequential generative process using decoder \({\varvec{\theta }}\). This process sequentially takes the latent variable \(\mathbf {z}\) (from encoder \({\varvec{\phi }}\)), stochastic variables \(\mathbf {z}_{\varvec{\theta }}^k\), and labels \(y_k\) for recovering input \(\mathbf {x}\). Note that \(\varvec{\mu }_{\varvec{\theta }}(\cdot |\cdot )\) determines the mean of Gaussian distribution that generates each \(\mathbf {z}_{\varvec{\theta }}^k\).

Full size image

Sequential Generative Models for Multi-label Classification. To address WS-MLC using sequential generative models, we assume that each instance \(\mathbf {x}\) is generated from \(\mathbf {y}\) with an additional latent variable \(\mathbf {z}\). Without the loss of generality and following most exisint generative models [16, 17], we further assume that \(p(\mathbf {z}) = \mathcal {N}(\mathbf {z}| 0,\mathbf {I})\), and have factorization of \(p(\mathbf {y})\) as \( p(\mathbf {y}) = \prod _{k=1}^K \mathtt {Bern}(y_k |\varvec{\gamma }_k), \) where \(y_k\) is the k-th label of \(\mathbf {y}\) and \(\varvec{\gamma }_k\) is the parameter of Bernoulli distribution for \(y_k\). We note that, one might consider a more representative prior based on the factorization of \(p(\mathbf {y}) = p(y_1)\cdot \prod _{k=2}^K p(y_k|y_1,\ldots ,y_{k-1})\). For simplicity, we consider the generation of different labels to be independent, and such an alternative prior is sufficiently satisfactory as confirmed later by our experiments. And, following the setting of [16], the priors \(p(\mathbf {y})\) and \(p(\mathbf {z})\) are set to be marginally independent.

Inspired by recent sequential methods for MLC [8, 21, 22, 30], our propose model also aims at leveraging information from multiple observed labels in a sequential manner during the learning process. More specifically, we choose to describe \(p_{{\varvec{\theta }}}(\mathbf {x}|\mathbf {y}, \mathbf {z})\), i.e., generation of multi-label data \(\mathbf {x}\), as a sequential generative process with an additional set of intermediate stochastic variables \(\{\mathbf {z}^k_{{\varvec{\theta }}}\}_{k=1}^{K}\) as shown in Fig. 2. To be more precise, this generative process is formulated as follows:

$$\begin{aligned} \begin{aligned}&p_{{\varvec{\theta }}}(\mathbf {x}|\mathbf {y}, \mathbf {z}) = g(\mathbf {x}|\mathbf {z}^{K}_{{\varvec{\theta }}}; {\varvec{\theta }}); \\&\mathbf {z}^k_{{\varvec{\theta }}} \sim \mathcal {N}( \varvec{\mu }_{{\varvec{\theta }}}(\mathbf {z}^{k-1}_{{\varvec{\theta }}}, y_k, \mathbf {z}) , \sigma ^2 \mathbf {I}); \; 1\le k \le K \\&\mathbf {z}^0_{{\varvec{\theta }}} = \mathbf {0}, \end{aligned} \end{aligned}$$
(1)

where \(g(\cdot |\cdot ;{\varvec{\theta }})\) is a likelihood function with parameters determined by non-linear transformation of \({\varvec{\theta }}^{K}\). For example, Gaussian distribution can be utilized for \(g(\cdot |\cdot )\) to describe the features with continuous values. In our framework, such a sequential generation process is realized by recurrent neural networks (RNN). That is, \(\varvec{\mu }_{{\varvec{\theta }}}(\cdot , \cdot , \cdot )\) outputs the mean vector from the non-linear transformation of \(\mathbf {z}\), \(\mathbf {z}^{k-1}_{{\varvec{\theta }}}\) and \(y_k\), which is implemented as the RNN cell that shares the model parameters across all labels \(y_k\).

With the above generative model \(p_{{\varvec{\theta }}}(\mathbf {x}| \mathbf {y}, \mathbf {z})\), we are able to learn the model parameters \({\varvec{\theta }}\) by maximizing the marginal likelihood of \(p_{{\varvec{\theta }}}(\mathbf {x}, \mathbf {y})\) (from fully-labeled data), \(p_{{\varvec{\theta }}}(\mathbf {x}, \mathbf {y}^{\mathbf {o}})\) (from partially-labeled data), and/or \(p_{{\varvec{\theta }}}(\tilde{\mathbf {x}})\) (from unlabeled data). In other words, we are able to obtain \({\varvec{\theta }}\) by solving

$$\begin{aligned} \underset{{\varvec{\theta }}}{\arg \max }\; \sum _{(\mathbf {x}, \mathbf {y})\in \mathcal {D}_\ell } \log p_{{\varvec{\theta }}}(\mathbf {x}, \mathbf {y}) + \sum _{(\mathbf {x}, \mathbf {y}^{\mathbf {o}})\in \mathcal {D}_o} \log p_{{\varvec{\theta }}}(\mathbf {x}, \mathbf {y}^{\mathbf {o}}) + \sum _{\tilde{\mathbf {x}} \in \mathcal {D}_u} \log p_{{\varvec{\theta }}}(\tilde{\mathbf {x}}). \end{aligned}$$
(2)

To perform MLC with a given \(\mathbf {x}\), classification can be achieved by \(p_{{\varvec{\theta }}}(\mathbf {y}|\mathbf {x}) \propto p_{{\varvec{\theta }}}(\mathbf {x}|\mathbf {y})p(\mathbf {y})\) with model parameter \({\varvec{\theta }}\).

Sequential Classification Model for Variational Inference of DSGM. Unfortunately, learning (i.e., exact inference) of \({\varvec{\theta }}\) by solving (2) is computationally prohibitive due to the need to compute intractable integral when applying Bayes rules. To enable an efficient approximated inference of \({\varvec{\theta }}\), we design a novel learning algorithm based on the principle of variational inference [4, 17]. In particular, we propose a deep sequential classification model for posterior inference approximation. We then derive the variational lower bound and the corresponding optimization procedure accordingly.

Fig. 3.
figure 3

Illustration of our sequential classification architecture \({\varvec{\phi }}\) in DSGM, which sequentially encodes input \(\mathbf {x}\) and labels \(y_k\) into stochastic variables \(\mathbf {z}_{\varvec{\phi }}^k\), with prediction layers \(f_k\) for determining label outputs \(\hat{y}_k\).

Full size image

We now discuss the design of our sequential classification model for the variational inference of \({\varvec{\theta }}\). The key ingredient of variational inference is to introduce a fixed form distribution \(q_{{\varvec{\phi }}}(\cdot |\cdot )\), so that the posterior inference from observed variables to the latent ones can be achieved via \(q_{{\varvec{\phi }}}(\cdot |\cdot )\) instead of using \(p_{{\varvec{\theta }}}(\cdot |\cdot )\) which is in practice intractable. In the case of learning with fully-labeled training data, we seek to infer \(\mathbf {z}\) from \((\mathbf {x}, \mathbf {y})\) directly. For dealing with weakly-labeled data, unobserved labels are viewed as latent variables, which need to be inferred from \(\mathbf {x}\) and the observed labels (if available).

With the above observation and motivation, the goal of \(q_{{\varvec{\phi }}}(\cdot |\cdot )\) is to achieve the following approximation of posterior inference:

$$\begin{aligned}&q_{{\varvec{\phi }}} (\mathbf {z} | \mathbf {x}, \mathbf {y}) \approx p_{{\varvec{\theta }}}(\mathbf {z}|\mathbf {x}, \mathbf {y}); \; \forall (\mathbf {x}, \mathbf {y}) \in \mathcal {D}_\ell \\&q_{{\varvec{\phi }}} (\mathbf {y}^{\mathbf {m}}, \mathbf {z} | \mathbf {x}, \mathbf {y}^{\mathbf {o}}) \approx p_{{\varvec{\theta }}}( \mathbf {y}^{\mathbf {m}}, \mathbf {z} |\mathbf {x}, \mathbf {y}^{\mathbf {o}}); \; \forall (\mathbf {x}, \mathbf {y}^{\mathbf {o}}) \in \mathcal {D}_o \\&q_{{\varvec{\phi }}} (\mathbf {y}, \mathbf {z} | \tilde{\mathbf {x}}) \approx p_{{\varvec{\theta }}}(\mathbf {y}, \mathbf {z}|\tilde{\mathbf {x}}); \; \forall (\tilde{\mathbf {x}}) \in \mathcal {D}_u, \end{aligned}$$

where we have partially-labeled data \((\mathbf {x}, \mathbf {y}^{\mathbf {o}}) \in \mathcal {D}_o\) in which \(\mathbf {y}^{\mathbf {m}}\) indicates the label vectors with missing ground truth. It is worth noting that, \(q(\mathbf {y}, \mathbf {z}| \tilde{\mathbf {x}})\) essentially performs classification as inference for unlabeled data, and will be applied as the classification model for the testing stage. Inspired by [8, 21, 22, 30] which approach MLC by solving the task of label sequence prediction, and to meet the sequential nature of our proposed generative process, our deep sequential classification model would serve as \(q_{{\varvec{\phi }}}(\cdot |\cdot )\) for addressing WS-MLC (see Fig. 3 for illustration).

We now elaborate the architecture of our sequential classification model \(q_{{\varvec{\phi }}}(\cdot |\cdot )\), and explain in details on how to perform posterior inference given either fully-labeled, partially-labeled or unlabeled data via a set of intermediate latent variables \(\{\mathbf {z}_{{\varvec{\phi }}}^k\}_{k=1}^K\).

For labeled data, the sequential posterior inference \(q_{{\varvec{\phi }}}(\mathbf {z}|\mathbf {x}, \mathbf {y})\) is performed as follows:

$$\begin{aligned}&q_{{\varvec{\phi }}}(\mathbf {z}| \mathbf {y}, \mathbf {x}) = \mathcal {N} (\mathbf {z}| \varvec{\mu }^q_{{\varvec{\phi }}}(\mathbf {z}_{{\varvec{\phi }}}^{K}), \varvec{\sigma }^q_{{\varvec{\phi }}}(\mathbf {z}_{{\varvec{\phi }}}^{K})) ; \end{aligned}$$
(3)
$$\begin{aligned}&\mathbf {z}^k_{{\varvec{\phi }}} \sim \mathcal {N}( \varvec{\mu }_{{\varvec{\phi }}}(\mathbf {z}^{k-1}_{{\varvec{\phi }}}, \mathbf {x}, y_k) , \sigma ^2 \mathbf {I}), \; 1 \le k \le K ; \end{aligned}$$
(4)
$$\begin{aligned}&\hat{y}_k \sim \mathtt {Bern}(f^k_{{\varvec{\phi }}}(\mathbf {z}_{{\varvec{\phi }}}^{k-1})),\; 2 \le k \le K \end{aligned}$$
(5)
$$\begin{aligned}&\hat{y}_1 \sim \mathtt {Bern}(f^1_{{\varvec{\phi }}}(\mathbf {x})); \end{aligned}$$
(6)
$$\begin{aligned}&\mathbf {z}^{0}_{{\varvec{\phi }}} = \mathbf {0}, \end{aligned}$$

where \(\hat{y}_k\) denotes the prediction of k-th label. Here \(\varvec{\mu }^q_{{\varvec{\phi }}}(\cdot )\) and \(\varvec{\sigma }^q_{{\varvec{\phi }}}(\cdot )\) are the deterministic functions that calculate the mean vector and diagonal covariance matrix for \(q_{\varvec{\phi }}(\mathbf {z}| \mathbf {x}, \mathbf {y})\), respectively. On the other hand, \(f^k_{{\varvec{\phi }}}(\cdot ,\cdot )\) determines the parameter of Bernouli distribution for prediction of \(\hat{y}_k\). The main intuition behind such a design of \(q_{{\varvec{\phi }}}(\cdot |\cdot )\) is to encode \(\mathbf {z}_{{\varvec{\phi }}}^k\) with the information from \( (\mathbf {x}, y_1,\ldots ,y_k)\). Such encoding allows us to resemble the following factorization by predicting each \(\hat{y}_{k+1}\) with \(\mathbf {z}_{{\varvec{\phi }}}^k\):

$$ q_{{\varvec{\phi }}}(\mathbf {y} | \mathbf {x}) = q_{{\varvec{\phi }}}(y_1 | \mathbf {x}) \prod _{k=2}^K q_{{\varvec{\phi }}}(y_k | \mathbf {x}, y_1, \ldots , y_{k-1}). $$

We see that, \(\mathbf {z}_{{\varvec{\phi }}}^{K}\) with such relation would encode information from all observed variables, and thus can be directly used to determine \(\mathbf {z}\) from \(\mathbf {x}\) and \(\mathbf {y}\).

For partially-labeled data in WS-MLC, we adopt the same posterior inference procedure as (3)–(6) except that we now consider the meanfield variational family \(q_{{\varvec{\phi }}}(\mathbf {y}^{\mathbf {m}}, \mathbf {z} | \mathbf {x}, \mathbf {y}^{\mathbf {o}}) = q_{{\varvec{\phi }}} (\mathbf {z} | \mathbf {x}, \mathbf {y}^{\mathbf {o}}) q_{{\varvec{\phi }}} (\mathbf {y}^{\mathbf {m}}| \mathbf {x}, \mathbf {y}^{\mathbf {o}})\). Nevertheless, despite the factorized probability representation, information from all labels should still be exploited to infer \(\mathbf {z}\), which is achieved by utilizing the predicted label \(\hat{y}_k\) instead (in the case where \(y_k\) is missing). To be more precise, we modify (4) to calculate \(\mathbf {z}_{{\varvec{\phi }}}^k\) by.

$$\begin{aligned} \mathbf {z}^k_{{\varvec{\phi }}} \sim {\left\{ \begin{array}{ll} \mathcal {N}( \varvec{\mu }_{{\varvec{\phi }}}(\mathbf {z}^{k-1}_{{\varvec{\phi }}}, \mathbf {x}, y_k) , \sigma ^2 \mathbf {I}),\; \text {if}\; y_k \in \mathbf {y}^{\mathbf {o}} \\ \mathcal {N}( \varvec{\mu }_{{\varvec{\phi }}}(\mathbf {z}^{k-1}_{{\varvec{\phi }}}, \mathbf {x}, \hat{y}_k) , \sigma ^2 \mathbf {I}),\; \text {if}\; y_k \notin \mathbf {y}^{\mathbf {o}}, \\ \end{array}\right. } \end{aligned}$$
(7)

where \(\hat{y}_k \in \{0,1\}\) is a binary sample based on the predicted probability that \(y_k = 1\) via (5). With such modification, our sequential classification model is able to infer \(\mathbf {z}\) with information from all labels even if some are unobserved.

As for unlabeled data in WS-MLC, we also utilize the meanfiled variational family \(q_{{\varvec{\phi }}} (\mathbf {y}, \mathbf {z} | \tilde{\mathbf {x}}) = q_{{\varvec{\phi }}} (\mathbf {z} | \tilde{\mathbf {x}}) q_{{\varvec{\phi }}} (\mathbf {y}| \tilde{\mathbf {x}})\). By realizing that unlabeled data is the data with all label missing, we perform posterior sequential posterior inference in exactly the same way as that for partially-labeled data. In this case, (7) would degenerate to the case with each \(y_k \notin \mathbf {y}^{\mathbf {o}}\).

Finally, we implement the above sequntial posterior inference with \(q_{{\varvec{\phi }}}(\cdot |\cdot )\) via RNN, as depicted in Fig. 3. That is, \(\varvec{\mu }_{{\varvec{\phi }}}(\cdot ,\cdot ,\cdot )\) used in both (4) and (7) is realized as an RNN cell, which is the same as those in our sequential generative model.

Objective for Variational Lower Bound. In this subsection, we discuss how we derive the objective of the lower bound for variational inference. Note that the calculation of \(q_{{\varvec{\phi }}}(\mathbf {z}| \mathbf {x}, \mathbf {y})\) requires the integral over the samples of \(\{\mathbf {z}_{{\varvec{\phi }}}^{k}\}_{k=1}^{K}\) even if \(\mathbf {x}\) and \(\mathbf {y}\) are known. This would be undesirable for the derivation of the variational lower bound, as such integrals cannot be analytically calculated.

By applying location-scale transform of Gaussian distributions, one would be able to determine the exact parameters of distribution \(q_{{\varvec{\phi }}}(\mathbf {z}| \mathbf {x}, \mathbf {y})\) (i.e., mean and covariance) by introducing a set of random variables \(\{{\varvec{\epsilon }}_{{\varvec{\phi }}}^{k}\}_{k=1}^{K}\). Thus, (4) can be rewritten as

$$\begin{aligned} \mathbf {z}^k_{{\varvec{\phi }}} = \varvec{\mu }_{{\varvec{\phi }}}(\mathbf {z}^{k-1}_{{\varvec{\phi }}}, \mathbf {x}, y_k) + \sigma ^2 {\varvec{\epsilon }}_{{\varvec{\phi }}}^{k}; \; 1 \le k \le K, \end{aligned}$$
(8)

where each \({\varvec{\epsilon }}_{{\varvec{\phi }}}^{k} \sim \mathcal {N}(0, \mathbf {I})\) is an independent sample of standard Gaussian distribution. Consequently, one can derive the variational lower bound by taking

$$ \mathbb {E}_{{\varvec{\epsilon }}^1_{\varvec{\phi }},\ldots ,{\varvec{\epsilon }}^{K}_{\varvec{\phi }}}[ \mathcal {KL}(q_{{\varvec{\phi }}}(\mathbf {z}|\mathbf {x}, \mathbf {y}, {\varvec{\epsilon }}^1_{{\varvec{\phi }}}, \ldots ,{\varvec{\epsilon }}^{K}_{{\varvec{\phi }}}) \, \Vert \, p_{{\varvec{\theta }}}(\mathbf {z}|\mathbf {x}, \mathbf {y}))]$$

as a starting point, where \(q_{{\varvec{\phi }}}(\mathbf {z}|\mathbf {x}, \mathbf {y}, {\varvec{\epsilon }}^1_{\varvec{\phi }}, \ldots ,{\varvec{\epsilon }}^{K}_{\varvec{\phi }})\) denotes the fixed distribution given the sampled value of \(\{{\varvec{\epsilon }}_{{\varvec{\phi }}}^{k}\}_{k=1}^{K}\).

Based on location-transform techniques of \(p_{{\varvec{\theta }}}(\mathbf {x}| \mathbf {y}, \mathbf {z}) = \mathbb {E}_{{\varvec{\epsilon }}_{{\varvec{\theta }}}}[ p_{{\varvec{\theta }}}(\mathbf {x}| \mathbf {y}, \mathbf {z}, {\varvec{\epsilon }}_{{\varvec{\theta }}})]\), where \({\varvec{\epsilon }}_{{\varvec{\theta }}} = \{{\varvec{\epsilon }}_{{\varvec{\theta }}}^k\}_{k=1}^{K}\) is another set of independent samples from standard Gaussian distribution in addition to \(\{{\varvec{\epsilon }}_{{\varvec{\phi }}}^k\}_{k=1}^{K}\) for \(q_{{\varvec{\phi }}}(\cdot |\cdot )\), the lower bound for the labeled data \((\mathbf {x}, \mathbf {y}) \in \mathcal {D}_\ell \) can now be expressed as \( \log p_{{\varvec{\theta }}}(\mathbf {x}, \mathbf {y}) \ge \mathbb {E}_{{\varvec{\epsilon }}_{{\varvec{\phi }}}} [ -\mathcal {L}(\mathbf {x}, \mathbf {y}, {\varvec{\epsilon }}_{{\varvec{\phi }}}) ] \) , where \({\varvec{\epsilon }}_{{\varvec{\phi }}} = \{{\varvec{\epsilon }}_{{\varvec{\phi }}}^k\}_{k=1}^K\). Finally, by Jensen’s inequality (for concave functions), we have

$$\begin{aligned} \begin{aligned} -\mathcal {L}(\mathbf {x}, \mathbf {y}, {\varvec{\epsilon }}_{{\varvec{\phi }}})&= \log p(\mathbf {y}) + \mathbb {E}_{q_{{\varvec{\phi }}}(\mathbf {z}| \mathbf {x}, \mathbf {y}, {\varvec{\epsilon }}_{{\varvec{\phi }}})} [ \mathbb {E}_{{\varvec{\epsilon }}_{{\varvec{\theta }}}} [ \log p_{{\varvec{\theta }}}(\mathbf {x}| \mathbf {y}, \mathbf {z}, {\varvec{\epsilon }}_{{\varvec{\theta }}}) ] ] \\&-\,\mathcal {KL}( q_{{\varvec{\phi }}}(\mathbf {z}| \mathbf {x}, \mathbf {y}, {\varvec{\epsilon }}_{{\varvec{\phi }}}) \Vert p(\mathbf {z})). \end{aligned} \end{aligned}$$
(9)

In order to deal with partially-labeled data \((\mathbf {x}, \mathbf {y}^{\mathbf {o}}) \in \mathcal {D}_o\), we need both \(q_{{\varvec{\phi }}}(\mathbf {y}^{\mathbf {m}}| \mathbf {x}, \mathbf {y}^{\mathbf {o}})\) and \(q_{{\varvec{\phi }}}(\mathbf {z}| \mathbf {x}, \mathbf {y}^{\mathbf {o}})\) for deriving the associated variational lower bound objective. However, as noted above, the sequential posterior inference with \(q_{{\varvec{\phi }}}(\cdot ,\cdot )\) using (7) involves sampling for unobserved labels. Even with the technique of location-scale transform on \(\{\mathbf {z}_{{\varvec{\phi }}}^k\}_{k=1}^K\), oue still needs to marginalize out the sampling regarding \(\mathbf {y}^{\mathbf {m}}\) to obtain \(q_{{\varvec{\phi }}}(\mathbf {y}^{\mathbf {m}}| \mathbf {x}, \mathbf {y}^{\mathbf {o}})\) and \(q_{{\varvec{\phi }}}(\mathbf {z}| \mathbf {x}, \mathbf {y}^{\mathbf {o}})\). To alleviate this problem, we choose to rewrite (7) as

$$\begin{aligned} \mathbf {z}^k_{{\varvec{\phi }}} = {\left\{ \begin{array}{ll} {\varvec{\mu }}_{{\varvec{\phi }}}(\mathbf {z}^{k-1}_{{\varvec{\phi }}}, \mathbf {x}, y_k) + \sigma ^2 {\varvec{\epsilon }}^k_{{\varvec{\phi }}},\;&{} \text {if}\; y_k \in \mathbf {y}^{\mathbf {o}} \\ \llbracket \alpha _k \ge p_k\rrbracket \varvec{\mu }_{{\varvec{\phi }}}(\mathbf {z}^{k-1}_{{\varvec{\phi }}}, \mathbf {x}, 0) + \llbracket \alpha _k < p_k\rrbracket \varvec{\mu }_{{\varvec{\phi }}}(\mathbf {z}^{k-1}_{{\varvec{\phi }}}, \mathbf {x}, 1) + \sigma ^2 {\varvec{\epsilon }}^k_{{\varvec{\phi }}},\;&{} \text {if}\; y_k \notin \mathbf {y}^{\mathbf {o}} \\ \end{array}\right. } \end{aligned}$$
(10)

where \(\alpha _k \sim U(0,1)\), \({\varvec{\epsilon }}_k \sim \mathcal {N}(0,\mathbf {I})\), \(\llbracket \cdot \rrbracket \) is the indicator function and \(p_k\) is the probability that \(y_k = 1\) from (5) and (6). We see that (10) is effectively a reparameterization of sampling of \(\mathbf {z}^k_{{\varvec{\phi }}}\) with \(\varvec{\alpha }= \{\alpha _k\}_{k=1}^K\) and \({\varvec{\epsilon }}_{{\varvec{\phi }}} = \{{\varvec{\epsilon }}^k_{{\varvec{\phi }}}\}_{k=1}^K\), which allows exact determinination of \(q_{{\varvec{\phi }}}(\mathbf {y}^{\mathbf {m}}| \mathbf {x}, \mathbf {y}^{\mathbf {o}})\) and \(q_{{\varvec{\phi }}}(\mathbf {z}| \mathbf {x}, \mathbf {y}^{\mathbf {o}})\) with a set of \((\varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}})\). With this observation, we have the lower bound objective for partially-labeled data as \( \log p_{{\varvec{\theta }}}(\tilde{\mathbf {x}}) \ge \mathbb {E}_{\varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}}} [ -\mathcal {M}(\mathbf {x}, \mathbf {y}^{\mathbf {o}}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}}) ] \) , where

$$\begin{aligned} \begin{aligned}&-\mathcal {M}(\mathbf {x}, \mathbf {y}^{\mathbf {o}}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}}) = \mathbb {E}_{q_{{\varvec{\phi }}}(\mathbf {y}^{\mathbf {m}} | \mathbf {x}, \mathbf {y}^{\mathbf {o}}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}})} [ \log p(\mathbf {y}) ] \\&+ \mathbb {E}_{q_{{\varvec{\phi }}}(\mathbf {z} | \mathbf {x}, \varvec{\alpha }, \mathbf {y}^{\mathbf {o}}, {\varvec{\epsilon }}_{{\varvec{\phi }}})} [ \mathbb {E}_{q_{{\varvec{\phi }}}(\mathbf {y}^{\mathbf {m}} | \mathbf {x}, \varvec{\alpha }, \mathbf {y}^{\mathbf {o}}, {\varvec{\epsilon }}_{{\varvec{\phi }}})} [ \mathbb {E}_{{\varvec{\epsilon }}_{{\varvec{\theta }}}} [ \log p_{{\varvec{\theta }}}(\mathbf {x}| \mathbf {y}, \mathbf {z}, {\varvec{\epsilon }}_{{\varvec{\theta }}}) ] ] ] \\&-\mathcal {KL}( q_{{\varvec{\phi }}}(\mathbf {z}| \mathbf {x}, \varvec{\alpha }, \mathbf {y}^{\mathbf {o}}, {\varvec{\epsilon }}_{{\varvec{\phi }}}) \Vert p(\mathbf {z})) + \mathcal {H}( q_{{\varvec{\phi }}}(\mathbf {y}^{\mathbf {m}}| \mathbf {x}, \varvec{\alpha }, \mathbf {y}^{\mathbf {o}}, {\varvec{\epsilon }}_{{\varvec{\phi }}})) \end{aligned} \end{aligned}$$
(11)

where \(\mathcal {H}(\cdot )\) is the entropy function by again realizing that the meanfield assumption still holds even with \(\varvec{\alpha }, {\varvec{\epsilon }}\) included due to the design of \(q_{{\varvec{\phi }}}(\cdot ,\cdot )\).

Finally, as for observation of unlabeled data \(\tilde{\mathbf {x}} \in \mathcal {D}_u\), the variational lower bound can be derived similarly to that of partially-labeled data by realizing that the reparameterization of \(\{\mathbf {z}_{{\varvec{\phi }}}^k\}_{k=1}^K\) using (10) degenerates to the case with each \(y_k \notin \mathbf {y}^{\mathbf {o}}\). Consequently, the lower bound objective for unlabeled data can be expressed as \( \log p_{{\varvec{\theta }}}(\tilde{\mathbf {x}}) \ge \mathbb {E}_{\varvec{\alpha },{\varvec{\epsilon }}_{{\varvec{\phi }}}} [ -\mathcal {U}(\tilde{\mathbf {x}}, {\varvec{\epsilon }}_{{\varvec{\phi }}}) ] \) , where

$$\begin{aligned} \begin{aligned}&-\mathcal {U}(\tilde{\mathbf {x}}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}}) = \mathbb {E}_{q_{{\varvec{\phi }}}(\mathbf {y} | \mathbf {x}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}})} [ \log p(y) ] \\&+ \mathbb {E}_{q_{{\varvec{\phi }}}(\mathbf {z} | \mathbf {x}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}})} [ \mathbb {E}_{q_{{\varvec{\phi }}}(\mathbf {y} | \mathbf {x}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}})} [ \mathbb {E}_{{\varvec{\epsilon }}_{{\varvec{\theta }}}} [ \log p_{{\varvec{\theta }}}(\mathbf {x}| \mathbf {y}, \mathbf {z}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\theta }}}) ] ] ] \\&-\mathcal {KL}( q_{{\varvec{\phi }}}(\mathbf {z}| \mathbf {x}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}}) \Vert p(\mathbf {z})) + \mathcal {H}(q_{{\varvec{\phi }}}(\mathbf {y}| \tilde{\mathbf {x}}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}})). \end{aligned} \end{aligned}$$
(12)

With (9), (11) and (12), we now obtain the lower bound objective of marginal likelihood regarding the data with weakly labels. As suggested in [16], it is preferable to have the classifier directly perform label prediction. Thus, we further augment the derived lower bound objective with a discriminative loss on the observed labels for fully-labeled and partial labeled data, resulting in the following final minimization objective:

$$\begin{aligned} \begin{aligned}&\sum _{(\mathbf {x}, \mathbf {y})\in \mathcal {D}_\ell } \mathbb {E}_{{\varvec{\epsilon }}_{{\varvec{\phi }}}}[ \mathcal {L}(\mathbf {x}, \mathbf {y}, {\varvec{\epsilon }}_{{\varvec{\phi }}}) - \log q_{{\varvec{\phi }}}(\mathbf {y}| \mathbf {x}, {\varvec{\epsilon }}_{{\varvec{\phi }}}) ] \\ +&\sum _{(\mathbf {x}, \mathbf {y}^{\mathbf {o}})\in \mathcal {D}_o} \mathbb {E}_{{\varvec{\epsilon }}_{\varvec{\alpha }, {\varvec{\phi }}}}[ \mathcal {M}(\mathbf {x}, \mathbf {y}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}}) - \log q_{{\varvec{\phi }}}(\mathbf {y}^{\mathbf {o}}| \mathbf {x}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}}) ] \\ +&\sum _{\tilde{\mathbf {x}} \in \mathcal {D}_u} \mathbb {E}_{\varvec{\alpha },{\varvec{\epsilon }}_{{\varvec{\phi }}}}[ \mathcal {U}(\tilde{\mathbf {x}}, \varvec{\alpha }, {\varvec{\epsilon }}_{{\varvec{\phi }}}) ]. \end{aligned} \end{aligned}$$
(13)

With the set-up of the above objectives, the resulting \(q_{{\varvec{\phi }}}(\mathbf {y} | \mathbf {x}, \varvec{\alpha }, {\varvec{\epsilon }}_{\varvec{\phi }})\) will be used to recognize future unseen test data. For testing, we determine the binary prediction of each label \(\hat{y}_k\) by directly thresholding the predicted probability with threshold of 0.5 (which is implemented by setting all \(\alpha _k = 0.5\)).

Learning of DSGM. We now detail the learning and optimization of our DGSM with the objective functions introduced above. For the loss of labeled data in (9), the KL-divergence term can be analytically computed for any \({\varvec{\epsilon }}_{{\varvec{\phi }}}\) as both \(q_{\varvec{\phi }}(\mathbf {z}|\cdot )\) and \(p(\mathbf {z})\) are Gaussian distributions. For the part \(\mathbb {E}_{q_{\varvec{\phi }}(\mathbf {z}|\cdot )}[\mathbb {E}_{{\varvec{\epsilon }}_{{\varvec{\theta }}}}[\log p_{{\varvec{\theta }}}(\mathbf {x}| \mathbf {y}, \mathbf {z}, {\varvec{\epsilon }}_{{\varvec{\theta }}})]]\) of the loss function, the gradient can be efficiently estimated using the reparameterization trick on \(q_{\varvec{\phi }}(\mathbf {z}|\cdot )\) [17] and a single sample of \({\varvec{\epsilon }}_{\varvec{\theta }}\). Since the gradient of the outer expectation \(\mathbb {E}_{{\varvec{\epsilon }}_{\varvec{\theta }}}[\cdot ]\) in (13) for the loss of fully-labeled data can be efficiently estimated using a single sample of \({\varvec{\epsilon }}_{\varvec{\theta }}\), we advance techniques of stochastic gradient descent (SGD) for optimizing our network parameters \(({\varvec{\theta }},{\varvec{\phi }})\) using fully-labeled data.

For the loss of partially-labeled data in (11), we apply aforementioned techniques with a sample of \(\varvec{\alpha }\) for gradient estimation. However, other optimization issues need to be addressed. First, we need to calculate the expectation \(\mathbb {E}_{q_{\varvec{\phi }}(\mathbf {y}^{\mathbf {m}}| \mathbf {x}, \mathbf {y}^{\mathbf {o}}, \cdot )}\log p_{\varvec{\theta }}(\mathbf {x}|\cdot )\) with respect to the predicted probability of missing labels \(\mathbf {y}^{\mathbf {o}}\) given \((\mathbf {x}, \mathbf {y}^{\mathbf {o}})\) (note that we omit \({\varvec{\epsilon }}_{\varvec{\theta }}\) and \({\varvec{\epsilon }}_{\varvec{\phi }}\) for presentation simplicity). The other issue is that, we need to handle the discontinuous indicator function in (7).

Regarding the calculation of \(\mathbb {E}_{q_{\varvec{\phi }}(\mathbf {y}^{\mathbf {m}}| \mathbf {x}, \mathbf {y}^{\mathbf {o}}, \cdot )}[\log p_{\varvec{\theta }}(\mathbf {x}|\cdot )]\), explicitly marginalizing out \({q_{\varvec{\phi }}(\mathbf {y}^{\mathbf {m}}| \mathbf {x}, \mathbf {y}^{\mathbf {o}}, \cdot )}\) is a possible solution. However, it would take \(\mathcal {O}(2^{|\mathbf {y}^{\mathbf {m}}|})\) time due to the need to examine each combination of missing labels, making it computationally prohibitive when the number of missing labels is large. To resolve the issue, we reparameterize the expectation to have the form

$$\mathbb {E}_{\varvec{\beta }}[\log p_{\varvec{\theta }}(\mathbf {x}|\cdot , \varvec{\beta }, q_{\varvec{\phi }}(\mathbf {y}^{\mathbf {m}}| \mathbf {x}, \mathbf {y}^{\mathbf {o}}, \cdot ))], $$

where \(\varvec{\beta }=\{\beta _k\}_{k=1}^K\), \(\beta _k \sim U(0,1)\) by rewriting the sampling of \(\mathbf {z}_{{\varvec{\theta }}}^k\) in (1) as

$$\begin{aligned} \mathbf {z}^k_{{\varvec{\theta }}} = {\left\{ \begin{array}{ll} \varvec{\mu }_{{\varvec{\theta }}}(\mathbf {z}^{k-1}_{{\varvec{\theta }}}, y_k, \mathbf {z}) + \sigma ^2 {\varvec{\epsilon }}^k_{{\varvec{\theta }}},\;&{} \text {if}\; y_k \notin \mathbf {y}^{\mathbf {m}} \\ \llbracket \beta _k \ge p_k\rrbracket \varvec{\mu }_{{\varvec{\theta }}}(\mathbf {z}^{k-1}_{{\varvec{\theta }}}, 0, \mathbf {z}) + \llbracket \beta _k < p_k\rrbracket \varvec{\mu }_{{\varvec{\theta }}}(\mathbf {z}^{k-1}_{{\varvec{\theta }}}, 1, \mathbf {z}) + \sigma ^2 {\varvec{\epsilon }}^k_{{\varvec{\theta }}},\;&{} \text {if}\; y_k \in \mathbf {y}^{\mathbf {m}}. \\ \end{array}\right. } \end{aligned}$$
(14)

where \(p_k\) is the predicted probability that \(y_k = 1\). It can be seen that, the above reparameterization is analogous to that of sampling \(\mathbf {z}_{{\varvec{\phi }}}^k\) with (7) for the sequential posterior inference with \(q_{{\varvec{\phi }}}{\cdot |\cdot }\). This allows us to efficiently estimate the gradient of the expectation \(\mathbb {E}_{q_{\varvec{\phi }}(\mathbf {y}^{\mathbf {m}}| \mathbf {x}, \mathbf {y}^{\mathbf {o}}, \cdot )}\log p_{\varvec{\theta }}(\mathbf {x}|\cdot )\) with an extra single sample of \(\varvec{\beta }\).

As for dealing with the discontinuity of the indicator function, we adopt the straight-through estimator (STE) in [3] for addressing this problem. More precisely, we calculate the loss in (11) in the forward pass using the normal indicator function, and replace the indicator function with identity function during the backward pass to calculate the gradient. The use of STE leads to promising performance as noted in [3].

For calculating the loss term of unlabeled data, we apply the same techniques and reparameterizing \(\mathbf {z}_{{\varvec{\theta }}}^k\) with (14) by observing that (14) degenerates to the case with each \(y_k \in \mathbf {y}^{\mathbf {m}}\) for unlabeled data.

With the above explanation and derivations, we are able to efficiently obtain the estimation of gradient with respect to (13) for both fully-labeled and weakly-labeled data. As a result, the final discriminative classifier \(q_{{\varvec{\phi }}}(\mathbf {y} | \mathbf {x})\) in our DSGM can be learned by updating \(({\varvec{\theta }}, {\varvec{\phi }})\) with SGD techniques.

3.3 Discussions

Finally, we discuss the connection and difference between our proposed DSGM and recent models for related learning tasks.

The use of deep generative models for semi-supervised mutli-class classification (not MLC) has been recently studied in [16]. In particular, [16] jointly trains their classification network \(q_{{\varvec{\phi }}}(y | \mathbf {x})\), inference network \(q_{{\varvec{\phi }}}(\mathbf {z}| \mathbf {x}, y)\), and generative network \(p_{\varvec{\theta }}(\mathbf {x}| \mathbf {z}, y)\) by optimizing the variational lower bound for likelihood of observed labeled and unlabeled data. However, applying the models of [16] for (semi-supervised) MLC requires explicit examination of all \(2^K\) possible label combinations when calculating the lower bound objective for unlabeled data. This is quite computationally infeasible especially when K is large. In contrast, the sequential architectures and the corresponding optimization procedure in our proposed DSGM provides linear dependency of K, which is in practice more applicable for semi-supervised or weakly-supervsied MLC tasks.

On the other hand, formulating MLC as a sequential label prediction has been studied in recent literature [8, 21, 22, 30]. For example, [21, 30] advances RNNs to sequentially predict the labels while implicitly observing their dependency. While the use of sequential label prediction has been widely investigated with promising performances, existing models cannot be easily extended to handle partially-labeled and unlabeled data (i.e., WS-MLC tasks). Such robustness is particularly introduced into our DSGM. As confirmed later by the experiments, our DSGM performs favorably against state-of-the-art deep MLC models in such challenging settings.

4 Experiments

4.1 Experiment Settings

To evaluate the performance of our proposed DSGM for WS-MLC, we consider the following datasets: iaprtc12, espgame, mirflickr, NUS-WIDE, and MSCOCO. The first three datasets are image recognition datasets used in [11], where 1000-dimensional of bag-of-words features based on SIFT. NUS-WIDE [7] and MSCOCO [19] are two other large scale datasets typically used for evaluation of image annotation. We summarize the key statistics of the above datasets in the appendix. For all datasets, we discard the instances with no positive labels as done in [10]. For NUS-WIDE and MSCOCO, we use the bottom four convolutional layers of a ResNet-152 [12] trained on Imagenet without fine-tuning to extract 2048-dimensional feature vectors in order to utilize both the high-level and low-level information of raw images.

Fig. 4.
figure 4

Performance comparisons in terms of Micro-f1 and Macro-f1 for datasets with varying labeled data ratios.

Full size image

In our DSGM architecture, we use gated-recurrent unit [6] as the recurrent cells to model \(\varvec{\mu }_{{\varvec{\phi }}}\) and \(\varvec{\mu }_{{\varvec{\theta }}}\). The dimensions of latent variables \(\{\mathbf {z}_{{\varvec{\theta }}}^k\}_{k=1}^K\) and \(\{\mathbf {z}_{{\varvec{\phi }}}^k\}_{k=1}^K\) are set to 128, while the dimension of \(\mathbf {z}\) is fixed as 64. The variance \(\sigma ^2\) of \(\{\mathbf {z}_{{\varvec{\theta }}}^k\}_{k=1}^K\) and \(\{\mathbf {z}_{{\varvec{\phi }}}^k\}_{k=1}^K\) is set to 0.005. When applying DSGM for WS-MLC, we reduce the dimension of feature vector \(\mathbf {x}\) to 512 by a linear transformation, which is parameterized as a fully connected layer without activation. Following [21, 30], the label order for sequential learning/prediction is set from the most frequent one to the rarest one (see such suggestions in [21]). Nevertheless, in our experiment, we do not observe significant differences between the choices of different label orders. To perform stochastic gradient descent for optimization, we exploit Adam [15] with a fixed learning rate of 0.003, and the batch size is fixed to 100. Note that for the experiment of semi-supervised MLC, we pretrai our DSGM with only labeled data for 100 epochs for faster convergence. Finally, both Micro-f1 and Macro-f1 are considered as evaluation metrics [27].

4.2 Comparisons with Semi-Supervised MLC Algorithms

We first evaluate our DSGM on the task of semi-supervised MLC (SS-MLC), where the dataset contains both fully-labeled and unlabeled data. Two state-of-the-arts SS-MLC algorithms are considered: Semi-supervised Low-rank Mapping (SLRM) [14] and Weakly Semi-supervised Deep Learning (Wesed) [33] (with its inductive setting viewed as a semi-supervised setting). In addition, we consider a naïve extension of state-of-the-art deep generative approach for semi-supervised multi-class classification (SS-MCC) [16], DGM-Naïve (detailed in supplementary). For completeness, we also include two well-known or state-of-the-art supervised MLC algorithms, ML-kNN [36] and RNN-m [21]. We follow [14, 33] to set the hyper parameters for SLRM and Wesed, and fix \(k=5\) for ML-kNN. For RNN-m, we use the same RNN cell and the feature transformation as those in our DSGM, and set the learning rate as 0.001. The training details of DGM-Naïve are discussed in the supplementary material. For each dataset, we randomly split into two subsets with equal sizes for training and testing. The average results of five random splits are presented.

Fig. 5.
figure 5

Micro-f1 and Macro-f1 with different missing label ratios.

Full size image

The comparison results are shown in Fig. 4, where the horizontal axis represents the ratio of labeled data with respect to the entire training set. Note that experiments of SLRM are not conducted on two large-scale datasets NUS-WIDE and MSCOCO, as SLRM requires pairwise information between training instances. From Fig. 4, we see that our DSGM achieved improved results when comparing to the state-of-the-art SS-MLC methods of SLRM and Wesed, as well as the extension of the recent generative SS-MCC approach, DGM-Naïve. We note that, for large-scale datasets of NUS-WIDE and MSCOCO, supervised MLC method of ML-kNN and RNN-m achieved comparable results as ours did. The above empirical results support our exploitation of unlabeled data for MLC tasks.

Further inspection on Fig. 4 reveals that the use of more powerful features (i.e., those calculated by Resnet 152) generally resulted in favorable performances (e.g., DGM-Naïve, ML-kNN, RNN-m, and ours). On the other hand, when it comes to the datasets iaprtc12, espgame and mirflickr using low-level features, our DSGM clearly outperformed DGM-Naïve, ML-kNN and RNN-m in most of the cases. Moreover, we observe that DSGM remarkably performed against DGM-Naïve on the above three datasets especially when the labeled data ratio becomes smaller. This demonstrates the effectiveness of our sequential architecture in exploiting unlabeled data for MLC.

4.3 Comparisons with Algorithms for MLC with Missing Labels

Next, we compare our proposed model with state-of-the-art MLC algorithms for WS-MLC, particularly the observation of partially-labeled data, or data with missing labels. The methods to be compared to include LEML [35], Multi-label Learning with Missing Labels (MLML) [31], and ML-PGD (Multi-label Learning with Missing Labels Using Mixed Graph) [32]. We also modify DSGM-Naïve to handle data missing label data for comparison of state-of-the-art deep generative approach in such settings. The scenario of missing labels is simulated by randomly dropping the ground truth labels, with ratio varying from \(10\%\) to \(50\%\).

Figure 5 illustrates and compares the performances, where the horizontal axis indicates the missing ratio. The results from Fig. 5 demonstrate that our algorithm performed against state-of-the-art algorithms, and confirmed the robustness of our methods for different MLC tasks (i.e., SS-MLC and MLC with missing labels). With a closer inspection between the results of DSGM and DGM-Naïve, we see that while DGM-Naïve reported promising and satisfactory results, DSGM in general still remarkably outperformed DGM-Naïve. This reflects the importance and the advantage of our sequential architecture which integrate generative models and discriminative classifiers for WS-MLC.

Fig. 6.
figure 6

Visualization of the derived latent vectors on mirflickr for standard CVAE and DSGM.

Full size image

4.4 Qualitative Studies

Finally, we provide qualitative studies regarding our sequential architecture of generative models. Specifically, we train a standard Conditional Variational Auto Encoder (CVAE) [25] and the sequential generative models of DSGM on mirflickr using the first 10 labels with the dimension of \(\mathbf {z}\) set to 2. This allows us to visualize the inferred latent vectors for each instance \(\mathbf {x}\). We plot the derived latent vectors of each \(\mathbf {x}\) corresponding to the 10 most common label combinations in Fig. 6, which reflects label correlation information. The 10 most common combinations cover over \(95\%\) of instances, and each latent vector is colored based on its associated label combination in Fig. 6.

From the visualization results shown in Fig. 6, it is clear that our proposed sequential generative model resulted in more representative latent vectors when comparing to those of CVAE. From this figure, we see that our model better represents and describes the relationship between data with different labels. This also supports the use of our proposed deep generative model of multi-labeled data in the weakly-supervised setting.

5 Conclusion

We proposed a deep generative model, DSGM for solving WS-MLC problems. DSGM integrates a unique deep sequential generative model to descrbe multi-label data as well as a novel deep sequential classification model for both posterior inference and classification. The variational lower bound is derived for the learning of our sequential generative model together with an efficient optimization procedure. Experiment results confirmed the superiority of our proposed DSGM over state-of-the-art semi-supervised MLC approaches, and those designed to handle MLC with missing labels. We further demonstrated that DSGM would be more effective than naïve utilization of deep generative models regarding WS-MLC, i.e., SS-MLC and MLC with missing labels.