Keywords

1 Introduction

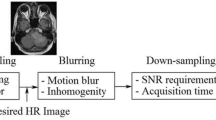
Diffusion-weighted imaging (DWI) and magnetic resonance spectroscopy imaging (MRSI) are important techniques for brain imaging. DWI is a specific MR imaging method based on mapping of diffusion process of water molecules in tissues [1]. It is an effective technique, which provides functional information of the brain tissues. DWI is a faster acquisition technique as compared to conventional MRI and it does not require any contrast agent as well. Most of the obtained images are acquired using high speed protocols with a low spatial resolution, reducing the patient stress but also producing low quality images [1]. On the other hand, MRSI is a non-invasive technique which gives information about the biochemical components within the tissues [7]. MRSI is particularly of great help in early diagnosis of brain lesions on the basis of the spectra obtained from different metabolite concentrations. MRSI also has the same advantage of fast scan time as DWI. In spite of advantages of DWI and MRSI, the rise in the cost of scans and poor signal-to-noise ratio limit their clinical use. These limits can be overcome by image super-resolution (SR) methods [2]. SR methods are categorized as either single-image SR (SISR) or multiple-image SR. SISR is more preferable in medical imaging as multiple images are difficult to be acquired in a particular cross-section, taking considerable scan time. Sparse representation approach has proved to be very effective in case of single-image SR. But the stabilization for the solution of inverse problems is a major issue in sparsity approach, which can be overcome by regularization. In this paper, we focus to develop a SISR method for MR images using sparse representation along with non-local total variation (NLTV) regularization.

The remaining part of the paper is written in following sections: In Sect. 2, a brief literature about of the regularization based SR methods is provided. Section 3 will describe the proposed methodology. Experimental results on different datasets of diffusion-weighted and spectroscopic MR images are explained in Sect. 4. Lastly, Sect. 5 gives a conclusion about the paper.

2 Background

Owing to the resolution limitations, there is a need to create high resolution images in a short acquisition time using post-processing techniques. Even though, basic interpolation methods are available, but these methods introduce blurring artifacts. Taking the disadvantages of the interpolation based techniques into consideration, SR had been developed, which has shown very influential and efficient results in HR image reconstruction. The SR methods tries to perform mapping between the LR and HR images via learning some prior information regarding similarity of the two images with their own image space [9]. Earlier works apply SR algorithm on medical imaging to generate HR images using multiple LR images with different angular views, but because of the insufficient number of low resolution images and unknown blurring operators, it becomes highly ill-posed in nature.

For solving the ill-posed problem of image SR, many recent regularization techniques are developed to get a more stabilized solution [6, 8]. Recently, sparse representation based SR reconstruction came into picture as a powerful tool for image restoration [4, 5]. Sparse representation is mainly concerned with the solution of inverse problems. In medical image processing, total variation (TV) regularization methods are successfully used as it shows excellent edge preservations. Despite its high effectiveness, problems like over-smoothing of image textures and odd artifacts may limit such methods. Lately, the non local means (NLM) based regularization approaches are also introduced for solving inverse problems like, image restoration, super-resolution and denoising, etc.,

3 Proposed Method

The performances of sparse representation algorithms for image SR are related to several phenomenons, like, quality of the dictionary trained, effectiveness of the constraint term selected for regularization, etc. The proposed method for SR reconstruction from a set of LR MR images is discussed in the following subsections. It consist of two parts: first, learning of LR and HR dictionaries and second, reconstruction of HR output image utilizing the learned dictionaries. The reconstruction algorithm is again can be divided into the following sub-tasks: first, extraction of high-frequency features of the patches, then solving a sparse prior based regularization and secondly, a non-local total variation regularization to restore the textural details remove the undesirable staircase artifact to recover the fine details and textures. Finally, a global image regularization is done that helps in incorporating the given LR image’s point spread function into the reconstructed HR images by utilizing the image acquisition model constraint.

3.1 Sparsity Based Image Super-Resolution

In the beginning, overlapping patches of size \(k \times k\) are extracted from the input LR image Y. The sparse coefficients \(\alpha \) corresponding to each low-resolution patch y is found with respect to the trained dictionaries \(D_{l}\) and \(D_{h}\). Next, these sparse coefficients are combined with high-resolution dictionary \(D_{h}\) to find high-resolution patches x.

The solution of the following sparse regularization problem gives the sparse coefficients corresponding to each low-resolution patch y:

$$\begin{aligned} {{ \alpha ^*}} = \arg \,\mathop {\min }\limits _{{\alpha }} \left\| {{{D^{'}\alpha }} - {{\tilde{y}}}} \right\| _2^2 + \lambda \left\| {{\alpha }} \right\| _1, \end{aligned}$$
(1)

where \({{ D^{'}}} = \left[ \begin{gathered} \,\,{{D}}_\ell \\ T{{D}}_h \\ \end{gathered} \right] \), \({{\tilde{y}}} = \left[ \begin{gathered} {{y}} \\ w \\ \end{gathered} \right] \), and \(\lambda \) is the regularization parameter. T is the overlap region extraction operator which finds the region which is common to both the presently reconstructing patch and the latest HR patch generated; w represents the overlapped pixels contained in the previously reconstructed HR image.

Following the computation of sparse coefficients \(\alpha ^{*}\) using Eq. 1, HR patches x are obtained by solving the following relation which supports the fact that the HR and LR dictionaries shares the same sparse representation.

$$\begin{aligned} x \approx D_h \alpha ^ * \end{aligned}$$
(2)

Arranging all the individual HR patches reconstructed by Eq. 2 on a single grid will yield to an intermediate HR image \(X_{0}\). Before finding the initial HR reconstructed image \(X_{0}\) by the minimization problem, non local total variation regularization is performed so that the patches to be reconstructed fit properly in the above minimization formulation. Again due to measurement errors, \(X_{0}\) may not fit the generalized model, \(Y=WX\), where Y is the input LR image, X is the desired HR image and W is the image sampling operator. For overcoming these limitations due to noise, a global reconstruction constraint is imposed by solving a minimization problem:

$$\begin{aligned} X^ * = \arg \mathop {\min }\limits _X ||WX - Y||_2^2 + \lambda ||X - X_0 ||_2^2 \end{aligned}$$
(3)

The above Eq. 4 is the gradient descent method, which is minimized iteratively to find the final reconstructed image \(X_{0}\).

3.2 NLTV Regularization

The non-local means (NLM) filtering implies the weighted average of the surrounding pixels within a search window for the computation of the new filtered pixel value. Two blocks of the HR image \(X_{0}\) having central pixels at \(x_{i}\) and \(x_{j}\) contributes to weight \(w_{ij}\) which is the gaussian distance \(l_{2}\) between the blocks [12]. Consider \(x_{i}\) and \(x_{j}\) denote the pixel at the center of \(b_s \times b_s\) blocks and it is assumed that \(x_{j}\) lies in the search window of \(x_{i}\). Weight \(w_{ij}\) is computed by:

$$\begin{aligned} w_{ij} = \exp ( - ||x_j - x_i ||_2^2 /f^2 )/c_i \end{aligned}$$
(4)

where f and \(c_{i}\) are controlling parameter and normalization factors, respectively. The new filtered pixel value is denoted by NLM (\(x_{i}\)), and this approach of filtering has lead to a new approach of regularization, known as nonlocal regularization. Consider all the pixels in the center organized as a column vector, represented as r and all the weights are also organized as column vector, represented as w. Mathematically, this nonlocal regularization can be represented as:

$$\begin{aligned} \sum \limits _{x_i \in x} {||x_i - w_i^T r_i ||_2^2 } \end{aligned}$$
(5)

These weights are updated iteratively and before the implementation of gradient descent method for final reconstruction, the nonlocal total variation (NLTV) regularization is implemented, the formulation of this approach is as:

$$\begin{aligned} \mathop {\min }\limits _x ||D_h \alpha ||\, + \,\alpha ||x - Wx||_2^2 \,\,\,\, \end{aligned}$$
(6)

The solution of the above formulation is the basis of the NLTV regularization. The HR image \(X_{0}\) obtained after the regularization is used in Eq. 4, which undergoes minimization iteratively to obtain the final SR image \(X^{*}\).

3.3 Dictionary Learning

Two training image patch pairs, set of high-resolution patches is represented by \(X^{h}={x_{1},x_{2},....,x_{k}}\) and set of low-resolution patches is represented by \(Y^{l}={y_{1},y_{2},....,y_{k}}\). These two dictionaries are jointly trained with the condition that both HR and LR image patches have a common sparse representations among them. A joint sparse representation regularization can be formulated involving the LR and HR image patches simultaneously. Mathematically,

$$\begin{aligned} \mathop {\min }\limits _{\{ D_h ,D_l ,Z\} } \frac{1}{R}||X^h - D_h Z||_2^2 \, + \,\frac{1}{S}||Y^l - D_l Z||_2^2 \, + \lambda (\frac{1}{R} + \frac{1}{S})||Z||_1 \end{aligned}$$
(7)

where LR and HR patches in vector form have dimensions S and R respectively. \(||Z||_{1}\) is a \({\ell _1}\)-norm term that enforces sparsity into both the dictionaries. Equation 7 is solved iteratively for three parameters simultaneously to obtain the HR and LR dictionaries \(D_{h}\) and \(D_{l}\).

4 Experiments and Evaluations

Simulations of the proposed work is carried out using MATLAB (R2015b) environment on PC having configurations as follows: OS- Windows 7, Processor: Intel core i5 (2.2 GHz), and RAM: 8 GB. The diffusion-weighted MRI data has been acquired from a GE HDx 1.5 T with the following parameters: TR/TE: 4225/76.6 ms; Slice thickness: 5 mm, spacing between scans: 5 mm; Field of view (FOV): \(100\times 100\); Flip angle: \(90^{0}\). The spectroscopic MRI images have also been acquired from a GE HDx 1.5 T with the following parameters: TR/TE: 150/1.372 ms; Slice thickness: 8 mm; spacing between scans: 5 mm; Field of view (FOV): \(100\times 100\); Flip angle: \(70^{0}\).

4.1 Simulations

First, the LR dictionary \(D_{l}\) and the HR dictionary \(D_{h}\) are trained jointly where both consist of 512 atoms in each. For training, a number of 1,00,000 LR/HR patch pairs are selected from about 30 standard MR images. The regularization parameter for the dictionary has been considered as \(\lambda =0.15\). This dictionary has been trained as per the approach proposed by Yang et al. [11].

Next, for the super-resolution reconstruction, two upscale factors have been considered, i.e., 2 and 3. For both the upscale factors, size of the LR input is \(128\times 128\). Size of the output HR image is \(256\times 256\) and \(384\times 384\) for upscale factor 2 and 3 respectively. The results of the proposed method and some other SR based methods has been given with their magnified view. In Tables 1 and 2, DWI results represent the SR results of diffusion-weighted MRI images and MRSI results represent the SR results of Spectroscopic MRI images.

Fig. 1.
figure 1

Results of DW MRI by using different SR techniques for upscale factor 2

Full size image
Fig. 2.
figure 2

Magnified view of results of DW image SR for upscale factor 2

Full size image
Fig. 3.
figure 3

Results of spectroscopic image SR by different techniques for upscale factor 2

Full size image
Fig. 4.
figure 4

Magnified view of results of spectroscopic image SR for upscale factor 2

Full size image
Fig. 5.
figure 5

Results of DW MR image SR by different techniques for upscale factor 3

Full size image
Fig. 6.
figure 6

Magnified view of results of DW MR image SR for upscale factor 3

Full size image
Fig. 7.
figure 7

Results of spectroscopic image SR by different techniques for upscale factor 3

Full size image
Fig. 8.
figure 8

Magnified view of results of Spectroscopic image SR for upscale factor 3

Full size image
Table 1. Quantitative evaluations of the DW image SR for different methods using upscale factor 2 and 3
Full size table
Table 2. Quantitative evaluations of the spectroscopic image SR for different methods using upscale factor 2 and 3
Full size table

4.2 Evaluations

The simulation results obtained are evaluated both visually and quantitatively. In Figs. 1, 2, 3, 4, 5, 6, 7 and 8, it is clearly seen that the fine details such as edges have been preserved efficiently in the proposed method. From Tables 1 and 2, it can be seen that evaluation parameters obtained for the proposed method are better in terms of peak signal-to-noise ratio (PSNR) as well as mean structural similarity index (MSSIM) compared to the traditional bicubic interpolation techniques. The proposed method has also shown better results as compared to ScSR proposed by Yang et al. [11] and LRTV proposed in [10]. Compared to the ground truth, bi-cubic interpolation, and LRTV methods produce blurry results. As far as ScSR is concerned, it does not produce blurring artifacts, but in comparison to the proposed method, it does not preserve equivalent edge details. We have compared the image quality using two more metrics mean-square error (MSE) and mutual information (MI) [3] between the ground truth and the SR result image. For better image quality, MSE should be less and MI should be more. All the images used in the experiments are brain images. The magnified views of the results clearly show the zoomed view of a specified portion of the results. It can be seen that fine details are recovered by the proposed method.

5 Conclusion

In this paper, we have shown that the implementation of non-local TV regularization for solving the regularization issues of the sparsity based approach can be a viable solution to the issues. This combination provides better consistency of patches, thereby giving better results. Quantitative comparisons show that the proposed method outperforms the existing regularization based approaches. Proposed method is computationally expensive due to the iterative process of regularization. As a future work, this can be extended to multi-core processing for computationally efficient results.