Keywords

1 Introduction

In the field of vision measurement [1,2,3,4,5,6], such as geometric dimension measurement, 3D profilometry measurement, 3D object classification recognition, and so on, it usually uses the camera to obtain the modulated light stripe to solve and reconstruct the contour data of the measured object. Structured light vision sensor is widely used because of its simple structure, low cost, non-contact, high efficiency. Thus, extracting the center line of the light stripe is a key step for 3D reconstruction. Further, in the field of medical image analysis [7,8,9,10,11], such as blood vessel detection in retina or fundus images, pulmonary nodule detection in CT images, information enhancement of ultrasound images, and so on. All of these need to detect the edge contour or the center for medical diagnosis. Moreover, in the field of remote sensing, the center of curvilinear structures are extracted from aerial and satellite images to determine key information such as rivers and roads [12,13,14]. Therefore, fast and accurate center extraction of lines are extremely important for visual measurement, and center detection of lines algorithm can also be applied to medical images and remote sensing images.

At present, the methods of extracting the center of light stripe can be divided into two categories according to the extracting accuracy. One is pixel-level accuracy, such as extreme value method [15,16,17,18], skeleton thinning method [19]; the other is sub-pixel accuracy, including direction template method [20, 21], gray centroid method [22, 23], curve fitting method [24, 25] and Hessian matrix method (Steger method) [26,27,28].

Extremum method and threshold method can detect and extract the light stripe center quickly, but the extraction accuracy is not high and is vulnerable to noise interference. The skeleton refinement method has fast extraction speed, but it has poor noise resistance and is prone to burrs. Directional template method has fast extraction speed, but its robustness and accuracy are not as good as curve fitting method and Hessian matrix method. Although the curve fitting method also has high accuracy, high stability and good robustness, the detection and extraction speed is slow, and it is not suitable for the detection of light stripe in complex background images. Gray centroid method is generally used in simple light stripe images because of its high accuracy, fast speed and good stability. Steger method is widely used to extract of the center of light stripe image in visual measurement, the center line of blood vessel in medical detection image and the center line of road in remote sensing image because of its high accuracy and good anti-noise ability.

Steger’s method has high accuracy, good stability and strong anti-noise ability, but the computational complexity caused by multiple convolutions is huge, resulting in a slower speed. In addition, if the whole image only uses the same Gauss convolution kernel size, it is difficult to accurately extract the center line and even lead to the discontinuity of the light stripe when the light stripe width distribution is uneven and the curvature varies greatly. At both ends of the light stripe, it is easy to generate multiple centers point of the light stripe because of discontinuity of light stripe and abrupt change of gray level. Similarly, if the light stripe is located at the edge of the image, there will also be multiple centers. If there are intersections in the light stripe, the center line of the light stripe near the intersection will often have a larger error.

For different problems, many papers also present various improvement methods. For example, aiming at the problem that multi-convolution of Gauss template increases the time of extracting the center of the light stripes, the processing range of stripe image is reduced by morphology and image recognition [29, 30], and the convolution times of image by Gauss template are reduced, so as to improve the speed of image extraction, or to improve the speed of image extraction by virtue of the performance of hardware [31]. In order to solve the problem of uneven distribution of light stripe width, adaptive template is often used to solve the problem of strip discontinuity caused by the change of light stripe width. However, adaptive template increases the number of convolutions, thus increasing the extraction time.

To solve these problems, we also propose an improved method based on the Hessian matrix. First, the original image is divided into several sub-blocks according to the number of CPU threads on the computer, and the extraction speed of the light stripe center is improved by multi-threaded parallel computing. Secondly, in sub-block images, morphological methods (corrosion, expansion, regional connectivity) and adaptive threshold methods are used to segment the light stripe image. Thirdly, the width of the light stripe is estimated by binary image using the multi-directional template. Thus, the size of the convolution template for Gaussian filter is determined and image convolution is carried out by adaptive template method, and candidate points of light stripe center are determined by Steger method using Hessian matrix. Finally, the eigenvalues of the Hessian matrix are normalized by the data normalization method. According to the discriminant conditions, the candidate points of the light stripe center are judged to be the center points of the light stripe. Finally, the light stripe center of the whole image is extracted.

2 Algorithms and Principles

2.1 Image Sub-block and Parallel Computing

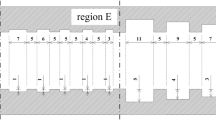
When structured light is used for dimension measurement or three-dimensional topographic scanning, the modulated light stripe projected on the measured object will change with the change of its surface shape. When the surface curvature of the object is large or at the corner of the object, it is easy to produce uneven width distribution of the cross section of the light stripe. The method based on Hessian matrix needs to estimate the light stripe width along the normal direction as the convolution template size of the Gauss filtering. Therefore, the best method is to use many different sizes of Gauss convolution templates, which usually leads to the reduction of image processing speed. At present, with the improvement of hardware performance, it is easy to improve the speed of the algorithm using the performance of hardware itself. So, we use a multi-threaded parallel computing method, as shown in Fig. 1.

Fig. 1.
figure 1

The flow chart of multi-threaded parallel computing presented in this paper.

Full size image

We use the method shown in Fig. 2 to segment the image. Different sub-images are obtained according to the number of threads in the CPU. There are some overlapping images between adjacent sub-images, so it is convenient to use the Gauss convolution template for convolution calculation. Of course, the width of overlapping area is larger than that of convolution template. Image segmentation is not only helpful to improve the speed of the algorithm, but also helpful to get more accurate thresholds for binary image processing.

Fig. 2.
figure 2

An image segmentation method proposed in this paper.

Full size image

According to the characteristics of the image, the upper edge noise of the image is more serious, while the other areas are more uniform. In addition, the light stripe in the image are generally vertical distribution. We divide the image into four horizontal sub-images.

2.2 Feature Segmentation of Light Stripe

Before image convolution, the region segmentation theory is used to segment the image automatically. Because of the great difference between the gray value of light stripe and background, the threshold of image segmentation is automatically determined by the method of maximum class square (OSTU method). In order to improve the running speed, we simplify it as follows.

For an image, if the maximum gray value is \({L_{\max }}\) and the minimum gray value is \({L_{\min }}\), then the distribution range of gray value is \(\left[ {{L_{\min }},{L_{\max }}} \right] \). If the number of pixels with gray value of L is \({n_L}\), then the total number of pixels is \(N = \sum \limits _{i = {L_{\min }}}^{i = {L_{\max }}} {{n_i}} \).

By normalizing the gray value, the following results can be obtained:

$$\begin{aligned} \sum \limits _{i = {L_{\min }}}^{i = {L_{\max }}} {{p_i}} = \sum \limits _{i = {L_{\min }}}^{i = {L_{\max }}} {\frac{{{n_i}}}{N}} = 1 \end{aligned}$$
(1)

The histogram defined by Eq. (1) is called a 2D histogram. There are \({L_{\max }} - {L_{\min }}\) straight lines that are perpendicular to the main diagonal line in a 2D histogram, as shown in Fig. 3.

Fig. 3.
figure 3

Straight-line intercept histogram.

Full size image

Assuming a gray value threshold is \(\tau \). The gray value threshold divides the pixels in the stripe image into two categories, namely \(\left[ {{L_{\min }},\tau } \right] \), and \(\left[ {\tau ,{L_{\max }}} \right] \). Then the probability of two kinds of occurrence is

$$\begin{aligned} \left\{ \begin{array}{l} {\rho _1} = \rho \left( \tau \right) = \sum \limits _{i = {L_{\min }}}^\tau {{p_i}} \\ {\rho _2} = \rho \left( \tau \right) = \sum \limits _{i = {L_{\min }}}^\tau {{p_i}} \end{array} \right. \end{aligned}$$
(2)

Then, the mean value is

$$\begin{aligned} \left\{ \begin{array}{l} {\mu _1}\left( \tau \right) = \sum \limits _{i = 0}^\tau {{{i{p_i}} / {{\omega _1}\left( \tau \right) = {{\mu \left( \tau \right) } / {{\omega _1}\left( \tau \right) }}}}} \\ {\mu _2}\left( \tau \right) = \sum \limits _{\tau + 1}^{{L_{\max }}} {{{i{p_i}} / {{\omega _2}\left( \tau \right) = \frac{{{\mu _\tau } - \mu \left( \tau \right) }}{{1 - {\omega _1}\left( \tau \right) }}}}} \end{array} \right. \end{aligned}$$
(3)

Where, \(\mu \left( \tau \right) = \sum \limits _{i = {L_{\min }}}^\tau {i{p_i}} ,{\mu _\tau } = \sum \limits _{i = {L_{\min }}}^{{L_{\max }}} {i{p_i}} \).

Then, the variance of the two groups of data is:

$$\begin{aligned} \left\{ \begin{array}{l} {\sigma _1} = \sum \limits _{i = {L_{\min }}}^\tau {{{{{\left( {i - {\mu _1}} \right) }^2}{p_i}} / {{\rho _1}}}} \\ {\sigma _2} = \sum \limits _{i = \tau + 1}^{{L_{\max }}} {{{{{\left( {i - {\mu _2}} \right) }^2}{p_i}} / {{\rho _2}}}} \end{array} \right. \end{aligned}$$
(4)

Between-class variance \(\sigma _B^2\) can be computed using:

$$\begin{aligned} \sigma _B^2\left( \tau \right) = {\rho _1}{\left[ {{\mu _1}\left( \tau \right) - {\mu _\tau }} \right] ^2} + {\rho _2}{\left[ {{\mu _2}\left( \tau \right) - {\mu _\tau }} \right] ^2} = {\rho _1}{\rho _2}{\left[ {{\mu _1}\left( \tau \right) - {\mu _2}\left( \tau \right) } \right] ^2} \end{aligned}$$
(5)

The optimal threshold \({\tau ^ * }\) can be selected from

$$\begin{aligned} \sigma _B^2\left( {{\tau ^ * }} \right) = \mathop {\max }\limits _{{L_{\min }} \le \tau \le {L_{amx}}} \sigma _B^2\left( \tau \right) \end{aligned}$$
(6)

After \(\tau \)‘\(*\) is obtained, all pixels can be classified using

$$\begin{aligned} f\left( {x,y} \right) = \left\{ \begin{array}{l} 0\\ 1 \end{array} \right. \quad \begin{array}{*{20}{c}} {if\;I\left( {x,y} \right) \le {\tau ^ * }}\\ {if\;I\left( {x,y} \right) > {\tau ^ * }} \end{array} \end{aligned}$$
(7)

where \(f\left( {x,y} \right) \) is the segmented image, \(I\left( {x,y} \right) \) is the gray value of the image at the point \(\left( {i,j} \right) \).

2.3 Width Estimation of Light Stripe

After we get the binary image, we need to determine the size of the convolution template for the next Gauss filtering. We propose a directional template method to determine the width of the cross section of the light stripe.

The gray value 1 in the binary image is regarded as the candidate point of the image light stripe. Four directional templates are used to convolute the candidate point in the light stripe image, and the minimum value of the four convolutions is taken as the light stripe width through the candidate point (Fig. 4).

Fig. 4.
figure 4

Light stripe width estimation based on multi-directional template

Full size image
$$\begin{aligned} {I_w}\left( {x,y} \right) = s \cdot \min \left( {I\left( {x,y} \right) * {T_i}} \right) \quad i = 1,2,3,4 \end{aligned}$$
(8)

Where, s is the compensation coefficient, and the ratio of the light stripe width in gray image to that in binary image is regraded as the value s. In this paper, s is \(\sqrt{2} \).

2.4 Calculation of the Hessian Matrix

In general, the intensity profile \(f\left( x \right) \) of a light stripe can be described by a Gaussian function as shown in Fig. 5. The Gauss function is as follow.

Fig. 5.
figure 5

Light stripe line-width estimation and Gaussian curve fitting

Full size image
$$\begin{aligned} f\left( x \right) = \frac{A}{{\sqrt{2\pi \sigma } }}\exp \left[ { - \frac{{{{\left( {x - \mu } \right) }^2}}}{{2{\sigma ^2}}}} \right] \end{aligned}$$
(9)

where A represents the intensity of the light stripe, and \({\sigma }\) represents the standard deviation width of light stripe.

For filtering the noise in the image, the image \(I\left( {x,y} \right) \) is convolved with Gaussian kernel \({g_\sigma }(x,y)\) and differential operators to calculate the derivatives of \(I\left( {x,y} \right) \). So, the center point of the light stripe is given by the first-order zero-crossing-point of the convolution result, which also reaches local extreme points in the second-order derivatives.

Therefore, we use the Gauss filter to eliminate the noise in the image. The Gauss filter is as follow.

$$\begin{aligned} {g_\sigma }\left( {x,y} \right) = \frac{1}{{2\pi {\sigma ^2}}}\exp \left( { - \frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}} \right) \end{aligned}$$
(10)

The first-order partial derivatives of the Gaussian function are expressed by

$$\begin{aligned} \left\{ \begin{array}{l} {g_x}\left( {x,y} \right) = \left( { - \frac{x}{{2\pi {\sigma ^4}}}} \right) \exp \left( { - \frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}} \right) \\ {g_y}\left( {x,y} \right) = \left( { - \frac{y}{{2\pi {\sigma ^4}}}} \right) \exp \left( { - \frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}} \right) \end{array} \right. \end{aligned}$$
(11)

The second-order partial derivatives of the Gaussian function are denoted by

$$\begin{aligned} \left\{ \begin{array}{l} {g_{xx}}\left( {x,y} \right) = \left( { - \frac{1}{{2\pi {\sigma ^4}}}} \right) \left( {1 - \frac{{{x^2}}}{{{\sigma ^2}}}} \right) \exp \left( { - \frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}} \right) \\ {g_{yy}}\left( {x,y} \right) = \left( { - \frac{1}{{2\pi {\sigma ^4}}}} \right) \left( {1 - \frac{{{y^2}}}{{{\sigma ^2}}}} \right) \exp \left( { - \frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}} \right) \\ {g_{xy}}\left( {x,y} \right) = \left( {\frac{{xy}}{{2\pi {\sigma ^6}}}} \right) \exp \left( { - \frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}} \right) \end{array} \right. \end{aligned}$$
(12)

According to the above Eqs. (11) and (12), the first-order derivative and the second-order derivative of the image can be convoluted by image and Gaussian kernel function.

$$\begin{aligned} \left\{ \begin{array}{l} {I_x}\left( {x,y} \right) = I\left( {x,y} \right) * {g_x}\left( {x,y} \right) \\ {I_y}\left( {x,y} \right) = I\left( {x,y} \right) * {g_y}\left( {x,y} \right) \end{array} \right. ,\left\{ \begin{array}{l} {I_{xx}}\left( {x,y} \right) = I\left( {x,y} \right) * {g_{xx}}\left( {x,y} \right) \\ {I_{yy}}\left( {x,y} \right) = I\left( {x,y} \right) * {g_{yy}}\left( {x,y} \right) \\ {I_{xy}}\left( {x,y} \right) = I\left( {x,y} \right) * {g_{xy}}\left( {x,y} \right) \end{array} \right. \end{aligned}$$
(13)

where \({I_{x}}\left( {x,y} \right) \), \({I_y}\left( {x,y} \right) \) are the first-order partial derivatives with the image \(I\left( {x,y} \right) \) along the x and y directions, and \({I_{xx}}\left( {x,y} \right) \), \({I_{yy}}\left( {x,y} \right) \), and \({I_{xy}}\left( {x,y} \right) \) represent the second-order partial derivatives with the image \(I\left( {x,y} \right) \), respectively.

So, the Hessian matrix of any point in an image is given by

$$\begin{aligned} H\left( {x,y} \right) = \left[ {\begin{array}{*{20}{c}} {{I_{xx}}\left( {x,y} \right) }&{}{{I_{xy}}\left( {x,y} \right) }\\ {{I_{xy}}\left( {x,y} \right) }&{}{{I_{yy}}\left( {x,y} \right) } \end{array}} \right] \end{aligned}$$
(14)

The eigenvalues of the Hessian matrix are the maximum and minimum of the second-order directional derivatives of the image at this point. The corresponding eigenvectors are the directional vectors of the two extremes, and the two vectors are orthogonal. For light stripe images, the normal direction is the eigenvector corresponding to the larger absolute eigenvalue of the Hessian matrix, and the eigenvector corresponding to the smaller absolute eigenvalue of the Hessian matrix is perpendicular to the normal direction.

Suppose \({\lambda _1}\) and \({\lambda _2}\) are the two eigenvalues of the Hessian matrix, and \({n_x}\) and \({n_y}\) are their corresponding eigenvectors. The eigenvalue \({\lambda _1}\) approaches zero, and the other eigenvalue \({\lambda _2}\) is far less than zero because the gray value of the edge of the light stripe is much larger than that of the background. Namely, \(\left\| {{\lambda _1}} \right\| \approx 0,{\lambda _2} \ll 0\).

Obviously, whether the above conditions are satisfied is a necessary condition for judging that the image point is the center of the light stripe. Therefore, we should choose two thresholds to judge the two eigenvalues. If the threshold is larger, the effective center of the light stripe will be lost, and the discontinuity of the light stripe will occur. If the threshold is smaller, multiple light stripe centers will be generated on the same cross-section of the light stripe.

In order to solve the above problems, we use the data normalization method commonly used in the neural network to normalize the above two eigenvalues. Therefore, we propose a normalized model based on Gauss function and an arc-tangent function.

2.5 Normalization of Hessian Matrix Eigenvalues and Discrimination of Light Stripe Centers

For smaller eigenvalues \({\lambda _1}\) tending to zero, we use standard Gauss function to normalize it. So, when the eigenvalue \({\lambda _1}\) tends to zero, the normalized value tends to 1. For the eigenvalue \({\lambda _2}\) with larger absolute value, we use the arc-tangent function to normalize it. When the absolute value of the eigenvalue \({\lambda _1}\) increases, the normalized value approaches to 1. These two normalization functions are as follows.

$$\begin{aligned} {h_1}\left( {{\lambda _1}} \right) = \exp \left( { - \frac{{\lambda _1^2}}{a}} \right) \end{aligned}$$
(15)

where \({\lambda _1}\) is the eigenvalue of the Hessian matrix corresponding to the axis direction of the light stripe. The gray value of the light stripe center varies tinily in its axis direction. a is a constant that we need to set.

$$\begin{aligned} {h_2}\left( {{\lambda _2}} \right) = \left\{ \begin{array}{l} 0\quad \;\quad \quad \quad \quad \\ \frac{2}{\pi }\mathrm{{atan}}\left( {\frac{{{\lambda _2}}}{b}} \right) {} {} {} \quad \end{array} \right. \;\begin{array}{*{20}{c}} {{\lambda _2} \ge 0}\\ {{\lambda _2} < 0} \end{array} \end{aligned}$$
(16)

where \({\lambda _2}\) is the eigenvalue of the Hessian matrix corresponding to the normal direction of the light stripe. The gray value of the light stripe center varies greatly in its normal direction. b is also a constant that we need to set.

We use the product of these two normalized functions as the final normalized function. The proposed function is illustrated in Fig. 6.

Fig. 6.
figure 6

The normalization function \(h\left( {{\lambda _1},{\lambda _2}} \right) \) for the eigenvalues \({\lambda _1}\), \({\lambda _2}\) of the Hessian matrix

Full size image
$$\begin{aligned} \left\{ \begin{array}{l} h\left( {{\lambda _1},{\lambda _2}} \right) = 0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ h\left( {{\lambda _1},{\lambda _2}} \right) = \frac{2}{\pi }\exp \left( { - \frac{{\lambda _1^2}}{a}} \right) a\tan \left( {\frac{{{\lambda _2}}}{b}} \right) \; \end{array} \right. \;\begin{array}{*{20}{c}} {{\lambda _2} \ge 0}\\ {{\lambda _2} < 0} \end{array} \end{aligned}$$
(17)

It should be noted that the values of a and b here are related to the stripe width of the actual image. We usually use the following formula to get the value.

$$\begin{aligned} \left\{ \begin{array}{l} a = 2*{{\sum \limits _{i = 1}^N {{I_w}\left( {x,y} \right) } } / N}\\ b = {{ - \sum \limits _{i = 1}^N {{I_w}\left( {x,y} \right) } } / N} \end{array} \right. \end{aligned}$$
(18)

Where, N is the sum of the gray value 1 of the segmented light stripe image. For this paper, a is set to 20 and b is set to \(-0.1\).

To obtain the sub-pixel center point of light stripe, let \(\left( {x + t{n_x},y + t{n_y}} \right) \) be the sub-pixel coordinates of the center coordinate \(\left( {x,y} \right) \) along the normal direction of the unit vector \(\left( {{n_x},{n_y}} \right) \) deduced by the Hessian matrix. The Taylor expansion of \(I\left( {x + t{n_x},y + t{n_y}} \right) \) at \(I\left( {x,y} \right) \) is

$$\begin{aligned} \begin{array}{l} I\left( {x + t{n_x},y + t{n_y}} \right) = I\left( {x,y} \right) + t{n_x}{I_x}\left( {x,y} \right) + t{n_y}{I_y}\left( {x,y} \right) + \\ \quad + 1/2\left( {{t^2}n_x^2{I_{xx}}\left( {x,y} \right) + 2{t^2}{n_x}{n_y}{I_{xy}}\left( {x,y} \right) + {t^2}n_y^2{I_{yy}}\left( {x,y} \right) } \right) \end{array} \end{aligned}$$
(19)

where \({I_x}\left( {x,y} \right) \), \({I_y}\left( {x,y} \right) \) are the convolution results of the first-order partial derivatives in x and y directions, and t is an unknown value. Because of the sub-pixel center exists on the normal vector of light stripe, the derivative of Eq. (19) is equal to 0, then

$$\begin{aligned} t = - \frac{{{n_x}{I_x}\left( {x,y} \right) + {n_y}{I_y}\left( {x,y} \right) }}{{n_x^2{I_{xx}}\left( {x,y} \right) + 2{n_x}{n_y}{I_{xy}}\left( {x,y} \right) + n_y^2{I_{yy}}\left( {x,y} \right) }} \end{aligned}$$
(20)

If \(t{n_x} \in \left[ { - {1 / {2,{1 / 2}}}} \right] \) and \(t{n_y} \in \left[ { - {1 / {2,{1 / 2}}}} \right] \), \(\left( {x + t{n_x},y + t{n_y}} \right) \) is the sub-pixel center point of the light stripe.

Fig. 7.
figure 7

Light stripe image of real object for size measurement of rails

Full size image

3 Experiment

3.1 Extraction of Light Stripe Center in Visual Measurement of Rails

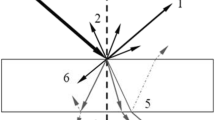
Line-structure vision sensor is often used in rail dimension vision measurement. Fast measurement of rail dimension is very important to ensure the safety of train running. Usually the rail is installed outdoors, and the outdoor light environment is always changing, which easily affects the accuracy of light stripe center extraction. We validate the effectiveness of the proposed method by extracting light strips from the image of rail size measurement. The light stripe image of size measurement of rails is shown in Fig. 7.

From Fig. 7, we can see that the background noise of the stripe image is more complex, and the light stripe width distribution is not uniform. The width of the light stripe at both ends is obviously thinner. In the area labeled 5 in Fig. 7, the curvature of the light stripe changes greatly. It is impossible to extract the center line of light stripe directly by using traditional Hessain matrix.

Fig. 8.
figure 8

(a) (b) (c) (d) Extraction of the center line of the light stripe in the area image labeled 1, 2, 3 and 4 in Fig. 7, respectively

Full size image

From Fig. 8(a), we can see that the background noise of the stripe area labeled 1 in Fig. 8 is more serious. The method proposed in this paper can still ensure the correct extraction of the center line of the light stripe.

From Fig. 8(b), we can see that in the area labeled 2 in Fig. 8, the light stripe fines obviously at the end. The method proposed in this paper can still ensure the correct extraction of the center line of the light stripe.

Fig. 9.
figure 9

(a) Center line extraction with great curvature change of light stripe. (b) Center line extraction with uneven change of light stripe width.

Full size image

From Fig. 9(a), we can see that when the curvature of the stripe curve changes greatly, the center line of the light stripe can still be correctly extracted.

From Fig. 9(b), we can see that when the width of the stripe curve is unevenly distributed, the center line of the light stripe can still be correctly extracted.

3.2 Extraction of Multiple Light Stripe Centers

We use the method based on Hessian matrix and the method proposed in this paper to extract the center lines of multiple light stripes in the image to verify the extraction accuracy.

Fig. 10.
figure 10

Multiple light stripe center extraction based on Hessian matrix

Full size image

From Fig. 10, we can see that it is obviously incorrect to extract the central points of two light stripes in the image by using the Hessian matrix method. There are obviously many center points of the light stripes at both ends of the light stripes. We need to delete the wrong center points of the light stripes. We can directly remove the center points of the stripes at both ends of the image, this method is simple, but it is easy to retain or delete the wrong center points of the stripes too much.

Fig. 11.
figure 11

(a) Extraction of the center line of the light stripe in the area image labeled 1 in Fig. 10. (b) Extraction of the center line of the light stripe in the area image labeled 2 in Fig. 10. (c) Extraction of the center line of the light stripe in the area image labeled 3 in Fig. 10. (d) Extraction of the center line of the light stripe in the area image labeled 4 in Fig. 10.

Full size image

From Fig. 11, we can see that after normalizing the eigenvalues of Hessian matrix proposed in this paper, excessive light stripe centers at both ends can be deleted obviously. It should be noted that the number of center points deleted depends on the size of the Gauss filter template.

3.3 Extraction of Intersecting Light Stripe Centers

We use the method based on Hessian matrix and the method proposed in this paper to extract the center line of intersecting light strips, respectively.

Fig. 12.
figure 12

(a) Extraction of the center line of intersecting light stripes based on Hessian matrix. (b) Extraction of the center line of intersecting light stripes based on the method proposed in this paper.

Full size image

From Fig. 12(a), we can see that at the intersection of the two curves, the extracted feature points are not the center of the two quadratic curves, so the wrong feature points need to be eliminated. The change direction of the points on each conic is continuous, and the change direction of the wrong feature points extracted at the intersection will change abruptly, and the angle between the mutation position and the change vector of the adjacent points will increase.

As can be seen from Fig. 12(b), the proposed method can not only filter out the multiple centers of the four endpoints of two curved strips, but also filter out the wrong centers at the intersection. If we need to get the center of the light strip, we can use the right center of the light strip which has been extracted to fit the curve. After fitting, we can get the intersection point, and then we can get the correct center line of the intersection.

3.4 Extraction of Curve Center in Medical Images

The adaptive template matching and Hessian matrix eigenvalue normalization method proposed in this paper are used to extract the central line of color retinal vessels to verify the effectiveness of the proposed method in complex multi-central line extraction.

Fig. 13.
figure 13

(a) Original retinal vascular image. (b) Extracted vascular images. (Color figure online)

Full size image

As shown in Fig. 13(a), it is a color image of retinal vessels. Figure 13(b) shows the extracted image. From the image, it can be seen that for the image without lesions, the blood vessels can be segmented completely.

3.5 Comparisons of Extraction Time

We use the configuration of the notebook computer: i5-3210M dual-core four-threaded CPU, 8G memory, compiled by Visual studio 2015 software, the resolution of 768*576 light stripe image to extract, that is, the image in Fig. 7. The calculating time is as shown in Table 1.

Table 1. Comparisons of extraction time between different method.
Full size table

Although the time of the proposed method is comparable to that of Steger’s method (the speed of the proposed method is a little slower), the calculation time can be reduced by increasing the number of threads in the CPU or using GPU acceleration.

4 Conclusion

A fast sub-pixel center extraction method based on adaptive template is proposed. The adaptive threshold method is used to reduce the image convolution area, and the multi-thread parallel operation is used to improve the speed of stripe center extraction. The multi-directional template is used to estimate the width of the light stripe along the normal direction. The size of the Gaussian convolution template is determined according to the actual width. The Hessian matrix is calculated and its eigenvalues are normalized to establish the criterion for the center of the light stripe. This method has fast processing speed, good robustness and high precision. It is suitable for vision measurement image, medical image, remote sensing image and other fields.