Dist-GAN: An Improved GAN Using Distance Constraints

Abstract

We introduce effective training algorithms for Generative Adversarial Networks (GAN) to alleviate mode collapse and gradient vanishing. In our system, we constrain the generator by an Autoencoder (AE). We propose a formulation to consider the reconstructed samples from AE as “real” samples for the discriminator. This couples the convergence of the AE with that of the discriminator, effectively slowing down the convergence of discriminator and reducing gradient vanishing. Importantly, we propose two novel distance constraints to improve the generator. First, we propose a latent-data distance constraint to enforce compatibility between the latent sample distances and the corresponding data sample distances. We use this constraint to explicitly prevent the generator from mode collapse. Second, we propose a discriminator-score distance constraint to align the distribution of the generated samples with that of the real samples through the discriminator score. We use this constraint to guide the generator to synthesize samples that resemble the real ones. Our proposed GAN using these distance constraints, namely Dist-GAN, can achieve better results than state-of-the-art methods across benchmark datasets: synthetic, MNIST, MNIST-1K, CelebA, CIFAR-10 and STL-10 datasets. Our code is published here (https://github.com/tntrung/gan) for research.

1 Introduction

Generative Adversarial Network [12] (GAN) has become a dominant approach for learning generative models. It can produce very visually appealing samples with few assumptions about the model. GAN can produce samples without explicitly estimating data distribution, e.g. in analytical forms. GAN has two main components which compete against each other, and they improve through the competition. The first component is the generator G, which takes low-dimensional random noise $\mathrm {z} \sim P_\mathrm {z}$ as an input and maps them into high-dimensional data samples, $\mathrm {x} \sim P_\mathrm {x}$. The prior distribution $P_\mathrm {z}$ is often uniform or normal. Simultaneously, GAN uses the second component, a discriminator D, to distinguish whether samples are drawn from the generator distribution $P_G$ or data distribution $P_\mathrm {x}$. Training GAN is an adversarial process: while the discriminator D learns to better distinguish the real or fake samples, the generator G learns to confuse the discriminator D into accepting its outputs as being real. The generator G uses discriminator’s scores as feedback to improve itself over time, and eventually can approximate the data distribution.

Despite the encouraging results, GAN is known to be hard to train and requires careful designs of model architectures [11, 24]. For example, the imbalance between discriminator and generator capacities often leads to convergence issues, such as gradient vanishing and mode collapse. Gradient vanishing occurs when the gradient of discriminator is saturated, and the generator has no informative gradient to learn. It occurs when the discriminator can distinguish very well between “real” and “fake” samples, before the generator can approximate the data distribution. Mode collapse is another crucial issue. In mode collapse, the generator is collapsed into a typical parameter setting that it always generates small diversity of samples.

Several GAN variants have been proposed [4, 22, 24, 26, 29] to solve these problems. Some of them are Autoencoders (AE) based GAN. AE explicitly encodes data samples into latent space and this allows representing data samples with lower dimensionality. It not only has the potential for stabilizing GAN but is also applicable for other applications, such as dimensionality reduction. AE was also used as part of a prominent class of generative models, Variational Autoencoders (VAE) [6, 17, 25], which are attractive for learning inference/generative models that lead to better log-likelihoods [28]. These encouraged many recent works following this direction. They applied either encoders/decoders as an inference model to improve GAN training [9, 10, 19], or used AE to define the discriminator objectives [5, 30] or generator objectives [7, 27]. Others have proposed to combine AE and GAN [18, 21].

In this work, we propose a new design to unify AE and GAN. Our design can stabilize GAN training, alleviate the gradient vanishing and mode collapse issues, and better approximate data distribution. Our main contributions are two novel distance constraints to improve the generator. First, we propose a latent-data distance constraint. This enforces compatibility between latent sample distances and the corresponding data sample distances, and as a result, prevents the generator from producing many data samples that are close to each other, i.e. mode collapse. Second, we propose a discriminator-score distance constraint. This aligns the distribution of the fake samples with that of the real samples and guides the generator to synthesize samples that resemble the real ones. We propose a novel formulation to align the distributions through the discriminator score. Comparing to state of the art methods using synthetic and benchmark datasets, our method achieves better stability, balance, and competitive standard scores.

2 Related Works

The issue of non-convergence remains an important problem for GAN research, and gradient vanishing and mode collapse are the most important problems [3, 11]. Many important variants of GAN have been proposed to tackle these issues. Improved GAN [26] introduced several techniques, such as feature matching, mini-batch discrimination, and historical averaging, which drastically reduced the mode collapse. Unrolled GAN [22] tried to change optimization process to address the convergence and mode collapse. [4] analyzed the convergence properties for GAN. Their proposed GAN variant, WGAN, leveraged the Wasserstein distance and demonstrated its better convergence than Jensen Shannon (JS) divergence, which was used previously in vanilla GAN [12]. However, WGAN required that the discriminator must lie on the space of 1-Lipschitz functions, therefore, it had to enforce norm critics to the discriminator by weight-clipping tricks. WGAN-GP [13] stabilized WGAN by alternating the weight-clipping by penalizing the gradient norm of the interpolated samples. Recent work SN-GAN [23] proposed a weight normalization technique, named as spectral normalization, to slow down the convergence of the discriminator. This method controls the Lipschitz constant by normalizing the spectral norm of the weight matrices of network layers.

Other work has integrated AE into the GAN. AAE [21] learned the inference by AE and matched the encoded latent distribution to given prior distribution by the minimax game between encoder and discriminator. Regularizing the generator with AE loss may cause the blurry issue. This regularization can not assure that the generator is able to approximate well data distribution and overcome the mode missing. VAE/GAN [18] combined VAE and GAN into one single model and used feature-wise distance for the reconstruction. Due to depending on VAE [17], VAEGAN also required re-parameterization tricks for back-propagation or required access to an exact functional form of prior distribution. InfoGAN [8] learned the disentangled representation by maximizing the mutual information for inducing latent codes. EBGAN [30] introduced the energy-based model, in which the discriminator is considered as energy function minimized via reconstruction errors. BEGAN [5] extended EBGAN by optimizing Wasserstein distance between AE loss distributions. ALI [10] and BiGAN [9] encoded the data into latent and trained jointly the data/latent samples in GAN framework. This model can learn implicitly encoder/decoder models after training. MDGAN [7] required two discriminators for two separate steps: manifold and diffusion. The manifold step tended to learn a good AE, and the diffusion objective is similar to the original GAN objective, except that the constructed samples are used instead of real samples.

In the literature, VAEGAN and MDGAN are most related to our work in term of using AE to improve the generator. However, our design is remarkably different: (1) VAEGAN combined KL divergence and reconstruction loss to train the inference model. With this design, it required an exact form of prior distribution and re-parameterization tricks for solving the optimization via back-propagation. In contrast, our method constrains AE by the data and latent sample distances. Our method is applicable to any prior distribution. (2) Unlike MDGAN, our design does not require two discriminators. (3) VAEGAN considered the reconstructed samples as “fake”, and MDGAN adopts this similarly in its manifold step. In contrast, we use them as “real” samples, which is important to restrain the discriminator in order to avoid gradient vanishing, therefore, reduce mode collapse. (4) Two of these methods regularize G simply by reconstruction loss. This is inadequate to solve the mode collapse. We conduct an analysis and explain why additional regularization is needed for AE. Experiment results demonstrate that our model outperforms MDGAN and VAEGAN.

3 Proposed Method

Mode collapse is an important issue for GAN. In this section, we first propose a new way to visualize the mode collapse. Based on the visualization results, we propose a new model, namely Dist-GAN, to solve this problem.

Fig. 1.

(a) Mode collapse observed by data samples of the MNIST dataset, and (b) their corresponding latent samples of an uniform distribution. Mode collapse occurs frequently when the capacity of networks is small or the design of generator/discriminator networks is unbalance.

3.1 Visualize Mode Collapse in Latent Space

Mode collapse occurs when “the generator collapses to a parameter setting where it always emits the same point. When collapse to a single mode is imminent, the gradient of the discriminator may point in similar directions for many similar points.” [26]. Previous work usually examines mode collapse by visualizing a few collapsed samples (generated from random latent samples of a prior distribution). Figure 1a is an example. However, the data space is high-dimensional, therefore it is difficult to visualize points in the data space. On the other hand, the latent space is lower-dimensional and controllable, and it is possible to visualize the entire 2D/3D spaces. Thus, it could be advantageous to examine mode collapse in the latent space. However, the problem is that GAN is not invertible to map the data samples back to the latent space. Therefore, we propose the following method to visualize the samples and examine mode collapse in the latent space. We apply an off-the-shelf classifier. This classifier predicts labels of the generated samples. We visualize these class labels according to the latent samples, see Fig. 1b. This is possible because, for many datasets such as MNIST, pre-trained classifiers can achieve high accuracy, e.g. 0.04% error rate.

Fig. 2.

Latent space visualization: The labels of 55 K 2D latent variables obtained by (a) DCGAN, (b) WGANGP, (c) our Dist-GAN$_2$ (without latent-data distance) and (d) our Dist-GAN$_3$ (with our proposed latent-data distance). The Dist-GAN settings are defined in the section of Experimental Results.

3.2 Distance Constraint: Motivation

Fig. 1b is the latent sample visualization using this technique, and the latent samples are uniformly distributed in a 2D latent space of $[-1, 1]$. Figure 1b clearly suggests the extent of mode collapse: many latent samples from large regions of latent space are collapsed into the same digit, e.g. ‘1’. Even some latent samples reside very far apart from each other, they map to the same digit. This suggests that a generator $G_{\theta }$ with parameter $\theta$ has mode collapse when there are many latent samples mapped to small regions of the data space:

$$\begin{aligned} \mathrm {x_i} = G_{\theta }(\mathrm {z_i}), \mathrm {x_j} = G_{\theta }(\mathrm {z_j}): f(\mathrm {x_i}, \mathrm {x_j}) < \delta _{\mathrm {x}} \end{aligned}$$

(1)

Here $\{\mathrm {z_i}\}$ are latent samples, and $\{\mathrm {x_i}\}$ are corresponding synthesized samples by $G_{\theta }$. f is some distance metric in the data space, and $\delta _{\mathrm {x}}$ is a small threshold in the data space. Therefore, we propose to address mode collapse using a distance metric g in latent space, and a small threshold $\delta _{\mathrm {z}}$ of this metric, to restrain $G_{\theta }$ as follows:

$$\begin{aligned} g(\mathrm {z_i}, \mathrm {z_j})> \delta _{\mathrm {z}} \rightarrow f(\mathrm {x_i}, \mathrm {x_j}) > \delta _{\mathrm {x}} \end{aligned}$$

(2)

However, determining good functions f, g for two spaces of different dimensionality and their thresholds $\delta _{\mathrm {x}}, \delta _{\mathrm {z}}$ is not straightforward. Moreover, applying these constraints to GAN is not simple, because GAN has only one-way mapping from latent to data samples. In the next section, we will propose novel formulation to represent this constraint in latent-data distance and apply this to GAN.

We have also tried to apply this visualization for two state-of-the-art methods: DCGAN [24], WGANGP [13] on the MNIST dataset (using the code of [13]). Note that all of our experiments were conducted in the unsupervised setting. The off-the-shelf classifier is used here to determine the labels of generated samples solely for visualization purpose. Figure 2a and b represent the labels of the 55 K latent variables of DCGAN and WGANGP respectively at iteration of 70K. Figure 2a reveals that DCGAN is partially collapsed, as it generates very few digits ‘5’ and ‘9’ according to their latent variables near the bottom-right top-left corners of the prior distribution. In contrast, WGANGP does not have mode collapse, as shown in Fig. 2b. However, for WGANGP, the latent variables corresponding to each digit are fragmented in many sub-regions. It is an interesting observation for WGANGP. We will investigate this as our future work.

3.3 Improving GAN Using Distance Constraints

We apply the idea of Eq. 2 to improve generator through an AE. We apply AE to encode data samples into latent variables and use these encoded latent variables to direct the generator’s mapping from the entire latent space. First, we train an AE (encoder $E_{\omega }$ and decoder $G_\theta$), then we train the discriminator $D_{\gamma }$ and the generator $G_{\theta }$. Here, the generator is the decoder of AE and $\omega , \theta , \gamma$ are the parameters of the encoder, generator, and discriminator respectively. Two main reasons for training an AE are: (i) to regularize the parameter $\theta$ at each training iteration, and (ii) to direct the generator to synthesize samples similar to real training samples. We include an additional latent-data distance constraint to train the AE:

$$\begin{aligned} \min _{\omega ,\theta } L_R(\omega ,\theta ) + \lambda _{\mathrm {r}} L_W(\omega ,\theta ) \end{aligned}$$

(3)

where $L_R(\omega ,\theta ) = ||\mathrm {x} - G_{\theta }(E_{\omega }(\mathrm {x}))||_2^2$ is the conventional AE objective. The latent-data distance constraint $L_W(\omega ,\theta )$ is to regularize the generator and prevent it from being collapsed. This term will be discussed later. Here, $\lambda _{\mathrm {r}}$ is the constant. The reconstructed samples $G_{\theta }(E_{\omega }(\mathrm {x}))$ can be approximated by $G_{\theta }(E_{\omega }(\mathrm {x})) = \mathrm {x} + \varepsilon$, where $\varepsilon$ is the reconstruction error. Usually the capacity of E and G are large enough so that $\epsilon$ is small (like noise). Therefore, it is reasonable to consider those reconstructed samples as “real” samples (plus noise $\varepsilon$). The pixel-wise reconstruction may cause blurry. To circumvent this, we instead use feature-wise distance [18] or similarly feature matching [26]: $L_R(\omega ,\theta ) = ||\varPhi (\mathrm {x}) - \varPhi (G_{\theta }(E_{\omega }(\mathrm {x})))||_2^2$. Here $\varPhi (\mathrm {x})$ is the high-level feature obtained from some middle layers of deep networks. In our implementation, $\varPhi (\mathrm {x})$ is the feature output from the last convolution layer of discriminator $D_{\gamma }$. Note that in the first iteration, the parameters of discriminator are randomly initialized, and features produced from this discriminator is used to train the AE.

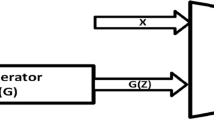
Our framework is shown in Fig. 3. We propose to train encoder $E_{\omega }$, generator $G_{\theta }$ and discriminator $D_{\gamma }$ following the order: (i) fix $D_{\gamma }$ and train $E_{\omega }$ and $G_{\theta }$ to minimize the reconstruction loss Eq. 3 (ii) fix $E_{\omega }$, $G_{\theta }$, and train $D_{\gamma }$ to minimize (Eq. 5), and (iii) fix $E_{\omega }$, $D_{\gamma }$ and train $G_{\theta }$ to minimize (Eq. 4).

Generator and Discriminator Objectives. When training the generator, maximizing the conventional generator objective $\mathbb {E}_{\mathrm {z}} \sigma (D_\gamma (G_\theta (\mathrm {z})))$ [12] tends to produce samples at high-density modes, and this leads to mode collapse easily. Here, $\sigma$ denotes the sigmoid function and $\mathbb {E}$ denotes the expectation. Instead, we train the generator with our proposed “discriminator-score distance". We align the synthesized sample distribution to real sample distribution with the $\ell _1$ distance. The alignment is through the discriminator score, see Eq. 4. Ideally, the generator synthesizes samples similar to the samples drawn from the real distribution, and this also helps reduce missing mode issue.

$$\begin{aligned} \min _{\theta }\mathcal {L}_G(\theta ) = |\mathbb {E}_{\mathrm {x}} \sigma (D_\gamma (\mathrm {x})) - \mathbb {E}_{\mathrm {z}} \sigma (D_\gamma (G_\theta (\mathrm {z})))| \end{aligned}$$

(4)

The objective function of the discriminator is shown in Eq. 5. It is different from original discriminator of GAN in two aspects. First, we indicate the reconstructed samples as “real”, represented by the term $L_C = \mathbb {E}_{\mathrm {x}} \log \sigma (D_\gamma (G_\theta (E_\omega (\mathrm {x}))))$. Considering the reconstructed samples as “real” can systematically slow down the convergence of discriminator, so that the gradient from discriminator is not saturated too quickly. In particular, the convergence of the discriminator is coupled with the convergence of AE. This is an important constraint. In contrast, if we consider the reconstruction as “fake” in our model, this speeds up the discriminator convergence, and the discriminator converges faster than both generator and encoder. This leads to gradient saturation of $D_\gamma$. Second, we apply the gradient penalty $L_P = (||\nabla _{\hat{\mathrm {x}}} D_\gamma (\hat{\mathrm {x}})||_2^2 - 1)^2$ for the discriminator objective (Eq. 5), where $\lambda _{\mathrm {p}}$ is penalty coefficient, and $\hat{\mathrm {x}} = \epsilon \mathrm {x} + (1 - \epsilon ) G(\mathrm {z})$, $\epsilon$ is a uniform random number $\epsilon \in U[0,1]$. This penalty was used to enforce Lipschitz constraint of Wasserstein-1 distance [13]. In this work, we also find this useful for JS divergence and stabilizing our model. It should be noted that using this gradient penalty alone cannot solve the convergence issue, similar to WGANGP. The problem is partially solved when combining this with our proposed generator objective in Eq. 4, i.e., discriminator-score distance. However, the problem cannot be completely solved, e.g. mode collapse on MNIST dataset with 2D latent inputs as shown in Fig. 2c. Therefore, we apply the proposed latent-data distance constraints as additional regularization term for AE: $L_W(\omega ,\theta )$, to be discussed in the next section.

$$\begin{aligned} \begin{aligned} \min _{\gamma }\mathcal {L}_D(\omega ,\theta ,\gamma )&= -(\mathbb {E}_{\mathrm {x}} \log \sigma (D_\gamma (\mathrm {x})) + \mathbb {E}_{\mathrm {z}} \log (1 - \sigma (D_\gamma (G_\theta (\mathrm {z})))) \\&+ \mathbb {E}_{\mathrm {x}} \log \sigma (D_\gamma (G_\theta (E_\omega (\mathrm {x})))) - \lambda _{\mathrm {p}}\mathbb {E}_{{\hat{\mathrm {x}}}}(||\nabla _{\hat{\mathrm {x}}} D_\gamma (\hat{\mathrm {x}})||_2^2 - 1)^2) \end{aligned} \end{aligned}$$

(5)

Regularizing Autoencoders by Latent-Data Distance Constraint. In this section, we discuss the latent-data distance constraint $L_W(\omega ,\theta )$ to regularize AE in order to reduce mode collapse in the generator (the decoder in the AE). In particular, we use noise input to constrain encoder’s outputs, and simultaneously reconstructed samples to constrain the generator’s outputs. Mode collapse occurs when the generator synthesizes low diversity of samples in the data space given different latent inputs. Therefore, to reduce mode collapse, we aim to achieve: if the distance of any two latent variables $g(\mathrm {z_i}, \mathrm {z_j})$ is small (large) in the latent space, the corresponding distance $f(\mathrm {x_i}, \mathrm {x_j})$ in data space should be small (large), and vice versa. We propose a latent-data distance regularization $L_W(\omega ,\theta )$:

$$\begin{aligned} L_W(\omega ,\theta ) = ||f(\mathrm {x},G_\theta (\mathrm {z})) - \lambda _{\mathrm {w}}g(E_\omega (\mathrm {x}),\mathrm {z})||_2^2 \end{aligned}$$

(6)

Fig. 3.

The architecture of Dist-GAN includes Encoder (E), Generator (G) and Discriminator (D). Reconstructed samples are considered as “real”. The input, reconstructed, and generated samples as well as the input noise and encoded latent are all used to form the latent-data distance constraint for AE (regularized AE).

Fig. 4.

(a) The 1D frequency density of outputs using $\mathrm {M_d}$ from uniform distribution of different dimensionality. (b) One example of the density when mode collapse occurs. (c) The 1D density of real data and generated data obtained by different methods: DCGAN (kldiv: 0.00979), WGANGP (kldiv: 0.00412), Dist-GAN$_2$ (without data-latent distance constraint of AE, kldiv: 0.01027), and Dist-GAN (kldiv: 0.00073).

where f and g are distance functions computed in data and latent space. $\lambda _{\mathrm {w}}$ is the scale factor due to the difference in dimensionality. It is not straight forward to compare distances in spaces of different dimensionality. Therefore, instead of using the direct distance functions, e.g. Euclidean, $\ell _1$-norm, etc., we propose to compare the matching score $f(\mathrm {x},G_\theta (\mathrm {z}))$ of real and fake distributions, and the matching score $g(E_\omega (\mathrm {x}),\mathrm {z})$ of two latent distributions. We use means as the matching scores. Specifically:

$$\begin{aligned} f(\mathrm {x},G_\theta (\mathrm {z})) = \mathrm {M_d}(\mathbb {E}_{\mathrm {x}}G_\theta (E_\omega (\mathrm {x})) - \mathbb {E}_{\mathrm {z}} G_\theta (\mathrm {z})) \end{aligned}$$

(7)

$$\begin{aligned} g(E_\omega (\mathrm {x}),\mathrm {z}) = \mathrm {M_d}(\mathbb {E}_{\mathrm {x}}E_\omega (\mathrm {x}) - \mathbb {E}_{\mathrm {z}}\mathrm {z}) \end{aligned}$$

(8)

where $\mathrm {M_d}$ computes the average of all dimensions of the input. Figure 4a illustrates 1D frequency density of 10000 random samples mapped by $\mathrm {M_d}$ from $[-1,1]$ uniform distribution of different dimensionality. We can see that outputs of $\mathrm {M_d}$ from high dimensional spaces have small values. Thus, we require $\lambda _\mathrm {w}$ in (6) to account for the difference in dimensionality. Empirically, we found $\lambda _\mathrm {w} = \sqrt{\frac{d_\mathrm {z}}{d_\mathrm {x}}}$ suitable, where $d_\mathrm {z}$ and $d_\mathrm {x}$ are dimensions of latent and data samples respectively. Figure 4b shows the frequency density of a collapse mode case. We can observe that the 1D density of generated samples is clearly different from that of the real data. Figure 4c compares 1D frequency densities of 55K MNIST samples generated by different methods. Our Dist-GAN method can estimate better 1D density than DCGAN and WGANGP measured by KL divergence (kldiv) between the densities of generated samples and real samples.

The entire algorithm is presented in Algorithm 1.

4 Experimental Results

4.1 Synthetic Data

All our experiments are conducted using the unsupervised setting. First, we use synthetic data to evaluate how well our Dist-GAN can approximate the data distribution. We use a synthetic dataset of 25 Gaussian modes in grid layout similar to [10]. Our dataset contains 50 K training points in 2D, and we draw 2 K generated samples for testing. For fair comparisons, we use equivalent architectures and setup for all methods in the same experimental condition if possible. The architecture and network size are similar to [22] on the 8-Gaussian dataset, except that we use one more hidden layer. We use fully-connected layers and Rectifier Linear Unit (ReLU) activation for input and hidden layers, sigmoid for output layers. The network size of encoder, generator and discriminator are presented in Table 1 of Supplementary Material, where $d_\mathrm {in} = 2$, $d_\mathrm {out} = 2$, $d_\mathrm {h} = 128$ are dimensions of input, output and hidden layers respectively. $N_\mathrm {h} = 3$ is the number of hidden layers. The output dimension of the encoder is the dimension of the latent variable. Our prior distribution is uniform $[-1,1]$. We use Adam optimizer with learning rate $\mathrm {lr} = 0.001$, and the exponent decay rate of first moment $\beta _1 = 0.8$. The learning rate is decayed every 10K steps with a base of 0.9. The mini-batch size is 128. The training stops after 500 epochs. To have fair comparison, we carefully fine-tune other methods (and use weight decay during training if this achieves better results) to ensure they achieve their best results on the synthetic data. For evaluation, a mode is missed if there are less than 20 generated samples registered into this mode, which is measured by its mean and variance of 0.01 [19, 22]. A method has mode collapse if there are missing modes. In this experiment, we fix the parameters $\lambda _{\mathrm {r}} = 0.1$ (Eq. 3), $\lambda _{\mathrm {p}} = 0.1$ (Eq. 5), $\lambda _{\mathrm {w}} = 1.0$ (Eq. 6). For each method, we repeat eight runs and report the average.

Fig. 5.

From left to right figures: (a), (b), (c), (d). The number of registered modes (a) and points (b) of our method with two different settings on the synthetic dataset. We compare our Dist-GAN to the baseline GAN [12] and other methods on the same dataset measured by the number of registered modes (classes) (c) and points (d).

First, we highlight the capability of our model to approximate the distribution $P_\mathrm {x}$ of synthetic data. We carry out the ablation experiment to understand the influence of each proposed component with different settings:

• Dist-GAN$_1$: uses the “discriminator-score distance” for generator objective ($\mathcal {L}_G$) and the AE loss $L_R$ but does not use data-latent distance constraint term ($L_W$) and gradient penalty ($L_P$). This setting has three different versions as using reconstructed samples ($L_C$) as “real”, “fake” or “none” (not use it) in the discriminator objective.

• Dist-GAN$_2$: improves from Dist-GAN$_1$ (regarding reconstructed samples as “real”) by adding the gradient penalty $L_P$.

• Dist-GAN: improves the Dist-GAN$_2$ by adding the data-latent distance constraint $L_W$. (See Table 3 in Supplementary Material for details).

The quantitative results are shown in Fig. 5. Figure 5a is the number of registered modes changing over the training. Dist-GAN$_1$ misses a few modes while Dist-GAN$_2$ and Dist-GAN generates all 25 modes after about 50 epochs. Since they almost do not miss any modes, it is reasonable to compare the number of registered points as in Fig. 5b. Regarding reconstructed samples as “real” achieves better results than regarding them as “fake” or “none”. It is reasonable that Dist-GAN$_1$ obtains similar results as the baseline GAN when not using the reconstructed samples in discriminator objective (“none” option). Other results show the improvement when adding the gradient penalty into the discriminator (Dist-GAN$_2$). Dist-GAN demonstrates the effectiveness of using the proposed latent-data constraints, when comparing with Dist-GAN$_2$.

To highlight the effectiveness of our proposed “discriminator-score distance” for the generator, we use it to improve the baseline GAN [12], denoted by GAN$_1$. Then, we propose GAN$_2$ to improve GAN$_1$ by adding the gradient penalty. We can observe that combination of our proposed generator objective and gradient penalty can improve stability of GAN. We compare our best setting (Dist-GAN) to previous work. ALI [10] and DAN-2S [19] are recent works using encoder/decoder in their model. VAE-GAN [18] introduces a similar model. WGAN-GP [13] is one of the current state of the art. The numbers of covered modes and registered points are presented in Fig. 5c and Fig. 5d respectively. The quantitative numbers of last epochs are shown in Table 2 of Supplementary Material. In this table, we report also Total Variation scores to measure the mode balance. The result for each method is the average of eight runs. Our method outperforms GAN [12], DAN-2S [19], ALI [10], and VAE/GAN [18] on the number of covered modes. While WGAN-GP sometimes misses one mode and diverges, our method (Dist-GAN) does not suffer from mode collapse in all eight runs. Furthermore, we achieve a higher number of registered samples than WGAN-GP and all others. Our method is also better than the rest with Total Variation (TV) [19]. Figure 6 depicts the detail proportion of generated samples of 25 modes. (More visualization of generated samples in Section 2 of Supplementary Material).

Fig. 6.

The mode balance obtained by different methods.

4.2 MNIST-1K

For image datasets, we use $\varPhi (\mathrm {x})$ instead $\mathrm {x}$ for the reconstruction loss and the latent-data distance constraint in order to avoid the blur. We fix the parameters $\lambda _{\mathrm {p}} = 1.0$, and $\lambda _{\mathrm {r}} = 1.0$ for all image datasets that work consistently well. The $\lambda _{\mathrm {w}}$ is automatically computed from dimensions of features $\varPhi (\mathrm {x})$ and latent samples. Our model implementation for MNIST uses the published code of WGAN-GP [13]. Figure 7 from left to right are the real samples, the generated samples and the frequency of each digit generated by our method for standard MNIST. It demonstrates that our method can approximate well the MNIST digit distribution. Moreover, our generated samples look realistic with different styles and strokes that resemble the real ones. In addition, we follow the procedure in [22] to construct a more challenging 1000-class MNIST (MNIST-1K) dataset. It has 1000 modes from 000 to 999. We create a total of 25,600 images. We compare methods by counting the number of covered modes (having at least one sample [22]) and computing KL divergence. To be fair, we adopt the equivalent network architecture (low-capacity generator and two crippled discriminators K/4 and K/2) as proposed by [22]. Table 1 presents the number of modes and KL divergence of compared methods. Results show that our method outperforms all others in the number of covered modes, especially with the low-capacity discriminator (K/4 architecture), where our method has 150 modes more than the second best. Our method reduces the gap between the two architectures (e.g. about 60 modes), which is smaller than other methods. For both architectures, we obtain better results for both KL divergence and the number of recovered modes. All results support that our proposed Dist-GAN handles better mode collapse, and is robust even in case of imbalance in generator and discriminator.

Fig. 7.

The real and our generated samples in one mini-batch. And the number of generated samples per class obtained by our method on the MNIST dataset. We compare our frequency of generated samples to the ground-truth via KL divergence: KL = 0.01.

Table 1. The comparison on MNIST-1K of methods. We follow the setup and network architectures from Unrolled GAN.

5 CelebA, CIFAR-10 and STL-10 Datasets

Furthermore, we use CelebA dataset and compare with DCGAN [24] and WGAN-GP [13]. Our implementation is based on the open source [1, 2]. Figure 8 shows samples generated by DCGAN, WGANGP and our Dist-GAN. While DCGAN is slightly collapsed at epoch 50, and WGAN-GP sometimes generates broken faces. Our method does not suffer from such issues and can generate recognizable and realistic faces. We also report results for the CIFAR-10 dataset using DCGAN architecture [24] of same published code [13]. The generated samples with our method trained on this dataset can be found in Sect. 4 of Supplementary Material. For quantitative results, we report the FID scores [15] for both datasets. FID can detect intra-class mode dropping, and measure the diversity and the quality of generated samples. We follow the experimental procedure and model architecture in [20]. Our method outperforms others for both CelebA and CIFAR-10, as shown in the first and second rows of Table 2. Here, the results of other GAN methods are from [20]. We also report FID score of VAEGAN on these datasets. Our method is better than VAEGAN. Note that we have also tried MDGAN, but it has serious mode collapsed for both these datasets. Therefore, we do not report its result in our paper.

Fig. 8.

Generated samples of DCGAN (50 epochs, results from [1]), WGAN-GP (50 epochs, results from [1]) and our Dist-GAN (50 epochs).

Table 2. Comparing FID score to other methods. First two rows (CelebA, CIFAR-10) follow the experimental setup of [20], and the remaining rows follow the experimental setup of [23] using standard CNN architectures.

Lastly, we compare our model with recent SN-GAN [23] on CIFAR-10 and STL-10 datasets with standard CNN architecture. Experimental setup is the same as [23], and FID is the score for the comparison. Results are presented in the third to fifth rows of Table 2. In addition to settings reported using synthetic dataset, we have additional settings and ablation study for image datasets, which are reported in Section 5 of Supplementary Material. The results confirm the stability of our model, and our method outperforms SN-GAN on the CIFAR-10 dataset. Interestingly, when we replace “log" by “hinge loss” functions in the discriminator as in [23], our “hinge loss" version performs even better with FID = 22.95, compared to FID = 25.5 of SN-GAN. It is worth noting that our model is trained with the default parameters $\lambda _p = 1.0$ and $\lambda _r = 1.0$. Our generator requires about 200 K iterations with the mini-batch size of 64. When we apply our “hinge loss” version on STL-10 dataset similar to [23], our model can achieve the FID score 36.19 for this dataset, which is also better than SN-GAN (FID = 43.2).

6 Conclusion

We propose a robust AE-based GAN model with novel distance constraints, called Dist-GAN, that can address the mode collapse and gradient vanishing effectively. Our model is different from previous work: (i) We propose a new generator objective using “discriminator-score distance”. (ii) We propose to couple the convergence of the discriminator with that of the AE by considering reconstructed samples as “real” samples. (iii) We propose to regularize AE by “latent-data distance constraint” in order to prevent the generator from falling into mode collapse settings. Extensive experiments demonstrate that our method can approximate multi-modal distributions. Our method reduces drastically the mode collapse for MNIST-1K. Our model is stable and does not suffer from mode collapse for MNIST, CelebA, CIFAR-10 and STL-10 datasets. Furthermore, we achieve better FID scores than previous works. These demonstrate the effectiveness of the proposed Dist-GAN. Future work applies our proposed Dist-GAN to different computer vision tasks [14, 16].