Abstract
Value-based decision making (VBDM) is a principle that states that humans and other species adapt their behavior according to the dynamic subjective values of the chosen or unchosen options. The neural bases of this process have been extensively investigated using task-based fMRI and lesion studies. However, the growing field of resting-state functional connectivity (RSFC) may shed light on the organization and function of brain connections across different decision-making domains. With this aim, we used independent component analysis to study the brain network dynamics in a large cohort of young males (N = 145) and the relationship of these dynamics with VBDM. Participants completed a battery of behavioral tests that evaluated delay aversion, risk seeking for losses, risk aversion for gains, and loss aversion, followed by an RSFC scan session. We identified a set of large-scale brain networks and conducted our analysis only on the default mode network (DMN) and networks comprising cognitive control, appetitive-driven, and reward-processing regions. Higher risk seeking for losses was associated with increased connectivity between medial temporal regions, frontal regions, and the DMN. Higher risk seeking for losses was also associated with increased coupling between the left frontoparietal network and occipital cortices. These associations illustrate the participation of brain regions involved in prospective thinking, affective decision making, and visual processing in participants who are greater risk-seekers, and they demonstrate the sensitivity of RSFC to detect brain connectivity differences associated with distinct VBDM parameters.
Similar content being viewed by others
An extensive body of literature has already investigated the influence of several personality traits and psychological constructs on value-based decision making (VBDM) during adolescence and early adulthood (Franken, van Strien, Nijs, & Muris, 2008; Romer, 2010; Zermatten, Van der Linden, d’Acremont, Jermann, & Bechara, 2005). However, a limited scope still exists, because the prior research usually focused on single constructs at a time. Beyond these earlier behavioral studies, this investigation offers a complementary neuroimaging approach for understanding the neural underpinnings of an array of VBDM components (i.e., delay aversion, risk seeking/risk aversion, and loss aversion) in healthy young males.
Delay aversion is often taken as an indicator of impulsivity and is usually assessed with delay-discounting tasks in experimental environments (Ainslie, 1975). Individuals may benefit from impulsive behavior because it allows them to take advantage of unexpected opportunities when quickly exploiting their options (Dickman, 1990). However, high degrees of impulsivity are related to a broad range of maladaptive behaviors, principally in young individuals (Story, Vlaev, Seymour, Darzi, & Dolan, 2014). In a similar manner, risk seeking has been pointed out as a predisposing factor for the development of addictive disorders and delinquent behavior during adolescence (Blum & Nelson-Mmari, 2004; Burnett, Bault, Coricelli, & Blakemore, 2010; Steinberg, 2008), especially in male participants (Ball, Farnill, & Wangeman, 1984). Conversely, high risk aversion (taken as the other extreme of the risk spectrum), as well as high loss aversion (Kahneman & Tversky, 1979), might indicate a negative learning bias that increases the risk of depression and anxiety disorders (Smoski et al., 2008).
On the neural level, task-based fMRI experiments and lesion studies have shown the brain circuitry underlying some of the behaviors mentioned above: Frontostriatal regions (i.e., medial prefrontal cortex, ventral striatum) are implicated in valuation processes and reinforcement learning (Bartra, McGuire, & Kable, 2013; Peters & Buchel, 2011; Ripke et al., 2012; Rushworth, Noonan, Boorman, Walton, & Behrens, 2011), whereas the so-called cognitive control network (i.e., posterior parietal cortex, lateral prefrontal cortex, anterior insula, and anterior cingulate cortex) was associated with the decision phase during intertemporal and probabilistic choices (Marco-Pallarés, Mohammadi, Samii, & Münte, 2010; McClure, Laibson, Loewenstein, & Cohen, 2004; Ripke et al., 2015; Ripke et al., 2012; Weber & Huettel, 2008). Additionally, developmental neuroimaging studies have postulated that stronger activation of regions involved in reward processing (e.g. nucleus accumbens) during adolescence encourages sensation seeking and risk taking at these ages (Barkley-Levenson & Galvan, 2014; Braams, van Duijvenvoorde, Peper, & Crone, 2015; Galvan, Hare, Voss, Glover, & Casey, 2007).
A complementary investigation of brain networks can be achieved through resting-state functional connectivity (RSFC), a robust technique for exploring low-frequency fluctuations (~ 0.01–0.1 Hz) in the BOLD signal (Biswal, Yetkin, Haughton, & Hyde, 1995). Resting-state fluctuations are coherently organized into intrinsic connectivity networks (ICN) that are believed to recapitulate task-based/stimulus activity (Mennes et al., 2010; Smith et al., 2009) and exhibit variations according to the different phenotypic characteristics of an individual (Vaidya & Gordon, 2013). These networks can be investigated using independent component analysis (ICA; Beckmann & Smith, 2004), a reliable method that allows the separation of ICNs from artifactual signals (Cole, Smith, & Beckmann, 2010), and thus supports the exploration of organized neural activity. The possibility that these ICNs differ across distinct VBDM styles has already promoted study of the relationship between various VBDM constructs and RSFC in young and vulnerable populations (Cservenka, Casimo, Fair, & Nagel, 2014; Weissman et al., 2015; Whelan et al., 2012). However, further investigations analyzing several VBDM components in a single study will increase our understanding of the neural bases of these behaviors.
Recent insights into the resting-state circuitries that may characterize impulsive decision making have described weaker connectivity between regulatory (frontal) and appetitive-drive (limbic) regions (Davis et al., 2013). Additionally, hyperconnectivity between the DMN and motor-planning regions was also reported in the same group of participants (Shannon et al., 2011), suggesting that higher activity at rest of limbic and motor regions may predispose young individuals to impulsive decision making. Similarly, hyperconnectivity between subcortical limbic structures (i.e., nucleus accumbens, amygdala) and middle frontal cortices may underlie the expression of risky behaviors in adolescents (DeWitt, Aslan, & Filbey, 2014). On the other hand, risk-averse decision making seems to follow the same activation pattern in both task-based and resting-state fMRI, with participation of a brain circuit comprising the right inferior frontal gyrus and insular cortex (Christopoulos, Tobler, Bossaerts, Dolan, & Schultz, 2009; Cox et al., 2010; Preuschoff, Quartz, & Bossaerts, 2008). Although these findings indicate that the functional brain architecture may accurately reflect individual differences in VBDM, studies with larger samples of healthy participants are still necessary in order to observe the neural dynamics that may underlie risky and impulsive choices at young ages. Furthermore, the relation between risky behaviors and RSFC has only been investigated in the gain domain (i.e., risk seeking/risk aversion for gains), but the distinction between gains and losses has not been reported thus far.
In the present study, we examined RSFC and its relation to VBDM, expressed through four constructs (delay aversion, risk aversion for gains, risk seeking for losses, and loss aversion) in a large cohort of young males. We hypothesized that the basal ganglia and default mode networks would exhibit higher functional connectivity in more delay-averse and risk-seeking participants, illustrating more reward-driven traits and therefore weaker functional connectivity in the cognitive-control and executive networks. Finally, we explored the relationship between brain functional networks, risk seeking for losses, and loss aversion, since existing studies have described the engagement of single brain structures, but the functional dynamics under rest have not yet been studied.
Methods and materials
The study protocol was approved by the local ethics committees of Charité Universitätsmedizin Berlin and Technische Universität Dresden, and was in accordance with national legislation and the Declaration of Helsinki. All participants provided written informed consent and received monetary compensation.
Participants
This study included data from 145 18-year-old, right-handed, healthy males, selected from a total sample of 201 individuals who took part in the ongoing longitudinal fMRI study “Learning Dysfunctions in Young Adults as Predictors for the Development of Alcohol Use Disorders” (LeAD, www.lead-studie.de; clinical trial number: NCT01744834) within the research group “Learning and Habituation as Predictors of the Development and Maintenance of Alcoholism” funded by the Deutsche Forschungsgemeinschaft (DFG). In this study, we used the sample already reported by Bernhardt et al. (2017), with the addition of two participants who were abstinent from alcohol and therefore had not been included in other studies from this research group (for details, see the description in Supplementary Material 1). All participants were recruited in Berlin and Dresden through their respective residents’ registration offices and were screened in order to exclude current or previous history of neurological or psychiatric diseases, drug abuse or dependence (except for nicotine dependence and alcohol abuse) and MRI incompatible conditions.
Value-based decision-making assessment
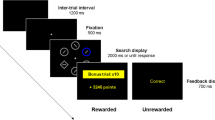
In the first session, participants completed an extensive behavioral and clinical assessment that included the value-based decision-making battery (VBDM; see Fig. 1). This set of tasks employs a Bayesian learning scheme to estimate the delay-discounting rate, the probability-discounting rates for gains and losses, and loss aversion.
Value-based decision-making battery with trial examples for each task. During all tasks, offers are randomly assigned to presentation on the left or the right side of the screen. We imposed no time limit for the selection in a given trial and provided no feedback after the choice. The selected choices were indicated within a red frame before presenting the next offer. Participants were informed that they would be paid on the basis of a randomly selected trial that they chose in each task. Crosse-out boxes represent the odds against winning or losing in the probabilistic tasks. In the mixed gambles task the crossed-out box represents the option to reject the gamble (Pooseh et al., 2018).
Delay aversion was assessed with a delay discounting (DD) task with 30 trials, in which participants needed to choose between receiving a smaller immediate amount of money or a greater delayed one (e.g., €2 now or €8 in one week). Monetary rewards ranged from €0.30 to €10. The evaluation of the offers is best described by a hyperbolic function (Mazur, 1988; Odum, 2011):
where V represents the subjective value of the amount A after a delay D in days (available delays: 3, 7, 14, 31, 61, 180, and 365 days) and k is a free parameter representing the discount rate. Larger k values represent preference for immediate amounts and therefore higher delay aversion.
The second and third tasks assessed risk aversion for gains and risk seeking for losses, using probability discounting for gains and losses, respectively (PDG and PDL; both with 30 trials), where participants needed to choose between a sure amount that they could win or lose and the probability of winning/losing a larger amount of money (e.g., 75% probability of winning €5 or winning €2 for sure, or a 50% probability of losing €8 or losing €3 for sure). The probability values were set to 2/3, 1/2, 1/3, 1/4, and 1/5. The amounts ranged from €0.30 to €10 for PDG, and – €0.30 to – €10 for PDL. Probability discounting can also be well described by a hyperbolic function (Green, Myerson, & Ostaszewski, 1999; Rachlin, Raineri, & Cross, 1991):
where V is the subjective value of a probabilistic amount A, k is a parameter that reflects the individual discounting rate due to the probability of the reward, and θ represents the odds against receiving the probabilistic amount (θ = [1 − p]/p), where p is the probability of receipt. In the probability discounting for gains, risk-averse behavior is defined as the preference for the certain amount over the probabilistic one, reflected by larger k values. On the other hand, probability discounting for losses produces larger k values when participants prefer the probabilistic offer over the certain one, therefore, exhibiting a more risk-seeking behavior (Shead & Hodgins, 2009).
The final task measuring loss aversion presented mixed gambles (MG; 40 trials), in which participants received a credit of €10 at the beginning of the game and then needed to decide whether to accept or reject an offer with a 50/50 chance of either gaining one amount of money or losing another amount (e.g., refusing to gamble or accepting a gamble that offered either winning €15 or losing €8). The amounts ranged from €1 to €40 for gains and from – €5 to – €20 for losses. The value function here was given by
where V is the expected value of the gamble. The coefficient 1/2 expresses a 50/50 chance of gaining or losing, G and L are the amounts of gains and losses, respectively, and λ is a measure of behavioral loss aversion that can be computed as the ratio of the contributions of loss to gain magnitude in the participant’s decisions. Larger λ values indicate higher loss aversion and are produced when participants reject the gamble because they perceived high differences between gains and losses (Tom, Fox, Trepel, & Poldrack, 2007).
In all tasks, the likelihood of choosing between the two offers followed a softmax probability function P(a1 │ k, β) = 1/(1 + exp[β(V2 − V1)]), where V1 and V2 are the subjective values of the offers and β > 0 serves as a consistency parameter such that its large values correspond to a high probability of taking the most valuable action. The algorithm started from liberal prior distributions on the parameters and, after observing a choice at each trial, updates the belief about the parameters using the Bayes’s rule P(k, β| choice) ∝ P(choice| k, β)P(k, β). The procedure continued for 30 (40 in mixed gambles) trials to reach a stable estimation. The estimates at the final trial were considered the best-fitting parameters for a participant. Further information is provided in Supplementary Material 2; details regarding the mathematical framework can be found in Pooseh, Bernhardt, Guevara, Huys, and Smolka (2018); and application of the battery in a clinical cohort is reported in Bernhardt et al. (2017).
Summary statistics and pairwise correlations were calculated using SPSS 22.0 (IBM-SPSS, Chicago, IL, USA) on the nonlogarithmic VBDM scores. To be used as regressors in the resting-state analysis (see the Single-Network Analysis section), the resulting main discounting parameters (k) were log-transformed in order to approximate them to a normal distribution. The mixed gambles parameter (λ) was normally distributed, therefore no transformation was necessary. To maximize the availability of the data, multiple imputation (MI; Little & Smith, 1987) was used to complete missing completely at random (MCAR) VBDM scores of nine participants who had only one incomplete subtest and Winsorization (Dixon, 1960) was used to change one extreme score (see the Results section). These processes did not change the descriptive statistics of the main scores.
MR data acquisition
The scanning protocols were identical in both study centers. The scanning session took place during a second appointment. Six-minute resting-state fMRI scans were acquired on a 3-T whole-body Magnetom Trio Tim MRI Scanner (Siemens Medical, Erlangen, Germany) equipped with a 12-channel head coil using a single-shot gradient echoplanar imaging (EPI) sequence with a repetition time (TR) of 2.41 s, an echo time (TE) of 25 ms, a flip angle of 80°, field of view of 192 × 192 mm, matrix size of 64 × 64 and voxel size of 3 mm × 3 mm × 2 mm. A total of 148 resting-state volumes were acquired, each consisting of 42 transversal slices (2 mm thick, 1-mm gap), tilted axially parallel to the anterior–posterior commissural line. For registration purposes, a T1-weighted high-resolution anatomic scan of the magnetization-prepared rapid gradient echo (MPRAGE) was acquired (TR = 1.90 s, TE = of 2.52 ms, TI = 1,100 ms, flip angle of 9°, FOV = 256 × 224 mm2, 192 slices, 1 mm × 1 mm × 1 mm voxel size, slice thickness of 1 mm, and no gap). Participants were given earplugs to protect hearing and foam pads to minimize head movement. They were instructed not to think about anything in particular and to lie as still as possible with their eyes closed.
Image preprocessing
The resting-state fMRI data were preprocessed using the Functional Magnetic Resonance Imaging of the Brain (FMRIB) Software Library (FSL Version 5.0.8, www.fmrib.ox.ac.uk/fsl; Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012). Because movement has a great impact on functional connectivity, DVARS (with D referring to the temporal derivative of the time courses and VARS referring to the RMS variance over voxels) and framewise displacement (FD; Power, Barnes, Snyder, Schlaggar, & Petersen, 2012) were calculated on the resting state data prior to any other preprocessing step with the tool fsl_motion_outliers. Participants whose sequences showed more than 10% of volumes over the 0.5% ΔBOLD for DVARS and/or over 0.5 mm for FD were excluded from the subsequent analysis (see Supplementary Material 1).
Preprocessing steps included motion correction with MCFLIRT, brain extraction of the EPI data with BET, spatial smoothing with a Gaussian kernel of full width at half maximum of 5 mm and high-pass temporal filter at 100 s. Registration parameters were derived from nonsmoothed and nonfiltered data. For registration, the T1-weighted images were registered to a common stereotaxic space (MNI152; 2 mm × 2 mm × 2 mm spatial resolution) using a 12-degree-of-freedom nonlinear registration implemented in FNIRT (warp resolution: 10 mm) and then, each participant’s functional dataset was registered to their corresponding T1-weighted image using a 6-degree-of-freedom linear affine transformation with FLIRT. After this process, all images were visually inspected to ensure the accuracy of the registration. Finally, FD measures were calculated again after preprocessing to ensure that the existing volumes with high motion were adequately handled by the motion correction algorithm. A more stringent cutoff was used with these data (FD ≥ 0.2 mm). One participant who exhibited more than 10% of volumes over this threshold was discarded from the high-level analysis.
Generation of intrinsic connectivity networks
We used group probabilistic independent component analysis as implemented in MELODIC Version 3.14 (Beckmann & Smith, 2004) to generate a set of spatially independent components (IC). The first stage of this group process uses principal component analysis (PCA) to temporally demean and concatenate all datasets, treating them as if they were a huge single dataset. However, this stage becomes excessively computationally demanding as the number of time points and participants increases. For this reason, we used the recently implemented MIGP algorithm (MELODIC’s Incremental Group-PCA; Smith, Hyvarinen, Varoquaux, Miller, & Beckmann, 2014), which has been shown to be more accurate than the current approaches used for multisubject resting-state studies with the advantage of having very low computing memory requirements. Following the process, the data were whitened and projected into a 50 dimensional subspace, variance was normalized and finally the estimated intensity maps were divided by the standard deviation of the residual noise and thresholded by fitting a Gaussian/gamma mixture model to the distribution of voxel intensities within spatial maps and controlling the local false discovery rate (FDR) at p < .5.
Single-network analyses
It should be noted that there is no current consensus about the ideal number of ICs, although the existing literature reports that higher dimensionalities produce a better brain parcellation and subdivision of networks, whereas low-order models are useful for identifying large-scale brain networks (Ray et al., 2013). Following the suggestion of Szewczyk-Krolikowski et al. (2014), a model order of 50 ICs (explaining 65% of the total variance) was found optimal to detect the basal ganglia among other 13 large-scale brain networks. Higher dimensionalities were also explored (70 ICs, 89 ICs), without any significant improvement.
To identify participant-specific spatial maps and associated time courses of the 14 ICNs, we performed a dual regression approach (Beckmann, Mackay, Nicola, & Smith, 2009; Filippini et al., 2009). During the first stage of this regression, the group-level spatial maps representing the identified 14 ICNs were linearly regressed against the functional data of each participant, resulting in individual time series for every ICN (spatial regression). In the second stage, these time series were normalized and regressed against the resting state datasets of the corresponding participant (temporal regression) to estimate participant-specific voxel-to-network spatial maps of every network. To remove sources of spurious variance that might affect estimation of the participants’ ICNs, the six individual motion parameters obtained during motion correction and time courses of white matter and CSF were added as nuisance regressors during this stage (Cole et al., 2013; Klumpers et al., 2012). To extract these last time courses, individual white matter and CSF masks were generated from the structural images and transformed into a participant-specific functional space before extracting their corresponding time series (see Supplementary Material 3).
This dual regression approach differs from other group-ICA methodologies (e.g. “back-projection”; Calhoun, Adali, Pearlson, & Pekar, 2001) in the way temporal and spatial dynamics at the subject level are estimated. In this method, the estimated spatial maps do not depend on the initial participant-specific major eigenspaces (PCA) and therefore, may lie outside the network’s boundaries (Beckmann et al., 2009). The regression coefficients contained in the resulting spatial maps from dual regression represent the weighted voxels associated with specific signal variations for a specific network. The strength of the voxel-to-network connectivity is given by the value of these coefficients (Cole et al., 2013; Klaassens et al., 2016).
Six ICNs were chosen as networks of interest due to their previously reported implication in decision making and related processes (frontal, default mode, left and right frontoparietal, cingulo-opercular, and basal ganglia networks; Davis et al., 2013; Shannon et al., 2011; Tom et al., 2007; Zhou et al., 2014). The resulting participant-specific maps of every network were concatenated across participants and saved in 4D files. The six networks of interest were tested voxel-wise for associations with the behavioral scores, using a nonparametric test based on criteria of exchangeability (10,000 permutations as implemented in FSL–Randomise; Nichols & Holmes, 2002) that included one GLM for each network with all four VBDM scores (demeaned log k and λ), a dichotomous variable to control for scan site, and mean DVARS measures to account for BOLD changes associated with motion that could not be removed by regression of the motion parameters. To assess the potential collinearity between the regressors of the model, we calculated the variance inflation factor (VIF). The highest VIF score (1.09) indicated that our model does not have a collinearity problem (VIF threshold = 5; Mumford, Poline, & Poldrack, 2015). A gray-matter mask was used during permutation testing. The results were identified using threshold-free cluster enhancement (TFCE; Smith & Nichols, 2009). A multiple-comparison correction was carried out voxel-wise using FDR at a nominal significance level of q < .05, using the fdr command in FSL. This procedure yielded an adjusted threshold of p < .0077. Further correction was carried out to account for the 24 test performed (four VBDM scores and six ICN), setting the significant p < .0003. As we previously mentioned, our results were not restricted to the networks’ boundaries, thus brain regions could exhibit significant changes in connectivity either inside or outside a given network (Reineberg, Andrews-Hanna, Depue, Friedman, & Banich, 2015). After permutation testing, the resulting significant regions indicated that the strength of the coupling between these regions and the tested network was associated with a given VBDM score.
Results
Behavioral results
Summary statistics of the obtained VBDM scores, pairwise correlations, and the numbers of imputed and Winsorized scores are presented in Table 1. The resulting discounting parameters (k) for delay discounting are comparable to those observed previously in healthy individuals, which are typically lower than in those with substance use disorders (Amlung, Vedelago, Acker, Balodis, & MacKillop, 2017). Further analyses showed that the participants of the present study were more risk-averse for gains (probability discounting for gains), more risk-seeking for losses (probability discounting for losses), and more loss-averse (mixed gambles) than a sample of alcohol-dependent patients (Bernhardt et al., 2017). Negative correlations between probability discounting for losses and delay discounting denoted that more risk-seeking (for losses) participants were more patient. Similarly, a negative correlation between probability discounting for losses and mixed gambles indicated that more risk-seeking (for losses) participants were not influenced by the difference between gain and loss in making the gamble.
We found no significant differences between the VBDM scores from the two research sites (see the supplementary material, Table S1). Additionally, we controlled for possible associations between VBDM scores and motion parameters, since a positive correlation between impulsivity and in-scanner motion has been reported in resting-state studies (Kong et al., 2014). The Spearman’s rank correlations resulting from these analyses were no higher than .06 (see the supplementary material, Table S2).
Intrinsic connectivity network selection
From the 50 initially estimated ICs, nine were identified as large-scale brain networks according to the templates from Smith et al. (2009), using a cross-correlation analysis implemented with the fslcc tool (see the supplementary material, Table S3). Five other ICs were also considered as plausible ICNs after visual inspection of the peak activations, inspection of plots of the time series obtained from the first stage of the dual regression, and comparison with other existing templates (Laird et al., 2011; Ray et al., 2013). The remaining 36 components were deemed movement artifacts, scanner drifts, and other activations of noninterest (i.e., white matter, CSF). Spatial maps of the 14 ICNs are described in Table 2 and presented in Fig. 2.
Spatial maps of the 14 ICNs listed in Table 2, displayed in neurological orientation (right = right) and thresholded at z ≥ 4. The z-scoring was carried out on the group ICs by dividing the voxel-wise estimated spatial maps by the standard deviation of the residual noise (Beckmann & Smith, 2004). The networks of interest are depicted at the top of the image. Brain areas were identified using the Harvard–Oxford Cortical and Subcortical Structural Atlases.
VBDM scores and single network variations
We found that increased connectivity between the DMN and the bilateral parahippocampal gyri was associated with higher risk seeking for losses, as measured with the probability discounting for losses task. The same scores were associated with higher connectivity between the DMN and both the right frontal pole and small clusters in the right inferior temporal gyrus and left orbitofrontal cortex (Fig. 3A, all ps < .0003, FDR-corrected). Moreover, increased connectivity between the left frontoparietal network and clusters located in the left occipital pole/cuneus and left lateral occipital cortex was also associated with higher probability discounting for losses scores (Fig. 3B, all ps < .0003, FDR-corrected). The complete results are presented in Table 3.
Higher risk seeking for losses (measured with the probability discounting for losses task) was associated with increased functional connectivity between (A) the default mode network (DMN) and the bilateral parahippocampal gyri (PHG), right frontal pole (FP), right inferior temporal gyrus (ITG), and left orbitofrontal cortex (OFC); and (B) the left frontoparietal network (FPN) and the left occipital pole/cuneus and lateral occipital cortex (LOC). In all brain figures, the DMN and left FPN regions are displayed in orange in the online version of the figure, and the significant clusters are shown in red. The scatterplots below the brain figures show the PDL scores (in a logarithmic scale on the x-axis), and the parameter estimates (“P.E”) of the significant clusters extracted from the participant-specific DMN and left FPN (in arbitrary units on the y-axis). The brain figures are displayed from the anterior to the posterior coronal plane in neurological orientation, with MNI coordinates (Y) next to each brain figure. Significant clusters are displayed at p < .0003, false discovery rate (FDR) corrected at q < .05 and adjusted for 24 tests. The brain areas were identified using the Harvard–Oxford Cortical and Subcortical Structural Atlases.
No significant associations were found neither for the remaining VBDM scores (delay discounting, probability discounting for gains, and mixed gambles) nor for the other selected ICN (frontal, basal ganglia, cingulo-opercular, or right frontoparietal).
Discussion
To our knowledge, this is the first study to investigate resting-state functional connectivity and its relation to a set of different value-based decision-making parameters. Our findings show that individuals who were more risk seeking for losses—that is, who prefer a larger but only probable loss to a smaller but certain loss (as measured with the probability discounting for losses task)—exhibited increased connectivity between the DMN and bilateral hippocampal gyri and frontal regions. Higher risk seeking for losses was also associated with greater connectivity between the left frontoparietal network, the occipital pole, and lateral occipital regions.
The “medial temporal lobe subsystem” of the DMN has been implicated in mnemonic scene construction (Andrews-Hanna, Reidler, Sepulcre, Poulin, & Buckner, 2010), as well as in the integration of autobiographical memories into current processing (Buckner, Andrews-Hanna, & Schacter, 2008). Along this line, research in economic decision making has already delineated a model involving the frontotemporal axis of the DMN as a binding neural pathway that connects internal memories with prospective actions (Buckner et al., 2008) and that might subserve self-related simulations of future scenarios in which, for example, potential losses did not occur. Although the notion is speculative, the participation of mnemonic processes in risk-seeking (for losses) individuals may also be supported by increased connectivity between the DMN and the bilateral parahippocampal gyri (PHG), brain structures that are highly involved in contextual associations and episodic memory. In addition, the PHG show several anatomical and functional connections with anterior and posterior hubs of the DMN (Aminoff, Kveraga, & Bar, 2013). Even when memory and decision making are studied independently, there is unquestionable integration of both functions for decomposing the representations of past experiences and integrating them to future events, aiming to produce adaptive behaviors (Murty, FeldmanHall, Hunter, Phelps, & Davachi, 2016). Given the complexity of these functions, our findings do not allow us to draw strong conclusions about their association, but they encourage future research to study the interplay between memory and risk-seeking choices.
Higher risk seeking for losses is also associated with increased coupling between the DMN, the frontopolar cortex, and small clusters located in left orbitofrontal regions. In this regard, neuroeconomic research has described specialized neurons within the OFC that appear to code the value of an expected reward and, in this way, guide behavior toward more advantageous options (Schoenbaum, Takahashi, Liu, & McDannald, 2011). Similarly, task-based fMRI has shown that the coupling between frontal DMN areas and the frontal pole provides information about the value of unchosen options and represents the value that these options might have in the near future (Rushworth et al., 2011).
Finally, our findings showed that higher risk seeking for losses modulated the coupling between the left frontoparietal network and occipital regions. This network has typically been associated with risk taking and impulsiveness in both task-based and resting-state studies (Vaidya & Gordon, 2013; Weber & Huettel, 2008), as well as with adaptive control and flexibility (Dosenbach et al., 2007). In the present study, the biggest cortical area connected with the frontoparietal network was the left occipital pole/cuneus, which is mainly involved in basic visual processing (Grill-Spector & Malach, 2004). Further studies have related the activity of this area with behavioral engagement (Zhang & Li, 2012) and risk-taking reactivity, especially in adolescents (Tamura et al., 2012) and in pathologies with aberrant decision making (Crockford, Goodyear, Edwards, Quickfall, & el-Guebaly, 2005). Similar to our findings, Tamura et al. (2012) reported greater activation of the cuneus in response to the observation of high risk-taking actions in late adolescents. Despite their existing methodological differences (i.e., resting-state, task-based fMRI), these studies suggest potential implications of the visual system in the expression of more risk-seeking behaviors in young individuals.
Prior research has investigated the relation between RSFC and risky behaviors only in the gain domain (i.e., risky choices to obtain higher gains). However, our study presents a different approach in which risk seeking for gains and losses was assessed separately according to the well-grounded prospect theory (Kahneman & Tversky, 1979). This theory describes how risk is evaluated when potential gains or losses are involved. In the gain domain, the observation that the value of a gain is discounted (i.e., less attractive) due to the risk of not receiving it has been termed risk seeking for gains. In the loss domain, the value of a loss is similarly discounted when a probability is added. However, due to the prospect of losing nothing at all, the discounted offer is perceived as the more attractive one and has a higher likelihood to be chosen. Therefore, this behavior has been termed risk seeking for losses. Usually, risk seeking for gains is interpreted as a facet of impulsivity and has been associated with mental disorders. Risk seeking for losses, on the other hand, indicates instead how susceptible individuals are to certain negative outcomes and how eager they are to avoid them. Increased risk seeking for losses therefore presents a more anxious decision-making style that may be understood as being opposite to an impulsive style. Data from our lab support this reasoning by showing that patients who suffer from alcohol use disorder exhibit increased risk seeking for gains and reduced risk seeking for losses (Bernhardt et al., 2017). In summary, we believe that impulsive choices in the gain and loss domains are characterized by increased risk seeking for gains but reduced risk seeking for losses.
Perhaps the above-mentioned differences between gains and losses played a role in the lack of connectivity changes in the networks comprising cortico-striatal and dopaminergic circuits, which are generally involved in impulsivity and reward-related behaviors (Baik, 2013; Weiland et al., 2014). For instance, connectivity changes in key regions of the basal ganglia and the cingulo-opercular network have previously been reported in both risk-taking and risk-averse behaviors (Cox et al., 2010; DeWitt et al., 2014), but changes in these networks were not evident in our study. Likewise, the relation between delay discounting, probability discounting for gains, and RSFC seems to be stronger in conduct and addiction disorders (Wei et al., 2016; Zhu, Cortes, Mathur, Tomasi, & Momenan, 2015), but more sensitive techniques seem to be necessary for the detection of such differences in healthy samples. Nevertheless, our results provide, for the first time, insight into the brain’s functional architecture that may underlie risk seeking with respect to losses in healthy young males.
Limitations
Our results must be viewed in light of several limitations. Our group-level analysis was carried out using nonparametric permutation testing, a method that provides an effective control for Type I error rates (Eklund, Nichols, & Knutsson, 2016), while requiring minimal assumptions about the data for valid statistical inference (Nichols & Holmes, 2002). Even when these facts favored the use of permutation tests with our data (Beckmann et al., 2009), we are aware that the biggest disadvantage of this method is weak control of outlying data points, as was recently shown by Mumford (2017). Another factor to consider is that the cluster sizes reported for three brain regions were smaller than the recommended k = 10 (Lieberman & Cunningham, 2009), as a result of the conservative statistical threshold applied. Therefore, for completeness, we reported all clusters that passed correction for multiple testing, but refrained from deep discussion of the results where the clusters contained fewer than ten voxels. Finally, our sample was restricted to a population of healthy, 18-year-old participants. Thus, it remains unclear whether our results can be generalized to older or younger individuals. Moreover, our sample was restricted to male participants. Existing studies have described remarkable gender differences in risk-seeking behaviors (Ball et al., 1984) and associated negative consequences (Turner & McClure, 2003), but, to date, only the study of Zhou et al. (2014) has addressed gender functional connectivity differences linked to risk-seeking behavior. Therefore, we believe that future decision-making research will benefit from the inclusion of both genders and different age ranges.
Conclusion
In summary, delay-averse, risk-averse for gains, and loss-averse behaviors did not influence the functional connectivity of large-scale brain networks in our sample, whereas risk seeking (as measured by probability discounting for losses), modulated the expansion of the default mode and left frontoparietal network to their adjacent areas, particularly those areas relevant for self-oriented prospective thinking, affective decision making, and visual processing. These findings suggest that distinct connectivity patterns of large-scale brain networks may underlie individual differences in decision making in healthy populations, and they strengthen the role of RSFC as a potential biomarker of different VBDM facets.
Author note
Y.I.D.A. performed the analyses, interpreted the results, and drafted the manuscript. S.N., M.S., and M.G. collected the data and conducted the study. P.T.N. assisted with the analysis and interpretation of the results; S.P. programmed the behavioral tasks; and A.H. and M.N.S. designed the study and supervised the project. All authors critically reviewed the article and agreed to its content. The authors thank Mark Jacob, Ilja M. Veer, and Michael Marxen for their useful comments on early versions of this article and for technical assistance during the analysis, and the LeAD study teams in Dresden and Berlin for their fruitful work. This research was supported by the German Research Foundation (Deutsche Forschungsgemeinschaft, Grants HE 2597/13-2, HE 2597/13-1, SM 80/7-1, SM 80/7-2, SFB 940/1, and SFB 940/2). Y.I.D.A. is supported by a scholarship of from German Academic Exchange Service (Deutscher Akademischer Austauschdienst). The authors declare no competing financial interests.
References
Ainslie, G. (1975). Specious reward: A behavioral theory of impulsiveness and impulse control. Psychological Bulletin, 82, 463–496.
Aminoff, E. M., Kveraga, K., & Bar, M. (2013). The role of the parahippocampal cortex in cognition. Trends in Cognitive Sciences, 17, 379–390. https://doi.org/10.1016/j.tics.2013.06.009
Amlung, M., Vedelago, L., Acker, J., Balodis, I., & MacKillop, J. (2017). Steep delay discounting and addictive behavior: A meta-analysis of continuous associations. Addiction, 112, 51–62. https://doi.org/10.1111/add.13535
Andrews-Hanna, J. R., Reidler, J. S., Sepulcre, J., Poulin, R., & Buckner, R. L. (2010). Functional-anatomic fractionation of the brain’s default network. Neuron, 65, 550–562. https://doi.org/10.1016/j.neuron.2010.02.005
Baik, J. H. (2013). Dopamine signalling in reward-related behaviours. Frontiers in Neural Circuits, 7, 152. https://doi.org/10.3389/fncir.2013.00152
Ball, I. L., Farnill, D., & Wangeman, J. F. (1984). Sex and age-differences in sensation seeking—Some national comparisons. British Journal of Psychology, 75, 257–265.
Barkley-Levenson, E., & Galvan, A. (2014). Neural representation of expected value in the adolescent brain. Proceedings of the National Academy of Sciences, 111, 1646–1651. https://doi.org/10.1073/pnas.1319762111
Bartra, O., McGuire, J. T., & Kable, J. W. (2013). The valuation system: A coordinate-based meta-analysis of BOLD fMRI experiments examining neural correlates of subjective value. NeuroImage, 76, 412–427. https://doi.org/10.1016/j.neuroimage.2013.02.063
Beckmann, C. F., Mackay, C. E., Nicola, F., & Smith, S. M. (2009). Group comparison of resting-state FMRI data using multi-subject ICA and dual regression. NeuroImage, 47(Suppl. 1), S148. https://doi.org/10.1016/S1053-8119(09)71511-3
Beckmann, C. F., & Smith, S. M. (2004). Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Transactions on Medical Imaging, 23, 137–152. Retrieved from www.ncbi.nlm.nih.gov/pubmed/14964560
Bernhardt, N., Nebe, S., Pooseh, S., Sebold, M., Sommer, C., Birkenstock, J., … Smolka, M. N. (2017). Impulsive decision making in young adult social drinkers and detoxified alcohol-dependent patients: A cross-sectional and longitudinal study. Alcoholism: Clinical and Experimental Research, 41, 1794–1807. https://doi.org/10.1111/acer.13481
Biswal, B., Yetkin, F. Z., Haughton, V. M., & Hyde, J. S. (1995). Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magnetic Resonance Medicine, 34, 537–541.
Blum, R. W., & Nelson-Mmari, K. (2004). The health of young people in a global context. Journal of Adolescent Health, 35, 402–418. https://doi.org/10.1016/j.jadohealth.2003.10.007
Braams, B. R., van Duijvenvoorde, A. C., Peper, J. S., & Crone, E. A. (2015). Longitudinal changes in adolescent risk-taking: A comprehensive study of neural responses to rewards, pubertal development, and risk-taking behavior. Journal of Neuroscience, 35, 7226–7238. https://doi.org/10.1523/JNEUROSCI.4764-14.2015
Buckner, R. L., Andrews-Hanna, J. R., & Schacter, D. L. (2008). The brain’s default network: Anatomy, function, and relevance to disease. Annals of the New York Academy of Sciences, 1124, 1–38. https://doi.org/10.1196/annals.1440.011
Burnett, S., Bault, N., Coricelli, G., & Blakemore, S. J. (2010). Adolescents’ heightened risk-seeking in a probabilistic gambling task. Cognitive Development, 25, 183–196. https://doi.org/10.1016/j.cogdev.2009.11.003
Calhoun, V. D., Adali, T., Pearlson, G. D., & Pekar, J. J. (2001). A method for making group inferences from functional MRI data using independent component analysis. Human Brain Mapping, 14, 140–151. https://doi.org/10.1002/hbm.1048
Christopoulos, G. I., Tobler, P. N., Bossaerts, P., Dolan, R. J., & Schultz, W. (2009). Neural correlates of value, risk, and risk aversion contributing to decision making under risk. Journal of Neuroscience, 29, 12574–12583. https://doi.org/10.1523/jneurosci.2614-09.2009
Cole, D. M., Beckmann, C. F., Oei, N. Y., Both, S., van Gerven, J. M., & Rombouts, S. A. (2013). Differential and distributed effects of dopamine neuromodulations on resting-state network connectivity. NeuroImage, 78, 59–67. https://doi.org/10.1016/j.neuroimage.2013.04.034
Cole, D. M., Smith, S. M., & Beckmann, C. F. (2010). Advances and pitfalls in the analysis and interpretation of resting-state FMRI data. Frontiers in Systems Neuroscience, 4, 8. https://doi.org/10.3389/fnsys.2010.00008
Cox, C. L., Gotimer, K., Roy, A. K., Castellanos, F. X., Milham, M. P., & Kelly, C. (2010). Your resting brain cares about your risky behavior. PLoS ONE, 5, e12296. https://doi.org/10.1371/journal.pone.0012296
Crockford, D. N., Goodyear, B., Edwards, J., Quickfall, J., & el-Guebaly, N. (2005). Cue-induced brain activity in pathological gamblers. Biological Psychiatry, 58, 787–795. https://doi.org/10.1016/j.biopsych.2005.04.037
Cservenka, A., Casimo, K., Fair, D. A., & Nagel, B. J. (2014). Resting state functional connectivity of the nucleus accumbens in youth with a family history of alcoholism. Psychiatry Research, 221, 210–219. https://doi.org/10.1016/j.pscychresns.2013.12.004
Davis, F. C., Knodt, A. R., Sporns, O., Lahey, B. B., Zald, D. H., Brigidi, B. D., & Hariri, A. R. (2013). Impulsivity and the modular organization of resting-state neural networks. Cerebral Cortex, 23, 1444–1452. https://doi.org/10.1093/cercor/bhs126
DeWitt, S. J., Aslan, S., & Filbey, F. M. (2014). Adolescent risk-taking and resting state functional connectivity. Psychiatry Research: Neuroimaging, 222, 157–164. https://doi.org/10.1016/j.pscychresns.2014.03.009
Dickman, S. J. (1990). Functional and dysfunctional impulsivity: Personality and cognitive correlates. Journal of Personality and Social Psychology, 58, 95–102.
Dixon, W. J. (1960). Simplified estimation from censored normal samples. Annals of Mathematical Statistics, 31, 385–391. https://doi.org/10.1214/aoms/1177705900
Dosenbach, N. U., Fair, D. A., Miezin, F. M., Cohen, A. L., Wenger, K. K., Dosenbach, R. A., … Petersen, S. E. (2007). Distinct brain networks for adaptive and stable task control in humans. Proceedings of the National Academy of Sciences, 104, 11073–11078. https://doi.org/10.1073/pnas.0704320104
Eklund, A., Nichols, T. E., & Knutsson, H. (2016). Cluster failure: Why fMRI inferences for spatial extent have inflated false-positive rates. Proceedings of the National Academy of Sciences, 113, 7900–7905. https://doi.org/10.1073/pnas.1602413113
Filippini, N., MacIntosh, B. J., Hough, M. G., Goodwin, G. M., Frisoni, G. B., Smith, S. M., … Mackay, C. E. (2009). Distinct patterns of brain activity in young carriers of the APOE-epsilon4 allele. Proceedings of the National Academy of Sciences, 106, 7209–7214. https://doi.org/10.1073/pnas.0811879106
Franken, I. H., van Strien, J. W., Nijs, I., & Muris, P. (2008). Impulsivity is associated with behavioral decision-making deficits. Psychiatry Research, 158, 155–163. https://doi.org/10.1016/j.psychres.2007.06.002
Galvan, A., Hare, T., Voss, H., Glover, G., & Casey, B. J. (2007). Risk-taking and the adolescent brain: Who is at risk? Developmental Science, 10, F8–F14. https://doi.org/10.1111/j.1467-7687.2006.00579.x
Green, L., Myerson, J., & Ostaszewski, P. (1999). Amount of reward has opposite effects on the discounting of delayed and probabilistic outcomes. Journal of Experimental Psychology: Learning, Memory, and Cognition, 25, 418–427.
Grill-Spector, K., & Malach, R. (2004). The human visual cortex. Annual Review of Neuroscience, 27, 649–677. https://doi.org/10.1146/annurev.neuro.27.070203.144220
Jenkinson, M., Beckmann, C. F., Behrens, T. E., Woolrich, M. W., & Smith, S. M. (2012). FSL. NeuroImage, 62, 782–790. https://doi.org/10.1016/j.neuroimage.2011.09.015
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47, 263–291. https://doi.org/10.2307/1914185
Klaassens, B. L., Rombouts, S. A. R. B., Winkler, A. M., van Gorsel, H. C., van der Grond, J., & van Gerven, J. M. A. (2016). Time related effects on functional brain connectivity after serotonergic and cholinergic neuromodulation. Human Brain Mapping, 38, 308–325. https://doi.org/10.1002/hbm.23362
Klumpers, L. E., Cole, D. M., Khalili-Mahani, N., Soeter, R. P., Te Beek, E. T., Rombouts, S. A., & van Gerven, J. M. A. (2012). Manipulating brain connectivity with delta(9)-tetrahydrocannabinol: a pharmacological resting state FMRI study. NeuroImage, 63, 1701–1711. https://doi.org/10.1016/j.neuroimage.2012.07.051
Kong, X. Z., Zhen, Z., Li, X., Lu, H. H., Wang, R., Liu, L., … Liu, J. (2014). Individual differences in impulsivity predict head motion during magnetic resonance imaging. PLoS ONE, 9, e104989. https://doi.org/10.1371/journal.pone.0104989
Laird, A. R., Fox, P. M., Eickhoff, S. B., Turner, J. A., Ray, K. L., McKay, D. R., … Fox, P. T. (2011). Behavioral interpretations of intrinsic connectivity networks. Journal of Cognitive Neuroscience, 23, 4022–4037.
Lieberman, M. D., & Cunningham, W. A. (2009). Type I and Type II error concerns in fMRI research: Re-balancing the scale. Social Cognitive and Affective Neuroscience, 4, 423–428. https://doi.org/10.1093/scan/nsp052
Little, R. J. A., & Smith, P. J. (1987). Editing and imputation for quantitative survey data. Journal of the American Statistical Association, 82, 58–68. https://doi.org/10.2307/2289125
Marco-Pallarés, J., Mohammadi, B., Samii, A., & Münte, T. F. (2010). Brain activations reflect individual discount rates in intertemporal choice. Brain Research, 1320, 123–129. https://doi.org/10.1016/j.brainres.2010.01.025
Mazur, J. E. (1988). Estimation of indifference points with an adjusting-delay procedure. Journal of the Experimental Analysis of Behavior, 49, 37–47. https://doi.org/10.1901/jeab.1988.49-37
McClure, S. M., Laibson, D. I., Loewenstein, G., & Cohen, J. D. (2004). Separate neural systems value immediate and delayed monetary rewards. Science, 306, 503–507. https://doi.org/10.1126/science.1100907
Mennes, M., Kelly, C., Zuo, X. N., Di Martino, A., Biswal, B. B., Castellanos, F. X., & Milham, M. P. (2010). Inter-individual differences in resting-state functional connectivity predict task-induced BOLD activity. NeuroImage, 50, 1690–1701. https://doi.org/10.1016/j.neuroimage.2010.01.002
Mumford, J. A. (2017). A comprehensive review of group level model performance in the presence of heteroscedasticity: Can a single model control Type I errors in the presence of outliers? NeuroImage, 147, 658–668. https://doi.org/10.1016/j.neuroimage.2016.12.058
Mumford, J. A., Poline, J. B., & Poldrack, R. A. (2015). Orthogonalization of regressors in fMRI models. PLoS ONE, 10, e0126255. https://doi.org/10.1371/journal.pone.0126255
Murty, V. P., FeldmanHall, O., Hunter, L. E., Phelps, E. A., & Davachi, L. (2016). Episodic memories predict adaptive value-based decision-making. Journal of Experimental Psychology: General, 145, 548–558. https://doi.org/10.1037/xge0000158
Nichols, T. E., & Holmes, A. P. (2002). Nonparametric permutation tests for functional neuroimaging: A primer with examples. Human Brain Mapping, 15, 1–25. https://doi.org/10.1002/hbm.1058
Odum, A. L. (2011). Delay discounting: I’m a k, you’re a k. Journal of the Experimental Analysis of Behavior, 96, 427–439. https://doi.org/10.1901/jeab.2011.96-423
Peters, J., & Buchel, C. (2011). The neural mechanisms of inter-temporal decision-making: Understanding variability. Trends in Cognitive Sciences, 15, 227–239. https://doi.org/10.1016/j.tics.2011.03.002
Pooseh, S., Bernhardt, N., Guevara, A., Huys, Q. J., & Smolka, M. N. (2018). Value-based decision-making battery: A Bayesian adaptive approach to assess impulsive and risky behavior. Behavior Research Methods, 50, 236–249. https://doi.org/10.3758/s13428-017-0866-x
Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L., & Petersen, S. E. (2012). Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. NeuroImage, 59, 2142–2154. https://doi.org/10.1016/j.neuroimage.2011.10.018
Preuschoff, K., Quartz, S. R., & Bossaerts, P. (2008). Human insula activation reflects risk prediction errors as well as risk. Journal of Neuroscience, 28, 2745–2752. https://doi.org/10.1523/JNEUROSCI.4286-07.2008
Rachlin, H., Raineri, A., & Cross, D. (1991). Subjective probability and delay. Journal of the Experimental Analysis of Behavior, 55, 233–244. https://doi.org/10.1901/jeab.1991.55-233
Ray, K. L., McKay, D. R., Fox, P. M., Riedel, M. C., Uecker, A. M., Beckmann, C. F., … Laird, A. R. (2013). ICA model order selection of task co-activation networks. Frontiers in Neuroscience, 7, 237. https://doi.org/10.3389/fnins.2013.00237
Reineberg, A. E., Andrews-Hanna, J. R., Depue, B. E., Friedman, N. P., & Banich, M. T. (2015). Resting-state networks predict individual differences in common and specific aspects of executive function. NeuroImage, 104, 69–78. https://doi.org/10.1016/j.neuroimage.2014.09.045
Ripke, S., Hubner, T., Mennigen, E., Muller, K. U., Li, S. C., & Smolka, M. N. (2015). Common neural correlates of intertemporal choices and intelligence in adolescents. Journal of Cognitive Neuroscience, 27, 387–399. https://doi.org/10.1162/jocn_a_00698
Ripke, S., Hubner, T., Mennigen, E., Muller, K. U., Rodehacke, S., Schmidt, D., … Smolka, M. N. (2012). Reward processing and intertemporal decision making in adults and adolescents: The role of impulsivity and decision consistency. Brain Research, 1478, 36–47. https://doi.org/10.1016/j.brainres.2012.08.034
Romer, D. (2010). Adolescent risk taking, impulsivity, and brain development: Implications for prevention. Developmental Psychobiology, 52, 263–276. https://doi.org/10.1002/dev.20442
Rushworth, M. F., Noonan, M. P., Boorman, E. D., Walton, M. E., & Behrens, T. E. (2011). Frontal cortex and reward-guided learning and decision-making. Neuron, 70, 1054–1069. https://doi.org/10.1016/j.neuron.2011.05.014
Schoenbaum, G., Takahashi, Y., Liu, T. L., & McDannald, M. A. (2011). Does the orbitofrontal cortex signal value? Annals of the New York Academy of Sciences, 1239, 87–99. https://doi.org/10.1111/j.1749-6632.2011.06210.x
Shannon, B. J., Raichle, M. E., Snyder, A. Z., Fair, D. A., Mills, K. L., Zhang, D., … Kiehl, K. A. (2011). Premotor functional connectivity predicts impulsivity in juvenile offenders. Proceedings of the National Academy of Sciences, 108, 11241–11245. https://doi.org/10.1073/pnas.1108241108
Shead, N. W., & Hodgins, D. C. (2009). Probability discounting of gains and losses: Implications for risk attitudes and impulsivity. Journal of the Experimental Analysis of Behavior, 92, 1–16. https://doi.org/10.1901/jeab.2009.92-1
Smith, S. M., Fox, P. T., Miller, K. L., Glahn, D. C., Fox, P. M., Mackay, C. E., … Beckmann, C. F. (2009). Correspondence of the brain’s functional architecture during activation and rest. Proceedings of the National Academy of Sciences, 106, 13040–13045. https://doi.org/10.1073/pnas.0905267106
Smith, S. M., Hyvarinen, A., Varoquaux, G., Miller, K. L., & Beckmann, C. F. (2014). Group-PCA for very large fMRI datasets. NeuroImage, 101, 738–749. https://doi.org/10.1016/j.neuroimage.2014.07.051
Smith, S. M., & Nichols, T. E. (2009). Threshold-free cluster enhancement: Addressing problems of smoothing, threshold dependence and localisation in cluster inference. NeuroImage, 44, 83–98. https://doi.org/10.1016/j.neuroimage.2008.03.061
Smoski, M. J., Lynch, T. R., Rosenthal, M. Z., Cheavens, J. S., Chapman, A. L., & Krishnan, R. R. (2008). Decision-making and risk aversion among depressive adults. Journal of Behavior Therapy and Experimental Psychiatry, 39, 567–576. https://doi.org/10.1016/j.jbtep.2008.01.004
Steinberg, L. (2008). A social neuroscience perspective on adolescent risk-taking. Developmental Review, 28, 78–106. https://doi.org/10.1016/j.dr.2007.08.002
Story, G. W., Vlaev, I., Seymour, B., Darzi, A., & Dolan, R. J. (2014). Does temporal discounting explain unhealthy behavior? A systematic review and reinforcement learning perspective. Frontiers in Behavioral Neuroscience, 8, 76. https://doi.org/10.3389/fnbeh.2014.00076
Szewczyk-Krolikowski, K., Menke, R. A., Rolinski, M., Duff, E., Salimi-Khorshidi, G., Filippini, N., … Mackay, C. E. (2014). Functional connectivity in the basal ganglia network differentiates PD patients from controls. Neurology, 83, 208–214. https://doi.org/10.1212/WNL.0000000000000592
Tamura, M., Moriguchi, Y., Higuchi, S., Hida, A., Enomoto, M., Umezawa, J., & Mishima, K. (2012). Neural network development in late adolescents during observation of risk-taking action. PLoS ONE, 7, e39527. https://doi.org/10.1371/journal.pone.0039527
Tom, S. M., Fox, C. R., Trepel, C., & Poldrack, R. A. (2007). The neural basis of loss aversion in decision-making under risk. Science, 315, 515–518. https://doi.org/10.1126/science.1134239
Turner, C., & McClure, R. (2003). Age and gender differences in risk-taking behaviour as an explanation for high incidence of motor vehicle crashes as a driver in young males. Injury Control and Safety Promotion, 10, 123–130. https://doi.org/10.1076/icsp.10.3.123.14560
Vaidya, C. J., & Gordon, E. M. (2013). Phenotypic variability in resting-state functional connectivity: Current status. Brain Connections, 3, 99–120. https://doi.org/10.1089/brain.2012.0110
Weber, B. J., & Huettel, S. A. (2008). The neural substrates of probabilistic and intertemporal decision making. Brain Research, 1234, 104–115. https://doi.org/10.1016/j.brainres.2008.07.105
Wei, Z., Yang, N., Liu, Y., Yang, L., Wang, Y., Han, L., … Zhang, X. (2016). Resting-state functional connectivity between the dorsal anterior cingulate cortex and thalamus is associated with risky decision-making in nicotine addicts. Scientific Reports, 6, 21778. https://doi.org/10.1038/srep21778
Weiland, B. J., Heitzeg, M. M., Zald, D., Cummiford, C., Love, T., Zucker, R. A., & Zubieta, J. K. (2014). Relationship between impulsivity, prefrontal anticipatory activation, and striatal dopamine release during rewarded task performance. Psychiatry Research, 223, 244–252. https://doi.org/10.1016/j.pscychresns.2014.05.015
Weissman, D. G., Schriber, R. A., Fassbender, C., Atherton, O., Krafft, C., Robins, R. W., … Guyer, A. E. (2015). Earlier adolescent substance use onset predicts stronger connectivity between reward and cognitive control brain networks. Developmental Cognitive Neuroscience, 16, 121–129. https://doi.org/10.1016/j.dcn.2015.07.002
Whelan, R., Conrod, P. J., Poline, J. B., Lourdusamy, A., Banaschewski, T., Barker, G. J., … Consortium, I. (2012). Adolescent impulsivity phenotypes characterized by distinct brain networks. Nature Neuroscience, 15, 920–925. https://doi.org/10.1038/nn.3092
Zermatten, A., Van der Linden, M., d’Acremont, M., Jermann, F., & Bechara, A. (2005). Impulsivity and decision making. Journal of Nervous and Mental Disease, 193, 647–650.
Zhang, S., & Li, C. S. R. (2012). Functional networks for cognitive control in a stop signal task: Independent component analysis. Human Brain Mapping, 33, 89–104. https://doi.org/10.1002/hbm.21197
Zhou, Y., Li, S., Dunn, J., Li, H., Qin, W., Zhu, M., … Jiang, T. (2014). The neural correlates of risk propensity in males and females using resting-state fMRI. Frontiers in Behavioral Neuroscience, 8, 2. https://doi.org/10.3389/fnbeh.2014.00002
Zhu, X., Cortes, C. R., Mathur, K., Tomasi, D., & Momenan, R. (2015). Model-free functional connectivity and impulsivity correlates of alcohol dependence: A resting-state study. Addiction Biology, 22, 206–217. https://doi.org/10.1111/adb.12272
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
ESM 1
(DOCX 83 kb)
Rights and permissions
About this article
Cite this article
Deza Araujo, Y.I., Nebe, S., Neukam, P.T. et al. Risk seeking for losses modulates the functional connectivity of the default mode and left frontoparietal networks in young males. Cogn Affect Behav Neurosci 18, 536–549 (2018). https://doi.org/10.3758/s13415-018-0586-4
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13415-018-0586-4