1 Introduction

Group decision making (GDM) problems commonly occur for situations in the real world. A GDM problem is defined as the problem of selecting the best solution from a given set of alternatives X={x1, x2, …, x n }, according to a group of experts E={e1, e2, …, e m }, based on their unique preferences {P1, P2, …, P m }. In general, experts are associated with various fields, and they may hold quite different or even contradictory opinions. Therefore, one important process involves reconciling all of these opinions to reach a consensus and then finding the best solution that is acceptable to all (Cabrerizo et al., 2013).

GDM problems consist of two main processes: consensus and selection (Cabrerizo et al., 2010). The consensus process is concerned with reaching a certain level of consensus among the groups. So far, various models have been proposed for GDM problems (Wang and Li, 2015). In general, a feedback mechanism has been incorporated into these models, to provide advice to experts to improve the degree of consensus. However, there remain some aspects to be addressed. As an example, consider a heterogeneous situation. The majority of consensus models in the literature take into account only the importance of the experts in the aggregation process (Herrera-Viedma et al., 2014). However, experts belong to various fields, and their opinions may carry different weights throughout the consensus-reaching process. Therefore, it is reasonable to distinguish among experts when providing recommendations to reach the highest consensus level. It is logical to assume that experts with low levels of importance should receive more advice than those with high levels. With this motivation, we propose that a new feedback mechanism should be generated which considers the experts’ different importance levels when addressing advice.

In most cases, it is difficult or impossible for experts to assign precise or numerical values when expressing their opinions (Cabrerizo et al., 2015a). Fuzzy set theory has been introduced to handle the imprecision and uncertainties in real-life situations (Sabahi and Akbarzadeh-T, 2014). However, most of the existing fuzzy methods focus only on type-1 fuzzy sets (T1 FSs). Type-2 fuzzy sets (T2 FSs) can be treated as an extension of T1 FSs. In most cases, the computational burden is too heavy to apply T2 FSs to real-life problems (Mendel et al., 2006). Hence, interval type-2 fuzzy sets (IT2 FSs), a special case of general T2 FSs, must be considered. Previously, IT2 FSs have been applied widely in perceptual computing (Mendel et al., 2010), control systems (Wu and Mendel, 2011), and other fields (Feng et al., 2014). For example, Chen and Lee (2010) proposed a new approach for dealing with multi-attribute GDM problems, based on the arithmetic operations of IT2 FSs. Moharrer et al. (2015) proposed a novel two-phase methodology based on IT2 FSs for modeling linguistic label perception. Although various applications of IT2 FSs exist in different fields, they have not been applied before to the consensus-reaching process for solving GDM problems.

This article proposes a new consensus model for GDM problems using an IT2 fuzzy environment, motivated by the extra room for flexibility that IT2 FSs can provide in real-life situations (Chen and Lee, 2010). Moreover, to improve on the methods of previous studies, a new feedback mechanism is generated, which is guided by the experts’ levels of importance throughout the consensus-reaching process. Moreover, a practical example is investigated and comparable models are executed, to illustrate the practicality and feasibility of the proposed model.

2 Interval type-2 fuzzy set

The main aim of this section is to provide some basic definitions related to the IT2 FS framework and its corresponding numerical operations.

Definition 1 (Mendel et al., 2006; Wang et al., 2012)

A T2 FS \(\tilde \tilde A\) in the universe of discourse X can be represented by a type-2 membership function \({\mu _{\tilde \tilde A}}\) as follows:

$$\begin{array}{*{20}c} {\tilde \tilde A = \left\{ {\left( {(x,\;u),\;{\mu _{\tilde \tilde A}}(x,\;u)} \right)\left| {\forall x} \right.} \right. \in X,\quad \quad \quad \quad \quad } \\ {\left. {\forall u \in {J_X} \subseteq \left[ {0,1} \right],0 \le {\mu _{\tilde \tilde A}}(x,\;u) \le 1} \right\},} \\ \end{array} $$
((1))

where J X denotes an interval in [0, 1]. Moreover, the T2 FS \({\tilde \tilde A}\) can be represented in an alternative form as follows:

$$\tilde \tilde A = \int\limits_{x \in X} {\int\limits_{u \in {J_X}} {{{{\mu _{\tilde \tilde A}}(x,\;u)} \over {(x,\;u)}},} } $$
((2))

where ∫∫ represents the union over all admissible x and u.

Definition 2 (Mendel et al., 2006) Let \({\tilde \tilde A}\) be a T2 FS in the universe of discourse X represented by a type-2 membership function \({\mu _{\tilde \tilde A}}\). If all \({\mu _{\tilde \tilde A}}(x,\;u) = 1\), then \({\tilde \tilde A}\) is called an IT2 FS and can be expressed as follows:

$$\tilde \tilde A = \int\limits_{x \in X} {\int\limits_{u \in {J_X}} {{1 \over {(x,\;u)}},} } $$
((3))

where J X has the same meaning as above.

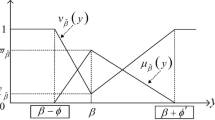
Definition 3 (Mendel et al., 2006) The upper and lower membership functions of an IT2 FS are type-1 membership functions, respectively. Fig. 1 shows a trapezoidal IT2 FS.

$$\begin{array}{*{20}c} {{{\tilde \tilde A}_i} = (\tilde A_i^{\rm{U}},\;\tilde A_i^{\rm{L}})\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;} \\ { = \left( {\left( {a_{i1}^{\rm{U}},\;a_{i2}^{\rm{U}},\;a_{i3}^{\rm{U}},\;a_{i4}^{\rm{U}}; {H_1}(\tilde A_i^{\rm{U}}),\;{H_2}(\tilde A_i^{\rm{U}})} \right),} \right.} \\ {\quad \left. {\left( {a_{i1}^{\rm{L}},\;a_{i2}^{\rm{L}},\;a_{i3}^{\rm{L}},\;a_{i4}^{\rm{L}}; {H_1}(\tilde A_i^{\rm{L}}),\;{H_2}(\tilde A_i^{\rm{L}})} \right)} \right),} \\ \end{array} $$
((4))

where \({H_j}(\tilde A_i^U)\) is the membership value of the element \(a_{i(j + 1)}^{\rm{U}}\) in the upper trapezoidal membership function \(\tilde A_i^{\rm{U}}\), \({H_j}(\tilde A_i^{\rm{L}})\) is the membership value of the element \(a_{i(j + 1)}^{\rm{L}}\) in the lower trapezoidal membership function \(\tilde A_i^{\rm{L}}\), and all of these membership values belong to [0, 1].

Fig. 1
figure 1

Illustration of a trapezoidal IT2 FS

Full size image

Definition 4 (Lee and Chen, 2008) Let

$$\begin{array}{*{20}c} {{{\tilde \tilde A}_1} = (\tilde A_1^{\rm{U}},\;\tilde A_1^{\rm{L}}) = \left( {\left( {a_{11}^{\rm{U}},\;a_{12}^{\rm{U}},\;a_{13}^{\rm{U}},\;a_{14}^{\rm{U}}; {H_1}(\tilde A_1^{\rm{U}}),\;{H_2}(\tilde A_1^{\rm{U}})} \right),} \right.\quad \quad \quad \quad \quad \quad \quad \quad } \\ {\left. {\left( {a_{11}^{\rm{L}},\;a_{12}^{\rm{L}},\;a_{13}^{\rm{L}},\;a_{14}^{\rm{L}}; {H_1}(\tilde A_1^{\rm{L}}),\;{H_2}(\tilde A_1^{\rm{L}})} \right)} \right)} \\ \end{array} $$

and

$$\begin{array}{*{20}c} {{{\tilde \tilde A}_2} = (\tilde A_2^{\rm{U}},\;\tilde A_2^{\rm{L}}) = \left( {\left( {a_{21}^{\rm{U}},\;a_{22}^{\rm{U}},\;a_{23}^{\rm{U}},\;a_{24}^{\rm{U}}; {H_1}(\tilde A_2^{\rm{U}}),\;{H_2}(\tilde A_2^{\rm{U}})} \right),} \right.\quad \quad \quad \quad \quad \quad \quad } \\ {\left. {\left( {a_{21}^{\rm{L}},\;a_{22}^{\rm{L}},\;a_{23}^{\rm{L}},\;a_{24}^{\rm{L}}; {H_1}(\tilde A_2^{\rm{L}}),\;{H_2}(\tilde A_2^{\rm{L}})} \right)} \right)} \\ \end{array} $$

be two trapezoidal IT2 FSs. Then, some of the main operations between them are defined as follows:

$$\begin{array}{*{20}c} {{{\tilde \tilde A}_1} \oplus {{\tilde \tilde A}_2} = (\tilde A_1^{\rm{U}},\;\tilde A_1^{\rm{L}}) \oplus (\tilde A_2^{\rm{U}},\;\tilde A_2^{\rm{L}})\quad \quad \quad \quad \quad \quad \quad \quad } \\ { = \left( {\left( {a_{11}^{\rm{U}} + } \right.a_{21}^{\rm{U}},\;a_{12}^{\rm{U}} + a_{22}^{\rm{U}},\;a_{13}^{\rm{U}} + a_{23}^{\rm{U}},\;a_{14}^{\rm{U}} + a_{24}^{\rm{U}}; } \right.\quad \quad \quad \quad \;} \\ {\left. {\min \left( {{H_1}(\tilde A_1^{\rm{U}}),\;{H_1}(\tilde A_2^{\rm{U}})} \right),\;\min \left( {{H_2}(\tilde A_1^{\rm{U}}),\;{H_2}(\tilde A_2^{\rm{U}})} \right)} \right),\;\;} \\ {\left( {a_{11}^{\rm{L}} + a_{21}^{\rm{L}},\;a_{12}^{\rm{L}} + a_{22}^{\rm{L}},\;a_{13}^{\rm{L}} + a_{23}^{\rm{L}},\;a_{14}^{\rm{L}} + a_{24}^{\rm{L}}; } \right.\quad \quad \quad \quad \quad \;} \\ {\left. {\left. {\min \left( {{H_1}(\tilde A_1^{\rm{L}}),\;{H_1}(\tilde A_2^{\rm{L}})} \right),\;\min \left( {{H_2}(\tilde A_1^{\rm{L}}),\;{H_2}(\tilde A_2^{\rm{L}})} \right)} \right)} \right),} \\ \end{array} $$
((5))
$$\begin{array}{*{20}c} {{{\tilde \tilde A}_1} \ominus {{\tilde \tilde A}_2} = (\tilde A_1^{\rm{U}},\;\tilde A_1^{\rm{L}}) \ominus (\tilde A_2^{\rm{U}},\;\tilde A_2^{\rm{L}})\quad \quad \quad \quad \quad \quad \quad \quad } \\ { = \left( {\left( {a_{11}^{\rm{U}} - } \right.a_{24}^{\rm{U}},\;a_{12}^{\rm{U}} - a_{23}^{\rm{U}},\;a_{13}^{\rm{U}} - a_{22}^{\rm{U}},\;a_{14}^{\rm{U}} - a_{21}^{\rm{U}};} \right.\quad \quad \quad \quad \;} \\ {\left. {\min \left( {{H_1}(\tilde A_1^{\rm{U}}),\;{H_1}(\tilde A_2^{\rm{U}})} \right),\;\min \left( {{H_2}(\tilde A_1^{\rm{U}}),\;{H_2}(\tilde A_2^{\rm{U}})} \right)} \right),\;\;} \\ {\left( {a_{11}^{\rm{L}} - a_{24}^{\rm{L}},\;a_{12}^{\rm{L}} - a_{23}^{\rm{L}},\;a_{13}^{\rm{L}} - a_{22}^{\rm{L}},\;a_{14}^{\rm{L}} - a_{21}^{\rm{L}};} \right.\quad \quad \quad \quad \quad \;} \\ {\left. {\left. {\min \left( {{H_1}(\tilde A_1^{\rm{L}}),\;{H_1}(\tilde A_2^{\rm{L}})} \right),\;\min \left( {{H_2}(\tilde A_1^{\rm{L}}),\;{H_2}(\tilde A_2^{\rm{L}})} \right)} \right)} \right),} \\ \end{array} $$
((6))
$$\begin{array}{*{20}c} {{{\tilde \tilde A}_1} \otimes {{\tilde \tilde A}_2} = (\tilde A_1^{\rm{U}},\;\tilde A_1^{\rm{L}}) \otimes (\tilde A_2^{\rm{U}},\;\tilde A_2^{\rm{L}})\quad \quad \quad \quad \quad \quad \quad \quad } \\ { = \left( {\left( {a_{11}^{\rm{U}} \times } \right.a_{21}^{\rm{U}},\;a_{12}^{\rm{U}} \times a_{22}^{\rm{U}},\;a_{13}^{\rm{U}} \times a_{23}^{\rm{U}},\;a_{14}^{\rm{U}} \times a_{24}^{\rm{U}};} \right.\quad \quad \quad \quad \quad } \\ {\left. {\min \left( {{H_1}(\tilde A_1^{\rm{U}}),\;{H_1}(\tilde A_2^{\rm{U}})} \right),\;\min \left( {{H_2}(\tilde A_1^{\rm{U}}),\;{H_2}(\tilde A_2^{\rm{U}})} \right)} \right),\quad } \\ {\left( {a_{11}^{\rm{L}} \times a_{21}^{\rm{L}},\;a_{12}^{\rm{L}} \times a_{22}^{\rm{L}},\;a_{13}^{\rm{L}} \times a_{23}^{\rm{L}},\;a_{14}^{\rm{L}} \times a_{24}^{\rm{L}};} \right.\quad \quad \quad \quad \quad \quad \quad } \\ {\left. {\left. {\min \left( {{H_1}(\tilde A_1^{\rm{L}}),\;{H_1}(\tilde A_2^{\rm{L}})} \right),\;\min \left( {{H_2}(\tilde A_1^{\rm{L}}),\;{H_2}(\tilde A_2^{\rm{L}})} \right)} \right)} \right).\quad } \\ \end{array} $$
((7))

Definition 5 (Lee and Chen, 2008) Some arithmetic operations between the trapezoidal IT2 FSs are defined as follows:

$$\begin{array}{*{20}c} {k{{\tilde \tilde A}_1} = \left( {\left( {ka_{11}^{\rm{U}},\;ka_{12}^{\rm{U}},\;ka_{13}^{\rm{U}},\;ka_{14}^{\rm{U}};{H_1}(\tilde A_1^{\rm{U}}),\;{H_2}(\tilde A_1^{\rm{U}})} \right),\quad \quad \quad } \right.} \\ {\left. {\left( {ka_{11}^{\rm{L}},\;ka_{12}^{\rm{L}},\;ka_{13}^{\rm{L}},\;ka_{14}^{\rm{L}};{H_1}(\tilde A_1^{\rm{L}}),\;{H_2}(\tilde A_1^{\rm{L}})} \right)} \right),} \\ \end{array} $$
((8))
$$\begin{array}{*{20}c} {{{{{\tilde \tilde A}_1}} \over k} = \left( {\left( {{{a_{11}^{\rm{U}}} \over k},\;{{a_{12}^{\rm{U}}} \over k},\;{{a_{13}^{\rm{U}}} \over k},\;{{a_{14}^{\rm{U}}} \over k};{H_1}(\tilde A_1^{\rm{U}}),\;{H_2}(\tilde A_1^{\rm{U}})} \right),} \right.\quad \quad } \\ {\left. {\left( {{{a_{11}^{\rm{L}}} \over k},\;{{a_{12}^{\rm{L}}} \over k},\;{{a_{13}^{\rm{L}}} \over k},\;{{a_{14}^{\rm{L}}} \over k};{H_1}(\tilde A_1^{\rm{L}}),\;{H_2}(\tilde A_1^{\rm{L}})} \right)} \right).} \\ \end{array} $$
((9))

Definition 6 (Lee and Chen, 2008) The ranking value Rank(\({\tilde \tilde A_i}\)) of a trapezoidal IT2 FS \({\tilde \tilde A_i}\) is defined as follows:

$$\begin{array}{*{20}c} {{\rm{Rank}}({{\tilde {\tilde A}}_i}) = } \\ {{M_1}(\tilde A_i^{\rm{U}}) + {M_1}(\tilde A_i^{\rm{L}}) + {M_2}(\tilde A_i^{\rm{U}}) + {M_2}(\tilde A_i^{\rm{L}}) + {M_3}(\tilde A_i^{\rm{U}}) + {M_3}(\tilde A_i^{\rm{L}})} \\ { - 0.25\left( {{S_1}(\tilde A_i^{\rm{U}}) + {S_1}(\tilde A_i^{\rm{L}}) + {S_2}(\tilde A_i^{\rm{U}}) + {S_2}(\tilde A_i^{\rm{L}})} \right.\quad \quad \quad \quad \quad \quad \quad } \\ {\left. { + {S_3}(\tilde A_i^{\rm{U}}) + {S_3}(\tilde A_i^{\rm{L}}) + {S_4}(\tilde A_i^{\rm{U}}) + {S_4}(\tilde A_i^{\rm{L}})} \right)\quad \quad \quad \quad \quad } \\ { + {H_1}(\tilde A_i^{\rm{U}}) + {H_1}(\tilde A_i^{\rm{L}}) + {H_2}(\tilde A_i^{\rm{U}}) + {H_2}(\tilde A_i^{\rm{L}}),\quad \quad \quad \quad \quad \quad \quad \quad \quad } \\ \end{array} $$
((10))

where \({M_p}(\tilde A_i^j)\quad (1 \le p \le 3)\) denotes the average value of the elements \(a_{ip}^j\) and \(a_{i(p + 1)}^j\), \({S_q}(\tilde A_i^j)\;\left( {1 \le q \le 3} \right)\) the standard deviation of the elements \(a_{ip}^j\) and \(a_{i(p + 1)}^j\), and \({S_4}(\tilde A_i^j)\) the standard deviation of the elements \(a_{i1}^j,\;a_{i2}^j,\;a_{i3}^j,\;a_{i4}^j\). That is,

$${M_p}(\tilde A_i^j) = {{a_{ip}^j + a_{i(p + 1)}^j} \over 2},\quad 1 \le p \le 3,\;j \in \{ {\rm{U}},\;{\rm{L}}\} ,$$
$$\begin{array}{*{20}c} {{S_q}(\tilde A_i^j) = \sqrt {{1 \over 2}\sum\limits_{k = q}^{q + 1} {{{(a_{ik}^j - {M_q}(\tilde A_i^j))}^2}} } ,\;1 \le q \le 3,\;j \in \{ {\rm{U,}}\;{\rm{L}}\} ,} \\ {{S_4}(\tilde A_i^j) = \sqrt {{1 \over 4}\sum\limits_{k = 1}^4 {\left( {a_{ik}^j - {1 \over 4}\sum\limits_{k = 1}^4 {a_{ik}^j} } \right)} } ,\;j \in \{ {\rm{U,}}\;{\rm{L}}\} .} \\ \end{array} $$

Note that a larger ranking value indicates a larger corresponding number.

Definition 7 (Zhang and Zhang, 2013) The Hamming distance between \({\tilde \tilde A_1}\) and \({\tilde \tilde A_2}\), denoted by \(D({\tilde \tilde A_1},\;{\tilde \tilde A_2})\), can be expressed as follows:

$$D({\tilde \tilde A_1},\;{\tilde \tilde A_2}) = {{{d_1} + {d_2}} \over 8},$$
((11))

where

$$\begin{array}{*{20}c} {{d_1} = \left| {a_{11}^{\rm{U}} - a_{21}^{\rm{U}}} \right| + \left| {a_{12}^{\rm{U}} \cdot {H_1}(\tilde A_1^{\rm{U}}) - a_{22}^{\rm{U}} \cdot {H_1}(\tilde A_2^{\rm{U}})} \right|\quad \quad \quad } \\ { + \left| {a_{13}^{\rm{U}} \cdot {H_2}(\tilde A_1^{\rm{U}}) - a_{23}^{\rm{U}} \cdot {H_2}(\tilde A_2^{\rm{U}})} \right| + \left| {a_{14}^{\rm{U}} - a_{24}^{\rm{U}}} \right|} \\ \end{array} $$

and

$$\begin{array}{*{20}c} {{d_2} = \left| {a_{11}^{\rm{L}} - a_{21}^{\rm{L}}} \right| + \left| {a_{12}^{\rm{L}} \cdot {H_1}(\tilde A_1^{\rm{L}}) - a_{22}^{\rm{L}} \cdot {H_1}(\tilde A_2^{\rm{L}})} \right|\quad \quad \quad } \\ { + \left| {a_{13}^{\rm{L}} \cdot {H_2}(\tilde A_1^{\rm{L}}) - a_{23}^{\rm{L}} \cdot {H_2}(\tilde A_2^{\rm{L}})} \right| + \left| {a_{14}^{\rm{L}} - a_{24}^{\rm{L}}} \right|.} \\ \end{array} $$

3 Consensus model under IT2 fuzzy environment

Various consensus models have been proposed for GDM problems in previous decades, the majority of which are based on consensus and proximity measures to guide the feedback mechanism. These two measures focus on guiding the consensus-reaching process until a satisfactory consensus level is reached. However, when generating advice for the experts associated with a particular problem, such models ignore the importance levels of the opinions given by experts (Pérez et al., 2014). Meanwhile, note that consensus is meant as a full agreement at the beginning, which has been proven to be unreasonable and makes no sense. Experts may have trouble assigning crisp values to alternatives when dealing with GDM problems in most real-life situations. Hence, fuzzy set theory has been introduced to handle such uncertainties. However, in existing studies, most consensus models are based on T1 FSs, which would be incapable of handling some complex situations in comparison with T2 FSs.

To handle these issues, we propose a new consensus model, incorporating a new feedback mechanism in an IT2 fuzzy environment. The new feedback mechanism generates different advice strategies based on the experts’ levels of importance, and IT2 FS can provide decision makers with more flexibility. To the best of our knowledge, this is the first time that such a framework has been presented. We believe that this can provide greater insight into the consensus-reaching process.

The consensus model consists of several stages, as shown in Fig. 2. First, the problem is presented to the experts. Then, the experts express their unique assessments, based on their own understanding, using an IT2 fuzzy environment. During the consensus-reaching process, consensus measures must be calculated to check whether the consensus level is satisfactory. If yes, then the selection process is applied to choose the appropriate solution from the given set of possibilities. Otherwise, the feedback mechanism is initiated, generating useful advice to the experts based on their levels of understanding of the problem. Several consensus rounds may be necessary to achieve a certain level of consensus. In the following subsections, different stages are presented in detail.

Fig. 2
figure 2

New consensus model for group decision making (GDM) using an IT2 environment

Full size image

3.1 Computing the consensus measures

Suppose that each expert from a group E={e1, e2, …, e m } is required to express his/her fuzzy preferences \(\{ {\tilde \tilde P_1},\;{\tilde \tilde P_2}, \ldots ,{\tilde \tilde P_m}\} \) on a given set of alternatives X={x1, x2, …, x n }, using the linguistic terms and their corresponding IT2 FSs shown in Table 1 (Chen and Lee, 2010). For an expert e k , \(\tilde \tilde P_{ij}^k\) denotes a preference for alternative x i over alternative x j .

Table 1 Fuzzy linguistic assessment variables
Full size table

When the preferences have been provided, the consensus measures need to be calculated to ascertain whether the current consensus level in the decision-making process is satisfactory. In general, the consensus measures can be calculated at three different levels (Herrera-Viedma et al., 2007; Pérez et al., 2014; Zhang et al., 2015):

  1. 1.

    Initially, a similarity matrix \({\bf{S}}{{\bf{M}}^{kl}} = ({\rm{sm}}_{ij}^{kl})\), measuring the agreement between each pair of experts (ek, el) (k=1, 2, …, m−1; l=k+1, k+2, …, m), is constructed as follows:

    $${\rm{sm}}_{ij}^{kl} = 1 - D(\tilde \tilde p_{ij}^k,\;\tilde \tilde p_{ij}^l),$$
    ((12))

    where \(D(\tilde \tilde p_{ij}^k,\;\tilde \tilde p_{ij}^l)\) is the distance between \(\tilde \tilde p_{ij}^k\) and \(\tilde \tilde p_{ij}^l\), calculated by using Eq. (11).

  2. 2.

    Subsequently, all of the constructed similarity matrices must be combined to obtain an aggregated consensus matrix, CM= (cm ij ), using the following relationship (Pérez et al., 2014):

    $${\rm{c}}{{\rm{m}}_{ij}} = 2\sum\limits_{k = 1}^{m - 1} {\sum\limits_{l = k + 1}^m {{{{\rm{sm}}_{ij}^{kl}} \over {m(m - 1)}}.} } $$
    ((13))

    It is held that cm ij ∈[0,1]. The lower and upper bounds indicate the presence of no consensus and a total consensus for preference p ij , respectively.

  3. 3.

    Finally, the consensus measures at three different levels are defined as follows:

    Consensus measure on preference:

    $${\rm{c}}{{\rm{d}}_{ij}} = {\rm{c}}{{\rm{m}}_{ij}}.$$
    ((14))

    Consensus measure on alternatives:

    $${\rm{C}}{{\rm{D}}_i} = \sum\limits_{j = 1,\;j \ne 1}^n {{{{\rm{c}}{{\rm{d}}_{ij}} + {\rm{c}}{{\rm{d}}_{ji}}} \over {2(n - 1)}}.} $$
    ((15))

    Consensus measure on the relation:

    $${\rm{CD}} = \sum\limits_{i = 1}^n {{{{\rm{C}}{{\rm{D}}_i}} \over n}} .$$
    ((16))

After the consensus measure CD is obtained, it must be compared with a threshold CR∈[0, 1], which is set beforehand as the minimum required consensus level. When CD≥CR, the consensus-reaching process is acceptable, and the model moves onto the selection process. Otherwise, the feedback mechanism is activated, to aid the experts in changing their preferences and to narrow their differences to reach a higher consensus level. Note that a maximum number of repetitions should be decided, in case CD never converges to CR (Mata et al., 2009).

3.2 Feedback mechanism

As mentioned above, we propose a new feedback mechanism to guide the experts in changing their preferences based on their levels of importance. In general, experts with low levels of importance require more advice than those with high levels. Thus, in this study, we need to classify the experts into different levels in advance.

In this regard, the weights of different experts need to be determined first. However, in most situations, it is impossible to determine weights for the experts. Therefore, we assign the experts different weights directly using the preferences expressed by them. Following Chen and Yang (2011), the closer an expert’s preference value is to the mean value, the larger the weight that should be assigned.

The mean preference value \({\bar \tilde \tilde p_{ij}}\) between two alternatives x i and x j is computed using Eq. (17):

$${\bar \tilde \tilde p_{ij}} = {1 \over k}\sum\limits_{k = 1}^m {\tilde \tilde p_{ij}^k} ,\quad i,\;j = 1,\;2,\; \ldots ,\;n.$$
((17))

Then, we compute the similarity between the preference of each expert and the mean preference as in Eq. (18):

$${S_k} = 1 - {1 \over {n(n - 1)}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1,\;j \approx 1}^n {D(\tilde \tilde p_{ij}^k,\;{{\bar \tilde \tilde p}_{ij}})} } .$$
((18))

The weight of expert e k is computed as follows:

$${W_k} = {{{S_k}} \over {\sum\limits_{i = 1}^m {{S_k}} }}.$$
((19))

Finally, we must classify the experts into three levels: low, medium, and high. The performance of this classification depends on the specific problem being dealt with.

After we obtain the weights and preferences of all experts, we combine all of the different comparison matrices into a single matrix for the group, \(\tilde \tilde P = ({\tilde \tilde P_{ij}})\), using the following formula:

$${\tilde \tilde P_{ij}} = \sum\limits_{k = 1}^m {{w_k}\tilde \tilde P_{ij}^k} .$$
((20))

Proximity measures are designed to measure the agreement between each individual’s preference and the collective group preference. This can be used to guide the feedback mechanism. We proceed by computing this metric at three different levels, as shown below:

Proximity measure on preferences of each expert \({\bf{P}}{{\bf{M}}^k} = ({\rm{pm}}_{ij}^k)\)

$${\rm{pm}}_{ij}^k = 1 - D(\tilde \tilde P_{ij}^k,\;{\tilde \tilde P_{ij}}).$$
((21))

Proximity measure on alternatives:

$${\rm{PM}}_i^k = {1 \over {2\left( {n - 1} \right)}}\sum\limits_{j = 1,\;j \ne i}^n {({\rm{pm}}_{ij}^k + {\rm{pm}}_{ji}^k).} $$
((22))

Proximity measure on the relation:

$${\rm{P}}{{\rm{M}}^k} = {1 \over n}\sum\limits_{i = 1}^n {{\rm{PM}}_i^k} .$$
((23))

Then, we propose three different strategies for providing advice to the experts with different importance levels (Zhang et al., 2015), after all of the related parameters have been calculated and obtained.

  1. (a)

    For low-importance experts:

    For experts at this level, we assume that they have little knowledge associated with the specific problem. Therefore, it is logical to assume that significant changes should be suggested by the feedback mechanism. To do this, we attempt to modify all of the preference values for which the consensus degree based on consensus measures is not high enough, as follows:

    $$R_{{\rm{Low}}}^k = \left\{ {(i,\;j)|{\rm{c}}{{\rm{d}}_{ij}} < {\alpha _1}} \right\},$$
    ((24))

    where \({\alpha _1} = {1 \over {n(n - 1)}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1,\;j \ne i}^n {{\rm{c}}{{\rm{d}}_{ij}}} } .\)

  2. (b)

    For medium-importance experts

    For experts at this level, fewer changes should be encouraged in comparison with the low-importance experts. Therefore, we focus on disagreements at the level of alternatives (Pérez et al., 2014). To do this, a vector β = [β i ] is determined, where \({\beta _i} = \sum\limits_{k - 1}^m {{\rm{PM}}_i^k/m\quad (i = 1,\;2, \ldots ,n)} \).

    We then define the preference values that need to be changed, based on consensus measures in conjunction with the proximity measures, as follows:

    $$R_{{\rm{Med}}}^k = \left\{ {(i,j)|{\rm{c}}{{\rm{d}}_{ij}} < {\alpha _1} \cap {\rm{C}}{{\rm{D}}_i} < {\rm{CD}} \cap {\rm{PM}}_i^k < {\beta _i}} \right\}.$$
    ((25))
  3. (c)

    For high-importance experts

    In general, the opinions of experts with higher levels of importance are more valuable, and it is logical to assume that their preferences should be preserved as much as possible, so that they can exert an influence on others. Thus, in this situation, we focus on the preference values that hinder agreement with the collective preference at pairs of alternatives (Pérez et al., 2014), based on the proximity measures:

    $$\begin{array}{*{20}c} {R_{{\rm{High}}}^k = \left\{ {(i,j)|{\rm{c}}{{\rm{d}}_{ij}} < {\alpha _1} \cap {\rm{C}}{{\rm{D}}_i} < {\rm{CD}}} \right.\quad \quad } \\ {\left. { \cap {\rm{PM}}_i^k{\rm{ < }}{\beta _{\rm{i}}} \cap {\rm{PM}}_{ij}^k < {\alpha _2}} \right\},} \\ \end{array} $$
    ((26))

    where

    $${\alpha _2} = {{\sum\limits_{i = 1}^n {\sum\limits_{j = 1,\;j \ne i}^n {{\rm{pm}}_{ij}^k} } } \over {n(n - 1)}}.$$

Once all of the preference values that need to be changed have been identified, different steps should then be followed in different cases. In this regard, an expert should increase the assessment when \(\tilde \tilde p_{ij}^k < {\tilde \tilde p_{ij}}\) or decrease it when \(\tilde \tilde p_{ij}^k < {\tilde \tilde p_{ij}}\).

3.3 Selection process

After a certain number of consensus rounds have been carried out and an acceptable agreement level is reached, i.e., CD≥CR, the selection process begins.

When we obtain the collective preference matrix \(\tilde \tilde P\), the alternatives can be furnished with the ranking values. As previously mentioned, a larger ranking value often corresponds to a larger trapezoidal IT2 FS. Hence, we define the dominance degree px i of each alternative x i as in the following equation:

$${\rm{p}}{{\rm{x}}_i} = \sum\limits_{j = 1,\;j \ne i}^n {{\rm{Rank}}} ({\tilde \tilde p_{ij}}).$$
((27))

Finally, a ranking order can be obtained for all the alternatives, and the alternative with the highest value for px i is the best solution.

4 Illustrative example

4.1 Proposed consensus model

In this section, we use an example to show the performance of the proposed model. Suppose that four experts from different fields are invited to make judgments between four alternatives, using the fuzzy linguistic terms in Table 1. Following a period of consideration, the preferences were obtained as follows:

$$\begin{array}{*{20}c} {{E^1} = \left[ {\begin{array}{*{20}c} - & {{\rm{VH}}} & {{\rm{VH}}} & {{\rm{VH}}} \\ {{\rm{VL}}} & - & {{\rm{MH}}} & {\rm{H}} \\ {\rm{L}} & {{\rm{ML}}} & - & {\rm{M}} \\ {\rm{L}} & {\rm{L}} & {\rm{M}} & - \\ \end{array} } \right],} \\ {{E^2} = \left[ {\begin{array}{*{20}c} - & {{\rm{VL}}} & {{\rm{ML}}} & {{\rm{ML}}} \\ {{\rm{VH}}} & - & {\rm{H}} & {{\rm{VH}}} \\ {{\rm{MH}}} & {\rm{L}} & - & {\rm{M}} \\ {\rm{H}} & {{\rm{VL}}} & {\rm{M}} & - \\ \end{array} } \right],} \\ {{E^3} = \left[ {\begin{array}{*{20}c} - & {\rm{M}} & {{\rm{ML}}} & {{\rm{ML}}} \\ {\rm{M}} & - & {\rm{L}} & {\rm{L}} \\ {\rm{H}} & {\rm{H}} & - & {\rm{M}} \\ {{\rm{MH}}} & {{\rm{MH}}} & {\rm{M}} & - \\ \end{array} } \right],} \\ {{E^4} = \left[ {\begin{array}{*{20}c} - & {\rm{M}} & {{\rm{ML}}} & {{\rm{ML}}} \\ {\rm{M}} & - & {\rm{L}} & {\rm{L}} \\ {\rm{H}} & {\rm{H}} & - & {\rm{M}} \\ {{\rm{MH}}} & {{\rm{MH}}} & {\rm{M}} & - \\ \end{array} } \right].} \\ \end{array} $$

The four linguistic matrices were then transformed into their corresponding IT2 FSs, as follows:

$$\begin{array}{*{20}c} {{{\tilde \tilde P}^1} = \left[ {\begin{array}{*{20}c} - & {\tilde \tilde p_{12}^1} & {\tilde \tilde p_{13}^1} & {\tilde \tilde p_{14}^1} \\ {\tilde \tilde p_{21}^1} & - & {\tilde \tilde p_{23}^1} & {\tilde \tilde p_{24}^1} \\ {\tilde \tilde p_{31}^1} & {\tilde \tilde p_{32}^1} & - & {\tilde \tilde p_{34}^1} \\ {\tilde \tilde p_{41}^1} & {\tilde \tilde p_{42}^1} & {\tilde \tilde p_{43}^1} & - \\ \end{array} } \right],} & {{{\tilde \tilde P}^2} = \left[ {\begin{array}{*{20}c} - & {\tilde \tilde p_{12}^2} & {\tilde \tilde p_{13}^2} & {\tilde \tilde p_{14}^2} \\ {\tilde \tilde p_{21}^2} & - & {\tilde \tilde p_{23}^2} & {\tilde \tilde p_{24}^2} \\ {\tilde \tilde p_{31}^2} & {\tilde \tilde p_{32}^2} & - & {\tilde \tilde p_{34}^2} \\ {\tilde \tilde p_{41}^2} & {\tilde \tilde p_{42}^2} & {\tilde \tilde p_{43}^2} & - \\ \end{array} } \right],} \\ {{{\tilde \tilde P}^3} = \left[ {\begin{array}{*{20}c} - & {\tilde \tilde p_{12}^3} & {\tilde \tilde p_{13}^3} & {\tilde \tilde p_{14}^3} \\ {\tilde \tilde p_{21}^3} & - & {\tilde \tilde p_{23}^3} & {\tilde \tilde p_{24}^3} \\ {\tilde \tilde p_{31}^3} & {\tilde \tilde p_{32}^3} & - & {\tilde \tilde p_{34}^3} \\ {\tilde \tilde p_{41}^3} & {\tilde \tilde p_{42}^3} & {\tilde \tilde p_{43}^3} & - \\ \end{array} } \right],} & {{{\tilde \tilde P}^4} = \left[ {\begin{array}{*{20}c} - & {\tilde \tilde p_{12}^4} & {\tilde \tilde p_{13}^4} & {\tilde \tilde p_{14}^4} \\ {\tilde \tilde p_{21}^4} & - & {\tilde \tilde p_{23}^4} & {\tilde \tilde p_{24}^4} \\ {\tilde \tilde p_{31}^4} & {\tilde \tilde p_{32}^4} & - & {\tilde \tilde p_{34}^4} \\ {\tilde \tilde p_{41}^4} & {\tilde \tilde p_{42}^4} & {\tilde \tilde p_{43}^4} & - \\ \end{array} } \right].} \\ \end{array} $$

Take \({{{\tilde \tilde P}^1}}\), for instance, where

$$\begin{array}{*{20}c} {\tilde \tilde p_{12}^1 = ((0.9,1,1,1;1,1),(0.95,1,1,1;0.9,0.9)),\quad \quad \quad \quad \;\;\;} \\ {\tilde \tilde p_{13}^1 = ((0.9,1,1,1;1,1),(0.95,1,1,1;0.9,0.9)),\quad \quad \quad \quad \;\;\;} \\ {\tilde \tilde p_{14}^1 = ((0.9,1,1,1;1,1),(0.95,1,1,1;0.9,0.9)),\quad \quad \quad \quad \;\;\;} \\ {\tilde \tilde p_{21}^1 = ((0,0,0,0.1;1,1),(0,0,0,0.05;0.9,0.9)),\quad \quad \quad \quad \;} \\ {\tilde \tilde p_{23}^1 = ((0.5,0.7,0.7,0.9;1,1),(0.6,0.7,0.7,0.8;0.9,0.9)),} \\ {\tilde \tilde p_{24}^1 = ((0.7,0.9,0.9,1;1,1),(0.8,0.9,0.9,0.95;0.9,0.9)),\;} \\ {\tilde \tilde p_{31}^1 = ((0,0.1,0.1,0.3;1,1),(0.05,0.1,0.1,0.2;0.9,0.9)),\;\;} \\ {\tilde \tilde p_{32}^1 = ((0.1,0.3,0.3,0.5;1,1),(0.2,0.3,0.3,0.4;0.9,0.9)),\;} \\ {\tilde \tilde p_{34}^1 = ((0.3,0.5,0.5,0.7;1,1),(0.4,0.5,0.5,0.6;0.9,0.9)),} \\ {\tilde \tilde p_{41}^1 = ((0,0.1,0.1,0.3;1,1),(0.05,0.1,0.1,0.2;0.9,0.9)),\;\;} \\ {\tilde \tilde p_{42}^1 = ((0,0.1,0.1,0.3;1,1),(0.05,0.1,0.1,0.2;0.9,0.9)),\;\;} \\ {\tilde \tilde p_{43}^1 = ((0.3,0.5,0.5,0.7;1,1),(0.4,0.5,0.5,0.6;0.9,0.9)).} \\ \end{array} $$
  1. 1.

    Computing the consensus measures

    First, the six similarity matrices SM12, SM13, SM14, SM23, SM24, and SM34 were obtained by computing the agreement between each pair of experts using Eq. (12). Subsequently, a consensus matrix CM was obtained using Eq. (13). Then, the consensus measures at the three different levels were obtained using Eqs. (14)–(16).

    Consensus measure on preference:

    $${\bf{CD}}{\rm{ = }}\left[ {\begin{array}{*{20}c} - & {0.53} & {0.67} & {0.67} \\ {0.53} & - & {0.53} & {0.46} \\ {0.60} & {0.53} & - & 1 \\ {0.63} & {0.57} & 1 & - \\ \end{array} } \right].$$

    Consensus measure on alternatives: \({\rm{C}}{{\rm{D}}_1} = 0.61,\;{\rm{C}}{{\rm{D}}_2} = 0.53,\;{\rm{C}}{{\rm{D}}_3} = 0.72,\;{\rm{C}}{{\rm{D}}_4} = 0.72.\) Consensus measure on the relation:

    $${\rm{CD}} = {1 \over 4}\sum\limits_{i = 1}^4 {{\rm{C}}{{\rm{D}}_i} = 0.645.} $$

    We set CL=0.7, and see that CD<CL. This means that the consensus level was unacceptable. Thus, the feedback mechanism was activated.

  2. 2.

    Feedback mechanism

    First, the weights of all of the experts were determined by using Eqs. (17)–(19).

    The results were w1=0.22, w2=0.24, w3=0.27, and w4=0.27. In this problem, we set experts e3 and e4 as high-importance experts, e2 as a medium-importance expert, and e1 as a low-importance expert.

    After determining all of the experts’ weights and their corresponding preferences, a global final comparison matrix was obtained by using Eq. (20), as follows:

    $$\tilde \tilde P = \left[ {\begin{array}{*{20}c} - & {{{\tilde \tilde p}_{12}}} & {{{\tilde \tilde p}_{13}}} & {{{\tilde \tilde p}_{14}}} \\ {{{\tilde \tilde p}_{21}}} & - & {{{\tilde \tilde p}_{23}}} & {{{\tilde \tilde p}_{24}}} \\ {{{\tilde \tilde p}_{31}}} & {{{\tilde \tilde p}_{32}}} & - & {{{\tilde \tilde p}_{34}}} \\ {{{\tilde \tilde p}_{41}}} & {{{\tilde \tilde p}_{42}}} & {{{\tilde \tilde p}_{43}}} & - \\ \end{array} } \right],$$

    where

    $$\begin{array}{*{20}c} {{{\tilde \tilde p}_{12}} = ((0.36,0.49,0.49,0.62;1,1),\quad \quad } \\ {\quad \quad \quad (0.43,0.49,0.49,0.56;0.9,0.9)),} \\ {{{\tilde \tilde p}_{13}} = ((0.28,0.45,0.45,0.61;1,1),\quad \quad \;} \\ {\quad \quad \quad (0.37,0.45,0.45,0.53;0.9,0.9)),} \\ {{{\tilde \tilde p}_{14}} = ((0.28,0.45,0.45,0.61;1,1),\quad \quad \;} \\ {\quad \quad \;\;(0.37,0.45,0.45,0.53;0.9,0.9)),} \\ {{{\tilde \tilde p}_{21}} = ((0.38,0.51,0.51,0.64;1,1),\quad \quad } \\ {\quad \quad \quad (0.44,0.51,0.51,0.58;0.9,0.9)),} \\ {{{\tilde \tilde p}_{23}} = ((0.28,0.42,0.42,0.61;1,1),\quad \quad } \\ {\quad \quad \quad (0.35,0.42,0.42,0.51;0.9,0.9)),} \\ {{{\tilde \tilde p}_{24}} = ((0.37,0.49,0.49,0.62;1,1),\quad \quad } \\ {\quad \quad \quad (0.43,0.49,0.49,0.56;0.9,0.9)),} \\ {{{\tilde \tilde p}_{31}} = ((0.50,0.68,0.68,0.82;1,1),\quad \;\quad } \\ {\quad \quad \;\;(0.59,0.68,0.68,0.75;0.9,0.9)),} \\ {{{\tilde \tilde p}_{32}} = ((0.4,0.58,0.58,0.72;1,1),\quad \quad \;\;\;} \\ {\quad \quad \;(0.49,0.58,0.58,0.65;0.9,0.9)),} \\ {{{\tilde \tilde p}_{34}} = ((0.3,0.5,0.5,0.7;1,1),\quad \quad \quad \quad \;\;} \\ {\;(0.4,0.5,0.5,0.6;0.9,0.9)),} \\ {{{\tilde \tilde p}_{41}} = ((0.44,0.62,0.62,0.79;1,1),\quad \quad \quad } \\ {\quad \quad (0.53,0.62,0.62,0.70;0.9,0.9)),} \\ {{{\tilde \tilde p}_{42}} = ((0.27,0.4,0.4,0.58;1,1),\quad \quad \quad \quad } \\ {\quad (0.34,0.4,0.4,0.49;0.9,0.9)),} \\ {{{\tilde \tilde p}_{43}} = ((0.3,0.5,0.5,0.7;1,1),\quad \quad \quad \quad \quad } \\ {(0.4,0.5,0.5,0.6;0.9,0.9)).} \\ \end{array} $$

    Proximity measures for each expert were then calculated using Eqs. (21)–(23):

    Proximity measure on preference:

    $$\begin{array}{*{20}c} {{\bf{P}}{{\bf{M}}^1} = \left[ {\begin{array}{*{20}c} - & {0.52} & {0.48} & {0.48} \\ {0.52} & - & {0.74} & {0.62} \\ {0.46} & {0.74} & - & {1.0} \\ {0.52} & {0.72} & {1.0} & - \\ \end{array} } \right],} \\ {{\bf{P}}{{\bf{M}}^2} = \left[ {\begin{array}{*{20}c} - & {0.54} & {0.85} & {0.85} \\ {0.54} & - & {0.56} & {0.53} \\ {0.97} & {0.56} & - & {1.0} \\ {0.74} & {0.62} & {1.0} & - \\ \end{array} } \right],} \\ {{\bf{P}}{{\bf{M}}^3} = \left[ {\begin{array}{*{20}c} - & {0.97} & {0.85} & {0.85} \\ {0.97} & - & {0.70} & {0.64} \\ {0.79} & {0.70} & - & {1.0} \\ {0.92} & {0.72} & {1.0} & - \\ \end{array} } \right],} \\ {{\bf{P}}{{\bf{M}}^4} = \left[ {\begin{array}{*{20}c} - & {0.97} & {0.85} & {0.85} \\ {0.97} & - & {0.70} & {0.64} \\ {0.79} & {0.70} & - & {1.0} \\ {0.92} & {0.72} & {1.0} & - \\ \end{array} } \right].} \\ \end{array} $$

    Proximity measure on alternatives:

    $$\begin{array}{*{20}c} {{\rm{PM}}_1^1 = 0.50,\;{\rm{PM}}_2^1 = 0.64,\;{\rm{PM}}_3^1 = 0.74,\;{\rm{PM}}_4^1 = 0.72,\,} \\ {{\rm{PM}}_1^2 = 0.75,\;{\rm{PM}}_2^2 = 0.54,\;{\rm{PM}}_3^2 = 0.74,\;{\rm{PM}}_4^2 = 0.79,} \\ {{\rm{PM}}_1^3 = 0.89,\;{\rm{PM}}_2^3 = 0.78,\;{\rm{PM}}_3^3 = 0.84,\;{\rm{PM}}_4^3 = 0.85,} \\ {{\rm{PM}}_1^4 = 0.89,\;{\rm{PM}}_2^4 = 0.78,\;{\rm{PM}}_3^4 = 0.84,\;{\rm{PM}}_4^4 = 0.85.} \\ \end{array} $$

    Proximity measure on relations:

    $${\rm{P}}{{\rm{M}}^1} = 0.65,\;{\rm{P}}{{\rm{M}}^2} = 0.73,\;{\rm{P}}{{\rm{M}}^3} = 0.84,\;{\rm{P}}{{\rm{M}}^4} = 0.84.$$

    Based on the rules and methods detailed above, the following different advice strategies were generated:

    1. (a)

      For low-importance expert e1:

      $$\begin{array}{*{20}c} {R_{{\rm{Low}}}^1 = \{ (i,j)|c{d_{ij}} < {\alpha _1}\} = \{ (i,j)|c{d_{ij}} < 0.64\} \quad \quad \quad } \\ { = \{ (1,2),(2,1),(2,3),(2,4),(3,1),(3,2),(4,1),(4,2)\} .} \\ \end{array} $$
    2. (b)

      For medium-importance expert e2: a vector β was determined as follows:

      $${\beta _1} = 0.76,\;{\beta _2} = 0.69,\;{\beta _3} = 0.81,\;{\beta _4} = 0.80.$$

      According to the suggested rules, the preferences that should be modified were identified as

      $$\begin{array}{*{20}c} {R_{{\rm{Med}}}^2 = \{ (i,j)|c{d_{ij}} < {\alpha _1} \cap {\rm{C}}{{\rm{D}}_i} < {\rm{CD}} \cap {\rm{PM}}_i^k < {\beta _i}\} \quad \quad \quad \;\;} \\ { = \{ (i,j)|c{d_{ij}} < 0.64 \cap {\rm{C}}{{\rm{D}}_i} < {\rm{0}}{\rm{.645}} \cap {\rm{PM}}_i^2 < {\beta _i}\} } \\ { = \{ (1,2),(2,1),(2,3),(2,4)\} .\quad \quad \quad \quad \quad \quad \quad \quad } \\ \end{array} $$
    3. (c)

      For high-importance experts e3 and e4:

      $$\begin{array}{*{20}c} {R_{{\rm{High}}}^3 = \{ (i,j)|c{d_{ij}} < {\alpha _1} \cap {\rm{C}}{{\rm{D}}_i} < {\rm{CD}}\quad \quad \quad \;\;} \\ { \cap {\rm{PM}}_i^k < {\beta _i} \cap {\rm{pm}}_{ij}^k < {\alpha _2}\} \quad \quad } \\ { = \{ (i,j)|c{d_{ij}} < 0.64 \cap {\rm{C}}{{\rm{D}}_i} < {\rm{0}}{\rm{.645}}} \\ { \cap {\rm{PM}}_i^3 < {\beta _i} \cap {\rm{pm}}_{ij}^3 < 0.84\} = \emptyset ,} \\ {R_{{\rm{High}}}^4 = \emptyset .\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad } \\ \end{array} $$

      Finally, the following four different recommendations were suggested to the experts to reach a higher consensus level in the next round:

      $$\begin{array}{*{20}c} {{R^1} = \left[ {\begin{array}{*{20}c} {} & - & = & = \\ + & {} & - & - \\ + & + & {} & = \\ + & + & = & {} \\ \end{array} } \right],\;{R^2} = \left[ {\begin{array}{*{20}c} {} & + & = & = \\ - & {} & - & - \\ = & = & {} & = \\ = & = & = & {} \\ \end{array} } \right],} \\ {{R^3} = \left[ {\begin{array}{*{20}c} {} & = & = & = \\ = & {} & = & = \\ = & = & {} & = \\ = & = & = & {} \\ \end{array} } \right],\;{R^2} = \left[ {\begin{array}{*{20}c} {} & = & = & = \\ = & {} & = & = \\ = & = & {} & = \\ = & = & = & {} \\ \end{array} } \right],} \\ \end{array} $$

      where r ij =+, −, or = denotes that the expert should increase, decrease, or maintain his/her preference accordingly.

      Note that the weight for each expert can be altered in each consensus round. We assume that the experts followed the advice and changed their preferences accordingly. In the next round, the whole group reached a higher consensus level of CD=0.77, which was greater than the minimum threshold. The experts’ new preference relations were now as follows:

      $$\begin{array}{*{20}c} {{E^1} = \left[ {\begin{array}{*{20}c} - & {{\rm{MH}}} & {{\rm{VH}}} & {{\rm{VH}}} \\ {{\rm{ML}}} & - & {\rm{M}} & {\rm{M}} \\ {\rm{M}} & {{\rm{MH}}} & - & {\rm{M}} \\ {\rm{M}} & {\rm{M}} & {\rm{M}} & - \\ \end{array} } \right],} \\ {{E^2} = \left[ {\begin{array}{*{20}c} - & {{\rm{ML}}} & {{\rm{ML}}} & {{\rm{ML}}} \\ {{\rm{MH}}} & - & {\rm{M}} & {{\rm{MH}}} \\ {{\rm{MH}}} & {\rm{L}} & - & {\rm{M}} \\ {\rm{H}} & {{\rm{VL}}} & {\rm{M}} & - \\ \end{array} } \right],} \\ {{E^3} = \left[ {\begin{array}{*{20}c} - & {\rm{M}} & {{\rm{ML}}} & {{\rm{ML}}} \\ {\rm{M}} & - & {\rm{L}} & {\rm{L}} \\ {\rm{H}} & {\rm{H}} & - & {\rm{M}} \\ {{\rm{MH}}} & {{\rm{MH}}} & {\rm{M}} & - \\ \end{array} } \right],} \\ {{E^4} = \left[ {\begin{array}{*{20}c} - & {\rm{M}} & {{\rm{ML}}} & {{\rm{ML}}} \\ {\rm{M}} & - & {\rm{L}} & {\rm{L}} \\ {\rm{H}} & {\rm{H}} & - & {\rm{M}} \\ {{\rm{MH}}} & {{\rm{MH}}} & {\rm{M}} & - \\ \end{array} } \right].} \\ \end{array} $$

      The new aggregated group preference matrix was the following:

      $$\begin{array}{*{20}c} {\tilde {\tilde P}_{new} = \left[ {\begin{array}{*{20}c} - & {\tilde {\tilde p}_{12}} & {\tilde {\tilde p}_{13}} & {\tilde {\tilde p}_{14}} \\ {\tilde {\tilde p}_{21}} & - & {\tilde {\tilde p}_{23}} & {\tilde {\tilde p}_{24}} \\ {\tilde {\tilde p}_{31}} & {\tilde {\tilde p}_{32}} & - & {\tilde {\tilde p}_{34}} \\ {\tilde {\tilde p}_{41}} & {\tilde {\tilde p}_{42}} & {\tilde {\tilde p}_{43}} & - \\ \end{array} } \right],} \\ \end{array}$$

      where

      $$\begin{array}{*{20}c} {{{\tilde {\tilde p}}_{12}} = ((0.30,0.50,0.50,0.70;1,1),\quad \quad } \\ {\quad \quad \quad (0.40,0.50,0.50,0.60;0.9,0.9)),} \\ {{{\tilde {\tilde p}}_{13}} = ((0.29,0.47,0.47,0.62;1,1),\quad \quad \;} \\ {\quad \quad \quad (0.38,0.47,0.47,0.54;0.9,0.9)),} \\ {{{\tilde {\tilde p}}_{14}} = ((0.29,0.47,0.47,0.62;1,1),\quad \quad \;} \\ {\quad \quad \;\;(0.38,0.47,0.47,0.54;0.9,0.9)),} \\ {{{\tilde {\tilde p}}_{21}} = ((0.30,0.50,0.50,0.70;1,1),\quad \quad } \\ {\quad \quad \quad (0.40,0.50,0.50,0.60;0.9,0.9)),} \\ {{{\tilde {\tilde p}}_{23}} = ((0.14,0.29,0.29,0.49;1,1),\quad \quad } \\ {\quad \quad \quad (0.22,0.29,0.29,0.39;0.9,0.9)),} \\ {{{\tilde {\tilde p}}_{24}} = ((0.19,0.34,0.34,0.54;1,1),\quad \quad } \\ {\quad \quad \quad (0.26,0.34,0.34,0.44;0.9,0.9)),} \\ {{{\tilde {\tilde p}}_{31}} = ((0.56,0.76,0.76,0.90;1,1),\quad \;\quad } \\ {\quad \quad \;\;(0.66,0.76,0.76,0.83;0.9,0.9)),} \\ {{{\tilde {\tilde p}}_{32}} = ((0.49,0.66,0.66,0.81;1,1),\quad \quad \;\;\;} \\ {\quad \quad \;(0.58,0.66,0.66,0.74;0.9,0.9)),} \\ {{{\tilde {\tilde p}}_{34}} = ((0.3,0.5,0.5,0.70;1,1),\quad \quad \quad \quad \;\;} \\ {\;(0.4,0.5,0.5,0.6;0.9,0.9)),} \\ {{{\tilde {\tilde p}}_{41}} = ((0.50,0.70,0.70,0.88;1,1),\quad \quad \quad } \\ {\quad \quad (0.60,0.70,0.70,0.79;0.9,0.9)),} \\ {{{\tilde {\tilde p}}_{42}} = ((0.33,0.49,0.49,0.66;1,1),\quad \quad \quad } \\ {(0.41,0.49,0.49,0.58;0.9,0.9)),} \\ {{{\tilde {\tilde p}}_{43}} = ((0.3,0.5,0.5,0.70;1,1),\quad \quad \quad \quad \;} \\ {(0.4,0.5,0.5,0.6;0.9,0.9)).} \\ \end{array} $$
  3. 3.

    Selection process

    Finally, the selection process was applied to select the appropriate solution using the dominance degree based on the rank value of each alternative, using Eq. (27). Thus, we obtained

    $${x_1} = 19.51,\;{x_2} = 17.76,\;{x_3} = 22.37,\;{x_4} = 21.02.$$

    As such, the final ranking list was x2 < x1 < x4 < x3, and therefore x3 was chosen to be the recommended solution.

4.2 Other consensus models

4.2.1 Statistical study

As mentioned in Section 3.1, different similarity matrices must be calculated to check the consensus measures, wherein different distance functions are used. Meanwhile, various distance functions have been used in existing studies. Therefore, it is worth carrying out some studies to determine whether different distance functions are able to influence the consensus-reaching process. To this aim, we apply five different distance functions commonly used in existing studies. These are the Manhattan, Euclidean, Cosine, Dice, and Jaccard distance functions (Chiclana et al., 2013).

Using the same preference values as in the above example, we conducted our experiment using the above five distance functions, and five different consensus measures at the relation level were obtained (Table 2).

Table 2 Consensus measures at the relation level using different distance functions
Full size table

It can be seen that the Cosine function produced the largest consensus level, followed by the Dice, Manhattan, Euclidean, and Jaccard distance functions. Moreover, the Manhattan and the Euclidean distance functions produced similar results. Thus, decision makers can use a specific distance function to reach a higher consensus level based on these comparative results, which can lead to a faster convergence.

Chiclana et al. (2013) carried out similar comparative statistical studies under different combinations of numbers of experts and linguistic ordered weighted averaging (OWA) operators. Their results were similar.

4.2.2 Comparative study

To demonstrate clearly the feasibility and practicality of our proposed model, three other consensus models were applied under the same assumptions. These were a Web-based consensus support system (Alonso et al., 2010), a linguistic consensus model (Alonso et al., 2013), and a trust-based consensus model (Wu et al., 2015).

The first model develops a Web-based consensus support system, based on consistency and consensus measures, and we found that it was good at maintaining individual consistency. The second model incorporates some delegation and a feedback mechanism to quicken the consensus-reaching process, and it was designed particularly to work in highly dynamic environments. The third model uses a trust-based estimation and aggregation method within a network social group.

Some reasonable hypotheses have been assumed while conducting the experiments. For example, the parameter to balance the weight of consensus and consistency criteria in the first model was set to 0.5, while the consistency level was set to 0.7. The trust weights in the second model and the average trust degrees for each expert were all settled as 0.25. After careful computations, the following three ranking results were obtained:

  1. (a)

    x4<x1<x3<x2,

  2. (b)

    x1<x4<x2<x3,

  3. (c)

    x4<x1<x2<x3.

The first model yielded a very different result from our model. The second alternative, x2, was found to be the best choice, while x3 came only in the second place. However, according to the opinions of the high-level importance experts in our proposed model, e3 and e4, x3 should be superior to x2. For the second and third models, the best alternative remained the same as in our model, but the ranking of the others varied significantly. The differences may be due to the different methods used to compute the weights. Moreover, variations in the determination of the corresponding parameters in the different models can affect the results. However, none of the three consensus models considered the experts’ weights when generating advice to the experts, and a greater number of consensus rounds were necessary to achieve a satisfactory consensus level. Thus, it is a logical and necessary procedure to distinguish the experts throughout the consensus-reaching process.

5 Conclusions

A new consensus model for GDM problems, using an IT2 fuzzy environment, is proposed. In our model, experts are asked to express their preferences using linguistic terms, which are characterized by IT2 FSs. Different weights for the experts are determined based on the experts’ opinions on the problem. Note that the weights do not necessarily remain the same in each consensus round. Two criteria are used simultaneously to guide the consensus-reaching process, and we propose a new feedback mechanism that generates different advice strategies based on the levels of the experts’ knowledge concerning the specific problem (Zhang et al., 2015). In general, experts with a lower level of importance receive more advice, and experts with a higher level of importance should alter their opinions less. To the best of our knowledge, this is the first time that a feedback mechanism that considers differences in experts’ knowledge levels in an IT2 fuzzy environment has been applied to a consensus model, which can certainly provide us with greater insight into the GDM process.

The following points summarize the advantages of our consensus model compared with other existing models:

  1. 1.

    The IT2 FSs used in this study can depict information with more vagueness and uncertainty, which can provide decision makers with more flexibility, and they can be used in other decision-making fields.

  2. 2.

    The automatic feedback mechanism, which is designed to generate specific advice to aid the consensus-reaching process, overcomes the problem of a traditional moderator. In addition, it yields promising results in practice.

  3. 3.

    The concept of the importance of the experts is considered throughout the decision-making process, which is one of the main novelties in this study. Furthermore, we believe that this is a reasonable addition to the model, and it can lead to a faster convergence.

However, the following disadvantages are also worth noting:

  1. 1.

    The consensus model cannot guarantee convergence. The feedback mechanism is responsible only for generating some suggestions to the experts to reach a higher consensus degree. However, it is the experts’ decision whether to accept it or not. In the future, some principles of persuasion and weapons of influence could be applied, to support the consensus-reaching process (Herrera-Viedma et al., 2014).

  2. 2.

    This consensus model fails to detect or forecast the consistency of the experts, which may lead to unreasonable results. Therefore, we intend to apply some mechanisms that can effectively check the consistency of the experts in a future study (Pérez et al., 2014).

  3. 3.

    One of the main drawbacks of our method lies in its computational difficulty. In this regard, creating some new consensus measures, along with the use of different distance functions, would be interesting.

In summary, there are still some new challenges associated with GDM problems that need to be solved. In particular, we should focus more on some new consensus approaches, particularly in social networks, due to their new characteristics and features in real-world applications (Cabrerizo et al., 2015b). Some initial efforts have been attempted in this direction (Wu and Chiclana, 2014; Wu et al., 2015). New preference structures applied in consensus approaches to represent the individuals’ preferences should be given enough attention. Some visualization tools and the development of software systems could be combined in the consensus-reaching process, to support a better understanding of different states and help reach a high consensus level (Cabrerizo et al., 2015b). We believe that these new challenges will help make this topic a hot one in the future.