Appendices
Appendix 1: Original Model Equations
Notes:
-
1.
A superscript J is used to denote endogenous IgG or mAb in most equations. If the equations describing the mAb and IgG are different two independent systems of equations are used.
-
2.
Dependent variables are described in amounts, not concentrations, as in (13).
-
3.
The original model (13) described binding to FcRn receptor as the change from initial FcRn concentration in different tissues and the initial conditions for this change is set to 0. In this work, FcRn receptor amounts were expressed as RfreeOrgan ‐ X.
-
4.
The original model used two estimated coefficients to reflect the non-FcRn dependent tissue uptake of mAb (13). In our study, simulations were performed without these coefficients.
I. plasma
Endogenous IgG
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{plasma}}^{\mathrm{endo}}}{\operatorname{d}t}\\ {}={K}_0\times {V}_{\mathrm{Plasma}}+\frac{Q_{\mathrm{Lung}}-{L}_{\mathrm{Lung}}}{V_{\mathrm{VAS}}^{\mathrm{Lung}}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{endo}}-\frac{L_{\mathrm{GIT}}+{L}_{\mathrm{Spleen}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{endo}}\\ {}-\frac{Q_{\mathrm{Liver}}+{Q}_{\mathrm{Heart}}+{Q}_{\mathrm{Kidney}}+{Q}_{\mathrm{Skin}}+{Q}_{\mathrm{Muscle}\ }}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{endo}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}^{\mathrm{endo}}\times {F}_{\mathrm{return}\ }\end{array}\hfill \\ {}\hfill \mathrm{IC}={A}_{\mathrm{plasma}}^{\mathrm{endo}}\mathrm{SS}\hfill \end{array} $$
(3)
Exogenous mAb
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{plasma}}}{\operatorname{d}t}\\ {}=\frac{Q_{\mathrm{Lung}}-{L}_{\mathrm{Lung}}}{V_{\mathrm{VAS}}^{\mathrm{Lung}}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}-\frac{L_{\mathrm{GIT}}+{L}_{\mathrm{Spleen}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}\\ {}-\frac{Q_{\mathrm{Liver}}+{Q}_{\mathrm{Heart}}+{Q}_{\mathrm{Kidney}}+{Q}_{\mathrm{Skin}}+{Q}_{\mathrm{Muscle}\ }}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}\times {F}_{\mathrm{return}\ }\end{array}\hfill \\ {}\hfill \mathrm{IC}={\mathrm{Dose}}_{\mathrm{mAb}}\hfill \end{array} $$
(4)
II. Organs
A. Vascular Space
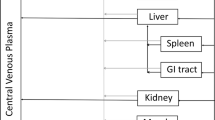
Equations for the vascular compartment in liver and lung are different from other organs.
i. lung
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{V}\mathrm{AS}\ \mathrm{Lung}}^J}{\operatorname{d}t}\\ {}=\frac{Q_{\mathrm{Liver}}-{L}_{\mathrm{Liver}}}{V_{\mathrm{V}\mathrm{AS}}^{\mathrm{Liver}}}\times {A}_{\mathrm{V}\mathrm{AS}\ \mathrm{Liver}}^J+\frac{Q_{\mathrm{Heart}}-{L}_{\mathrm{Heart}}}{V_{\mathrm{V}\mathrm{AS}}^{\mathrm{Heart}}}\times {A}_{\mathrm{V}\mathrm{AS}\ \mathrm{Heart}}^{\mathrm{J}}+\frac{Q_{\mathrm{Kidney}}-{L}_{\mathrm{Kidney}}}{V_{\mathrm{V}\mathrm{AS}}^{\mathrm{Kidney}}}\times {A}_{\mathrm{V}\mathrm{AS}\ \mathrm{Kidney}}^{\mathrm{J}}\\ {}+\frac{Q_{\mathrm{Skin}}-{L}_{\mathrm{Skin}}}{V_{\mathrm{V}\mathrm{AS}}^{\mathrm{Skin}}}\times {A}_{\mathrm{V}\mathrm{AS}\ \mathrm{Skin}}^{\mathrm{J}}+\frac{Q_{\mathrm{Muscle}}-{L}_{\mathrm{Muscle}}}{V_{\mathrm{V}\mathrm{AS}}^{\mathrm{Muscle}}}\times {A}_{\mathrm{V}\mathrm{AS}\ \mathrm{Muscle}}^{\mathrm{J}}-\frac{Q_{\mathrm{Lung}}-{L}_{\mathrm{Lung}}}{V_{\mathrm{V}\mathrm{AS}}^{\mathrm{Lung}}}\times {A}_{\mathrm{V}\mathrm{AS}\ \mathrm{Lung}}^{\mathrm{J}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Lung}}}{{\mathrm{V}}_{\mathrm{V}\mathrm{AS}}^{\mathrm{Lung}}}\\ {}\times {A}_{\mathrm{V}\mathrm{AS}\ \mathrm{Lung}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{V}\mathrm{AS}}\right)\times \frac{L_{\mathrm{Lung}}}{V_{\mathrm{V}\mathrm{AS}}^{\mathrm{Lung}}}\times {A}_{\mathrm{V}\mathrm{AS}\ \mathrm{Lung}}^{\mathrm{J}}+ FR\times \frac{C{L}_{\mathrm{Uptake}}^{\mathrm{Lung}}}{V_{\mathrm{END}}^{\mathrm{Lung}}}\times {\mathrm{ARCPX}}_{\mathrm{Lung}\hbox{-} 5}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{V}\mathrm{AS}\ \mathrm{Lung}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{V}\mathrm{AS}\ \mathrm{Lung}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{V}\mathrm{AS}\ \mathrm{Lung}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(5)
ii. liver
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}}{\operatorname{d}t}\\ {}=\frac{Q_{\mathrm{GIT}}-{L}_{\mathrm{GIT}}}{V_{\mathrm{VAS}}^{\mathrm{GIT}}}\times {A}_{\mathrm{VAS}\ \mathrm{GIT}}^J+\frac{Q_{\mathrm{Spleen}}-{L}_{\mathrm{Spleen}}}{V_{\mathrm{VAS}}^{\mathrm{Spleen}}}\times {A}_{\mathrm{VAS}\ \mathrm{Spleen}}^J+\frac{L_{\mathrm{GIT}}+{L}_{\mathrm{Spleen}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^J\\ {}+\frac{Q_{\mathrm{Liver}}-{Q}_{\mathrm{GIT}}-{Q}_{\mathrm{Spleen}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^J-\frac{Q_{\mathrm{Liver}}-{L}_{\mathrm{Liver}}}{V_{\mathrm{VAS}}^{\mathrm{Liver}}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^J-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Liver}}}{V_{\mathrm{VAS}}^{\mathrm{Liver}}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^J-\left(1-{\sigma}_{\mathrm{VAS}}\right)\\ {}\times \frac{L_{\mathrm{Liver}}}{V_{\mathrm{VAS}}^{\mathrm{Liver}}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}+\mathrm{FR}\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Liver}}}{V_{\mathrm{END}}^{\mathrm{Liver}}}\times {\mathrm{ARCPX}}_{\mathrm{Liver}\hbox{-} 5}^J\end{array}\hfill \\ {}\hfill {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(6)
iii. Other Organs (heart, kidney, skin, muscle, GIT, spleen)
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}}{\operatorname{d}t}\\ {}=\frac{Q_{\mathrm{Organ}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-\frac{Q_{\mathrm{Organ}}-{L}_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\\ {}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\mathrm{FR}\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{endo}}\operatorname{ss};{A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(7)
B. Interstitial Space (Applies for all organs including liver and lung, all termed “Organ”)
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}}{\operatorname{d}t}\\ {}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}+\left(1-\mathrm{FR}\right)\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\\ {}\times {\mathrm{A}\mathrm{RCPX}}_{\mathrm{Organ}\hbox{-} 5}^J-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{endo}}\mathrm{IC}={\mathrm{A}}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(8)
C. Endosomal Space (Applies for all organs including liver and lung, all termed “Organ”)
i. Subcompartment 1
Endogenous IgG
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}}{\operatorname{d}t}\\ {}=\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{endo}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{endo}}-k\frac{k_{\mathrm{on}\hbox{-} 1}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}\right.\\ {}\left.-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}\right)+{k}_{\mathrm{off}\hbox{-} 1}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}-\frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}\mathrm{ss}\hfill \end{array} $$
(9)
Exogenous mAb
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}}{\operatorname{d}t}\\ {}=\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{exo}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{exo}}-\frac{k_{\mathrm{on}\hbox{-} 1}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}\right.\\ {}\left.-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}\right)+{k}_{\mathrm{off}\hbox{-} 1}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}-\frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(10)
Endogenous IgG-FcRn complex
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}}{\operatorname{d}t}\\ {}=\frac{k_{\mathrm{on}\hbox{-} 1}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}\right)-{k}_{\mathrm{off}\hbox{-} 1}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}\\ {}-\frac{1}{\tau}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}\end{array}\hfill \\ {}\hfill {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}\mathrm{IC}={\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}\mathrm{ss}\hfill \end{array} $$
(11)
Exogenous mAb-FcRn complex
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}}{\operatorname{d}t}\\ {}=\frac{k_{\mathrm{on}\hbox{-} 1}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}\right)-{k}_{\mathrm{off}\hbox{-} 1}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}\\ {}-\frac{1}{\tau}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}\end{array}\hfill \\ {}\hfill {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(12)
ii. Subcompartments 2, 3 and 4 (i = 2, 3, 4)
Endogenous IgG
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}}{\operatorname{d}t}\\ {}=\frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \left(\mathrm{i}\hbox{-} 1\right)}^{\mathrm{endo}}-\frac{k_{\mathrm{on}\hbox{-} \mathrm{i}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}\right)\\ {}+{k}_{\mathrm{off}\hbox{-} \mathrm{i}}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}-\frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}\operatorname{ss}\hfill \end{array} $$
(13)
Exogenous mAb
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}}{\operatorname{d}t}\\ {}=\frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \left(\mathrm{i}\hbox{-} 1\right)}^{\mathrm{exo}}-\frac{k_{\mathrm{on}\hbox{-} \mathrm{i}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}\right)\\ {}+{k}_{\mathrm{off}\hbox{-} \mathrm{i}}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}-\frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(14)
Endogenous IgG-FcRn complex
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}}{\operatorname{d}t}\\ {}=\frac{1}{\tau}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \left(\mathrm{i}\hbox{-} 1\right)}^{\mathrm{endo}}+\frac{k_{\mathrm{on}\hbox{-} \mathrm{i}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}\right)\\ {}-{k}_{\mathrm{off}\hbox{-} \mathrm{i}}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}-\frac{1}{\tau}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}\end{array}\hfill \\ {}\hfill {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}\mathrm{IC}={\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}\mathrm{ss}\hfill \end{array} $$
(15)
Exogenous mAb-FcRn complex
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}}{\operatorname{d}t}\\ {}=\frac{1}{\tau}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \left(\mathrm{i}\hbox{-} 1\right)}^{\mathrm{exo}}+\frac{k_{\mathrm{on}\hbox{-} \mathrm{i}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}\right)\\ {}-{k}_{\mathrm{off}\hbox{-} \mathrm{i}}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}-\frac{1}{\tau}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}\end{array}\hfill \\ {}\hfill {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(16)
iii. Subcompartment 5
Endogenous IgG
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}}{\operatorname{d}t}\\ {}=\frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 4}^{\mathrm{endo}}-\frac{k_{\mathrm{on}\hbox{-} 5}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\right)+{k}_{\mathrm{off}\hbox{-} 5}\\ {}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}-\frac{{\mathrm{CL}}_{\mathrm{Proteolysis}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}\mathrm{ss}\hfill \end{array} $$
(17)
Exogenous mAb
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\operatorname{END} Organ-5}^{\mathrm{exo}}}{\operatorname{d}t}\\ {}=\frac{1}{\tau}\times {A}_{\operatorname{END} Organ-4}^{\mathrm{exo}}-\frac{k_{\operatorname{on}-5}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\operatorname{END} Organ-5}^{\mathrm{exo}}\times \left({\operatorname{Rtotal}}_{Organ-5}-{\operatorname{ARCPX}}_{\operatorname{Organ}-5}^{\mathrm{exo}}-{\operatorname{ARCPX}}_{\operatorname{Organ}-5}^{\mathrm{endo}}\right)+{k}_{\operatorname{off}-5}\\ {}\times {\operatorname{ARCPX}}_{\operatorname{Organ}-5}^{\mathrm{exo}}-\frac{{\operatorname{CL}}_{\mathrm{Proteolysis}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\operatorname{END} Organ-5}^{\mathrm{exo}}\end{array}\hfill \\ {}\hfill {A}_{\operatorname{END} Organ-5}^{\mathrm{exo}}\operatorname{IC}=0\hfill \end{array} $$
(18)
Endogenous IgG-FcRn complex
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}}{\operatorname{d}t}\\ {}=\frac{1}{\tau}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 4}^{\mathrm{endo}}+\frac{k_{\mathrm{on}\hbox{-} 5}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\right)\\ {}-{k}_{\mathrm{off}\hbox{-} 5}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}\end{array}\hfill \\ {}\hfill {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}\mathrm{IC}={\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}\mathrm{ss}\hfill \end{array} $$
(19)
Exogenous mAb-FcRn complex
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}}{\operatorname{d}t}\\ {}=\frac{1}{\tau}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 4}^{\mathrm{exo}}+\frac{k_{\mathrm{on}\hbox{-} 5}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\right)\\ {}-{k}_{\mathrm{off}\hbox{-} 5}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\end{array}\hfill \\ {}\hfill {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(20)
III. Lymph Node
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{LN}}^{\mathrm{J}}}{\operatorname{d}t}\\ {}=\left(1-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{Lung}}}{V_{\mathrm{ISF}}^{\mathrm{Lung}}}\times {A}_{\mathrm{ISF}\ \mathrm{Lung}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{Liver}}}{V_{\mathrm{ISF}}^{\mathrm{Liver}}}\times {A}_{\mathrm{ISF}\ \mathrm{Liver}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{GIT}}}{V_{\mathrm{ISF}}^{\mathrm{GIT}}}\times {A}_{\mathrm{ISF}\ \mathrm{GIT}}^{\mathrm{J}}+\left(1\right.\\ {}\left.-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{Spleen}}}{V_{\mathrm{ISF}}^{\mathrm{Spleen}}}\times {A}_{\mathrm{ISF}\ \mathrm{Spleen}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{Heart}}}{V_{\mathrm{ISF}}^{\mathrm{Heart}}}\times {A}_{\mathrm{ISF}\ \mathrm{Heart}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{Kidney}}}{V_{\mathrm{ISF}}^{\mathrm{Kidney}}}\times {A}_{\mathrm{ISF}\ \mathrm{Kidney}}^{\mathrm{J}}+\left(1\right.\\ {}\left.-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{Skin}}}{V_{\mathrm{ISF}}^{\mathrm{Skin}}}\times {A}_{\mathrm{ISF}\ \mathrm{Skin}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{Muscle}}}{V_{\mathrm{ISF}}^{\mathrm{Muscle}}}\times {A}_{\mathrm{ISF}\ \mathrm{Muscle}}^{\mathrm{J}}-\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{LN}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{LN}}^{\mathrm{endo}}\operatorname{ss};{A}_{\mathrm{LN}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(21)
Appendix 2: Fast Endosomal Transfer and Rapid Binding Assumptions
Transfer of mAb/IgG between endosomal compartments is fast relative to the time scale of other processes such as changes in plasma and lymph as well as the rate of binding of mAb/IgG to FcRn. The assumption that the endosomal transfer rate is faster than FcRn binding process holds true for earlier compartments where FcRn binding is considered negligible (in the first endosomal subcompartment) or low (in intermediate compartments). As the drug is transferred to later compartments, rate of binding increases and thus rapid binding assumption is applied to the last compartment where the majority of binding to FcRn takes place. Physiologically these 2 processes (transfer and binding) might interfere with each other. However, since these 2 assumptions (i.e., fast endosomal transfer and rapid binding) are applied sequentially, the 2 assumptions do not contradict each other, at least from a theoretical aspect.
Assumption: Endosomal transfer of mAb/IgG between endosomal compartments is very fast relative to the time scale of other processes:
It can be shown that input in to the first endosomal compartment will be transferred to the terminal compartment as τ → 0 (Please refer to Appendix 9),
$$ \frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 4}\to \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}+\frac{C{L}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}\;\mathrm{as}\kern0.37em \tau \to 0 $$
(23)
Thus, equation for free mAb/IgG in the terminal compartment can be expressed as:
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}}{\operatorname{d}t}=\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{exo}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{exo}}-\frac{k_{\mathrm{on}\hbox{-} 5}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}\right.\hfill \\ {}\left.-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\right)+{k}_{\mathrm{off}\hbox{-} 5}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}-\frac{{\mathrm{CL}}_{\mathrm{Proteolysis}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\hfill \end{array} $$
(24)
and the equation for complex mAb/IgG in the terminal compartment can be expressed as:
$$ \begin{array}{l}\frac{\operatorname{d}{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}}{\operatorname{d}t}=\frac{k_{\mathrm{on}\hbox{-} 5}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\right)-{k}_{\mathrm{off}\hbox{-} 5}\hfill \\ {}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {\operatorname{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\hfill \end{array} $$
(25)
Assumption: Free drug, the target and the complex are at rapid equilibrium meaning that the binding and dissociation rates are much faster than other processes (18).
Thus,
$$ \begin{array}{l}\frac{k_{\mathrm{on}\hbox{-} 5}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\right)-{k}_{\mathrm{off}\hbox{-} 5}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\hfill \\ {}=0\hfill \end{array} $$
(26)
And
$$ {k}_{\mathrm{off}\hbox{-} 5}/\frac{k_{\mathrm{on}\hbox{-} 5}}{V_{\mathrm{END}}^{\mathrm{Organ}}}={\mathrm{KD}}_{\mathrm{END}} $$
(27)
Solve for ARCPX
exoOrgan ‐ 5
$$ {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}=\frac{A_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}\right)}{{\mathrm{KD}}_{\mathrm{END}}+{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}} $$
(28)
Similarly,
$$ {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}=\frac{A_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\right)}{{\mathrm{KD}}_{\mathrm{END}}+{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{endo}}} $$
(29)
Substitute ARCPX
endoOrgan ‐ 5
in Eq. 27 to solve for ARCPX
exoOrgan ‐ 5
in terms of the free amounts of endogenous (A
endoEND Organ ‐ 5
) IgG and exogenous mAb (A
exoEND Organ ‐ 5
)
$$ {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}=\frac{A_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}\times {\mathrm{KD}}_{\mathrm{END}}\ }{\left[{\mathrm{KD}}_{\mathrm{END}}+{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\right]\times \left[{\mathrm{KD}}_{\mathrm{END}}+{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}\right]-{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{exo}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{endo}}} $$
(30)
and A
END Organ ‐ i and A
endoEND Organ ‐ i
are negligible compared to KDEND (A
exoEND Organ ‐ 5
< < KDEND and A
endoEND Organ ‐ 5
< < KDEND) (Please refer to Supplementary Figure 2)
Thus, Eq. 29 for ARCPX
JOrgan ‐ 5
can be simplified to
$$ {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}=\frac{A_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}}{{\mathrm{KD}}_{\mathrm{END}}\ } $$
(31)
Equations derived for ARCPX
JOrgan ‐ 5
showed that the IgG/mAb-FcRn complex is proportional to the free IgG/mAb. In the following section, equations for free IgG/mAb (Eq. 27) and complex (Eq. 28) are added to get A
JTotal END Organ ‐ 5
$$ {\mathrm{ARCPX}}_{\mathrm{Total}\ \mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}={A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}+{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{J}} $$
(32)
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{Total}\ \mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}}{\operatorname{d}t}\hfill \\ {}=\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}-\frac{{\mathrm{CL}}_{\mathrm{Proteolysis}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\hfill \\ {}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}\hfill \end{array} $$
(33)
Assumption: total mAb/IgG in compartment 5 is in equilibrium, i.e.
$$ \frac{\operatorname{d}{A}_{\mathrm{Total}\ \mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}}{\operatorname{d}t}=0 $$
(34)
Consequently,
$$ \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}-\frac{{\mathrm{CL}}_{\mathrm{Proteolysis}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}=0 $$
(35)
Substituting ARCPX
JOrgan ‐ 5
by Eq. 31 allows one to solve Eq. 43 for A
END Organ ‐ 5
$$ {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}=\frac{\left(\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}\right)}{\left(\frac{{\mathrm{CL}}_{\mathrm{Proteolysis}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times \frac{{\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}}{{\mathrm{KD}}_{\mathrm{END}}\ }\right)} $$
(36)
Substituting A
JEND Organ ‐ 5
from Eqs. 38 and 34 allows solving for ARCPX
JOrgan ‐ 5
in terms of vascular and interstitial amounts
$$ {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}={A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}\times \frac{\frac{{\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}}{{\mathrm{KD}}_{\mathrm{END}}}\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}}{\frac{{\mathrm{CL}}_{\mathrm{Proteolysis}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times \frac{{\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}}{{\mathrm{KD}}_{\mathrm{END}}}}+{A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}\times \frac{\frac{{\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}}{{\mathrm{KD}}_{\mathrm{END}}}\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}}{\frac{{\mathrm{CL}}_{\mathrm{Proteolysis}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times \frac{{\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 5}}{{\mathrm{KD}}_{\mathrm{END}}\ }} $$
(37)
Let the terms multiplying A
JVAS Organ
and A
JISF Organ
be k
1 and k
2, respectively. Thus,
$$ {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 5}^{\mathrm{J}}={A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}\times {k}_1+{A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}\times {k}_2 $$
(38)
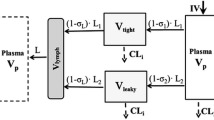
Substitute ARCPXOrgan ‐ 5 in the equation for vascular and interstitial compartments (Please refer to Fig. 3):
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}}{\operatorname{d}t}=\frac{Q_{\mathrm{Organ}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-\frac{Q_{\mathrm{Organ}}-{L}_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times \hfill \\ {}{A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\mathrm{FR}\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_1\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\mathrm{FR}\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_2\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}\hfill \end{array} $$
(39)
Introduce the input term from the vascular to the interstitial compartment: (This term appears in the interstitial compartment)
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}}{\operatorname{d}t}=\frac{Q_{\mathrm{Organ}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-\frac{Q_{\mathrm{Organ}}-{L}_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times \hfill \\ {}{A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\mathrm{FR}\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_1\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\mathrm{FR}\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_2\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}-\left(1-\mathrm{FR}\right)\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_1\times \hfill \\ {}{A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\left(1-\mathrm{FR}\right)\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_1\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}\hfill \end{array} $$
(40)
which can be simplified to:
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Organ}}}{\operatorname{d}t}=\frac{Q_{\mathrm{Organ}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-\frac{Q_{\mathrm{Organ}}-{L}_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times \hfill \\ {}{A}_{\mathrm{VAS}\;\mathrm{Organ}}^{\mathrm{J}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_1\times {A}_{\mathrm{VAS}\;\mathrm{Organ}}^{\mathrm{J}}+\mathrm{FR}\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_2\times {A}_{\mathrm{ISF}\;\mathrm{Organ}}^{\mathrm{J}}-\left(1-\mathrm{FR}\right)\times \frac{C{L}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_1\times \hfill \\ {}{A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}\hfill \end{array} $$
(41)
A similar substitution of ARCPX
JOrgan ‐ 5
in the equation for the interstitial compartment yields:
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}}{\operatorname{d}t}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\operatorname{VAS} Organ}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\operatorname{ISF} Organ}^{\mathrm{J}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\operatorname{ISF} Organ}^{\mathrm{J}}+\hfill \\ {}\left(1-\operatorname{FR}\right)\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_1\times {A}_{\operatorname{VAS} Organ}^{\mathrm{J}}+\left(1-\operatorname{FR}\right)\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_2\times {A}_{\operatorname{ISF} Organ}^{\mathrm{J}}\hfill \end{array} $$
(42)
Introduce the input term from the interstitial to the vascular compartment: (This term appears in the vascular compartment and should be accounted for)
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\operatorname{ISF} Organ}^J}{\operatorname{d}t}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\operatorname{VAS} Organ}^J-\left(1-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\operatorname{ISF} Organ}^J-\frac{C{L}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\operatorname{ISF} Organ}^J+\hfill \\ {}\left(1-\mathrm{FR}\right)\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_1\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\left(1-\mathrm{FR}\right)\times \frac{C{L}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_2\times {A}_{\operatorname{ISF} Organ}^{\mathrm{J}}+ FR\times \frac{{\operatorname{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_2\times \hfill \\ {}{A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}-\mathrm{FR}\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_2\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}\hfill \end{array} $$
(43)
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Organ}}}{\operatorname{d}t}\hfill \\ {}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\operatorname{VAS} Organ}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\operatorname{ISF} Organ}^{\mathrm{J}}-\frac{{\operatorname{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\operatorname{ISF} Organ}^{\mathrm{J}}+\left(1\right.\hfill \\ {}\left.-\operatorname{FR}\right)\times \frac{{\operatorname{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_1\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_2\times {A}_{\operatorname{ISF} Organ}^{\mathrm{J}}-\operatorname{FR}\hfill \\ {}\times \frac{{\operatorname{CL}}_{Uptake}^{Organ}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_2\times {A}_{\operatorname{ISF} Organ}^{\mathrm{J}}\hfill \end{array} $$
(44)
Let \( \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_1 \) be a first-order input from the vascular compartment to itself (k
OrganVAS ‐ VAS
)
Let \( \mathrm{FR}\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_2 \) be a first-order input from interstitial compartment to vascular compartment (k
OrganISF ‐ VAS
)
Let \( \left(1-\mathrm{FR}\right)\times \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_1 \) be a first-order input from vascular compartment to interstitial compartment (k
OrganVAS ‐ ISF
)
Let \( \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {k}_2 \) be a first-order input from the interstitial compartment to itself (k
OrganISF ‐ ISF
).
The final equations for vascular and interstitial compartments can be written as:
A. Vascular Space
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}}{\operatorname{d}t}\hfill \\ {}=\frac{Q_{\mathrm{Organ}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}-\frac{Q_{\mathrm{Organ}}-{L}_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\hfill \\ {}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Organ}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Organ}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Organ}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}\hfill \end{array} $$
(45)
B. Interstitial Space
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}}{\operatorname{d}t}\hfill \\ {}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times \frac{L_{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}-\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}\hfill \\ {}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Organ}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{ISF}}^{\mathrm{Organ}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Organ}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}\hfill \end{array} $$
(46)
Appendix 3: Simplified Model Equations After Rapid Binding and Fast Endosomal Transfer Assumptions (Step 1)
I. plasma
Endogenous IgG
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{plasma}}^{\mathrm{endo}}}{\operatorname{d}t}\\ {}={K}_0\times {V}_{\mathrm{Plasma}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{endo}}-\frac{L_{\mathrm{GIT}}+{L}_{\mathrm{Spleen}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{endo}}-\frac{Q_{\mathrm{Liver}}+{Q}_{\mathrm{Heart}}+{Q}_{\mathrm{Kidney}}+{Q}_{\mathrm{Skin}}+{Q}_{\mathrm{Muscle}\ }}{V_{\mathrm{Plasma}}}\times \\ {}{A}_{\mathrm{Plasma}}^{\mathrm{endo}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}^{\mathrm{endo}}\times {F}_{\mathrm{return}\ }\end{array}\hfill \\ {}\hfill \mathrm{IC}={A}_{\mathrm{plasma}}^{\mathrm{endo}}\mathrm{SS}\hfill \end{array} $$
(47)
Exogenous mAb
$$ \begin{array}{ll}\frac{\operatorname{d}{A}_{\mathrm{plasma}}}{\operatorname{d}t}=\hfill & {k}_{VAS- circul.}^{\mathrm{Lung}}\times {A}_{\operatorname{VAS} Lung}-\frac{L_{\mathrm{GIT}}+{L}_{\mathrm{Spleen}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}\hfill \\ {}\hfill & -\frac{Q_{\mathrm{Liver}}+{Q}_{\mathrm{Heart}}+{Q}_{\mathrm{Kidney}}+{Q}_{\mathrm{Skin}}+{Q}_{\mathrm{Muscle}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}+\frac{1}{{\operatorname{Tau}}_{LN}}\times {A}_{\mathrm{LN}}\times {F}_{\mathrm{return}}\hfill \\ {}\hfill & \operatorname{IC}={\operatorname{Dose}}_{\mathrm{mAb}}\hfill \end{array} $$
(48)
II. Organs
A. Vascular Space
Equations for the vascular compartment in liver and lung are different from other organs.
i. lung
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}}{\operatorname{d}t}\\ {}={k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Liver}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Heart}}\times {A}_{\mathrm{VAS}\ \mathrm{Heart}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Kidney}}\times {A}_{\mathrm{VAS}\ \mathrm{Kidney}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Skin}}\times {A}_{\mathrm{VAS}\ \mathrm{Skin}}^{\mathrm{J}}\\ {}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Muscle}}\times {A}_{\mathrm{VAS}\ \mathrm{Muscle}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Lung}}\\ {}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Lung}}\times {A}_{\mathrm{ISF}\ \mathrm{Lung}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(49)
ii. liver
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}}{\operatorname{d}t}={k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{GIT}}\times {A}_{\mathrm{VAS}\ \mathrm{GIT}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Spleen}}\times {A}_{\mathrm{VAS}\ \mathrm{Spleen}}^{\mathrm{J}}+\frac{L_{\mathrm{GIT}}+{L}_{\mathrm{Spleen}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}+\frac{Q_{\mathrm{Liver}}-\left({Q}_{\mathrm{GIT}}+{Q}_{\mathrm{Spleen}}\right)}{V_{\mathrm{Plasma}}}\ast {A}_{Plasma}^{endo}-\\ {}{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Liver}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Liver}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Liver}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Liver}}\times \\ {}{A}_{\mathrm{VAS}\ \mathrm{Liver}}^J+{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Liver}}\times {A}_{\mathrm{ISF}\ \mathrm{Liver}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Liver}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(50)
iii. Other Organs (heart, kidney, skin, muscle, GIT, spleen)
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}}{\operatorname{d}t}\\ {}=\frac{Q_{\mathrm{Organ}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Organ}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Organ}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Organ}}\\ {}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Organ}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Organ}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Organ}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(51)
B. Interstitial Space (Applies for all organs including liver and lung, all termed “Organ”)
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}}{\operatorname{d}t}\\ {}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Organ}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Organ}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{EL}}^{\mathrm{Organ}}\\ {}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Organ}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{ISF}}^{\mathrm{Organ}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Organ}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(52)
III. Lymph Node
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{LN}}^{\mathrm{J}}}{\operatorname{d}t}\\ {}=\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Lung}}\times {A}_{\mathrm{ISF}\ \mathrm{Lung}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Liver}}\times {A}_{\mathrm{ISF}\ \mathrm{Liver}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{GIT}}\\ {}\times {A}_{\mathrm{ISF}\ \mathrm{GIT}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Spleen}}\times {A}_{\mathrm{ISF}\ \mathrm{Spleen}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Heart}}\times {A}_{\mathrm{ISF}\ \mathrm{Heart}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\\ {}\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Kidney}}\times {A}_{\mathrm{ISF}\ \mathrm{Kidney}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Skin}}\times {A}_{\mathrm{ISF}\ \mathrm{Skin}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Muscle}}\times {A}_{\mathrm{ISF}\ \mathrm{Muscle}}^{\mathrm{J}}\\ {}-\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{LN}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{LN}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{LN}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(53)
Appendix 4: Model Equations for Lumping of GIT and Spleen (Splanchnic) and Heart, Kidney, Skin, and Muscle (Visceral)
This is Step #2 in the model development. Please refer to Fig. 3 for model structure and Table I for model parameters.
I. plasma
Endogenous IgG
For the lumped compartment, the lymphatic can be described as the sum of flow for each individual organ as:
$$ \begin{array}{l}{L}_{\mathrm{Splanchnic}}={L}_{\mathrm{GIT}}+{L}_{\mathrm{Spleen}}\hfill \\ {}{L}_{\mathrm{Visceral}}={L}_{\mathrm{Heart}}+{L}_{\mathrm{Kidney}}+{L}_{\mathrm{Skin}}+{L}_{\mathrm{Muscle}\ }\hfill \end{array} $$
Similarly, the plasma flow for the lumped compartment can be described as:
$$ \begin{array}{l}{Q}_{\mathrm{Splanchnic}}={Q}_{\mathrm{GIT}}+{Q}_{\mathrm{Spleen}}\hfill \\ {}{Q}_{\mathrm{Visceral}}={Q}_{\mathrm{Heart}}+{Q}_{\mathrm{Kidney}}+{Q}_{\mathrm{Skin}}+{Q}_{\mathrm{Muscle}\ }\hfill \end{array} $$
Then the equation for endogenous IgG in plasma becomes:
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{plasma}}^{\mathrm{endo}}}{\operatorname{d}t}={K}_0\times {V}_{\mathrm{Plasma}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{endo}}-\frac{L_{\mathrm{Splanchnic}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{endo}}-\frac{Q_{\mathrm{Liver}}+{Q}_{\mathrm{Visceral}\ }}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{endo}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times \\ {}{A}_{\mathrm{LN}}^{\mathrm{endo}}\times {F}_{\mathrm{return}\ }\end{array}\hfill \\ {}\hfill IC={A}_{\mathrm{plasma}}^{\mathrm{endo}}\mathrm{SS}\hfill \end{array} $$
(54)
Exogenous mAb
$$ \begin{array}{c}\hfill \frac{\operatorname{d}{A}_{\mathrm{plasma}}}{\operatorname{d}t}={k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}-\frac{L_{\mathrm{Splanchnic}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}-\frac{Q_{\mathrm{Liver}}+{Q}_{\mathrm{Visceral}\ }}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}\times {F}_{\mathrm{return}\ }\hfill \\ {}\hfill \mathrm{IC}={\mathrm{Dose}}_{\mathrm{mAb}}\hfill \end{array} $$
(55)
II. Organs
A. Vascular Space
Equations for the vascular compartment in liver and lung are different from other organs.
i. lung
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}}{\operatorname{d}t}\\ {}={k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Liver}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}\\ {}\begin{array}{c}\hfill -\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Lung}}\times {A}_{\mathrm{ISF}\ \mathrm{Lung}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}\hfill \\ {}\hfill {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array}\end{array} $$
(56)
ii. Liver
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}}{\operatorname{d}t}={k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}+\frac{L_{\mathrm{Splanchnic}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}+\frac{Q_{\mathrm{Liver}}-\left({Q}_{\mathrm{Splanchnic}}\right)}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Liver}}\times \\ {}{A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Liver}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Liver}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Liver}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}+\\ {}\ {k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Liver}}\times {A}_{\mathrm{ISF}\ \mathrm{Liver}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Liver}}\times {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Liver}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(57)
iii. splanchnic (GIT and spleen lumped)
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}}{\operatorname{d}t}=\frac{Q_{\mathrm{Splanchnic}}\ }{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}-\left(1-\right.\\ {}\left.{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}-\\ {}{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}\\ {}{A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{exo}}\mathrm{IC}=0\end{array} $$
(58)
iv. visceral (heart, kidney, skin, muscle lumped)
$$ \begin{array}{c}\hfill \frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}}{\operatorname{d}t}=\frac{Q_{\mathrm{Visceral}}\ }{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times \hfill \\ {}\hfill {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Visceral}}\times {A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}\hfill \\ {}\hfill {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(59)
B. Interstitial Space
i. lung, liver
(All organs but splanchnic and visceral)
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}}{\operatorname{d}t}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\operatorname{LY} VAS- ISF}^{\mathrm{Organ}}\times {A}_{\operatorname{VAS} Organ}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\operatorname{LY} ISF- LN}^{\mathrm{Organ}}\times {A}_{\operatorname{ISF} Organ}^{\mathrm{J}}-{k}_{\operatorname{ISF}- EL}^{\mathrm{Organ}}\times \\ {}{A}_{\operatorname{ISF} Organ}^{\mathrm{J}}+{k}_{\operatorname{VAS}- ISF}^{\mathrm{Organ}}\times {A}_{\operatorname{VAS} Organ}^{\mathrm{J}}+{k}_{\operatorname{ISF}- ISF}^{\mathrm{Organ}}\times {A}_{\operatorname{ISF} Organ}^{\mathrm{J}}-{k}_{\operatorname{ISF}- VAS}^{\mathrm{Organ}}\times {A}_{\operatorname{ISF} Organ}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\operatorname{ISF} Organ}^{\mathrm{endo}}\operatorname{IC}={A}_{\operatorname{ISF} Organ}^{\mathrm{endo}}\operatorname{ss};{A}_{\operatorname{ISF} Organ}^{\mathrm{exo}}\operatorname{IC}=0\hfill \end{array} $$
(60)
ii. splanchnic (GIT and spleen lumped)
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{d{A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}}{ dt}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}\\ {}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{EL}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{ISF}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Splanchnic}}\times \\ {}{A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(61)
iii. visceral (heart, kidney, skin, muscle lumped)
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}}{\operatorname{d}t}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Visceral}}\times {A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{EL}}^{\mathrm{Visceral}}\times \\ {}{A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{ISF}}^{\mathrm{Visceral}}\times {A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Visceral}}\times {A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(62)
III. Lymph Node
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{LN}}^{\mathrm{J}}}{\operatorname{d}t}\\ {}=\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Lung}}\times {A}_{\mathrm{ISF}\ \mathrm{Lung}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Liver}}\times {A}_{\mathrm{ISF}\ \mathrm{Liver}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\\ {}\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Visceral}}\times {A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}-\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{LN}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{LN}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{LN}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(63)
Appendix 5: Model Equations after fast transfer from liver to lung (Step#3)
Liver compartment no longer exists and the appearance of \( \frac{Q_{\mathrm{Liver}}}{V_{\mathrm{Plasma}}} \) is solely indicative of the transfer from plasma to lung. Finally, splanchnic is now positioned to be parallel to other organs, i.e., visceral.
I. plasma
Endogenous IgG
$$ \begin{array}{l}\begin{array}{l}\frac{d{A}_{\mathrm{plasma}}^{\mathrm{endo}}}{ dt}={K}_0\times {V}_{\mathrm{Plasma}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{endo}}-\frac{Q_{\mathrm{Splanchnic}}+{Q}_{\mathrm{Visceral}}+{Q}_{\mathrm{Liver}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{endo}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}^{\mathrm{endo}}\times \\ {}\ {F}_{\mathrm{return}\ }\end{array}\hfill \\ {}\hfill \mathrm{IC}={A}_{\mathrm{plasma}}^{\mathrm{endo}}\mathrm{SS}\hfill \end{array} $$
(64)
Exogenous mAb
$$ \begin{array}{c}\hfill \frac{d{A}_{\mathrm{plasma}}}{ dt}={k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}-\frac{Q_{\mathrm{Splanchnic}}+{Q}_{\mathrm{Visceral}}+{Q}_{\mathrm{Liver}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}\times {F}_{\mathrm{return}\ }\hfill \\ {}\hfill \mathrm{IC}={\mathrm{Dose}}_{\mathrm{mAb}}\hfill \end{array} $$
(65)
II. Organs
A. Vascular Space
Equations for the vascular compartment in lung are different from other organs.
i. lung
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{d{A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}}{ dt}={k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}+\frac{Q_{\mathrm{Liver}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Lung}}\times \\ {}{A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}+\\ {}{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Lung}}\times {A}_{\mathrm{ISF}\ \mathrm{Lung}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(66)
ii. splanchnic (GIT and spleen lumped)
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{endo}}}{\operatorname{d}t}=\frac{Q_{\mathrm{Splanchnic}}\ }{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}-\left(1-\right.\\ {}\left.{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}-\\ {}{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Splanchnic}}\times {A}_{\operatorname{VAS}\kern0.50em Splanchnic}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\operatorname{VAS}\kern0.5em Splanchnic}^{\mathrm{endo}}\operatorname{IC}={A}_{\mathrm{VAS}\kern0.5em \mathrm{Splanchnic}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(67)
iii. visceral (heart, kidney, skin, muscle lumped)
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}}{\operatorname{d}t}=\frac{Q_{\mathrm{Visceral}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times \\ {}{k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Visceral}}\times {A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(68)
B. Interstitial Space
i. lung
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Lung}}^{\mathrm{J}}}{\operatorname{d}t}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Lung}}\times {A}_{\mathrm{ISF}\ \mathrm{Lung}}^{\mathrm{J}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{EL}}^{\mathrm{Lung}}\times \\ {}{A}_{\mathrm{ISF}\ \mathrm{Lung}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{ISF}}^{\mathrm{Lung}}\times {A}_{\mathrm{ISF}\ \mathrm{Lung}}^{\mathrm{J}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Lung}}\times {A}_{\mathrm{ISF}\ \mathrm{Lung}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(69)
ii. splanchnic (GIT and spleen lumped)
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}}{\operatorname{d}t}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}-\\ {}{k}_{\mathrm{ISF}\hbox{-} \mathrm{EL}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{VAS}\ \mathrm{Splanchnic}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{ISF}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Splanchnic}}\times \\ {}{A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(70)
iii. visceral (heart, kidney, skin, muscle lumped)
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\operatorname{ISF} Visceral}^{\mathrm{J}}}{\operatorname{d}t}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Visceral}}\times {A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{EL}}^{\mathrm{Visceral}}\times \\ {}{A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Visceral}}\times {A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{ISF}}^{\mathrm{Visceral}}\times {A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Visceral}}\times {A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(71)
III. Lymph Node
Endogenous IgG
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{LN}}^{\mathrm{J}}}{\operatorname{d}t}=\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Lung}}\times {A}_{\mathrm{ISF}\ \mathrm{Lung}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Splanchnic}}\times {A}_{\mathrm{ISF}\ \mathrm{Splanchnic}}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times \\ {}{k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Visceral}}\times {A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{J}}-\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{LN}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{LN}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{LN}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(72)
Appendix 6: Model Equations for Lumping Splanchnic and Visceral into Peripheral (Step#4)
I. plasma
Endogenous IgG
$$ \begin{array}{c}\hfill \frac{\operatorname{d}{A}_{\mathrm{plasma}}^{\mathrm{endo}}}{\operatorname{d}t}={K}_0\times {V}_{\mathrm{Plasma}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{endo}}-\frac{Q_{\mathrm{Peripheral}}+{Q}_{\mathrm{Liver}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{endo}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}^{\mathrm{endo}}\times {F}_{\mathrm{return}\ }\hfill \\ {}\hfill \mathrm{IC}={A}_{\mathrm{plasma}}^{\mathrm{endo}}\mathrm{SS}\hfill \end{array} $$
(73)
Exogenous mAb
$$ \begin{array}{c}\hfill \frac{\operatorname{d}{A}_{\mathrm{plasma}}}{\operatorname{d}t}={k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Lung}}\times {A}_{\mathrm{VAS}\ \mathrm{Lung}}-\frac{Q_{\mathrm{Peripheral}}+{Q}_{\mathrm{Liver}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}\times {F}_{\mathrm{return}\ }\hfill \\ {}\hfill \mathrm{IC}={\mathrm{Dose}}_{\mathrm{mAb}}\hfill \end{array} $$
(74)
II. Organs
A. Vascular Space
Equations for the vascular compartment in lung are different from other organs.
i. lung
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Lung}}^{\mathrm{J}}}{\operatorname{d}t}={k}_{VAS- circul.}^{\mathrm{Peripheral}}\times {A}_{\operatorname{VAS} Peripheral}^{\mathrm{J}}+\frac{Q_{\mathrm{Liver}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-{k}_{VAS- circul.}^{\mathrm{Lung}}\times {A}_{\operatorname{VAS} Lung}^{\mathrm{J}}-{k}_{\operatorname{VAS}- EL}^{\mathrm{Lung}}\times \\ {}\ {A}_{\operatorname{VAS} Lung}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\operatorname{LY} VAS- ISF}^{\mathrm{Lung}}\times {A}_{\operatorname{VAS} Lung}^{\mathrm{J}}+{k}_{\operatorname{VAS}- VAS}^{\mathrm{Lung}}\times {A}_{\operatorname{VAS} Lung}^{\mathrm{J}}+{k}_{\operatorname{ISF}- VAS}^{\mathrm{Lung}}\times {A}_{\operatorname{ISF} Lung}^{\mathrm{J}}\\ {}-{k}_{\operatorname{VAS}- ISF}^{\mathrm{Lung}}\times {A}_{\operatorname{VAS} Lung}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\operatorname{VAS} Lung}^{\mathrm{endo}}\mathrm{IC}={A}_{\operatorname{VAS} Lung}^{\mathrm{endo}}\mathrm{ss};{A}_{\operatorname{VAS} Lung}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(75)
ii. Peripheral (splanchnic and visceral lumped)
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}}{\operatorname{d}t}=\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}-\left(1-\right.\\ {}\left.\ {\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}^{\mathrm{J}}-\\ {}{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(76)
B. Interstitial Space
Peripheral
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{d{A}_{\operatorname{ISF} Peripheral}^{\mathrm{J}}}{ dt}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\operatorname{LY} VAS- ISF}^{\mathrm{Peripheral}}\times {A}_{\operatorname{VAS} Peripheral}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\operatorname{LY} ISF- LN}^{\mathrm{Peripheral}}\times {A}_{\operatorname{ISF} Peripheral}^{\mathrm{J}}-\\ {}{k}_{\operatorname{ISF}- EL}^{\mathrm{Peripheral}}\times {A}_{\operatorname{ISF} Peripheral}^{\mathrm{J}}+{k}_{\operatorname{VAS}- ISF}^{\mathrm{Peripheral}}\times {A}_{\operatorname{VAS} Peripheral}^{\mathrm{J}}+{k}_{\operatorname{ISF}- ISF}^{\mathrm{Peripheral}}\times {A}_{\operatorname{ISF} Peripheral}^{\mathrm{J}}-{k}_{\operatorname{ISF}- VAS}^{\mathrm{Peripheral}}\times \\ {}{A}_{\operatorname{ISF} Peripheral}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}^{\mathrm{endo}}\operatorname{IC}={A}_{\mathrm{ISF}\ Visceral}^{\mathrm{endo}}\operatorname{ss};{A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(77)
III. Lymph Node
Endogenous IgG
$$ \begin{array}{c}\hfill \frac{\operatorname{d}{A}_{\mathrm{LN}}^{\mathrm{J}}}{\operatorname{d}t}=\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\operatorname{LY} ISF- LN}^{\mathrm{Lung}}\times {A}_{\operatorname{ISF} Lung}^{\mathrm{J}}+\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\operatorname{LY}\kern0.5em ISF- LN}^{\mathrm{Peripheral}}\times {A}_{\operatorname{ISF} Peripheral}^{\mathrm{J}}-\frac{1}{{\operatorname{Tau}}_{LN}}\times {A}_{\mathrm{LN}}^{\mathrm{J}}\hfill \\ {}\hfill {A}_{\mathrm{LN}}^{\mathrm{endo}}\operatorname{IC}={A}_{\mathrm{LN}}^{\mathrm{endo}}\operatorname{ss};{A}_{\mathrm{LN}}^{\mathrm{exo}}\operatorname{IC}=0\hfill \end{array} $$
(78)
Appendix 7: Model Equations for Fast Transfer from Lung to Plasma (Step#5)
(Figure 4d)
I. plasma
Endogenous IgG
$$ \begin{array}{c}\hfill \frac{\operatorname{d}{A}_{\mathrm{plasma}}^{\mathrm{endo}}}{\operatorname{d}t}={K}_0\times {V}_{\mathrm{Plasma}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{endo}}-\frac{Q_{\mathrm{Peripheral}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{endo}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}^{\mathrm{endo}}\times {F}_{\mathrm{return}\ }\hfill \\ {}\hfill \mathrm{IC}={A}_{\mathrm{plasma}}^{\mathrm{endo}}\mathrm{SS}\hfill \end{array} $$
(79)
Exogenous mAb
$$ \begin{array}{c}\hfill \frac{\operatorname{d}{A}_{\mathrm{plasma}}}{\operatorname{d}t}={k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}-\frac{Q_{\mathrm{Peripheral}}}{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}\times {F}_{\mathrm{return}\ }\hfill \\ {}\hfill \mathrm{IC}={\mathrm{Dose}}_{\mathrm{mAb}}\hfill \end{array} $$
(80)
II. Peripheral
A. Vascular Space
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}}{\operatorname{d}t}=\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}\times {A}_{\mathrm{Plasma}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}\\ {}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}^{\mathrm{J}}-\\ {}\ {k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{VAS}\ \mathrm{Visceral}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(81)
B. Interstitial Space
Peripheral
$$ \begin{array}{c}\hfill \begin{array}{l}\frac{d{A}_{\mathrm{ISF}\ \mathrm{Peripheral}}^{\mathrm{J}}}{ dt}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}^{\mathrm{J}}-\\ {}{k}_{\mathrm{ISF}\hbox{-} \mathrm{EL}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}^{\mathrm{J}}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}^{\mathrm{J}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}^{\mathrm{J}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Peripheral}}\times \\ {}{A}_{\mathrm{ISF}\ \mathrm{Peripheral}}^{\mathrm{J}}\end{array}\hfill \\ {}\hfill {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{ISF}\ \mathrm{Visceral}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(82)
III. Lymph Node
$$ \begin{array}{c}\hfill \frac{\operatorname{d}{A}_{\mathrm{LN}}^{\mathrm{J}}}{\operatorname{d}t}=\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}^{\mathrm{J}}-\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}^{\mathrm{J}}\hfill \\ {}\hfill {A}_{\mathrm{LN}}^{\mathrm{endo}}\mathrm{IC}={A}_{\mathrm{LN}}^{\mathrm{endo}}\mathrm{ss};{A}_{\mathrm{LN}}^{\mathrm{exo}}\mathrm{IC}=0\hfill \end{array} $$
(83)
Appendix 8: Rapid equilibrium between plasma and Vascular compartments forming Central compartment (Model Equations) (Step#6)
(Figure 5) (Supplementary Table 4)
In this step, rapid equilibrium from plasma to vascular compartment is assumed. The rate of transfer from plasma to vascular compartment of Peripheral organs \( \left(\frac{Q_{\mathrm{Peripheral}}}{V_{\mathrm{Plasma}}}\right) \) is of the same order as transfer rate from the vascular compartment of Peripheral organs to plasma (k
PeripheralVAS ‐ circul.
). These two rates are assumed to be faster than rates governing transfer between vascular and interstitial spaces:
$$ \begin{array}{l}\begin{array}{cccccc}\hfill {k}_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}\gg \hfill & \hfill {k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Peripheral}},\hfill & \hfill {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}},\hfill & \hfill {k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Peripheral}},\hfill & \hfill {k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}.}^{\mathrm{Peripheral}},\hfill & \hfill {k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}\hfill \end{array}\\ {}\begin{array}{cccccc}\hfill \begin{array}{cccccccccc}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \frac{1}{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}\sim 0\hfill & \hfill \hfill \end{array}\end{array} $$
(Table III):
Further, we assume that the vascular compartment is in rapid equilibrium such that the rate of change is negligible (i.e., \( \frac{\mathrm{d}{A}_{\mathrm{VAS}\ \mathrm{Peripheral}}}{\mathrm{d}t} \) is much smaller than the right hand side of the differential equation)
Dividing Eqs. 114/115 by k
PeripheralVAS ‐ circul.
leads to
$$ 0=\frac{\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}}{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}\ast {A}_{\mathrm{Plasma}}-{A}_{\mathrm{VAS}\ \mathrm{Peripheral}}-0-0+0+0-0 $$
(84)
After rearrangement
$$ {A}_{\mathrm{Plasma}}=\frac{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}{\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}}\times {A}_{\mathrm{VAS}\ \mathrm{Peripheral}} $$
(85)
Introduce a new variable for the total amount in vascular and plasma compartments (Central)
$$ {A}_{\mathrm{Central}}={A}_{\mathrm{Plasma}}+{A}_{\mathrm{VAS}\ \mathrm{Peripheral}} $$
(86)
Then
$$ {A}_{\mathrm{Plasma}}=\frac{A_{\mathrm{Central}}}{\ \left(1+\frac{\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}}{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}\right)} $$
(87)
and
$$ {A}_{\mathrm{VAS}\ \mathrm{Peripheral}}=\frac{A_{\mathrm{Central}}}{\ \left(1+\frac{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}{\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}}\right)} $$
(88)
Adding differential equations for vascular and plasma compartments to get the differential equation for A
Central results in
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{Central}}}{\operatorname{d}t}=-{k}_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Peripheral}}\times \frac{A_{\mathrm{Central}}}{\ \left(1+\frac{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}{\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}}\right)}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}\times \frac{A_{\mathrm{Central}}}{\ \left(1+\frac{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}{\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}}\right)}+{k}_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Peripheral}}\times \\ {}\frac{A_{\mathrm{Central}}}{\left(1+\frac{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}{\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}}\right)}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{VAS}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}-{k}_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}\times \frac{A_{\mathrm{Central}}}{\ \left(1+\frac{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}{\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}}\right)}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}\times {F}_{\mathrm{return}\ }\end{array} $$
(89)
Regroup rates and change parameter names to reflect new model structure
Let
$$ {k}_{\mathrm{EL}}^{\mathrm{Central}}=\frac{k_{\mathrm{VAS}\hbox{-} \mathrm{EL}}^{\mathrm{Peripheral}}}{\ \left(1+\frac{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}{\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}}\right)} $$
be elimination rate from the central compartment
Let \( \frac{k_{\mathrm{LY}\ \mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}}{\left(1+\frac{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}{\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}}\right)} \) be transfer rate from the central to interstitial (i.e., peripheral) compartment via lymphatic flow
Let \( \frac{k_{\mathrm{VAS}\hbox{-} \mathrm{VAS}}^{\mathrm{Peripheral}}}{\left(1+\frac{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}{\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}}\right)} \) first-order input from central compartment to itself which reflects the impact of recycled drug from endosomal compartment
Let \( \frac{k_{\mathrm{VAS}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}}{\left(1+\frac{k_{\mathrm{VAS}\hbox{-} \mathrm{circul}.}^{\mathrm{Peripheral}}}{\frac{Q_{\mathrm{Peripheral}}\ }{V_{\mathrm{Plasma}}}}\right)} \) be first-order input from central to interstitial compartment
Let k
PeripheralISF ‐ VAS
be termed k
PeripheralISF ‐ Central
to reflect the updated model structure
Thus equations for Central, Peripheral and lymph node compartments are provided as follows,
Central Compartment
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{Central}}\ }{\operatorname{d}t}=-{k}_{\mathrm{EL}}^{\mathrm{Central}}\times {A}_{\mathrm{Central}}-\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\hbox{-} \mathrm{ISF}}^{\mathrm{Central}}\times {A}_{\mathrm{Central}}+{k}_{\mathrm{Central}}^{\mathrm{Central}}\times {A}_{\mathrm{Central}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{Central}}^{\mathrm{Peripheral}}\times \\ {}{A}_{\mathrm{ISF}\ \mathrm{Peripheral}}-{k}_{\mathrm{Central}\hbox{-} \mathrm{ISF}}^{\mathrm{Central}}\times {A}_{\mathrm{Central}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}\times {F}_{\mathrm{return}\ }\end{array} $$
(90)
Peripheral Compartment
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Peripheral}}}{\operatorname{d}t}=\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\hbox{-} \mathrm{ISF}}^{\mathrm{Central}}\times {A}_{\mathrm{Central}}-\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{EL}}^{\mathrm{Peripheral}}\\ {}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}+{k}_{\mathrm{Central}\hbox{-} \mathrm{ISF}}^{\mathrm{Central}}\times {A}_{\mathrm{Central}}+{k}_{\mathrm{ISF}\hbox{-} \mathrm{ISF}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}-{k}_{\mathrm{ISF}\hbox{-} \mathrm{Central}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}\end{array} $$
(91)
Lymph Node
$$ \frac{d{A}_{\mathrm{LN}}}{\operatorname{d}t}=\left(1-{\sigma}_{LY}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}-\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}} $$
(92)
Rearrange equation for A
Central and A
ISF Peripheral
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{Central}}\ }{\operatorname{d}t}=-\left({k}_{\mathrm{EL}}^{\mathrm{Central}}-{k}_{\mathrm{Central}}^{\mathrm{Central}}\right)\times {A}_{\mathrm{Central}}-\left(\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\mathrm{LY}\hbox{-} \mathrm{ISF}}^{\mathrm{Central}}+{k}_{\mathrm{Central}\hbox{-} \mathrm{ISF}}^{\mathrm{Central}}\right)\times {A}_{\mathrm{Central}}+\\ {}{k}_{\mathrm{ISF}\hbox{-} \mathrm{Central}}^{\mathrm{Peripheral}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}+\frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}\times {A}_{\mathrm{LN}}\times {F}_{\mathrm{return}\ }\end{array} $$
(93)
$$ \begin{array}{l}\frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Peripheral}}}{\operatorname{d}t}=\\ {}\ \left(\left(1-{\sigma}_{\mathrm{VAS}}\right)\times {k}_{\operatorname{LY}- ISF}^{\mathrm{Central}}+{k}_{\operatorname{Central}- ISF}^{\mathrm{Central}}\right)\times {A}_{\mathrm{Central}}-\left(\left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\operatorname{LY}\kern0.5em ISF- LN}^{\mathrm{Peripheral}}+{k}_{\operatorname{ISF}- Central}^{\mathrm{Peripheral}}\right)\times \\ {}{A}_{\operatorname{ISF}\kern0.5em Peripheral}-\left({k}_{\operatorname{ISF}- EL}^{\mathrm{Peripheral}}-{k}_{\operatorname{ISF}- ISF}^{\mathrm{Peripheral}}\right)\times {A}_{\operatorname{ISF}\kern0.5em Peripheral}\end{array} $$
(94)
Subsequently, the following rearrangements and assumptions were made:
-
1-
Rearrangement: Subtracting the rate of recycling of mAb from the endosomes back to the central compartment (k
CentralCentral
, 5.8E-06 h−1) which acts as an input to the central compartment from the central compartment elimination, (k
CentralEL
, 6.1E-06 h−1) results in a slower elimination rate termed, k
CEL
(3E-07 h−1).
$$ {k}_{\mathrm{EL}}^{\mathrm{C}\mathrm{entral}}-{k}_{\mathrm{C}\mathrm{entral}}^{\mathrm{C}\mathrm{entral}}={k}_{\mathrm{EL}}^{\mathrm{C}} $$
(95)
Similarly, subtracting the rate of recycling of mAb from the endosomes back to the peripheral compartment (k
PeripheralPeripheral
, 2.73E−06 h−1) from the peripheral compartment elimination, k
PeripheralEL
(2.85E−06 h−1) results in a slower peripheral elimination rate termed, k
PEL
(1.2E−07 h−1).
$$ {k}_{\mathrm{EL}}^{\mathrm{P}\mathrm{eripheral}}-{k}_{\mathrm{P}\mathrm{eripheral}}^{\mathrm{P}\mathrm{eripheral}}={k}_{\mathrm{EL}}^{\mathrm{P}} $$
(96)
-
2-
Rearrangement: Transfer from central to peripheral compartments via lymphatic flow and the reflection of the fraction mAb-FcRn complex recycled are combined into one term that describes the sum of the two processes.
$$ \left(1-{\sigma}_{\mathrm{V}}\right)\times {k}_{\mathrm{LY}\ \mathrm{Cen}\hbox{-} \mathrm{P}\mathrm{er}}+{k}_{\mathrm{C}\mathrm{en}\hbox{-} \mathrm{P}\mathrm{er}}={k}_{\mathrm{C}\hbox{-} \mathrm{P}} $$
(97)
-
3-
Assumption: Rate of return of mAb to the lymph node via lymphatic flow ((1 − σ
LY) × k
PeripheralLY ISF ‐ LN
, 0.39 h−1) is faster than the reflection of the fraction mAb-FcRn complex recycled , (k
PeripheralISF ‐ Central
, 1.95E-06 h−1)
$$ \left(1-{\sigma}_{\mathrm{LY}}\right)\times {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Peripheral}}\gg {k}_{\mathrm{ISF}\hbox{-} \mathrm{Central}}^{\mathrm{Peripheral}} $$
(98)
-
4-
Assumption: Rate of return from peripheral compartment to lymph node ((1 − σ
LY) × k
PeripheralLY ISF ‐ LN
, 0.39 h−1) is comparable to rate of return from lymph node to central compartment (\( \frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}} \), 0.11 h−1)
$$ \left(1-{\sigma}_{\mathrm{LY}}\right)\ast {k}_{\mathrm{LY}\ \mathrm{ISF}\hbox{-} \mathrm{LN}}^{\mathrm{Peripheral}}\sim \frac{1}{{\mathrm{Tau}}_{\mathrm{LN}}}={k}_{\mathrm{LN}} $$
(99)
-
5-
Assumption: 100% of the drug in the lymph node is subject to return to the central compartment (i.e., F
return = 1)
Rewrite Eqs. 93, and 94
$$ \frac{\operatorname{d}{A}_{\mathrm{C}\mathrm{entral}}\ }{\operatorname{d}t}=-{k}_{\mathrm{EL}}^{\mathrm{C}}\times {A}_{\mathrm{C}\mathrm{entral}}-{k}_{\mathrm{C}\mathrm{P}}\times {A}_{\mathrm{C}\mathrm{entral}}+{k}_{\mathrm{LN}}\times {A}_{\mathrm{LN}} $$
(100)
$$ \frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Peripheral}}}{\operatorname{d}t}={k}_{\mathrm{CP}}\times {A}_{\mathrm{Central}}-{k}_{\mathrm{LN}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}-{k}_{\mathrm{EL}}^{\mathrm{P}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}} $$
(101)
Further, k
CEL
∼ k
PEL
= k
EL. Thus, Final model equations can be written as:
A. Central Compartment
$$ \begin{array}{ll}\frac{\operatorname{d}{A}_{\mathrm{Central}}\ }{\operatorname{d}t}=\hfill & -{k}_{\mathrm{EL}}\times {A}_{\mathrm{Central}}-{k}_{\mathrm{CP}}\times {A}_{\mathrm{Central}}+{k}_{\mathrm{LN}}\times {A}_{\mathrm{LN}}\hfill \\ {}\hfill & \mathrm{IC}={\mathrm{Dose}}_{\mathrm{mAb}}\hfill \end{array} $$
(102)
B. Peripheral Compartment
$$ \begin{array}{ll}\frac{\operatorname{d}{A}_{\mathrm{ISF}\ \mathrm{Peripheral}}}{\operatorname{d}t}=\hfill & {k}_{\mathrm{CP}}\times {A}_{\mathrm{Central}}-{k}_{\mathrm{LN}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}-{k}_{\mathrm{EL}}\times {A}_{\mathrm{ISF}\ \mathrm{Peripheral}}\hfill \\ {}\hfill & \mathrm{IC}=0\hfill \end{array} $$
(103)
C. Lymph node Compartment
$$ \begin{array}{ll}\frac{\operatorname{d}{A}_{\mathrm{LN}}}{\operatorname{d}t}=\hfill & {k}_{\mathrm{LN}}\times \left({A}_{\mathrm{ISF}\ \mathrm{Peripheral}}-{A}_{\mathrm{LN}}\right)\hfill \\ {}\hfill & \mathrm{IC}=0\hfill \end{array} $$
(104)
Appendix 9: Derivation of the Output Function in Transit Compartment System with Fast Transfer
In this appendix, we show that the output from the last of N transit compartments equals to the input, if the transfer rate between transit compartments is fast compared to other processes. We assume that all model variables describing amounts are nonnegative. We also skip the proofs of the following statements:
$$ 0\le {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}},0\le {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}},0\le {\mathrm{ARCPX}}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}},0\le {\mathrm{ARCPX}}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}},i=1,2,3,4 $$
(105)
and
$$ {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{endo}}+{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{exo}}\le {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} \mathrm{i}},i=1,2,3,4 $$
(106)
and there exist positive constants M
endo and M
exo such that
$$ \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}\le {M}^{\mathrm{J}},\mathrm{J}=\mathrm{endo}\ \mathrm{or}\ \mathrm{exo} $$
(107)
First we will show that for i = 1, 2, 3, 4, J = endo or exo
$$ \frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{J}}\le {M}^{\mathrm{J}}+{k}_{\mathrm{off}\hbox{-} 1}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}+\dots +{k}_{\mathrm{off}\hbox{-} \mathrm{i}}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} \mathrm{i}} $$
(108)
and
$$ \frac{1}{\tau}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{J}}\le \tau \times \frac{k_{\mathrm{on}\hbox{-} \mathrm{i}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}\times \left({M}^{\mathrm{J}}+{k}_{\mathrm{off}\hbox{-} 1}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}+\dots +{k}_{\mathrm{off}\hbox{-} \mathrm{i}}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}\right) $$
(109)
Applying the integrating factor e
t/τ to (9) and (10) one can obtain the following solution for A
JEND Organ ‐ 1
:
$$ \begin{array}{l}\ {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(t)={\displaystyle \underset{0}{\overset{t}{\int }}}\left(\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\ast {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}(z)+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\ast {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}(z)\right)\ast {e}^{\frac{z-t}{\tau }}\operatorname{d}z\\ {}-\frac{k_{\mathrm{on}\hbox{-} 1}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\ast {\displaystyle \underset{0}{\overset{t}{\int }}}{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}\ast \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(z)-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(z)\right)\times {e}^{\frac{z-t}{\tau }}\operatorname{d}z\\ {}+{k}_{\mathrm{off}\hbox{-} 1}\times {\displaystyle \underset{0}{\overset{t}{\int }}}{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(z)\times {e}^{\left(z-t\right)/\tau}\operatorname{d}z\end{array} $$
(110)
and
$$ \begin{array}{l}\ {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(t)=\\ {}\frac{k_{\mathrm{on}\hbox{-} 1}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {\displaystyle \underset{0}{\overset{t}{\int }}}{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(z)-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(z)\right)\times {e}^{\frac{z-t}{\tau }}\operatorname{d}z\\ {}-{k}_{\mathrm{off}\hbox{-} 1}\times {\displaystyle \underset{0}{\overset{t}{\int }}}{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(z)\times {e}^{\left(z-t\right)/\tau}\operatorname{d}z\end{array} $$
(111)
(107) and (108) imply that
$$ {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(t)\le {M}^{\mathrm{J}}\times {\displaystyle \underset{0}{\overset{t}{\int }}}{e}^{\frac{z-t}{\tau }}\operatorname{d}z+{k}_{\mathrm{off}\hbox{-} 1}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}\times {\displaystyle \underset{0}{\overset{t}{\int }}}{e}^{\frac{z-t}{\tau }}\operatorname{d}z\le \tau \times \left({M}^{\mathrm{J}}+{k}_{\mathrm{off}\hbox{-} 1}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}\right) $$
(112)
and
$$ {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(t)\le \frac{k_{\mathrm{on}\hbox{-} 1}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}\times {\displaystyle \underset{0}{\overset{t}{\int }}}{A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}\times {e}^{\frac{z-t}{\tau }}\operatorname{d}z $$
(113)
From (113) it follows
$$ {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(t)\le {\tau}^2\times \left({M}^{\mathrm{J}}+{k}_{\mathrm{off}\hbox{-} 1}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}\right)\times \frac{k_{\mathrm{on}\hbox{-} 1}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1} $$
This proves (109) and (110) for i = 1. The proof of cases i = 2, 3, 4 is analogous.
In the next step we will show that for i = 1, 2, 3, 4, J = endo or exo
$$ \frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \mathrm{i}}^{\mathrm{J}}\to \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}\;\mathrm{as}\;\tau \to 0 $$
(114)
That will yield (23) for i = 4. Consider first the case i = 1. Multiplying (110) by 1/τ results in
$$ \begin{array}{l}\frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(t)={\displaystyle \underset{0}{\overset{t}{\int }}}\left(\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}(z)+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}(z)\right)\times \frac{1}{\tau }{e}^{\frac{z-t}{\tau }}\operatorname{d}z-\frac{k_{\mathrm{on}\hbox{-} 1}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times \\ {}{\displaystyle \underset{0}{\overset{t}{\int }}}\frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}\times \left({\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(z)-{\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(z)\right)\times {e}^{\frac{z-t}{\tau }}\operatorname{d}z+{k}_{\mathrm{off}\hbox{-} 1}\times \\ {}{\displaystyle \underset{0}{\overset{t}{\int }}}\frac{1}{\tau}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(z)\times {e}^{\left(z-t\right)/\tau}\operatorname{d}z\end{array} $$
(115)
From (107) and (112) the following bound applies to the integral
$$ \begin{array}{l}{\displaystyle \underset{0}{\overset{t}{\int }}}\frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}\ast \left({\operatorname{Rtotal}}_{Organ-1}-{\operatorname{ARCPX}}_{Organ-1}^J(z)-{\operatorname{ARCPX}}_{Organ-1}^J(z)\right)\times {e}^{\frac{z-t}{\tau }}\operatorname{d}z\le \\ {}\left({M}^{\mathrm{J}}+{k}_{\mathrm{off}\hbox{-} 1}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}\right)\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}\times \tau \end{array} $$
(116)
This means that the integral in (117) approaches 0 as τ → 0. Similarly, (110) implies that the last integral in (116) can be bound as follows:
$$ {\displaystyle \underset{0}{\overset{t}{\int }}}\frac{1}{\tau}\times {\mathrm{ARCPX}}_{\mathrm{Organ}\hbox{-} 1}^{\mathrm{J}}(z)\times {e}^{\left(z-t\right)/\tau}\operatorname{d}z\le {\tau}^2\times \frac{k_{\mathrm{on}\hbox{-} \mathrm{i}}}{V_{\mathrm{END}}^{\mathrm{Organ}}}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} \mathrm{i}}\times \left({M}^{\mathrm{J}}+{k}_{\mathrm{off}\hbox{-} 1}\times {\mathrm{Rtotal}}_{\mathrm{Organ}\hbox{-} 1}\right) $$
(117)
which implies that this integral approaches 0 as τ → 0. To conclude that
$$ \begin{array}{l}{\displaystyle \underset{0}{\overset{t}{\int }}}\left(\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}(z)+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}(z)\right)\times \frac{1}{\tau }{e}^{\frac{z-t}{\tau }}\operatorname{d}z\to \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}(t)+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times \\ {}{A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}(t)\end{array} $$
(118)
we observe that
$$ \gamma (t)=\frac{1}{\tau }{e}^{\frac{-t}{\tau }} $$
is the gamma probability density function which possesses the approximate identity property (22,23)
$$ {\displaystyle \underset{0}{\overset{t}{\int }}}f(z)\gamma \left(t-z\right)\operatorname{d}z\to f(t)\;\mathrm{as}\;\tau \to 0 $$
(119)
for any continuous function f(t). This completes proof of (114) for i = 1. The proof of cases i = 2, 3, 4 is differs only in the part:
$$ {\displaystyle \underset{0}{\overset{t}{\int }}}\frac{1}{\tau}\times {A}_{\mathrm{END}\ \mathrm{Organ}\hbox{-} \left(\mathrm{i}\hbox{-} 1\right)}^{\mathrm{J}}(z)\times \frac{1}{\tau }{e}^{\frac{z-t}{\tau }} dz\to \frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{VAS}}^{\mathrm{Organ}}}\times {A}_{\mathrm{VAS}\ \mathrm{Organ}}^{\mathrm{J}}(t)+\frac{{\mathrm{CL}}_{\mathrm{Uptake}}^{\mathrm{Organ}}}{V_{\mathrm{ISF}}^{\mathrm{Organ}}}\times {A}_{\mathrm{ISF}\ \mathrm{Organ}}^{\mathrm{J}}(t)\;\mathrm{as}\;\tau \to 0 $$
(120)
However, by induction, (107) implies (108) which concludes Appendix 9.