Introduction

In the past decades, digital fringe projection (DFP) methods have been proposed as one of the most reliable techniques to reconstruct the surface of objects because of their accuracy and efficiency [1,2,3]. Because it is easier and more convenient to generate fringe patterns and project patterns with a high speed, 3D shape measurement of dynamic objects has been rapidly expanding [4, 5]. However, conventional DFP technique has major limitations: the projection nonlinearity and speed bottleneck [6,7,8,9]. These shortcomings make it difficult to be applied to high-quality and high-speed 3D shape measurement.

To overcome the bottleneck, binary defocusing technique is recently developed which has successfully made speed breakthrough [10,11,12]. However, binary defocusing technique cannot achieve the same measurement capability compared with conventional DFP methods: (1) the measurement accuracy decreases due to high-frequency harmonics influence and (2) the measurement range is smaller since the projector must be properly focused for high-quality measurement [13,14,15]. Lately, pulse width modulation (PWM) [16] and optimal pulse width modulation (OPWM) [17] techniques are proposed to improve the fringe quality by eliminating high-frequency harmonics. However improvement is limited to wide fringe stripes, because the modulation is only one-dimensional without making full use of two-dimensional information.

Dithering technology is developed to take advantage of two-dimensional binary images so it could improve fringe quality of wide fringe stripes [18,19,20,21]. These techniques maintain low-frequency component so that the overall image is similar to the original pattern when a low-pass filter is applied. However, if fringe stripes are narrow, the improvement is rather small because high-frequency sinusoidal fringe patterns are usually desirable since they provide better measurement quality when the period of fringe pattern is small.

Taking advantage of two-dimensional (2D) nature of the structured patterns, dithering optimization methods are developed for DFP systems [22,23,24]. According to their objective functions, these optimization methods can be classified into two categories: intensity-based optimization [25, 26] and phase-based optimization [27, 28]. The former makes the dithered pattern approximation for an ideal sinusoidal fringe after defocusing. They are robust to projector defocusing levels but they can not reduce phase errors efficiently. Since the ultimate goal of optimization is to generate high-quality phase, it is natural to optimize the pattern in the phase domain [29]. The latter makes the phase close to the desired linear phase when properly focused. However, the phase-based optimization method is sensitive to different defocusing levels.

In order to address the aforementioned challenge, this paper proposes a weight object function combining normalized mean squared error and intensity residual error. Instead of optimizing the whole pattern, our framework is optimizing pixels group by group to find the best binary patches, and then tiling the best patch to generate the full-size pattern utilizing symmetry and periodicity structure of the sinusoidal pattern. The proposed fringe patterns belong to dithering binary stripes so they inherit the property of dithering binary pattern which means that they can increase the measurement speed without using 8-bit information. It can also be used to overcome the gamma of projector without projector non-linearity calibration. Moreover, these patterns can overcome the shortcomings from phase-based optimization and intensity-based optimization.

Both simulation and experiments demonstrate that the proposed method can achieve substantial phase quality improvements when the projector is at different defocusing levels.

The rest of the paper is organized as follows. Section Methods explains the principles concerned in this technique and the process of fringe pattern generation. Section Results and Discussion presents simulation results, experimental results and the merits of the proposed technique. Section Conclusions summarizes this paper.

Methods

Three-step phase-shifting algorithm

Sinusoidal phase shifting algorithms are very widely used in conventional optical metrology due to their fast speed and high accuracy [30]. Typically, the more numbers of fringe patterns are used, the better measurement quality can be achieved. For high-speed 3D shape measurement, a three-step phase-shifting algorithm is usually adopted since it requires the minimum number of patterns to get the phase uniquely point by point. Since our research focuses on high-speed 3D shape measurement, a simple three-step phase-shifting algorithm with a phase shift of 2π/3is used to evaluate the proposed optimization algorithm. Three fringe images can be described as:

$$ {I}_1=A\left(x,y\right)+B\left(x,y\right)\cos \left[\varphi \left(x,y\right)-2\pi /3\right] $$
(1)
$$ {I}_2=A\left(x,y\right)+B\left(x,y\right)\cos \left[\varphi \left(x,y\right)\right] $$
(2)
$$ {I}_3=A\left(x,y\right)+B\left(x,y\right)\cos \left[\varphi \left(x,y\right)+2\pi /3\right] $$
(3)

Where A(x, y) is average intensity. B(x, y) is intensity modulation. ϕ(x, y) is the phase to be solved for:

$$ \phi \left(x,y\right)={\tan}^{-1}\frac{\sqrt{3}\left({I}_1-{I}_3\right)}{2{I}_2-{I}_1-{I}_3} $$
(4)

This equation provides the phase ranging [−π, π) with 2π discontinuities. A continuous phase map can be obtained by adopting a spatial or temporal phase unwrapping algorithm. In this research, we use the temporal phase unwrapping method with three frequency phase-shifting algorithms.

Bayer-dithering technique

Dithering techniques have been developed to convert a higher bit depth into a lower bit depth, and this is analogous to halftone technique used in printing. Various dithering algorithms can be used to approximate an ideal sinusoidal fringe pattern, such as simple thresholding, random dithering, and ordered dithering [31].

Among these dithering methods, Bayer-ordered dithering has been extensively utilized in many applications due to its simplicity and efficiency, which is adopted in this study. The Bayer dithering technique compares the original image with a 2D grid of thresholds called Bayer kernel, and then the original image is quantized according to corresponding pixels in the Bayer kernel: if the grayscale value is larger than the kernel, the pixel is turned to 1 (or 255 grayscale value), otherwise to 0. Neighboring pixels do not affect each other. Different kernels can generate completely different dithering effects. Among the kernels used, Bayer has shown that if the sizes of the matrices are 2N (N is an integer), there is an optimal dither kernel that results in the pattern noise being as high-frequency as possible. A low-pass filter can suppress the high-frequency noises. The Bayer kernel can be obtained by:

$$ {M}_1=\left[\begin{array}{l}0\kern2em 2\\ {}3\kern2em 1\end{array}\right] $$
(5)

Where M1 is the smallest base, and other larger patterns can be obtained by:

$$ {M}_{n+1}=\left[\begin{array}{l}\kern2.5em 4{M}_n\kern4.5em 4{M}_n+2{U}_n\\ {}4{M}_n+3{U}_n\kern3.5em 4{M}_n+{U}_n\end{array}\right] $$
(6)

Where Un is n-dimensional unit matrix. In this research, we find that the Bayer kernel 8 × 8 produces the best results for all tested fringe stripes, and then it is utilized.

Weight objection function

Dithering optimization technique has been researched in reducing its overall phase error. The objective function of all these optimization techniques is to get the best fit of the binary patterns [32]. The optimization process can be described as a norm function such as Frobenius norm function:

$$ \underset{B,G}{\min}\left\Vert I\left(x,y\right)-G\left(x,y\right)\ast B{\left(x,y\right)}_F\right\Vert $$
(7)

Where ‖•‖ represents the Frobenius norm. I(x, y) is the ideal sinusoidal intensity pattern. G(x, y) represents a 2D Gaussian function. B(x, y) is a 2D binary pattern and ∗ represents convolution. The optimization function evaluates the global intensity similarity between the dithering pattern and its corresponding ideal pattern, but it just considers the global similarity without focusing on local structure similarity. In addition, NP problem makes it difficult to calculate the object function [15].

The objective of all these optimization techniques is to obtain the best fit of the binary patterns which are close to the ideal sinusoidal pattern. The optimized binary patterns should be as close as possible to the ideal sinusoidal patterns after applying Gaussian filter. The local detailed structure is one of the important resources in an image. It contains particular high-frequency components. In order to contain local similarity in the objective function, we propose a weighted object function (WOF). The objective function combines two parts: a global intensity part and a local structure part. The global intensity measurement is based on the normalized mean squared error (NMSE). The local structure measurement is based on the residual error of intensity (REI). If the intensity of ideal pattern are I and the intensity of dithering pattern is Id, WOF can be expressed as:

$$ WOF={\omega}_1 NMSE\left(I,{I}_d\right)+{\omega}_2 REI\left(I,{I}_d\right) $$
(8)

Where NMSE(I, Id) measures the global similarity and REI(I, Id) measures the local similarity, respectively. WOF gets the synthetic error between the ideal pattern I and the dithering pattern Id. ω1 and ω2 are weighted factors limited by ω1 + ω2 = 1. Figure 1 illustrates phase root mean square error values RMS (rad) when weighted factor ω1 = 0~1. In order to simplify the description, we call it phase RMS error in the following parts. The lowest point of the broken line in Fig. 1 means the root mean square error values RMS value is the smallest when ω1 is 0.7. Thus, in this research, we set ω1 = 0.7.

Fig. 1
figure 1

The phase root mean square error values RMS with different weighted value ω1

Full size image

First a global intensity similarity is introduced into the WOF expression. NMSE(I, Id) can evaluate the global intensity similarity between the dithering pattern and the corresponding ideal pattern. NMSE(I, Id) can be shown as:

$$ NMSE\left(I,{I}_d\right)=\frac{\sum_H{\sum}_W{\left(I\left(x,y\right)-{I}_d\left(x,y\right)\right)}^2}{\sum_H{\sum}_W{\left(I\left(x,y\right)\right)}^2} $$
(9)

Where H and W respectively represent height and width of the pattern. NMSE(I, Id) method reflects statistical errors from the whole fringe pattern intensity. Thus, the smaller the NMSE(I, Id) is, the better the whole pattern quality becomes. However NMSE(I, Id) only focuses on the global similarity, so REI(I, Id) is introduced as an optimization term to evaluate the local structure similarity between the dithering pattern and the corresponding ideal pattern.

Because the existence of the third harmonics does not induce any phase errors for three-step phase-shifting algorithm [33], it can be proved that if the intensity error varies periodically at the frequency which is multiple of 3f0 (f0is the fundamental frequency of the desired sinusoidal pattern). The obtained phase map could be as same as the ideal phase map. The intensity error could not vary periodically but it is possible to separate the 3f0 harmonics from the total intensity error. Therefore, the intensity residual error function REI(I, Id) is designed as:

$$ REI\left(I,{I}_d\right)=E\left(x,y\right)-{E}_{3{f}_0}\left(x,y\right) $$
(10)
$$ E\left(x,y\right)=G\left(x,y\right)\ast B\left(x,y\right)-I\left(x,y\right) $$
(11)

Where E(x, y) is the total intensity error between the defocused binary pattern and the ideal sinusoidal pattern. \( {E}_{3{f}_0}\left(x,y\right) \) is the periodically harmonics. G(x, y) is a Gaussian function. B(x, y) is the binary dithered pattern. * is convolution. I(x, y) is the ideal sinusoidal pattern intensity.

It can be assumed that a periodical signal s(x) varies along x direction for one period T(T = 3 N) and s3N(x) is one part of s(x). In order to extract the harmonics sN(x) from the whole signal s3N(x), discrete Fourier transform is employed to obtain its spectrum S3N(k). After that, all those harmonics at the frequency (3l)th should be retained and other harmonics should be removed. Therefore, the new sampled spectrum SN(k) can be described as:

$$ {S}_N(k)={S}_{3N}(k)\cdot H(k) $$
(12)
$$ {\displaystyle \begin{array}{l}H(k)=\frac{1}{3} comb\left(\frac{k}{3}\right)=\frac{1}{3}\sum \limits_{l=0}^{N-1}\delta \left(\frac{k}{3}-l\right)\\ {}\kern4em =\sum \limits_{l=0}^{N-1}\delta \left(k-3l\right)\end{array}} $$
(13)

Where H(k) is the Dirac comb function and every δ function is separated from each other at 3. According to discrete Fourier transform theory and convolution principle, the filtering process in the spatial domain can be described as:

$$ {s}_N(x)={s}_{3N}(x)\ast h(x) $$
(14)
$$ {\displaystyle \begin{array}{l}h(x)=\frac{1}{3N} comb\left(\frac{x}{N}\right)=\frac{1}{3N}\sum \limits_{m=0}^2\delta \left(\frac{x}{N}-m\right)\\ {}\kern4em =\frac{1}{3}\sum \limits_{m=0}^2\delta \left(x- Nm\right)\end{array}} $$
(15)

Where h(x) is the spatial filtering function. ∗ represents convolution. It turns out that h(x) is a Dirac comb function, but it is composed of three δ functions and the extent decreases to one-third. Therefore, the (3l)th harmonics of sN(x) can be solved for:

$$ {\displaystyle \begin{array}{l}{s}_N(x)={s}_{3N}(x)\ast \frac{\delta (x)+\delta \left(x-N\right)+\delta \left(x-2N\right)}{3}\\ {}=\frac{s_{3N}(x)+{s}_{3N}\left(x-N\right)+{s}_{3N}\left(x-2N\right)}{3}\end{array}} $$
(16)

Therefore, the (3l)th intensity error \( {E}_{3{f}_0}\left(x,y\right) \) can be extracted from the intensity error E(x, y), which can be described as the following function:

$$ {E}_{3{f}_0}\left(x,y\right)=\frac{1}{3}\left[E\left(x,y\right)+E\left(x+\frac{T}{3},y\right)+E\left(x+\frac{2T}{3},y\right)\right] $$
(17)

This function demonstrates a simple way to extract the (3l)th harmonics sN(x) out of signal without discrete Fourier transform. Firstly, s3N(x) is divided into three segments at the same length N. Secondly, three segments are added together to calculate an average segment. And finally, the (3l)th harmonics sN(x) are generated by periodically extending the average segment along x direction three times. Then, the intensity residual error REI(I, Id) can be calculated.

Implementation in the best patch optimization framework

Instead of optimizing the whole fringe pattern, we use an idea which called binary patch, and then the patch are tiled to generate full-size patterns using symmetry and periodicity. Assuming that the desired sinusoidal fringe patterns vary along x direction: the best-fit binary pattern should be symmetric along x direction for one fringe period (T); and it should be periodic along the y direction. The period in every row Sy is defined as the period along y direction. In this paper, we take Sx = T/2 as the patch column period and T is the fringe period. The row period Sy for a best patch is set to different widths which are optimized respectively and from which the best one is chosen. This framework also includes two parts, the global intensity optimization and the further combined optimization. The process of optimization can be divided into the following major steps:

  • Step 1: Initial patch generation. Bayer dithered sinusoidal fringes are generated firstly. The patch size of the row period Sy ranges from 2 to 10. Then, according to the symmetry of the sinusoidal pattern and the optimization efficiency, the patch column period Sx is set to T/2 which is one half of fringe period.

  • Step 2: Patch optimization based on weighted error function. Each pixel (i, j) are mutated from 0 to 1 or from 1 to 0. Because three step phase-shifting algorithm is used, there are eight groups: (0,0,0), (0,01), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1). They are filtered by a Gaussian filter with size G = 5. Weighted error function is further optimized for each group and the group error ζ is kept from the one with biggest absolute phase error to the smallest one. The further optimization is performed iteratively until phase RMS error is less than 0.01% or the number of iteration reaches maximum times. Figure 2 shows the phase RMS error after each round of optimization.

  • Step 3: Patch shifting. The global optimization binary patch is tiled and shifted to produce phase shifted fringes.

  • Step 4: Patch selection. After a number of patch mutations, a set of optimized patches are generated. From these patches, the best patch is selected based on the following two rules: (1) phase error does not change drastically if different sizes of Gaussian filter are applied; and (2) the resultant phase error is consistently small. These two rules imply that the best patch under one defocusing level may not be chosen.

  • Step 5: Fringe pattern generation. Utilizing symmetry and periodicity properties of fringe patterns, the desired size fringe pattern is generated by tiling the best patch together.

Fig. 2
figure 2

The phase root mean square error values RMS after each round of optimization

Full size image

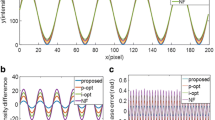
Figure 3 shows binary patterns before and after applying the optimization algorithms. Figure 3a shows the desired sinusoidal pattern. The period of every fringe pattern is T = 20pixels. Figure 3b, c and d show three binary patterns comparison, which are respectively generated by utilizing intensity-based optimization, phase-based optimization and the proposed method.

Fig. 3
figure 3

Example of binary patterns after applying different algorithms. a Ideal sinusoidal pattern (T = 20pixels); b intensity-based optimization pattern; c phase-based optimization pattern; d proposed method optimization pattern

Full size image

Phase-based optimization (p-opt) and intensity-based optimization (i-opt) are also two main categories to improve the quality of fringe patterns. In order to show the superiority of the proposed optimization method, we compare it with the norm Frobenius (NF), the p-opt [17], i-opt [14] and ideal sinusoidal fringe patterns under the same condition. Figure 3 shows the comparison among different optimization. Figure 4a shows the comparison between the ideal sinusoidal curve and cross-sections from different fringe patterns. Figure 4b and c give the intensity difference and phase difference with i-opt, o-opt, NF and the proposed method. From the results we can find that the optimization framework can generate better quality and less phase error. Because NF just compares the global similarity without considering the local structure similarity, in the following section we just compare the intensity-based optimization, phase-based optimization and the proposed optimization.

Fig. 4
figure 4

The cross-section fringe comparison of different optimization. a The comparison between ideal sinusoidal curve and cross section fringe pattern with different optimization. b The intensity difference among four methods. c The phase error comparison among four methods

Full size image

Results and discussion

We evaluate the proposed algorithm through simulation where different periods are used. In this simulation, we use fringe periods T = 30,50,70 and 90 pixels. Different defocusing levels are expressed by applying different sizes of Gaussian filters. The size of Gaussian filterGranges from 5 to 17 and standard deviation is σ = G/3.

When the size of Gaussian filter is 5 × 5 (σ = 5/3), it represents the case that the projector is nearly focused. When the size of Gaussian filter is 17 × 17 (σ = 17/3), it represents the case that the projector is defocused to a much more degree. In this simulation, the wrapped phase is obtained based on three-step phase-shifting algorithm and the phase RMS error is obtained by calculating the difference between the phase obtained from the binary patterns and the phase obtained from the ideal sinusoidal fringe pattern. Figure 5 shows the phase RMS error comparison among phase-based optimization (Phase-opt) [17], intensity-based optimization (Intensity-opt) [14] and the proposed best-patch optimization (Proposed-opt).

Fig. 5
figure 5

The phase RMS error comparison among the phase optimized fringes (P-opt), intensity optimized fringes (I-opt) and the proposed fringes of best-patch optimization (Proposed)

Full size image

By analyzing the simulation, we can find that when the projector is nearly focused (Gaussian filter size is 5 × 5 and standard deviation is 5/3), the phase-based optimization has the lowest phase RMS error. When the period changes from 20 pixels to 90 pixels, the phase-based has the best phase quality. While with the Gaussian filter size increasing, the quality from phase-based optimization decreases because it is sensitive to filter sizes. When the projector is slightly defocused (Gaussian filter size is 11 × 11 and standard deviation is 11/3 pixels). The phase error from the intensity-based optimization and the phase error from the proposed method decrease greatly as the filter size increases and they produce better results. They have the same tendency when the filter sizes increases. From simulation results, we can also find when the filter size is small, the proposed optimization almost have smaller phase RMS errors than the intensity-based optimization. It means that when projector is nearly focused(the filter size is small), the proposed optimization can perform better than intensity-based optimization. Besides it is robust to defocusing levels. When the projector is slightly focused and strongly defocused (the filter size is large), the proposed optimization can still get high quality fringe pattern with less phase RMS error. Simulation has verified the superiority of the proposed optimization technique which can produce fringes with high phase quality under different defocusing levels.

We also develop a 3D shape measurement system to verify the proposed method which consists of a DLP projector (Samsung SP-P310MEMX) and a digital CCD camera (Daheng MER-500-14U3M/C-L). The camera is attached with a 16 mm focal length lens (Computar M1614-MP) and the lens resolution is 1024 × 768. The resolution of projector is 800 × 600 and it has 0.49–2.80 m projection distance.

A uniform flat board is measured based on different optimization under three defocusing levels. Because phase-shifting algorithm with (n + 2) steps is insensitive to high-order harmonics up to the nth-order [20]. So in this research, the ideal phase is obtained by a ten-step phase-shifting algorithm and the period of fringe patterns is set to 20 pixels. Figure 6a-c show dithering fringe patterns which are optimized based on the proposed method from nearly focused, slightly defocused and strongly defocused respectively. Figure 6d-f show the corresponding phase RMS errors and the phase RMS errors comparison from intensity-based optimization and phase-based optimization. This experimental results show that when the projector is nearly focused, the proposed method and phase-based method have better phase quality and the intensity-based method has the largest rms error. With the defocusing levels increasing, the intensity-based method performs better than the phase-based method while the proposed method has small fluctuate. However phase errors are still smaller. It indicates that the proposed method performs consistently well to get the better phase quality under three defousing levels.

Fig. 6
figure 6

Experimental phase quality comparison among intensity-based optimization, phase-based optimization and the proposed method under different amounts of defocusing. a-c show dithering fringe patterns under different defocusing levels; d-f show the corresponding phase RMS errors

Full size image

Furthermore, a more complex 3D statue is measured to compare these optimization methods under the same projector defocusing levels respectively. Figure 7 shows the deformed fringe pattern under nearly focused, slightly defocused and strongly defocused respectively. The measurement results are shown in Fig. 8. In order to compare the quality of results, Figs. 9, 10 and 11 show the results based on phase optimization and the results based on intensity optimization at the same defocusing levels respectively. From the measurement results, it can be found that when the projector is nearly focused, the result from the phase-based optimization appears slightly better than the intensity-based optimization method. Under slightly defocused and strongly defoucsed, the results from the intensity-based optimization method have less errors than the results from phase-based optimization method. Because the proposed method decreases the phase error and it optimizes the intensity errors, the proposed method can reconstruct smoother surface than both optimization methods.

Fig. 7
figure 7

The deformed fringe pattern under different defocusing levels. a the deformed fringe pattern under nearly focused; b the deformed fringe pattern under slightly defocused; c the deformed fringe pattern under strongly defocused

Full size image
Fig. 8
figure 8

The measurement results based on proposed method with different projector focusing levels

Full size image
Fig. 9
figure 9

The measurement results based on phase optimization and intensity optimization with projector nearly focused

Full size image
Fig. 10
figure 10

The measurement results based on phase optimization and intensity optimization with projector slightly defocused

Full size image
Fig. 11
figure 11

The measurement results based on phase optimization and intensity optimization with projector strongly defocused

Full size image

In order to give a more clear comparison, the phase errors of three dithering methods are calculated and they are shown in Fig. 12 according to Figs. 8, 9, 10 and 11. When the projector is nearly focused, phase RMS errors of intensity-based optimization, phase-based optimization and the proposed optimization are 0.057 rad, 0.048 rad, and 0.045 rad. When the projector is slightly defocused, the corresponding phase RMS errors are 0.049 rad, 0.055 rad, and 0.045 rad for slightly defocused and when the projector is strongly defocused, the phase RMS errors are 0.045 rad, 0.058 rad and 0.042 rad. Table 1 lists the corresponding measurement time based on Fig. 12. By comparison between the measurement time, it can be found that the proposed method can increase measurement speed.

Fig. 12
figure 12

The phase error comparison of measurement results

Full size image
Table 1 The measurement time comparison between different optimization methods. (Unit:s)
Full size table

These results also clearly show that phase-based optimization technology can improve phase quality under a certain condition but it is sensitive to the amount of defocusing. The intensity-based optimization technology is able to improve the fringe quality with the defocusing levels increasing, but it can not reduce phase errors efficiently. The proposed technique has the same tendency with intensity-based optimization but it can increase the phase quality under different defocusing levels. The results are consistent with the simulation analysis.

Conclusions

This paper has presented an optimization method based on the weight objective function to generate high-quality sinusoidal fringe patterns. By using normalized mean squared error and residual error of intensity, the global similarity and local similarity can be optimized. Utilizing symmetry and periodicity properties of the fringe patterns, the desired fringe pattern is generated by tiling the best patch together. Simulation shows that the proposed fringes maintain high phase quality under different filter sizes. Experimental results also verify the feasibility and advantage of the proposed technique that the proposed method can generate high-quality binary fringes under different defocusing levels.