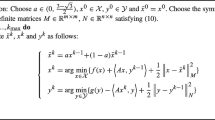Abstract
This paper revisits the numerical shape-from-shading method proposed in early 1980s. The original problem is non-convex due to the unit norm constraint for surface normal, and the existing approaches including the original Ikeuchi and Horn’s work uses approximate solution strategies for the original problem. This paper instead studies relaxation strategies for the original non-convex constraint and describes corresponding solution techniques that are built upon advanced convex optimization. We analyze the effect of the relaxations in terms of resulting accuracy and computational complexity.
Similar content being viewed by others
1 Introduction
Shape-from-shading [11] is a problem of determining shape in the form of surface normal from the shading distribution observed in a single image. While a human can naturally achieve this task, it is computationally non-trivial and still remains as one of the central problems in computer vision.
The major difficulty arises from the fact that the problem is under-constrained, i.e., there are many solutions that satisfy the image formation model. In other words, there exists a set of shapes that yields exactly the same shading appearance under a fixed lighting condition. To overcome this issue, previous approaches incorporate additional priors, such as the smoothness constraint [13]. With such priors, it has been shown that the shape-from-shading problem can be better constrained.
There is another difficulty in shape-from-shading that is often overlooked, the non-convex nature of the problem due to the unit norm constraint. Even assuming a linear (Lambertian) reflectance model, the problem of inferring shape in the form of surface normal requires the surface normal vector to be in the unit norm, namely, ∥n∥2 = 1, for a surface normal vector \(\mathbf {n} \in \mathbb {R}^{3}\). Oftentimes, a two-parameter notation of a surface normal vector (p,q,1)⊤ is used, but it comes with the normalization of its magnitude, resulting in \(\mathbf {n}~=~(p,q,1)^{\top } / \sqrt {p^{2}~+~q^{2}~+~1}\). It makes the unit norm constraint somehow implicit; however, the problem is fundamentally unchanged and the non-convexity of the problem still remainsFootnote 1.
This paper studies the effect of the unit norm constraint (∥n∥2 = 1) that always appears in shape-from-shading problems, under the conventional assumptions of orthographic projection and calibrated point light source. This constraint makes the overall problem non-convex; therefore, it is important to understand its property and develop work-around if any for the method to be applied in practical situations. We illustrate various relaxation strategies and corresponding solution methods and assess the effect of the approximations. Our study puts its basis on the early work of numerical shape-from-shading [13] and revisits the problem with advanced convex relaxation and optimization methods that have been more recently developed.
1.1 Related works
Since Horn’s original work [11], the problem of shape-from-shading has been one of the central problems in computer vision. While the shape-from-shading problem can be described in a simple manner, it exhibits a mathematically rich structure. There have been a numerous number of previous works that study shape-from-shading, and an excellent survey of the early methods is found in [45]. The survey categorizes the approaches into four classes: minimization [5, 13], propagation [11, 19], basis representation [23, 28], and linear approximation [27, 37] approaches. Our method falls in the class of minimization approaches, in which the smoothness of the surface normal is maximized under some constraints. The vast majority of the early works focuses on the solution strategies; however, surprisingly very few works explicitly discussed the issue of the non-convex nature of the problem until more recently [7, 18]. Early methods tried to avoid the issue of non-convexity by their customized solution technique. For example, Ikeuchi and Horn [13] iterate between solving the problem without the non-convex constraint and normalizing the surface normal. Szeliski’s work [35] has used a gradient-descent method for obtaining the surface normal in conjunction with a hierarchical basis representation based on scale-space theory [38] for shape and its gradient, effectively avoiding local minimas. More recently, Xiong et al. [43] used a locally quadratic shape representation for robust inference of the global shape. A newer survey of shape-from-shading [6] provided a comprehensive summary of recent shape-from-shading methods.
Most of the existing methods, including the original shape-from-shading [11] and our method, assume an orthographic camera projection and calibrated light condition, i.e., the light source direction is known. Recently, methods to alleviate with these restrictions have been proposed. Tankus et al. [36] proposed a shape-from-shading method under a perspective projection based on an extension of fast marching [20]. They have evaluated their method using synthetic images and the medical images recorded by an endoscopy and demonstrated improvement in accuracy by the perspective projection model. Richter et al. [30] used a learning-based approach for estimating surface normal under perspective and uncalibrated conditions. Their method uses a regression forest for determining surface normal trained with synthetic data and has shown promising results.
While most of the methods assume a point light source, Queau et al. [29] proposed a shape-from-shading method under natural illumination. They used a variational method for ensuring smoothness of surface normal through regularization by solving partial differential equations. Their method demonstrates robustness in estimation without tedious tuning of a regularization parameter.
For the purpose of making shape-from-shading applicable to real-world scenarios, there are threads of works that aim at relaxation of restrictive assumptions. They include the relaxations of known and uniform albedo assumption [2] using a coarse depth information, spatially uniform illumination assumption [8], and known illumination assumption [31] with a discriminative learning approach. With these advancements, shape-from-shading has been successfully applied to some real-world applications, such as endoscopy [42], recovery of shape with high-frequency details [41, 44], and face recognition [3, 34] to list a few. Our study also aims at broadening the use of shape-from-shading, and this paper particularly studies the unit norm constraint that is inherent in shape-from-shading problems. Unlike previous approaches that introduce new assumptions for making the problem more tractable, our focus is to analyze the behavior of the unit norm constraint and its relaxed surrogates.
2 Background
Given a measurement vector \(\mathbf {m} \in \mathbb {R}^{p}\) that consists of p-pixel observations under a distant light \(\mathbf {l} \in \mathbb {R}^{3}\), ∥l∥2 = 1, we wish to recover the surface normal map (scaled by albedo) \(\mathbf {N} \in \mathbb {R}^{3\times p}\) based on the Lambertian image formation model
We revisit the original numerical shape-from-shading formulation [13] using a matrix notation because of its simplicity of notations. The three constraints introduced in the original work [13]—brightness, smoothness, and occluding boundary constraints—can be written as follows:
Brightness constraint. The brightness constraint ensures the agreement among observations m, lighting l, and surface normal N via the Lambertian image formation model:
Smoothness constraint. Smoothness constraint ensures the surface normal estimates have locally smooth variations. Using a 2D Laplacian matrix \(\mathbf {D} \in \mathbb {R}^{p\times p}\) defined over grid locations in a valid image region, the smoothness constraint can be written as
Occluding boundary constraint. At pixels on an occluding boundary, it is assumed that the surface orientation information is available. Namely, it assumes that the surface normal direction is perpendicular to the tangent line of the object boundary, looking outward. Let F, a diagonal p × p matrix, indicate the pixel locations where the occluding boundary constraint is applicable (1 for such pixels and 0 otherwise), and a matrix \(\mathbf {G} \in \mathbb {R}^{3 \times p}\) contains the corresponding surface normal information. For example, if the ith pixel is at the occluding boundary, Fi,i = 1 and g i = n i , where g i and n i correspond to the ith column vectors of G and N, respectively. For non-occluding boundary pixels, Fj,j = 0 and g j = 0. With these notations, the occluding boundary constraint can be written as
Unit norm constraint. Another important constraint is a unit norm constraint for surface normal vectors. Namely, the norm of a surface normal vector \(\mathbf {n}_{i} \in \mathbb {R}^{3}\), corresponding to a column vector of N(=[n1,…,n p ]) needs to satisfy
In addition, we are interested in surface normals that are visible from a camera; thus, an additional constraint 0≤n z can be placed.
In the original formulation [13], the smoothness constraint (3) is regarded as an objective function to minimize while the rest are treated as hard constraints as
This problem is a non-convex QCQP (quadratically constrained quadratic program) due to the non-convex constraint \(\|\mathbf {n}_{i}\|^{2}_{2} = 1\) and understood as a NP-hard problem. In other words, the computational difficulty arises solely due to the unit norm constraint \(\|\mathbf {n}_{i}\|_{2}^{2} = 1\). The original paper [13] tackled the problem essentially by iteratively solving a relaxed subproblem without the norm constraint. This paper revisits this problem and studies possible relaxations of the norm constraint and their effects.
3 Relaxations and solution methods
In the original formulation (6), the unit norm constraint for surface normal is a non-convex quadratic equality, which is the source of the non-convexity of the overall problem. This section describes convex relaxation strategies for shape-from-shading and their solution methods. We consider the following three types of convex relaxations in addition to the original non-convex problem:
Figure 1 shows feasible regions of the original unit norm constraint and the relaxed constraints. The “ORIGINAL” constraint says that the norm of surface normal must be on the hemisphere formed by \(\|\mathbf {n}_{i}\|_{2}^{2}=1\) and n z ≥0. The “INSIDE” relaxation is a convex surrogate for the unit norm constraint, turning the original constraint into a quadratic inequality constraint. The “BOX” relaxation uses a looser convex approximation to the original constraint to form linear inequality constraints that correspond to ranges of each elements of surface normal. Finally, the “OPEN” relaxation fully removes the unit norm constraint and allows solutions anywhere in the half-space n z ≥0. Aside from the ORIGINAL constraint, the three relaxed constraints are all convex, and thus, they turn the whole problem into convex. In what follows, we discuss solution methods for these settings.
3.1 ORIGINAL constraint
Because the feasible region of the original unit norm constraint is non-convex, deriving its exact solution is generally difficult. To make it computationally tractable, the original problem can be approximated to either Lagrangian relaxation or semidefinite programming (SDP) relaxation [1, 7]. In general, the SDP relaxation, which becomes a convex problem, better approximates the original problem unless the weighting factors for Lagrangian relaxation is carefully chosen and yields higher accuracy. However, linearization in SDP relaxation generates a huge dense matrix \({\text {vec}}(\mathbf {N})^{\top {\text {vec}}}(\mathbf {N}) \left (\in \mathbb {R}^{3p \times 3p}\right)\), which prohibits the method to work only with small images as pointed out in [7]. We now discuss the Lagrangian relaxation of the original problem (6) with weight parameters λ1, λ2, and λ3:
For convenience of later discussion, we vectorize N as \(\mathbf {x} = \text {vec}(\mathbf {N}) \,=\, \left [\mathbf {n}_{1}^{\top }, \ldots, \mathbf {n}_{p}^{\top }\right ]^{\top }\) and reformulate the problem (7) as:
where
with ⊗ representing the Kronecker product operator and I3 being a 3×3 identity matrix.
While the problem (8) is a non-convex nonlinear least-squares problem with boundary conditions 0≤n iz , we can apply a variant of Levenberg-Marquardt algorithm [24, 26] that is designed for (convex) constrained problems [16] to seek a local minima. The updating formula from x at iteration k denoted by x(k) to x(k+1) is given as:
The parameter \(\mathbf {d}^{(k)} \left (\in \mathbb {R}^{3p}\right)\) indicates the search direction of Levenberg-Marquardt algorithm and is determined by solving the subproblem described in Appendix 1.
Lagrangian relaxation yields a good approximate solution to the original problem when λ1, λ2, and λ3 are available and if we could solve the problem by overcoming the non-convexity. However, due to the non-convexity, the Levenberg-Marquardt method (or any other convex optimization methods) may be trapped in local minima depending on the initial guess x0. In addition, the best choice of λ1, λ2, and λ3 depends on the target image, and unfortunately, the ideal values are generally inaccessible.
3.2 INSIDE relaxation
The INSIDE relaxation of the problem is formulated as:
where \(\mathbf {s}_{i} \left (\in \mathbb {R}^{3p}\right)\) are single-entry vectors with one in row i and zero elsewhere, and K i is a block diagonal matrix:
The relaxed problem is convex QCQP, which can be solved as a second-order cone program (SOCP) [25]. The details of the solution method are described in Appendix 2. While this SOCP problem can be solved more efficiently than the SDP relaxation to the original problem, it is still computationally demanding when the size of input image is large.
3.3 BOX relaxation
The Box relaxation problem, in which the unit norm constraint is replaced by range constraints of surface normal elements, can be written as:
This problem is a linear constrained quadratic programming (LCQP) and also can be solved by the primal-dual interior point method [40]. Because the Karush-Kuhn-Tucker (KKT) conditions for the BOX relaxation involve less quadratic terms than those for the INSIDE relaxation, the KKT equations for this case can be efficiently solved by a standard Newton’s method (Appendix 3).
3.4 OPEN relaxation
The case for OPEN relaxation is rather straightforward. The problem in this case can be written in the form of LCQP as
and, again, it can be efficiently solved by a primal-dual interior point method [40].
3.5 Piecewise solution method
While the INSIDE relaxation approach shows higher accuracy than other relaxation strategies that are described above, its computational complexity rapidly grows along with the image size. Motivated by propagation approaches in shape-from-shading (see Section 2.2 of [45]), we develop an efficient piecewise solution strategy.
The proposed method splits the image into small patches having some overlaps to the neighbors and estimates surface normal using the INSIDE relaxation starting from the most reliable patch. The reliability is determined by the number of the occluding boundary constraints in a patch; the more the constraints are provided, the better surface normal estimate is expected. Once the surface normal map \(\hat {\mathbf {x}}\) for the most reliable patch is determined by the INSIDE relaxation method, the normal maps x of its neighbors are estimated by taking the surface normal estimates \(\hat {\mathbf {x}}\) of the overlapped pixels as new constraints. Namely, the following additional constraint between \(\hat {\mathbf {x}}\) and x is further enforced to the INSIDE relaxation setting:
where R is a matrix that selects pixel locations where the surface normal estimates \(\hat {\mathbf {x}}\) is available in the overlapped regions, i.e., R=diag[r0,…,r p ], and r i =1 if the pixel location i has the estimated normal \(\hat {\mathbf {x}}\) and r i =0 otherwise. Since the surface normal estimates \(\hat {\mathbf {x}}\) are subject to error, putting them as hard constraints has a chance of making the problem infeasible. Therefore, we treat the new constraints as a soft constraint with a positive weight parameter λ. The procedure for a target patch is written as
Since solving the INSIDE relaxation setting by SOCP requires O(n3) computational complexity, where n is the number of unknowns (3p in our case), this patch splitting strategy makes the problem significantly more efficient at the cost of degradation of the accuracy. For example, when the patch size is set 1/10 of the entire image size, it becomes 100 times faster (1/103 computation is repeated 10 times).
As described, the solution method is sequential, i.e., if the initial estimate fails, the error may propagate to the rest of the estimation. However, by starting with the most reliable patch, this effect is alleviated, and in practice, we found the strategy is sufficiently reliable.
4 Experiments
This section shows experimental results using both synthetic and real-world images for the various settings for the unit norm constraint. The performance of the ORIGINAL problem and INSIDE, BOX, and OPEN relaxations are examined in terms of their accuracy and computation times. We also evaluate the effectiveness of the piecewise solution method described in Section 3.5. In addition, we compare these strategies with the original numerical shape-from-shading algorithm proposed by Ikeuchi and Horn [13] (labeled “ITERATIVE” hereafter), a polynomial shape-from-shading method proposed by Ecker and Jepson [7] (labeled “P-SFS”), and local shape prediction method proposed by Xiong et al. [43] (labeled “XIONG”).
For the ITERATIVE method [13], following the original method’s procedure, we repeat the Newton step for the following problem for a few times (set to 5 in this evaluation based on our empirical test) starting from the initial guess n=(0,0,1)⊤:
and normalize the current estimate of the surface normal to ∥n i ∥2=1. As such, it iteratively optimizes without the unit norm constraint, and during the iterations, it enforces the surface normal to have the unit norm by normalization. In the work of the P-SFS method [7], they propose an iterative procedure with exact line search, which is inherently non-convex, and its convex SDP relaxation. Since their method does not require boundary conditions, we align the setting to their setting and compare the performance with their SDP relaxation method. We use Gurobi OptimizerFootnote 2 as a solver for SDP problems. XIONG method [43] assumes the quadratic representation of local shape and infers the local shape for each small image patches separately. We use their implementation that is publicly availableFootnote 3 and their default parameters for our experiment. In our all experiments, the feasibility tolerance for constraints of LCQP, QCQP, and SDP is set to 1×10−6 and the tolerance for the stopping criteria is set to 1×10−6.
4.1 Synthetic scenes
In this section, we show some experiments on synthetic dataset [15]. The dataset consists of ten objects, which have a smooth shape, and the dataset contains ideally complete 3D shape data. There is another dataset for evaluating the shape-from-shading or photometric stereo method ([9, 33]), but [15] is designed for synthetic evaluation and suits our evaluation. We show the results of five objects among them, labeled “blob01” to “blob05,” rendered under a directional light source l=(0,0,1)⊤. Figure 2 summarizes the results of various settings: (a) ORIGINAL setting with the Lagrangian relaxation, (b) INSIDE relaxation, (c) BOX relaxation, (d) OPEN relaxation, (e) PIECEWISE solution method described in Section 3.5, and (f) ITERATIVE method of [10]. For each scene, top row shows the estimated surface normal, and the bottom row depicts the angular error map and corresponding mean angular error (MAE). For the ORIGINAL method with Lagrangian relaxation, we carefully picked the weight parameters (λ1,λ2,λ3)=(512,2048,32) with numerical simulation based on ground truth. It shows that aside from the ORIGINAL method, the INSIDE relaxation tends to yield favorable result compared to BOX and OPEN relaxations. The trend is inherited in the PIECEWISE method that uses the INSIDE relaxation in a sequential manner. The ITERATIVE method also shows higher accuracy compared to BOX and OPEN relaxations. The ORIGINAL setting shows the highest accuracy in two scenes, but the weight (hyper) parameters of the Lagrangian relaxation have been carefully chosen for producing the results.
Results on Blobby dataset [15]. From left to right, surface normal and angular error maps are shown for (a) ORIGINAL, (b) INSIDE, (c) BOX, (d) OPEN, (e) PIECEWISE, and (f) ITERATIVE methods. GT indicates the ground truth normal maps, and the values represent corresponding MAEs
Discussion on Lagrangian relaxation for ORIGINAL. The Lagrangian relaxation of the ORIGINAL setting has two obvious issues. One is the non-convexity of the problem, which implies that the solution may depend on the initial guess. The other is that the hyper parameters λ1, λ2, and λ3 of [8] need to be properly chosen for expecting accurate estimates; however, unfortunately, the optimal hyper parameters are generally unknown and scene-dependent.
Figure 3 shows the plot of MAEs that are obtained by changing the initial guess of the surface normal for the blob01 and blob02 scenes using the Lagrangian relaxation of the ORIGINAL setting. In the figures, x- and y-axes correspond to the azimuth θ and polar ϕ angles of the initial guess of the surface normal. The MAE drastically varies with the small variations of initial guess for the surface normal, and the variation has dependency on the scene.
Variation of mean angular errors (MAEs) with respect to the initial guess of surface normal using the Lagrangian relaxation of the ORIGINAL setting for blob01 (left) and blob02 (right) scenes. The initial guess of normal vectors are uniformly sampled from the hemisphere in the spherical coordinates (θ,ϕ). The star markers in the figure represent the best initial guesses
To see the effect of the choice of hyper parameters, we altered the hyper parameters λ1, λ2, and λ3 of [8] and observed the resulting MAEs. One of the results using the blob03 scene is shown in Fig. 4, in which the hyper parameters are set to λ1=λ2=λ3∈{1,10,100,1000,10000}. The MAE varies significantly depending on the choice of the parameters, and it illustrates the difficulty of applying the Lagrangian relaxation of the ORIGINAL problem.
Comparison to existing methods. We compared our method with P-SFS and XIONG. While our method requires the boundary conditions to work properly, in order to compare with the P-SFS and XIONG methods that do not require them, we eliminate the boundary condition from the INSIDE relaxation. As a result, there remains a rotation ambiguity in the solution. Therefore, we applied rotation alignment of the estimated normal map for the purpose of comparison. We determine the rotation matrix \(\mathbf {R}\ {\in }\ \mathbb {R}^{3 \times 3}\) by solving the following problem:
where N∗ and \(\hat {\mathbf {N}}\) are the ground truth and estimated normal maps, respectively. This problem is known as the orthogonal Procrustes problem [12], and the solution method is proposed in [32]. XIONG directly estimates the depth rather than surface normal; therefore, to compare with other methods in the space of surface normal, we compute the normal map from the estimated depth map. Figure 5 shows one of the representative results. From left to right, it shows the ground truth normal map, (a) result of the INSIDE relaxation with boundary conditions, (b) INSIDE relaxation without boundary conditions, (c) P-SFS method, and (d) XIONG method. “(b) - aligned” and “(c) - aligned” are the rotation aligned results of (b) and (c). While the result of (a) is convincing, (b) and (c) are rather far from the ground truth due to that the surface normals are not anchored by boundary conditions, containing the rotation ambiguity. Also, compared with (d), (a) achieves the better estimation.
Comparison of INSIDE relaxation with P-SFS and XIONG. From left to right, the surface normal maps of the ground truth, (a) INSIDE with boundary conditions, (b) INSIDE without boundary conditions, (c) P-SFS method, and (d) XIONG method are shown. “(b) - aligned” and “(c) - aligned” are the results of (b) and (c) aligned to the ground truth. Resulting mean angular errors are shown in the bottom
Speed and accuracy. Figure6 summarizes the computation times and accuracies of various methods applied to blob01–blob05 datasets. The x- and y-axes represent the log-scale processing time and MAE respectively. The mean scores of MAEs are plotted by circle, and their minimum and maximum time/accuracy are indicated by the associated bars. It can be seen that the PIECEWISE method significantly reduces the computation time compared to the INSIDE relaxation with retaining the accuracy. OPEN and BOX relaxations are faster; however, they suffer from inaccuracy due to the loose relaxation. The ORIGINAL method with Lagrangian relaxation shows a good trade-off as we have carefully selected a good set of hyper parameters. The MAE may significantly vary depending on the selection of hyper parameters as discussed earlier. The ITERATIVE method is the most efficient one among them, while MAEs were consistently larger than PIECEWISE, INSIDE, and ORIGINAL methods.
4.2 Real-world data
Real-world data contains observations that deviate from the assumed image formation model. Namely, there are two major factors: non-uniform diffuse albedos and non-Lambertian surface reflectances. Due to these unmodelled errors, the brightness [2] and boundary [4] constraints can conflict, resulting in no feasible solutions. For the real-world data experiment, we therefore relax these hard constraints as soft ones as:
INSIDE relaxation:
BOX relaxation:
The results are summarized in Fig. 7. In the figure, “cat” data is from DiLiGenT [33] dataset, in which the ground truth is taken by the laser sensor. We picked up “cat” in DiLiGenT because it is the most Lambertian-like object. For other data, we have obtained the ground truth by a conventional least-squares photometric stereo [39] using 16 light sources. We selected these four objects: “wall-paper,” “coin,” and “logo,” which have diffuse surfaces. From left to right, it shows the estimated surface normal and angular error maps of (a) ORIGINAL with Lagrangian relaxation, (b) INSIDE, (c) BOX, (d) OPEN, (e) PIECEWISE, and (f) ITERATIVE methods. Although the surface details are smoothed out due to the smoothness constraint, overall structures can be better observed by properly accounting for the unit norm constraint with a tight relaxation by (b) compared to the result of (a) and (f). The PIECEWISE method in (e) also yields lower accuracy as well in this case but still producing results closer to the ground truth compared to (a) and (f).
Results on the real-world data. “cat” data is from DiLiGenT [33], and “wall-paper,” “coin,” and “logo” are recorded by ourselves. “GT” is the ground truth normal map, and for our own data, they are computed by photometric stereo. From left to right, surface normal maps and angular error maps of (a) ORIGINAL, (b) INSIDE, (c) BOX, (d) OPEN, (e) PIECEWISE, and (f) ITERATIVE are shown. The values show corresponding MAEs
Discussions on Lagrangian relaxation for the real-world data We examine Lagrangian relaxations of INSIDE, BOX, and OPEN methods using the real-world data for assessing their capabilities of handling unmodelled errors. The formulations are all convex problems; therefore, the solution does not depend on the initial guess. Here, we discuss the effect of the choice of hyper parameters λ1 and λ2.
We alter the hyper parameters λ1 and λ2 and observe the resulting mean angular errors (MAEs). The results using the “cat,” “wall-paper,” “coin,” and “logo” scenes are summarized in Fig. 8, in which the hyper parameters are set to λ1=λ2=λ∈{1,100,10000}.
While this result shows that the choice of hyper parameters has little effect on overall MAEs, it still locally affects surface normal estimates. For example, errors near ear and forefoot of “cat” are decreased with large hyper parameters in Fig. 9. Because the areas of ear and forefoot are not smooth, surface normal can be correctly estimated by emphasizing on the brightness and occluding boundary constraints rather than the smoothness constraint.
5 Discussion
This paper studied the unit norm constraint that appears in general shape-from-shading problems. We showed various convex relaxation strategies for the unit norm constraint, as well as a non-convex relaxation of the original problem using a Lagrangian relaxation. It has been shown that the INSIDE relaxation, which gives a tight convex surrogate for the original unit norm constraint, yields favorable results, and we developed a piecewise solution method for accelerating the shape estimation.
It has been shown that with carefully selected hyper-parameters, Lagrangian relaxation works well in terms of its speed and accuracy. However, unfortunately, such a priori knowledge is generally unavailable in real-world situations. For shape-from-shading to work with real-world applications, the INSIDE relaxation appears to be a favorable option when dealing with the unit norm constraint. With advanced convex optimization techniques and mature linear algebra packages, the computation of shape-from-shading is made significantly more efficient. We are interested in fusing this basic study into other recent works that use other prior knowledge for making shape-from-shading further applicable.
As a practical issue, the proposed method needs the annotation of the occluding boundary. In a controlled setting, this annotation could be semi-automated by sophisticated segmentation tools, such as [10, 14, 21], and we consider that this information is somewhat accessible in practice as various previous shape-from-shading works assumed.
6 Appendix 1. Lagrange relaxation subproblem
Search direction d(k) for the Levenberg-Marquardt algorithm is determined by solving the following subproblem:
A positive parameter κ k is used to control regularization by \(\|\mathbf {d}^{(k)}\|_{2}^{2}\). f(x(k)) and f′(x(k)) are given by
The subproblem [12] is a convex quadratic programming problem and thus has a unique solution for d(k).
7 Appendix 2: SOCP for INSIDE relaxation
The SOCP minimizes u for the upper bound of \(\frac {1}{2}\|\mathbf {D}_{\otimes } \mathbf {x}\|_{2}^{2}\) as
SOCP can be efficiently solved by a primal-dual interior-point method, which solves the following modified KKT (Karush-Kuhn-Tucker) conditions [17, 22] with letting y denote y=[u,x⊤]⊤:
where \(\mu \in \mathbb {R}^{2p+1}\) and \(\nu \in \mathbb {R}^{6p}\) are Lagrange multipliers and t is a parameter to control approximation in the barrier method. Parameters ∇ y u, H(y), \(\mathcal {D}H(\mathbf {y})\), A, and b are given by
where
The modified KKT equations can be solved by Newton’s method that changes y, μ, and ν by Newton steps Δy, Δμ, and Δν. The newton step is characterized by the following linear equations [4]
which results in a system of linear equations
where rdual, rcent, and rpri are residuals that are evaluated on the first, second, and third row block matrices in the KKT Eq. (13), respectively, after the previous Newton step.
8 Appendix 3: KKT for Box relaxation
The KKT conditions for the BOX relaxation case are:
where
The Newton steps Δy, Δμ, and Δν are derived by solving the following equations
where \(\mathbf {D}^{2}_{\otimes }=D^{\top }_{\otimes } D_{\otimes }\), and r dual , r cent , and r pri are residuals that are respectively evaluated on the first, second, and third row block matrices in the modified KKT Eq. (14) after the previous Newton step.
Notes
The non-convexity of the problem discussed in this paper is different from the concave/convex ambiguity that inherently appears in shape-from-shading problems.
Gurobi Optimizer: http://www.gurobi.com/products/gurobi-optimizer
References
Anstreicher KM (2009) Semidefinite programming versus the reformulation-linearization technique for nonconvex quadratically constrained quadratic programming. J Glob Optim 43(2-3):471–484.
Barron JT, Malik J (2011) High-frequency shape and albedo from shading using natural image statistics In: Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2521–2528.. IEEE, New Jersey.
Blanz V, Vetter T (2003) Face recognition based on fitting a 3d morphable model. IEEE Trans Pattern Anal Mach Intell 25(9):1063–1074.
Boyd S, Vandenberghe L (2004) Convex optimization. Cambridge University Press, New York.
Brooks MJ, Horn BKP (1985) Shape and source from shading In: Proceedings of International Joint Conference on Artificial Intelligence, 932–936.. Association for the Advancement of Artificial Intelligence, California.
Durou J-D, Falcone M, Sagona M (2008) Numerical methods for shape-from-shading: a new survey with benchmarks. Comp Vision Image Underst 109(1):22–43.
Ecker A, Jepson AD (2010) Polynomial shape from shading In: Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 145–152.. IEEE, New Jersey.
Forsyth DA (2011) Variable-source shading analysis. Int J Comput Vis 91(3):280–302.
Frankot RT, Chellappa R (1988) A method for enforcing integrability in shape from shading algorithms. PAMI 10(4):439–451.
Geman D, Geman S, Graffigne C, Dong P (1990) Boundary detection by constrained optimization. IEEE Trans Pattern Anal Mach Intell 12(7):609–628.
Horn BKP (1970) Shape from shading: a method for obtaining the shape of a smooth opaque object from one view. Technical Report AITR-232. MIT.
Hurley JR, Cattell RB (1962) The procrustes program: producing direct rotation to test a hypothesized factor structure. Syst Res Behav Sci 7(2):258–262.
Ikeuchi K, Horn BKP (1981) Numerical shape from shading and occluding boundaries. Artif Intell 17(1-3):141–184.
Isola P, Zoran D, Krishnan D, Adelson EH (2014) Crisp boundary detection using pointwise mutual information. Springer, Switzerland.
Johnson MK, Adelson EH (2011) Shape estimation in natural illumination In: Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2553–2560.. IEEE, New Jersey.
Kanzow C, Yamashita N, Fukushima M (2004) Levenberg-Marquardt methods with strong local convergence properties for solving nonlinear equations with convex constraints. J Comput Appl Math 172(2):375–397.
Karush W (1939) Minima of Functions of Several Variables with Inequalities as Side Conditions. Master’s thesis, Department of Mathematics. University of Chicago, Chicago, IL.
Khan N, Tran L, Tappen M (2009) Training many-parameter shape-from-shading models using a surface database In: Computer Vision Workshops (ICCV Workshops.. IEEE, New Jersey.
Kimmel R, Bruckstein AM (1992) Shape from shading via level sets. Israel Institute of Technology. Technical Report CIS Report.
Kimmel R, Sethian JA (2001) Optimal algorithm for shape from shading and path planning. J Math Imaging Vision 14(3):237–244.
Kokkinos I (2010) Highly accurate boundary detection and grouping In: Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, CVPR, 2520–2527.. IEEE, New Jersey.
Kuhn HWTucker AW (1951) Nonlinear programming In: Proceedings of 2nd Berkeley Symposium, 481–492.. University of California Press, Berkeley.
Lee CH, Rosenfeld A (1985) Improved methods of estimating shape from shading using the light source coordinate system. Artif Intell 26(2):125–143.
Levenberg K (1944) A method for the solution of certain non-linear problems in least squares. Q Appl Math 2(2):164–168.
Lobo MS, Vandenberghe L, Boyd S, Lebret H (1998) Applications of second-order cone programming. Linear Algebra Appl 284(1):193–228.
Marquardt DW (1963) An algorithm for least-squares estimation of nonlinear parameters. J Soc Ind Appl Math 11(2):431–441.
Pentland A (1989) Shape information from shading: a theory about human perception. Spat Vis 4(2):165–182.
Pentland AP (1982) Local shading analysis. Technical, Report Technical Note 272. SRI International.
Queau Y, Melou J, Castan F, Cremers D, Durou J-D (2017) A variational approach to shape-from-shading under natural illumination In: Energy Minimization Methods in Computer Vision and Pattern Recognition.. Springer International Publishing, Switzerland.
Richter SR, Roth S (2015) A discriminative approach to perspective shape from shading in uncalibrated illumination. Comput Graph 53:72–81.
Richter SR, Roth S (2015) Discriminative shape from shading in uncalibrated illumination In: Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 1128–1136.. IEEE, New Jersey.
Schönemann PH (1966) A generalized solution of the orthogonal procrustes problem. Psychometrika 31(1):1–10.
Shi B, Wu Z, Mo Z, Duan D, Yeung S-K, Tan P (2016) A benchmark dataset and evaluation for non-lambertian and uncalibrated photometric stereo In: Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR).. IEEE, New Jersey.
Smith WAP, Hancock ER (2002) Face recognition using shape-from-shading In: Proceedings of British Machine Vision Conference (BMVC), 1–10.. The British Machine Vision Association and Society for Pattern Recognition, Durham.
Szeliski R (1990) Fast shape from shading. In: Faugeras O (ed)Proceedings of European Conference on Computer Vision (ECCV), 359–368.. IEEE, New Jersey.
Tankus A, Sochen N, Yeshurun Y (2005) Shape-from-shading under perspective projection. IJCV 63(1):21–43.
Tsai PS, Shah M (1994) Shape from shading using linear approximation. Image Vis Comput J 12(8):487–498.
Witkin AP (1983) Scale-space filtering In: Proceedings of International Joint Conference on Artificial Intelligence, 1019–1021.
Woodham RJ (1980) Photometric method for determining surface orientation from multiple images. Opt Engineerings 19(I):139–144.
Wright SJ (1997) Primal-Dual Interior-Point Methods. Society for Industrial and Applied Mathematics, Philadelphia.
Wu C, Wilburn B, Matsushita Y, Theobalt C (2011) High-quality shape from multi-view stereo and shading under general illumination In: Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 969–976.. IEEE, New Jersey.
Wu C, Narasimhan SG, Jaramaz B (2010) A multi-image shape-from-shading framework for near-lighting perspective endoscopes. Int J Comput Vis 86(2):211–228.
Xiong Y, Chakrabarti A, Basri R, Gortler SJ, Jacobs DW, Zickler TE (2015) From shading to local shape. IEEE Trans Pattern Anal Mach Intell 37(1):67–79.
Yu L-F, Yeung S-K, Tai Y-W, Lin S (2013) Shading-based shape refinement of rgb-d images In: Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 1415–1422.. IEEE, New Jersey.
Zhang R, Tsai P-S, Cryer JE, Shah M (1999) Shape from shading: A survey. IEEE Trans Pattern Anal Mach Intell 21(8):690–706.
Funding
This work was supported by JSPS Grant-in-Aid for Scientific Research (A) (KAKENHI), grant number JP16H01732. The funders had no role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Availability of data and materials
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Author information
Authors and Affiliations
Contributions
HS carried out derivation of the solution methods, implementation, data acquisition, and experimentation, and drafted the manuscript. MS participated in the design of the convex optimization techniques described in the manuscript, contributed to developing solution methods, and helped to draft the manuscript. MT participated in the sequence alignment. YM conceived of the study, participated in its design and coordination, and helped to draft the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Santo, H., Samejima, M. & Matsushita, Y. Numerical shape-from-shading revisited. IPSJ T Comput Vis Appl 10, 8 (2018). https://doi.org/10.1186/s41074-018-0044-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41074-018-0044-9