1 Introduction

In this article, we investigate Fatou components for polynomial maps in two variables. More specifically, we fix our study in skew-product polynomial maps \(F(t,z) = (h(t), f(t,z))\) with an invariant fiber, \(h(t_0) = t_0\).

In a recent joint paper with Peters [7], we studied the geometrically attracting case, that is \(0<|h'(t_0)| <1\) inspired by results of Lilov’s thesis. Lilov’s theorem [4] deals with the superattracting case, i.e., \(h'(t_0)=0\).

In this article, we focus on the parabolic case. That is, we study the dynamics close to the fixed fiber for the case when \(h'(t_0)=1\). To put our result into context, let us explain the results of [4] as well as [7].

Consider a skew-product polynomial map \(F(t,z)= (h(t), f_t(z))\) such that \(h(t_0)=t_0\), with the condition that there exists an open attracting basin \(A \subset \mathbb C_t\) for \(t_0\), that is \(h(A)\subset A\), \(\lim _{n\rightarrow \infty }h^n(z)=t_0\) for all \(z \in A\), where \(t_0 \in \overline{A}\) (where \(\mathbb C_t= \{(0,t), t\in \mathbb C\}\)). Then the only options for \(h'(t_0)\) are the ones above, either the map h is superattracting, geometrically attracting or parabolic (up to an iterate). We want to investigate the dynamics of F on the set \(A\times \mathbb C\). Since \(f_{t_0}\) is a polynomial, by the non-wandering theorem of Sullivan [8], we know that all the one-dimensional Fatou components of \(f_{t_0}\) are nonwandering (and in fact, pre-periodic). Under our conditions on the existence of A as above, each one-dimensional Fatou component of \(f_{t_0}\) is therefore contained, or in the boundary, of a two-dimensional Fatou component of F. Lilov [4] proved that in the superattracting case all Fatou components in \(A\times \mathbb C\) are eventually mapped onto one of these fattened pre-periodic Fatou components. As a consequence in the superattracting case, there are no wandering Fatou components in \(A\times \mathbb C\). Lilov proved this by proving a stronger result, namely:

Theorem

(Lilov [4]) Let \(t_1 \in A\), and let D be an open one-dimensional disk lying in the \(t_1\)-fiber. Then the forward orbit of D must intersect one of the fattened Fatou components of \(f_{t_0}\).

In a joint paper with Peters [7], we proved that this result does not hold in the geometrically attracting case. More precisely, we prove the following:

Theorem

(Peters [7]) There exist skew-product polynomial maps of the form \(F(t, z) = (\alpha t, p(z) + q(t))\), where \(\alpha < 1\) and p and q are polynomials and a vertical holomorphic disk \(D \subset \{t=t_0\}\) whose forward orbit accumulates at a point \((0, z_0)\), where \(z_0\) is a repelling fixed point in the Julia set of p.

The proof of this theorem relies on a parametrization theorem for skew product maps where the map on the parameter fiber is attracting (similar to [3]).

A natural question is whether the same construction can be extended for skew-product maps that are parabolic, or if as in Lilov’s case, all Fatou components in \(A\times \mathbb C\) are non-wandering. Fatou components on the attracting skew-product case have been explored also by Peters and Smit [6]. We prove in this article that, in the parabolic case, a similar construction can be done as in the case of geometrically attracting.

The first step is to prove an analogous parametrization theorem for the parabolic case. Under an additional condition, we accomplish this and believe that this result can be useful, independently of the application given here. Let us state the additional condition and the parametrization theorem here.

Definition 1.1

We say F is a special parabolic skew product if F is of the form:

$$\begin{aligned} F(t,z) = \left( \frac{t}{1+t}, f_t(z)\right) , \end{aligned}$$

and each \(f_t(z)\) is of the form:

$$\begin{aligned} f_t(z) = z + \alpha z^2 + \alpha ^2 z^3 + O(|z|^4,|tz|^4) \end{aligned}$$

for some \(\alpha \in {\mathbb C}^{*}\).

Theorem

(Theorem 2.4) Let

$$\begin{aligned} F(t,z) = \left( \frac{t}{1+t}, f_t(z)\right) , \end{aligned}$$

where F is a special parabolic skew product as in Definition 1.1. Then there exists \(\epsilon >0\) and an open domain \(V_{\alpha ,\epsilon }\) with the origin at its boundary such that

$$\begin{aligned} \phi _n(t) = \pi _2 F^{n}\left( \frac{\alpha t}{1+(n+1)\alpha t},\frac{t}{1+\alpha nt}\right) \end{aligned}$$

converges for t in \(V_{\alpha ,\epsilon }\). Even more, the limit \(\phi\) is the parametrization of the unstable manifold of \(f_0\), i.e.,

$$\begin{aligned} \phi \left( \frac{t}{1-\alpha t}\right) = f_0(\phi (t)) . \end{aligned}$$

After we prove this parametrization theorem, we use a similar strategy to the one in [7] to prove that in the parabolic case, forward orbits of one-dimensional disks D that lie above A do not necessarily intersect fattened Fatou components. Therefore, Lilov’s theorem is false in general for the parabolic case. Consequently, we see that the dynamics inside the set \(A\times \mathbb C\) is more complicated in the parabolic case than in the superattracting one. More explicitly, we prove that there exist wandering Fatou disks for skew parabolic maps. We deduce this by proving the following theorem:

Theorem

(Theorem 3.5) There exist skew-product maps of the form \(F(t, z) = (\frac{t}{1+t}, f_t(z))\) where \(f_t(z) = f(t,z)\) polynomial in two variables, and a vertical holomorphic disk \(D \subset \{t=t_1\}\) for well chosen \(t_1\), whose \(\omega\)-limit set contains the parabolic fixed point (0, 0) which is completely contained in the Julia set of \(f_0\).

The organization of the paper is as follows: in the next section we prove the parametrization theorem for parabolic skew product maps (Theorem 2.4). We first prove a result for maps in one dimension and use it to prove the result for skew-products. In Sect. 3, we construct parabolic skew product maps that have wandering Fatou disks (Theorem 3.5). We also prove that our Fatou disks cannot be enlarged to Fatou components.

2 Parametrization of unstable manifolds of parabolic maps in one dimension

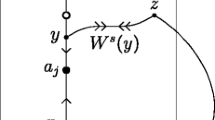
Given a parabolic map \(F(z) = z + a_kz^k+O(z^{k+1}), a_k \ne 0, k \ge 2\), the Leau–Fatou theorem say that there exist \(k-1\) regions in which each point is attracted to the origin under iterates by F, and also \(k-1\) regions in which the orbits are going towards the origin under the iterates of \(F^{-1}\) (see [5] for more details). We can think of these regions as stable and unstable manifolds of F. In each one of these regions is possible to find a Fatou coordinate, that is, a change of coordinates map \(\phi\) such that F is conjugate to a translation. To find the change of coordinates \(\phi\), there is not in general an iterative process as it is the case for hyperbolic maps.

However, for a certain class of maps, the change of coordinates can be recovered using iterations of our parabolic map. Let us introduce a needed condition before we state and prove our theorem.

Definition 2.1

We say f is special, if f is of the following form:

$$\begin{aligned} f(z) = z + \alpha z^2 + \alpha ^2 z^3 + O(z^4), \end{aligned}$$

for some \(\alpha \in {\mathbb C}^{*}\).

The condition of f being special is equivalent to f being formally conjugated to a translation \(h(z) = z-1\) in a whole neighborhood of the origin. It is well known that this formal conjugacy is indeed holomorphic when we restrict to wedges for which the origin is a boundary point (see for example the appendix at [2]).

Our starting point is that this holomorphic conjugacy map restricted to the unstable manifold of f can also be recovered using appropriate iterates of f. Even more, we prove precise estimates on the rate of convergence of these iterates.

Theorem 2.2

Let f be special as in definition 2.1. Define:

$$\begin{aligned} \phi _n(z):= f^n\left( \frac{z}{1+\alpha nz}\right) . \end{aligned}$$

Then there exists \(\epsilon >0\) such that \(\phi _n\) converges to a map \(\phi\) defined in \(V_{\alpha ,\epsilon } = \{z \in \mathbb C, |\alpha z-\epsilon | < \epsilon \}\), which is a parametrization of the unstable manifold of f:

$$\begin{aligned} \phi \left( \frac{t}{1-\alpha t}\right) =f(\phi (t)). \end{aligned}$$
(1)

Even more, if \(z \in V_{\alpha ,\epsilon }\), then

$$\begin{aligned} |\phi _{n+1}(z)-\phi _n(z)|< \frac{C'|\alpha z^2|}{(1+n|\alpha z|)^2} < \frac{C'}{n^2|\alpha |}. \end{aligned}$$

Proof

First, we assume, \(\alpha =1\) and prove the theorem for this case. We change coordinates of f to infinity. Let \(\iota (z) = 1/z\). Then the map \(g=\iota \circ f \circ \iota\) is given by

$$\begin{aligned} g(w) = w - 1 + \eta (w) = w-1+O\left( \frac{1}{w^2}\right) . \end{aligned}$$

We define the sequence \(\psi _n(w) = g^n(w+n)\). Clearly \(\phi _n = \iota \circ \psi _n \circ \iota\). So proving convergence for \(\phi _n\) is equivalent to proving convergence for \(\psi _n\). We consider the inverse map h of g. Close to infinity, we have \(h(u) = u + 1 + O(1/u^2)\). It is a classical result to prove that the sequence \(\gamma _n(u) = h^n(u) - n\) is convergent when \(\text {Re}(u) > R'\) for \(R'\) large enough and that the limit \(\gamma (u)\) satisfies \(\gamma (u) +1 = \gamma (h(u))\) (see for eg. Theorem 10.9 in Milnor’s book [5]). Since \(\gamma _n \circ \psi _n = \text {Id}\), then we have that \(\psi _n\) converges to \(\psi\) on the image of \(\gamma _n\), which contains a domain of the same form \(\text {Re}(w) > R\). Then \(\psi (w) = g \circ \psi (w +1)\). Therefore, \(\phi _n\) converges on the domain \(V=\{|z - 1/2R| <1/2R \}\) and we obtain

$$\begin{aligned} \phi (z) =f \circ \phi \left( \frac{z}{1+z}\right) , \end{aligned}$$

which is equivalent to (1).

To obtain estimates on the speed at which the \(\phi _n\) converges, we also look at the speed and estimates for the limit function \(\gamma\). We have that

$$\begin{aligned} \gamma _n(u) = u + \sum _{i=0}^{n-1} O\left(\frac{1}{u_i^2}\right), \end{aligned}$$

and by the estimates above, for \(R'\) large and \(\text {Re}(u) > R'\) then \(|h(u)-u-1|<1/2\) since \(|h(u)-u-1|=O(1/u^2)\). Applying to the sum above: \(|\gamma _n(u) - u| < \frac{C}{|u|} - \frac{C}{|u+n/2|}\). Then the limit function satisfies \(|\gamma (u) - u| < \frac{C}{|u|}\). Since the inverse of the limit of \(\gamma _n\) is the limit \(\psi\) of the sequence \(\psi _n\), we also have the estimate

$$\begin{aligned} |\psi (w) - w|< \frac{C}{|\psi (w)|} < \frac{C'}{|w|}. \end{aligned}$$

And now using \(\phi = \iota \circ \psi \circ \iota\), we obtain

$$\begin{aligned} |\phi (z) - z|< C'|z|^2|\phi (z)| < C''|z|^3. \end{aligned}$$

Likewise, we can make exactly the same estimates for the differences. From

$$\begin{aligned} |\gamma _{n+1}(u) - \gamma _n(u)| < \frac{C}{|h_n(u)|^2} \end{aligned}$$

we obtain

$$\begin{aligned} |\phi _{n+1}(z) -\phi _n(z)| < \frac{C|z|^2}{(1+n|z|)^2}. \end{aligned}$$

For the general case \(\alpha \ne 0,1\), apply the result above for the map \(\tilde{f}(z) = \alpha f(z/\alpha )\). We have \(\widetilde{\phi _n}\), as well as \(\widetilde{\phi }\) with the estimates above corresponding to \(\alpha =1\). Define \(\phi _n(z) = \frac{1}{\alpha } \widetilde{\phi _n}(\alpha z)\) and \(\phi (z) = \frac{1}{\alpha } \widetilde{\phi }(\alpha z)\). It is immediate to see that these maps satisfy the equations above.

This concludes the proof of the theorem. \(\square\)

Remark 2.3

Note that the theorem above indicates the speed at which the \(\phi _n\) approach \(\phi\). If we would like a faster convergence, we need to prescribe higher orders of f (not only the cubic term). More explicitly, given any integer \(k>0\), there exists \(f_k(z) = z +O(z^2)\) polynomial of degree k vanishing at the origin, such that for any \(f = f_k + O(z^{k+1})\) then

$$\begin{aligned} |\phi (z) - \phi _n(z)| < O(1/n^k) . \end{aligned}$$

for |z| bounded in a region as above, where \(\phi\) is the limit of the sequence \(\phi _n\) and \(\phi _n\) is defined as above.

Since we will be dealing with convergence for values of t in a domain as defined on Theorem 2.2, from now when we write \(V_{\alpha , \epsilon }\) we mean a domain like the one above:

$$\begin{aligned} V_{\alpha ,\epsilon } := \{z \in \mathbb C, |\alpha z-\epsilon | < \epsilon \}, \end{aligned}$$
(2)

where \(\alpha \ne 0\) and \(\epsilon >0\) is as small as necessary. We also write \(V_\epsilon := V_{1,\epsilon }\).

Now we are ready to prove an analogous theorem for a skew product type of map \((t,z) \rightarrow (g(t),f_t(z))\) where \(g(0)=0, |g'(0)| =1\) and each \(f_t\) is special.

We see that F has an invariant fiber \(t=0\), and at this invariant fiber the action is given by the one-dimensional map \(f_0(z)\). Under the given conditions, there exists an invariant manifold associated to \(f_0\) inside the fixed fiber. Our following theorem gives us a parametrization of this invariant manifold using iterates of F and projecting.

Theorem 2.4

Let F be a special parabolic skew product as in Definition 1.1 in Sect. 1. Let

$$\begin{aligned} \phi _n(t) = \pi _2 F^{n}\left( \frac{\alpha t}{1+(n+1)\alpha t},\frac{t}{1+\alpha nt}\right) . \end{aligned}$$

Then \(\{\phi _n\}_{n\ge 1}\) converges for t in a domain \(V_{\alpha ,\epsilon }\) defined as in (2).

Even more, the limit \(\phi\) gives a parametrization of the unstable manifold of \(f_0\):

$$\begin{aligned} \phi \left( \frac{t}{1-\alpha t}\right) = f_0(\phi (t)). \end{aligned}$$
(3)

Proof

As in the one-dimensional case, we write F in a simpler form, by changing coordinates to infinity, now in both variables. As before, we can assume \(\alpha =1\) and the general result follows from a linear change of variables \(\rho (t,z) = (t,\alpha z)\). Let \((u,w) = I(t,z) = (1/t,1/z)\). In these new variables,

$$\begin{aligned} G(u,w) = I \circ F \circ I = \left( u+1, g_u(w)\right) , \end{aligned}$$

where \(1/g_u(w) =f_{1/u}(1/w)\) or \(\iota \circ g_u\circ \iota =f_{1/u}\). We want to prove that the sequence

$$\begin{aligned} \phi _n(t) = f_{t_{n}}\circ \ldots f_{t_2}\circ f_{t_1}\left( \frac{t}{1+nt}\right) \end{aligned}$$

converges, where \(t_i = t/(1+(n+i)t)\). Let \(u = \iota (t) = 1/t\) then \(t=\iota (u)\). Denote by \(u_i :=1/t_i = (n+i) + u\). Proving convergence for \(\phi _n\) is equivalent to proving convergence for \(\psi _n = \iota \circ \phi _n \circ \iota\). It is easy to see that

$$\begin{aligned} \psi _n(u) = g_{u+2n}\circ \ldots g_{u+n+2}\circ g_{u+n+1}(u+n) . \end{aligned}$$
(4)

From the following equation:

$$\begin{aligned} \psi _{n+1}(u) = g_{u+2(n+1)} \circ \psi _n(u+1), \end{aligned}$$

we see that proving convergence of the sequence \(\psi _n\) immediately implies (3).

As in one variable we see that \(g_u(w) =w - 1 +O (1/w^2,1/(uw^2))\). Denote

$$\begin{aligned} \theta _u(w) := g_u(w) - w + 1. \end{aligned}$$
(5)

Denote R such that, for \(|w|>R\) and \(|u|>R\), then \(|\theta _u(w)| < A/|w|^2\) and \(\frac{d\theta _u(w)}{dw} < A/|w|^3\), where A is fixed.

We first choose R large enough so that for \(|w|>R\), then \(|\theta _u(w)| < 1/10\). Clearly, we have that for any u: \(\text {Re}(g_u(w)) > \text {Re}(w)\), and the domain \(W = \{\text {Re}(w) > R\}\) is invariant by \(g_u\). In this domain, we also have the easy estimates, for \(w\in W\), \(|w|+9/10< |g_u(w)| <|w|+11/10,\) and therefore, \(|w|+9k/10< |g^k_u(w)| <|w|+11k/10.\)

Let us define:

$$\begin{aligned} u_{n,i} := g_{u+n+i}\circ \ldots \circ g_{u+n+1}(u+n), 1 \le i \le n, \end{aligned}$$
(6)

and \(u_{n,0} := u+n\). Comparing (4) and (6) we see that \(\psi _n(u) = u_{n,n}\). Choose \(R' > R + A/R\), then we have

Lemma 2.5

If \(\text {Re}(u) > R'\) , then:

$$\begin{aligned} \text {Re}(u_{n,i}) > R+n-i \end{aligned}$$

for \(0\le i\le n\) .

Proof

The proof follows easily by induction. For \(i=0\) the statement is trivial. Assume by induction it is valid for \(i\le k\), where \(k \le n-1\). Using

$$\begin{aligned} u_{n,k+1}&= u_{n,0} -(k+1)+ \sum _{i=0}^k \theta _{u+n+i+1}(u_{n,i}), \end{aligned}$$

and by induction, and equation (5) up to k for each term

$$\begin{aligned} |\theta _{u+n+i+1}(u_{n,i})|< \frac{A}{|u_{n,i}|^2} < \frac{A}{(R+n-i)^2}; \end{aligned}$$

we obtain the estimate for \(i=k+1\). \(\square\)

Recall the estimates after Eq. (5): \(|\theta _u(w)| < A/|w|^2\text { for }|w|> R, |u|>R\).

Lemma 2.6

Let \(R<S<|x|,|y|\) and \(|u|, |v| >R\) . Then

$$\begin{aligned} |\theta _u(x) - \theta _v(y)| \le |x-y|\left( \frac{2A}{S^3}\right) + |u-v|\frac{A}{|u||v|S^2} . \end{aligned}$$

Proof

It follows easily from the definition of \(\theta _u\) and from

$$\begin{aligned} |\theta _u(x) - \theta _u(y)| \le |x-y|\left( \frac{2A}{|x|^3}\right) \,\text{ and }\,|\theta _u(y) - \theta _v(y)| \le |u-v|\frac{A}{|u||v||y|^2}. \end{aligned}$$

where the first estimate follows from \(d\theta _u(w)/dw=O(1/w^3)\) and the second one from \(d\theta _u(w)/du=O(1/u^2w^2).\) \(\square\)

Lemma 2.7

For \(0 \le k \le n\) , let

$$\begin{aligned} |u_{n+1,k+1} - u_{n,k}|\le C_k . \end{aligned}$$

Then

$$\begin{aligned} C_k < \frac{4A}{(R+k)^2}. \end{aligned}$$

Proof

We prove this by induction also. For \(k=0\) the inequality follows directly from the estimate on \(|\theta _{u+n+2}(u+n+1)|\). We assume the estimate on \(C_i\) is valid for \(i \le k-1\). Using the definition for \(u_{n,k}\) as in (6) we write \(u_{n+1,k+1}= g_{u+n+k+2}(u_{n+1,k})\) and \(u_{n,k} = g_{u+n+k}(u_{n,k-1})\). Then

$$\begin{aligned} u_{n+1,k+1} - u_{n,k} = u_{n+1,k} + \theta _{u+n+k+2}(u_{n+1,k}) - u_{n,k-1} - \theta _{u+n+k}(u_{n,k-1}). \end{aligned}$$

We use Lemmas 2.5, 2.6 and the estimate for \(i=k-1\) to prove that \(|u_{n+1,k+1} - u_{n,k}| \le C_k\) where

$$\begin{aligned} C_k=C_{k-1}\left( 1 + \frac{2A}{(R+n+1-k)^3}\right) +\frac{2A}{(R+n+k)^2(R+n-k)^2}. \end{aligned}$$

Using

$$\begin{aligned} \prod _{i=1}^k\left( 1 + \frac{2A}{(R+k+1-i)^3}\right) \sim \exp \sum _{i=1}^k \frac{2A}{(R+k+1-i)^3}<< \exp (\frac{A}{R^2}) , \end{aligned}$$

we see

$$\begin{aligned} C_k \le 2C_{0} + \sum _{i=1}^k \frac{4A}{(R+k+i)^2(R+k-i)^2}. \end{aligned}$$

From here, the estimate for \(i=k\) follows. \(\square\)

From Lemma 2.7 and recalling notation (4):

$$\begin{aligned}|\psi _{n+1}(u) - \psi _{n}(u)| < \frac{4A}{(R+n)^2}.\end{aligned}$$

It is easy to go back to the t coordinate and obtain the following estimate:

$$\begin{aligned} |1/\phi _{n+1}(t) - 1/\phi _{n}(t)|< \frac{4A}{(R+n)^2} \Rightarrow |\phi _{n+1}(t) - \phi _{n}(t)| < \frac{A'}{(1+n\epsilon )^2}, \end{aligned}$$

where \(\epsilon = 1/R\), \(t \in V_{\epsilon /2} = \{|t-\epsilon /2|<\epsilon /2\}\) and \(A'\) is bounded by \(A, \epsilon\) and the supremum of \(\phi\) in \(V_\epsilon\).

We have

$$\begin{aligned} |\phi (t) - \phi _n(t)| < \frac{A'}{1+n\epsilon } \end{aligned}$$

for \(t \in V_\epsilon\). It is immediate to see that the limit \(\phi\) satisfies (3). This concludes the proof of Theorem 2.4. \(\square\)

So far, our map \(\phi\) is only defined in the domain \(V_{\alpha ,\epsilon }\). We can extend \(\phi\) to all of \(\mathbb C\) using the functional Eq. (3). Let \(t\in \mathbb C, t\ne 0\), for any t there exists \(N=N(t)\) such that \(\frac{t}{1+\alpha Nt} \in V_{\epsilon ,\alpha }\). We define

$$\begin{aligned} \phi (t) := f_0^N\left( \phi \left( \frac{t}{1+\alpha Nt}\right) \right) . \end{aligned}$$

It is easy to prove that \(\phi (t)\) can also be defined in terms of the iterates of F, as follows. Assume for simplicity \(\alpha =1\). Define

$$\begin{aligned} \phi _{N+n}(t) := \pi _2F^{N}\left( \frac{t}{1+(N+2n+1)t},\phi _n\left( \frac{t}{1+Nt}\right) \right) , \quad n \ge 0. \end{aligned}$$

All the terms inside the parenthesis in the right hand side are well defined and we have good estimates for the differences for \(\phi _n\) and \(\phi _{n+1}\). Then, we have

$$\begin{aligned} \phi (t) = \lim _{n \rightarrow \infty } \phi _{N+n}(t). \end{aligned}$$

Then, for all \(t \in \mathbb C\), there exists a \(N=N(t)\), and a constant \(C=C(N)\) such that

$$\begin{aligned} \left| \phi _{n+1}(t) - \phi _n(t)\right| < C\frac{A}{(1+(n-N)\epsilon )^2}\end{aligned}$$
(7)
$$\begin{aligned} \text { and } \left| \phi _{n+1}(t) - \phi (t)\right| < C\frac{A}{1+(n-N)\epsilon }, \end{aligned}$$
(8)

for any \(n \ge N+1\).

It is well known that the range of \(\phi\) is the whole complex plane \(\mathbb C\). See [5] for a proof.

3 Skew parabolic maps with Fatou disks

We use the parametrization theorem of the last section for a dynamical application. As explained in the introduction, we prove a theorem similar to the one in [7]. That is, we prove that there exists some skew product parabolic maps that have wandering Fatou disks. Our construction, however, does not allow us to fatten the disks. We prove that statement at the end of this section. Let us recall the definition of Fatou disks following Ueda [9].

Definition 3.1

Let \(f: X\rightarrow X\) be a holomorphic endomorphism of a complex manifold X. A holomorphic disks \(D \subset X\) is a Fatou disk for f if the restriction of \(\{f^n\}\) to the disk D is a normal family.

One-dimensional disks contained in the Fatou set of any map are clearly Fatou disks. However, we will prove that we cannot enlarge our Fatou disks into a Fatou component.

We need to add another couple of hypothesis to the ones in Definition 1.1. Since we want to construct Fatou disks, we will make then centered at \(z_0\), a critical point of \(f_0\) and not centered at 0 as the iterates used on the Theorem 2.4. We also add the condition \(\alpha =1\) to simplify the computations. Let us put together those additional conditions on the following definition:

Definition 3.2

Let

$$\begin{aligned} F(t,z) = \left( \frac{t}{1+t}, f_t(z)\right) \end{aligned}$$

be a special parabolic skew product map as in Definition 1.1 with \(\alpha =1\). We say that F satisfies \((\ddag )\) if the following conditions are satisfied:

  • There exists \(z_0\ne 0\) a critical point of \(f_0\), such that \(f_t(z_0) = t\) for all t.

  • \(z_0\) a critical point of \(f_0\) of order at least 4.

The following corollary is an immediate consequence of Theorem 2.4.

Corollary 3.3

Given F that satisfies \((\ddag )\) as above, for any t define the iterates

$$\begin{aligned} \phi _n(t) = \pi _2 F^{n+1}\left( \frac{t}{1+nt}, z_0\right) . \end{aligned}$$

Then the \(\phi _n\) converges to the parametrization of the unstable manifold of \(f_0\)

$$\begin{aligned} \phi \left( \frac{t}{1-t}\right) =f_0(\phi (t)). \end{aligned}$$

Proof

We easily see that

$$\begin{aligned} F\left( \frac{t}{1+nt}, z_0\right) = \left( \frac{t}{1+(n+1)t}, \frac{t}{1+nt}\right) , \end{aligned}$$

and now we apply Theorem 2.4 with \(\alpha =1.\) \(\square\)

Example

We give an explicit map for which condition (\(\ddag\)) is satisfied:

$$\begin{aligned} F(t,z) = \left( \frac{t}{1+t}, (z+1)^4(z-3z^2+7z^3)+t(1+(z+1)^4(-1+4z-10z^2+20z^3))\right) . \end{aligned}$$

We have \(f_t(z) = z + z^2 + z^3 + O(z^4,z^4t)\). Then \(z_0=-1, f_t(z_0) = t\) and \(z_0\) is a critical point of \(f_t\) of order 4.

Let \(t_0 \in \mathbb C\) be such that \(\phi (t_0) = z_0\). We refer to the complex lines \(\displaystyle {\{t_n = \frac{t_0}{1+nt_0}\}}\), \(n\ge 1\), as critical fibers.

Definition 3.4

We define the vertical disks \(D_n\), \(n\ge 1\), as follows:

$$\begin{aligned} D_n := \left\{ \left( \frac{t_0}{1+nt_0}, z\right) \mid |z - z_0| < n^{-3/4} \right\} . \end{aligned}$$

Note that \(t_0\) might not be contained in \(V_\epsilon\). However, there exists \(N'=N(t_0)\) such that \(\frac{t_0}{1+Nt_0}\) is in \(V_\epsilon\), for \(N \ge N'\). From now on, we restrict our estimates to the disks \(D_n\), \(n \ge N'\).

Now we are ready to prove Theorem 3.5. Let us restate here:

Theorem 3.5

There exist skew-product maps of the form \(F(t, z) = (\frac{t}{1+t}, f_t(z))\) where \(f_t(z) = f(t,z)\) is a polynomial in two variables, and a vertical holomorphic disk \(D_m \subset \{t=t_{m}\}\) whose \(\omega\) -limit set contains the parabolic fixed point (0, 0) that is in the Julia set of \(f_0\) .

Proof

Consider a special skew product map that satisfies condition (\(\ddag\)). Then we will prove that the forward orbits of \(D_m\) accumulate at the point \((0,z_0)\), and therefore, we prove that for n sufficiently large, the forward orbits of the disks \(D_n\) all avoid the bulged Fatou components of F.

Note that \(t_0\) might not be in our domain \(V_\epsilon\) above. However, for a fixed \(N'=N(t_0)\), we do have that \(\frac{t_0}{1+Nt_0}\) is in \(V_\epsilon\), for \(N>N'\). Therefore, we can obtain all the estimates for iterates of F after we iterate F, \(N'\) times.

We need the following lemma:

Lemma 3.6

Let (t, z) and (t, w), be such that \(t,z \in V_\epsilon\) and \(|w-z| < \frac{C}{n^3}\). Then

$$\begin{aligned} |\pi _2(F^n(t,z) -F^n(t,w))| < Cn^2|z-w|, \end{aligned}$$

where C is fixed independent of n.

Proof

If \(z=0\), then we have

$$\begin{aligned} |\pi _2F^n(t,w))| = |f_{t_n}\circ \ldots f_{t}(w)| \end{aligned}$$

and recall that each \(f_t\) is of the form \(f_t(z) = z + z^2 + O(z^3)\). Let \(w_{k+1} = f_{t_k}(w_k)\) and \(w_0=w\). Then we have that at infinity

$$\begin{aligned} \frac{1}{w_1} =\frac{1}{w} -1+O(w). \end{aligned}$$

Our assumption implies \(|w| < C/n^3\), then \(|1/w| > n^3/C\), so when we apply n times our map \(f_t\), we have \(|1/w_n| > |1/w_0| - n(1+K)\), where \(K=O(1/n^2)\). Going back to the original coordinates

$$\begin{aligned} |w_n|< \frac{1}{|1/w_0| - n(1+K)} = \frac{|w_0|}{1 - n|w_0|(1+K)} < Cn^2|w_0|. \end{aligned}$$

When \(z \ne 0\) then there exists n large so that \(|w-z| < \frac{C}{n^3}\) implies \(w \in V_\epsilon\). Then we have much stronger estimates than needed. \(\square\)

All we need to complete the proof of Theorem 3.5 is the following lemma.

Lemma 3.7

For n sufficiently large we have that

$$\begin{aligned} F^{n+1}(D_n) \subset D_{2n+1}. \end{aligned}$$

Proof

First, we assume \(n>N'\) so that \(t_{n} \in V_\epsilon\). For the center, we use corollary 3.3:

$$\begin{aligned} F^{n+1}\left( t_n,z_0 \right) = \left( t_{2n+1},\phi _n(t_0)\right) \end{aligned}$$

and from Eq. (7) we have

$$\begin{aligned} C\frac{A}{1+(n-N')\epsilon } = |\phi _n(t_0) - z_0| < r(2n+1) = (2n+1)^{-3/4}, \end{aligned}$$

for n large enough this inequality is satisfied. Now for the rest of the disk we use the last lemma. Let \((t_n,z_0+\rho ) \in D_n\), \(|\rho |<r(n)\). Since \(z_0\) is a critical point of order at least 4, then

$$\begin{aligned} F\left( t_n,z_0+\rho \right) - F\left( t_n,z_0 \right) = (0, \rho ^4C), \end{aligned}$$

where C is bounded independent of n. We use Lemma 3.6 for \((t,w)=F\left( t_n,z_0+\rho \right)\) and \((t,z)=F\left( t_n,z_0 \right) =(t_{n+1},t_n)\), so

$$\begin{aligned} \left| \pi _2\left( F^{n+1}\left( t_n,z_0 + \rho \right) - F^{n+1}\left( t_n,z_0 \right) \right) \right| < C'n^2|\rho |^4 . \end{aligned}$$

For n large we have the last inequality in the following line:

$$\begin{aligned} C'n^2|\rho |^4< C'n^2r(n)^4 = C'n^{-1} < r(2n+1) = (2n+1)^{-3/4} , \end{aligned}$$

therefore, we obtain that for n large \(F^{n+1}(D_n) \subset D_{2n+1}.\) \(\square\)

An immediate consequence of Lemma 3.7 is that for sufficiently large \(n \in \mathbb N\) there exists a sequence of \(l_n \rightarrow \infty\) so that \(F^{l_n}(D_n) \rightarrow (0,z_0)\) as \(\ell \rightarrow \infty\), and the proof of Theorem 3.5 is complete. \(\square\)

Lemma 3.8

The disks \(D_n\) are Fatou disks for F.

Proof

We need to prove that the sequence \(F^k\) restricted to each of the disks \(D_n\) is a normal family. We see that the t coordinate of each disk \(D_n\) is going to 0 and therefore stays bounded. For the z coordinate we have that the sequence \(\{\pi _2 F^{2^k(n+1)}, k\ge 0\}\). It is easy to see also that if (t, z) is such that \(|z| > R\) and \(|t| < 1\) then \(F^n(t,z) \rightarrow \infty\). Then it follows that the entire second coordinate of the iterates of F must stay bounded. By Montel’s Theorem this implies that \(F^k\) is a normal family when restricted to each \(D_n.\) \(\square\)

Remark 3.9

However, we see that we cannot enlarge our one-dimensional disks into domains of a polidisk shape. Assume that for each n, there exists a domain \(B_n = U_n\times D_n\) where \(U_n\) is an open ball around each \(t_n\), that is \(U_n = \{|t-t_n|<\delta _n\}\). We will let \(\delta _n\) vary for each n. Clearly, \(D_n \subset B_n\). We will argue by contradiction; assume that there exists a sequence of \(\delta _n >0\) so that \(F^{n+1}(B_n) \subset B_{2n+1}\) for n large enough.

Let \((s,z_0) \in B_n\) where \(0<|s-t_n| < \delta _n\). By assumption \(F^{n+1}(s,z_0) \in B_{2n+1}\), therefore, \(\pi _2(F^{n+1}(s,z_0)) \in D_{2n+1}\) which is equivalent to

$$\begin{aligned} L := |\pi _2(F^{n+1}(s,z_0)) - z_0| < (2n+1)^{-3/4}. \end{aligned}$$
(9)

We will see that this is not possible for any choice of \(\delta _n\).

We estimate L by below

$$\begin{aligned} L = |\pi _2 F^{n+1}(s,z_0) - z_0| \ge |\pi _2 F^{n+1}(s,z_0) - \phi _n(t_0)|-|\phi _n(t_0)-z_0| . \end{aligned}$$
(10)

For n large we have an estimate on the second term of the right hand side of (10):

$$\begin{aligned} |\phi _n(t_0)-z_0| = |\phi _n(t_0)-\phi (t_0)| < C'/n. \end{aligned}$$

For the first term on the right hand side of (10), we have:

$$\begin{aligned} |\pi _2 F^{n+1}(s,z_0) - \phi _n(t_0)| = |\phi _n(s') - \phi _n(t_0)| \ge C|s'-t_0| , \end{aligned}$$

where \(\frac{s'}{1+ns'} = s\) or equivalently \(s' = s / (1-ns)\). Since \(\delta '_n = |s-t_n| \ne 0\), then \(\delta '_0 = |s'-t_0| \ne 0\). Back in (10)

$$\begin{aligned} L = |\pi _2 F^{n+1}(s,z_0) - z_0| \ge C\delta '_0 - C'/n ,\end{aligned}$$

which together with the bound (9) gives us a contradiction. Therefore, it is not possible to fatten the disks above. For a more recent result on open wandering domains for skew product maps see [1]. Their technique, based on an idea of M. Lyubich, is to use parabolic implosion.