Abstract
Background
We propose an a posteriori estimator of the error of hyper-reduced predictions for elastoviscoplastic problems. For a given fixed mesh, this error estimator aims to forecast the validity domain in the parameter space, of hyper-reduction approximations. This error estimator evaluates if the simulation outputs generated by the hyper-reduced model represent a convenient approximation of the outputs that the finite element simulation would have predicted. We do not account for the approximation error related to the finite element approximation upon which the hyper-reduction approximation is introduced.
Methods
We restrict our attention to generalized standard materials. Upon use of incremental variational principles, we propose an error in constitutive relation. This error is split into three terms including a tailored norm of the hyper-reduction approximation error. This error norm is defined by using the convexity of an incremental potential introduced to state the constitutive equations. The second term of the a posteriori error is related to the stress recovery technique that generates stresses fulfilling the finite element equilibrium equations. The last term is a coupling term between the hyper-reduction approximation error at each time step and the errors committed before this time step. Unfortunately, this last term prevents error certification. In this paper, we restrict our attention to outputs extracted by a Lipschitz function of the displacements.
Results
In the proposed numerical examples, we show very good preliminary results in predicting the validity domain of hyper-reduction approximations. The average computational time of the predictions obtained by hyper reduction, is accelerated by a factor of 6 compared to that of finite element simulations. This speed-up incorporates the computational time devoted to the error estimation.
Conclusions
The numerical implementation of the proposed error estimator is straightforward. It does not require the computation of the incremental potential. In the numerical results, the estimated validity domain of hyper-reduced approximations is inside the reference validity domain. This paper is a first attempt for a posteriori error estimation of hyper-reduction approximations.
Similar content being viewed by others
Background
Reduced-Order models aim at reducing the computational time required to obtain solutions of Partial Differential Equations (PDE) which are physically-based and parameter dependent. They reduce the computational complexity of optimization procedures or parametric analyses [1-3].
Reduced-Order Models are very useful to model complex mechanical phenomena, when parametric studies are mandatory to setup convenient nonlinear constitutive equations or boundary conditions. In such situations, many open questions about physical assumptions arise and the scientist’s intuition alone cannot guarantee that convenient simplified numerical approximations are chosen. Here, we consider hyper-reduced (HR) simulations, involving both a reduced-basis approximation and reduced-coordinate estimation by using a mesh restricted to Reduced Integration Domain (RID) [4,5]. The introduction of the RID is crucial for elastoviscoplastic models, because in many practical cases, no speed-up is achieved if the mesh is not restricted to the RID. In such a framework, error estimation provides a valuable algorithmic approach to check if hyper-reduced simulations have been performed in the validity domain of the hyper-reduced model, and if they allow a physical understanding of the simulation outputs.
HR simulations may not be performed in faster time than predictions using metamodeling, response surface methods, or virtual charts [6]. But, unlike these methods, Reduced-Order Models involve equations related to physical principles (i.e. the balance of momentum), physical constitutive equations and data, validated by experiments. Such an approach enables certification of outputs of interest [7], or error estimation of predictions obtained by using Reduced-Order Models [7-11]. Moreover, error estimation is mandatory in many model reduction of parametric Partial Differential Equations, when one needs to evaluate, in the parameter space, a trust region or a validity domain related to Reduced-Basis accuracy [12-14]. Error estimation is also mandatory to perform a priori model reduction by using greedy algorithms [15,16] or the A Priori Hyper-reduction method [4].
Unfortunately, in nonlinear mechanics of materials, parametric PDEs are rarely affine in parameter, and it is quite difficult to reduce equations and data to an approximate affine form as proposed in [15] by using the Empirical Interpolation Method [17,18]. The novelty of this paper is the use of an incremental variational principle [19-21] to develop an a posteriori estimator of errors for HR predictions in case of generalized standard elastoviscoplastic models. As usual, the finite element (FE) solution fulfills incremental equations in time, but no differential equations related to the continuous time variable. The incremental variational principle enables to preserve formulations discrete in time when comparing the HR solution to the FE solution. This approach enables to state a relationship between a tailored norm of the hyper-reduction approximation error and the a posteriori estimator of this error. Here, we term hyper-reduction approximation error (HRAE) the difference between the FE solution of the PDE and its estimation by the hyper-reduced model. The reference solution is the FE solution, not the exact solution of the PDE. In the sequel, the proposed tailored norm of the displacement is denoted by ∥u∥ u , where u is the predicted displacement over the domain Ω. The error estimator is denoted by η. We follow the theory of constitutive relation error (CRE) proposed by P. Ladevèze [22]. This kind of a posteriori error has been developed for a large set of constitutive equations [9,23-26]. Although constitutive relation error (CRE) can handle all approximation errors due to time discretization, FE approximation, and eventually a separated representation of the displacements [27], we restrict our attention to approximation errors due to the additional assumptions incorporated in the numerical model by the hyper-reduced formulation. Here, the CRE η requires the construction of stresses fulfilling FE equilibrium equations.
In the numerical part of this paper, we apply the error estimation to forecast the validity domain of hyper-reduced predictions of simulation outputs. Adjoint sensitivity analyses have been introduced for certification of outputs in [8,28]. In case of time dependent problems, the adjoint equation or the mirror problem [25] is solved backward in time from T to 0. Here, we circumvent such a complex numerical solution by restricting our attention to Lipschitz functions of the displacements for simulation outputs, similarly to [29]. The output function is denoted by \(s(\textbf {u}) \in \mathcal {R}^{N_{s}}\). The Lipschitz continuity of the output s(u) reads:
where \(\mathcal {V}_{h}\) is the convenient Hilbert space related to the FE approximation of the PDE, ∥·∥ F is the Frobenius norm on \(\mathbb {R}^{N_{s}}\). The elastoviscoplastic problem is both discretized in space and in time by the finite element method and the forward Euler scheme. The solution of this FE problem at discrete time \(\phantom {\dot {i}\!}t^{n} \in \{t^{o}, \ldots, t^{N_{t}} \}\) is denoted by \(\textbf {u}^{n}_{\textit {FE}}\):
where \(({\boldsymbol \xi }_{i})_{i=1}^{N_{\xi }}\) are the FE shape functions, x the space coordinate, μ is a vector of parameters and  is a given parameter space.The hyper-reduction approximation of this FE solution is denoted by \(\textbf {u}^{n}_{\textit {HR}}\):
is a given parameter space.The hyper-reduction approximation of this FE solution is denoted by \(\textbf {u}^{n}_{\textit {HR}}\):
where \((\boldsymbol {\psi }_{k})_{k=1}^{N_{\psi }}\) is a given reduced-basis, \(({\gamma ^{n}_{k}})_{k=1}^{N_{\psi }}\) are the reduced coordinates evaluated by using equilibrium equations set-up on the RID denoted by Ω Z , Ω Z ⊂Ω, by following the hyper-reduction method [5]. The HRAE is denoted by e n, \(\textbf {e}^{n} = \textbf {u}^{n}_{\textit {FE}} - \textbf {u}^{n}_{\textit {HR}}\). Because of the time discretization, we cannot consider the approximation error e n separately for each time index n. We must account for the error at all discrete times simultaneously. Therefore, the upper bound of interest related to the Lipschitz continuity reads:
The reference validity domain of the hyper-reduced model is denoted by \(\mathcal {D}_{V}\). Its definition reads:
where ε D is a given tolerance. The proposed numerical error estimation aims to forecast a reliable approximation of \(\mathcal {D}_{V}\) by the recourse to hyper-reduced simulations, a posteriori estimations of errors and a FE simulation used to generate reduced-bases. The approximate validity domain is denoted by \(\widetilde {\mathcal {D}}_{V}\):
where c η is a substitute for the Lipschitz constant c o , η is a substitute for the tailored norm of the HRAE, \((\textbf {u}^{n}_{\textit {HR}})_{n=1}^{N_{t}}\) is the sequence of hyper-reduced predictions over the full time interval and \((\widehat {{\boldsymbol \sigma }}^{n})_{n=1}^{N_{t}}\) is a sequence of stresses fulfilling the FE equilibrium equation at each discrete time t n, where \(\widehat {{\boldsymbol \sigma }}^{n}\) is an affine function of the stress estimated from \(\textbf {u}^{n}_{\textit {HR}}\). In the sequel, both sequences \((\textbf {u}^{n}_{\textit {HR}})_{n=1}^{N_{t}}\) and \((\widehat {{\boldsymbol \sigma }}^{n})_{n=1}^{N_{t}}\) are denoted by u HR and \(\widehat {{\boldsymbol \sigma }}\) respectively.
Various Reduced-Basis construction methods can be incorporated into the hyper-reduced model. For the sake of simplicity, in the following numerical examples, the Reduced-Basis is provided by a Proper Orthogonal Decomposition [30-32] of the FE solution related to a given parameter value \(\boldsymbol {\mu }^{1} \in \mathcal {D}\). The POD modes are orthonormal solutions of the following mimization problem:
where <·,·> is the L 2 scalar product defined on Ω and \(\| \cdot \|_{L^{2}(\Omega)}\phantom {\dot {i}\!}\) is the related norm. The hyper-reduced model is set-up in order to provide an accurate approximate solution for μ=μ 1:
where ε HR is a given tolerance. Hence \(\boldsymbol {\mu }^{1} \in \widetilde {\mathcal {D}}_{V}\). Moreover c η fulfills the following constraint:
In this paper μ 1 is arbitrary chosen. Nevertheless, the knowledge of an approximate validity domain aims to validate this choice or to adapt it. In the sequel, for clarity, we do not mention the vector of parameters μ in the notations.
Methods
This section is organized as follows. The generalized standard constitutive equations are presented first. They are based on an incremental variational principle proposed in [33]. Then, we introduce the hyper-reduced incremental problem to be solved. The following section is devoted to the construction of the FE-equilibrated stress within the framework of the hyper-reduced modeling. The next sections introduce the error estimator, the tailored norm related to the CRE and the partition of the CRE. We finish by remarks on the numerical implementation of the proposed approach.
Incremental potential for the constitutive equations
The constitutive laws are described by using an incremental potential in the framework of the irreversible thermodynamic processes. A priori error estimators and incremental variational formulations were introduced in [33] for mechanical problems of bodies undergoing large dynamic deformations. Extensions of this approach were proposed in [20,21] for effective response predictions of heterogeneous materials. The strain history is taken into account by using internal variables denoted by α. These variables are the lump sum of the history of material changes. This approach has its roots in the works by Biot [34], Ziegler [35], Germain [36] or Halpen and Nguyen [37] and has proven its ability to cover a broad spectrum of models in viscoelasticity, viscoplasticity, plasticity and also continuum damage mechanics. The FE solution is approximated by an hyper-reduced predictions denoted by \(\textbf {u}_{\textit {HR}}^{n}\), \(\boldsymbol {\alpha }_{\textit {HR}}^{n}\), \(\boldsymbol {\sigma }_{\textit {HR}}^{n}\) respectively for the displacements, the internal variables and the Cauchy stress, at discrete time t n. For the sake of simplicity, we denote by \(\boldsymbol {\varepsilon }_{\textit {HR}}^{n}\) the strain tensor \(\boldsymbol {\varepsilon }(\textbf {u}_{\textit {HR}}^{n})\), in the framework of the infinitesimal strain theory.
According to the framework of the incremental variational formulations, the constitutive law is defined by a condensed incremental potential, denoted by \(w_{\Delta }(\boldsymbol {\varepsilon }_{\textit {HR}}^{n})\), such that:
In practice, we do not implement the computation of the partial derivative of w Δ with respect to the component of the strain tensor. Nevertheless, Equation (10) is fulfilled up to the computer precision. The internal variables are solutions of the following equation [21]:
where w(ε,α) is the free energy of the material, and \(\varphi (\dot {\boldsymbol {\alpha }})\) is its dissipation potential [36]. The two potentials w and φ are convex functions of their arguments (ε,α) and \(\dot {\boldsymbol {\alpha }}\) respectively, according to the theory of generalized standard materials [36,37]. Examples of constitutive laws can be found in [38]. A detailed example is given in the last section of this paper.
The convexity of w Δ is proved in [21] under the assumption that w and φ are convex functions. In the sequel, the explicit knowledge of the condensed incremental potential is not required for the mathematical formulation of the error estimator.
By recourse to the Legendre transformation, the dual potential of w Δ , denoted by \(w^{\star }_{\Delta }\), reads:
We restrict our attention to convex functions w Δ , hence:
Therefore:
The definition of the partial derivatives \(\frac {\partial w_{\Delta }}{\partial \boldsymbol {\varepsilon }}\) and \(\frac {\partial w^{\star }_{\Delta }}{\partial \boldsymbol {\sigma }}\) is extended to fulfill the following equations:
Hence, by construction, \(\boldsymbol {\sigma }^{n}_{\textit {HR}}\) and \(\boldsymbol {\varepsilon }_{\textit {HR}}^{n}\) fulfill the following equation:
Hyper-reduced setting
The continuous medium is occupying a domain Ω. The boundary ∂ Ω of Ω is denoted by ∂ U Ω∪∂ F Ω. On ∂ U Ω, there is the Dirichlet condition u=u c . On ∂ F Ω, there is a given force field F n. The FE displacement field belongs to a function space \(\textbf {u}_{c} +\mathcal {V}_{h}\). The reduced subspace is denoted by \(\mathcal {V}_{\textit {ROM}}\):
We denote by V the matrix form of empirical modes defined on the FE basis:
By following the hyper-reduction method [39], we generate the RID Ω
Z
by using the empirical modes \(({\boldsymbol \psi }_{k})_{k=1}^{N_{\psi }}\) and the strain modes \((\boldsymbol {\varepsilon }(\boldsymbol {\psi }_{k}))_{k=1}^{N_{\psi }}\). When the RID is known, we determine the set of available FE residual entries when the stress estimation is restricted to Ω
Z
. This set is denoted by  such that:
such that:
Therefore, we can define truncated test functions insuring a weak form of the balance of momentum restricted to the domain Ω Z , since these test functions are set to zero over Ω∖Ω Z. These truncated test functions are denoted by \(({\boldsymbol {\psi }_{k}^{Z}})_{k=1}^{N_{\psi }}\) such that:
The statement of the hyper-reduced incremental problem is the following. Given a parameter vector μ, find an estimation of the reduced coordinates γ n such that \(\textbf {u}_{\textit {HR}}^{n} \in \textbf {u}_{c} + \mathcal {V}_{\textit {ROM}}\) fulfills the constitutive equations and the principle of virtual work:
where : is the contracted product for second-order tensors. We must emphasize the fact that Equation (24) gives access to the displacement in all the domain Ω although the equilibrium is set only on Ω Z . Hence, when the hyper-reduced solution is known, the stress \(\boldsymbol {\sigma }^{n}_{\textit {HR}}\) can be estimated on the full domain Ω by using Equation (10).
The FE equations are obtained by substituting in equations (24) to (26), the following items:
-
the shape functions \((\boldsymbol {\xi }_{i})_{i=1}^{N_{\xi }}\) for \((\boldsymbol {\psi }_{k})_{k=1}^{N_{\psi }}\),
-
the test functions \((\boldsymbol {\xi }_{i})_{i=1}^{N_{\xi }}\) for \(({\boldsymbol {\psi }_{k}^{Z}})_{k=1}^{N_{\psi }}\),
-
the full domain Ω for Ω Z ,
-
the variables \(((q_{i})_{i=1}^{N_{\xi }},\textbf {u}^{n}_{\textit {FE}}, \boldsymbol {\sigma }^{n}_{\textit {FE}}, \boldsymbol {\alpha }^{n}_{\textit {FE}})\) for \(\left ((\gamma _{k})_{k=1}^{N_{\psi }},\textbf {u}^{n}_{\textit {HR}}, \boldsymbol {\sigma }^{n}_{\textit {HR}}, \boldsymbol {\alpha }^{n}_{\textit {HR}}\right)\).
However, in Equation (27), the incremental potential related to the hyper-reduced prediction is not the incremental potential of the FE prediction, because \(\boldsymbol {\alpha }^{n-1}_{\textit {FE}}\) and \(\boldsymbol {\alpha }^{n-1}_{\textit {HR}}\) may differ. So, \(\boldsymbol {\sigma }^{n}_{\textit {FE}}\) fulfills the constitutive equation, but it may not be a derivative of w Δ . Therefore, we introduce a correction term in stress, denoted by δ σ n, such that:
where \(\boldsymbol {\varepsilon }_{\textit {FE}}^{n} = \boldsymbol {\varepsilon }(\textbf {u}_{\textit {FE}}^{n})\) and δ σ n account for the variation of the internal variables due to the difference between \(\left (\boldsymbol {\varepsilon }_{\textit {FE}}^{i}\right)_{i=1}^{n-1}\) and \(\left (\boldsymbol {\varepsilon }_{\textit {HR}}^{i}\right)_{i=1}^{n-1}\) at time instants before t n. The convexity of w and ϕ insures that the FE solution is unique, if no rigid mode is available.
Dual reduced-subspace
In this section, we introduce the technique of construction of the stress fields \(\widehat {\boldsymbol {\sigma }}^{n}\) fulfilling the finite element equilibrium equation at each discrete time t n. These stress fields are used in the next sections to build a CRE. The FE equilibrium equation is a linear equation upon stresses denoted by σ n. It defines an affine space such that \(\boldsymbol {\sigma }^{n} \in \boldsymbol {\sigma }^{n}_{N} + \mathcal {S}_{h}\), where \(\boldsymbol {\sigma }^{n}_{N}\) is a particular solution of Neumann boundary conditions (i.e. in the linear elastic case for instance), and \(\mathcal {S}_{h}\) is the following vector space:
The following linear elastic problem gives us \(\boldsymbol {\sigma }^{n}_{N}\):
where \(E_{o} \in \mathbb {R}^{+}\) is an abritary constant.
By the recourse to the stress predicted by the FE simulation for μ=μ 1, we obtain the snapshots of stress fields \(\left (\boldsymbol {\sigma }^{n}_{\textit {FE}}(\cdot ;\boldsymbol {\mu }^{1}) - \boldsymbol {\sigma }^{n}_{N}\right)_{n=1}^{N_{t}}\) that span a subspace of \(\mathcal {S}_{h}\):
Similarly to the approach proposed in [10] for elasticity, we introduce a dual reduced-subspace denoted by \(\mathcal {S}_{\textit {ROM}} \subset \mathcal {S}_{h}\). \(\mathcal {S}_{\textit {ROM}}\) is generated by the usual POD applied to \(\left (\boldsymbol {\sigma }^{n}_{\textit {FE}}(\cdot ;{\boldsymbol \mu }^{1}) - \boldsymbol {\sigma }^{n}_{N}\right)_{n=1}^{N_{t}}\). Its dimension is denoted by \(N^{\sigma }_{\psi }\), and it is such that \(N^{\sigma }_{\psi } \le N_{t}\).
Hence, the hyper-reduced predictions of the stress tensor can be projected into the space of admissible stresses fulfilling the FE equilibrium equation. This projection reads:
The above minimization problem is a global L 2 projection of the stress \(\boldsymbol {\sigma }^{n}_{\textit {HR}}\) onto the reduced basis that span \(\mathcal {S}_{\textit {ROM}}\). The dual basis being a POD basis, it is orthonormal with respect to the L 2 scalar product. So the computational complexity of the stresses projection scales linearly with the number of Gauss points of the mesh and \(N^{\sigma }_{\psi }\). In practice, this computational complexity is negligible compared to the complexity of the evaluation of \(\boldsymbol {\sigma }^{n}_{\textit {HR}}\), by using the constitutive equations.
The constitutive relation error and its partition
The reference solution being incremental in time, no continuous formulation in time is considered for the error estimator. The error estimation proposed in [33] for incremental variational formulation, is related to an asymptotic convergence assumption in order to get an upper bound of the approximation error related to the FE discretization. This upper bound depends on a constant related of the weak form of the partial differential equations. Here, we propose to apply the Constitutive Relation Error method proposed in [22] to estimate the constant c η without assuming an asymptotic convergence of the HRAE.
Following the method proposed in [22], a constitutive relation error, denoted by η, can be introduced as follows:
where \(\widehat {\boldsymbol {\sigma }}^{n}\) is defined by Equation (34). The following properties hold:
The first property (36) comes from the Legendre transformation (14). The property (37) comes from Equation (19). The proof of Property (38) is the following. If \(\eta (\textbf {u}^{n}_{\textit {HR}}, \: \widehat {\boldsymbol {\sigma }}^{n}) = 0\forall \: n \in \{1,\ldots,N_{t}\}\) then \((\textbf {u}^{n}_{\textit {HR}}, \widehat {\boldsymbol {\sigma }}^{n}, \boldsymbol {\alpha }^{n}_{\textit {HR}})\) fulfills the constitutive equations, the Dirichlet conditions and the FE equilibrium equation. As \((\textbf {u}^{n}_{\textit {HR}}, \widehat {\boldsymbol {\sigma }}^{n}, \boldsymbol {\alpha }^{n}_{\textit {HR}})\) fulfills all the equations of the FE problem, it is a solution of the FE problem and e n=0.
We propose for ∥e n∥ u an Hilbert norm parametrized by the approximate solution \(\textbf {u}^{n}_{\textit {HR}}\) and the exact solution \(\textbf {u}^{n}_{\textit {FE}}\). This parametrized norm is defined by:
where ε(·) is the symmetric part of the gradient and G a symmetric positive-definite fourth-order tensor. If the identity tensor is substituted for G, we obtain a usual H 1(Ω) norm. We assume that there is no rigid mode, neither in the FE solution nor in the reduced basis.
The following mathematical developments aim to establish a relation between \(\eta (\textbf {u}_{\textit {HR}}, \: \frac {\partial w_{\Delta }}{\partial \boldsymbol {\varepsilon }}(\boldsymbol {\varepsilon }_{\textit {FE}}))\) and the tailored norm ∥e n∥ u . We choose G by the recourse to the convexity of the incremental potential w Δ . According to the Legendre transformation, we have:
Hence, we can remove the contribution of the dual potential \(w_{\Delta }^{*}\) in \(\eta \left (\textbf {u}_{\textit {HR}}, \: \frac {\partial w_{\Delta }}{\partial \boldsymbol {\varepsilon }}(\boldsymbol {\varepsilon }_{\textit {FE}}) \right)\):
Let us define the scalar function f(λ):
We assume that f is C 2 on [0,1]. The application of the Taylor Lagrange formula at order 2 leads to:
The function evaluation and its derivatives read:
Therefore, by choosing:
we obtain the following property:
This property is an intermediate result before establishing the relationship between \(\| \textbf {e}^{n} \|_{u}^{2}\) and the error estimator. The incremental potential being strictly convex, G is definite positive. A schematic view of \(\sum _{n=1}^{N_{t}} \| \textbf {e}^{n} \|_{u}^{2}\) is shown on Figure 1.
Tailored norm. Schematic view of the physically-based norm of the approximation error, related to the convexity of the incremental potential. The ordinates of points on the dashed line are given by \(z\left (\varepsilon ^{\star }\right) = \sum _{n=1}^{N_{t}} \int _{\Omega } w_{\Delta }\left (\varepsilon ^{n}_{\textit {FE}}\right) + \frac {\partial w_{\Delta }}{\partial \varepsilon }\left (\varepsilon ^{n}_{\textit {FE}}\right) :\left (\varepsilon ^{\star n}- \varepsilon ^{n}_{\textit {FE}} \right) \: d\Omega \).
Similarly, a norm on stresses can be defined to measure the distance between the admissible stress \(\widehat {\boldsymbol {\sigma }}^{n}\) and \(\boldsymbol {\sigma }_{\textit {FE}}^{n} - \delta \boldsymbol {\sigma }^{n}\), by the recourse to the dual potential \(w_{\Delta }^{\star }\) such that:
where H is a positive symmetric fourth order tensor. To establish the relation between H and the Hessian matrix of the potential \(w^{\star }_{\Delta }\), we consider \(\eta (\textbf {u}_{\textit {FE}}, \widehat {\boldsymbol {\sigma }})\). Intermediate stresses \((\textbf {S}^{n}(\lambda))_{n=1}^{N_{t}}\) are introduced such that:
By the recourse to the Taylor Lagrange formula, we obtain the following property:
Property.
The proposed constitutive relation error fulfills the following partition:
The last term of the sum is a coupling term between the error e n and the HRAE committed before the discrete time t n. Since we can’t certify that this term is positive, η is not an upper bound of the HRAE.
Thanks to the definition of δ σ by Equation (28), we have the following properties:
We start proving the partition property by considering the following sum of terms:
In  , the contributions of w
Δ
and \(w^{\star }_{\Delta }\) are canceled when considering the definition of η, and we obtain:
, the contributions of w
Δ
and \(w^{\star }_{\Delta }\) are canceled when considering the definition of η, and we obtain:
Then:
where \(\boldsymbol {\varepsilon }_{\textit {FE}}^{n}- \boldsymbol {\varepsilon }_{\textit {HR}}^{n} = \boldsymbol {\varepsilon }(\textbf {e}^{n})\). Therefore, according to properties (53), (55) and (56), the following partition is fulfilled:
Since \(\textbf {e}^{n} \in \mathcal {V}_{h}\) and \(\boldsymbol {\sigma }_{\textit {FE}}^{n} - \widehat {\boldsymbol {\sigma }}^{n} \in \mathcal {S}_{h}\), then:
This ends the proof.
Property.
If e n=0, for n∈{1,…,N t } then \(\textbf {u}^{n}_{\textit {HR}} = \textbf {u}^{n}_{\textit {FE}}\), \(\boldsymbol {\alpha }^{n}_{\textit {HR}} = \boldsymbol {\alpha }^{n}_{\textit {FE}}\), δ σ n=0 and:
In the general case, the closer \(\widehat {\boldsymbol {\sigma }}^{n}\) to \(\boldsymbol {\sigma }_{\textit {FE}}^{n} - \delta \boldsymbol {\sigma }^{n}\) the better the error estimation. The proposed error estimator incorporates errors related to the projection of the stress onto the dual reduced basis.
Numerical implementation of the CRE
The numerical implementation of the incremental potential and its dual is not required for the error estimation. Let’s consider the following function of a scalar coordinate λ:
Then:
Therefore, the following property holds:
Here, \(\widehat {\boldsymbol {\varepsilon }}^{n}(\lambda)\) is the strain tensor given by the constitutive equation upon the stress τ(λ) at time t n and the internal variables \(\boldsymbol {\alpha }^{n-1}_{\textit {HR}}\) at time t n−1. Hence, the numerical estimation of \(\widehat {\boldsymbol {\varepsilon }}^{n}(\lambda)\) can be performed by the usual implementation of the constitutive equations of generalized standard materials [40-42].
In the following numerical simulations, we have estimated the integral on λ by the value of first derivative of g for λ=1.
Numerical estimation of the constant c η
In practice, we have more modes than necessary to achieve accurate predictions for μ=μ 1, because the POD of \((\textbf {u}^{n}_{\textit {FE}}(\cdot, \: \boldsymbol {\mu }^{1}))_{n=1}^{N_{t}}\) is accurate up to the numerical precision. The total number of available modes is denoted by \(\overline {N}_{\psi }\) such that \(\overline {N}_{\psi } \le \min (N_{\xi }, N_{t})\) and \(N_{\psi } \le \overline {N}_{\psi }\). This gives access to several hyper-reduced models by restricting the number of modes involved in the reduced basis related to the displacements. The constant c η is set-up by using these approximate hyper-reduced solutions and the known stresses predicted by the FE model:
Hence the constraint (9) is fulfilled. Let us denote by \(N^{c}_{\psi }\) the number of displacement modes for which the maximum in Equation (66) is reached. In our opinion, if we expect that the error estimator behaves like an upper bound, we should not take \(N^{c}_{\psi }\) modes to generate the final HR model. In the following example, we are setting \(N_{\psi } = N^{c}_{\psi }+1\).
Results and discussion
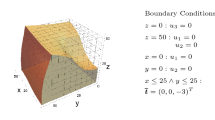
We apply the estimation of the validity domain to a beam composed with a layer of tin alloy (SnX) on a layer of copper (Cu). This is a cantilever beam shown in Figure 2. The thickness of the tin is 0.155 mm, the thickness of the copper in 0.111 mm, the width and the length of the beam are respectively 2. mm and 12. mm. These are the dimensions of an experimental specimen used at the Centre des Matériaux. The simulation output is the difference between an experimental transverse displacement at point A, shown in Figure 2, and its prediction by the mechanical model:
where y is the transverse axis and \(u_{\textit {exp}}^{n}\) is a given experimental measurement of the transverse displacement of the point A. The copper is assumed to be elastic and isotropic. Its Young modulus is 63000. MPa and its Poisson coefficient is 0.3. The tin alloy is isotropic and elastoviscoplastic with a linear kinematic hardening. The potentials of the tin alloy read:
where E=80000. MPa, ν=0.3, m=8., R o =0.1 MPa. These material coefficients are reasonably good enough to fit experiments performed at the Centre des Matériaux. The parameters of the mechanical model are the material coefficients h and C related to viscoplasticity and kinematic hardening respectively. The range of variation for μ=(h,C) is [15. MPa, 30. MPa]×[3000. MPa, 40000. MPa]. The pointwise load follows a sinusoidal time variation:
The FE simulation used to generate the reduced basis is performed on an arbitrary sampling point μ 1=(20. MPa, 30000. MPa). The POD of the FE solution gives \(\overline {N}_{\psi } = 9\) displacement modes with non-zero eigenvalue. It also provides \(\overline {N}_{\psi }^{\sigma } = 48\) admissible stress modes. We denote by \((\boldsymbol {\psi }_{k}^{\sigma })_{k=1}^{\overline {N}_{\psi }^{\sigma }}\) the statically admissible modes related to the POD of \((\boldsymbol {\sigma }^{n}_{\textit {FE}}(\cdot ;\boldsymbol {\mu }^{1}) - \boldsymbol {\sigma }^{n}_{N})_{n=1}^{N_{t}}\). Some of these modes are shown in Figure 3.
Figure 4 shows that the proposed error estimator incorporates errors related to the projection of the stress onto the dual reduced basis. In this example, if the number of modes of the dual reduced-basis is too small (i.e. smaller than 24), the error estimator does not account for the improvement of u HR when the reduced-basis \((\psi _{k})_{k=1}^{N_{\psi }}\) has more than 3 modes. The convenient choice of \(N_{\psi }^{\sigma }\) is set-up by considering its influence on the smallest value of η for large values of N ψ . Here, \(N_{\psi }^{\sigma } = 29\) makes this influence negligible for all values of N ψ . When \(N_{\psi }^{\sigma }\) has been fixed, we can estimate c η according to Equation (66). Figure 5 shows the curve related to the HRAE and the error estimator c η η obtained for the sampling point μ=μ 1, when varying the number of displacement modes for the maximization problem (66).
For the proposed example, inside the plastic zone, the stress field through the thickness of the beam is very sensitive to modifications of the parameters h and C. Here, the validity domain of the hyper-reduction approximations is defined by \(\epsilon _{D} = 0.05^{2} \: \sum _{n=1}^{N_{t}} (u_{\textit {exp}}^{n})^{2}\). It is shown in Figure 6. The hyper-reduced model is set-up by choosing \(\epsilon _{\textit {HR}} = \frac {\epsilon _{D}}{25. \: 10^{2}}\). Then, N ψ =7 and the related RID Ω Z , shown in Figure 2, involves 31 elements over a total of 120 elements. The average number of Newton-Raphson iterations is 4 per time step. The speed-up obtained with this hyper-reduced model, including the error estimation, is 6. Without error estimation the speed-up is 8. Hence, the cost of error estimation is quite reasonable and the computational-complexity reduction is preserved. Here, the FE model is very simple. The bigger the FE model, the larger we expect the speed-up to be.
Error prediction on outputs. On the left, in blue, the reference validity domain \(\mathcal {D}_{V}\) over the parameter space  , on the right the approximate one \(\widetilde {\mathcal {D}}_{V}\). The white star is located at the sampling point μ
1. The black dashed line is the limit of the reference validity domain defined by an error on the outputs lower than 5%.
, on the right the approximate one \(\widetilde {\mathcal {D}}_{V}\). The white star is located at the sampling point μ
1. The black dashed line is the limit of the reference validity domain defined by an error on the outputs lower than 5%.
The estimation of the validity domain is shown on the right of Figure 6. It is quite restrictive. This means that most of the points in \(\widetilde {\mathcal {D}}_{V}\) are in the reference validity domain \(\mathcal {D}_{V}\). Here, for small values of the parameter h, the prediction of the validity domain is too conservative. Such a situation can appear when the average influence of a parameter on the solution is larger than its influence on the output, because the error estimator is linked to the HRAE in an average sense.
We have tried the proposed numerical approach in case of \(N_{\psi } = N_{\psi }^{c}\) (here \(N_{\psi }^{c} = 6\)), by using the same RID. The estimated validity domain and the boundary of the reference validity domain for the related HR model are shown in Figure 7. This modification has significant influence on the numerical results. Once again, all the points in \(\widetilde {\mathcal {D}}_{V}\) are in the reference validity domain.
We have performed additional numerical simulations by substituting a Dirichlet boundary condition to the pointwise load. In this case, the time evolution of the load is:
Figure 8 shows the estimation of the validity domain of the hyper-reduced model compared to the boundary of \(\mathcal {D}_{V}\), for this case of a non-zero Dirichlet boundary condition. Both reference validity domain and its estimation are different compared to the previous ones because the reduced bases are different. They have a better accuracy with respect to N ψ =7 and \(N_{\psi }^{\sigma } = 29\).
Error prediction on outputs in case of non-zero Dirichlet boundary condition. In blue, the approximate validity domain \(\widetilde {\mathcal {D}}_{V}\). The white star is located at the sampling point μ 1. The black dashed line is the limit of the reference validity domain defined by an error on the outputs lower than 5%.
We can notice that the higher h and C, the smaller the plastic strains in the beam. Since the hyper-reduced model is accurate for low plastic strains, the validity domain covers the high values of h and C.
Conclusions
We propose an a posteriori estimator of hyper-reduction errors that aims to evaluate if the simulation outputs predicted by hyper-reduced models are convenient approximations of the outputs that the finite element simulation would have predicted. By choosing a tailored norm of the approximation error on displacement, we show how the proposed error estimator is related to the HR approximation error. This error estimator receives the contribution of a coupling term between the error at time step n and the error committed before. We show that this term prevents rigorous error certification. But in practice, numerical examples show a restrictive estimation of the validity domain of the HR model. By restrictive, we mean that this domain is inside the reference validity domain computed by using both the FE solution and the HR solution. The speed-up achieved by the HR model including the estimation of the constitutive relation error is 6 on the proposed numerical elasto-viscoplastic examples. The estimation of the validity domain requires the computation of a constant similar to a Lipschitz constant. This constant is estimated without any additional simulation of FE solution, but the FE solution at the sampling point μ=μ 1. As shown in is this paper, the numerical implementation of the proposed error estimator is very simple. It does not require the computation of the incremental potential or of its dual. This paper is a first attempt for a posteriori error estimation of hyper-reduction approximations. More numerical experiments are in preparation for the assessment of the proposed numerical approach.
Abbreviations
- PDE:
-
Partial differential equation
- RID:
-
Reduced integration domain
- HR:
-
Hyper-reduced
- FE:
-
Finite element
- HRAE:
-
Hyper-reduction approximation error
- CRE:
-
Constitutive relation error
References
Ganapathysubramanian B, Zabaras N (2008) A non-linear dimension reduction methodology for generating data-driven stochastic input models. J Comput Phys 227(13): 6612–6637.
Balima O, Favennec Y, Petit D (2007) Model reduction for heat conduction with radiative boundary conditions using the modal identification method. Numer Heat Transfer Part B-Fundam 52(2): 107–130.
Daescu DN, Navon IM (2007) Efficiency of a pod-based reduced second-order adjoint model in 4d-var data assimilation. Int J Numer Methods Fluids 53(6): 985–1004.
Ryckelynck D (2005) A priori hyperreduction method: an adaptive approach. J Comput Phys 202(1): 346–366. doi:10.1016/j.jcp.2004.07.01.
Ryckelynck D (2009) Hyper-reduction of mechanical models involving internal variables. Int J Numer Methods Eng 77(1): 75–89.
Chinesta F, Keunings R, Leygue A (2014) The Proper Generalized Decomposition for Advanced Numerical Simulations: a Primer. SpringerBriefs in applied sciences and technology. Springer, New Haven.
Ngoc Cuaong N, Veroy K, Patera AT (2005) Certified real-time solutin of parametrized partial differential equations. In: Yip (ed)Handbook of Material Modeling, 1529–1564.. Springer, Sidney. doi:10.1007/978-1-4020-3286-8_76.
Ammar A, Chinesta F, Diez P, Huerta A (2010) An error estimator for separated representations of highly multidimensional models. Comput Methods Appl Mech Eng 199(25-28): 1872–1880. doi:10.1016/j.cma.2010.02.012.
Ladevèze P, Chamoin L (2011) On the verification of model reduction methods based on the proper generalized decomposition. Comput Methods Appl Mech Eng 200(23-24): 2032–2047. doi:10.1016/j.cma.2011.02.019.
Kerfriden P, Ródenas JJ, Bordas SP-A (2014) Certification of projection-based reduced order modelling in computational homogenisation by the constitutive relation error. Int J Numer Meth Engng 97: 395–422.
de Almeida JPM (2013) A basis for bounding the errors of proper generalised decomposition solutions in solid mechanics. Int J Numer Methods Eng 94(10): 961–984. doi:10.1002/nme.4490.
Arian E, Fahl M, Sachs EW (2000) Trust-region proper orthogonal decomposition for flow control In: NASA/CR-. 2000-210124, No. 2000-25.. ICASE Report, Ohio University.
Michel B, Laurent C (2008) Optimal control of the cylinder wake in the laminar regime by trust-region methods and pod reduced-order models. J Comput Phys 227: 7813–7840.
Bui D, Hamdaoui M, De Vuyst F (2013) Pod-isat: An efficient pod-based surrogate approach with adaptive tabulation and fidelity regions for parametrized steady-state pde discrete solutions. Int J Numer Methods Eng 94(7): 648–671. doi:10.1002/nme.4468.
Rozza G, Huynh DBP, Patera AT (2008) Reduced basis approximation and a posteriori error estimation for affinely parametrized elliptic coercive partial differential equations. Arch Comput Methods Eng 15(3): 229–275.
Le Bris C, Lelièvre T, Maday Y (2009) Results and questions on a nonlinear approximation approach for solving high-dimensional partial differential equations. Constructive Approximation 30(3): 621–651. doi:10.1007/s00365-009-9071-1.
Barrault M, Maday Y, Nguyen NC, Patera AT (2004) An ‘empirical interpolation’ method: application to efficient reduced-basis discretization of partial differential equations. Comptes Rendus Mathematique 339(9): 667–672.
Nguyen NC, Patera AT, Peraire J (2008) A ‘best points’ interpolation method for efficient approximation of parametrized functions. Int J Numer Methods Eng 73(4): 521–543.
Ortiz M, Stainier L (1999) The variational formulation of viscoplastic constitutive updates. Comput Methods Appl Mech Engrg 171: 419–444.
Miehe C (2002) Strain-driven homogenization of inelastic micro-structures and composites based on an incremental variational formulation. Int J Numer Meth Eng55: 1285–1322.
Lahellec N, Suquet P (2007) On the effective behavior of nonlinear inelastic composites: I. incremental variational principles. J Mech Phys Solids 55(9): 1932–1963. doi:10.1016/j.jmps.2007.02.003.
Ladevèze P, Leguillon D (1983) Error estimate procedure in the finite element method and applications. SIAM J Numer Anal 20: 485–509.
Gallimard L, Ladevèze P, Pelle JP (1996) Error estimation and adaptivity in elastoplasticity. Int J Numer Methods Eng 39(2): 189–217.
Ladevèze P, Moes N (1998) A posteriori constitutive relation error estimators for nonlinear finite element analysis and adaptive control. In: Ladevèze P Oden JT (eds)In Advances in Adaptive Computational Methods in Mechanics. Studies in Applied Mechanics, 231–256.. Elsevier Publication, The University of Texas at Austin, TX, USA.
Ladevèze P, Blaysat B, Florentin E (2012) Strict upper bounds of the error in calculated outputs of interest for plasticity problems. Comput Methods Appl Mech Eng245-46(0): 194–205. doi:10.1016/j.cma.2012.07.009.
Bouclier R, Louf F, Chamoin L (2013) Real-time validation of mechanical models coupling pgd and constitutive relation error. Comput Mech 52(4): 861–883. doi:10.1007/s00466-013-0850-y.
Pelle J-P, Ryckelynck D (2000) An efficient adaptive strategy to master the global quality of viscoplastic analysis. Comput Struct 78(1-3): 169–183. doi:10.1016/S0045-7949(00)00107-3.
Paraschivoiu M, Peraire J, Patera AT (1997) A posteriori finite element bounds for linear-functional outputs of elliptic partial differential equations. Comput Methods Appl Mech Eng 150(1-4): 289–312. doi:10.1016/S0045-7825(97)00086-8. Symposium on Advances in Computational Mechanics.
Wirtz D, Haasdonk B (2012) Efficient a-posteriori error estimation for nonlinear kernel-based reduced systems. Syst Control Lett 61(1): 203–211. doi:10.1016/j.sysconle.2011.10.012.
Karhunen K (1947) Über lineare methoden in der wahrscheinlichkeitsrechnung. Ann Academiae Scientiarum Fennicae 37: 3–79. series: Mathematica-Physica.
Loève MM (1963) Probability Theory, The University Series in Higher Mathematics. 3rd edn. Van Nostrand, Princeton, NJ.
Sirovich L (1987) Turbulence and the dynamics of coherent structures. 1. coherent structures. Q Appl Mathematics 45(3): 561–571.
Radovitzky R, Ortiz M (1999) Error estimation and adaptive meshing in strongly nonlinear dynamic problems. Comput Methods Appl Mech Engrg 172: 203–240.
Biot MA (1965) Mechanics of Incremental Deformations. Wiley, New York.
Ziegler H (1963) Some Extremum Principles in Irreversible Thermodynamics with Applications to Continuum Mechanics vol. Progress in Solid Mechanics, vol. IV.(Sneddon IN, Hill R, eds.), North-Holland, Amsterdam.
Germain P, Nguyen QS, Suquet P (1983) Continuum thermodynamics. J Appl Mech 50: 1010–1020.
Halphen B, Nguyen QS (1975) Generalized standard materials. J De Mecanique 14(1): 39–63.
Lemaitre J, Chaboche J-L (1985) Mecanique des Materiaux Solides. 1st edn. Dunod, English version published by Cambridge University Press: Cambridge, Paris.
Ryckelynck D (2009) Hyper-reduction of mechanical models involving internal variables. Int J Numer Methods Eng 77(1): 75–89.
Besson J, Cailletaud G, Chaboche J-L, Forest S (2009) Non-linear mechanics of materials In: Solid Mechanics and Its Applications. 167 2010.
Fritzen F, Bhlke T (2011) Nonlinear homogenization using the nonuniform transformation field analysis. PAMM 11(1): 519–522. doi:10.1002/pamm.201110250.
Fritzen F, Leuschner M (2013) Reduced basis hybrid computational homogenization based on a mixed incremental formulation. Comput Methods Appl Mech Eng 260(0): 143–154. doi:10.1016/j.cma.2013.03.007.
Acknowledgements
We would like to thank Pierre Ladevèze, Gérard Coffignal and Yvon Maday for the discussions we had about this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The theory represents joint work by DR and LG. Numerical results represents joint work by DR and SJ. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ryckelynck, D., Gallimard, L. & Jules, S. Estimation of the validity domain of hyper-reduction approximations in generalized standard elastoviscoplasticity. Adv. Model. and Simul. in Eng. Sci. 2, 6 (2015). https://doi.org/10.1186/s40323-015-0027-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40323-015-0027-7