Abstract
Background
Biologgers incorporating triaxial magnetometers and accelerometers can record animal movements at infra-second frequencies. Such data allow the Dead-Reckoned (DR) path of an animal to be reconstructed at high resolution. However, poor measures of speed, undocumented movements caused by ocean currents, confounding between movement and gravitational acceleration and measurement error in the sensors, limits the accuracy and precision of DR paths. The conventional method for calculating DR paths attempts to reduce random errors and systematic biases using GPS observations without rigorous statistical justification or quantification of uncertainty in the derived swimming paths.
Methods
We developed a Bayesian Melding (BM) approach to characterize uncertainty and correct for bias of DR paths. Our method used a Brownian Bridge process to combine the fine-resolution (but seriously biased) DR path and the sparse (but precise and accurate) GPS measurements in a statistically rigorous way. We also exploited the properties of underlying processes and some approximations to the likelihood to dramatically reduce the computational burden of handling large, high-resolution data sets. We implemented this approach in an R package “BayesianAnimalTracker”, and applied it to bio-logging data obtained from northern fur seals (Callorhinus ursinus) foraging in the Bering Sea. We also tested the accuracy of our method using cross-validation analysis and compared it to the conventional bias correction of DR and linear interpolation between GPS observations (connecting two consecutive GPS observations by a straight line).
Results
Our BM approach yielded accurate, high-resolution estimated paths with uncertainty quantified as credible intervals. Cross-validation analysis demonstrated the greater prediction accuracy of the BM method to reconstruct movements versus the conventional and linear interpolation methods. Moreover, the credible intervals covered the true path points albeit with probabilities somewhat higher than 95 %. The GPS corrected high-resolution path also revealed that the total distance traveled by the northern fur seals we tracked was 40–50 % further than that calculated by linear interpolation of the GPS observations.
Similar content being viewed by others
Background
Pseudotracks of animal movements calculated from tri-axial magnetometer and accelerometer tags are derived from infra-second sensor readings providing movement details at a scale that imply a high degree of accuracy and precision. However, error propagates through the pseudotrack calculating algorithm additively so that errors in actual location estimates can be relatively high, and quantifying the various sources of error, such as ocean currents and the confounding between gravitational and animal movement acceleration, is difficult. Current methods for fitting pseudotracks to known locations (such as ARGOS or GPS locations) do so deterministically making no attempt to account for the degree of error between the pseudotracks and known locations of animals or providing any sort of measure of error in the georeferenced pseudotracks. We therefore developed a BM approach to correct the high-resolution path of marine mammals reconstructed from tri-axial magnetometer and accelerometer tags with GPS observations, and quantify the combined uncertainty from all sources in the corrected path.
Bio-logging tags are increasingly being attached to animals to log and relay data about the movements and behaviour of animals that cannot be directly observed [1, 2]. Many of these tags incorporate Global Positioning System (GPS) sensors to directly and accurately determine animal locations. Unfortunately, GPS tags have a limited sampling frequency due to battery life, and often have limited exposure to satellites due to animal behaviour and habitat. This is particularly true for marine mammals that dive frequently and are only on the surface for a relatively small proportion of time. Thus, GPS can only provide a sparse and irregularly spaced record of animal locations.
The gaps in locations between infrequent GPS observations can be filled by concurrently deploying a “Dead-Reckoning” (DR) tag consisting of an accelerometer, a magnetometer, a time-depth recorder (TDR) and other supporting components [1, 3]. Such DR tags can sample at infra-second frequencies (e.g., 16 Hz) and provide a detailed record of an animal’s movement. Data downloaded from the tag can be processed by a Dead-Reckoning Algorithm (DRA) to reconstruct the DR path of the animal [1, 4, 5].
The detailed implementation of a DRA may vary in different applications [1, 4, 6], but the basic idea is as follows. First, the animal’s orientation (direction of velocity) is estimated from the smoothed accelerometer and magnetometer readings via an approximate solution to the Wahba’s problem [7]. Next, the animal’s speed can be estimated by data from other sensors, such as a TDR or speed sensor [8], or it can be derived from acceleration data or assumed to be a constant value. Speed is in turn combined with the orientation and a known starting point to create the DR path.
The DR path provides remarkably detailed information about an animal’s movements, especially fine-scale fluctuations that GPS cannot capture. However, the DR path can be biased because of poor measures of swim speeds, systematic and random error in the accelerometer and magnetometer sensors, undocumented animal movements caused by ocean currents, confounding between movement and gravitational acceleration, and discretization in the integration of the speed all lead to errors in the DR path [1, 9–11]. These biases and errors can be significant if not corrected using the relatively accurate GPS observations (by as much as 100 km at the end of a seven-day trip in the case study we explored below).
The conventional approach for correcting for DR path bias has been to add a linear bias correction term to the DR path, which directly shifts the DR path to the locations indicated by the GPS observations [1]. However, this approach lacks rigorous statistical justification and does not consider measurement error in the GPS observations. It also does not provide any measure of uncertainty about the correct path taken by the animal, because it is fully deterministic.
Our goal was to develop a statistically rigorous method for track reconstruction that overcomes the limitations of the conventional approach to determine DR paths of moving animals. We thus sought to correct the biased DR paths and quantify the uncertainty in the corrected paths.
Methods
We collected Dead-Reckoning data from northern fur seals (Callorhinus ursinus) tagged in the Bering Sea, and determined their swimming paths using 1) the conventional method for DR path reconstruction [1] and 2) our proposed Bayesian Melding approach.
Animal tagging and data processing
Two lactating northern fur seal were captured and tagged on Bogoslof Island (Alaska, USA) as part of the Bering Sea Integrated Research Program (BSIERP) [3, 12]. Three tags were attached to the fur of each seal with 5 min epoxy: a DR “Daily Diary” tag and TDR MK 10-F with Fastloc® GPS technology (both produced by Wildlife computers), and a VHF tag, which was used to ensure the success of retrieving the other tags. The accelerometers and magnetometers of the DR tag were set to sample 16 times per second (16 Hz) while the TDR pressure sensor sampled at 1 Hz. The GPS sensor was programmed to make one attempt every 15 min to connect with the satellite.
We produced the DR path for two foraging trips made by the two female seals (denoted as “Trip 1” and “Trip 2”) using the “TrackReconstruction” R package on the 16 Hz data set. This R package was developed based on [1, 4] and its detailed information can be found in [13]. We sub-sampled the DR path to 1 Hz, using only the first of the 16 locations in each second to construct the corrected animal path. We projected the GPS observations of longitude and latitude to Easting and Northing in kilometers (km) in a point-wise fashion as per [1].
Conventional bias correction method
The conventional correction method [1] can be summarized as follows: 1) denote the DR path (in one dimension) by \(x_1, x_2, \ldots , x_T\) at times \(t=1, 2, \ldots , T\) and the GPS observations at times 1 and T by \(y_1\) and \(y_T\), respectively; 2) assume \(x_1 = y_1=0\) and calculate the corrected path \(\hat{\eta }_t\) as
which shifts the DR path in-between two GPS observations directly to the locations indicated by the GPS observations, namely \(\hat{\eta }_1= y_1\) and \(\hat{\eta }_T= y_T\); 3) repeat this procedure for all the sections of the path between GPS observations, to correct the entire path.
Bayesian Melding
The Bayesian Melding (BM) approach was pioneered to combine direct observations of air-pollutant concentrations from a sparse network of monitoring stations and the computer model outputs at each pixel of a map, based on known pollutant sources and geophysical information [14]. This BM approach was later adapted by different fields to characterize such things as hurricane surface winds [15], ozone levels [16], and wet deposition [17]. All of these applications have demonstrated the remarkable flexibility and effectiveness of the BM approach.
The GPS observations obtained from our fur seals are analogous to the monitoring station measurements in the first BM application [1], and the DR path of our moving seals is similar to the computer model output of drifting air-pollutants. Using the GPS to correct DR paths combines the location information from two independent sources (the GPS and DR path), which is the strength of Bayesian Melding.
Model choice
Animal’s true path In our BM approach, we assumed the one-dimensional path \(\eta (t)\) of the animal was a Brownian Bridge process, whose mean f(t) at a time t and covariance function \(R(s, t) = \mathrm{Cov}\,(\eta (s), \eta (t))\) for two time points s, t are:
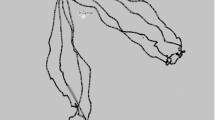
where \(\eta (1)=A\) and \(\eta (T)=B\) are the known start and end points of the trip. \(\sigma ^2_H\) is the variance parameter, which reflects the mobility of the animal (i.e., it is larger when the animal is more active). We chose the Brownian Bridge process because the animal’s trip displayed a “bridge” structure (i.e., it had fixed start and end points on the island where the tag was deployed and retrieved; and appeared random in the middle as shown in Fig. 1). The Brownian Bridge model can be used to model the habitat used for a wide range of animal species [18] and is generally well accepted by biologists and ecologists [19–21]. Humphries et al. [22] found that Brownian Motion (Bridge) model fit well with the movements of some marine mammals in environments with abundant resources. The ocean around Bogoslof Island, where our case study fur seals foraged, is believed to be such a resource abundant environment [23].
The longitude of the GPS observations of the two trips in our case study of northern fur seals. Both trips started and ended at Bogoslof Island (Alaska) and the horizontal line indicates the longitude −168.035E of the island. The time unit is the proportion of the total time of this trip. Notice the “bridge” structure of these trips, i.e., their difference is small at the beginning and end, but very large in the middle. This “bridge” structure is described by the Brownian Bridge process
GPS observations of the two trips and the corrected paths from our BM approach. The GPS measured latitude and longitude of the two trips of the northern fur seal began and ended at Bogoslof Island in the summer of 2009. The GPS observations in Trip 1 are indicated by the round points and those for Trip 2 are indicated by the triangular points. The pink curve is the corrected path from our BM model for Trip 1 and the blue curve is for Trip 2. Trip 1 lasted from 21 July 2009 09:30:00 to 28 July 2009 09:49:00, and Trip 2 lasted from 20 July 2009 07:41:59 to 27 July 2009 23:22:47
GPS observations The GPS observations of the locations were denoted by \(Y(t_k), k=1, 2, \ldots , K, t_1=1, t_K=T, t_k \in \{2, \ldots , T-1\}, k=2, \ldots , K-2\), which are unbiased observations of the true location:
for \(k=2, \ldots , K-2\). \(Y(t_k)\) can thus be viewed as the true value \(\eta (t_k)\) plus a normal noise with variance \(\sigma ^2_G\). For \(k=1\) and \(k=K\), \(Y(t_1) = \eta (t_1)\), and \(Y(t_K) = \eta (t_K)\), as the start and end points are known. Notice here that k stands for the k-th GPS observation obtained in this trip and the \(t_1, t_2, \ldots , t_K\) are irregularly spaced in (1, T).
DR path We used \(X(t), t=1, 2, \ldots , T\) to denote the DR path without any error correction and incorporated the bias of the DR path by assuming:
where h(t) is a parametric function designed to capture the systematic bias, and \(\xi (t)\) is a Brownian Motion process of mean zero, which can model the unstructured error in the DR path.
In principle, h(t) could capture the structured error that can be expressed as a deterministic function of time in the DR path, such as those caused by a constant bias in the accelerometer readings, the currents, and other external forces. However, there are still some “random” errors caused by the measurement error in the accelerometer, magnetometer, or speed measurements that cannot be expressed as a deterministic function of time. These random errors may add white noise to the velocity estimates (speed in two dimensions) in the DRA, which will accumulate in the DR path. The sum of white noises over time results in a Brownian Motion process. Thus, we considered \(\xi (t)\) to be a Brownian Motion process, whose covariance function is \(C(s, t) =\sigma ^2_D (\min (s, t)-1)\), where \(\sigma ^2_D\) can be viewed as the variance of the white noise added to the velocity in the DRA.
Various models can be considered for h(t), such as \(h(t)= \sum _{i=1}^Q \beta _i t^{i-1}\). For simplicity, we chose to illustrate our method using \(h(t) = \beta _0\). We had explored more complicated models [11] and found them to have little impact on the corrected paths and uncertainty in the two fur seal data sets we tested.
This simple model in (2) can cover various factors of biases or errors in the DR path. For example, if there was a constant bias in the speed estimate, the integration of this constant bias over time is a linear function of time, which can be captured by our h(t) part. On the other hand, the random error in the animal’s speed is absorbed into the \(\xi (t)\). This model choice may not be the best to describe all the bias and error factors, but it worked well for our data sets, as shown below.
Priors for parameters The final ingredients in our BM model were the prior distributions of the parameters. We fixed \(\sigma ^2_G\) at 0.0625 based on the extensive tests of the Fastloc® GPS device [24, 25] and the average observed number of satellites present during the two fur seal foraging trips. Non-informative priors were chosen for the remaining parameters, such that \(p(\sigma ^2_H) \propto \frac{1}{\sigma ^2_H}\) and \(p(\sigma ^2_D) \propto \frac{1}{\sigma ^2_D}\), and \(p(\beta _0) \propto 1\).
Univariate versus bivariate modeling The two dimensions of the path (i.e., Northing or Easting) were analyzed separately in our BM approach. In theory, our method could be improved if we simultaneously analyzed the two dimensions by considering them as a bivariate Brownian Bridge process. Using a bivariate model would require us to consider a time varying correlation parameter to avoid assuming the animal constantly moves in one direction for the whole trip. However, it is unclear whether the additional parameters needed to represent the time varying correlation function would actually improve its prediction performance. This should be explored in future studies.
Computation of the BM model
We used a Bayesian approach to calculate the posterior distribution of \(\eta (t)\) based on the priors and the data (the GPS observations and DR path). More specifically, the posterior mean of \(\eta (t)\), denoted by \(\tilde{\eta }(t)\), was the corrected path and the posterior standard error (SE), denoted by \(\tilde{\sigma }(t)\), provided an uncertainty statement about the estimated path. The point-wise 95 % credible interval (CI, Bayesian version of the confidence interval) for \(\eta (t)\) was constructed as
The algorithm to calculate \(\tilde{\eta }(t)\) and \(\tilde{\sigma }(t)\) can be summarized in the following steps:
-
1.
Find a set of reasonable values of \(\sigma ^2_H\) and \(\sigma ^2_G\) based on the GPS observations and the DR path at the corresponding time points. The weight of each pair \(\sigma ^2_H\) and \(\sigma ^2_G\) was decided using the likelihood of the data.
-
2.
Conditioning on each \(\sigma ^2_H\) and \(\sigma ^2_G\), calculate the conditional posterior of \(\eta (t)\) in two steps:
-
(a)
The posterior of \(\eta (t)\) at the GPS time points and parameters in h(t) were decided based on the GPS observations and the DR path at the corresponding time points.
-
(b)
The rest of \(\eta (t)\) was broken into periods separated by the GPS observations and updated based on the DR path only for the period together with the posterior of \(\eta (t)\) at the two GPS end points.
-
(a)
-
3.
Numerically integrate the conditional posterior with the weights found in Step 1.
The above algorithm was designed to avoid dealing directly with the long sequence of \(\eta (t)'s\) and to reduce the computational burden of the Bayesian calculation. Approximations to the posterior were applied in Step 1 and Step 2-(a). Step 2-(b) was designed based on the conditional independence property of the Brownian Bridge process and Brownian Motion process. The full technical details of these steps are provided in [11] and the algorithm is implemented in a package called “BayesianAnimalTracker” [26]. This package can be freely used in R [27] and this paper includes an additional file to illustrate how to use this package (Additional file 1).
In the simplified situation where h(t) (systematic bias) is a constant zero, our algorithm in Step 2-(b) flattened the conventional bias correction by a factor of \(\frac{\sigma ^2_H}{\sigma ^2_D + \sigma ^2_H}\) and added it to the linear interpolation between the two consecutive GPS observations. As the GPS observations were relatively precise, the linear interpolation decided the general direction of the animal’s movement. The DR path nevertheless offered detailed information on the animal’s movement, in sprite of some of these details being just errors of the DR path. Under our model, the animal’s true path, the Brownian Bridge process, contributed \(\sigma ^2_H\) variance to the DR path while the error process \(\xi (t)\) accounted for \(\sigma ^2_D\) variance. Therefore, a proportion \(\frac{\sigma ^2_H}{\sigma ^2_D + \sigma ^2_H}\) of the details from the DR path could be treated as a “signal” from the animal’s true path, which we added to the linear interpolation. In other words, Step 2-(b) can be viewed as a compromise between linear interpolation and conventional bias correction, where the weights on each method in the compromise were decided based on \(\sigma ^2_D\) and \(\sigma ^2_H\). This compromise is illustrated below.
Setting \(h(t)=0\) for all t is a simplified situation that helps explain one step of our method. In practice, however, our BM method also considered the bias function h(t) in Step 2-(b) and marginalized the randomness of the variance parameters \(\sigma ^2_D\) and \(\sigma ^2_H\) in Step 3. As a consequence, the correct path from our BM approach is not just a weighted average of the linear interpolation and the conventional method, and does not have a mathematical formula that can be easily interpreted.
In summary, our BM approach requires the inputs of projected GPS observations (Northing or Easting), the corresponding Northing or Easting of the uncorrected DR path, and the variance of the GPS observation \(\sigma ^2_G\). These inputs return the posterior mean of \(\tilde{\eta }(t)\) as the corrected path, and the posterior standard error \(\tilde{\sigma }(t)\) serves as an uncertainty statement about the corrected path.
Cross-validation
We carried out a cross-validation analysis to examine how well the corrected DR path (from either the conventional method, linear interpolation, or our BM) can predict or estimate the animal’s location when the GPS observations are not available. This procedure has long been used to test a method when real ground-truth is not available and the cross-validation procedure enabled us to compare our predictions to some “ground-truth” created from our observed data. Specifically, we imagined m consecutive GPS observations (m = 1 or 5) were unavailable and carried on correcting the DR path without these m GPS observations. We then compared the predictions from the corrected path to the left-out GPS observations. This procedure was repeated for all the GPS observations except for the start and end points. The difference between the observations \(Y(t_k)\) and the predictions \(\check{\eta }(t_k)\) were summarized as the cross-validation root mean squared error:
where \(\check{\eta }(t_k)\) can be the predictions from the conventional method [1], our BM approach, or linear interpolation of the GPS observations. For linear interpolation, we ignored the DR path and directly connected two GPS observations by a straight line. For our BM approach, we also checked whether each \(Y(t_k)\) was covered by the CI at \(t_k\) obtained without \(Y(t_k)\) and the coverage percentage was defined as the proportion of the \(Y(t_k)\) that was covered by the CI.
Results and discussion
Exploratory data analysis about GPS observations
The two foraging trips made by the fur seals were each about 1 week. Trip 1 was 7 days and had 276 valid GPS observations, while Trip 2 lasted about 7.5 days and had 129 GPS observations (Fig. 2). Some of the gaps between the GPS observations were quite large as shown by the histograms of time gaps and (great circle) distances (in km) between any two consecutive GPS observations (Fig. 3). Although a large proportion of the time gaps were within 1 h, 13 % of those in Trip 1 and 30 % of those in Trip 2 were greater than 1 h—with time gaps averaging 36 min for Trip 1 and 82 min for Trip 2. In terms of distances between GPS locations, 7 % of the spatial gaps in Trip 1 and 17 % in Trip 2 were greater than 5 km. The largest between-GPS distance in these two trips was nearly 50 km. Thus, the GPS observations were irregularly spaced in time and space, and the gaps between them were quite large.
Bayesian Melding results
Applying our Bayesian Melding approach to the Easting and Northing of the two trips to fill in the gaps between GPS observations successfully corrected the bias of the DR path in all four analyses (Fig. 2). Plotting the corrected path together with the CI in the analysis and the DR path of Trip 1 further illustrates our method (Fig. 4). Bias of the DR path dramatically increased with time (and was about 100 km by the end of this trip—Fig. 4), and the DR path contained fluctuations consistent with the fluctuations of the GPS observations. As shown by the black curve (Fig. 4), our BM approach successfully produced a path that passed through the GPS observations. Similar plots were obtained from the analysis of the other three data sets (data not shown).
Zooming in on a portion of the track shown in Fig. 4 reveals how our approach works in the fine scale (see Fig. 5). Figure 5 also provides a way to visually compare the conventional method and linear interpolation (ignoring the DR path and connecting the consecutive GPS observations by straight lines)—and shows that our method differs from linear interpolation between GPS observations by keeping some of the tortuosity exhibited by the DR path (also seen in Fig. 2). The posterior mean from our BM approach appears to be a flattened version of the conventional bias correction, where the bumps in the conventional method are damped to the linear interpolation between two GPS points. A mathematical explanation of this is provided by [11].
The CI for \(\eta (t)\) in Fig. 5 shows a clear “bridge” structure. Namely, the CI was narrow when \(\eta (t)\) was close to the GPS observations and became wider between two GPS points. The posterior SE at the GPS points almost equaled the \(\sigma _G = 0.25\) (km) in the input to our BM, which decided the upper limit of our precision about the corrected path. For the time points between two GPS points, we had less accurate information from the DR path, which increased the posterior SE.
As an overall summary of the accuracy of our corrected paths, we calculated the averaged posterior SE (APSE, \(\frac{1}{T}\sum _{t=1}^T \tilde{\sigma }(t)\)). For Trip 1, the APSE was 0.524 km in the Easting direction and 0.444 km in the Northing. In contrast, the APSE of Trip 2 Easting and Northing were 1.45 and 1.28 km respectively, which were greater than those from Trip 1. This indicates that the BM corrected path for Trip 2 was less accurate than that for Trip 1. It also reflects the fact that fewer GPS observations were obtained for Trip 2, and the gaps between consecutive GPS observations were larger, which means that there was less accurate information to correct the biased DR path.
Coverage percentage of our CI
The results of our cross-validation analyses with \(m= 1\) (leave-1 out cross-validation; Table 1) and \(m = 5\) (leave-5-out cross-validation; Table 2) revealed that the coverage percentage of our BM CI was above the nominal level of 95 % in most of our cross-validations, which indicates, therefore, that we overestimated the uncertainty in the corrected path and that the CI was conservative. However, the averaged posterior SE was just around 1 km, which was sufficiently precise for most applications (e.g., utilization distribution and resource selection [28] or providing in situ temperature record [3]). In this way, the conservativeness of the CI may not be a big concern [11]. The coverage percentage was also found to decrease when more GPS observations were left out (Tables 1, 2), as there was less accurate information about the path with sparser GPS observations.
Comparisons with the conventional method and linear interpolation
Our BM approach had a smaller CV-RMSE than linear interpolation in all the four data sets, while the conventional method had a larger CV-RMSE than linear interpolation in some cases (e.g., Trip 1 Easting and Trip 2 Northing in the LOOCV). Heuristically, more data should give better results. The conventional method had more data than the linear interpolation (where the DR path was ignored) and thus it should have had a smaller CV-RMSE than linear interpolation, which was not true in our case study. In this way, the conventional method failed to use the additional information properly to produce better predictions.
In the comparison of our BM to the conventional method, the CV-RMSE of our BM approach was smaller than those from the conventional method in seven out of the eight cross-validations. For Trip 2 Easting in LOOCV, the CV-RMSE of our method was slightly larger than that of the conventional method. This might be caused by \(h(t) = \beta _0\) failing to capture the bias of the DR path sufficiently well. This issue can be addressed by allowing more flexible structure as in h(t) [11].
Tables 1 and 2 imply that our BM approach improved the linear interpolation estimates by 100–700m, which may not be enough improvement to justify using the DR tag and our method. However, the main reason that the linear interpolation was good in our case study is because a lot of these GPS observations were close to each other in both time and space, as shown in the histograms of Fig. 3. Cases where two consecutive GPS observations were very close had a small bias in linear interpolation. For example, an animal traveling at a constant speed of 3 m/s (which was the assumed speed in our DRA) with a time gap between two GPS observations of 15 min would have a maximum possible bias of linear interpolation of 15 × 60 × 3/2 = 1350m (the denominator of “2” reflects the animal having to reach the later GPS location). Thus, the 100–700 m improvement achieved by our method is non-trivial when compared to this 1350 m maximum bias.
Histograms of the time gaps and distances between GPS locations. The top two panels are the histograms of the time gap between two consecutive GPS observations in our two data sets; and the bottom two panels show the distances between two consecutive GPS observations. Red histograms are for Trip 1, and blue are for Trip 2
Bayesian Melding results for Trip 1 Northing. The red points are the GPS observations and the blue curve shows the uncorrected DR path. The black curve is the posterior mean of \(\tilde{\eta }(t)\) from our BM model and the gray curves connect the 95 % point-wise credible intervals at all the time points
Close up of the 2000–2400min portion of the track shown in Fig. 4. The blue curve is the uncorrected DR path, and the black curve is the posterior mean \(\eta (t)\) from our BM model. The gray curves connect the 95 % point-wise credible intervals at all the time points. The conventional bias correction is also included as the brown curve, and the green line is the linear interpolation between GPS observations
Although many of the consecutive GPS observations in our case study were close, there were some huge gaps (e.g., a 4-h time gap and 50 km distance gap) as shown in the large right tail of the histograms in Fig. 3. In these cases, linear interpolation did not work, while our method provided a good estimate/prediction of the animal’s location based on the DR path. This was not as apparent in the tabulated results of our cross-validation analyses because most of the gaps were small. This conclusion is also reflected by the improvement that resulted from our method when going from the leave-one-out CV to leave-5-out CV (Tables 1, 2). In practice, the DR tag and our BM method significantly improve track reconstruction when the gap between GPS observations cannot be controlled.
Another advantage of our BM approach over the conventional method is that it can calculate an improved bias correction and credible interval at a reasonable computational cost. The computational times of our method and the conventional method are listed in Table 3 along with the computational time of the DRA as a benchmark. Although our BM approach took longer to compute, it was reasonable given the time it took to calculate the DR path. In addition, downloading the data from the tag and reading it into the software to perform DRA usually takes much longer than the actual calculation of DRA. Thus, the computation cost of our BM approach should not be of concern.
Distance traveled by the animal
With the corrected path from our BM, we more accurately calculated the distance traveled by the fur seals during their foraging trip (Table 4). Distances calculated using our approach were 40 % greater for Trip 1 and 49 % greater for Trip 2 than those calculated by linear interpolation of the GPS observations. This once again demonstrates that the corrected DR path is needed to fill-in the gaps between the GPS observations. Calculating the distance traveled by the animal with the conventional bias correction method revealed it to be twice the distance calculated based on GPS observations, which further illustrates that our BM is a comprise between linear interpolation and conventional DR correction.
Conclusions
We found that the GPS observations were too sparse and irregular to sufficiently describe the foraging paths of northern fur seals. The uncorrected DR paths included useful detailed information about the paths, but were severely inaccurate. Our proposed BM approach successfully provides a corrected path along with credible intervals of uncertainty—and can be further improved with more flexible parameterization [11]. Our analysis of the BM method also provides a statistically rigorous foundation for using the DR path to answer many other bio-logging questions.
Our BM approach requires some statistical knowledge and takes more time to compute when compared to linear interpolation and conventional bias correction methods. However, our method can be directly applied using our R package (as shown in additional file 1 of this paper) without understanding all of the formulas, and the computational time is reasonable when compared to the time to download the data and perform the DRA. Moreover, our method achieves greater prediction accuracy than the other two methods as shown by the cross-validation studies—and also quantifies the uncertainty in the corrected path with credible intervals, which cannot be obtained in the linear interpolation nor the conventional method. Further improvement of BM approach is likely to come with the inclusion of multivariate and non-stationary modeling of the animal’s path.
References
Wilson RP, Liebsch N, Davies IM, Quintana F, Weimerskirch H, Storch S, Lucke K, Siebert U, Zankl S, Müller G, Zimmer I, Scolaro A, Campagna C, Plötz J, Bornemann H, Teilmann J, McMahon CR. All at sea with animal tracks; methodological and analytical solutions for the resolution of movement. Deep Sea Res Part II. 2007;54(3–4):193–210. doi:10.1016/j.dsr2.2006.11.017.
Rutz C, Hays GC. New frontiers in biologging science. Biol Lett. 2009;5(3):289–92.
Nordstrom CA, Benoit-Bird KJ, Battaile BC, Trites AW. Northern fur seals augment ship-derived ocean temperatures with higher temporal and spatial resolution data in the eastern Bering Sea. Deep Sea Res Part. 2013;II(94):257–73. doi:10.1016/j.dsr2.2013.03.022.
Wilson RRP, Wilson MP. Dead reckoning-a new technique for determining penguin movements at sea. Meeresforschung Rep Marine Res. 1988;32:155–8.
Johnson MP, Tyack PL. A digital acoustic recording tag for measuring the response of wild marine mammals to sound. IEEE J Ocean Eng. 2003;28(1):3–12.
Elkaim GH, Decker EB, Oliver G, Wright B. Marine Mammal Marker (MAMMARK) dead reckoning sensor for in-situ environmental monitoring. In: Position, Location, And Navigation Symposium, IEEE/ION. 2006. p. 976–987.
Wahba G. A least squares estimate of satellite attitude. SIAM Rev. 1965;7(3):409.
Mitani Y, Sato K, Ito S, Cameron MF, Siniff DB, Naito Y. A method for reconstructing three-dimensional dive profiles of marine mammals using geomagnetic intensity data: results from two lactating weddell seals. Polar Biol. 2003;26(5):311–7.
Shiomi K, Narazaki T, Sato K, Shimatani K, Arai N, Ponganis PJ, Miyazaki N. Data-processing artefacts in three-dimensional dive path reconstruction from geomagnetic and acceleration data. Aquat Biol. 2010;8:299–304.
Schmidt V, Weber TC, Wiley DN, Johnson MP. Underwater tracking of humpback whales (Megaptera novaeangliae) with high-frequency pingers and acoustic recording tags. IEEE J Ocean Eng. 2010;35(4):821–36. doi:10.1109/JOE.2010.2068610.
Liu Y, Battaile BC, Zidek JV, Trites AW. Bayesian melding of the Dead-reckoned path and GPS measurements for an accurate and high-resolution path of marine mammals. 2014. arXiv preprint arXiv:1411.6683.
Benoit-Bird KJ, Battaile BC, Heppell SA, Hoover B, Irons D, Jones N, Kuletz KJ, Nordstrom CA, Paredes R, Suryan RM, Waluk CM, Trites AW. Prey patch patterns predict habitat use by top marine predators with diverse foraging strategies. PloS One. 2013;8(1):53348. doi:10.1371/journal.pone.0053348.
Battaile B. TrackReconstruction: reconstruct animal tracks from magnetometer, accelerometer, depth and optional speed data. 2014. R package version 1.1. http://CRAN.R-project.org/package=TrackReconstruction.
Fuentes M, Raftery AE. Model evaluation and spatial interpolation by bayesian combination of observations with outputs from numerical models. Biometrics. 2005;61(1):36–45.
Foley KM, Fuentes M. A statistical framework to combine multivariate spatial data and physical models for Hurricane surface wind prediction. J Agric Biol Environ Stat. 2008;13(1):37–59. doi:10.1198/108571108X276473.
Liu Z, Le ND, Zidek JV. An empirical assessment of Bayesian melding for mapping ozone pollution. Environmetrics. 2011;22(3):340–53. doi:10.1002/env.1054.
Sahu SK, Gelfand AE, Holland DM. Fusing point and areal level space-time data with application to wet deposition. J Royal Stat Soc Series C (Applied Statistics). 2010;59(1):77–103.
Horne JS, Garton E, Krone S, Lewis J. Analyzing animal movements using Brownian bridges. Ecology. 2007;88(9):2354–63.
Sawyer H, Kauffman MJ, Nielson RM, Horne JS. Identifying and prioritizing ungulate migration routes for landscape-level conservation. Ecol Appl. 2009;19(8):2016–25.
Kranstauber B, Kays R, LaPoint SD, Wikelski M, Safi K. A dynamic Brownian bridge movement model to estimate utilization distributions for heterogeneous animal movement. J Anim Ecol. 2012;81(4):738–46.
Kranstauber B, Safi K, Bartumeus F. Bivariate Gaussian bridges: directional factorization of diffusion in Brownian bridge models. Mov Ecol. 2014;2(1):5.
Humphries NE, Queiroz N, Dyer JRM, Pade NG, Musyl MK, Schaefer KM, Fuller DW, Brunnschweiler JM, Doyle TK, Houghton JDR, Hays GC, Jones CS, Noble LR, Wearmouth VJ, Southall EJ, Sims DW. Environmental context explains Lévy and Brownian movement patterns of marine predators. Nature. 2010;465(7301):1066–9. doi:10.1038/nature09116.
Benoit-Bird KJ, Battaile BC, Nordstrom CA, Trites AW. Foraging behavior of northern fur seals closely matches the hierarchical patch scales of prey. Mar Ecol Prog Ser. 2013;479:283–302.
Bryant E. 2D Location accuracy statistics for Fastloc RCores running firmware versions 2.2 and 2.3. UK: Wildtrack Telemetry Systems Ltd; 2007.
Hazel J. Evaluation of fast-acquisition GPS in stationary tests and fine-scale tracking of green turtles. J Exp Marine Biol Ecol. 2009;374(1):58–68. doi:10.1016/j.jembe.2009.04.009.
Liu YS. BayesianAnimalTracker: Bayesian melding of GPS and DR path for animal tracking. 2014. R package version 1.2.
R Core Team. R: a Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna; 2014. http://www.R-project.org/.
Hooten MB, Garlick MJ, Powell JA. Computationally efficient statistical differential equation modeling using homogenization. J Agric Biol Environ Stat. 2013;18(3):405–28. doi:10.1007/s13253-013-0147-9.
Authors' contributions
YL developed and implemented the proposed Bayesian Melding approach, carried the data analysis and cross-validation studies, and drafted this paper. BB edited the paper, collected the biologging data and provided YL guidance on analyzing the Dead-Reckoning path. JZ first suggested the Bayesian Melding approach and oversaw YL’s research. AT oversaw the animal tagging experiment and edited the paper. All authors read and approved the final manuscript.
Acknowledgements
Yang Liu and James Zidek thank the National Sciences and Engineering Research Council of Canada for supporting their research, and Prof. Nancy Heckman for additional financial support. All data collection procedures were conducted under the National Oceanic and Atmospheric Administration (NOAA) Permit No. 14329 and abided by the guidelines of the Committee on Animal Care at the University of British Columbia (Permit No. A09–0345). We are indebted to A. Baylis, J. Gibbens, R. Marshall, R. Papish, A. Will, C. Berger, A. Harding, R. Towell, B. Fadley, K. Call, C. Kuhn and N. Liebsch for assistance or advice with animal captures and instrument deployment. The data was collected as part of the BEST–BSIERP “Bering Sea Project” funded jointly by the US National Science Foundation and the North Pacific Research Board.
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Additional information
Brian C. Battaile, Andrew W. Trites and James V. Zidek contributed equally to this work.
Additional file
40317_2015_80_MOESM1_ESM.r
Additional file 1. Most of the analyses in this paper can be reproduced by the “BayesianAnimalTracker” R package. Available at http://cran.r-project.org/web/packages/BayesianAnimalTracker/index.html. Based on this package and the data set included in it, the additional file 1 is a vignette of this package, with step-by-step instructions on how we corrected the DR path of the Trip 1 data and plotted Figures 2, 4 and 5.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Liu, Y., Battaile, B.C., Trites, A.W. et al. Bias correction and uncertainty characterization of Dead-Reckoned paths of marine mammals. Anim Biotelemetry 3, 51 (2015). https://doi.org/10.1186/s40317-015-0080-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40317-015-0080-5