1 Introduction

The exact solutions to NLEEs lead to basic knowledge of the structure of physical phenomena. Therefore researchers have been interested in studying and seeking the derived exact solutions and made a great effort in it due to the great importance in nonlinear science. It is a fact that there is no unique method which is fruitful to solve all kinds of nonlinear wave problems. Exact traveling wave solutions to nonlinear systems of PDEs are essential for analyzing natural phenomena in wide areas of the physical sciences [1–15].

The exploitation of a symbolic computation package will make it realistic to propose a number of direct analytical methods. The research of traveling wave solutions of some nonlinear evolution equations derived from such fields played an important role in the analysis of some phenomena such as the exp\((-\varphi(\xi)\) method, Bernoulli’s sub-ODE method, the homogeneous balance method, the modified simple equation method, the modified extended direct algebraic method, the modified extended mapping method, the Kudryashov method, the extended sinh–cosh and sin–cos methods, the Lie symmetry method, the soliton ansatz method and many more methods [15–40].

Previous authors in [24] applied a new auxiliary technique on the complex fractional Kundu–Eckhaus equation and in [23] applied six methods on the van der Waals normal form for fluidized granular matter wave equations. Further the authors in [26] derived results on a Benney-like equation with the help of a modified simple equation method. Similarly, in [28] one employed an auxiliary equation method for the \((3 + 1)\)-dimensional modified Korteweg–de Vries–Zakharov–Kuznetsov equation. But here our decision is to investigate a novel soliton of models in Eq. (1), Eq. (23), Eq. (58) and Eq. (100) by employing the modified F-expansion method. Our obtained solutions are more powerful than those in the previous existing literature. These solutions have potential applications to handle nonlinear problems in mathematics and physics.

This article is organized as follows: Applications of the modified F-expansion method are described in Sect. 2, Discussion of our results with other results is in Sect. 3. Our conclusion is in Sect. 4.

2 Applications

2.1 The nonlinear integer order Kundu–Eckhaus equation

Consider the general form of the complex fractional Kundu–Eckhaus equation [24],

$$ i\frac{\partial^{\alpha}v}{\partial t^{\alpha}}+v_{xx}-2\beta \vert v \vert ^{2}v+\gamma^{2} \vert v \vert ^{4}v+2i\gamma \bigl( \vert v \vert ^{2} \bigr)_{x}v =0,\quad 0< \alpha< 1. $$
(1)

The above model having applications in optical fiber, quantum field theory and in dispersive water waves. Let a wave transformation be \(v(x, t)=u(\xi)e^{i\eta}\) and, moreover, \(\xi=ik(x-\frac{2\mu t^{\alpha}}{\alpha})\), \(\eta=(\mu x+\frac{\epsilon t^{\alpha}}{\alpha})\) in Eq. (1) for conversion of the complex fractional Kundu–Eckhaus equation to integer order; for further details about the conformable fractional derivative see [20–22]. We have

$$\begin{aligned} \begin{aligned} &\frac{\partial^{\alpha}v}{\partial t^{\alpha}}=i\bigl(\epsilon u-2\mu k u' \bigr)e^{i\eta},\qquad \frac{\partial^{2}v}{\partial x^{2}}=-\bigl(\mu^{2}u+2\mu k u'+k^{2}u''\bigr)e^{i\eta}, \\ &\frac{\partial }{\partial x}\bigl( \vert v \vert ^{2}v\bigr) =2ik u^{2}u'e^{i\eta}. \end{aligned} \end{aligned}$$
(2)

Substituting (2) in (1), this action gives an ODE such that

$$ -\bigl( \epsilon+\mu^{2}\bigr)u-k^{2}u''-2 \beta u^{3}+\gamma^{2}u^{5}-4\gamma k u^{2}u'=0. $$
(3)

Balancing between \(u''\) and \(u^{5}\) in (3), we obtain \(N=\frac {1}{2}\). Now using another transformation \(u(\xi)=\Psi^{\frac{1}{2}})\) on (3), we obtain

$$ -4\bigl( \epsilon+\mu^{2}\bigr)\Psi^{2}+k^{2} \Psi^{\prime2}-2k^{2}\Psi\Psi''-8 \beta\Psi ^{3}+4\gamma^{2}\Psi^{4}-8 k \Psi^{2}\Psi'=0. $$
(4)

Balancing between the highest derivative and nonlinear term in (4), we obtain N=1. Assuming (4) has a solution [25],

$$ \Psi(\xi)= a_{0}+a_{1}F(\xi)+b_{1}F^{-1}( \xi), $$
(5)

where F satisfies the Ricatti equation [25]

$$ F'( \xi)= B_{1}+B_{2}F+B_{3}F^{2}. $$
(6)

Put (5) with (6) in (4), we obtain numerous equations involving these parameters, \(a_{0}\), \(a_{1}\), \(b_{1}\), \(B_{1}\), \(B_{2}\), \(B_{3}\), β, γ, k, μ and ϵ, after solving this equation system, we have the following solution possibilities.

2.1.1 The soliton-like solutions of Eq. (1)

If \(B_{1}=0\), \(B_{2}=1\), \(B_{3}=-1\), then we have the following results:

$$ \begin{aligned}&k= \frac{\sqrt{7} \beta+\beta}{2 \gamma},\qquad \mu=\pm\frac{\sqrt {-\frac{\sqrt{7} \beta^{2}}{\gamma^{2}}-\frac{4 \beta^{2}}{\gamma^{2}}-8 \epsilon}}{2 \sqrt{2}},\\ & `a_{1}= \frac{5 \beta-\sqrt{7} \beta}{4 \gamma^{2}},\qquad a_{0}= 0,\qquad b_{1}= 0. \end{aligned}$$
(7)

Put (7) in (5), then the solution of (1) becomes

$$ \Psi_{1}(\xi)= \biggl(\frac{5 \beta-\sqrt{7} \beta}{8 \gamma ^{2}} \biggl(1+\tanh \biggl(\frac{1}{2}\xi\biggr) \biggr) \biggr)^{\frac {1}{2}}e^{i\eta} . $$
(8)

If \(B_{1}=0\), \(B_{2}=-1\), \(B_{3}=1\), then we have the following results:

$$ \begin{aligned}& k= \frac{-\sqrt{7} \beta-\beta}{2 \gamma}, \qquad \mu=\pm\frac{\sqrt {-\frac{\sqrt{7} \beta^{2}}{\gamma^{2}}-\frac{4 \beta^{2}}{\gamma^{2}}-8 \epsilon}}{2 \sqrt{2}},\\ & a_{1}= \frac{5 \beta-\sqrt{7} \beta}{4 \gamma^{2}}, \qquad a_{0}= 0,\qquad b_{1}= 0 . \end{aligned}$$
(9)

Substitute (9) in (5)

$$ \Psi_{2}(\xi)= \biggl(\frac{5 \beta-\sqrt{7} \beta}{8 \gamma ^{2}} \biggl(1-\coth \biggl(\frac{1}{2}\xi\biggr) \biggr) \biggr)^{\frac {1}{2}}e^{i\eta} . $$
(10)

If \(B_{1}=\frac{1}{2}\), \(B_{2}=0\), \(B_{3}=-\frac{1}{2}\), then we have the following results:

$$ \begin{aligned} &k= \frac{3 (\sqrt{7} \beta-2 \beta )}{ (\sqrt {7}-5 ) \gamma}, \qquad \mu= \pm\frac{\sqrt{8 (5 \sqrt {7}-16 ) \gamma^{2} \epsilon+9 (4 \sqrt{7}-11 ) \beta^{2}}}{2 (\sqrt{7}-5 ) \gamma},\\ &a_{1}= -\frac{9 \beta}{4 (\sqrt{7}-5 ) \gamma^{2}},\qquad a_{0}= \frac{\sqrt {7} \beta+5 \beta}{8 \gamma^{2}},\qquad b_{1}= 0. \end{aligned}$$
(11)

Put (11) in (5), we obtain

$$ \Psi_{3}(\xi)= \biggl(\frac{\sqrt{7} \beta+5 \beta}{8 \gamma ^{2}}- \frac{9 \beta}{4 (\sqrt{7}-5 ) \gamma^{2}} \bigl(\coth(\xi)\pm csch(\xi) \bigr) \biggr) ^{\frac{1}{2}}e^{i\eta} . $$
(12)

If \(B_{1}=1\), \(B_{2}=0\), \(B_{3}=-1\), then we have the following results:

$$\begin{aligned} \begin{aligned} &k= -\frac{3 (\sqrt{7} \beta-2 \beta )}{ (\sqrt {7}-5 ) \gamma},\qquad \mu= \pm\frac{\sqrt{8 (5 \sqrt {7}-16 ) \gamma^{2} \epsilon+9 (4 \sqrt{7}-11 ) \beta^{2}}}{2 (\sqrt{7}-5 ) \gamma},\\ &a_{1}= \frac{9 \beta }{4 (\sqrt{7}-5 ) \gamma^{2}},\qquad a_{0}= \frac{\sqrt{7} \beta+5 \beta}{8 \gamma^{2}},\qquad b_{1}= 0. \end{aligned} \end{aligned}$$
(13)

Put (13) in (5),

$$ \Psi_{4}= \biggl(\frac{\sqrt{7} \beta+5 \beta}{8 \gamma^{2}}+\frac {9 \beta}{4 (\sqrt{7}-5 ) \gamma^{2}} \bigl(\tanh(\xi ) \bigr) \biggr)^{\frac{1}{2}}e^{i\eta} . $$
(14)

2.1.2 The trigonometric function solutions of Eq. (1)

If \(B_{1}=\frac{1}{2}\), \(B_{2}=0\), \(B_{3}=\frac{1}{2}\), then we have the following results:

$$\begin{aligned} \begin{aligned} &k= \frac{ (\sqrt{7}-2 ) \sqrt{32+10 \sqrt{7}} \sqrt{-\beta^{2}}}{6 \gamma}, \qquad\mu=\pm\frac{\sqrt{-8 \gamma^{2} \epsilon+\sqrt{7} \beta^{2}-4 \beta^{2}}}{2 \sqrt{2} \gamma}, \\ &a_{1}= \frac{\sqrt{-5 \sqrt{7} \beta^{2}-16 \beta^{2}}}{4 \sqrt{2} \gamma^{2}},\qquad a_{0}=\frac{\sqrt{7} \beta+5 \beta}{8 \gamma ^{2}},\qquad b_{1}= 0. \end{aligned} \end{aligned}$$
(15)

Putting (15) in (5), then solution (1) is

$$ \Psi_{5}(\xi)= \biggl(\frac{\sqrt{7} \beta+5 \beta}{8 \gamma ^{2}}+ \frac{\sqrt{-5 \sqrt{7} \beta^{2}-16 \beta^{2}}}{4 \sqrt{2} \gamma^{2}} \bigl(\sec(\xi)+\tan(\xi) \bigr) \biggr)^{\frac {1}{2}}e^{i\eta} . $$
(16)

If \(B_{1}=-\frac{1}{2}\), \(B_{2}=0\), \(B_{3}=-\frac{1}{2}\), then we have the following results:

$$\begin{aligned} \begin{aligned} &k=-\frac{ (\sqrt{7}-2 ) \sqrt{32+10 \sqrt{7}} \sqrt{-\beta^{2}}}{6 \gamma},\qquad \mu= \pm\frac{\sqrt{-8 \gamma^{2} \epsilon+\sqrt{7} \beta^{2}-4 \beta^{2}}}{2 \sqrt{2} \gamma}, \\ &a_{1}=\frac{\sqrt{-5 \sqrt{7} \beta^{2}-16 \beta^{2}}}{4 \sqrt{2} \gamma^{2}},\qquad a_{0}= \frac{\sqrt{7} \beta+5 \beta}{8 \gamma ^{2}},\qquad b_{1}= 0. \end{aligned} \end{aligned}$$
(17)

Put (17) in Eq. (5),

$$ \Psi_{6}(\xi)= \biggl(\frac{\sqrt{7} \beta+5 \beta}{8 \gamma ^{2}}+ \frac{\sqrt{-5 \sqrt{7} \beta^{2}-16 \beta^{2}}}{4 \sqrt{2} \gamma^{2}} \bigl(\sec(\xi)-\tan(\xi) \bigr) \biggr)^{\frac {1}{2}}e^{i\eta} . $$
(18)

If \(B_{1}=1(-1)\), \(B_{2}=0\), \(B_{3}=1(-1)\), then we have the following results:

$$\begin{aligned} \begin{aligned} &k=-\frac{ (\sqrt{7}-2 ) \sqrt{8+\frac{5 \sqrt {7}}{2}} \sqrt{-\beta^{2}}}{6 \gamma}, \qquad \mu=\pm\frac{\sqrt{-8 \gamma^{2} \epsilon+\sqrt{7} \beta^{2}-4 \beta^{2}}}{2 \sqrt{2} \gamma }, \\ &a_{1}= \frac{\sqrt{-5 \sqrt{7} \beta^{2}-16 \beta^{2}}}{4 \sqrt {2} \gamma^{2}},\qquad a_{0}= \frac{\sqrt{7} \beta+5 \beta}{8 \gamma ^{2}},\qquad b_{1}= 0. \end{aligned} \end{aligned}$$
(19)

Replace (19) in (5),

$$ \Psi_{7}(\xi)= \biggl(\frac{\sqrt{7} \beta+5 \beta}{8 \gamma ^{2}}+ \frac{\sqrt{-5 \sqrt{7} \beta^{2}-16 \beta^{2}}}{4 \sqrt{2} \gamma^{2}} \bigl(\tan(\xi) \bigl(\cot(\xi)\bigr) \bigr) \biggr)^{\frac {1}{2}}e^{i\eta} . $$
(20)

2.1.3 The rational function solutions of Eq. (1)

If \(B_{3}=0\), then we have the following results:

$$ \begin{aligned}& k= \frac{\sqrt{7} \beta-\beta}{2 B_{2} \gamma},\qquad \mu\pm\frac {\sqrt{\frac{\sqrt{7} \beta^{2}}{\gamma^{2}}-\frac{4 \beta^{2}}{\gamma ^{2}}-8 \epsilon}}{2 \sqrt{2}},\\ & a_{1}= 0,\qquad a_{0}= 0,\qquad b_{1}= \frac {-\sqrt{7} B_{1} \beta-5 B_{1} \beta}{4 B_{2} \gamma^{2}} . \end{aligned}$$
(21)

Transfer (21) in (5),

$$ \Psi_{8}(\xi)= \biggl(\frac{-\sqrt{7} B_{1} \beta-5 B_{1} \beta}{4 \gamma^{2}} \biggl( \frac{1}{ (\exp(B_{2}\xi)-B_{1})} \biggr) \biggr)^{\frac{1}{2}}e^{i\eta} . $$
(22)

2.2 The van der Waals normal form for fluidized granular matter wave equation

Consider the generalized form of the nonlinear the van der Waals normal form for fluidized granular matter wave model [23] given by

$$ \frac{\partial^{2} v}{\partial t^{2}}+\frac{\partial^{2}}{\partial x^{2}} \biggl(\frac{\partial^{2}v}{\partial x^{2}}- \eta\frac{\partial v}{\partial t}-v^{3}-\epsilon v \biggr)=0, $$
(23)

where η is the bulk viscosity, ϵ is for the bifurcation parameter. The extreme advantage of this model is that it is used to explain the basic physical phase phenomenon in nonlinear science.

Let us make a traveling wave transformation for (23),

$$ v(x,t)=\Psi(\xi),\qquad \xi=kx+\omega t. $$
(24)

Substituting (24) in (23) and twice integrating with zero constant, we obtain

$$ \Psi+k^{4}\frac{1}{\omega^{2} (1-\frac{\text{k$\epsilon $}}{\omega^{2}} )}\Psi''+ \frac{\eta k^{2} \Psi'}{\omega (1-\frac{\text{k$\epsilon$}}{\omega^{2}} )}+ \frac{k^{2} \Psi ^{3}}{\omega^{2} (1-\frac{\text{k$\epsilon$}}{\omega^{2}} )}=0. $$
(25)

Suppose that (25) has the same solution form (5), we obtain collections of equations involving these parameters, \(a_{0}\), \(a_{1}\), \(b_{1}\), \(B_{1}\), \(B_{2}\), \(B_{3}\), k and ω. After solving we have the following results.

2.2.1 The soliton-like solutions of Eq. (23)

If \(B_{1}=0\), \(B_{2}=1\), \(B_{3}=-1\), then we have the following results:

$$ \begin{aligned}& k= \frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{9-2 \eta^{2}}}, \qquad \omega= \frac{3 \sqrt[3]{-1} \sqrt[3]{\eta} \epsilon ^{2/3}}{ (9-2 \eta^{2} )^{2/3}},\\ &a_{1} =\pm\frac{\sqrt [6]{-1} \sqrt{2} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{9-2 \eta ^{2}}},\qquad a_{0}=\pm\frac{\sqrt[6]{-1} \sqrt{2} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt[3]{9-2 \eta^{2}}},\qquad b_{1}= 0. \end{aligned}$$
(26)

Put (26) in (5),

$$ \Psi_{9}(\xi)=\frac{\sqrt[6]{-1} \sqrt{2} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt[3]{9-2 \eta^{2}}} \biggl(\pm1\pm \frac{1 }{2} \biggl(1+\tanh\biggl(\frac{1}{2}\xi\biggr) \biggr) \biggr) . $$
(27)

If \(B_{1}=0\), \(B_{2}=-1\), \(B_{3}=1\), then we have the following results:

$$ \begin{aligned}& k= \frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{9-2 \eta^{2}}},\qquad \omega= \frac{3 \sqrt[3]{-1} \sqrt[3]{\eta} \epsilon ^{2/3}}{ (9-2 \eta^{2} )^{2/3}},\qquad a_{1}=\pm\frac{\sqrt [6]{-1} \sqrt{2} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{9-2 \eta ^{2}}},\\ & a_{0}=\pm\frac{\sqrt[6]{-1} \sqrt{2} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt[3]{9-2 \eta^{2}}},\qquad b_{1}= 0. \end{aligned}$$
(28)

Put (28) in (5), then the solution of (23) becomes

$$ \Psi_{10}(\xi)=\frac{\sqrt[6]{-1} \sqrt{2} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt[3]{9-2 \eta^{2}}} \biggl(\pm1\pm \frac{1 }{2} \biggl(1-\coth\biggl(\frac{1}{2}\xi\biggr) \biggr) \biggr) . $$
(29)

If \(B_{1}=\frac{1}{2}\), \(B_{2}=0\), \(B_{3}=-\frac{1}{2}\), then we have the following results:

$$\begin{aligned} \begin{aligned} &k=\pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon }}{2^{2/3} \sqrt[3]{9-2 \eta^{2}}}, \qquad \omega\pm\frac{3 (-1)^{5/6} \sqrt[3]{\eta} \epsilon^{2/3}}{\sqrt[3]{2} \sqrt[6]{9-2 \eta^{2}} \sqrt{2 \eta^{2}-9}},\\ & a_{1}=\pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt [6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{2 \sqrt[6]{2} \sqrt{2 \eta ^{2}-9}}, \\ &a_{0}=\pm\frac{\sqrt[6]{-\frac{1}{2}} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt[3]{9-2 \eta^{2}}},\qquad b_{1}= \pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{2 \sqrt[6]{2} \sqrt{2 \eta^{2}-9}}. \end{aligned} \end{aligned}$$
(30)

Replace (30) in Eq. (5),

$$\begin{aligned} \Psi_{11}(\xi)={}&\frac{\sqrt[6]{-\frac{1}{2}} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt[3]{9-2 \eta^{2}}} \\ &{}\pm\frac{(-1)^{2/3} \eta ^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{2 \sqrt[6]{2} \sqrt{2 \eta^{2}-9}} \biggl(\coth(\xi)\pm csch(\xi)+\frac{1}{\coth (\xi)\pm csch(\xi) } \biggr) . \end{aligned}$$
(31)

If \(B_{1}=1\), \(B_{2}=0\), \(B_{3}=-1\), then we have the following results:

Family I

$$\begin{aligned} \begin{aligned} &k= \frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon }}{2^{2/3} \sqrt[3]{9-2 \eta^{2}}}, \qquad \omega=\pm\frac{3 (-1)^{5/6} \sqrt[3]{\eta} \epsilon^{2/3}}{\sqrt[3]{2} \sqrt[6]{9-2 \eta^{2}} \sqrt{2 \eta^{2}-9}},\qquad a_{1}= 0, \\ &a_{0}= -\frac{\sqrt[6]{-\frac {1}{2}} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{9-2 \eta ^{2}}},\qquad b_{1}= \pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{\sqrt[6]{2} \sqrt{2 \eta^{2}-9}}. \end{aligned} \end{aligned}$$
(32)

Substitute (32) in (5),

$$ \Psi_{12}(\xi)=-\frac{\sqrt[6]{-\frac{1}{2}} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt[3]{9-2 \eta^{2}}}\pm\frac{(-1)^{2/3} \eta ^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{\sqrt[6]{2} \sqrt {2 \eta^{2}-9}} \biggl(\frac{1}{\tanh(\xi) } \biggr) . $$
(33)

Family II

$$\begin{aligned} \begin{aligned} &k= \frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon }}{2^{2/3} \sqrt[3]{9-2 \eta^{2}}},\qquad \omega\pm\frac{3 (-1)^{5/6} \sqrt[3]{\eta} \epsilon^{2/3}}{\sqrt[3]{2} \sqrt[6]{9-2 \eta^{2}} \sqrt{2 \eta^{2}-9}}, \\ &a_{1}=\pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt [6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{\sqrt[6]{2} \sqrt{2 \eta ^{2}-9}},\qquad a_{0}= \frac{\sqrt[6]{-\frac{1}{2}} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt[3]{9-2 \eta^{2}}},\qquad b_{1}= 0. \end{aligned} \end{aligned}$$
(34)

Put (34) in (5),

$$ \Psi_{13}=\frac{\sqrt[6]{-\frac{1}{2}} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt[3]{9-2 \eta^{2}}}\pm\frac{(-1)^{2/3} \eta ^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{\sqrt[6]{2} \sqrt {2 \eta^{2}-9}} \bigl( \tanh(\xi) \bigr) . $$
(35)

Family III

$$\begin{aligned} \begin{aligned} &k= \frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{2 \sqrt[3]{2} \sqrt[3]{9-2 \eta^{2}}},\qquad \omega=\pm\frac{3 (-1)^{5/6} \sqrt[3]{\eta} \epsilon^{2/3}}{2^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt {2 \eta^{2}-9}},\\ &a_{1}=\pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{2^{5/6} \sqrt{2 \eta^{2}-9}},\qquad \\ &a_{0}= \frac{\sqrt[6]{-2} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{9-2 \eta^{2}}},\qquad `b_{1}=\pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt[6]{9-2 \eta ^{2}} \sqrt[3]{\epsilon}}{2^{5/6} \sqrt{2 \eta^{2}-9}}. \end{aligned} \end{aligned}$$
(36)

Transfer (36) in Eq. (5),

$$ \Psi_{14}=\frac{\sqrt[6]{-2} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt [3]{9-2 \eta^{2}}}\pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt[6]{9-2 \eta ^{2}} \sqrt[3]{\epsilon}}{2^{5/6} \sqrt{2 \eta^{2}-9}} \biggl(\tanh(\xi )+\frac{1}{\tanh(\xi) } \biggr) . $$
(37)

2.2.2 The trigonometric function solutions of Eq. (23)

If \(B_{1}=\frac{1}{2}\), \(B_{2}=0\), \(B_{3}=\frac{1}{2}\), then we have the following results:

Family I

$$ \begin{aligned}& k=-\frac{\sqrt[3]{-1} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{2 \eta^{2}-9}}, \qquad \omega=\pm\frac{3 \sqrt[6]{-1} \sqrt[3]{\eta} \epsilon^{2/3}}{ (2 \eta^{2}-9 )^{2/3}},\qquad a_{1}= \pm\frac {(-1)^{5/6} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}}, \\ & a_{0}= -\frac{\sqrt[3]{-1} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}},\qquad b_{1}= 0. \end{aligned}$$
(38)

Substitute (38) in (5),

$$ \Psi_{15}=-\frac{\sqrt[3]{-1} \eta^{2/3} \sqrt[3]{\epsilon }}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}}\pm\frac{(-1)^{5/6} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}} \bigl(\sec(\xi )+\tan(\xi) \bigr) . $$
(39)

Family II

$$ \begin{aligned}& k= \frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{2 \eta ^{2}-9}}, \qquad \omega=\pm\frac{3 (-1)^{5/6} \sqrt[3]{\eta} \epsilon ^{2/3}}{ (2 \eta^{2}-9 )^{2/3}},\qquad a_{1}= 0, \\ & a_{0}=\pm\frac {(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}},\qquad b_{1}= - \frac{\sqrt[6]{-1} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}}. \end{aligned}$$
(40)

Put (40) in (5),

$$ \Psi_{16}=\pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon }}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}}-\frac{\sqrt[6]{-1} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}} \biggl(\frac {1}{\sec(\xi)+\tan(\xi)} \biggr) . $$
(41)

Family III

$$\begin{aligned} \begin{aligned} &k= -\frac{\eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{36-8 \eta^{2}}},\qquad \omega=\pm\frac{3 \sqrt[3]{\eta} \epsilon ^{2/3}}{\sqrt[6]{36-8 \eta^{2}} \sqrt{2 \eta^{2}-9}},\qquad a_{1}= \frac {\eta^{2/3} \sqrt[6]{36-8 \eta^{2}} \sqrt[3]{\epsilon}}{2 \sqrt{2} \sqrt{2 \eta^{2}-9}}, \\ &a_{0}=\pm\frac{\sqrt{2} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt[3]{36-8 \eta^{2}}},\qquad b_{1}= -\frac{\eta^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{2 \sqrt[6]{2} \sqrt{2 \eta^{2}-9}}. \end{aligned} \end{aligned}$$
(42)

Replace (42) in (5),

$$\begin{aligned} \Psi_{17}={}&\pm\frac{\sqrt{2} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt [3]{36-8 \eta^{2}}}+\frac{\eta^{2/3} \sqrt[6]{36-8 \eta^{2}} \sqrt [3]{\epsilon}}{2 \sqrt{2} \sqrt{2 \eta^{2}-9}} \bigl(\sec(\xi)+\tan (\xi) \bigr) \\ &{}-\frac{\eta^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt [3]{\epsilon}}{2 \sqrt[6]{2} \sqrt{2 \eta^{2}-9}} \biggl(\frac {1}{\sec(\xi)+\tan(\xi)} \biggr) . \end{aligned}$$
(43)

If \(B_{1}=-\frac{1}{2}\), \(B_{2}=0\), \(B_{3}=-\frac{1}{2}\), then we have the following results:

Family I

$$ \begin{aligned} &k= \frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{2 \eta ^{2}-9}},\qquad `\omega=\pm\frac{3 (-1)^{5/6} \sqrt[3]{\eta} \epsilon ^{2/3}}{ (2 \eta^{2}-9 )^{2/3}},\qquad a_{1}= \frac{\sqrt[6]{-1} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt{2} \sqrt[3]{2 \eta ^{2}-9}},\\ & a_{0}= \frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon }}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}},\qquad b_{1}= 0. \end{aligned}$$
(44)

Put (44) in (5),

$$ \Psi_{18}=\frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt {2} \sqrt[3]{2 \eta^{2}-9}}+\frac{\sqrt[6]{-1} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}} \bigl( \sec(\xi )-\tan(\xi) \bigr) . $$
(45)

Family II

$$ \begin{aligned}&k= \frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{2 \eta ^{2}-9}}, \qquad \omega=\pm\frac{3 (-1)^{5/6} \sqrt[3]{\eta} \epsilon ^{2/3}}{ (2 \eta^{2}-9 )^{2/3}},\qquad a_{1}= 0,\\ & a_{0}=\pm\frac {(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}}, \qquad b_{1}= \frac{\sqrt[6]{-1} \eta^{2/3} \sqrt[3]{\epsilon }}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}}. \end{aligned}$$
(46)

Substitute (46) in Eq. (5),

$$ \Psi_{19}(\xi)=\pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon }}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}}+\frac{\sqrt[6]{-1} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt{2} \sqrt[3]{2 \eta^{2}-9}} \biggl(\frac {1}{\sec(\xi)-\tan(\xi)} \biggr) . $$
(47)

Family III

$$\begin{aligned} \begin{aligned} &k= -\frac{\eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{36-8 \eta^{2}}},\qquad \omega= \pm\frac{3 \sqrt[3]{\eta} \epsilon^{2/3}}{\sqrt [6]{36-8 \eta^{2}} \sqrt{2 \eta^{2}-9}},\qquad a_{1}= \pm\frac{\eta^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{2 \sqrt[6]{2} \sqrt{2 \eta^{2}-9}}, \\ &a_{0}= \pm\frac{\sqrt{2} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt[3]{36-8 \eta^{2}}},\qquad b_{1}= \frac{\eta^{2/3} \sqrt[6]{36-8 \eta^{2}} \sqrt[3]{\epsilon}}{2 \sqrt{2} \sqrt{2 \eta^{2}-9}}. \end{aligned} \end{aligned}$$
(48)

Put (48) in (5),

$$\begin{aligned} \Psi_{20}(\xi)={}&\pm\frac{\sqrt{2} \eta^{2/3} \sqrt[3]{\epsilon }}{\sqrt[3]{36-8 \eta^{2}}}+\frac{\eta^{2/3} \sqrt[6]{36-8 \eta^{2}} \sqrt[3]{\epsilon}}{2 \sqrt{2} \sqrt{2 \eta^{2}-9}} \biggl(\frac {1}{\sec(\xi)-\tan(\xi)} \biggr) \\ &{}\pm\frac{\eta^{2/3} \sqrt [6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{2 \sqrt[6]{2} \sqrt{2 \eta ^{2}-9}} \bigl(\sec(\xi)-\tan(\xi) \bigr) . \end{aligned}$$
(49)

If \(B_{1}=1(-1)\), \(B_{2}=0\), \(B_{3}=1(-1)\), then we have the following results:

Family I

$$ \begin{aligned}& k= -\frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{36-8 \eta^{2}}},\qquad \omega=\pm\frac{3 \sqrt[3]{-1} \sqrt[3]{\eta} \epsilon^{2/3}}{\sqrt[6]{36-8 \eta^{2}} \sqrt{2 \eta ^{2}-9}},\\ &a_{1}=\pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{\sqrt[6]{2} \sqrt{2 \eta^{2}-9}}, \qquad a_{0}= -\frac {(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[6]{2} \sqrt [3]{9-2 \eta^{2}}},\qquad b_{1}= 0. \end{aligned}$$
(50)

Replace (50) in (5),

$$ \Psi_{21}(\xi)=-\frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon }}{\sqrt[6]{2} \sqrt[3]{9-2 \eta^{2}}}\pm\frac{(-1)^{2/3} \eta ^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{\sqrt[6]{2} \sqrt {2 \eta^{2}-9}} \bigl(\tan(\xi) \bigl(\cot(\xi)\bigr) \bigr) . $$
(51)

Family II

$$ \begin{aligned} &k= -\frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{36-8 \eta^{2}}}, \qquad \omega\pm\frac{3 \sqrt[3]{-1} \sqrt[3]{\eta} \epsilon^{2/3}}{\sqrt[6]{36-8 \eta^{2}} \sqrt{2 \eta^{2}-9}},\qquad a_{1}= 0,\\ & a_{0}\pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt [6]{2} \sqrt[3]{9-2 \eta^{2}}}, \qquad b_{1}= - \frac{(-1)^{2/3} \eta^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{\sqrt[6]{2} \sqrt{2 \eta^{2}-9}}. \end{aligned}$$
(52)

Substituting (52) in (5),

$$ \Psi_{22}(\xi)=\pm\frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon }}{\sqrt[6]{2} \sqrt[3]{9-2 \eta^{2}}}-\frac{(-1)^{2/3} \eta^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{\sqrt[6]{2} \sqrt{2 \eta ^{2}-9}} \biggl(\frac{1}{\tan(\xi)(\cot(\xi)) } \biggr) . $$
(53)

Family III

$$\begin{aligned} \begin{aligned} &k= -\frac{\eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{144-32 \eta^{2}}}, \qquad\omega=\pm\frac{3 \sqrt[3]{\eta} \epsilon ^{2/3}}{\sqrt[6]{144-32 \eta^{2}} \sqrt{2 \eta^{2}-9}},\\ & a_{1}= -\frac {\eta^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{2^{5/6} \sqrt {2 \eta^{2}-9}}, \\ &a_{0}=\pm\frac{2 \sqrt{2} \eta^{2/3} \sqrt [3]{\epsilon}}{\sqrt[3]{144-32 \eta^{2}}},\qquad b_{1}=\pm \frac{\eta ^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{2^{5/6} \sqrt{2 \eta^{2}-9}}. \end{aligned} \end{aligned}$$
(54)

Put (54) in (5),

$$ \Psi_{23}(\xi)=\pm\frac{2 \sqrt{2} \eta^{2/3} \sqrt[3]{\epsilon }}{\sqrt[3]{144-32 \eta^{2}}}- \frac{\eta^{2/3} \sqrt[6]{9-2 \eta^{2}} \sqrt[3]{\epsilon}}{2^{5/6} \sqrt{2 \eta^{2}-9}} \biggl( \tan(\xi ) \bigl(\cot(\xi)\bigr)+\frac{1}{\tan(\xi)(\cot(\xi)) } \biggr) . $$
(55)

2.2.3 The rational function solutions of Eq. (23)

If \(B_{3}=0\), then we have the following results:

$$ \begin{aligned}&k= \frac{(-1)^{2/3} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{9 B_{2}^{2}-2 B_{2}^{2} \eta^{2}}},\qquad \omega= \frac{3 \sqrt[3]{-1} B_{2} \sqrt [3]{\eta} \epsilon^{2/3}}{ (-B_{2}^{2} (2 \eta^{2}-9 ) )^{2/3}},\qquad a_{1}= 0, \\ & a_{0}= \pm\frac{\sqrt[6]{-1} \sqrt{2} B_{2} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{-B_{2}^{2} (2 \eta ^{2}-9 )}}, \qquad b_{1}= \pm\frac{\sqrt[6]{-1} \sqrt{2} B_{1} \eta ^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{-B_{2}^{2} (2 \eta^{2}-9 )}}. \end{aligned}$$
(56)

Put (56) in (5),

$$ \Psi_{24}(\xi)=\pm\frac{\sqrt[6]{-1} \sqrt{2} B_{2} \eta^{2/3} \sqrt[3]{\epsilon}}{\sqrt[3]{-B_{2}^{2} (2 \eta^{2}-9 )}}\pm \frac{\sqrt[6]{-1} \sqrt{2} B_{1} \eta^{2/3} \sqrt[3]{\epsilon }}{\sqrt[3]{-B_{2}^{2} (2 \eta^{2}-9 )}} \biggl(\frac{B_{2}}{ (\exp(B_{2}\xi)-B_{1})} \biggr) . $$
(57)

2.3 The Benney–Luke equation

Let us consider the general form of the Benney–Luke equation in [26],

$$ u_{tt}-u_{xx}+\beta u_{xxxx}-\gamma u_{xxtt}+u_{t}u_{xx}+2u_{x}u_{xt}=0. $$
(58)

This equation is also called a water wave equation, it is used to describe two-way water wave propagation. Let \(u(x,t)=\Psi(\xi)\), \(\xi =x-kt\); substituting in (58), integrating and by removal of the constant of integration,

$$ \bigl(k^{2}-1 \bigr) \Psi'+ \Psi^{'''} \bigl(\beta-\gamma k^{2} \bigr)-\frac{3}{2}k \Psi^{'2}=0. $$
(59)

We assumed that (5) is the solution of (59). Substitute Eq. (5) with (6) in (59), After solving these equations system, we have following solution cases.

2.3.1 The soliton-like solutions of Eq. (58)

If \(B_{1}=0\), \(B_{2}=1\), \(B_{3}=-1\), then we have the following results:

$$ k= \pm\frac{\sqrt{\beta-1}}{\sqrt{\gamma-1}},\qquad a_{1}= \frac{4 (\gamma-\beta)}{\sqrt{(\beta-1)( \gamma-1)}},\qquad b_{1}= 0. $$
(60)

Put (60) in (5),

$$ \Psi_{25}=a_{0}+\frac{2 (\gamma-\beta)}{\sqrt{(\beta-1)( \gamma -1)}} \biggl(1+ \tanh\biggl(\frac{1}{2}\xi\biggr) \biggr),\quad \beta>1, \gamma>0. $$
(61)

If \(B_{1}=0\), \(B_{2}=-1\), \(B_{3}=1\), then we have the following results:

$$ k= \pm\frac{\sqrt{\beta-1}}{\sqrt{\gamma-1}},\qquad a_{1}= \frac{4 (\beta-\gamma)}{\sqrt{(\beta-1)( \gamma-1)}},\qquad b_{1}= 0. $$
(62)

Replace (62) in (5),

$$ \Psi_{26}=a_{0}+\frac{2 (\beta-\gamma)}{\sqrt{(\beta-1)( \gamma -1)}} \biggl(1- \coth\biggl(\frac{1}{2}\xi\biggr) \biggr),\quad \beta>1, \gamma>0. $$
(63)

If \(B_{1}=\frac{1}{2}\), \(B_{2}=0\), \(B_{3}=-\frac{1}{2}\), then we have the following results:

Family I

$$ k= \pm\frac{\sqrt{\beta-1}}{\sqrt{\gamma -1}},\qquad a_{1}=0,\qquad b_{1}= \frac{2 (\beta-\gamma)}{\sqrt{(\beta -1)(\gamma-1)}}. $$
(64)

Put (64) in (5),

$$ \Psi_{27}=a_{0}-\frac{2 (\beta-\gamma)}{\sqrt{(\beta-1)(\gamma -1)}} \biggl( \frac{1}{\coth(\xi)\pm csch(\xi) } \biggr),\quad \beta >1, \gamma>0. $$
(65)

Family II

$$ k= \pm\frac{\sqrt{\alpha-1}}{\sqrt{\beta -1}},\qquad b_{1}=0,\qquad a_{1}= \frac{2 (\beta-\gamma)}{\sqrt{(\beta -1)(\gamma-1)}} . $$
(66)

Transfer (66) in (5),

$$ \Psi_{28}=a_{0}+\frac{2 (\beta-\gamma)}{\sqrt{(\beta-1)(\gamma -1)}} \bigl( \coth(\xi)\pm csch(\xi) \bigr), \quad \beta>1, \gamma>1. $$
(67)

Family III

$$ k= \pm\frac{\sqrt{1-4 \beta}}{\sqrt{1-4 \gamma}},\qquad a_{1}=\frac{2 (\beta-\gamma)}{\sqrt{1-4 \beta} \sqrt{1-4 \gamma}},\qquad b_{1}=\frac {2 (\beta-\gamma)}{\sqrt{1-4 \beta} \sqrt{1-4 \gamma}} . $$
(68)

Replace (68) in (5),

$$\begin{aligned} &\Psi_{29}=a_{0}+\frac{2 (\beta-\gamma)}{\sqrt{1-4 \beta} \sqrt {1-4 \gamma}} \biggl( \bigl(\coth(\xi)\pm csch(\xi)\bigr)+\frac{1}{\coth(\xi )\pm csch(\xi) } \biggr), \\ & \quad \beta< \frac{1}{4}, \gamma< \frac{1}{4}. \end{aligned}$$
(69)

If \(B_{1}=1\), \(B_{2}=0\), \(B_{3}=-1\), then we have the following results:

Family I

$$ k=\pm\frac{\sqrt{1-4 \beta}}{\sqrt{1-4 \gamma }},\qquad a_{1}=0,\qquad b_{1}=- \frac{4 (\beta-\gamma)}{\sqrt{1-4 \beta} \sqrt {1-4 \gamma}}. $$
(70)

Put (70) in (5),

$$ \Psi_{30}=a_{0}-\frac{4 (\beta-\gamma)}{\sqrt{1-4 \beta} \sqrt {1-4 \gamma}} \biggl( \frac{1}{\tanh(\xi)} \biggr), \quad\beta< \frac {1}{4}, \gamma< \frac{1}{4}. $$
(71)

Family II

$$ k= \frac{\sqrt{1-4 \beta}}{\sqrt{1-4 \gamma }},\qquad b_{1}=0,\qquad a_{1}=- \frac{4 (\beta-\gamma)}{\sqrt{1-4 \beta} \sqrt {1-4 \gamma}} . $$
(72)

Replace (72) in (5),

$$ \Psi_{31}=a_{0}-\frac{4 (\beta-\gamma)}{\sqrt{1-4 \beta} \sqrt {1-4 \gamma}} \bigl( \tanh(\xi) \bigr), \quad \beta< \frac {1}{4}, \gamma< \frac{1}{4}. $$
(73)

Family III

$$ k= \pm\frac{\sqrt{1-16 \beta}}{\sqrt{1-16 \gamma}},\qquad a_{1}=\frac {4 (\beta-\gamma)}{\sqrt{1-16 \beta} \sqrt{1-16 \gamma }},\qquad b_{1}=\frac{4 (\beta-\gamma)}{\sqrt{1-16 \beta} \sqrt{1-16 \gamma}} . $$
(74)

Put (60) in (5),

$$ \Psi_{32}=a_{0}+\frac{4 (\beta-\gamma)}{\sqrt{1-16 \beta} \sqrt {1-16 \gamma}} \biggl( \tanh(\xi)+\frac{1}{\tanh(\xi)} \biggr), \quad \beta< \frac{1}{16}, \gamma< \frac{1}{16}. $$
(75)

2.3.2 The trigonometric function solutions of Eq. (58)

If \(B_{1}=\frac{1}{2}\), \(B_{2}=0\), \(B_{3}=\frac{1}{2}\), then we have the following results:

Family I

$$ k=\pm\frac{\sqrt{\beta+1}}{\sqrt{\gamma+1}},\qquad a_{1}= \frac{2 (\beta-\gamma)}{\sqrt{\beta+1} \sqrt{\gamma+1}},\qquad b_{1}= 0, $$
(76)

Substitute (76) in (5),

$$ \Psi_{33}(\xi)=a_{0}+\frac{2 (\beta-\gamma)}{\sqrt{\beta+1} \sqrt{\gamma+1}} \bigl(\sec(\xi)+\tan(\xi) \bigr), \quad \beta >-1, \gamma>-1. $$
(77)

Family II

$$ k=\pm\frac{\sqrt{\beta+1}}{\sqrt{\gamma+1}},\qquad b_{1}= \frac{2 (\gamma-\beta)}{\sqrt{\beta+1} \sqrt{\gamma+1}},\qquad a_{1}= 0. $$
(78)

Put (78) in (6),

$$ \Psi_{34}(\xi)=a_{0}+\frac{2 (\gamma-\beta)}{\sqrt{\beta+1} \sqrt{\gamma+1}} \biggl(\frac{1}{\sec(\xi)+\tan(\xi)} \biggr),\quad \beta>-1, \gamma>-1. $$
(79)

Family III

$$ k=\pm\frac{\sqrt{-4 \beta-1}}{\sqrt{-4\gamma-1}}, \qquad a_{1}= \frac{2 (\beta-\gamma)}{\sqrt{4 \beta+1} \sqrt{4 \gamma+1}},\qquad b_{1}= -\frac{2 (\beta-\gamma)}{\sqrt{4 \beta+1} \sqrt{4\gamma+1}}. $$
(80)

Put (80) in (5),

$$\begin{aligned} & \Psi_{35}=a_{0}+\frac{2 (\beta-\gamma)}{\sqrt{4 \beta+1} \sqrt{4 \gamma+1}} \biggl( \sec(\xi)+\tan(\xi)-\frac{1}{\sec(\xi)+\tan (\xi)} \biggr), \\ &\quad \beta>\frac{-1}{4}, \gamma>\frac{-1}{4}. \end{aligned}$$
(81)

If \(B_{1}=-\frac{1}{2}\), \(B_{2}=0\), \(B_{3}=-\frac{1}{2}\), then we have the following results:

Family I

$$ k=\pm\frac{\sqrt{\beta+ 1}}{\sqrt{\gamma+1}},\qquad a_{1}= \frac{2 (\gamma-\beta)}{\sqrt{\beta +1} \sqrt{\gamma+1}},\qquad b_{1}= 0. $$
(82)

Put (82) in(6),

$$ \Psi_{(}\xi)=a_{0}+\frac{2 (\gamma-\beta)}{\sqrt{\beta+1} \sqrt {\gamma+1}} \bigl(\sec(\xi)- \tan(\xi) \bigr),\quad \beta >-1, \gamma-1. $$
(83)

Family II

$$ k=\pm\frac{\sqrt{\beta+1}}{\sqrt{\gamma+1}},\qquad b_{1}=\frac{2 (\beta-\gamma)}{\sqrt{\beta+1} \sqrt{\gamma+1}},\qquad a_{1}= 0. $$
(84)

Put (84) in (5),

$$ \Psi_{37}=a_{0}+\frac{2 (\beta-\gamma)}{\sqrt{\beta+1} \sqrt {\gamma+1}} \biggl( \frac{1}{\sec(\xi)-\tan(\xi)} \biggr), \quad\beta >-1, \gamma-1. $$
(85)

Family III

$$ k=\pm\frac{\sqrt{-4 \beta-1}}{\sqrt{-4 \gamma-1}},\qquad a_{1}=-\frac {2 (\beta-\gamma)}{\sqrt{4 \beta+1} \sqrt{4 \gamma +1}},\qquad b_{1}=\frac{2 (\beta-\gamma)}{\sqrt{4 \beta+1} \sqrt{4 \gamma+1}}. $$
(86)

Replace (86) in (5),

$$\begin{aligned} & \Psi_{38}=a_{0}-\frac{2 (\beta-\gamma)}{\sqrt{4 \beta+1} \sqrt{4 \gamma+1}} \biggl( \bigl(\sec(\xi)-\tan(\xi)\bigr) -\frac{1}{\sec(\xi)-\tan (\xi)} \biggr), \\ &\quad \beta>- \frac{1}{4}, \gamma>-\frac{1}{4}. \end{aligned}$$
(87)

If \(B_{1}=1(-1)\), \(B_{2}=0\), \(B_{3}=1(-1)\), then we have the following results:

Family I

$$ k\pm\frac{\sqrt{4 \beta+1}}{\sqrt{4 \gamma+1}},\qquad a_{1}=\frac{4 (\beta-\gamma)}{\sqrt{4 \beta+1} \sqrt{4 \gamma+1}},\qquad b_{1}=0, $$
(88)

Put (88) in (5),

$$ \Psi_{39}=a_{0}+\frac{4 (\beta-\gamma)}{\sqrt{4 \beta+1} \sqrt{4 \gamma+1}} \bigl( \tan(\xi) \bigl(\cot(\xi)\bigr) \bigr), \quad \beta>-\frac {1}{4}, \gamma>- \frac{1}{4}. $$
(89)

Family II

$$ k=\pm\frac{\sqrt{4 \beta+1}}{\sqrt{4 \gamma+1}},\qquad b_{1}=-\frac{4 (\beta-\gamma)}{\sqrt{4 \beta+1} \sqrt{4 \gamma+1}},\qquad a_{1}=0. $$
(90)

Replace (90) in (5),

$$ \Psi_{40}(\xi)=a_{0}-\frac{4 (\beta-\gamma)}{\sqrt{4 \beta+1} \sqrt{4 \gamma+1}} \biggl(\frac{1}{\tan(\xi)(\cot(\xi)} \biggr),\quad \beta>-\frac{1}{4}, \gamma>- \frac{1}{4}. $$
(91)

Family III

$$ k=\pm\frac{\sqrt{16 \beta+1}}{\sqrt{16 \gamma+1}},\qquad a_{1}=-\frac {4 (\beta-\gamma)}{\sqrt{16 \beta+1} \sqrt{16 \gamma +1}},\qquad b_{1}=\frac{4 (\beta-\gamma)}{\sqrt{16\beta+1} \sqrt{16 \gamma+1}}. $$
(92)

Transfer (92) in (5),

$$\begin{aligned} &\Psi_{41}=a_{0}-\frac{4 (\beta-\gamma)}{\sqrt{16 \beta+1} \sqrt {16 \gamma+1}} (\tan( \xi) \biggl(\cot(\xi) -\frac{1}{\tan(\xi )(\cot(\xi)} \biggr), \\ & \quad \beta>-\frac{1}{16}, \gamma>-\frac{1}{16}. \end{aligned}$$
(93)

2.3.3 The rational function solutions of Eq. (58)

If \(B_{1}=0\), \(B_{2}=0\), then we have the following results:

$$ k= \pm1,\qquad a_{1}= \pm4B_{3} (\beta-\gamma),\qquad b_{1}= 0, $$
(94)

Substitute (94) in (5),

$$ \Psi_{42}=a_{0}+4B_{3} \biggl( \frac{(\beta-\gamma)}{A_{3}\xi+\epsilon } \biggr) . $$
(95)

If \(B_{2}=0\), \(B_{3}=0\), then we have the following results:

$$ k= \pm1,\qquad b_{1}= \pm4B_{1} (\beta-\gamma),\qquad a_{1}= 0. $$
(96)

Put (96) in (5),

$$ \Psi_{43}=a_{0}\pm4 \biggl( \frac{(\beta-\gamma)}{\xi} \biggr) . $$
(97)

If \(B_{1}\neq0\), \(B_{2}\neq0\), \(B_{3}=0\), then we have the following results:

$$ k= \frac{\sqrt{\beta B_{2}^{2}-1}}{\sqrt{\gamma B_{2}^{2}-1}}, \qquad b_{1}= \frac {4 B_{1} (\beta-\gamma)}{\sqrt{\beta B_{2}^{2}-1} \sqrt{\gamma B_{2}^{2}-1}},\qquad a_{1}= 0. $$
(98)

Replace (98) in (5),

$$ \Psi_{44}=a_{0}+\frac{4 B_{1} (\beta-\gamma)}{\sqrt{\beta B_{2}^{2}-1} \sqrt{\gamma B_{2}^{2}-1}} \biggl( \frac{B_{2}}{ (\exp(B_{2}\xi)-B_{1})} \biggr). $$
(99)

2.4 The \((3 + 1)\)-dimensional modified Korteweg–de Vries–Zakharov–Kuznetsov equation

Let us consider the general form in [28],

$$ u_{t}+\alpha u^{2}u_{x}+\beta u_{xxx}+\gamma(u_{yy}+u_{zz})_{x}=0. $$
(100)

Consider the wave transformation for Eq. (100),

$$ u(x,y,z,t)=\Psi(\xi), \quad\xi=x+y+z-\eta t. $$
(101)

Put Eq. (101) in Eq. (100) and after integrating we have the following ODE form:

$$ -\eta\Psi+\alpha\frac{\Psi^{3}}{3}+(\beta+2\gamma) \Psi''=0. $$
(102)

Let (5) be a solution of (102). Substitute (5) with (6) in (102); after solving we have the following solution possibilities.

2.4.1 The soliton-like solutions of Eq. (100)

If \(B_{1}=0\), \(B_{2}=1\), \(B_{3}=-1\), then we have the following results:

$$ a_{1}= \pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha}},\qquad \eta = \frac{1}{2} (-\beta-2 \gamma),\qquad a_{0}= \pm\frac{\sqrt{-3\beta -6\gamma} }{ \sqrt{2\alpha}},\qquad b_{1}= 0. $$
(103)

Put (103) in (5), we have

$$ \Psi_{45}= \pm\frac{\sqrt{-3\beta-6\gamma} }{ \sqrt{2\alpha }}\pm\frac{ \sqrt{-6\beta-12 \gamma}}{2 \sqrt{\alpha}} \biggl(1+\tanh\biggl(\frac{1}{2}\xi\biggr) \biggr) . $$
(104)

If \(B_{1}=0\), \(B_{2}=-1\), \(B_{3}=1\), then we have the following results:

$$ \begin{aligned}&a_{1}= \pm\frac{ \sqrt{-6(\beta+2 \gamma) }}{\sqrt{\alpha }}, \qquad \eta= \frac{1}{2} (-\beta-2 \gamma), \\ & a_{0}= \pm\frac{\sqrt {-3(\beta+2\gamma)} }{ \sqrt{2\alpha}},\qquad b_{1}= 0. \end{aligned}$$
(105)

Replace (105) in (5),

$$ \Psi_{46}=\pm\frac{\sqrt{-3(\beta+2\gamma)} }{ \sqrt{2\alpha }}\pm\frac{ \sqrt{-6(\beta+2 \gamma) }}{2 \sqrt{\alpha}} \biggl(1-\coth\biggl(\frac{1}{2}\xi\biggr) \biggr) . $$
(106)

If \(B_{1}=\frac{1}{2}\), \(B_{2}=0\), \(B_{3}=-\frac{1}{2}\), then we have the following results:

Family I

$$ a_{1}= 0,\qquad \eta= -\frac{1}{2} (\beta+2 \gamma),\qquad a_{0}= 0,\qquad b_{1}= \pm \frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}} . $$
(107)

Substitute (107) in (5),

$$ \Psi_{47}=\pm\frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha }} \biggl( \frac{1}{\coth(\xi)\pm csch(\xi) } \biggr) . $$
(108)

Family II

$$ b_{1}= 0,\qquad \eta= -\frac{1}{2} (\beta+2 \gamma),\qquad a_{0}= 0,\qquad a_{1}= \pm \frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}} . $$
(109)

Put (109) in (5),

$$ \Psi_{48}=\pm\frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha }} \bigl(\coth(\xi)\pm csch(\xi) \bigr) . $$
(110)

Family III

$$ b_{1}= \pm\frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}},\qquad \eta = (\beta+2 \gamma),\qquad a_{0}= 0,\qquad a_{1}= \pm\frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}} . $$
(111)

Putting (111) in (5),

$$ \Psi_{49}=\pm\frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha }} \biggl( \bigl(\coth( \xi)\pm csch(\xi)\bigr)+\frac{1}{\coth(\xi)\pm csch(\xi) } \biggr) . $$
(112)

If \(B_{1}=1\), \(B_{2}=0\), \(B_{3}=-1\), then we have the following results:

Family I

$$ a_{1}= 0,\qquad \eta= -2 (\beta+2 \gamma),\qquad a_{0}= 0,\qquad b_{1}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha}} . $$
(113)

Replacing (113) in (5),

$$ \Psi_{50}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha }} \biggl( \frac{1}{\tanh(\xi)} \biggr). $$
(114)

Family II

$$ b_{1}= 0, \qquad \eta= -2 (\beta+2 \gamma), \qquad a_{0}= 0,\qquad a_{1}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha}} . $$
(115)

Put (115) in (5),

$$ \Psi_{51}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha }} \bigl(\tanh(\xi) \bigr). $$
(116)

Family III

$$ b_{1}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha}},\qquad \eta= -8 (\beta+2 \gamma),\qquad a_{0}= 0,\qquad a_{1}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha}} . $$
(117)

Substitute (117) in (5),

$$ \Psi_{52}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha }} \biggl(\tanh(\xi)+ \frac{1}{\tanh(\xi)} \biggr). $$
(118)

2.4.2 The trigonometric function solutions of Eq. (100)

If \(B_{1}=\frac{1}{2}\), \(B_{2}=0\), \(B_{3}=\frac{1}{2}\), then we have the following results:

Family I

$$ a_{1}= \pm\frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}},\qquad \eta = \frac{1}{2} (\beta+2 \gamma), \qquad a_{0}= 0, \qquad b_{1}= 0. $$
(119)

Put (119) in (5),

$$ \Psi_{53}=\pm\frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}} \bigl(\sec(\xi)+\tan( \xi) \bigr). $$
(120)

Family II

$$ b_{1}= \pm\frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}}, \qquad \eta = \frac{1}{2} (\beta+2 \gamma),\qquad a_{0}= 0, \qquad a_{1}= 0. $$
(121)

Put (121) in (5),

$$ \Psi_{54}=\pm\frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha }} \biggl( \frac{1}{\sec(\xi)+\tan(\xi)} \biggr). $$
(122)

Family III

$$ b_{1}= \pm\frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}},\qquad \eta = (2\beta+4 \gamma),\qquad a_{0}= 0,\qquad a_{1}= \pm\frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}} . $$
(123)

Replace (123) in Eq. (5),

$$ \Psi_{55}= \pm\frac{ \sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha }} \biggl(\bigl(\sec( \xi)+\tan(\xi)\bigr)+\frac{1}{\sec(\xi)+\tan(\xi)} \biggr). $$
(124)

If \(B_{1}=-\frac{1}{2}\), \(B_{2}=0\), \(B_{3}=-\frac{1}{2}\), then we have the following results:

Family I

$$ a_{1}= \pm\frac{\sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}},\qquad \eta= \frac{1}{2} (\beta+2 \gamma),\qquad a_{0}= 0,\qquad b_{1}= 0. $$
(125)

Substitute (125) in (5),

$$ \Psi_{56}=\pm\frac{\sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha }} \bigl(\sec(\xi)-\tan( \xi) \bigr). $$
(126)

Family II

$$ b_{1}= \pm\frac{\sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}},\qquad \eta= \frac{1}{2} (\beta+2 \gamma),\qquad a_{0}= 0, \qquad a_{1}= 0. $$
(127)

Put (127) in (5),

$$ \Psi_{57}=\pm\frac{\sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha }} \biggl( \frac{1}{\sec(\xi)-\tan(\xi)} \biggr). $$
(128)

Family III

$$ b_{1}= \pm\frac{\sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}}, \qquad \eta= (-\beta-2 \gamma),\qquad a_{0}= 0, \qquad a_{1}= \pm\frac{\sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha}}. $$
(129)

Put (129) in (5),

$$ \Psi_{58}= \pm\frac{\sqrt{-3\beta-6 \gamma}}{\sqrt{2\alpha }} \biggl(\bigl(\sec( \xi)-\tan(\xi)\bigr) +\frac{1}{\sec(\xi)-\tan(\xi)} \biggr). $$
(130)

If \(B_{1}=1(-1)\), \(B_{2}=0\), \(B_{3}=1(-1)\), then we have the following results:

Family I

$$ a_{1}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha}},\qquad \eta= 2 (\beta+2 \gamma),\qquad a_{0}= 0,\qquad b_{1}= 0. $$
(131)

Put (131) in (5),

$$ \Psi_{59}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha}} \bigl(\tan(\xi) \bigl( \cot(\xi)\bigr) \bigr). $$
(132)

Family II

$$ b_{1}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha}},\qquad \eta= 2 (\beta+2 \gamma),\qquad a_{0}= 0,\qquad a_{1}= 0. $$
(133)

Replace (133) in (5),

$$ \Psi_{60}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha}} \biggl( \frac{1}{\tan(\xi)(\cot(\xi)} \biggr). $$
(134)

Family III

$$ b_{1}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha}},\qquad \eta =- 4 (\beta+2 \gamma), \qquad a_{0}= 0,\qquad a_{1}=\pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha}} . $$
(135)

Substitute (135) in (5),

$$ \Psi_{61}= \pm\frac{ \sqrt{-6\beta-12 \gamma}}{\sqrt{\alpha }} (\tan(\xi) \biggl( \cot(\xi) +\frac{1}{\tan(\xi)(\cot(\xi )} \biggr). $$
(136)

2.4.3 The rational function solution of Eq. (100)

If \(B_{1}\neq0\), \(B_{2}\neq0\), \(B_{3}=0\), then we have the following results:

$$ \begin{aligned}& a_{1}= 0, \qquad \eta= \frac{1}{2} \bigl(-\beta B_{2}^{2}-2 B_{2}^{2} \gamma \bigr),\\ & a_{0}= \pm\frac{B_{2} \sqrt{-\beta-2 \gamma}}{\sqrt{\alpha }},\qquad b_{1}=\pm\frac{ B_{1} \sqrt{-6 (\beta+2 \gamma)}}{\sqrt{\alpha } } . \end{aligned}$$
(137)

Put (137) in (5),

$$ \Psi_{62}= \pm\frac{B_{2} \sqrt{-\beta-2 \gamma}}{\sqrt{\alpha}} \pm\frac{ B_{1} \sqrt{-6 (\beta+2 \gamma)}}{\sqrt{\alpha} } \biggl(\frac{B_{2}}{ (\exp(B_{2}\xi)-B_{1})} \biggr) . $$
(138)

3 Discussion of the results

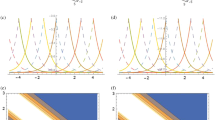
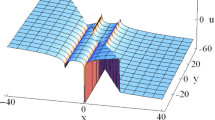
After successfully employing the modified F-expansion method on four important models, now in this section we shall discuss the similarities and dissimilarities of our novel constructed results with other results in the previous literature. By choosing different values of \(a_{i}\) and \(b_{i}\) in Eq. (5) with Eq. (6), we have obtained a collection of different solutions. Few of our results are similar to others, our solution (15) and (19) approximate in the same way as (2.37), (2.59) in [24], respectively. In the same way our constructed solutions (39) and (39) are similar to the solutions (22) and (26) in [23], respectively. Furthermore our solutions (49) and (81) are approximately similar solutions to (3.16) and (3.14) in [27]. The results of all our constructed solutions of both models are new and have not been investigated before in any previous research literature. The discussion of the results and graphically illustration of some solution demonstrate that our methods are more efficient, and a reliable and powerful tool to solve nonlinear problems.

4 Conclusion

From this study, we have seen the analytical structure of the complex fractional Kundu–Eckhaus, the van der Waals normal form for fluidized granular matter, the Benny–Luke and the \((3 + 1)\)-dimensional modified Korteweg–de Vries–Zakharov–Kuznetsov waves models for constructing the exact, solitary wave solutions by employing the modified F-expansion method. The constructed solutions are novel and more general. These results facilitate us to explore the physical phenomena of these nonlinear models. The obtained results having potential applications in mathematical physics.