Abstract
In this paper, a single-species discrete model with stage structure is investigated. By analyzing the corresponding characteristic equations, the local asymptotic stability of non-negative equilibrium points and the existence of flip bifurcation are discussed. Using the center manifold theory, the stability of the non-hyperbolic equilibrium point is obtained. Based on bifurcation theory, we obtain the direction and the stability of a flip bifurcation at the positive equilibrium with the birth rate as the bifurcation parameter. Finally, some numerical simulations, including phase portraits, chaotic bands with period windows, and Lyapunov exponent methods, are performed to validate the theoretical results, which extends the results in previous papers.
Similar content being viewed by others
1 Introduction
It is generally known that in the theory of population dynamics, there are two kinds of mathematical models: the continuous models governed by differential equations and the discrete models governed by difference equations. When the population size is small or when births and deaths all occur at discrete times, discrete models would be more appropriate than the continuous models. Meanwhile, discrete models give rise to more efficient computational models for numerical simulations and these results exhibit rich dynamics of the discrete models compared with the continuous ones. In fact, even in one-dimensional discrete models denoted by iterated quadratic maps, like the well-known logistic map, periodic and chaotic trajectories can easily be observed. Moreover, two-dimensional discrete models can reveal a plethora of complicated asymptotic behaviors, from convergence to a fixed point or a periodic cycle until a quasi-periodic orbit along a closed invariant curve or even an erratic motion inside a bounded chaotic attractor (see e.g. [1–5]).
For many animal species, such as crustaceans, insects and amphibians, the individuals take on different morphological shapes before reaching their final adult state. This multiplicity of developmental stages causes individuals with a complex life cycle. The age-specific reproduction and mortality rate of a population is one of the most fundamental parameters in both the theory and practice of population dynamics and demography. The characteristics of the vital rates (rates of reproduction, mortality and development) depending on age, size or development stage have often been argued (both theoretically and experimentally) to be crucial determining factors in the resulting dynamical growth and age distribution of the population [6, 7]. In recent years, stage structure models have received a lot of attention (see, e.g., [8–16]). Tang and Chen [17] proposed that a single-species population has stage structure, and the population is divided into immature and mature classes, and only the mature population can reproduce as follows:
where \(x(t)\) and \(y(t)\) are the immature and mature populations, respectively, with \(N(t)=x(t)+y(t)\); \(B(N(t))y(t)\) is the birth rate function with \(B(N(t))=b\mathrm{e}^{-N(t)}>0\) being known as the Ricker function; \(d>0\) denotes the death rate constant, and \(\delta>0\) is the maturity rate, which determines the mean length of the juvenile period. The boundedness and global stability of equilibria of model (1) were discussed. Tang and Chen [17] supposed that the death rates of immature and mature population are equal. It is unreasonable to our natural world. Subsequently, Gao and Chen [18] assumed that the death rates of immature and mature populations are different. According to model (1), they proposed the discrete single-species population model with stage structure
where \(N_{0}\) denotes the set of non-negative integers. \(x_{n}\) and \(y_{n}\) are the immature and mature populations at generation n, respectively. \(d_{1}\) and \(d_{2}\) (\(d_{i}>0\), \(i=1,2\)) are the death rate constants of immature and mature, respectively. The parameters b and δ have the same biological interpretations as those in model (1). In model (2), only the mature population have reproductive ability. Let \(\alpha=1-d_{1}-\delta,\beta=1-d_{2}\). For ecological reasons, we assume that \(0<\alpha<1\), \(0<\beta<1\), \(\delta\neq\beta\). Substituting α and β in model (2), we obtain the following model:
In [18], Gao and Chen pointed out that if \(b\delta>(1-\alpha )(1-\beta)\), then the positive equilibrium point of model (3) is globally asymptotically stable, however, if \(b\delta<(1-\alpha)(1-\beta )\), then the trivial equilibrium point is globally asymptotically stable. They did not consider the stability of equilibrium point when \(b\delta =(1-\alpha)(1-\beta)\). Moreover, by our results (see Theorem 2.2), it is clear to see that the condition \(b\delta>(1-\alpha )(1-\beta)\) is not sufficient for the stability of positive equilibrium point.
To date no paper has appeared in the literature which discusses the bifurcation problem for model (3). Our work mainly focuses on the stability of trivial equilibrium point when it is non-hyperbolic, i.e., \(b\delta=(1-\alpha)(1-\beta)\), the stability of positive equilibrium point, the existences and directions of the flip bifurcation of positive equilibrium point with the birth rate b as bifurcation parameter by applying the bifurcation theory.
The paper is organized as follows. In Sect. 2, we analyze the distribution of characteristic roots associated with model (3), and obtain the stability of equilibrium points, especially, the stability of non-hyperbolic equilibrium point. In Sect. 3, the direction and stability of flip bifurcations for model (3) are determined. In Sect. 4, some numerical simulations are performed to illustrate the theoretical results. A brief discussion is given in Sect. 5.
2 Stability of equilibrium points
In this section, we study the distribution of characteristic roots of model (3) by employing the relation between roots and coefficients of the quadratic equation, and discuss the stability of non-hyperbolic equilibrium point by center manifold theorem.
It is obvious that solutions of model (3) always exist and stay positive. Moreover, model (3) is dissipative (see [18]). Note that the local stability of an equilibrium point \((x,y)\) is determined by the modules of the roots of the characteristic equation at the equilibrium point. Clearly, \(E_{0}=(0,0)\) is the trivial equilibrium point of model (3). There exists a unique positive equilibrium point
provided that \(b\delta>(1-\alpha)(1-\beta)\).
Now, we investigate the local stability of model (3) around equilibrium points. The Jacobian matrix of model (3) at any state variable is given by
The characteristic equation of the Jacobian matrix \(J(x,y)\) is given by
where \(\mathrm{Tr}(J)\) and \(\mathrm{Det}(J)\) are the trace and determinant of the Jacobian matrix \(J(x,y)\), respectively. For model (3), \(\mathrm{Tr}(J)=-b\mathrm{e}^{-(x+y)}y+\alpha+\beta\) and \(\mathrm{Det}(J)=(-b\mathrm{e}^{-(x+y)}y+\alpha)\beta-(1-y)b\mathrm {e}^{-(x+y)}\delta\).
In order to analyze the stability of equilibria for model (3), we give the following lemma (see [19]), which can easily be proved by the relation between roots and coefficients of the characteristic equation (5) of model (3). Denote by \(\vert \lambda \vert \) the modulus of λ.
Lemma 2.1
Let \(F(\lambda)=\lambda^{2}-\widehat{B}\lambda+\widehat{C}\). Suppose that \(F(1)>0\), \(\lambda_{1}\) and \(\lambda_{2}\) are the two roots of \(F(\lambda)=0\). Then
-
(i)
\(\vert \lambda_{1} \vert <1\) and \(\vert \lambda_{2} \vert <1\) if and only if \(F(-1)>0\) and \(\widehat{C}<1\).
-
(ii)
\(\vert \lambda_{1} \vert <1\) and \(\vert \lambda_{2} \vert >1\) (or \(\vert \lambda_{1} \vert >1\) and \(\vert \lambda_{2} \vert <1\)) if and only if \(F(-1)<0\).
-
(iii)
\(\vert \lambda_{1} \vert >1\) and \(\vert \lambda_{2} \vert >1\) if and only if \(F(-1)>0\) and \(\widehat{C}>1\).
-
(iv)
\(\lambda_{1}=-1\) and \(\vert \lambda_{2} \vert \neq1\) if and only if \(F(-1)=0\) and \(\widehat{C}\neq1\).
-
(v)
\(\lambda_{1}\) and \(\lambda_{2}\) are complex and \(\vert \lambda _{1} \vert = \vert \lambda_{2} \vert =1\) if and only if \(\vert \widehat{B} \vert <2\) and \(\widehat{C}=1\).
In the following, we give the stability of trivial equilibrium point \(E_{0}\).
It follows from (5) that the characteristic equation of the equilibrium point \(E_{0}\) is given by
Obviously, Eq. (6) has two distinct real roots:
Note that if \(b\delta=(1-\alpha)(1-\beta)\), then \(\lambda_{1}=1\), \(\lambda _{2}=\alpha+\beta-1\). In this case, \(E_{0}\) is non-hyperbolic. However, due to \(-1<\lambda_{2}=\alpha+\beta -1<1\), it is difficult to determine the stability of \(E_{0}\). Now, by the center manifold theorem, we will analyze the stability for \(E_{0}\) when \(b\delta=(1-\alpha)(1-\beta)\).
Let \(\mathcal{T}= \bigl ( {\scriptsize\begin{matrix}{} 1-\beta& \alpha-1\cr \delta& \delta \end{matrix}} \bigr )\) and use the translation \(\bigl ( {\scriptsize\begin{matrix}{} x_{n}\cr y_{n} \end{matrix}} \bigr )= \mathcal{T}\bigl ( {\scriptsize\begin{matrix}{} \widetilde{x}_{n}\cr\widetilde{y}_{n} \end{matrix}} \bigr )\), then model (3) becomes
where
According to the center manifold theorem (see [20]), the center manifold for the map (7) can be represented as follows:
To obtain the specific expression of the center manifold, we take
Then the center manifold satisfies
Substituting (9) into (10) and equating coefficients, we obtain
Thus the map (7) restricted to the center manifold is given by
By Theorem 2.3 in [21], since \(-(1-\beta)<0\), the fixed point 0 of the map (11) is semi-asymptotically stable from the right. Thus \(E_{0}\) of model (3) is locally asymptotically stable in \(\{(x,y): x\geq0,y\geq0\}\) if \(b\delta=(1-\alpha)(1-\beta)\).
By Lemma 2.1 and the discussion above, we list the stability of trivial equilibrium point \(E_{0}\) for all permissible values of parameters in Table 1.
Now, we discuss the stability of the equilibrium \(E^{\ast}\). The characteristic equation of the equilibrium \(E^{\ast}\) can be represented as
where \(\mathrm{Tr}(J(E^{\ast}))=x^{\ast}(\alpha-1)+\alpha+\beta\) and \(\mathrm{Det}(J(E^{\ast}))=(x^{\ast}(\alpha-1)+\alpha)\beta-(x^{\ast }(\alpha-1)\delta+(1-\alpha)(1-\beta))\).
Clearly,
Note that \(\delta\neq\beta\). Let \(m_{1}=\mathrm{e}^{\frac{2(\alpha+\beta)(1+\delta-\beta)}{(1+\beta -\delta)(1-\alpha)(1-\beta)}}\) and \(m_{2}=\mathrm{e}^{\frac{(2-\alpha -\beta)(1+\delta-\beta)}{(\delta-\beta)(1-\alpha)(1-\beta)}}\). Then \(F(-1)>0\) if and only if \(b\delta<(1-\alpha)(1-\beta)m_{1}\). Meanwhile, when \(\delta<\beta\), always \(\mathrm{Det}(J(E^{\ast}))<1\). In fact, under the condition \(\delta<\beta\), one obtains
However, when \(\delta>\beta\), \(\mathrm{Det}(J(E^{\ast}))<1\) is equivalent to \(b\delta<(1-\alpha)(1-\beta)m_{2}\). To determine the size relation between \(m_{1}\) and \(m_{2}\), we consider the following two cases.
Case 1: \(\delta<\beta\). It is obvious that \(m_{2}<1<m_{1}\).
Case 2: \(\delta>\beta\). Note that \(\alpha+\beta<\alpha+\delta<1\). It is easy to obtain
Thus, in this case, \(m_{2}>m_{1}>1\).
By Lemma 2.1, we have the following results as regards the stability of the equilibrium point \(E^{\ast}\).
Theorem 2.2
Suppose that \(b\delta>(1-\alpha)(1-\beta)\).
-
(i)
If \(b\delta<(1-\alpha)(1-\beta)m_{1}\), then \(F(-1)>0\) and \(\mathrm{Det}(J(E^{\ast}))<1\). By Lemma 2.1, we have \(\vert \lambda_{1} \vert <1\) and \(\vert \lambda_{2} \vert <1\). Therefore, \(E^{\ast}\) is a sink.
-
(ii)
If \(b\delta>(1-\alpha)(1-\beta)m_{1}\), then \(F(-1)<0\). By Lemma 2.1, we have \(\vert \lambda_{1} \vert <1\) and \(\vert \lambda_{2} \vert >1\) (or \(\vert \lambda_{1} \vert >1\) and \(\vert \lambda_{2} \vert <1\)). Therefore, \(E^{\ast}\) is a saddle.
-
(iii)
If \(b\delta=(1-\alpha)(1-\beta)m_{1}\)lem1, we have \(\lambda_{1}=-1\) and \(\vert \lambda_{2} \vert \neq1\). Therefore, \(E^{\ast}\) is non-hyperbolic.
In the following, we will prove that it is impossible that Eq. (12) has a pair of conjugate complex roots with modulus 1. Assume that \(b\delta=(1-\alpha)(1-\beta)m_{2}\), i.e., \(\mathrm {Det}(J(E^{\ast}))=1\). We have \(\delta>\beta\) and
Thus,
It shows that \(\mathrm{Tr}(J(E^{\ast}))<-2\). As a result, Eq. (12) has no a pair of conjugate complex roots with modulus 1 for all permissible values of parameters. It implies that model (3) does not undergo a Neimark–Sacker bifurcation at the positive equilibrium point \(E^{\ast}\).
Denote \(M_{1}=\{(b,\delta,\alpha,\beta)| b\delta=(1-\alpha)(1-\beta )m_{1}\}\). From the above analysis, it follows that if \((b,\delta,\alpha,\beta)\in M_{1}\), then one of the two eigenvalues of the equilibrium \(E^{\ast}\) is −1 and the other is neither 1 nor −1. Therefore, model (3) may undergo flip bifurcation at \(E^{\ast}\) if the parameters vary in the small neighborhood of \(M_{1}\).
3 Flip bifurcation
In this section, we choose the birth rate b as a bifurcation parameter to study the flip bifurcation of the equilibrium point \(E^{\ast}\) by using the bifurcation approach in [22].
Let \(u_{n}=x_{n}-x^{\ast},v_{n}=y_{n}-y^{\ast}\). Then model (3) becomes
By introducing a new variable \(X_{n}=(u_{n},v_{n})^{T}\), we can rewrite (13) in the form
where \(G=(G_{1},G_{2})^{T}\) with
For the map (14), we obtain
where \(A=J(E^{\ast})\), \(B(X_{n},X_{n})\) and \(C(X_{n},X_{n},X_{n})\) are multilinear functions with
and
Consider the flip bifurcation case. Denote the critical value \(b=\frac {1}{\delta}(1-\alpha)(1-\beta)m_{1}\) by \(b^{\ast}\) at which the map (14) may undergo a flip bifurcation at the origin. In this case, A has a simple critical eigenvalue \(\lambda_{1}=-1\), and the corresponding critical eigenspace \(T^{C}\) is one-dimensional and spanned by an eigenvector \(q\in\mathbb{R}^{2}\) such that \(Aq=-q\). Let \(p\in\mathbb{R}^{2}\) be the adjoint eigenvector, that is, \(A^{T}p=-p\), where \(A^{T}\) is the transposed matrix. Normalize p with respect to q such that \(\langle p, q\rangle=1\), where \(\langle p, q\rangle =p_{1}q_{1}+p_{2}q_{2}\) is the scalar product in \(\mathbb{R}^{2}\). For satisfying the normalization \(\langle p, q\rangle=1\), we choose
Based on the theories developed by Kuznetsov [22], the restriction of the map (14) to its one-dimensional center manifold at the critical parameter values \(b^{\ast}\) can be transformed into the normal form
where
with
and I is the unit \(2\times2\) matrix.
Note that
Thus, we can obtain the stability and direction of flip bifurcation at the equilibrium \(E^{\ast}\) as follows.
Theorem 3.1
If \({\gamma}\neq0\), then model (3) undergoes a flip bifurcation at the equilibrium \(E^{\ast}\) when the parameter b varies and passes through \(b^{\ast}\). Moreover, if \({\gamma}>0\) (respectively, \({\gamma}<0\)), then the flip bifurcation of model (3) at \(b=b^{\ast}\) is supercritical (respectively, subcritical) and the period-doubling cycle is stable (respectively, unstable).
4 Numerical simulations
In this section we will give examples to illustrate the analytic results.
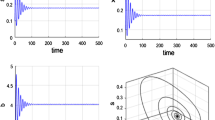
Fix parameters \(\alpha=0.1\), \(\beta=0.3\) and \(\delta=0.2\). Take \(b=3.15\). Clearly, \(b\delta=(1-\alpha)(1-\beta)\). The characteristic roots corresponding to trivial equilibrium point \(E_{0}\) are \(\lambda_{1}=1\) and \(\lambda_{2}=-0.6\), respectively. It follows from Table 1 that \(E_{0}\) is non-hyperbolic and stable. Figure 1 shows that the trivial equilibrium point \(E_{0}\) is stable. Further, take \(b=3.4\). It is easy to that \(\frac{2-\alpha-\beta }{2+\alpha+\beta}+\beta-\delta=0.7667\) and \((1-\alpha)(1-\beta)m_{1}-b\delta=1.1006\). From Theorem 2.2(i), it follows that the positive equilibrium point \((0.0594, 0.017)\) is stable (see Fig. 2).
In the following, we will give the diagrams of flip bifurcation and Lyapunov exponents. For model (3), fix the parameters \(\alpha =0.2\), \(\beta=0.4\) and \(\delta=0.1\), respectively. Take \(b=b^{\ast}=15.4141\). By the simple calculation, one obtains \(\gamma=0.5328>0\). From Theorem 3.1, the flip bifurcation emerges from equilibrium \((1, 0.1667)\) at \(b=b^{\ast}\). Vary b in the range \(12\leq b\leq150\). As b increases beyond \(b^{\ast}\), model (3) passes through a series of bifurcations that eventually lead to chaotic dynamics. Figure 3 shows bifurcation diagrams for model (3). After the flip bifurcation, the model undergoes a series of period-doubling bifurcations wherein \(2^{k}\)-cycle loses stability and a stable \(2^{k+1}\)-cycle is born as b increases. Subsequently, there is a cascade of period-doubling bifurcations leading to chaos. The Lyapunov exponent diagram corresponding to Fig. 3 is given in Fig. 4. Figure 5 shows that when \(b=120\), model (3) possesses two chaotic sets.
Lyapunov exponents corresponding to Fig. 3
5 Conclusion and discussion
There has been much work discussing the stability and bifurcation of single-species model with stage structure, but most of them dealt with only the continuous system. In this paper, we discuss the dynamical behaviors of a single-species discrete model with the Ricker function as the birth rate and only the mature population reproducing. By analyzing the location of the roots in the characteristic equation, some conditions are derived to ensure the asymptotically stable of equilibria of model (3). In [18], the authors provided the result that \(E^{\ast}\) is asymptotically stable if \(b\delta>(1-\alpha)(1-\beta)\). However, according to Theorem 2.2, we see that \(b\delta>(1-\alpha)(1-\beta )\) is not the sufficient condition under which \(E^{\ast}\) is asymptotically stable. Moreover, by the results of [17], we find the interesting phenomenon that \(E^{\ast}\) of the continuous model corresponding to model (3) is globally asymptotically stable if \(b\delta>(1-\alpha )(1-\beta)\).
As pointed out by [17], \(R_{0}=\frac{b\delta}{(1-\alpha)(1-\beta )}\) represents the intrinsic net reproductive number, which combines the age-specific fertility rates and the age-specific survival rates and gives the expected number of offspring per individual over its life time. \(R_{0}=1\) is a threshold which controls whether or not the population will survive. From Table 1, if \(R_{0}\leq1\), then the trivial equilibrium \((0,0)\) is asymptotically stable, that is, if on average individuals do not replace themselves before they die, then the population becomes extinct. From Theorem 2.2, if \(1< R_{0}< m_{1}\), then the positive equilibrium point \(E^{\ast}\) is asymptotically stable. It means that the population can survive over the long term. If \(R_{0}=m_{1}\), the positive equilibrium point \(E^{\ast }\) is non-hyperholic, that is, it may lose stability. Moreover, as the birth rate b increases, the positive equilibrium of model (3) exchanges its stability and occurs flip bifurcation. In fact, we see that for the continuous model corresponding to model (3) does not occur the bifurcation at the equilibrium \(E^{\ast}\). Furthermore, the direction and stability of flip bifurcation are determined. Numerical simulations also show the rich dynamical behavior of model (3), including cascades of period-doubling bifurcations in orbit of period 2, 4, 8 and chaotic sets and invariant circles.
References
Beddington, J.R., Free, C.A., Lawton, J.H.: Dynamic complexity in predator–prey models framed in difference equations. Nature 255(1), 58–60 (1975)
Liu, X., Xiao, D.: Complex dynamic behaviors of a discrete-time predator–prey system. Chaos Solitons Fractals 32(1), 80–94 (2007)
Hu, Z., Teng, Z., Zhang, L.: Stability and bifurcation analysis of a discrete predator–prey model with nonmonotonic functional response. Nonlinear Anal., Real World Appl. 12(4), 2356–2377 (2011)
Chen, B., Chen, J.: Complex dynamic behaviors of a discrete predator–prey model with stage structure and harvesting. Int. J. Biomath. 10(01), 1750013 (2017)
Gámez, M., López, I., Rodríguez, C., et al.: Ecological monitoring in a discrete-time prey–predator model. J. Theor. Biol. 429, 52–60 (2017)
Ebenman, B., Persson, L.: Size-Structured Population: Ecology and Evolution. Springer, Berlin (1988)
Metz, J., Diekmann, O.: The Dynamics of Physiologically Structured Populations. Lecture Notes in Biomathematics. Springer, New York (1986)
Bergh, O., Getz, W.M.: Stability of discrete age-structured and aggregated delay difference population models. J. Math. Biol. 26(5), 551–581 (1988)
Aiello, W.G., Freedman, H.I.: A time-delay model of single-species growth with stage structure. Math. Biosci. 101(2), 139–153 (1990)
Aiello, W.G., Freedman, H.I., Wu, J.: Analysis of a model representing stage-structured population growth with state-dependent time delay. SIAM J. Appl. Math. 52(3), 855–869 (1992)
Bernard, O., Souissi, S.: Qualitative behavior of stage-structure populations: application to structure validation. J. Math. Biol. 37(4), 291–308 (1998)
Fang, H.: Chaos in a single-species discrete population model with stage structure and birth pulses. Adv. Differ. Equ. 2014, 175 (2014)
Tang, S., Chen, L.: Multiple attractors in stage-structured population models with birth pulses. Bull. Math. Biol. 65(3), 479–495 (2003)
Khajanchi, S.: Dynamic behavior of a Beddington–DeAngelis type stage structured predator–prey model. Appl. Math. Comput. 244(4), 344–360 (2014)
Song, Y., Tao, Y., Shu, H.: Dynamics of a ratio-dependent stage-structured predator–prey model with delay. Math. Methods Appl. Sci. 40(18), 6451–6467 (2017)
Guo, H., Chen, L.: A study on time-limited control of single-pest with stage-structure. Appl. Comput. Math. 217(2), 677–684 (2010)
Tang, S., Chen, L.: Density-dependent birth rate, birth pulses and their population dynamic consequences. J. Math. Biol. 44(2), 185–199 (2002)
Gao, S., Chen, L.: The effect of seasonal harvesting on single-species discrete population model with stage structure and birth pulses. Chaos Solitons Fractals 24(4), 1013–1023 (2005)
Murray, J.: Mathematical Biology. Springer, New York (1993)
Carr, J.: Application of Center Manifold Theorem. Springer, New York (1981)
Dannan, F.M., Elaydi, S.N., Ponomarenko, V.: Stability of hyperbolic and nonhyperbolic fixed points of one-dimensional maps. J. Differ. Equ. Appl. 9(5), 449–457 (2003)
Kuznetsov, Y.A.: Elements of Applied Bifurcation Theory, 2nd edn. Springer, New York (2004)
Acknowledgements
The work is partially supported by the National Natural Science Foundation of China (No. 31570417), and by the Natural Science Foundation of Anhui Province of China (Nos. 1608085MA14, 1608085MC63), and by the Key Project of Natural Science Research of Anhui Higher Education Institutions of China (Nos. KJ2015A152, gxyqZD2016205).
Author information
Authors and Affiliations
Contributions
All authors contributed equally in this article. They read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wu, D., Zhao, M. & Zhang, H. Stability and bifurcation analysis for a single-species discrete model with stage structure. Adv Differ Equ 2018, 116 (2018). https://doi.org/10.1186/s13662-018-1559-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1559-1