New construction and proof techniques of projection algorithm for countable maximal monotone mappings and weakly relatively non-expansive mappings in a Banach space

Li Wei; Ravi P. Agarwal

doi:10.1186/s13660-018-1657-3

Journal of Inequalities and Applications

December 2018, 2018:64 | Cite as

New construction and proof techniques of projection algorithm for countable maximal monotone mappings and weakly relatively non-expansive mappings in a Banach space

Authors
Authors and affiliations

Li Wei
Ravi P. Agarwal

Open Access

Research

First Online: 27 March 2018

Received: 01 February 2018

Accepted: 16 February 2018

1 Shares
363 Downloads

Abstract

In a real uniformly convex and uniformly smooth Banach space, some new monotone projection iterative algorithms for countable maximal monotone mappings and countable weakly relatively non-expansive mappings are presented. Under mild assumptions, some strong convergence theorems are obtained. Compared to corresponding previous work, a new projection set involves projection instead of generalized projection, which needs calculating a Lyapunov functional. This may reduce the computational labor theoretically. Meanwhile, a new technique for finding the limit of the iterative sequence is employed by examining the relationship between the monotone projection sets and their projections. To check the effectiveness of the new iterative algorithms, a specific iterative formula for a special example is proved and its computational experiment is conducted by codes of Visual Basic Six. Finally, the application of the new algorithms to a minimization problem is exemplified.

Keywords

Maximal monotone mapping Weakly relatively non-expansive mapping Projection Limit of a sequence of sets Uniformly convex and uniformly smooth Banach space

MSC

47H05 47H09 47H10

1 Introduction and preliminaries

Let E be a real Banach space with $E^{*}$ its dual space. Suppose that C is a nonempty closed and convex subset of E. The symbol 〈⋅, ⋅〉 denotes the generalized duality pairing between E and $E^{*}$. The symbols “→” and “⇀” denote strong and weak convergence either in E or in $E^{*}$, respectively.

A Banach space E is said to be strictly convex [1] if for $\forall x,y \in E$ which are linearly independent,

$$ \Vert x + y \Vert < \Vert x \Vert + \Vert y \Vert . $$

The above inequality is equivalent to the following:

$$ \Vert x \Vert = \Vert y \Vert = 1, \quad x \ne y \quad \Rightarrow \quad \biggl\Vert \frac{x + y}{2} \biggr\Vert < 1. $$

A Banach space E is said to be uniformly convex [1] if for any two sequences $\{ x_{n} \} $ and $\{ y_{n} \} $ in E such that $\Vert x_{n} \Vert = \Vert y_{n} \Vert = 1$ and $\lim_{n \to \infty} \Vert x_{n} + y_{n} \Vert = 2$, $\lim _{n \to \infty } \Vert x_{n} - y_{n} \Vert = 0$ holds.

If E is uniformly convex, then it is strictly convex.

The function $\rho_{E}:[0, + \infty ) \to [0, + \infty )$ is called the modulus of smoothness of E [2] if it is defined as follows:

$$ \rho_{E}(t) = \sup \biggl\{ \frac{1}{2} \bigl(\Vert x + y \Vert + \Vert x - y \Vert \bigr) - 1:x,y \in E, \Vert x \Vert = 1, \Vert y \Vert \le t \biggr\} . $$

A Banach space E is said to be uniformly smooth [2] if $\frac{\rho_{E}(t)}{t} \to 0$, as $t \to 0$.

The Banach space E is uniformly smooth if and only if $E^{*}$ is uniformly convex [2].

We say E has Property (H) if for every sequence $\{ x_{n}\} \subset E$ which converges weakly to $x \in E$ and satisfies $\Vert x_{n} \Vert \to \Vert x \Vert $ as $n \to \infty $ necessarily converges to x in the norm.

If E is uniformly convex and uniformly smooth, then E has Property (H).

With each $x \in E$, we associate the set

$$ J(x) = \bigl\{ f \in E^{*}: \langle x,f \rangle = \Vert x \Vert ^{2} = \Vert f \Vert ^{2} \bigr\} ,\quad \forall x \in E. $$

Then the multi-valued mapping $J:E \to 2^{E^{*}}$ is called the normalized duality mapping [1]. Now, we list some elementary properties of J.

Lemma 1.1

([1, 2])

(1)

IfEis a real reflexive and smooth Banach space, thenJis single valued;
(2)

ifEis reflexive, thenJis surjective;
(3)

ifEis uniformly smooth and uniformly convex, then$J^{ - 1}$is also the normalized duality mapping from$E^{*}$into E. Moreover, bothJand$J^{ - 1}$are uniformly continuous on each bounded subset ofEor$E^{*}$, respectively;
(4)

for$x \in E$and$k \in ( - \infty, + \infty )$, $J(kx) = kJ(x)$.

For a nonlinear mapping U, we use $F(U)$ and $N(U)$ to denote its fixed point set and null point set, respectively; that is, $F(U) = \{ x \in D(U):Ux = x\}$ and $N(U) = \{ x \in D(U):Ux = 0\}$.

Definition 1.2

([3])

A mapping $T \subset E \times E^{*}$ is said to be monotone if, for $\forall y_{i} \in Tx_{i}$, $i = 1,2$, we have $\langle x_{1} - x_{2},y_{1} - y_{2} \rangle \ge 0$. The monotone mapping T is called maximal monotone if $R(J + \theta T) = E^{*}$ for $\theta > 0$.

Definition 1.3

([4])

The Lyapunov functional $\varphi :E \times E^{*} \to (0, + \infty )$ is defined as follows:

$$ \varphi (x,y) = \Vert x \Vert ^{2} - 2 \bigl\langle x,j(y) \bigr\rangle + \Vert y \Vert ^{2},\quad \forall x,y \in E,j(y) \in J(y). $$

Definition 1.4

([5])

Let $B:C \to C$ be a mapping, then

(1)

an element $p \in C$ is said to be an asymptotic fixed point of B if there exists a sequence $\{ x_{n}\}$ in C which converges weakly to p such that $x_{n} - Bx_{n} \to 0$, as $n \to \infty $. The set of asymptotic fixed points of B is denoted by $\hat{F}(B)$;
(2)

$B:C \to C$ is said to be strongly relatively non-expansive if $\hat{F}(B) = F(B) \ne \emptyset $ and $\varphi (p,Bx) \le \varphi (p,x)$ for $x \in C$ and $p \in F(B)$;
(3)

an element $p \in C$ is said to be a strong asymptotic fixed point of B if there exists a sequence $\{ x_{n}\}$ in C which converges strongly to p such that $x_{n} - Bx_{n} \to 0$, as $n \to \infty $. The set of strong asymptotic fixed points of B is denoted by $\tilde{F}(B)$;
(4)

$B:C \to C$ is said to be weakly relatively non-expansive if $\tilde{F}(B) = F(B) \ne \emptyset $ and $\varphi (p,Bx) \le \varphi (p,x)$ for $x \in C$ and $p \in F(B)$.

Remark 1.5

It is easy to see that strongly relatively non-expansive mappings are weakly relatively non-expansive mappings. However, an example in [6] shows that a weakly relatively non-expansive mapping is not a strongly relatively non-expansive mapping.

Lemma 1.6

([5])

LetEbe a uniformly convex and uniformly smooth Banach space andCbe a nonempty closed and convex subset of E. If$B:C \to C$is weakly relatively non-expansive, then$F(B)$is a closed and convex subset of E.

Lemma 1.7

([3])

Let$T \subset E \times E^{*}$be maximal monotone, then

(1)

$N(T)$is a closed and convex subset ofE;
(2)

if$x_{n} \to x$and$y_{n} \in Tx_{n}$with$y_{n} \rightharpoonup y$, or$x_{n} \rightharpoonup x$and$y_{n} \in Tx_{n}$with$y_{n} \to y$, then$x \in D(T)$and$y \in Tx$.

Definition 1.8

([4])

(1)

If E is a reflexive and strictly convex Banach space and C is a nonempty closed and convex subset of E, then for each $x \in E$ there exists a unique element $v \in C$ such that $\Vert x - v \Vert = \inf \{ \Vert x - y \Vert :y \in C\}$. Such an element v is denoted by $P_{C}x$ and $P_{C}$ is called the metric projection of E onto C.
(2)

Let E be a real reflexive, strictly convex, and smooth Banach space and C be a nonempty closed and convex subset of E, then for $\forall x \in E$, there exists a unique element $x_{0} \in C$ satisfying $\varphi (x_{0},x) = \inf \{ \varphi (y, x) :y \in C\}$. In this case, $\forall x \in E$, define $\Pi_{C}:E \to C$ by $\Pi_{C}x = x_{0}$, and then $\Pi_{C}$ is called the generalized projection from E onto C.

It is easy to see that $\Pi_{C}$ is coincident with $P_{C}$ in a Hilbert space.

Maximal monotone mappings and weakly or strongly relatively non-expansive mappings are different types of important nonlinear mappings due to their practical background. Much work has been done in designing iterative algorithms either to approximate a null point of maximal monotone mappings or a fixed point of weakly or strongly relatively non-expansive mappings, see [5, 6, 7, 8, 9, 10] and the references therein. It is a natural idea to construct iterative algorithms to approximate common solutions of a null point of maximal monotone mappings and a fixed point of weakly or strongly relatively non-expansive mappings, which can be seen in [11, 12, 13, 14, 15] and the references therein. Now, we list some closely related work.

In [12], Wei et al. presented the following iterative algorithms to approximate a common element of the set of null points of the maximal monotone mapping $T \subset E \times E^{*}$ and the set of fixed points of the strongly relatively non-expansive mapping $S \subset E \times E$, where E is a real uniformly convex and uniformly smooth Banach space:

$$\begin{aligned}& \textstyle\begin{cases} x_{1} \in E,\quad r_{1} > 0, \\ y_{n} = (J + r_{n}T)^{ - 1}J(x_{n} + e_{n}), \\ z_{n} = J^{ - 1}[\alpha_{n}Jx_{n} + (1 - \alpha_{n})Jy_{n}], \\ u_{n} = J^{ - 1}[\beta_{n}Jx_{n} + (1 - \beta_{n})JSz_{n}], \\ H_{n} = \{ z \in E:\varphi (z,z_{n}) \le \alpha_{n}\varphi (z,x_{n}) + (1 - \alpha_{n})\varphi (z,x_{n} + e_{n})\}, \\ V_{n} = \{ z \in E:\varphi (z,u_{n}) \le \beta_{n}\varphi (z,x_{n}) + (1 - \beta_{n})\varphi (z,z_{n})\}, \\ W_{n} = \{ z \in E: \langle z - x_{n},Jx_{1} - Jx _{n} \rangle \le 0\}, \\ x_{n + 1} = \Pi_{H_{n} \cap V_{n} \cap W_{n}}(x_{1}),\quad n \in N, \end{cases}\displaystyle \end{aligned}$$

(1.1)

$$\begin{aligned}& \textstyle\begin{cases} x_{1} \in E,\quad r_{1} > 0, \\ y_{n} = (J + r_{n}T)^{ - 1}J(x_{n} + e_{n}), \\ z_{n} = J^{ - 1}[\alpha_{n}Jx_{1} + (1 - \alpha_{n})Jy_{n}], \\ u_{n} = J^{ - 1}[\beta_{n}Jx_{1} + (1 - \beta_{n})JSz_{n}], \\ H_{n} = \{ z \in E:\varphi (z,z_{n}) \le \alpha_{n}\varphi (z,x_{1}) + (1 - \alpha_{n})\varphi (z,x_{n} + e_{n})\}, \\ V_{n} = \{ z \in E:\varphi (z,u_{n}) \le \beta_{n}\varphi (z,x_{1}) + (1 - \beta_{n})\varphi (z,z_{n})\}, \\ W_{n} = \{ z \in E:\langle z - x_{n},Jx_{1} - Jx _{n}\rangle \le 0\}, \\ x_{n + 1} = \Pi_{H_{n} \cap V_{n} \cap W_{n}}(x_{1}),\quad n \in N, \end{cases}\displaystyle \end{aligned}$$

(1.2)

and

$$ \textstyle\begin{cases} x_{1} \in E,\quad r_{1} > 0, \\ y_{n} = (J + r_{n}T)^{ - 1}J(x_{{n}} + e_{n}), \\ z_{n} = J^{ - 1}[\alpha_{n}Jx_{n} + (1 - \alpha_{n})Jy_{n}], \\ u_{n} = J^{ - 1}[\beta_{n}Jx_{n} + (1 - \beta_{n})JSz_{n}], \\ H_{1} = \{ z \in E:\varphi (z,z_{1}) \le \alpha_{1}\varphi (z,x_{1}) + (1 -\alpha_{1})\varphi (z,x_{1} + e_{1})\}, \\ V_{1} = \{ z \in E:\varphi (z,u_{1}) \le \beta_{1}\varphi (z,x_{1}) + (1 - \beta_{1})\varphi (z,z_{1})\}, \\ W_{1} = E, \\ H_{n} = \{ z \in H_{n - 1} \cap V_{n - 1} \cap W_{n - 1}:\varphi (z,z _{n}) \le \alpha_{n}\varphi (z,x_{n}) + (1 - \alpha_{n})\varphi (z,x_{n} + e _{n})\}, \\ V_{n} = \{ z \in H_{n - 1} \cap V_{n - 1} \cap W_{n - 1}:\varphi (z,u _{n}) \le \beta_{n}\varphi (z,x_{n}) + (1 - \beta_{n})\varphi (z,z_{n})\}, \\ W_{n} = \{ z \in H_{n - 1} \cap V_{n - 1} \cap W_{n - 1}: \langle z - x_{n},Jx_{1} - Jx_{n} \rangle \le 0\}, \\ x_{n + 1} = \Pi_{H_{n} \cap V_{n} \cap W_{n}}(x_{1}),\quad n \in N. \end{cases} $$

(1.3)

Under some mild assumptions, $\{ x_{n}\}$ generated by (1.1), (1.2), or (1.3) is proved to be strongly convergent to $\Pi_{N(T) \cap F(S)}(x _{1})$. Compared to projective iterative algorithms (1.1) and (1.2), iterative algorithm (1.3) is called monotone projection method since the projection sets $H_{{n}}$, $V_{n}$, and $W_{n}$ are all monotone in the sense that $H_{n + 1} \subset H_{n}$, $V_{n + 1} \subset V_{n}$, and $W_{{n} + 1} \subset W_{n}$ for $n \in N$. Theoretically, the monotone projection method will reduce the computation task.

In [13], Klin-eam et al. presented the following iterative algorithm to approximate a common element of the set of null points of the maximal monotone mapping $A \subset E \times E^{*}$ and the sets of fixed points of two strongly relatively non-expansive mappings $S,T \subset C \times C$, where C is the nonempty closed and convex subset of a real uniformly convex and uniformly smooth Banach space E.

$$ \textstyle\begin{cases} u_{n} = J^{ - 1}[\alpha_{n}Jx_{n} + (1 - \alpha_{n})JT{z}_{ {n}}], \\ {z}_{n} = J^{ - 1}[\beta_{n}Jx_{n} + (1 - \beta_{n})JS( {J} + {r}_{{n}}{A})^{ - 1}{Jx}_{ {n}}], \\ H_{n} = \{ z \in C:\varphi (z,u_{n}) \le \varphi (z,x_{n})\}, \\ V_{n} = \{ z \in C: \langle z - x_{n},Jx_{1} - Jx_{n} \rangle \le 0\}, \\ x_{n + 1} = \Pi_{H_{n} \cap V_{n}}(x_{1}),\quad n \in N. \end{cases} $$

(1.4)

Under some assumptions, $\{ x_{n}\}$ generated by (1.4) is proved to be strongly convergent to $\Pi_{N(A) \cap F(S) \cap F(T)}(x_{1})$.

In [14], Wei et al. extended the topic to the case of finite maximal monotone mappings $\{ T_{i}\}_{i = 1}^{{m}_{1}}$ and finite strongly relatively non-expansive mappings $\{ S_{j}\}_{j = 1}^{ {m}_{2}}$. They constructed the following two iterative algorithms in a real uniformly convex and uniformly smooth Banach space E:

$$ \textstyle\begin{cases} x_{1} \in E,\quad r > 0, \\ y_{n} = J^{ - 1}[\beta_{{n}}Jx_{n} + \sum_{i = 1}^{m_{1}} \beta_{n,i}J(J + rT_{i})^{ - 1}Jx_{n}], \\ x_{n + 1} = J^{ - 1}[\alpha_{n}Jx_{n} + \sum_{j = 1}^{m_{2}}\alpha_{n,j}J S_{j} y_{n}],\quad n \in N, \end{cases} $$

(1.5)

and

$$ \textstyle\begin{cases} x_{1} \in E,\quad r > 0, \\ y_{n} = J^{ - 1}[\beta_{{n}}Jx_{n} + (1 - \beta_{n})J(J + rT _{1})^{ - 1}J(J + rT_{2})^{ - 1}J \cdots (J + rT_{m_{1}})^{ - 1}Jx_{n}], \\ x_{n + 1} = J^{ - 1}[\alpha_{n}Jx_{n} + (1 - \alpha_{n})JS_{1}S_{2}\cdots S_{m_{2}}y_{n}],\quad n \in N. \end{cases} $$

(1.6)

Under some assumptions, $\{ x_{n}\}$ generated by (1.5) or (1.6) is proved to be weakly convergent to $v = \lim_{n \to \infty } \Pi_{( \bigcap_{i = 1}^{m_{1}}N(T_{i})) \cap ( \bigcap_{j = 1}^{m_{2}}F(S _{j}))}(x_{{n}})$.

Inspired by the previous work, in Sect. 2.1, we shall construct some new iterative algorithms to approximate the common element of the sets of null points of countable maximal monotone mappings and the sets of fixed points of countable weakly relatively non-expansive mappings. New proof techniques can be found, restrictions are mild, and error is considered. In Sect. 2.2, an example is listed and a specific iterative formula is proved. Computational experiments which show the effectiveness of the new abstract iterative algorithms are conducted. In Sect. 2.3, an application to the minimization problem is demonstrated.

The following preliminaries are also needed in our paper.

Definition 1.9

([16])

Let $\{ C_{n}\}$ be a sequence of nonempty closed and convex subsets of E, then

(1)

$s\mbox{-}\lim \inf C_{n}$, which is called strong lower limit, is defined as the set of all $x \in E$ such that there exists $x_{n} \in C_{n}$ for almost all n and it tends to x as $n \to \infty $ in the norm.
(2)

$w\mbox{-}\lim \sup C_{n}$, which is called weak upper limit, is defined as the set of all $x \in E$ such that there exists a subsequence $\{ C_{n_{k}}\}$ of $\{ C_{n}\}$ and $x_{n_{k}} \in C_{n_{k}}$ for every $n_{k}$ and it tends to x as $n_{k} \to \infty $ in the weak topology;
(3)

if $s\mbox{-}\lim \inf C_{n} = w\mbox{-}\lim \sup C_{n}$, then the common value is denoted by $\lim C_{n}$.

Lemma 1.10

([16])

Let$\{ C_{n}\}$be a decreasing sequence of closed and convex subsets ofE, i.e., $C_{n} \subset C_{m}$if$n \ge m$. Then$\{ C_{n}\}$converges in E and$\lim C_{n} = \bigcap_{n = 1}^{\infty } C_{n}$.

Lemma 1.11

([17])

Suppose thatEis a real reflexive and strictly convex Banach space. If$\lim C_{n}$exists and is not empty, then$\{ P_{c_{n}}x\}$converges weakly to$P_{\lim C_{n}}x$for every$x \in E$. Moreover, ifEhas Property (H), the convergence is in norm.

Lemma 1.12

([18])

LetEbe a real smooth and uniformly convex Banach space, and let$\{ u_{n}\}$and$\{ v_{n}\}$be two sequences of E. If either$\{ u_{n}\}$or$\{ v_{n}\}$is bounded and$\varphi (u_{n},v_{n}) \to 0$, as$n \to \infty $, then$u_{n} - v_{n} \to 0$, as$n \to \infty $.

Lemma 1.13

([19])

LetEbe a real uniformly convex Banach space and$r \in (0, + \infty )$. Then there exists a continuous, strictly increasing, and convex function$\omega : [0,2r] \to [0, +\infty)$with$\omega (0) = 0$such that

$$ \bigl\Vert kx + (1 - k)y \bigr\Vert ^{2} \le k\Vert x \Vert ^{2} + (1 - k)\Vert y \Vert ^{2} - k(1 - k)\omega \bigl( \Vert x - y \Vert \bigr) $$

for$k \in [0,1],x,y \in E$with$\Vert x \Vert \le r$and$\Vert y \Vert \le r$.

2 Strong convergence theorems and experiments

2.1 Strong convergence for infinite maximal monotone mappings and infinite weakly relatively non-expansive mappings

In this section, we suppose that the following conditions are satisfied:

(A1)

E is a real uniformly convex and uniformly smooth Banach space and $J:E \to E^{*}$ is the normalized duality mapping;
(A2)

$T_{i} \subset E \times E^{*}$ is maximal monotone and $S_{i}:E \to E$ is weakly relatively non-expansive for each $i \in N$;
(A3)

$\{ s_{n,i}\}$ and $\{ \tau_{n}\}$ are two real number sequences in ($0, + \infty $) for $i,n \in N$. $\{ \alpha_{n}\}$ is a real number sequence in ($0,1$) for $n \in N$;
(A4)

$\{ \varepsilon_{n}\}$ is the error sequence in E.

Algorithm 2.1

Step 1. Choose $u_{1},\varepsilon_{1} \in E$. Let $s_{1,i} \in (0, + \infty )$ for $i \in N$. $\alpha_{1} \in (0,1)$ and $\tau_{1} \in (0, + \infty )$. Set $n = 1$, and go to Step 2.

Step 2. Compute $v_{n,i} = (J + s_{n,i}T_{i})^{ - 1}J(u_{n} + \varepsilon_{n})$ and $w_{n,i} = J^{ - 1}[\alpha_{n}Ju_{n} + (1 - \alpha_{n})JS_{i}v_{n,i}]$ for $i \in N$. If $v_{n,i} = u_{n} + \varepsilon_{n}$ and $w_{n,i} = J^{ - 1}[\alpha_{n}Ju_{n} + (1 - \alpha_{n})J(u_{n} + \varepsilon_{n})]$ for all $i \in N$, then stop; otherwise, go to Step 3.

Step 3. Construct the sets $V_{n}$, $W_{n}$, and $U_{n}$ as follows:

$$\begin{aligned}& \textstyle\begin{cases} V_{1} = E, \\ V_{n + 1,i} = \{ z \in E: \langle v_{n,i} - z,J(u_{n} + \varepsilon_{n}) - Jv_{n,i} \rangle \ge 0\}, \\ V_{n + 1} = (\bigcap_{i = 1}^{\infty } V_{n + 1,i}) \cap V_{n}, \end{cases}\displaystyle \\& \textstyle\begin{cases} W_{1} = E, \\ W_{n + 1,i} = \{ z \in V_{n + 1,i}:\varphi (z,w_{n,i}) \le \alpha_{n} \varphi (z,u_{n}) + (1 - \alpha_{n})\varphi (z,v_{n,i})\}, \\ W_{n + 1} = (\bigcap_{i = 1}^{\infty } W_{n + 1,i}) \cap W_{n}, \end{cases}\displaystyle \end{aligned}$$

and

$$ U_{n + 1} = \bigl\{ z \in W_{n + 1}:\Vert u_{1} - z \Vert ^{2} \le \bigl\Vert P_{{W}_{n + 1}}(u_{1}) - u_{1} \bigr\Vert ^{2} + \tau_{n + 1} \bigr\} , $$

go to Step 4.

Step 4. Choose any element $u_{n + 1} \in U_{n + 1}$ for $n \in N$.

Step 5. Set $n = n + 1$, and return to Step 2.

Theorem 2.1

If, in Algorithm 2.1, $v_{n,i} = u_{n} + \varepsilon_{n}$and$w_{n,i} = J^{ - 1}[\alpha_{n}Ju_{n} + (1 - \alpha _{n})J(u_{n} + \varepsilon_{n})]$for all$i \in N$, then$u_{n} + \varepsilon_{n} \in (\bigcap_{i = 1}^{\infty } N(T_{i})) \cap ( \bigcap_{i = 1}^{\infty } F(S_{i}))$.

Proof

Since $v_{n,i} = u_{n} + \varepsilon_{n}$, then from Step 2 in Algorithm 2.1, we know that $Jv_{n,i} + s_{n,i}T_{i}v_{n,i} = Jv _{n,i}$ for all $i \in N$, which implies that $s_{n,i}T_{i}v_{n,i} = 0$ for $i \in N$. Therefore, $u_{n} + \varepsilon_{n} \in \bigcap_{i = 1} ^{\infty } N(T_{i})$.

Since $w_{n,i} = J^{ - 1}[\alpha_{n}Ju_{n} + (1 - \alpha_{n})J(u_{n} + \varepsilon_{n})] = J^{ - 1}[\alpha_{n}Ju_{n} + (1 - \alpha_{n})JS _{i}v_{n,i}]$, then in view of Lemma 1.1$v_{n,i} = S_{i}v_{n,i}$ for $i,n \in N$. Thus $v_{n,i} = u_{n} + \varepsilon_{n} \in \bigcap_{i = 1}^{\infty } F(S_{i})$, $n \in N$.

This completes the proof. □

Theorem 2.2

Suppose$(\bigcap_{i = 1}^{\infty } N(T_{i})) \cap (\bigcap_{i = 1}^{\infty } F(S_{i})) \ne \emptyset, \inf_{n}s _{n,i} > 0$for$i \in N$, $0 < \sup_{n}\alpha_{n} < 1$, $\tau_{n} \to 0$, and$\varepsilon_{n} \to 0$, as$n \to \infty $. Then the iterative sequence$u_{n} \to y_{0} = P_{\bigcap_{n = 1}^{\infty } W _{n}} (u_{1})\in (\bigcap_{i = 1}^{\infty } N(T_{i})) \cap (\bigcap_{i = 1}^{\infty } F(S_{i}))$, as$n \to \infty $.

Proof

We split the proof into eight steps.

Step 1. $V_{n}$ is a nonempty subset of E.

In fact, we shall prove that $(\bigcap_{i = 1}^{\infty } N(T_{i})) \cap (\bigcap_{i = 1}^{\infty } F(S_{i})) \subset V_{n}$, which ensures that $V_{n} \ne \emptyset $.

For this, we shall use inductive method. Now, $\forall p \in ( \bigcap_{i = 1}^{\infty } N(T_{i})) \cap (\bigcap_{i = 1}^{\infty } F(S _{i}))$.

If $n = 1$, it is obvious that $p \in V_{1} = E$. Since $T_{i}$ is monotone, then

$$ \bigl\langle v_{1,i} - p, J(u_{1} + \varepsilon_{1})-Jv_{1,i} \bigr\rangle = \langle v_{1,i} - p,s_{1,i}T_{i}v_{1,i} - s_{1,i}T_{i}p \rangle \ge 0. $$

Thus $p \in V_{2,i}$, which ensures that $p \in V_{2}$.

Suppose the result is true for $n = k + 1$. Then, if $n = k + 2$, we have

$$ \bigl\langle v_{k + 1,i} - p, J(u_{k + 1} + \varepsilon_{k + 1})-Jv_{k+1,i}\bigr\rangle = \langle v_{k + 1,i} - p,s_{k + 1,i}T_{i}v_{k + 1,i} - s_{k + 1,i}T_{i}p \rangle \ge 0. $$

Then $p \in V_{k + 2,i}$, which ensures that $p \in V_{k + 2}$.

Therefore, by induction, $(\bigcap_{i = 1}^{\infty } N(T_{i})) \cap ( \bigcap_{i = 1}^{\infty } F(S_{i})) \subset V_{n}$ for $n \in N$.

Step 2. $W_{n}$ is a nonempty closed and convex subset of E for $n \in N$.

Since $\varphi (z,w_{n,i}) \le \alpha_{n} \varphi (z,u_{n}) + (1 - \alpha_{n})\varphi (z,v_{n,i})$ is equivalent to $\langle z,2\alpha_{n}Ju_{n} + 2(1 - \alpha_{n})Jv_{n,i} - 2Jw_{n,i} \rangle \leq \alpha_{n}\Vert u _{n} \Vert ^{2} + (1 - \alpha_{n})\Vert v_{n,i} \Vert ^{2} - \Vert w_{n,i} \Vert ^{2}$, then it is easy to see that $W_{n,i}$ is closed and convex for $i,n \in N$. Thus $W_{n}$ is closed and convex for $n \in N$.

Next, we shall use inductive method to show that $(\bigcap_{i = 1} ^{\infty } N(T_{i})) \cap (\bigcap_{i = 1}^{\infty } F(S_{i})) \subset W_{n}$ for $n \in N$, which ensures that $W_{n} \ne \emptyset $ for $n \in N$.

In fact, $\forall p \in (\bigcap_{i = 1}^{\infty } N(T_{i})) \cap ( \bigcap_{i = 1}^{\infty } F(S_{i}))$.

If $n = 1$, it is obvious that $p \in W_{1} = E$. Then, from the definition of weakly relatively non-expansive mappings, we have

$$\begin{aligned} \varphi (p,w_{n,i}) &\le \alpha_{1}\varphi (p,u_{1}) + (1 - \alpha_{1}) \varphi (p,S_{i}v_{1,i}) \\ &\le \alpha_{1}\varphi (p,u_{1}) + (1 - \alpha_{1}) \varphi (p,v_{1,i}). \end{aligned}$$

Combining this with Step 1, we know that $p \in W_{2,i}$ for $i \in N$. Therefore, $p \in W_{2}$.

Suppose the result is true for $n = k + 1$. Then, if $n = k + 2$, we know from Step 1 that $p \in V_{k + 2,i}$ for $i,k \in N$. Moreover,

$$\begin{aligned} \varphi (p,w_{k + 1,i}) &\le \alpha_{k + 1}\varphi (p,u_{k + 1}) + (1 -\alpha_{k+ 1})\varphi (p,S_{i}v_{k + 1,i}) \\ & \le \alpha_{k + 1}\varphi (p,u_{k + 1}) + (1 -\alpha_{k + 1}) \varphi (p,v_{k + 1,i}), \end{aligned}$$

which implies that $p \in W_{k + 2,i}$, and then $p \in (\bigcap_{i = 1}^{\infty } W_{k + 2,i}) \cap W_{k +1} = W_{k + 2}$. Therefore, by induction,

$$\begin{aligned} \emptyset \ne \Biggl(\bigcap_{i = 1}^{\infty } N(T_{i}) \Biggr) \cap \Biggl(\bigcap_{i = 1}^{\infty } F(S_{i}) \Biggr) \subset W_{n} \quad\mbox{for } n \in N. \end{aligned}$$

Step 3. Set $y_{n} = P_{W_{n + 1}}(u_{1})$. Then $y_{n} \to y_{0} = P_{\bigcap_{n = 1}^{\infty } W_{n}} (u_{1})$, as $n \to \infty $.

From the construction of $W_{n}$ in Step 3 of Algorithm 2.1, $W_{n + 1} \subset W_{n}$ for $n \in N$. Lemma 1.10 implies that $\lim W_{n}$ exists and $\lim W_{n} = \bigcap_{n = 1}^{\infty } W_{n} \ne \emptyset $. Since E has Property (H), then Lemma 1.11 implies that $y_{n} \to y_{0} = P_{\bigcap_{n = 1}^{\infty } W_{n}} (u_{1})$, as $n \to \infty $.

Step 4. $\{ u_{n}\}$ is well defined.

It suffices to show that $U_{n} \ne \emptyset $. From the definitions of $P_{W_{n + 1}}(u_{1})$ and infimum, we know that for $\tau_{n + 1}$ there exists $b_{n} \in W_{n + 1}$ such that

$$ \Vert u_{1} - b_{n} \Vert ^{2} \le \Bigl(\inf_{z \in W_{n + 1}}\Vert u_{1} - z \Vert \Bigr)^{2} + \tau_{n + 1} = \bigl\Vert P_{W_{n + 1}}(u_{1}) - u _{1} \bigr\Vert ^{2} + \tau_{n + 1}. $$

This ensures that $U_{n + 1} \ne \emptyset $ for $n \to \infty $.

Step 5. $u_{n + 1} - y_{n} \to 0$ as $n \to \infty $.

Since $u_{n + 1} \in U_{n + 1} \subset W_{n + 1}$, then in view of Lemma 1.13 and the fact that $W_{n}$ is convex, we have, for $\forall k \in (0,1)$,

$$\begin{aligned} \Vert y_{n} - u_{1} \Vert ^{2} &\le \bigl\Vert ky_{n} + (1 - k)u_{n + 1} - u_{1} \bigr\Vert ^{2} \\ &\le k\Vert y_{n} - u_{1} \Vert ^{2} + (1 - k)\Vert u_{n + 1} - u_{1} \Vert ^{2} - k(1 - k) \omega \bigl(\Vert y _{n} - u_{n + 1} \Vert \bigr). \end{aligned}$$

Therefore,

$$\begin{aligned} k\omega \bigl(\Vert y_{n} - u_{n + 1} \Vert \bigr) \le \Vert u_{n + 1} -u_{1} \Vert ^{2} - \Vert y_{n} -u_{1} \Vert ^{2} \le \tau_{n + 1}. \end{aligned}$$

Letting $k \to 1$, then $y_{n} - u_{n + 1} \to 0$ as $n \to \infty $. Since $y_{n} \to y_{0}$, then $u_{n} \to y_{0}$, as $n \to \infty $.

Step 6. $u_{n} - v_{n,i} \to 0$ for $i \in N$, as $n \to \infty $.

Since $y_{n + 1} \in W_{n + 2} \subset W_{n + 1} \subset V_{n + 1}$, then

$$\begin{aligned} 0 &\le 2 \bigl\langle v_{n,i} - y_{n + 1},J(u_{n} + \varepsilon_{n}) - Jv _{n,i} \bigr\rangle \\ &= 2 \bigl\langle y_{n + 1} - v_{n,i},Jv_{n,i} - J(u _{n} + \varepsilon_{n}) \bigr\rangle \\ &= \varphi (y_{n + 1},u_{n} + \varepsilon_{n}) - \varphi (y_{n + 1},v_{n,i}) - \varphi (v_{n,i},u_{n} + \varepsilon_{n}) \\ &\le \varphi (y_{n + 1},u_{n} + \varepsilon_{n}) - \varphi (v_{n,i},u_{n} + \varepsilon_{n}). \end{aligned}$$

Thus, by using Step 5 and by letting $\varepsilon_{n} \to 0$, we have

$$\begin{aligned} \varphi (v_{n, i},u_{n} + \varepsilon_{n}) &\le \varphi (y_{n + 1},u_{n} + \varepsilon_{n}) \\ &= \varphi (y_{n + 1},y_{n}) + \varphi (y_{n},u_{n} + \varepsilon_{n}) + 2 \bigl\langle y_{n + 1} - y_{n},Jy_{n} - J(u_{n} + \varepsilon_{n}) \bigr\rangle \\ &\le \bigl(\Vert y_{n + 1} \Vert \Vert Jy_{n + 1} - Jy_{n} \Vert + \Vert y_{n + 1} - y_{n} \Vert \Vert y_{n} \Vert \bigr) \\ &\quad {}+ \bigl(\Vert y_{n} \Vert \bigl\Vert Jy_{n} - J(u_{n} + \varepsilon_{n}) \bigr\Vert + \Vert y_{n + 1} - u_{n} - \varepsilon_{n} \Vert \Vert u_{n} + \varepsilon_{n} \Vert \bigr) \\ &\quad {}+ 2\Vert y_{n + 1} - y_{n} \Vert \bigl\Vert Jy_{n} - J(u_{n} + \varepsilon_{n}) \bigr\Vert \to 0, \end{aligned}$$

as $n \to \infty $. Using Lemma 1.12, $v_{n,i} - u_{n} - \varepsilon _{n} \to 0$ for $i \in N$, as $n \to \infty $. Since $\varepsilon_{n} \to 0$, then $v_{n,i} - u_{n} \to 0$ for $i \in N$, as $n \to \infty $. Since $u_{n} \to y_{0}$, then $v_{n,i} \to y_{0}$ for $i \in N$, as $n \to \infty $.

Step 7. $w_{n,i} - u_{n} \to 0$ for $i \in N$, as $n \to \infty $.

Since $u_{n + 1} \in U_{n + 1} \subset W_{n + 1}$, then noticing Steps 5 and 6,

$$\begin{aligned} \varphi (u_{n + 1},w_{n,i}) \le \alpha_{n}\varphi (u_{n + 1},u_{n}) + (1 - \alpha_{n})\varphi (u_{n + 1},v_{n,i}) \to 0, \end{aligned}$$

as $n \to \infty $. Lemma 1.12 implies that $u_{n + 1} - w_{n,i} \to 0$, as $n \to \infty $. Since $u_{n} \to y_{0}$, then $w_{n,i} \to y_{0}$ for $i \in N$, as $n \to \infty $.

Step 8. $y_{0} = P_{\bigcap_{n = 1}^{\infty } W_{n}} (u_{1}) \in (\bigcap_{i = 1}^{\infty } N(T_{i})) \cap (\bigcap_{i = 1}^{\infty } F(S _{i}))$.

Since $v_{n,i} = (J + s_{n,i}T_{i})^{ - 1}J(u_{n} + \varepsilon_{n})$, then $Jv_{n,i} + s_{n,i}T_{i}v_{n,i} = J(u_{n} + \varepsilon_{n})$. Since $v_{n,i} \to y_{0}$, $u_{n} \to y_{0}$, $\varepsilon_{n} \to 0$ and $\inf_{n}s_{n,i} > 0$, then $T_{i}v_{n,i} \to 0$ for $i \in N$, as $n \to \infty $. Using Lemma 1.7, $y_{0} \in \bigcap_{i = 1}^{\infty } N(T_{i})$.

Since $w_{n,i} = J^{ - 1}[\alpha_{n}Ju_{n} + (1 - \alpha_{n})JS_{i}v_{n,i}]$, then in view of Lemma 1.1, $S_{i}v_{n,i} \to y_{0}$, as $n \to \infty $. Lemma 1.6 implies that $y_{0} \in \bigcap_{i = 1}^{\infty } F(S_{i})$.

This completes the proof. □

Corollary 2.3

If$i \equiv 1$, denote byTthe maximal monotone mapping and bySthe weakly relatively non-expansive mapping, then Algorithm 2.1reduces to the following:

$$\begin{aligned} \textstyle\begin{cases} u_{1} \in E,\quad \varepsilon_{1} \in E, \\ v_{n} = (J + s_{n}T)^{ - 1}J(u_{n} + \varepsilon_{n}), \\ w_{n} = J^{ - 1}[\alpha_{n}Ju_{n} + (1 - \alpha_{n})JSv_{n}], \\ V_{1} = W_{1} = E, \\ V_{n + 1} = \{ z \in E: \langle v_{n} - z,J(u_{n} + \varepsilon _{n}) - Jv_{n} \rangle \ge 0\} \cap V_{n}, \\ W_{n + 1} = \{ z \in V_{n + 1}:\varphi (z,w_{n}) \le \alpha_{n}\varphi (z,u _{n}) + (1 - \alpha_{n})\varphi (z,v_{n})\} \cap W_{n}, \\ U_{n + 1} = \{ z \in W_{n + 1}:\Vert u_{1} - z \Vert ^{2} \le \Vert P_{W_{n + 1}}(u_{1}) - u_{1} \Vert ^{2} + \tau_{n + 1}\}, \\ u_{n + 1} \in U_{n + 1},\quad n \in N, \end{cases}\displaystyle \end{aligned}$$

where$\{ \varepsilon_{n}\} \subset E$, $\{ s_{n}\} \subset (0,\infty )$, $\{ \tau_{n}\} \subset (0,\infty )$, and$\{ \alpha_{n}\} \subset (0,1)$. Then

(1)

Similar to Theorem 2.1, if$v_{n} = u_{n} + \varepsilon_{n}$and$w_{n} = J^{ - 1}[\alpha_{n}Ju_{n} + (1 - \alpha_{n})J(u_{n} + \varepsilon_{n})]$for all$n \in N$, then$u_{n} + \varepsilon_{n} \in N(T) \cap F(S)$.
(2)

Suppose thatE, $\{ \varepsilon_{n}\}$, $\{ \tau_{n}\}$, and$\{ \alpha_{n}\}$satisfy the same conditions as those in Theorem 2.2. If$N(T) \cap F(S) = \emptyset $and$\inf_{n}s_{n} > 0$, then the iterative sequence$u_{n} \to y_{0} = P_{\bigcap_{n= 1}^{\infty } W_{n}} (u_{1}) \in N(T) \cap F(S)$, as$n \to \infty $.

Algorithm 2.2

Only doing the following changes in Algorithm 2.1, we get Algorithm 2.2:

$$ w_{n,i} = J^{ - 1} \bigl[\alpha_{n}Ju_{1} + (1 - \alpha_{n})JS_{i}v_{n,i} \bigr] \quad \mbox{for all } i \in N, $$

and

$$ \textstyle\begin{cases} W_{1} = E, \\ W_{n + 1, i} = \{ z \in V_{n + 1, i}:\varphi (z,w_{n,i}) \le \alpha_{n}\varphi (z,u _{1}) + (1 - \alpha_{n})\varphi (z,v_{n,i})\}, \\ W_{n + 1} = (\bigcap_{i = 1}^{\infty } W_{n + 1,i} )\cap W_{n}. \end{cases} $$

Theorem 2.4

If, in Algorithm 2.2, $v_{n,i} = u_{n} + \varepsilon_{n}$and$w_{n,i} = J^{ - 1}[\alpha_{n}Ju_{1} + (1 - \alpha_{n})J(u_{n} + \varepsilon_{n})]$for all$i \in N$, then$u_{n} + \varepsilon_{n} \in (\bigcap_{i = 1}^{\infty } N(T_{i} )) \cap (\bigcap_{i = 1}^{\infty } F(S_{i} ))$.

Proof

Similar to Theorem 2.1, the result follows. □

Theorem 2.5

We only change the condition that$0 < \sup_{n} \alpha_{n} < 1$in Theorem 2.2by$\alpha_{n} \to 0$, as$n \to \infty $. Then the iterative sequence$u_{n} \to y_{0} = P_{\bigcap _{n = 1}^{\infty } W_{n}} (u_{1}) \in (\bigcap_{i = 1}^{\infty } N(T_{i} )) \cap (\bigcap_{i = 1}^{\infty } F(S_{i} ))$, as$n \to \infty $.

Proof

Copy Steps 1, 3, 4, 5, and 6 in Theorem 2.2 and make slight changes in the following steps.

Step 2. $W_{n}$ is a nonempty closed and convex subset of E for $n \in N$.

Since $\varphi (z,w_{n,i}) \le \alpha_{n}\varphi (z,u_{1}) + (1 - \alpha _{n})\varphi (z,v_{n,i})$ is equivalent to $\langle z,2\alpha_{n}Ju _{1} + 2(1 - \alpha_{n})Jv_{n,i} - 2Jw_{n,i} \rangle \le \alpha _{n}\Vert u_{1} \Vert ^{2} + (1 - \alpha_{n})\Vert v_{n,i} \Vert ^{2} - \Vert w_{n,i} \Vert ^{2}$, then it is easy to see that $W_{n,i}$ is closed and convex for $i,n \in N$. Thus $W_{n}$ is closed and convex for $n \in N$.

Next, we shall use inductive method to show that $(\bigcap_{i = 1} ^{\infty } N(T_{i} )) \cap (\bigcap_{i = 1}^{\infty } F(S_{i} )) \subset W_{n}$ for $n \in N$, which ensures that $W_{n} \ne \emptyset $ for $n \in N$.

In fact, $\forall p \in (\bigcap_{i = 1}^{\infty } N(T_{i} )) \cap ( \bigcap_{i = 1}^{\infty } F(S_{i} ))$.

If $n = 1$, it is obvious that $p \in W_{1} = E$. Then, from the definition of weakly relatively non-expansive mappings, we have

$$\begin{aligned} \varphi (p,w_{1,i}) &\le \alpha_{1}\varphi (p,u_{1}) + (1 - \alpha_{1}) \varphi (p,S_{i}v_{1,i}) \\ &\le \alpha_{1}\varphi (p,u_{1}) + (1 - \alpha_{1}) \varphi (p,v_{1,i}). \end{aligned}$$

Combining this with Step 1, we know that $p \in W_{2,i}$ for $i \in N$. Therefore, $p \in W_{2}$.

Suppose the result is true for $n = k + 1$. Then, if $n = k + 2$, we know from Step 1 that $p \in V_{k + 2,i}$ for $i,k \in N$. Moreover,

$$\begin{aligned} \varphi (p,w_{k + 1,i}) &\le \alpha_{k + 1}\varphi (p,u_{1}) + (1 - \alpha_{k + 1})\varphi (p,S_{i}v_{k + 1,i}) \\ &\le \alpha_{k + 1}\varphi (p,u _{1}) + (1 - \alpha_{k + 1})\varphi (p,v_{k + 1,i}), \end{aligned}$$

which implies that $p \in W_{k + 2,i}$ and then $p \in (\bigcap_{i = 1}^{\infty } W_{k + 2,i} ) \cap W_{k + 1} = W_{k + 2}$. Therefore, by induction, $\emptyset \ne (\bigcap_{i = 1}^{\infty } N(T_{i} )) \cap (\bigcap_{i = 1}^{\infty } F(S_{i} )) \subset W_{n}$ for $n \in N$.

Step 7. $w_{n,i} - u_{n} \to 0$ for $i \in N$, as $n \to \infty $.

Since $u_{n + 1} \in U_{n + 1} \subset W_{n + 1}$, then in view of the facts that $\alpha_{n} \to 0$ and Step 6,

$$ \varphi (u_{n + 1},w_{n,i}) \le \alpha_{n}\varphi (u_{n + 1},u_{1}) + (1 - \alpha_{n}) \varphi (u_{n + 1},v_{n,i}) \to 0, $$

as $n \to \infty $, for $i \in N$. Lemma 1.12 implies that $w_{n,i} - u_{n} \to 0$ for $i \in N$, as $n \to \infty $.

Step 8. $y_{0} = P_{\bigcap_{n = 1}^{\infty } W_{n}} (u_{1}) \in ( \bigcap_{i = 1}^{\infty } N(T_{i} )) \cap (\bigcap_{i = 1}^{\infty } F(S _{i} ))$.

In the same way as Step 8 in Theorem 2.2, we have $y_{0} \in \bigcap_{i = 1}^{\infty } N(T_{i})$. Since $w_{n,i} = J^{ - 1}[\alpha _{n}Ju_{1} + (1 - \alpha_{n})JS_{i}v_{n,i}]$, then $S_{i}v_{n,i} \to y _{0}$, as $n \to \infty $. Thus in view of Lemma 1.6, $y_{0} \in \bigcap_{i = 1}^{\infty } F(S_{i})$.

This completes the proof. □

Corollary 2.6

If$i \equiv 1$, denote byTthe maximal monotone mapping and bySthe weakly relatively non-expansive mapping, then Algorithm 2.2reduces to the following:

$$ \textstyle\begin{cases} u_{1} \in E,\quad \varepsilon_{1} \in E, \\ v_{n} = (J + s_{n}T)^{ - 1}J(u_{n} + \varepsilon_{n}), \\ w_{n} = J^{ - 1}[\alpha_{n}Ju_{1} + (1 - \alpha_{n})JSv_{n}], \\ V_{1} = W_{1} = E, \\ V_{n + 1} = \{ z \in E: \langle v_{n} - z,J(u_{n} + \varepsilon _{n}) - Jv_{n} \rangle \ge 0\} \cap V_{n}, \\ W_{n + 1} = \{ z \in V_{n + 1}:\varphi (z,w_{n}) \le \alpha_{n}\varphi (z,u_{1})+ (1 - \alpha_{n})\varphi (z,v_{n})\} \cap W_{n}, \\ U_{n + 1} = \{ z \in W_{n + 1}:\Vert u_{1} - z \Vert ^{2} \le \Vert P_{W_{n + 1}}(u_{1}) - u_{1} \Vert ^{2} + \tau_{n + 1}\}, \\ u_{n + 1} \in U_{n + 1},\quad n \in N, \end{cases} $$

where$\{ \varepsilon_{n}\} \subset E$, $\{ s_{n}\} \subset (0,\infty )$, $\{ \tau_{n}\} \subset (0,\infty )$and$\{ \alpha_{n}\} \subset (0,1)$. Then

(1)

Similar to Theorem 2.4, if$v_{n} = u_{n} + \varepsilon_{n}$and$w_{n} = J^{ - 1}[\alpha_{n}Ju_{1} + (1 - \alpha_{n})J(u_{n} + \varepsilon_{n})]$, then$u_{n} + \varepsilon_{n} \in N(T) \cap F(S)$for all$n \in N$.
(2)

Suppose thatE, $\{ \varepsilon_{n}\}$, $\{ \tau_{n}\}$, and$\{ \alpha_{n}\}$satisfy the same conditions as those in Theorem 2.5. If$N(T) \cap F(S) = \emptyset $and$\inf_{n}s_{n} > 0$, then the iterative sequence$u_{n} \to y_{0} = P_{\bigcap_{n = 1}^{\infty } W_{n}} (u_{1})\in N(T) \cap F(S)$as$n \to \infty $.

Remark 2.7

Compared to the existing related work, e.g., [12, 13, 14], strongly relatively non-expansive mappings are extended to weakly relatively non-expansive mappings. Moreover, in our paper, the discussion on this topic is extended to the case of infinite maximal monotone mappings and infinite weakly relatively non-expansive mappings.

Remark 2.8

Calculating the generalized projection $\Pi_{H_{n} \cap V_{n} \cap W_{n}}(x_{1})$ in [12] or $\Pi_{H_{n} \cap V_{n}}(x_{1})$ in [13] is replaced by calculating the projection $P_{W_{n + 1}}(u_{1})$ in Step 3 in our Algorithms 2.1 and 2.2, which makes the computation easier.

Remark 2.9

A new proof technique for finding the limit $y_{0} = P_{\bigcap_{n = 1}^{\infty } W_{n}} (u_{1})$ is employed in our paper by examining the properties of the projective sets $W_{n}$ sufficiently, which is quite different from that for finding the limit $\Pi_{N(T) \cap F(S)}(x_{1})$ in [12] or $\Pi_{N(A) \cap F(S) \cap F(T)}(x _{1})$ in [13].

Remark 2.10

Theoretically, the projection is easier for calculating than the generalized projection in a general Banach space since the generalized projection involves a Lyapunov functional. In this sense, iterative algorithms constructed in our paper are new and more efficient.

2.2 Special cases in Hilbert spaces and computational experiments

Corollary 2.11

IfEreduces to a Hilbert space H, then iterative Algorithm 2.1becomes the following one:

$$\begin{aligned} \textstyle\begin{cases} u_{1} \in H,\quad \varepsilon_{1} \in H, \\ v_{n,i} = (I + s_{n,i}T_{i})^{ - 1}(u_{n} + \varepsilon_{n}), \\ w_{n,i} = \alpha_{n}u_{n} + (1 - \alpha_{n})S_{i}v_{n,i}, \\ V_{1} = W_{1} = H, \\ V_{n + 1,i} = \{ z \in H: \langle v_{n,i} - z,u_{n} + \varepsilon _{n} - v_{n,i} \rangle \ge 0\}, \\ V_{n + 1} = (\bigcap_{i = 1}^{\infty } V_{n + 1,i} ) \cap V_{n}, \\ W_{n + 1,i} = \{ z \in V_{n + 1,i}:\Vert z - w_{n,i} \Vert ^{2}\le \alpha_{n}\Vert z - u_{n} \Vert ^{2} + (1 - \alpha_{n})\Vert z - v_{n,i} \Vert ^{2}\}, \\ W_{n + 1} = (\bigcap_{i = 1}^{\infty } W_{n + 1,i} ) \cap W_{n}, \\ U_{n + 1} = \{ z \in W_{n + 1}:\Vert u_{1} - z \Vert ^{2} \le \Vert P_{W_{n + 1}}(u_{1}) - u_{1} \Vert ^{2} + \tau_{n + 1}\}, \\ u_{n + 1} \in U_{n + 1},\quad n \in N. \end{cases}\displaystyle \end{aligned}$$

(2.1)

The results of Theorems 2.1 and 2.2 are true for this special case.

Corollary 2.12

IfEreduces to a Hilbert space H, then iterative Algorithm 2.2becomes the following one:

$$ \textstyle\begin{cases} u_{1} \in H,\quad \varepsilon _{1} \in H, \\ v_{n,i} = (I + s_{n,i}T_{i})^{ - 1}(u_{n} + \varepsilon_{n}), \\ w_{n,i} = \alpha_{n}u_{1} + (1 - \alpha_{n})S_{i}v_{n,i}, \\ V_{1} = W_{1} = H, \\ V_{n + 1,i} = \{ z \in H: \langle v_{n,i} - z,u_{n} + \varepsilon_{n} - v_{n,i} \rangle \ge 0\}, \\ V_{n + 1} = (\bigcap_{i = 1}^{\infty } V_{n + 1,i} ) \cap V_{n},\\ W_{n + 1,i} = \{ z \in V_{n + 1,i}:\Vert z - w_{n,i} \Vert ^{2} \le \alpha_{n}\Vert z - u_{1} \Vert ^{2} + (1 - \alpha_{n})\Vert z - v_{n,i} \Vert ^{2}\}, \\ W_{n + 1} = (\bigcap_{i = 1}^{\infty } W_{n + 1,i} ) \cap W_{n}, \\ U_{n + 1} = \{ z \in W_{n + 1}:\Vert u_{1} - z \Vert ^{2} \le \Vert P_{W_{n + 1}}(u_{1}) - u_{1} \Vert ^{2} + \tau_{n + 1}\}, \\ u_{n + 1} \in U_{n + 1},\quad n \in N. \end{cases} $$

(2.2)

The results of Theorems 2.4 and 2.5 are true for this special case.

Corollary 2.13

If, further$i \equiv 1$, then (2.1) and (2.2) reduce to the following two cases:

$$ \textstyle\begin{cases} u_{1} \in H,\quad \varepsilon _{1} \in H, \\ v_{n} = (I + s_{n}T)^{ - 1}(u_{n} + \varepsilon_{n}), \\ w_{n} = \alpha_{n}u_{n} + (1 - \alpha_{n})Sv_{n}, \\ V_{1} = W_{1} = H, \\ V_{n + 1} = \{ z \in H: \langle v_{n} - z,u_{n} + \varepsilon_{n} - v_{n} \rangle \ge 0\} \cap V_{n}, \\ W_{n + 1} = \{ z \in V_{n + 1}:\Vert z - w_{n} \Vert ^{2} \le \alpha_{n}\Vert z - u_{n} \Vert ^{2} + (1 - \alpha_{n})\Vert z - u_{n} \Vert ^{2}\} \cap W_{n}, \\ U_{n + 1} = \{ z \in W_{n + 1}:\Vert u_{1} - z \Vert ^{2} \le \Vert P_{W_{n + 1}}(u_{1}) - u_{1} \Vert ^{2} + \tau_{n + 1}\}, \\ u_{n + 1} \in U_{n + 1},\quad n \in N, \end{cases} $$

(2.3)

and

$$ \textstyle\begin{cases} u_{1} \in H,\quad \varepsilon _{1} \in H, \\ v_{n} = (I + s_{n}T)^{ - 1}(u_{n} + \varepsilon_{n}), \\ w_{n} = \alpha_{n}u_{1} + (1 - \alpha_{n})Sv_{n}, \\ V_{1} = W_{1} = H, \\ V_{n + 1} = \{ z \in H: \langle v_{n} - z,u_{n} + \varepsilon_{n} - v_{n} \rangle \ge 0\} \cap V_{n}, \\ W_{n + 1} = \{ z \in V_{n + 1}:\Vert z - w_{n} \Vert ^{2} \le \alpha_{n}\Vert z - u_{1} \Vert ^{2} + (1 - \alpha_{n})\Vert z - u_{n} \Vert ^{2}\} \cap W_{n}, \\ U_{n + 1} = \{ z \in W_{n + 1}:\Vert u_{1} - z \Vert ^{2} \le \Vert P_{W_{n + 1}}(u_{1}) - u_{1} \Vert ^{2} + \tau_{n + 1}\}, \\ u_{n + 1} \in U_{n + 1},\quad n \in N. \end{cases} $$

(2.4)

The results of Corollaries 2.3 and 2.6 are true for the special cases, respectively.

Remark 2.14

Take $H = ( - \infty, + \infty )$, $Tx = 2x$, and $Sx = x$ for $x \in ( - \infty, + \infty )$. Let $\varepsilon_{n} = \alpha_{n} = \tau_{n} = \frac{1}{n}$ and $s_{n} = 2^{n - 1}$ for $n \in N$. Then T is maximal monotone and S is weakly relatively non-expansive. Moreover, $N(T) \cap F(S) = \{ 0\}$.

Remark 2.15

Taking the example in Remark 2.14 and choosing the initial value $u_{1} = 1 \in ( - \infty, + \infty )$, we can get an iterative sequence $\{ u_{n}\}$ by algorithm (2.3) in the following way:

$$\begin{aligned} \textstyle\begin{cases} u_{1} = 1 \in ( - \infty, + \infty ), \\ u_{n + 1} = \frac{u_{1} + v_{n} - \sqrt{(u_{1} - v_{n})^{2} + \tau_{n + 1}}}{2},\quad n \in N, \end{cases}\displaystyle \end{aligned}$$

(2.5)

where $v_{n} = \frac{u_{n} + \varepsilon_{n}}{1 + 2s_{n}}$, $n \in N$. Moreover, $u_{n} \to 0 \in N(T) \cap F(S)$, as $n \to \infty $.

Proof

We can easily see from iterative algorithm (2.3) that

$$ v_{n} = \frac{u_{n} + \varepsilon_{n}}{1 + 2s_{n}}\quad \mbox{for } n \in N $$

(2.6)

and

$$ w_{n} = \alpha_{n}u_{n} + (1 - \alpha_{n})v_{n}\quad \mbox{for } n \in N. $$

(2.7)

To analyze the construction of set $W_{n}$, we notice that $\vert z - w_{n} \vert ^{2} \le \alpha_{n}\vert z - u_{n} \vert ^{2} + (1 - \alpha_{n})\vert z - v_{n} \vert ^{2}$ is equivalent to

$$ \bigl[2\alpha_{n}u_{n} + 2(1 - \alpha_{n})v_{n} - 2w_{n} \bigr]z \le \alpha_{n}u _{{n}}^{2} + (1 - \alpha_{n})v_{n}^{2} - w_{n}^{2}. $$

(2.8)

In view of (2.7), compute the left-hand side of (2.8):

$$\begin{aligned} &\bigl[2\alpha_{n}u_{n} + 2(1 - \alpha_{n})v_{n}- 2w_{n} \bigr]z \\ &\quad = \bigl[2\alpha_{n}u _{n} + 2(1 - \alpha_{n})v_{n} - 2\alpha_{n}u_{n} - 2(1 - \alpha_{n})v _{n} \bigr]z \\ &\quad \equiv 0\quad \mbox{for }n \in N. \end{aligned}$$

(2.9)

Meanwhile, compute the right-hand side of (2.8):

$$\begin{aligned} &\alpha_{n}u_{{n}}^{2} + (1 - \alpha_{n})v_{n}^{2} - w_{n}^{2} \\ &\quad = \alpha_{n}u_{{n}}^{2} + (1 - \alpha_{n})v_{n}^{2} - \alpha_{n}^{2}u _{n}^{2} - 2\alpha_{n}(1 - \alpha_{n})u_{n}v_{n} - (1 - \alpha_{n})^{2}v _{n}^{2} \\ &\quad = \alpha_{n}(1 - \alpha_{n})u_{n}^{2} + \alpha_{n}(1 - \alpha_{n})v _{n}^{2} - 2\alpha_{n}(1 - \alpha_{n})u_{n}v_{n} \\ &\quad = \alpha_{n}(1 - \alpha_{n}) (u_{n} - v_{n})^{2}\quad \mbox{for } n \in N. \end{aligned}$$

(2.10)

Using (2.8)–(2.10), we get

$$ W_{n + 1} = V_{n + 1} \cap W_{n}\quad \mbox{for } n \in N. $$

(2.11)

Next, we shall use inductive method to show that

$$\begin{aligned} \textstyle\begin{cases} 0 < v_{n + 1} < v_{n} < 1, \\ v_{n} > \frac{1}{2^{n + 1}(n + 1)}, \\ V_{n + 1} = ( - \infty,v_{n}], \\ W_{n + 1} = V_{n + 1}, \\ U_{n + 1} = [u_{1} - \sqrt{(u_{1} - v_{n})^{2} + \tau_{n + 1}},v _{n}], \\ \textrm{we may choose } u_{n + 1} = \frac{u_{1} + v _{n} - \sqrt{(u_{1} - v_{n})^{2} + \tau_{n + 1}}}{2}\quad \mbox{for } n\in N. \end{cases}\displaystyle \end{aligned}$$

(2.12)

In fact, if $n = 1$, then $v_{1} = \frac{u_{1} + \varepsilon_{1}}{1 + 2s_{1}} = \frac{2}{3}$, thus $V_{2} = ( - \infty,v_{1}] \cap V_{1} = ( - \infty,v_{1}]$. From (2.11), $W_{2} = V_{2} \cap W_{1} = V_{2}$. And then $P_{W_{2}}(u_{1}) = v_{1} = \frac{2}{3}$. So we have

$$\begin{aligned} U_{2} &= \bigl\{ z \in W_{2}:\vert u_{1} - z\vert \le \sqrt{ \bigl\vert P_{W _{2}}(u_{1}) - u_{1} \bigr\vert ^{2} + \tau_{2}} \bigr\} \\ &= \biggl[1 - \sqrt{\frac{1}{9} + \frac{1}{2}}, 1 + \sqrt{ \frac{1}{9} + \frac{1}{2}} \biggr] \cap \biggl( - \infty,\frac{2}{3} \biggr] \\ &= \biggl[1 - \sqrt{\frac{1}{9} + \frac{1}{2}}, \frac{2}{3} \biggr] \\ &= \bigl[u_{1} - \sqrt{(u_{1} - v_{1})^{2} + \tau_{2}},v_{1} \bigr]. \end{aligned}$$

Therefore, we may choose $u_{2} \in U_{2}$ as follows:

$$ u_{2} = \frac{u_{1} + v_{1} - \sqrt{(u_{1} - v_{1})^{2} + \tau_{2}}}{2}. $$

From (2.6), $v_{2} = \frac{u_{2} + \varepsilon_{2}}{1 + 2s_{2}} = \frac{4}{15} - \frac{\sqrt{22}}{60}$. Then $0 < v_{2} < v_{1} < 1$. And it is easy to see $v_{1} > \frac{1}{2^{1 + 1}(1 + 1)}$. Thus (2.12) is true for $n + 1$.

Suppose (2.12) is true for $n = k$, that is,

$$\begin{aligned} \textstyle\begin{cases} 0 < v_{k + 1} < v_{k} < 1, \\ v_{k} > \frac{1}{2^{k + 1}(k + 1)}, \\ V_{k + 1} = ( - \infty,v_{k}], \\ W_{k + 1} = V_{k + 1}, \\ U_{k + 1} = [u_{1} - \sqrt{(u_{1} - v_{k})^{2} + \tau_{k + 1}},v _{k}], \\ \mbox{we may choose } u_{k + 1} = \frac{u_{1} + v_{k} - \sqrt{(u_{1} - v_{k})^{2} + \tau_{k + 1}}}{2}. \end{cases}\displaystyle \end{aligned}$$

Then, for $n = k + 1$, we first analyze the set $V_{k + 2}$.

Note that $u_{k + 1} + \varepsilon_{k + 1} - v_{k + 1} = (1 + 2s_{k + 1})v_{k + 1} - v_{k + 1} = 2s_{k + 1}v_{k + 1} > 0$, then $\langle v_{k + 1} - z,u_{k + 1} + \varepsilon_{k + 1} - v_{k + 1} \rangle \ge 0$ is equivalent to $z \le v_{k + 1}$. Then

$$ V_{k + 2} = ( - \infty,v_{k + 1}] \cap V_{k + 1}= ( -\infty,v_{k +1}] \cap ( - \infty,v_{k}] = ( - \infty ,v_{k + 1}]. $$

From (2.11),

$$ W_{k+ 2} =V_{k + 2} \cap W_{k + 1} = ( -\infty,v_{k + 1}] \cap V_{k + 1} = V_{k + 2}. $$

Now, we analyze set $U_{k + 2}$.

Since $0 < v_{k + 1} < 1 = u_{1}$, then $P_{W_{k + 2}}(u_{1}) = v_{k + 1}$. Thus $\vert u_{1} - z \vert \le \sqrt{ \vert P_{W_{k + 2}}(u _{1}) - u_{1} \vert ^{2} + \tau_{k + 2}}$ is equivalent to $u_{1} - \sqrt{(u_{1} - v_{k + 1})^{2} + \tau_{k + 2}} \le z \le u _{1} + \sqrt{(u_{1} - v_{k + 1})^{2} + \tau_{k + 2}}$.

It is easy to check that $u_{1} + \sqrt{(u_{1} - v_{k + 1})^{2} + \tau_{k + 2}} > 1 > v_{k + 1}$, and $u_{1} - \sqrt{(u_{1} - v_{k + 1})^{2} + \tau_{k + 2}} < u_{1} - (u_{1} - v_{k + 1}) = v_{k + 1}$.

Thus $U_{k + 2} = [u_{1} - \sqrt{(u_{1} - v_{k + 1})^{2} + \tau_{k + 2}},v_{k + 1}]$. Then we may choose $u_{k + 2} \in U_{k + 2}$ such that

$$ u_{k + 2} = \frac{u_{1} + v_{k + 1} - \sqrt{(u_{1} - v_{k + 1})^{2} + \tau_{k + 2}}}{2}. $$

Now, we show that $v_{k + 2} > 0$.

Since

$$\begin{aligned} v_{k + 2} &= \frac{u_{k + 2} + \varepsilon_{k + 2}}{1 +2s_{k + 2}} \\ &= \frac{\frac{u_{1} + v_{k + 1} - \sqrt{(u_{1} - v_{k + 1})^{2} +\tau_{k + 2}}}{2} +\frac{1}{k + 2}}{1+2^{k+2}} \\ &= \frac{1}{(k + 2)(1 + 2^{k + 2})} + \frac{1 + v_{k + 1} - \sqrt{(u _{1} - v_{k + 1})^{2} + \frac{1}{k + 2}}}{2(1 + 2^{k + 2})}, \end{aligned}$$

then

$$\begin{aligned} v_{k + 2} > 0 &\quad \Leftrightarrow \quad \frac{1}{k + 2} + \frac{1 + v_{k + 1}}{2} > \frac{\sqrt{(1 - v_{k + 1})^{2} + \frac{1}{k + 2}}}{2} \\ &\quad \Leftrightarrow \quad \frac{1}{(k + 2)^{2}} + \frac{1}{k + 2} + \frac{v_{k + 1}}{k + 2} + v_{k + 1} > \frac{1}{4(k + 2)}, \end{aligned}$$

which is obviously true. Thus $v_{k + 2} > 0$.

Next, we show that $v_{k + 1} > \frac{1}{2^{k + 2}(k + 2)}$.

Since $v_{k + 1} = \frac{u_{k + 1} + \varepsilon_{k + 1}}{1 + 2s_{k + 1}} = \frac{(k + 1)u_{k + 1}}{(k + 1)(1 + 2^{k + 1})} + \frac{1}{(k + 1)(1 + 2^{k + 1})}$, then

$$\begin{aligned} \begin{aligned}[b] &v_{k + 1} > \frac{1}{2^{k + 2}(k + 2)} \\ &\quad \Leftrightarrow\quad (k + 1)u_{k + 1} + 1 > \frac{(k + 1)(1 + 2^{k + 1})}{2^{k + 2}(k + 2)} \\ &\quad \Leftrightarrow\quad (k + 1)\frac{1 + v_{k} - \sqrt{(1 - v_{k})^{2} + \frac{1}{k + 1}}}{2} > \frac{k + 1 - k2^{k + 1} - 3\cdot 2^{k + 1}}{2^{k + 2}(k + 2)} \\ &\quad \Leftrightarrow\quad (1 + v_{k}) + \frac{3 + k}{(k + 1)(k + 2)} - \frac{1}{2^{k + 1}(k + 2)} > \sqrt{(1 - v_{k})^{2} + \frac{1}{k + 1}} \\ &\quad \Leftrightarrow \quad \biggl[\frac{3 + k}{(k + 1)(k + 2)} - \frac{1}{2^{k + 1}(k + 2)} \biggr]^{2} + 4v_{k} + 2v_{k}\biggl[ \frac{3 + k}{(k + 1)(k + 2)} - \frac{1}{2^{k + 1}(k + 2)}\biggr] \\ &\qquad \quad \quad {}+ 2\biggl[\frac{3 + k}{(k + 1)(k + 2)} - \frac{1}{2^{k + 1}(k + 2)}\biggr] > \frac{1}{k}. \end{aligned} \end{aligned}$$

(2.13)

Note that

$$ 2 \biggl[\frac{3 + k}{(k + 1)(k + 2)} - \frac{1}{2^{k + 1}(k + 2)} \biggr] - \frac{1}{k+1} = \frac{k2^{k + 1} + 2^{k + 3} - 2k - 2}{2^{k + 1}(k + 1)(k + 2)} > 0, $$

then (2.13) is true, which implies that $v_{k + 1} > \frac{1}{2^{k + 2}(k + 2)}$.

Finally, we show that $v_{k + 2} < v_{k + 1}$.

From the definition of $u_{k + 2}$, we have $u_{k + 2} < \frac{1 + v _{k + 1} - (1 - v_{k + 1})}{2} = v_{k + 1}$. Then $v_{k + 2} < \frac{v _{k + 1} + \frac{1}{k + 2}}{1 + 2^{k + 2}}$. Since $v_{k + 1} > \frac{1}{2^{k + 2}(k + 2)}$, then $\frac{v_{k + 1} + \frac{1}{k + 2}}{1 + 2^{k + 2}} - v_{k + 1} = \frac{\frac{1}{k + 2} - 2^{k + 2}v_{k + 1}}{1 + 2^{k + 2}} < 0$, which implies that $v_{k + 2} < v_{k + 1}$.

Therefore, by induction, (2.12) is true for $n \in N$. Since $0 < v_{n + 1} < v_{n} < 1$, then $\lim_{n \to \infty } v_{n}$ exists. Set $a = \lim_{n \to \infty } v_{n}$. From (2.12), $\lim_{n \to \infty } u_{n} = a$ and from (2.6), $a = 0$. Then in view of (2.7), $\lim_{n \to \infty } w_{n} = 0$. That is, $\lim_{n \to \infty } w_{n} = \lim_{n\to\infty } v_{n} = \lim_{n \to \infty } u_{n} = 0$.

This completes the proof. □

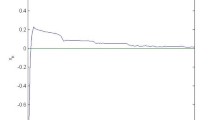
Remark 2.16

We next do a computational experiment on (2.5) in Remark 2.15 to check the effectiveness of iterative algorithm (2.3). By using the codes of Visual Basic Six, we get Table 1 and Fig. 1, from which we can see the convergence of $\{ u_{n}\}$, $\{ v_{n}\}$, and $\{ w_{n}\}$.

Figure 1
Convergence of $\{ u_{n}\}$, $\{ v_{n}\}$, and $\{ w_{n} \}$

Table 1

Numerical results of $\{ u_{n}\}$, $\{ v_{n}\}$, and $\{ w_{n}\}$ with initial $u_{1} = 1.0$

n	$v_{n}$	$w_{n}$	$u_{n}$
1	0.666666666666667	1.00000000000000	1.00000000000000
2	0.188493070669609	0.315479212008828	0.442465353348047
3	0.047734978022387	0.063917141637640	0.096281468868147
4	0.013887781581545	0.006938907907725	−0.01390771311373
5	0.005016751133393	−0.00287604161289	−0.03444721259803
6	0.002022073632571	−0.00418691873111	−0.03523188054954
7	0.000854971429905	−0.00391942854572	−0.03256582839944
8	0.000371596957448	−0.00362300404227	−0.02949958193595
9	0.000164574841194	−0.00281862431655	−0.02668421757849
10	0.000073908605586	−0.002357850182411	−0.02424367927438

Remark 2.17

Similar to Remark 2.15, considering the same example in Remark 2.14 and choosing the initial value $u_{1} = 1 \in ( - \infty, + \infty )$, we can get an iterative sequence $\{ u_{n}\}$ by algorithm (2.4) in the following way:

$$\begin{aligned} \textstyle\begin{cases} u_{1} = 1 \in ( - \infty, + \infty ), \\ u_{n + 1} = \frac{u_{1} + v_{n} - \sqrt{(u_{1} - v_{n})^{2} + \tau_{n + 1}}}{2},\quad n \in N, \end{cases}\displaystyle \end{aligned}$$

(2.14)

where $v_{n} = \frac{u_{n} + \varepsilon_{n}}{1 + 2s_{n}}$ and $w_{n} = \alpha_{n}u_{1} + (1 - \alpha_{n})v_{n}$ for $n \in N$. Then $\{ u_{n}\}$, $\{ v_{n}\}$, and $\{ w_{n}\}$ converge strongly to $0 \in N(T) \cap F(S)$, as $n \to \infty $.

Remark 2.18

We do a computational experiment on (2.14) in Remark 2.17 to check the effectiveness of iterative algorithm (2.4). By using the codes of Visual Basic Six, we get Table 2 and Fig. 2, from which we can see the convergence of $\{ u_{n}\}$, $\{ v_{n}\}$, and $\{ w_{n}\}$.

Figure 2
Convergence of $\{ u_{n}\}$, $\{ v_{n}\}$, and $\{ w_{n} \}$

Table 2

Numerical esults of $\{ u_{n}\}$, $\{ v_{n}\}$, and $\{ w_{n}\}$ with initial $u_{1} = 1.0$

n	$v_{n}$	$w_{n}$	$u_{n}$
1	0.666666666666667	1.00000000000000	1.00000000000000
2	0.188493070669609	0.594246535334805	0.442465353348047
3	0.047734978022387	0.365156652014924	0.096281468868147
4	0.013887781581545	0.260415836186159	−0.01390771311373
5	0.005016751133393	0.204013400906715	−0.03444721259803
6	0.002022073632571	0.168351728027143	−0.03523188054954
7	0.000854971429905	0.143589975511347	−0.03256582839944
8	0.000371596957448	0.125325147337767	−0.02949958193595
9	0.000164574841194	0.111257399858839	−0.02668421757849
10	0.000073908605586	0.100066517745027	−0.02424367927438
11	0.000033552200238	0.090939592909307	−0.02216063262202
12	0.000015364834636	0.083347417765083	−0.02038360583157
13	0.000007086981657	0.076929618752290	−0.01885943628695
14	0.000003288762206	0.071431625279192	−0.01754220267938
15	0.000001534136645	0.066668098527535	−0.01639454294823
16	0.000000718881060	0.062500673950994	−0.01538669196834
17	0.000000338196904	0.058823847714733	−0.01449504667360
18	0.000000159662486	0.055555706347903	−0.01370083322728
19	0.000000075612039	0.052631650579827	−0.01298901840146
20	0.000000035908223	0.050000034112812	−0.01234746359706

2.3 Applications to minimization problems

Let $h:E \to ( - \infty, + \infty]$ be a proper convex, lower-semicontinuous function. The subdifferential ∂h of h is defined as follows: $\forall x \in E$,

$$ \partial h(x) = \bigl\{ z \in E^{*}:h(x) + \langle y - x,z \rangle \le h(y), \forall y \in E \bigr\} . $$

Theorem 2.19

LetE, S, $\{ \varepsilon_{n}\}$, $\{ s_{n}\}$, $\{ \tau_{n}\}$, and$\{ \alpha_{n}\}$be the same as those in Corollary 2.3. Let$h:E \to ( - \infty, + \infty]$be a proper convex, lower-semicontinuous function. Let$\{ u_{n}\}$be generated by

$$ \textstyle\begin{cases} u_{1} \in E,\quad \varepsilon _{1} \in E, \\ v_{n} = \arg \min_{z \in E}\{ h(z) + \frac{1}{2s_{n}}\Vert z \Vert ^{2} - \frac{1}{s_{n}} \langle z,J(u_{n} + \varepsilon_{n}) \rangle \}, \\ w_{n} = J^{ - 1}[\alpha_{n}Ju_{n} + (1 - \alpha_{n})JSv_{n}], \\ V_{1} = W_{1} = E, \\ V_{n + 1} = \{ z \in E: \langle v_{n} - z,J(u_{n} + \varepsilon _{n}) - Jv_{n} \rangle \ge 0\} \cap V_{n}, \\ W_{n + 1} = \{ z \in V_{n + 1}:\varphi (z,w_{n}) \le \alpha_{n}\varphi (z,u _{n}) + (1 - \alpha_{n})\varphi (z,v_{n})\} \cap W_{n}, \\ U_{n + 1} = \{ z \in W_{n + 1}:\Vert u_{1} - z \Vert ^{2} \le \Vert P_{W_{n + 1}}(u_{1}) - u_{1} \Vert ^{2} + \tau_{n + 1}\}, \\ u_{n + 1} \in U_{n + 1},\quad n \in N. \end{cases} $$

Then

(1)

if$v_{n} = u_{n} + \varepsilon_{n}$and$w_{n} = J^{ - 1}[\alpha_{n}Ju_{n} + (1 - \alpha_{n})J(u_{n} + \varepsilon_{n})]$for all$n \in N$, then$u_{n} + \varepsilon_{n} \in N(\partial h) \cap F(S)$.
(2)

If$N(\partial h) \cap F(S) \ne \emptyset $and$\inf_{n}s _{n} > 0$, then the iterative sequence$u_{n} \to y_{o} = P_{\bigcap_{n = 1}^{\infty }W_{n}} (u_{1}) \in N(\partial h) \cap F(S)$, as$n \to \infty $.

Proof

Similar to [11], $v_{n} = \arg \min_{z \in E}\{ h(z) + \frac{1}{2s_{n}}\Vert z \Vert ^{2} - \frac{1}{s_{n}} \langle z,J(u _{n} + \varepsilon_{n}) \rangle \}$ is equivalent to $0 \in \partial h(v_{n}) + \frac{1}{s_{n}}Ju_{n} - \frac{1}{s_{n}}J(u_{n} + \varepsilon_{n})$. Then $v_{n} = (J + s_{n}\partial h)^{ - 1}J(u_{n} + \varepsilon_{n})$. So, Corollary 2.3 ensures the desired results.

This completes the proof. □

Theorem 2.20

We only do the following changes in Theorem 2.19: $w_{n} = J^{ - 1}[\alpha_{n}Ju_{1} + (1 - \alpha_{n})JSv_{n}]$and$W_{n + 1} = \{ z \in V_{n + 1}:\varphi (z,w_{n}) \le \alpha_{n}\varphi (z,u_{1}) + (1 - \alpha_{n})\varphi (z,v_{n})\} \cap W_{n}$. Then, under the assumptions of Corollary 2.6, we still have the result of Theorem 2.19.

Notes

Acknowledgements

Supported by the National Natural Science Foundation of China (11071053), Natural Science Foundation of Hebei Province (A2014207010), Key Project of Science and Research of Hebei Educational Department (ZD2016024), Key Project of Science and Research of Hebei University of Economics and Business (2016KYZ07), Youth Project of Science and Research of Hebei University of Economics and Business (2017KYQ09) and Youth Project of Science and Research of Hebei Educational Department (QN2017328).

Authors’ contributions

All authors contributed equally to the manuscript. All authors read and approved the final manuscript.

Competing interests

The authors declare that they have no competing interests.

References

1.
Takahashi, W.: Nonlinear Functional Analysis. Fixed Point Theory and Its Applications. Yokohama Publishers, Yokohama (2000) zbMATHGoogle Scholar
2.
Agarwal, R.P., O’Regan, D., Sahu, D.R.: Fixed Point Theory for Lipschitz-Type Mappings with Applications. Springer, Berlin (2008) zbMATHGoogle Scholar
3.
Pascali, D., Sburlan, S.: Nonlinear Mappings and Monotone Type. Sijthoff and Noordhoff, The Netherlands (1978) CrossRefzbMATHGoogle Scholar
4.
Alber, Y.I.: Metric and generalized projection operators in Banach spaces: properties and applications. In: Kartsatos, A.G. (ed.) Theory and Applications of Nonlinear Operators of Accretive and Monotone Type. Lecture Notes in Pure and Applied Mathematics, vol. 178, pp. 15–50. Dekker, New York (1996) Google Scholar
5.
Zhang, J.L., Su, Y.F., Cheng, Q.Q.: Simple projection algorithm for a countable family of weak relatively nonexpansive mappings and applications. Fixed Point Theory Appl. 2012, Article ID 205 (2012) MathSciNetCrossRefzbMATHGoogle Scholar
6.
Zhang, J.L., Su, Y.F., Cheng, Q.Q.: Hybrid algorithm of fixed point for weak relatively nonexpansive multivalued mappings and applications. Abstr. Appl. Anal. 2012, Article ID 479438 (2012) MathSciNetzbMATHGoogle Scholar
7.
Matsushita, S., Takahashi, W.: A strong convergence theorem for relatively nonexpansive mappings in a Banach space. J. Approx. Theory 134, 257–266 (2005) MathSciNetCrossRefzbMATHGoogle Scholar
8.
Liu, Y.: Weak convergence of a hybrid type method with errors for a maximal monotone mapping in Banach spaces. J. Inequal. Appl. 2015, Article ID 260 (2015) MathSciNetCrossRefzbMATHGoogle Scholar
9.
Su, Y.F., Li, M.Q., Zhang, H.: New monotone hybrid algorithm for hemi-relatively nonexpansive mappings and maximal monotone operators. Appl. Math. Comput. 217, 5458–5465 (2011) MathSciNetzbMATHGoogle Scholar
10.
Wei, L., Tan, R.: Iterative schemes for finite families of maximal monotone operators based on resolvents. Abstr. Appl. Anal. 2014, Article ID 451279 (2014). https://doi.org/10.1155/2014/451279 MathSciNetGoogle Scholar
11.
Wei, L., Cho, Y.J.: Iterative schemes for zero points of maximal monotone operators and fixed points of nonexpansive mappings and their applications. Fixed Point Theory Appl. 2008, Article ID 168468 (2008) MathSciNetCrossRefzbMATHGoogle Scholar
12.
Wei, L., Su, Y.F., Zhou, H.Y.: Iterative convergence theorems for maximal monotone operators and relatively nonexpansive mappings. Appl. Math. J. Chin. Univ. Ser. B 23(3), 319–325 (2008) MathSciNetCrossRefzbMATHGoogle Scholar
13.
Klin-eam, C., Suantai, S., Takahashi, W.: Strong convergence of generalized projection algorithms for nonlinear operators. Abstr. Appl. Anal. 2009, Article ID 649831 (2009) MathSciNetCrossRefzbMATHGoogle Scholar
14.
Wei, L., Su, Y.F., Zhou, H.Y.: Iterative schemes for strongly relatively nonexpansive mappings and maximal monotone operators. Appl. Math. J. Chin. Univ. Ser. B 25(2), 199–208 (2010) MathSciNetCrossRefzbMATHGoogle Scholar
15.
Inoue, G., Takahashi, W., Zembayashi, K.: Strong convergence theorems by hybrid methods for maximal monotone operator and relatively nonexpansive mappings in Banach spaces. J. Convex Anal. 16(16), 791–806 (2009) MathSciNetzbMATHGoogle Scholar
16.
Mosco, U.: Convergence of convex sets and of solutions of variational inequalities. Adv. Math. 3(4), 510–585 (1969) MathSciNetCrossRefzbMATHGoogle Scholar
17.
Tsukada, M.: Convergence of best approximations in a smooth Banach space. J. Approx. Theory 40, 301–309 (1984) MathSciNetCrossRefzbMATHGoogle Scholar
18.
Kamimura, S., Takahashi, W.: Strong convergence of a proximal-type algorithm in a Banach space. SIAM J. Optim. 13(3), 938–945 (2012) MathSciNetCrossRefzbMATHGoogle Scholar
19.
Xu, H.K.: Inequalities in Banach spaces with applications. In: Nonlinear Analysis, vol. 16, pp. 1127–1138 (1991) Google Scholar

Copyright information

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

Li Wei
- 1
Email authorView author's OrcID profile
Ravi P. Agarwal
- 2

1.School of Mathematics and StatisticsHebei University of Economics and BusinessShijiazhuangChina
2.Department of MathematicsTexas A&M University-KingsvilleKingsvilleUSA

New construction and proof techniques of projection algorithm for countable maximal monotone mappings and weakly relatively non-expansive mappings in a Banach space

Abstract

Keywords

MSC

1 Introduction and preliminaries

Lemma 1.1

Definition 1.2

Definition 1.3

Definition 1.4

Remark 1.5

Lemma 1.6

Lemma 1.7

Definition 1.8

Definition 1.9

Lemma 1.10

Lemma 1.11

Lemma 1.12

Lemma 1.13

2 Strong convergence theorems and experiments

2.1 Strong convergence for infinite maximal monotone mappings and infinite weakly relatively non-expansive mappings

Algorithm 2.1

Theorem 2.1

Proof

Theorem 2.2

Proof

Corollary 2.3

Algorithm 2.2

Theorem 2.4

Proof

Theorem 2.5

Proof

Corollary 2.6

Remark 2.7

Remark 2.8

Remark 2.9

Remark 2.10

2.2 Special cases in Hilbert spaces and computational experiments

Corollary 2.11

Corollary 2.12

Corollary 2.13

Remark 2.14

Remark 2.15

Proof

Remark 2.16

Remark 2.17

Remark 2.18

2.3 Applications to minimization problems

Theorem 2.19

Proof

Theorem 2.20

Notes

Acknowledgements

Authors’ contributions

Competing interests

References

Copyright information

Authors and Affiliations

Personalised recommendations