Abstract
Indoor positioning navigation technologies have developed rapidly, but little effort has been expended on integrity monitoring in Pedestrian Dead Reckoning (PDR) and WiFi indoor positioning navigation systems. PDR accuracy will drift over time. Meanwhile, WiFi positioning accuracy decreases in complex indoor environments due to severe multipath propagation and interference with signals when people move about. In our research, we aimed to improve positioning quality with an integrity monitoring algorithm for a WiFi/PDR-integrated indoor positioning system based on the unscented Kalman filter (UKF). The integrity monitoring is divided into three phases. A test statistic based on the innovation of UKF determines whether the positioning system is abnormal. Once a positioning system abnormality is detected, a robust UKF (RUKF) is triggered to achieve higher positioning accuracy. Again, the innovation of RUKF is used to judge the outliers in observations and identify positioning system faults. In the last integrity monitoring phase, users will be alerted in time to reduce the risk from positioning fault. We conducted a simulation to analyze the computational complexity of integrity monitoring. The results showed that it did not substantially increase the overall computational complexity when the number of dimensions in the state vector and observation vector in the system is small (< 20). In practice, the number of dimensions of state vector and observation vector in an indoor positioning system rarely exceeds 20. The proposed integrity monitoring algorithm was tested in two field experiments, showing that the proposed algorithm is quite robust, yielding higher positioning accuracy than the traditional method, using only UKF.
Similar content being viewed by others
1 Introduction
The technology for seamless indoor and outdoor positioning has undergone unprecedented development due to the increasing demand for location-based services (LBS). In outdoor environments, Global Navigation Satellite System (GNSS) technology guarantees high positioning accuracy, but in most indoor environments, the GNSS signal is very weak, or even be no signal at all [1]. Thus, some new positioning technologies, such as radio frequency (RF) signals, sensor-based, and multi-source fusion positioning methods, are applied indoors [2]. Indoor positioning means using WiFi fingerprinting positioning, Bluetooth, ultra-wideband, magnetic field positioning technologies, and Pedestrian Dead Reckoning (PDR) [3,4,5,6,7], which were developed to solve this problem. Among those approaches, WiFi fingerprinting positioning and PDR are the two most popular techniques, as they do not need additional hardware devices. However, due to severe multipath propagation, high fluctuation in WiFi signals, and the cumulative error in PDR, indoor positioning accuracy is low. Therefore, a high precision and robust indoor positioning system is urgently needed.
WiFi access points (APs) are widely deployed in indoor environments, such as offices, hospitals, airports, and university buildings. In general, WiFi-based indoor positioning is instrumented with smartphones, with a low deployment cost, tolerable errors, and limited use of computational resources [8, 9]. WiFi fingerprinting positioning with Received Signal Strength Indication (RSSI) observation is considered as one preferred method of indoor positioning. WiFi fingerprinting positioning uses RSSI to measure the environmental variation, so there is no need to know the exact location of the APs.
For PDR, smartphones using self-contained sensors such as accelerometer, gyroscope, and magnetometer can progressively infer the position of users by combining displacement of the current step with the position of the previous step. The displacement of the current step is calculated with the help of walking step detection, step length estimation, and user heading estimation [10]. The integration of WiFi fingerprinting positioning and PDR is one challenging technology of higher indoor positioning accuracy [11,12,13,14,15,16].
Although a variety of indoor positioning solutions are presently available, there is little research on the complete quality evaluation of the indoor positioning system. In particular, many researchers have paid attention to the optimization techniques of only positioning accuracy, rather than the complete quality of integrity, continuity, and availability. Nevertheless, in practice, the reliability and integrity of positioning systems are indispensable quality evaluation indicators. If an application system only outputs information but lacks a reliable description of that information, the service is incomplete essentially. In some high-risk indoor applications scenarios, like firefighting, peacekeeping, emergency evacuation, disaster relief, mobile health monitoring, and smart city businesses, the integrity of indoor positioning is a performance indicator that cannot be ignored.
At present, there are several initial solutions to this problem. In [17], one WLAN-oriented indoor positioning algorithm enhanced with threshold-specified integrity monitoring was proposed. This integrity monitoring algorithm utilizes redundancy among APs and removes each AP with a damaged feature to improve the system robustness. Likewise, literature [18] has studied the continuous availability of WLAN APs and proposed an integrity monitoring algorithm that identifies and removes rogue APs to improve positioning accuracy. Under the special considerations involved in integrity monitoring, the comprehensive performance of the indoor positioning system is improved. Ascher et al. investigated a UWB/INS positioning system and proposed an integrity monitoring algorithm based on extended Kalman innovation, which can effectively detect and remove the Time Difference of Arrival (TDOA) observation outliers for improving positioning accuracy [19]. The integrity monitoring algorithm proposed in [17, 18] only applied to a single WLAN system, but at present, one of the hottest trends in indoor positioning is multi-source integration positioning. These integrity monitoring algorithms all lack an alert mechanism for cases in which positioning accuracy completely dissatisfies user requirements.
Integrity monitoring will be a desirable option to improve multi-source integration positioning quality. In our research, we proposed an integrity monitoring algorithm for a WiFi/PDR-integrated indoor positioning system based on the unscented Kalman filter (UKF). The positioning accuracy of the UKF-based WiFi/PDR is generally improved; however, the factors of PDR cumulative error over time, severe multipath propagation and high fluctuation in WiFi signals, lead to the poor integrated positioning accuracy. In this paper, once the integrated positioning accuracy drops below a certain threshold and no longer meets user requirements, the integrity monitoring algorithm will be actively triggered for performance optimization. Due to the complexity of indoor environments and the influence of various observation factors such as severe multipath propagation, measurement gross errors often appear in actual positioning measurements. If these gross errors are not detected and eliminated, the position estimation will be poor and the filter may be divergent. To overcome this issue, a RUKF is employed to eliminate the gross errors in the phase of integrity monitoring and the measured outliers related to system faults are identified. When current measurements are identified as outliers, the gain matrix of RUKF is adjusted to reduce the influence of outliers on the filtering results. Again, once a fault is detected, the user will be alerted in time to reduce risk from the positioning fault. Experiments on in situ measurements have shown that the proposed algorithm can effectively identify and eliminate outliers, avoid the divergence of the filter, and improve the robustness and accuracy of positioning.
The main text of this paper is organized as follows: Related work is introduced in Section 2. The integration positioning approach and integrity monitoring algorithm are conceptually proposed in Section 3. Section 4 presents the Bayesian WiFi fingerprinting positioning, PDR, UKF-integrated WiFi fingerprinting positioning and PDR, and the integrity monitoring algorithm. Subsequently, the computational complexities of the UKF and integrity monitoring are analyzed in Section 5. The experimental setup, asymptotic and exact computational complexity analysis, field experiments results, and discussion are reported in Section 6. The conclusions are given in the last section.
2 Related work
The concept of integrity first appeared in the civil aviation applications of the Global Positioning System (GPS). It refers to the ability of a satellite navigation system to provide timely notifications or terminate signal when an error in the satellite navigation system exceeds the alert limit and makes the satellite navigation system unavailable [20]. Straightforwardly, integrity is a confidence measure, concerned with the accuracy of positioning and navigation system. The function of integrity is twofold: to detect and identify the fault or abnormality that affects positioning accuracy, and to inform the user in a timely way that positioning service is unavailable. There is a lot of research on integrity monitoring related to GNSS applications, among which the Receiver Autonomous Integrity Monitoring (RAIM) algorithm is widely used. This integrity monitoring algorithm on the client side has many advantages, such as independent of external devices, has a low cost, and is easy to implement. The classical integrity monitoring algorithms include pseudo-range comparison, least-squares residuals, and parity vectors [21], but these algorithms do not use the inertial navigation data, so these algorithms have certain technical limitations in PDR. The indoor environment is usually much complex than the outdoors, and severe multipath propagation, wireless signal interruption, and the indoor structural complexity make the GNSS integrity monitoring algorithm not fully applicable in indoor scenarios. However, the concept of integrity as proposed in the context of GPS is still applicable to the performance evaluation of indoor navigation systems.
WiFi fingerprinting positioning and PDR have their advantages and disadvantages. Due to the high fluctuation in WiFi signals, WiFi fingerprinting positioning error is large, but is stationary, and is not accumulative. PDR positioning has higher positioning accuracy over a short time, but its positioning result is relative, and its error is accumulated due to the noisy inertia sensors. To complement each other, integrated WiFi fingerprinting positioning and PDR sub-systems can reduce the signal fluctuations in WiFi by using PDR and obtaining the initial position of PDR by using WiFi fingerprinting positioning. Ultimately, data integration in WiFi fingerprinting positioning and PDR reduces the cumulative error of PDR for improving the overall positioning accuracy [22].
In most technically, data integration of indoor positioning is implemented through filters [11,12,13,14,15,16], such as particle filter (PF) [11, 12], Kalman filtering (KF) [13, 14], and extended Kalman filtering (EKF) [15, 16]. The PF can achieve high positioning accuracy only if a large number of representative particles are deployed, but large computational capacity and storage is needed. Particularly, intelligent terminals like the smartphones have very limited computing power, power supplies, and storage capacity [2], so PF is not the optimal choice on the smartphone platforms. The KF and EKF will work effectively only under the condition that the system state and observation operators are linear or slightly nonlinear. In fact, the PDR is highly nonlinear. Moreover, if the KF and EKF are used to integrate WiFi fingerprinting positioning and PDR, the improvements in positioning accuracy can be limited, and even the filter can become divergent. The UKF is a nonlinear filtering algorithm based on the unscented transform (UT) that overcomes the limitations of lower filter precision-caused truncation error, and widely applied in nonlinear estimation. The UKF abandons the traditional method of linearizing nonlinear functions and uses the UT to handle the nonlinear transfer of mean and covariance. The UKF approximates the probability density function of a nonlinear function, using a series of determined samples to approximate the posterior probability density of the system state, instead of approximating the nonlinear function. UKF does not ignore higher-order terms, so it has higher calculation accuracy for nonlinear distributions, which effectively overcomes the shortcomings of low accuracy and poor stability in EKF estimation. The estimated results from UKF will at least be equivalent at the precision of the second-order Taylor expansion of nonlinear models. Moreover, the computational complexity of UKF is much lower than that of PF.
In our research, we make a tradeoff between computational complexity and positioning accuracy and use UKF to integrate WiFi fingerprinting positioning and PDR. To further improve the performance of the indoor positioning system, an integrity monitoring algorithm is proposed. The related conceptions and processes of the integrity monitoring algorithm are elaborated in Sections 3 and 4.4.
3 Integrated positioning approach and integrity monitoring algorithm
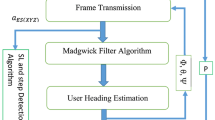
Figure 1 shows the technical chart for the proposed approach of integrated positioning and integrity monitoring.
As discussed, WiFi fingerprinting positioning accuracy is not high, due to wireless signal outages, severe multipath propagation, and signals encounter interference when people walk around. PDR has high positioning accuracy in a short time, but the error will cumulative fast over time. We use the UKF to integrate the two positioning approaches to exploit the respective advantages of the two positioning approaches and avoid their disadvantages. In this paper, the main novelty of our research is an integrity monitoring algorithm that delivers a robust integrated positioning system and offers users the confidence of in time positioning accuracy.
When the positioning system is working properly, the UKF is the optimal state estimation, and so the innovation of UKF obeys a Gaussian distribution with zero-mean. According to this principle, we designed the proposed integrity monitoring algorithm. We divided the integrity monitoring into three phases and set up three integrity flags, IF1, IF2, and IF3, as shown in Fig. 1, in blue. The first phase of our proposed integrity monitoring algorithm is what we call the Innovation-Based Integrity Monitoring (IBIM) algorithm. In this phase, UKF innovation is used to construct a test statistic and then determine whether the test statistic exceeds a threshold. If the test statistic is below the detection threshold (IF1 = 0), the UKF positioning results will be directly sent to the user. If it exceeds the detection threshold (IF1 ≠ 0), a RUKF is triggered to achieve higher positioning accuracy in the second phase.
Although the RUKF has corrected some anomaly range values and improved the positioning accuracy, observation noise and process noise are not fully estimated in real time during the filtering process because of the complexity of indoor environments; as a result, some outliers may still exist. The existence of outliers not only makes the positioning accuracy lower but will likely cause the filter to diverge. Abnormality in an observation can be reflected by the innovation of the filter; thus, RUKF innovation is used to identify further possible outliers in the second phase of integrity monitoring. If there are no outliers (IF2 = 0), the positioning results of RUKF will be output to the user. If there is an outlier detected (IF2≠ 0), the integrity monitoring will enter the last phase. In the last phase, the identified outliers are eliminated, and the system outliers and faults are distinguished individually. If the current observation is an outlier (IF3 = 0), else then (IF3≠ 0). See Section 4.4 for the details of this process.
4 Methodology
4.1 WiFi fingerprinting positioning
WiFi fingerprinting positioning consists of two phases including offline radio map-learning and online location inference; the WiFi fingerprinting positioning process is shown in Fig. 2.
In offline radio map-learning, a fingerprint database named a radio map [23] is constructed by collecting RSSI values of multiple APs at predetermined calibration points, and the collected RSSI values are stored therein. In online location inference, real-time RSSI measurements received by the smartphone are matched with the radio map to estimate the location of the smartphone [10, 24, 25].
Fingerprinting matching is done selectively with deterministic and stochastic algorithms [26]. Typical deterministic algorithms are the nearest neighbor (NN) algorithm, k nearest neighbor (KNN) algorithm, and the weighted k nearest neighbor (WKNN) algorithm [27]. Stochastic algorithms are mostly based on Gaussian distribution assumption [28] and Bayesian estimation [9, 29]. The deterministic algorithms are relatively simple and have a wide range of applications. However, WiFi signals are susceptible to interference in indoor environments, and there is no one-to-one mapping of signal features onto physical location [30]. Empirically, probabilistic algorithms can provide higher positioning accuracy and good usability than deterministic algorithms. In most cases, the Bayesian estimation algorithm is superior to the WKNN algorithm [30, 31]. Therefore, we use a Bayesian estimation of the Weibull signal model in [9] as a WiFi fingerprinting positioning scheme.
4.1.1 Bayesian estimation of the Weibull signal model
In WiFi fingerprinting positioning, the Weibull signal model often used probability density function for modeling the signal strength of radio waves [32], and it is expressed as follows:
Accordingly, the Cumulative Distribution Function (CDF) can be given as follows:
where x is the variable of the function, k is the shape parameter, λ is the scale parameter, and θ is the shift parameter [31, 33].
The parameters of the Weibull signal model can be estimated with a limited number of RSSI sample measurements. The model parameters (\( \lambda, k,\mathrm{and}\ \theta \)) can be calculated with [34, 35]:
where\( \overline{O} \) is the mean value of RSSI measurements set Oi, STD is the standard deviation, and Γ is the gamma function. The value (k + 0.15) is an approximation result of the expression \( 1/\sqrt{\Gamma \left(1+\frac{2}{k}\right)-{\Gamma}^2\left(1+\frac{1}{k}\right)} \) when 1.5≤k ≤ 2.5 [31].
Therefore, the distribution probability of each RSSI measurement in the fingerprint database can be expressed as:
In our research, in order to improve the computation process and weaken the RSSI measurements of signal strength singularity, a bin-based solution is adopted. When the conventional algorithm established the fingerprint database to 10 dB for a range of signal strength measurements RSSI by 30–100 divided into seven ranges, plus 0–30 dB for a single range, with a total of eight ranges, each range can be regarded as a bin. With a fingerprint database and the Weibull signal model, we can calculate the probability of an RSSI measurement. For the sake of computational efficiency, the RSSI measurements are rounded to integers. The probability for each bin in the fingerprint database can be expressed as:
where w is the width of the bin and x is the RSSI value at the left boundary value of the bin.
The fingerprinting method using the radio map based on the Weibull–Bayesian density model can be represented by a set of Weibull signal models that simulate the distribution of RSSI measurements. Each Weibull signal model of three parameters (\( \lambda, k,\mathrm{and}\ \theta \)) empirically represents the probability distribution of RSSI measurements between APAm and a smartphone at a reference point Ri. The structure of the radio map can be greatly simplified in this way because it only stores three parameters of the Weibull function to restore the complete probability density [9]; therefore, it is not necessary to store the empirical probability distribution of separate RSSI bins.
4.1.2 Fingerprinting positioning using the Bayesian estimation of the Weibull signal model
The fingerprinting algorithm based on the Weibull signal model with dynamic calculation probability, parameterized with three parameters, can be calculated with few samples, for a probability density with higher accuracy than the traditional histogram method. The fingerprinting positioning algorithm used in this paper is based on the Bayesian theory [36]. The principle is to use the conditional probability model for location fingerprinting and Bayesian inference mechanism to estimate the position of the smartphone [37]. Also called the Bayesian probability algorithm, the basic principle can be expressed as:
where x is a reference point in the fingerprint database, y is the RSSI measurements of AP received by the smartphone at the anchor point, and p(x|y) is the probability that the anchor point is the reference point x when the RSSI measurement is y. The value p(y|x) is the likelihood of the RSSI measurement being y at the reference point x. p(x) is the probability of a reference point x, and the default assumption is the equal probability of all reference points. The term p(y) is the probability of RSSI measurement, and the default APs are mutually independent in statistics. From Eq. (10), when the value of p(x|y) is maximum, the probability of reference point x occurring when the RSSI value received at the anchor point is y also reaches a maximum. The best match with the anchor point can be used as the positioning output. Therefore, the maximum a posteriori (MAP) estimation algorithm is used to find the maximum value of p(x|y) at which x is the positioning result, and the formula can be expressed as follows:
In order to obtain the maximum value of p(x|y), we know that p(x) and p(y) are the same at each fingerprint point by the Bayesian theory formula. The maximum value of p(x|y) can be transformed to solve the maximum likelihood of p(y|x) which means the probability of the RSSI measurements of each AP received at the fingerprint point x. Since each AP is independent, the formula for a maximum value of the probability product for the RSSI measurements of each AP can be expressed as:
where nMAC is the total number of AP received by smartphone at the anchor point, x is a fingerprinting point in the fingerprinting database, and yj is the RSSI measurements of the jth AP received by the smartphone at the anchor point. Therefore, the traditional probability product of all the APs at each fingerprinting point is calculated. The corresponding fingerprinting point is the positioning result.
The dynamic calculation probability method differs from the traditional fingerprinting method in that it takes the uncertainty of RSSI measurements into account and may vary from the received AP in a range from +5 to −5 dB [9]. Subsequently, we can dynamically obtain a possible range for RSSI measurements and then calculate the probability, which can more accurately estimate the probability of occurrence of an AP. The probability of RSSI measurements from all APs received at the anchor point can be expressed as:
where x is the RSSI value of the AP Am received by smartphone at the fingerprint point Ri. The three parameters of the Weibull signal model are stored in the fingerprint database to rebuild the probability distribution of the RSSI measurements between an AP Am and a smartphone at a fingerprint point Ri, and then calculates the probability value of the range dynamically in real time.
4.2 Pedestrian Dead Reckoning
PDR leverages inertial sensors such as a gyroscope, accelerometer, and magnetometer to obtain users’ movement information, then combines it with the previous location of a user to estimate current location by the equation:
where Pt is the position at timestamp t, Lt is the step length, and θt is the heading direction at timestamp t.
Smartphones integrate many sensors, such as accelerometers, gyroscopes, magnetometers, and barometers, which makes PDR more feasible and convenient. A classic PDR mainly contains three parts: step detection, step length estimation, and heading direction estimation.
4.2.1 Step detection
When the pedestrian walks horizontally, periodical variations can be detected from accelerometer readings as shown in Fig. 3. By the accelerometer of the smartphone, it is easy to determine whether the pedestrian is stationary or walking. As can be seen from Fig. 3, the green circle represents the detected steps, the actual number of steps is 52, and the detected number of steps is also 52. The pedestrian overall acceleration can be expressed as follows:
where the ax, ay, az denote the smartphone three-axis accelerometer values and g is the local gravity acceleration. By performing peak detection with a given threshold, pedestrian steps can be recognized in real time [38].
4.2.2 Step length estimation
The people step models vary widely, making the general model less accurate; the step lengths are determined by various factors, including height, attitude, and walking frequency [39, 40]. For the same person, the step length mainly depends on the walking speed [41]. Therefore, we apply the empirical model [42] to estimate the step length:
where Accmax and Accmin represent the maximum and minimum of value of the acceleration in the vertical direction during a step, k is the personalized coefficients for different pedestrians. The coefficient can be easily estimated by counting steps when pedestrians travel a known distance. In our research, the k is 0.57 m.
4.2.3 Heading direction estimation
To reduce the circumstance disturbances as well as accumulative error, we combine gyroscopes and magnetometers to estimate the heading direction. The smartphone heading direction comes from the gyroscope angular velocity and initial direction. It works steadily when facing external disturbance, but error accumulates rapidly over time. The smartphone heading direction can be determined by integrating the Z-axis angular velocity of a gyroscope:
where Ht is the current smartphone heading direction and wt is the angular velocity at step t. Magnetic direction can be directly obtained from a direction sensor (magnetometer), which is easily disturbed by circumstances. The magnetic heading angle is calculated as:
where Mx and My are the Earth’s magnetic field components along x and y axes of the reference frame. The combination method refers to [43], the heading direction calculated as follows:
where W is the weight of the magnetic data and empirically taking the value 0.01 [43].
4.3 UKF integrated WiFi fingerprinting positioning and PDR
WiFi fingerprinting positioning accuracy is low, its positioning error is relatively stable, and there is no cumulative error over time. In contrast, PDR delivers higher positioning accuracy in a short time, but error gradually accumulates. The integration of WiFi fingerprinting positioning and PDR over time forms a relatively robust indoor positioning system.
4.3.1 UKF model
The UKF is a nonlinear filtering algorithm based on the unscented transform (UT) that overcomes the limitations of lower filter precision-caused truncation error, and widely applied in nonlinear estimation. Assume the state model and measurement model of a system as follows:
where f is the nonlinear state function, h is the nonlinear observation function,Wk and Vk are the process noise and measurement noise, respectively, which are both uncorrelated zero-mean white Gaussian noise, and their covariances are Qk and Rk, respectively, that is Wk~N(0,Qk), Vk~N(0,Rk). Finally, \( {\upmu}_{k-1} \) is the control input of the model.
The first step in unscented Kalman filtering is to sample the pre-state distribution of the system, that is, to generate a series of points named Sigma points by UT. Consider an n-dimensional random variable X with a mean of \( \hat{\mathrm{x}} \) and a covariance of P, transformed by a nonlinear function f (⋅). The UT will generate a Sigma Vector X with a dimension of 2n + 1 and a set of weighted points W, as specified by the following procedures:
where \( {\left(\sqrt{\left(n+\uplambda \right)\mathrm{P}}\right)}_i \) represents column i of the square root matrix. λ is a scaling parameter, which is used to reduce the total prediction error, α determines the propagation speed of the Sigma sampling point around \( \hat{x} \), and α is usually set to a small positive number, (1E−4 ≤ α ≤ 1). In the calculation, κ usually takes 0, and the candidate parameter β is a non-negative weight coefficient, which is usually 2 [22]. \( {\mathrm{W}}_i^{\left(\mathrm{m}\right)} \) represents the weight of the mean of the ith sigma sample point, and \( {\mathrm{W}}_i^{\left(\mathrm{c}\right)} \) represents the weight of the covariance of the ith Sigma sample point.
After the Sigma sampling point is obtained, the time domain update of the unscented Kalman filter is executed in the following steps:
where \( {\upxi}_{\mathrm{k}}^{-} \) represents a one-step prediction state vector of Sigma sample points after the system nonlinear state function transform at different times k, \( {\overset{\wedge }{\mathrm{x}}}_{\mathrm{k}}^{-} \) is the priori state estimation, \( {\mathrm{P}}_{\mathrm{k}}^{-} \) is a priori covariance matrix of the state vector, \( {\left({\mathrm{Z}}_{\mathrm{k}}^{-}\right)}_i \) represents the observation vector, and \( {\overset{\wedge }{\mathrm{z}}}_{\mathrm{k}}^{-} \) denotes the observation prediction vector.
The measurement update of the UKF is completed as in the following steps:
where Pzz represents the observation prediction error covariance matrix, Pxz is the cross-covariance matrix of state vector and observation vector, Kk is the gain matrix of UKF, \( {\overset{\wedge }{\mathrm{x}}}_{\mathrm{k}} \) represents a posteriori state estimation, and Pk denotes a posteriori covariance matrix of state vector.
4.3.2 Implementation of UKF integration [22]
The results of WiFi fingerprinting positioning and PDR are integrated by using the above UKF algorithm. The system state is modeled by a nonlinear expression based on the pedestrian state information. The system model can be expressed as:
where xk and yk are the locations after k steps, θk is the heading direction after k steps, wk − 1 is three-dimensional system process noise, \( \overline{l} \) is the step length of step k, and \( \overline{\uptheta} \) is the variation of the heading direction in step k. The measurement model is as follows:
where xk and yk are the position of pedestrian inferred from WiFi fingerprinting positioning, lk is the step length of step k inferred from PDR positioning, Δθk is the variation of heading direction of step k inferred from the gyroscope, θk is the heading direction of step k inferred from the magnetometer, and Vk is the five-dimensional system measurement noise.
4.4 Integrity monitoring
4.4.1 Innovation-based Integrity Monitoring
Innovation of Kalman filtering is defined as the difference between the real observation and the predicted observation. Then the innovation can be written as:
It can be shown that when there are no faults of state prediction and observation, the innovation or residual error obeys Gaussian distribution with zero-mean [44], namely:
rk~N(\( 0 \), Dk) (29)
where Dk is the innovation covariance matrix:
in the process of measurement update, assuming that there is a gross error in the measurement result of the positioning sensors, the observation equation at time k can be expressed as:
where B is fault-caused gross error,\( \mathrm{B}=\left[{b}_1,{b}_2,\cdots, {b}_n\right] \). If the ith positioning sensor fails, bi ≠ 0, and if there is no fault, bi = 0. At this time, the innovation affected by the gross error can be written as:
The innovation vector at this time is no longer zero [45], namely:
The test statistic of fault or gross error in innovation can be expressed as [46]:
where rk is the innovation of Kalman filter at time k while Dk is the covariance matrix of the innovation at time k. In statistics, if there is no gross error (no fault), the test statistic λavg obeys the center \( {\chi}^2 \) distribution with the degree of freedom m, where m is the dimension of the current moment Zk observation vector:
If there is a gross error, the test statistic λavg obeys a non-central χ2 distribution with a degree of freedom of m:
where λ is a non-central parameter, \( \lambda ={\mathrm{B}}^{\mathrm{T}}{{\mathrm{D}}_k}^{-1}\mathrm{B} \). The threshold TD of gross error detection according to the Neyman–Pearson criterion [47], where the false alarm rate Pfa = α, here the value is 0.333 × 10−6, TD can be expressed as:
thus, the abnormality judgment of the hypothesis test is:
The expressions (38) can be used to determine whether the system is abnormal. If there is no abnormality in the system, the positioning results of UKF will be sent to the user (as can be seen from Fig. 1, IF1 = 0 at this time). If an abnormality occurs in the system (IF1 ≠0), the RUKF is triggered to remove the gross errors and obtain higher positioning accuracy. See Section 4.4.2 for details.
4.4.2 The robust UKF model
Multipath propagation and the complex indoor environment interfere with positioning lead to gross errors during the UKF measurement and updating process. The presence of gross errors can result in decreased positioning accuracy and even the filter may be divergent. In order to reduce this effect, it is reasonable to perform a robust estimation. A robust estimator is a reasonable alternative to obtain reliable parameter estimation in most cases [48,49,50]. We use the robust estimation of the measurement noise matrix Rk, a revised covariance matrix of Rk is defined as \( {\overline{\mathrm{R}}}_k \).
where αk = diag [\( {\upalpha}_1,{\upalpha}_2,\cdots, {\upalpha}_m \)] is an equal weight matrix of observations Zk, m is the dimension of the observation vector Zk at the current time. It can be obtained empirically using the Huber weight function or IGG functions. The IGG III weight function [51] is selected. Namely, the equivalent weight is calculated as [51, 52]:
where \( {k}_0 \) and \( {k}_1 \) are constants, theoretically having the values of \( {k}_0 \)= 2.5~3.5 and \( {k}_1 \) = 3.5~4.5, respectively. In our research, \( {k}_0 \) = 2.5 and k1 = 3.5. si is the normalized residual of the ith observation [53]. Thus, the update process in RUKF is as follows:
where \( {\overline{\mathrm{P}}}_{\mathrm{zz}} \) denotes the observation prediction error covariance matrix and \( {\overline{\mathrm{K}}}_k \)denotes the gain matrix of RUKF.
4.4.3 Outlier and fault judgment
Although the RUKF has corrected some range observation anomalies and somewhat improved the positioning accuracy, positioning accuracy is still quite limited because there is no real-time estimation of system and observation noise due to complex indoor environments and severe multipath propagation, and some outliers may remain in the system. If these outliers are not detected and removed, position estimation will not be optimal and the filter will probably diverge, which reduces the performance of the positioning system. To solve this problem, outlier identification and elimination algorithms are proposed; see Sections 4.4.3.1 and 4.4.3.2 for the details of this process.
The frequency of the appearance of outliers is much higher than the frequency of system fault in the positioning process. If no distinction is made between outliers and faults, it is easy to judge an outlier point in the system as a fault, which will cause system false alarm, increase false alarm rate, and make the system output values discontinuous. In reference to [54], the test statistic at time k exceeds a certain detection threshold (as can be seen from Fig. 4, red line), and it will be considered as an outlier.
Outliers are in the form of an isolated point (a certain moment), while other data in a certain field of k is normal. For a continuous occurrence of test statistic exceeding the detection threshold during a period, it can be considered as a fault. For example, the test statistics exceed the detection threshold at the time kn, and at \( {k}_{n+1} \), \( {k}_{n+2} \), ⋯, both kn + p times exceed the detection threshold (as can be seen from Fig. 4, the elliptical part).
Outlier identification
The innovation of RUKF, rk as shown in Eq. (28), and the covariance matrix of innovation \( {\overline{\mathrm{P}}}_{\mathrm{zz}} \) is given by Eq. (41). The rk and \( {\overline{\mathrm{P}}}_{\mathrm{zz}} \) are used to judge whether each component of observation zk is an outlier. The judgment criterion can be expressed as:
where (i, i) is the ith element on the diagonal of \( {\overline{\mathrm{P}}}_{\mathrm{zz}} \), (rk)i is the ith component of rk. C is constant and determined according to the actual physical background, in our research, C = 3. If Eq. (42) holds, then (zk)i is a normal observation (IF2 = 0 at this time). Conversely, (zk)i is considered to be an outlier (IF3 = 0), where (zk)i is the ith component of zk. If a large number of outliers appear successively, the observation can be considered a fault (IF3 ≠0), and then the system will alert the user in time.
The identification method is simple and feasible, with a clear physical explanation. More importantly, this method can effectively identify which component in an observation that exceeds the error limit, so that the target motion state model and noise statistical characteristics presupposed in advance, can be improved in a targeted manner, thereby improving filtering accuracy.
Outlier elimination
In the UKF, posteriori state estimation \( {\hat{\mathrm{x}}}_k \) is recursively corrected using the difference between new observation zk and predicted observation \( {\hat{\mathrm{z}}}_k^{-} \) (i.e., innovation); thus, the magnitude of the effect of zk on state estimation depends largely on gain matrix \( {\overline{\mathrm{K}}}_k \). Therefore, to get the correct estimate \( {\hat{x}}_k \), zk must be normal. When zk is distorted or includes an outlier, the \( {\overline{\mathrm{K}}}_k \) needs to be adjusted to obtain an accurate estimation \( {\hat{x}}_k \). When the ith component of the observation zk is not satisfied (42), that is, when (zk)i is an outlier, then the \( {\overline{\mathrm{K}}}_k \) is adjusted, so that,
continues to find the filter estimate \( {\hat{\mathrm{x}}}_k \) and the filter estimate posteriori covariance matrix of state vector Pk. Thus, the effect of an outlier point is eliminated when estimating the target parameter.
5 Computational complexity analysis
Computing the number of Floating Point Operations (FLOPs) of an algorithm is an effective method to analyze the computational complexity, especially when matrix operations are involved. One FLOP is an operation to add, subtract, multiply, or divide between two floating points. The number of FLOPs can be considered as a quantitative description of algorithm complexity [55]. In our research, WiFi fingerprinting positioning and PDR are scalar operations, while the UKF algorithm and the integrity monitoring algorithm both involve matrix operations. For the sake of brevity, in this instance, we consider only FLOPs for the UKF and integrity monitoring algorithms and neglect the computationally small, WiFi fingerprinting positioning and PDR scalar operations. The number of FLOPs required for common operations between matrices can be expressed as follows [56, 57]:
-
1.
Matrix addition and subtraction: A ∈ Rn × m, B ∈ Rn × m, then A ± B requires mn FLOPs.
-
2.
Matrix multiplication: A ∈ Rn × m, B ∈ Rm × h, 2mnh − nh FLOPs are required to obtain AB.
-
3.
Matrix inversion: A ∈ Rn × n, A−1 is computed using n3 FLOPs.
-
4.
Cholesky factorization: A ∈ Rn × n,n3/3 FLOPs are required for the chol(A).
The computational complexities of the UKF and the integrity algorithms introduced in this paper were quantitatively analyzed according to these rules.
5.1 UKF algorithm complexity analysis
We denote the total computational complexity in FLOPs by ζ. In the following, m represents the number of dimensions in the state vector in the indoor positioning system, while n represents the number of dimensions in the observation vector. The UKF algorithm complexity analysis, according to the steps in Section 4.3.1, is as follows:
-
1)
In UT transformation, n3/3 + 3n2 FLOPs are needed to generate Sigma sample point X.
-
2)
In the time domain updating, the one-step prediction state vector \( {\upxi}_k^{-} \) of Sigma sample points requires −n + 4n2 FLOPs. The priori state estimation \( {\hat{\mathrm{x}}}_{\mathrm{k}}^{-} \) requires 2n + 2n2 FLOPs, the priori covariance matrix of state vector \( {\mathrm{P}}_k^{-} \) is computed using 2n + 5n2 + 4n3 FLOPs, the observation vector \( {\mathrm{Z}}_k^{-} \) needs n3/3 + 3n2 FLOPs, and the observation prediction vector \( {\hat{\mathrm{z}}}_{\mathrm{k}}^{-} \) requires 2m + 2mn FLOPs.
-
3)
In the measurement updating process, to obtain the observation prediction error covariance Pzz, 2m + 3m2 + 2mn + 4m2n FLOPs are needed, to determine the cross-covariance of the state vector and observation vector Pxz requires 2n + 2mn + 2n2 + 4mn2 FLOPs, the gain matrix Kk of the UKF costs m3 + 2m2n − mn FLOPs, the posteriori state estimation \( {\hat{\mathrm{x}}}_k \) is computed using 2mn + m FLOPs, and the posteriori covariance matrix of state vector Pk needs 2m2n − mn + 2mn2 FLOPs.
Therefore, the total computational complexity of UKF is:
5.2 Integrity monitoring algorithm computational complexity analysis
The integrity monitoring algorithm is designed on the basis of UKF. Therefore, the algorithm computational complexity is higher than that of the UKF regardless of whether any system abnormality is detected. According to Sections 3 and 4.4, the integrity monitoring process can be divided into three phases. As discussed in Section 4.4.1, the gross error detection threshold TD can be calculated in advance. In the first phase (i.e., IBIM), if no system abnormality is detected, only formula (34) participates in the calculation, it costs m3 + 2m2 + m − 1 FLOPs. So the total computational complexity of integrity monitoring at this time can be expressed by the sum of UKF and IBIM FLOPs, i.e.,
If a system abnormality is detected, the RUKF is triggered. At this time, as in Section 4.4.2, the total computational complexity of integrity monitoring algorithm can be expressed as follows:
According to Section 4.4.3.2, if outliers are detected, the total computational complexity of the integrity monitoring is:
6 Experimental evaluation
In this section, two field experiments conducted to evaluate the performance of the proposed algorithm are presented and analyzed. The experimental setup is introduced in detail, and the asymptotic exact computational complexities of the UKF and integrity monitoring algorithm (IM) are analyzed. The implications of results and analysis are discussed.
6.1 Experimental setup
We developed an Android application for the experiments to collect positioning data and analyzed the data with MATLAB (R2019a, The MathWorks, Nitick, MA, USA). The device involved in the experiments was a smartphone running on the Android 8.0 operating system. The phone model was a HUAWEI Honor8 (4GB Ram/64 GB Rom) (Shenzhen, China). To evaluate the performance of the proposed algorithm, two field tests were conducted on the first floor and the third floor of an office building of the Earth Space Information Science International Research Center, Wuhan University. The office building has five floors, and a typical office environment, including corridors, office rooms, and computer rooms. Figure 5 shows the layout of the experiment area and the trajectories of the test true path (blue solid line). The lengths of the two true paths are 124 m and 93 m. The red stars are the locations of the APs. The experimental scene on the first floor includes the corridor, a VIP reception room marked by A as shown in Fig. 5a and a computer room marked by B as shown in Fig. 5a. Also, the experimental scene on the third floor had only the selected corridor, as shown in Fig. 5b.
6.2 Asymptotic and exact computational complexity analysis
We found that the computational complexities depend on state vector dimension (n) and observation vector dimension (m) of the positioning system, based on an analysis of the computational complexities of the UKF and integrity monitoring algorithms as in Section 5. In our research, n is 3 and m is 5. We compared the asymptotic and exact computational complexities of the UKF and the three phases of integrity monitoring in Figs. 6 and 7. In those figures, we plotted the curve of the computational complexity, describing the FLOPs against state vector and observation vector dimensions.
The computational complexity values FLOPs of the UKF and IM-Phase1 are the same when the m is a constant. Figure 6a shows the asymptotic exact computational complexity when the m equals 5, and the n varies from 1 to 60. Figure 6b shows the asymptotic exact computational complexity when the n is 3, and m varies from 1 to 60. It can be seen from Fig. 6a that the computational complexity values FLOPs of the UKF and IM-Phase1 are the same. This implies that under the condition of constant m, the first phase of integrity monitoring has no impact on the overall computational complexity. From Fig. 6b, as the number of dimension in observation vector of indoor positioning system gradually increases (m > 20), the computational complexity values FLOPs of UKF and IM-Phase1 are no longer the same, which indicates that under the condition of constant n, the number of dimension in observation of indoor positioning system gradually increases has a certain effect on the computational complexity of the first phase of integrity monitoring algorithm.
The integrity monitoring algorithm does not substantially increase in overall computational complexity when the number of dimensions in the state vector and observation vector in indoor positioning system is no more than 20. From Fig. 6, we can see that the computational complexity values FLOPs of the UKF, IM-Phase1, IM-Phase2, and IM-Phase3 are almost the same when the m and n are less than 20. The number of dimensions in the state vector and observation vector in the system is less than 20 in most use cases. It illustrates that the integrity monitoring algorithm does not substantially increase in overall computational complexity when the number of dimensions in the state vector and observation vector in indoor positioning system is small (< 20), which also means that the integrity monitoring algorithm has no significant impact on the real-time performance of the positioning system. Figure 7 shows the asymptotic exact computational complexities of the UKF, IM-Phase1, IM-Phase2, and IM-Phase3 when the state vector dimension n and the observation vector dimension m are 20 simultaneously.
It can be seen from Fig. 7 that the overall trend of the computational complexities of these algorithms is consistent with that of Fig. 6, but as the n and m are increasing, the algorithm complexity values FLOPs also increase. Figure 7 again shows that the integrity algorithm does not substantially increase the overall computational complexity when the number of dimensions in the state vector and observation vector in the positioning system is less than 20.
6.3 Experimental results and discussion
The first experiment was conducted on the first floor, the author entered two rooms, the first room is a VIP reception room, the second room is a computer room, and the rest of the test scene was completed in the corridor. Another experiment scenario was the corridor of the third floor. Figure 8 shows the true path of the two sets of experiments, as well as the trajectory of positioning results of WiFi, PDR, UKF, and IM.
The smartphone was always held flat in the two experiments. During the experiment, the WiFi fingerprinting positioning error was relatively stable, and there was no cumulative error over time. In contrast, PDR has a high accuracy within a short distance, but there was a significant cumulative error as walking distance increased. It can be seen from Fig. 8a that PDR positioning accuracy was relatively high at the beginning when the author entered the VIP reception room, the positioning trajectory of PDR deviated from the real trajectory significantly, and the cumulative error was 0.8 m at this time, and 1.8 m when the author arrived at the computer room. In the end, the maximum cumulative error of PDR was 6.49 m. We found that during the third floor experimental test, the average cumulative error of the PDR was less than that on the first floor. That is because the test scene on the first floor is more complicated, and the test route length is larger. Due to the cumulative error of PDR over time, the integrated positioning accuracy declined. However, after using WiFi fingerprinting positioning and IM, the positioning accuracy is improved.
In the first floor experiment, the average positioning errors of WiFi and PDR were 2.37 m and 2.49 m, respectively. The average positioning error after UKF integrated was 1.38 m, while the error using the proposed IM was 1.02 m. The average positioning errors were reduced by 41.7% and 44.6%, respectively, through UKF for WiFi/PDR integration. After applying the IM, the average positioning errors were reduced by 57% and 59%, respectively. In the third floor experiment, the average positioning errors for WiFi and PDR were 2.18 m and 2.16 m, respectively, and the average positioning error after UKF integrated was 1.22 m, while the error with the proposed IM was 0.85 m. After UKF for WiFi/PDR integration, the average positioning errors were reduced by 44.0% and 43.5%, respectively. Applying the IM, the average positioning errors were reduced by 61.0% and 60.6%, respectively.
The Cumulative Distribution Functions (CDF) of positioning errors in two experimental scenes are demonstrated in Fig. 9. The errors at a 95% confidence level for WiFi was 4.35 m and 5.17 m for PDR. For UKF, the error was 2.51 m, and for IM, the error was 1.96 m in the first floor experiment. In the third floor experiment, the error at a 95% confidence level WiFi was 3.69 m; for PDR, the error was 4.54 m, and for UKF, the error was 2.38 m. For IM in the third floor experiment, the error was 1.65 m.
In the IM test, we determine the current integrity phase by setting the integrity flags (IF 1, IF2, and IF3). In each experimental phase of integrity monitoring, we set a corresponding counter. When the corresponding integrity phase is entered, the counter is incremented by one. In test experiments on the first floor and the third floor, the number of times the counter entered the first phase of IM were 38 and 23, respectively; the number of times the counter entered the second phase were 17 and 8, respectively; and the number of times the third phase were 1 and 0 times, respectively. In the last phase of the two experiments, the large cumulative error of PDR resulted in reduced integrated accuracy. In particular, in the last phase of the experiment on the first floor, the cumulative PDR error increased, leading to a continuous increase of error in the integrated positioning results over some time, which triggered the third phase of integrity, an alarm message was sent to the user in time. This demonstrates the ability of IM to warn the user in time when the positioning accuracy does not meet user requirements. After applying our proposed IM algorithm, not only the positioning accuracy and robustness of the system are improved, but also the confidence of the positioning accuracy is guaranteed.
7 Conclusions and future work
This paper presents an integrity monitoring algorithm for WiFi/PDR/smartphone-integrated indoor positioning system based on the UKF. Using UKF for WiFi/PDR integration positioning, we make a tradeoff between computational complexity and positioning accuracy. To this end, our algorithm can be effectively applied to smart terminals such as smartphones. We found that after the UKF integration of WiFi fingerprinting positioning and PDR, the positioning accuracy of the integrated system is higher than the positioning accuracy of WiFi fingerprinting positioning and PDR individually.
The main contribution of this paper is the proposed integrity monitoring algorithm. A RUKF is employed to achieve higher positioning accuracy in the integrity monitoring phase. Besides, a highly feasible and effective method is proposed to identify the outliers and faults of the indoor positioning system. Once a fault is detected, the user will be alerted in time to reduce the potential risk. In safety-sensitive applications of indoor positioning, the timely alarm is an important means to avoid the loss or reduce the risk probability when the positioning accuracy no longer meets the user’s requirements.
Furthermore, by analyzing the computational complexities of the UKF and integrity monitoring algorithm, we concluded that the algorithm does not substantially increase in overall computational complexity when the number of dimensions in the state vector and observation vector in an indoor positioning system is less than 20. In practice, the number of dimensions in the state vector and observation vector in an indoor positioning system rarely exceeds 20. In this sense, our proposed integrity monitoring algorithm is efficient.
Finally, we used a smartphone equipped with the proposed WiFi/PDR-integrated indoor positioning system to collect positioning data and analyzed the experimental results in MATLAB. It is shown that the UKF algorithm with integrity monitoring improved the positioning quality, accuracy, and performance.
In our future work with integrity monitoring algorithms, we will focus on multi-fault detection to tackle isolated, damaged, or problematic WiFi APs for further improving WiFi fingerprinting positioning accuracy. Integrity monitoring will improve the positioning accuracy of the integrated positioning sources and increase the robustness of the integrated positioning system.
Availability of data and materials
The datasets used and analyzed during the current study are available from the corresponding author on reasonable request.
Abbreviations
- IM:
-
Integrity monitoring
- GNSS:
-
Global navigation satellite system
- PDR:
-
Pedestrian dead reckoning
- PF:
-
Particle filter
- KF:
-
Kalman filtering
- EKF:
-
Extended kalman filtering
- UKF:
-
Unscented kalman filter
- RUKF:
-
Robust unscented kalman filter
- LBS:
-
Location-based services
- APs:
-
Access points
- RSSI:
-
Received signal strength indication
- RAIM:
-
Receiver autonomous integrity monitoring
- IBIM:
-
Innovation-based integrity monitoring
- NN:
-
Nearest neighbor
- KNN:
-
k nearest neighbor
- WKNN:
-
Weighted k nearest neighbor
- MAP:
-
Maximum a posteriori
References
O. Garcia, Review for multipath facts in the realm of weak GNSS signal[J]. CADDM 20(2), 92–99 (2010). https://doi.org/10.19583/j.1003-4951.2010.02.014
R.Z. Chen, L. Chen, Indoor positioning with smartphones: the state-of-the-art and the challenges[J]. Act. Geodaetica Cartographica Sin. 46(10), 118–128 (2017)
C. Yang, H.R. Shao, WiFi-based indoor positioning[J]. Commun. Mag. IEEE 53(3), 150–157 (2015)
F. Forno, G. Malnati, G. Portelli, Design and implementation of a Bluetooth ad hoc network for indoor positioning[J]. IEE Proc. Softw. 152(5), 1 (2005)
A. Alarifi, A.M. Alsalman, M. Alsaleh, et al., Ultra wideband indoor positioning technologies: analysis and recent advances[J]. Sensors 16(5), 1–36 (2016)
V. Pasku, A.D. Angelis, G.D. Angelis, et al., Magnetic field-based positioning systems[J]. IEEE Commun. Surv. Tutorials 19(3), 2003–2017 (2017)
X. Wang, M.X. Jiang, Z.W. Guo, N.J. Hu, et al., An indoor positioning method for smartphones using landmarks and PDR. Sensors 16(12) (2016)
J. Torres-Sospedra, A. Jiménez, M. Adriano, et al., Off-line evaluation of mobile-centric indoor positioning systems: the experiences from the 2017 IPIN competition[J]. Sensors 18(2), 487–489 (2018)
Z. Li, J. Liu, F. Yang, et al., A Bayesian density model based radio signal fingerprinting positioning method for enhanced usability[J]. Sensors 18(11), 2135 (2018)
J. Yu, Z. Na, X. Liu, et al., WiFi/PDR-integrated indoor localization using unconstrained smartphones. Wireless Com. Network[J] 41(1) (2019). https://doi.org/10.1186/s13638-019-1365-9
M. Raitoharju, H. Nurminen, R. Piché, Kalman filter with a linear state model for PDR+WLAN positioning and its application to assisting a particle filter[J]. EURASIP J. Adv. Signal Process. 2015(1), 33 (2015)
N. Zhu, H. Zhao, W. Feng, et al., A novel particle filter approach for indoor positioning by fusing WiFi and inertial sensors[J]. Chin. J. Aeronaut. 28(6), 1725–1734 (2015)
Z. Chen, H. Zou, H. Jiang, et al., Fusion of WiFi, Smartphone sensors and landmarks using the Kalman filter for indoor positioning[J]. Sensors 15(1), 715–732 (2015)
R. Zhou, X.Z. Yuan, Y.M. Huang, WiFi-PDR fused indoor positioning based on Kalman filtering. Journal of University of Electronic Science and Technology of China. 45(3), 399–404 (2016). https://doi.org/10.3969/j.issn.1001-0548.2016.02.015
Z.A. Deng, G. Wang, D. Qin, et al., Continuous indoor positioning fusing WiFi, smartphone sensors and landmarks[J]. Sensors 16(9), 1427–1435 (2016)
X. Li, J. Wang, C. Liu, L. Zhang, Z. Li, Integrated WiFi/PDR/smartphone using an adaptive system noise extended Kalman filter algorithm for indoor positioning. ISPRS Int. J. Geo-Information 5(2), 8 (2016). https://doi.org/10.3390/ijgi5020008
A. Melkonyan, S. Yalamanchili, D. Akopian, Integrity monitoring and thresholding-based WLAN indoor positioning algorithm for mobile devices[J]. Int. Conf. Syst. Syst. Eng., 191–196 (2011). https://doi.org/10.1109/SYSOSE.2011.5966596
S.P. Yerubandi, B. Kalgikar, M. Gunturu, et al., Integrity monitoring in WLAN positioning systems[C]// Mobile Multimedia/image Processing, Security, & Applications (International Society for Optics and Photonics, Orlando, Florida, United States, 2009). https://doi.org/10.1117/12.818338
C. Ascher, L. Zwirello, T. Zwick and G. Trommer, Integrity monitoring for UWB/INS tightly coupled pedestrian indoor scenarios, 2011 International Conference on Indoor Positioning and Indoor Navigation, Guimaraes,1-6 (2011) doi:https://doi.org/10.1109/IPIN.2011.6071948
M.J. Rycroft, Understanding GPS. Principles and applications[J]. J. Atmos. Solar-Terrestrial Phys. 59(5), 598–599 (1997)
R.G. BROWN, A baseline GPS RAIM scheme and a note on the equivalence of three RAIM methods[J]. Navigation, 39(3):301-316 (1992). https://doi.org/https://doi.org/10.1002/j.2161-4296.1992.tb02278.x
G.L. Chen, X.L. Meng, Y.J. Wang, et al. Integrated WiFi/PDR/smartphone using an unscented Kalman filter algorithm for 3D indoor positioning[J]. Sensors, 15(9):24595-24614 (2015). https://doi:https://doi.org/10.3390/s150924595
L. Chen, B. Li, K. Zhao, et al., An improved algorithm to generate a WiFi fingerprint database for indoor positioning[J]. Sensors 13(8), 11085–11096 (2013)
B. Li, Y. Wang, H.K. Lee, A. Dempster, C. Rizos, Method for yielding a database of location fingerprints in WLAN. IEE Proc. Commun. 152(5), 580–586 (2005)
O. M. Badawy and M. A. B. Hasan, Decision tree approach to estimate user location in WLAN based on location fingerprinting, 2007 National Radio Science Conference, Cairo, pp. 1-10 (2007)
Y. Sun, Y. Xu, L. Ma, et al. KNN-FCM Hybrid algorithm for indoor location in WLAN. In Proceedings of the 2nd International Conference on Power Electronics and Intelligent Transportation System (PEITS), Shenzhen, China, pp. 251–254 (2009)
P. Davidson, R. Piché, A survey of selected indoor positioning methods for smartphones[J]. IEEE Commun. Surv. Tutorials 19(2), 1347–1370 (2017)
I. Bisio, F. Lavagetto, M. Marchese, et al. Smart probabilistic fingerprinting for WiFi-based indoor positioning with mobile devices[J]. Pervasive Mobile Comput., 31, 107-123 (2016). https://doi.org/https://doi.org/10.1016/j.pmcj.2016.02.001
L. Zheng, J. Liu, Z. Wang, et al. A novel fingerprinting method of WiFi indoor positioning based on Weibull signal model[C]// China satellite navigation academic annual conference. (2018). http://doi:https://doi.org/10.1007/978-981-13-0005-9_25
W. Zhang, X. Hua, W. Qiu, et al., A new combinatorial optimization algorithm for WiFi positioning. Eng. Surveying Mapp. 26, 14–18 (2017)
P. Ling, R. Chen, J. Liu, et al., Inquiry-based bluetooth indoor positioning via RSSI probability distributions[C]// International Conference on Advances in Satellite & Space Communications, Athens. Greece, 151–156 (2010)
N.C. Sagias, G.K. Karagiannidis, Gaussian class multivariate Weibull distributions: theory and applications in fading channels[J]. IEEE Trans. Inf. Theory 51(10), 3608–3619 (2005)
J. Liu, R. Chen, L. Pei, W. Chen, T. Tenhunen, et all. Accelerometer assisted robust wireless signal positioning based on a hidden Markov model. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, USA, 488–497 (2010).
J. Liu et al., Accelerometer assisted robust wireless signal positioning based on a hidden Markov model, IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, 298, 488-497 (2010).
A. Papoulis, J.G. Hoffman, Probability, random variables, and stochastic processes[J]. Phys. Today 20(1), 135–135 (1967)
M.A. Youssef, A. Agrawala, A.U. Shankar, WLAN location determination via clustering and probability distributions. In Proceedings of the First IEEE International Conference on Pervasive Computing and Communications, FortWorth, TX, USA, 143–150 (2003)
T. Roos, K.P. Myllym, H. Tirri, et al., A probabilistic approach to WLAN user location estimation[J]. Int. J. Wireless Inf. Netw. 9(3), 155–164 (2002)
F. Yang, J. Xiong, J.B. Liu, C.Q. Wang, Z. Li, P.F. Tong, R.Z. Chen, A pairwise SSD fingerprinting method of smartphone indoor localization for enhanced usability[J]. Remote Sensing, 11(5), 566 (2019).https://doi.org/https://doi.org/10.3390/rs11050566
F. Li, C.H. Zhao, G.Z. Ding, et al. A reliable and accurate indoor localization method using phone inertial sensors. In Proceedings of the 2012 ACM Conference on Ubiquitous Computing (UbiComp '12). ACM, New York, NY, USA, 421-430 (2012). http://dx.doi.org/https://doi.org/10.1145/2370216.2370280
J. Jahn, U. Batzer, J. Seitz, L. Patino-Studencka and J. Gutiérrez Boronat, Comparison and evaluation of acceleration based step length estimators for handheld devices, 2010 International Conference on Indoor Positioning and Indoor Navigation, Zurich, 1-6 (2010)
A.D. Zhi, H. Ying, et al., Extended Kalman filter for real time indoor localization by fusing WiFi and smartphone inertial sensors[J]. Micromachines 6(4), 523–543 (2015)
H. Weinberg, Using the ADXL202 in pedometer and personal navigation applications; Application Notes AN-602, vol 2 (Analog Devices Inc, Norwood, MA, USA, 2002), pp. 1–6
L. Kling, T. Wark, in Proceedings of the International Conference on Information Processing in Sensor Networks, St louis, MO, USA, 39–50. A wireless sensor network for real-time indoor localisation and motion monitoring (2008)
D. Simon. Optimal state estimation: Kalman, H∞, and nonlinear approaches[M]// Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches. (Wiley-Interscience, 2006), P.297.
H. Sha, F. Tian, D. Wang, et al., A new robust extended Kalman filter method for eliminating the slowly growing pseudo-range error[J]. Guofang Keji Daxue Xuebao/J. Natl. Univ. Defense Technol. 36(5), 131–135 (2014)
U.I. Bhatti, W.Y. Ochieng, S. Feng, Integrity of an integrated GPS/INS system in the presence of slowly growing errors. Part II: analysis[J]. Gps Solut. 11(3), 183–192 (2007)
Y.Y. Qin, H.Y. Zhang, S.H. Wang. Kalman filtering and integrated navigation principle [M]. (Northwestern Polytechnical University Press 2012), P.280.
Y. Yang, Robust estimation of geodetic datum transformation[J]. J. Geodesy 73(5), 268–274 (1999)
Y. Yang, M.K. Cheng, C.K.S. hum, et al., Robust estimation of systematic errors of satellite laser range[J]. J. Geodesy 73(7), 345–349 (1999)
J.L. Wang, J. Wang, Mitigating the effect of multiple outliers on GNSS navigation with M-estimation schemes. IGNSS2007 Symp. on GPS/GNSS, Sydney, Australia, p. 70 (2007)
J. Wang, Y. Gao, Z. Li, X. Meng, et al., A tightly-coupled GPS/INS/UWB cooperative positioning sensors system supported by V2I communication. Sensors[J] 16(7), 944 (2016)
C. Jiang, S. Zhang, Q. Zhang, Equivalent weight function and robust estimation method with adaptive criterion [J]. J. China Univ. Mining Technol.. 46, 911–916 (2017)
Y.X. Yang, Y.Y. Xu, GNSS receiver autonomous integrity monitoring (RAIM) algorithm based on robust estimation. Geodesy Geodynamics 7(2), 117–123 (2016)
Z. Yi, L. Jing-jing, Algorithm of outlier rejecting unscented Kalman filter[J]. Comput. Eng. Appl 48(33), 153–156 (2012)
P.M.W. Gill, J.A. Pople, The prism algorithm for two-electron integrals[J]. Int. J. Quantum Chem. 40(6), 753–772 (1991)
R. Hunger, Floating point operations in matrix-vector calculus. Technische Univ. Münch. Version 1, 16 (2007)
N. Shariati, E. Bjornson, M. Bengtsson, et al., Low-complexity polynomial channel estimation in large-scale MIMO with arbitrary statistics[J]. IEEE J. Selected Topics Signal Proc. 8(5), 815–830 (2014)
Acknowledgements
The authors would like to thank Stephen McClure for his valuable suggestions through the review phase, and thanks to Jinbing Liu and Zhenbing Zhang for their technical support of WiFi fingerprint positioning and PDR. Also, the authors are grateful to four anonymous reviewers for their valuable comments which improved our manuscript.
Funding
This work is supported jointly by the National Key Research Development Program of China (No. 2016YFB0502204 and No. 2017YFB0503604), National Natural Science Foundation of China (No.61971316), and State Key Laboratory of Satellite Navigation System and Equipment Technology. Those funds are mainly used for hardware support.
Author information
Authors and Affiliations
Contributions
HY, HS, ZJ, and BGM proposed the original idea and developed the proposed indoor localization approach. HY wrote the paper. YS developed the user heading estimation algorithm. HY, BGM, and HS analyzed the data and revised the paper. The authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yao, H., Shu, H., Sun, H. et al. An integrity monitoring algorithm for WiFi/PDR/smartphone-integrated indoor positioning system based on unscented Kalman filter. J Wireless Com Network 2020, 246 (2020). https://doi.org/10.1186/s13638-020-01809-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-020-01809-y