Abstract
The natural acoustic system used by marine mammals and the artificial sonar system used by humans coexist in the underwater cognitive sonar communication networks (CSCN). They share the spectrum when they are in the same waters. The CSCN detects the natural acoustic signal depending on cooperative spectrum sensing of sonar nodes. In order to improve spectrum sensing performance of CSCN, the optimization of cooperative spectrum sensing and data transmission is investigated. We seek to obtain spectrum efficiency maximization (SEM) and energy efficiency maximization (EEM) of CSCN through jointly optimizing sensing time, subchannel allocation, and transmission power. We have formulated a class of optimization problems and obtained the optimal solutions by alternating direction optimization and Dinkelbach’s optimization. The simulation results have indicated that SEM can achieve higher spectrum efficiency while EEM may get higher energy efficiency.
Similar content being viewed by others
1 Introduction
Cognitive radio (CR) can improve spectrum utilization greatly through letting secondary user (SU) to access the idle spectrum licensed to the primary user (PU) [1]. However, the SU has to detect the absence of the PU through performing spectrum sensing, in order to guarantee the normal communications of the PU [2]. Energy detection is widely used as an effective spectrum sensing method due to the unnecessary prior information of the detected signal [3]. But the performance of energy detection will decrease if the PU is in fading or shadowing path, which is called “hidden terminal problem.” Cooperative spectrum sensing has been proposed to cope with this problem through letting multiple SUs detect the PU and exchange the sensing information collaboratively [4].
Recently, underwater communication network has attracted the attention, which can be used in underwater environment monitoring and submarine resource exploration. The underwater communication network transmits data using the underwater acoustic channel [5]. However, there are often multiple different underwater acoustic systems in the same water area, which may cause the interference to each other. In order to improve the spectrum utilization, CR has been introduced in the underwater communication network, called as cognitive sonar communication networks (CSCN) [6]. CSCN can use the sonar nodes to detect the presence of the other underwater acoustic systems in the surrounding water environment and transmit data on the premise of detecting the idle underwater acoustic channel. The underwater acoustic environment in the ocean is very complex, and usually, multiple acoustic systems coexist in the same water area, such as artificial echolocation systems, monitoring systems, and the nature acoustic systems of marine mammals [7]. The spectrum sharing of artificial acoustic network system and natural acoustic system will affect the transmission efficiency and the survival of marine mammals. The CSCN can realize the coexistence of a variety of artificial underwater acoustic systems in the protection of marine animals [8]. Thus, in the CSCN, the sonar node and the nature acoustic system can be seen as a SU and a PU, respectively.
Spectrum efficiency is an important index to evaluate the transmission performance of CSCN. Most of the previous works focused on optimizing either cooperative sensing or data transmission to maximize the spectrum efficiency of the CSCN. For instance, the listening-before-transmitting spectrum access is proposed, which can maximize the spectrum efficiency through optimizing sensing time [9]; both [10] and [11] assumed that each SU had a fixed transmission power, which ignored the potential gain of dynamic resource optimization. The water filling algorithm could maximize the spectrum efficiency of multichannel CSCN through optimizing subchannel power [12]. Recently, green communications have attracted the attentions of the scholars. Energy efficiency has been proposed to measure the effectiveness of energy utilization [13].
In this paper, we investigate the joint parameter optimization of cooperative spectrum sensing and data transmission for multichannel CSCN. The contributions of the paper are listed as follows:
-
We seek to maximize spectrum efficiency and energy efficiency of CSCN, respectively, while considering both spectrum sensing performance for detecting the nature acoustic system and the power constraint of each sonar node.
-
We have formulated the cooperative spectrum sensing and data transmission optimization as a class of optimization problems about sensing time, subchannel allocation, and transmission power. In the optimization problem, the nature acoustic system is fully protected, while the transmission performance of the CSCN is improved as much as possible.
-
The joint optimization algorithm is proposed to obtain the solutions to the optimization problems, which is based on the alternating direction optimization and the Dinkelbach optimization.
2 System modeling
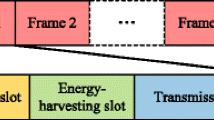
We consider L nature acoustic systems occupying L subchannels, which are seen as PUs and a CSCN constituting of N sonar nodes, which are seen as SUs. We also suppose that in an artificial acoustic system, there is an access point that controls the channel usage of the SUs in the locating water, which can be seen as a fusion center. In order to avoid causing harmful interference to the PU, the SU has to detect the utilization state of the licensed spectrum and decide the activation of the PU. Hence, the periodic cooperative spectrum sensing based on “listening before transmitting” is proposed in this paper, which divides the communication time into several frames, each of which constitutes of three time slots including local sensing slot, cooperative interaction slot, and data transmission slot, as shown in Fig. 1. In the local sensing slot, all the SUs sense the activation of the PU in L subchannels and obtain the local sensing information.
Then, in the cooperative interaction slot, each SU uses one common channel to report the local sensing information to the fusion center, which makes a final decision on the activation of the PU by the soft-decisional combination of the local sensing information. To avoid the mutual interference, the SUs cannot report from the common channel simultaneously at the same time. Hence, in order to save the bandwidth of the common channel, the SU adopts time division multiple access (TDMA) to report the local sensing information. Finally, in the data transmission slot, the SUs access the licensed spectrum to communicate according to the decision result of the fusion center.
2.1 Underwater acoustic channel model
The fusion center maintains a collection of free channels and the corresponding channel gain matrix in the underwater acoustic region by scanning and spectrum sensing. Supposing that h n,l is the channel gain of SU n using subchannel l, the channel gain matrix H, can be given by
Due to the reflection of the sea surface, submarine, and underwater medium, there are complicated multipath propagation in shallow sea acoustic channel, which can be considered as generalized uncorrelated scattering condition in general wireless channel. When the number of multipaths is relatively large, the underwater acoustic channel obeys the Rayleigh distribution. Thus, the channel gain distribution is given by
where \(\bar {h}_{n,l}\) is the statistical average of h n,l .
2.2 Cooperative spectrum sensing
The sensing signal of SU n for n=1,2,…,N in subchannel l for l=1,2,…,L, y n,l (m), is denoted as follows:
where θ l =0 and θ l =1 denote the absence and presence of the PU in subchannel l, respectively; h n,l denotes the subchannel gain from SU n to the PU; \(p^{s}_{l}\) is the transmission power of the PU in subchannel l; \(\sigma _{l}^{2}\) is the power of the noise in subchannel l; and M is the number of the samplings. M is given by M=τ f s , where τ is the local sensing time and f s is the sampling frequency. We can get the energy statistic of the sensing signal y n,l by accumulating the energy of M samplings as follows:
Each SU reports ψ n,l to a fusion center, which combines ψ n,l of N SUs to get an overall energy statistic of the PU signal in subchannel l as follows:
The overall energy statistic Ψ l is compared with a threshold λ. If Ψ l ≥λ, the presence of the PU is detected; otherwise, the absence of the PU is determined. When M is large enough, Ψ l obeys the Gaussian distribution approximatively according to the central limit theorem. Hence, the cooperative probabilities of false alarm and detection for subchannel l is given as follows:
where \(\bar {\gamma }_{l}=\frac {1}{N} {\sum _{n=1}^{N} {\frac {p^{s}_{l} h_{n,l}^{2}}{\sigma _{l}^{2}}}}\) is the average sensing SNR of N SUs in subchannel l, and the function \(Q(x)=\frac {1}{\sqrt {2\pi }}\int _{x}^{+\infty }\exp \left (-\frac {z^{2}}{2}\right) \ \mathbf{d} z\).
In order to avoid causing harmful interference to other underwater acoustic systems, the detection probability must be guaranteed. The sensing threshold λ can be obtained by fixing \(Q^{d}_{l}\) with some value, which is given as follows:
The selection of sensing threshold is important to the sensing performance. The detection probability will improve with the increasing of sensing threshold; however, the false alarm probability will also increase, thus decreasing the spectrum access probability. Through removing the threshold λ, \(Q^{f}_{l}\) is denoted by \(Q^{d}_{l}\) as follows:
In underwater, since the channel between the signal source and the sonar is often in severe fading, the received signal by one sonar may be too weak to be detected accurately. However, with cooperative spectrum sensing, the same signal can be received by multiple sonars from different paths. If the received signal by one sonar is too weak, the detection performance cannot be decreased through sharing the sensing information with the other sonars. Thus, the sensing diversity gain can be achieved to improve the final detection performance through cooperative spectrum sensing.
2.3 Spectrum efficiency maximization (SEM)
Spectrum efficiency is an important indicator to evaluate the spectrum sensing performance. In spectrum sensing, the decreasing of detection performance may decrease the spectrum access opportunity of the SU because of the increasing false alarm probability; however, improving detection performance needs to increase the sensing time, which decreases the data transmission time. Hence, we need to optimize the sensing parameters to maximize the spectrum efficiency. The SU can transmit data effectively only when the absence of the PU is detected accurately. The accurate idle detection probability of subchannel l is \(P_{r}(\theta _{l}=0)\left (1-Q^{f}_{l}\right)\), and the transmission rate of SU n in subchannel l is given by \( R_{n,l}=a_{n,l}\log \left (1+\frac {p_{n,l} g_{n,l}^{2}}{\sigma _{l}^{2}}\right)\), where a n,l ={0,1} denotes whether subchannel l is allocated to SU n, p n,l indicates the transmission power of the SU n in subchannel l, and g n,l denotes the subchannel gain between receiver and transmitter of SU n. Supposing the frame duration is T and the length of each cooperative interaction slot is ε, the overall spectrum efficiency of N SUs over L subchannels is given as follows:
Our goal is to maximize the spectrum efficiency of the SU by jointly optimizing sensing time, subchannel allocation, and transmission power, subject to the constraints that the detection probability is above the lower limit \(Q_{d}^{\text {min}}\), the total power of SU n is below the maximal power \(p^{\text {max}}_{n}\), and one subchannel is only allocated to one SU. Supposing the spectrum sensing power is p c , the optimization problem of SEM is given as follows:
For simplifying the optimization problem (10), we relax the integer a n,l with any value within [0,1] and let ω n,l =a n,l p n,l . Then, we have \(R_{n,l}=a_{n,l}\log \left (1+\frac {\omega _{n,l} g_{n,l}^{2}}{a_{n,l} \sigma _{l}^{2}}\right)\). From (8) and (9), η SE improves with the decreasing of \(Q^{f}_{l}\) while \(Q^{f}_{l}\) reduces with the decreasing of \(Q^{d}_{l}\). Hence, η SE may reach the maximum only when \(Q^{d}_{l} = Q_{d}^{\text {min}}\). The optimization problem is rewritten as follows:
where \(\kappa =Q^{-1}(Q_{d}^{\text {min}})(\bar {\gamma }_{l}+1)\) and \(\hat {p}^{\text {max}}_{n}=p^{\text {max}}_{n}-p_{c}\). Then, we will give the following theorem.
Theorem 1
Problem (11) is a convex optimization problem.
Proof
We often let \(Q_{f}^{l}\leq 0.5\) and then have \(\kappa +\bar {\gamma }_{l}\sqrt {N \tau f_{s}}\geq 0\). Fixing R n,l , We can get the secondary derivative of η SE in τ as follows:
which indicates that η SE is convex in τ. Moreover, R n,l is obviously convex in (a n,l ,ω n,l ). Since η SE is the nonnegative linear combination of R n,l , η SE is also convex in ({a n,l },{ω n,l }). Hence, η SE is a convex optimization problem about (τ,{a n,l },{ω n,l }). □
We use the alternating direction optimization (ADO) to get the solution to the optimization problem. Firstly, fixing τ, we optimize (a n,l ,ω n,l ). Using the Lagrange multiplier, the optimization function is given by
where \(\rho _{l}=P_{r}(\theta _{l}=0)\left (1-Q^{f}_{l}\right)\) is constant and μ n for n=1,…,N and ν l for l=1,…,L are the Lagrange multipliers. Through calculating \(\frac {\partial \Gamma }{\partial a_{n,l}}=0\) and \(\frac {\partial \Gamma }{\partial \omega _{n,l}}=0\), we have
where \(\Phi _{n,l}(\mu _{n})=\rho _{l} \left (\log \left (\frac {g_{n,l}^{2}}{\mu _{n} \sigma _{l}^{2}}\right)+\frac {\mu _{n} \sigma _{l}^{2}}{g_{n,l}^{2}}-1\right)\). Then, the Lagrange multipliers μ n and ν l can be obtained by using the gradient method that leads to the following update equations
where t≥0 is the iteration index and ζ 1(t) and ζ 2(t) are both the positive step sizes. Then, the updated Lagrange multipliers in (16) is used for updating the power allocation in (14). Secondly, we fix R n,l with the optimized (a n,l ,ω n,l ). Using the Newton iteration method, we can get the optimal τ through iteratively updating τ {k} until it is convergent, as follows:
where k≥0 is the iteration index. As mentioned above, we use ADO to optimize (a n,l ,ω n,l ) and τ alternatively until a n,l , ω n,l , and τ are all convergent, as shown in Algorithm 1. Then, if a n,l =0, the transmission power p n,l =0; otherwise, \(p_{n,l}=\frac {\omega _{n,l}}{a_{n,l}}\). Since η SE is convex in τ, a and ω, η SE is non-decreasing during each iteration, which is described as follows:

Hence, the convergence of η SE can be obtained after some iterations.
Supposing the estimation error is δ, η SE will be convergent when τ (k),{a n,l }(k), and {ω n,l }(k) are all convergent. Thus, the iterative complexity of the joint optimization algorithm is given by \(O\left (\frac {1}{\delta ^{3}}\right)\).
2.4 Energy efficiency maximization (EEM)
Compared to the traditional communication system, the SU may consume more energy due to spectrum sensing power. Thus, we use energy efficiency to evaluate the energy consumption of cooperative spectrum sensing. We define the energy efficiency as spectrum efficiency to energy consumption ratio. The consumed total energy for spectrum sensing and data transmission within unit time is given by
Hence, the energy efficiency of cooperative spectrum sensing is given by
We seek to maximize η EE by jointly optimizing {τ,{a n,l },{ω n,l }}. The optimization problem of EEM is given by
We have proven η SE(τ,{a n,l },{p n,l }) to be a continuous positive convex function. As E T (τ,{a n,l },{p n,l }) is a linear positive function, we can solve the optimization problem (21) by the Dinkelbach optimization [14].
Setting \(q=\frac {\eta _{\text {SE}}(\tau,\{a_{n,l}\},\{p_{n,l}\})}{E_{T}(\tau,\{a_{n,l}\},\{p_{n,l}\})}\), the optimization problem (21) can be rewritten as follows:
Supposing the feasible region of the solutions to (21) is denoted as S, the joint optimization algorithm based on the Dinkelbach optimization is described in Algorithm 2.

3 Simulations and discussions
In the simulations, the number of SUs is N=10, the number of subchannels is L=32, the channels obey the Rayleigh distribution with the mean −10 dB, the absence probability of the PU is P r (θ l =0)=0.5, the frame duration is T=100 ms, the length of cooperative interaction slot is ε=1 ms, the sampling frequency is f s =100 KHz, the maximal power of each SU is \(p_{n}^{\text {max}}=10\) mW, the sensing power p c =1 mW, and the noise power is \(\sigma _{l}^{2}=0.01\) mW.
Figures 2 and 3 show spectrum efficiency η SE and energy efficiency η EE varying with sensing time τ, respectively. We can see that there exists an optimal τ to maximize η SE or η EE. When τ is smaller, the detection performance will degrade to decrease the spectrum access; however, when τ is larger, both transmission time and transmission energy will decrease. Thus, there is a tradeoff between spectrum sensing and data transmission. We also see that η SE and η EE improve as detection probability decreases and sensing SNR increases. Figures 4 and 5 compare spectrum efficiency and energy efficiency of SEM and EEM, respectively. We can see that SEM can obtain higher spectrum efficiency while EEM may achieve higher energy efficiency, due to the different optimization objectives of SEM and EEM.
Then, we use power utilization ratio ρ to describe the usage of power in CSCN, which represents the power consumption required to accomplish the desired communication task when the maximum power is limited. ρ can be formulated as the ratio of the total consumed power to the total transmission power, as follows:
Figure 6 indicates the power utilization ratio comparison with detection probability. It can be seen that, as Q d grows, the power utilization ratio of SEM is always 100%. SEM only focuses on maximizing spectrum efficiency and ignores the power consumption. Thus, it tends to use the entire power to maximize the spectrum efficiency during the optimization, leading to the 100% power utilization ratio. However, in EEM, the power consumption gains lots of attention and the power utilization ratio always keeps a low level, which indicates that detection performance is improved via setting a limit to the power consumption. Figure 7 shows the power utilization ratio comparison with maximal power. It is seen that EEM can also achieves higher power utilization compared with SEM.
4 Conclusions
In this paper, we have maximized spectrum efficiency and energy efficiency of periodic cooperative spectrum sensing for multichannel CSCN, respectively, through formulating optimization problems and jointly optimizing sensing time, subchannel allocation, and transmission power. We have got the following conclusions: (1) there is a tradeoff between spectrum sensing and data transmission; (2) SEM can obtain higher spectrum efficiency while EEM may achieve higher energy efficiency.
References
J Mitola, Cognitive radio for flexible mobile multimedia communications. Mob. Netw. Appl. 6(5), 435–41 (2001).
M Jia, X Gu, Q Guo, W Xiang, N Zhang, Broadband hybrid satellite-terrestrial communication systems based on cognitive radio toward 5G. IEEE Wirel. Commun. 23(6), 96–106 (2016).
J Shen, S Liu, Y Wang, Robust energy detection in cognitive radio. IET Commun. 3(6), 1016–23 (2009).
X Liu, J Min, X Tan, Threshold optimization of cooperative spectrum sensing in cognitive radio network. Radio Sci. 48(1), 23–32 (2013).
P Casari, M Zorzi, Protocol design issues in underwater acoustic networks. Comput. Commun. 34(17), 2013–2015 (2011).
AA Syed, W Ye, J Heidemann, in Proc. IEEE 27th Conf. Comput. Commun. (INFOCOM). T-Lohi A new class of MAC protocols for underwater acoustic sensor networks (IEEE, Phoenix, 2008), pp. 231–235.
M Stojanovic, On the relationship between capacity and distance in an underwater acoustic communication channel. ACM SIGMOBILE Mobile Comput. Commun. Rev. 11(4), 34–43 (2007).
JR Nedwell, J Lovell, AW Turnpenny, Experimental validation of a species-specific behavioral impact metric for underwater noise. J. Acoust. Soc. Amer. 118(3), 2019 (2005).
X Liu, X Tan, Optimization algorithm of periodical cooperative spectrum sensing in cognitive radio. Int. J. Commun. Syst. 27(5), 705–20 (2014).
YC Liang, Y Zeng, ECY Peh, Sensing-throughput tradeoff for cognitive radio networks. IEEE Trans. Wirel. Commun. 7(4), 1326–36 (2008).
R Fan, H Jiang, Optimal multi-channel cooperative sensing in cognitive radio networks. IEEE Trans. Wirel. Commun. 9(3), 1128–38 (2010).
P He, L Zhao, S Zhou, Z Niu, Water-filling: a geometric approach and its application to solve generalized radio resource allocation problems. IEEE Trans. Wirel. Commun. 12(7), 3637–47 (2013).
X Liu, M Jia, X Gu, J Yan, J Zhou, Optimal spectrum sensing and transmission power allocation in energy-efficiency multichannel cognitive radio with energy harvesting. Int. J. Commun. Syst. 30(5), 1–15 (2017).
W Zhong, K Chen, X Liu, Joint optimal energy-efficient cooperative spectrum sensing and transmission in cognitive radio. China Commun. 14(1), 98–110 (2017).
Acknowledgements
This work was supported by the National Natural Science Foundations of China under Grant Nos. 61601221, 91438205, and 61671183; the Natural Science Foundations of Jiangsu Province under Grant No. BK20140828; the China Postdoctoral Science Foundations under Grant No. 2015M580425; the Fundamental Research Funds for the Central Universities under Grant No. DUT16RC(3)045; and the Open Research Fund of State Key Laboratory of Space-Ground Integrated Information Technology under Grant No. 2015_SGIIT_KFJJ_TX_02.
Author information
Authors and Affiliations
Contributions
XL conceived and designed the study. MJ performed the simulation experiments. XL wrote the paper. MJ reviewed and edited the manuscript. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, X., Jia, M. Cooperative spectrum sensing and data transmission optimization for multichannel cognitive sonar communication network. J Wireless Com Network 2017, 171 (2017). https://doi.org/10.1186/s13638-017-0962-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-017-0962-8