Background

Cellular biomechanics can be manipulated by strong electric fields. For example, undulation can be induced on a poorly conductive membrane [1] by an electric field. Tension and poration can be generated in the cell membranes by a microelectrode close to a cell [2]. As a consequence, the cell membrane undergoes geometrical changes. Strong direct current (DC) electric fields cause deformation in the cell membrane with predicable patterns [3, 4]. Stem cells derived from human adipose tissue elongated inside a DC electric field, in a direction that is perpendicular to the field [5]. Electric field-induced mechanical signals can be transferred into the biological system and cause a diversity of biological responses, including cell proliferation and apoptosis, hypertrophy (increased cell size), extracellular matrix remodeling, and DNA/RNA synthesis [6].

A DC electric field can also cause cell migration, which has significant impact on normal cellular physiology. The first observation that cells can migrate inside an applied electric field, or galvanotaxis, was reported nearly a century ago [7]. It has been suggested that mechanic forces generated on the cell could be partially responsible for cell migration in the electric field [8]. Cell electrophoresis is a method for estimating the surface charge of a cell by looking at its rate of movement in a DC electrical field [9]. It has been widely used for the characterization of the surface properties of the membrane, as well as for the separation of uniform cell subpopulations in a cell mixture [9]. In addition, electric fields are used for axonal guidance [10, 11], and migration of stem cells [12] or neurons within neural networks [13].

To investigate the cellular biomechanics under electric fields, investigators use artificially generated giant vesicles, which mimic the phospholipid bilayer in the cell membrane [14, 15]. These vesicles are usually formed with neutral molecules including L-a-phosphatidylcholine [15,16,17]. Similar to biological cells, vesicles deformed in a very strong DC field [16]. Vesicles exposed to the DC electric pulses can be deformed into elliptical [18] or cylindrical shapes [15]. Deformation of the vesicle depends on the “conductivity ratio” between the cytoplasm and the extracellular medium. The vesicle elongates in the field direction along its axis (prolate) if the cytoplasmic conductivity is higher than the medium. Conversely, the vesicle shortens (oblate) in the field direction if the medium is more conductive. Theoretical works have been proposed to investigate this interior-to-exterior conductivity ratio-dependent membrane deformation, using analytical [15, 19, 20] or numerical methods [21,22,23]. Interestingly, vesicle migration has not been observed in the strong DC electric field (2.0 Kv/cm), despite the observed electroporation and pore formation on the membrane [16].

We use a modeling approach to reconcile the kinematic difference between a biological cell and a vesicle under a DC electric field, with a “shell-like” membrane structure that separates the extracellular medium from the cytoplasm. We analyzed the biomechanics of this 3D structure by computing the steady-state pressure and forces imposed on the fixed membrane surface by the DC electric field. The model confirms the impact of the conductivity ratio on the buildup of the electric pressure on the membrane. The model suggests that the kinematic difference between the vesicle and the biological cell inside a DC electric field can be explained by the lack of charged molecules in the vesicle membrane.

Methods

“Shell model’ of a spherical vesicle/cell in a DC electric field

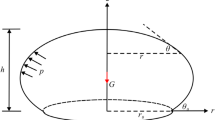
Figure 1 illustrates the configuration of a modeled vesicle/cell inside the extracellular medium (0#). The model contains a spherical membrane shell (1#) and intracellular cytoplasm (2#). The center of the sphere is at point O. To simplify calculations, we assume that each modeled region is electrically homogenous and isotropic. The dielectric permittivities and the conductivities in the three regions are ε 0, ε 1, ε 2 and σ 0, σ 1, σ 2, respectively. The inner and outer radii of the membrane are R_ and R +, respectively. The membrane thickness is d = R +-R_. The cell is exposed to a uniform external field \( \overrightarrow{E}=E\overrightarrow{Z} \), where \( \overrightarrow{Z} \) is the unitary vector in the direction of the external field. Similar model configurations have been used to study the bioelectricity of cells under electromagnetic field exposure [24,25,26].

Fig. 1
figure 1

The spherical vesicle/cell model and the spherical coordinate system (r, θ, ϕ). The vesicle/cell model includes three homogenous, isotropic regions: the extracellular medium, the membrane, and the cytoplasm. The axis of the electric field overlaps with the OZ axis

Full size image

Model parameters

Table 1 summarizes the parameters for the model, which are chosen from previous publications [27, 28]. These parameters include geometrical and electrical parameters of the cell and the medium. The electric field intensity was 200,000 V/m, sufficient to deform the cell membrane [15, 16].

Table 1 Model parameters
Full size table

Equations and boundary conditions

Expression of electric potentials in the extracellular medium, the membrane, and the cytoplasm are obtained by solving Laplace’s equation [29] with appropriate boundary conditions

$$ {\nabla}^2V=0 $$
(1)

Several boundary conditions are considered in the model: (1) Across the boundary of two different media, electric potential is continuous; (2) Across the boundary of two different media, the normal component of the current density is continuous. To account for the dielectric permittivity of the material, “complex conductivity”, defined as S = σ + jωε, was used [26, 30]. ω is the angular frequency. It is zero for the DC electric field. \( j=\sqrt{-1} \) is the imaginary unit. Therefore, across the extracellular medium/membrane interface (0#1#),

$$ {S}_0{E}_{0r}-{S}_1{E}_{1r}=0 $$
(2)

Across the membrane/cytoplasm interface (1#2#),

$$ {S}_1{E}_{1r}-{S}_2{E}_{2r}=0 $$
(3)

where S 0 = σ 0 + jωε 0 , S 1 = σ 1 + jωε 1 , S 2 = σ 2 + jωε 2. (3) Presence of the vesicle/cell in the electric field does not perturb field distribution at an infinite distance; and (4), the electric potential inside the vesicle/cell is finite.

In spherical coordinates (r, θ, ϕ), expressions of electric fields are given by

$$ \overset{\rightharpoonup }{E}=-\nabla V=-\left(\frac{\partial V}{\partial r},\frac{1}{r}\frac{\partial V}{\partial \theta },\frac{1}{r\sin \theta}\frac{\partial V}{\partial \varphi}\right) $$
(4)

Surface charge distribution and mechanical pressure on the “shell”

Under electromagnetic exposure, free charges accumulate on the interface of the two inhomogeneous media [31]. At the 0#1# interface (r = R+), the surface charge density is \( {\rho}_{s01}=\overrightarrow{n}\bullet \left({\varepsilon}_1{\overrightarrow{E}}_1-{\varepsilon}_0{\overrightarrow{E}}_0\right) \) or

$$ {\rho}_{s01}\left(R,\theta, \phi \right)={\varepsilon}_1{E}_{1r}-{\varepsilon}_0{E}_{0r} $$
(5)

At the 1#2# interface (r = R−), the surface charge density is \( {\rho}_{s12}=\overrightarrow{n}\bullet \left({\varepsilon}_2{\overrightarrow{E}}_2-{\varepsilon}_1{\overrightarrow{E}}_1\right) \) or

$$ {\rho}_{s12}\left(R,\theta, \phi \right)={\varepsilon}_2{E}_{2r}-{\varepsilon}_1{E}_{1r}, $$
(6)

where \( \overrightarrow{n} \) denoted the outward unit normal vector.

Interaction between the free charges and the electric field produces electric pressure, whose radial component can be calculated as the product of the charge density and the averaged electric field on both sides of the interface surface [29]. Quantitatively significant pressure produced by high-intensity electric field could cause cell membrane deformation [32]. On the 0#1# interface (r = R+), the radial pressure is

$$ {\rho}_{r01}=\frac{1}{2}\left({E}_{0r}+{E}_{1r}\right){\rho}_{s01} $$
(7)

On the 1#2# interface (r = R−), the radial pressure is

$$ {\rho}_{r12}=\frac{1}{2}\left({E}_{1r}+{E}_{2r}\right){\rho}_{s12} $$
(8)

Since the membrane is thin and uncompressible, the net radial electric stress is computed as [33]

$$ {P}_r={P}_{r01}+{P}_{r12} $$
(9)

Results

Analytical solutions for the electric fields and surface charges

Laplace’s equation was solved with boundary conditions (1–4) to yield the expression of the electric potentials (Additional file 1). The potential distributions in the three regions are

$$ {V}_0=\left(\frac{1}{r^2}\frac{3{S}_0\left(2{S}_1+{S}_2\right){R}_{+}^6+3{S}_0\left({S}_1-{S}_2\right){R}_{+}^3{R}_{-}^3}{2\left({S}_1-{S}_0\right)\left({S}_1-{S}_2\right){R}_{-}^3-\left({S}_1+2{S}_0\right)\left(2{S}_1+{S}_2\right){R}_{+}^3}+\frac{R_{+}^3}{r^2}-r\right)E\cos \theta $$
(10.1)
$$ {V}_1=\frac{3{S}_0{R}_{+}^3\left[r\left(2{S}_1+{S}_2\right)+\left({S}_1-{S}_2\right)\frac{R_{-}^3}{r^2}\right]}{2\left({S}_1-{S}_0\right)\left({S}_1-{S}_2\right){R}_{-}^3-\left({S}_1+2{S}_0\right)\left(2{S}_1+{S}_2\right){R}_{+}^3}E\cos \theta $$
(10.2)
$$ {V}_2=\frac{9{S}_0{S}_1{R}_{+}^3r}{2\left({S}_1-{S}_0\right)\left({S}_1-{S}_2\right){R}_{-}^3-\left({S}_1+2{S}_0\right)\left(2{S}_1+{S}_2\right){R}_{+}^3}E\cos \theta $$
(10.3)

We further calculate the electric field distribution in the extracellular space, the shell membrane, and the cytoplasm using Eq. (4). The expressions for the electric field around the cell, in the extracellular medium (0#) are:

$$ {E}_{0r}=\left[1-\frac{2{R}_{+}^3}{r^3}\frac{R_{-}^3\left({S}_0+2{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left({S}_0-{S}_1\right)\left(2{S}_1+{S}_2\right)}{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}\right]E\cos \theta $$
(11.1)
$$ {E}_{0\theta }=-\left[1+\frac{R_{+}^3}{r^3}\frac{R_{-}^3\left({S}_0+2{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left({S}_0-{S}_1\right)\left(2{S}_1+{S}_2\right)}{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}\right]E\sin \theta $$
(11.2)
$$ {E}_{0\varphi }=0 $$
(11.3)

The electric fields inside the membrane (1#) are:

$$ {E}_{1r}=\frac{3{R}_{+}^3}{r^3}\frac{S_0\left[2{R}_{-}^3\left(-{S}_1+{S}_2\right)+{r}^3\left(2{S}_1+{S}_2\right)\right]}{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}E\cos \theta $$
(12.1)
$$ {E}_{1\theta }=-\frac{3{R}_{+}^3}{r^3}\frac{S_0\left[{R}_{-}^3\left({S}_1-{S}_2\right)+{r}^3\left(2{S}_1+{S}_2\right)\right]}{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}E\sin \theta $$
(12.2)
$$ {E}_{1\varphi }=0 $$
(12.3)

The electric fields inside the cytoplasm (2#) are:

$$ {E}_{2r}=\frac{9{S}_0{S}_1{R}_{+}^3}{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}E\cos \theta $$
(13.1)
$$ {E}_{2\theta }=-\frac{9{S}_0{S}_1{R}_{+}^3}{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}E\sin \theta $$
(13.2)
$$ {E}_{1\varphi }=0 $$
(13.3)

From Eq. (5), the electrically-induced charge density on the 0#1# interface is (Additional file 2)

$$ {\rho}_{s01}\left(R,\theta, \varphi \right)=-\frac{3\left[2{R}_{-}^3\left({S}_1-{S}_2\right)-{R}_{+}^3\left(2{S}_1+{S}_2\right)\right]}{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}\left({S}_1{\varepsilon}_0-{S}_0{\varepsilon}_1\right)E\cos \theta $$
(14.1)

One the 1#2# interface (Additional file 3)

$$ {\rho}_{s12}\left(R,\theta, \varphi \right)=-\frac{9{R}_{+}^3{S}_0}{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}\left({S}_2{\varepsilon}_1-{S}_1{\varepsilon}_2\right)E\cos \theta $$
(14.2)

Figure 2 illustrates the surface charge distributions on these two interfaces, which depend on the orientation of the cell to the electric field (i.e., cos θ term). The densities of the induced surface charges are also functions of the electric properties of the medium, the membrane, and the cytoplasm. The two pole areas carry the greatest density of induced charges. Since the cos θ term presents in both Eqs. (14.1) and (14.2), charge distribution on both 0#1# interface (Fig. 2a) and 1#2# interface (Fig. 2b) are similar. However, charges carried by the two interfaces have different polarities at the same location (latitude and longitude).

Fig. 2
figure 2

Electrically-induced surface charge distribution on the a medium/membrane interface (ρs01) and b membrane/cytoplasm interface (ρs12). Membrane thickness is exaggerated to show the inner and outer membrane interfaces. The plot demonstrates the geometrical pattern of the induced surface charge distribution in the DC electric field. The orientation of the shell structure to the field is the same as that shown in Fig. 1. The color represents the amount of the charge density (C/m2) calculated with σ0 = 0.3 S/m and σ2 = 1.2 S/m and E = 200,000 V/m

Full size image

Surface charge density is a function of the field intensity. We compute the maximal surface charge (at θ=0) with parameters presented in Table 1 (E = 200,000 V/m, σ0 = 0.3 S/m and σ2 = 1.2 S/m). The induced charge density is −0.025 C/m2 on the 0#1# interface, and is 0.025 C/m2 on the 1#2# interface. Those values are comparable to the charge density carried by the intrinsic membrane proteins [8, 34].

Since induced charges are restricted on the membrane surface [35], the net induced charge should be zero on both the 0#1# and 1#2# interfaces. This could be confirmed by integrating the surface charge density over the whole surface area.

$$ {Q}_{s01}=\underset{\theta, \phi }{\iint }{\rho}_{s01}{da}_{01}=\underset{\theta, \phi }{\iint }{\rho}_{s01}{R}_{+}^2\sin \theta d\theta d\phi =0 $$
(15.1)
$$ {Q}_{s12}=\underset{\theta, \phi }{\iint }{\rho}_{s12}{da}_{12}=\underset{\theta, \phi }{\iint }{\rho}_{s12}{R}_{-}^2\sin \theta d\theta d\phi =0 $$
(15.2)

Here, \( d{\overset{\frown }{a}}_{01}={R}_{+}^2\sin \theta d\theta d\phi \overset{\frown }{r} \) is the surface element on the 0#1# interface and \( d{\overset{\frown }{a}}_{12}={R}_{\_}^2\sin\ \theta d\theta d\phi \overset{\frown }{r} \) is the surface element on the 1#2# interface in the \( \overset{\frown }{r} \) direction.

Steady state radial pressure

Mechanical pressure can be generated when the electric field interacts with the induced surface charges [32]. The pressure on the radial \( \overset{\frown }{r} \) direction is essential for cytoskeletal compression and extension [32]. On the 0#1# interface, the steady state radial pressure is (Additional file 2)

$$ {P}_{r01}=-\frac{9{E}^2\left({S}_0+{S}_1\right){\left[{R}_{+}^3\left(2{S}_1+{S}_2\right)-2{R}_{\_}^3\left({S}_1-{S}_2\right)\right]}^2}{2{\left[2{R}_{\_}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)\right]}^2}\left({S}_0{\varepsilon}_1-{S}_1{\varepsilon}_0\right){\mathrm{cos}}^2\theta $$
(16.1)

On the 1#2# interface, it is expressed as (Additional file 3)

$$ {P}_{r12}=-\frac{81{E}^2{R}_{+}^6{S}_0^2\left({S}_1+{S}_2\right)}{2{\left[2{R}_{\_}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)\right]}^2}\left({S}_1{\varepsilon}_2-{S}_2{\varepsilon}_1\right){\mathrm{cos}}^2\theta $$
(16.2)

Figure 3 illustrates the radial pressure distribution on both sides of the “shell” membrane. The chosen parameters are σ0 = 0.3 S/m, σ2 = 1.2 S/m and E = 200,000 V/m. The pressure on the outer membrane surface compresses the membrane (Fig. 3a), while the pressure on the inner membrane surface stretches and expands the membrane (Fig. 3b). On both membrane interfaces, the maximal pressure was generated on the two poles (θ = 0 or π).

Fig. 3
figure 3

Distribution of the radial pressure (arrows) on the a medium/membrane interface (Pr01) and on the b membrane/cytoplasm interface (Pr12). Color represents surface charges as defined in Fig. 2. Parameters are the same as in Fig. 2. Bottom: zoom-in views

Full size image

Dependency of net radial pressure on medium conductivity

We calculate the net pressure on the fixed membrane structure (Eq. (9), also see Additional file 4). For E = 200,000 V/m, the maximal magnitude of the pressure is 3 × 104 N/m2. This computed result is significant in comparison with those used for membrane deformation, including atomic force microscopy (AFM), optical trapping, micropipette aspiration and magnetic bead mocrorheology (twisting and pulling) [6].

Previous research indicates that the compressing/pulling pressure on the cell membrane could change its direction, depending on the ratio between the conductivities of the medium and the cytoplasm. The pressure is pulling if the cytoplasm is more conductive and compressing if the medium is more conductive [14, 19]. We used this observation to validate the model by varying the conductivity of the medium and computing the net radial pressure. Figure 4 illustrates that the direction of the net radial pressure switches from pulling to compressing when the medium conductivity suppresses cytoplasmic conductivity. In Fig. 4a, σ0 = 0.3 S/m, σ1 = 5 × 10−3 S/m and σ2 = 1.2 S/m, the mechanic pressure pulls the membrane outwardly. In Fig. 4b, σ0 = 4 S/m, σ1 = 5 × 10−3 S/m and σ2 = 1.2 S/m, the pressure compresses the membrane.

Fig. 4
figure 4

Net radial pressure on the cell membrane under a strong DC electric field. a The pressure pulls the membrane along the z-axis when σ0 = 0.3 S/m and σ2 = 1.2 S/m; b The pressure compresses the membrane along the z-axis when σ0 = 1.2 S/m and σ2 = 0.3 S/m. Membrane conductivity is σ1 = 5 × 10−3 S/m in this plot

Full size image

Membrane conductivity could significantly increase in a strong electric field due to electroporation [25, 36]. We test the effect of membrane conductivity on net radial pressure at various conductivity ratio (σ0/σ2). When the membrane conductivity remains low (σ1 < 5 × 10−5 S/m), the net radial pressure is always pulling, an indication of prolate elongation along the electric field. Varying medium conductivity and σ0/σ2 ratio could not cause a switch in the sign of the compressing force. In contrast, when the membrane conductivity becomes high (σ1 > 5 × 10−4 S/m), the net radial pressure can switch from pulling (when σ0/σ2 < 1) to compressing (when σ0/σ2 > 1) in the field direction (Fig. 5), indicating an oblate shape.

Fig. 5
figure 5

Dependency of the radial pressure on the conductivities of the medium, the cytoplasm, and the membrane. When membrane conductivity (σ1) is low, the radial pressure is always pulling. When membrane conductivity is high (>5 × 10−4 S/m), the radial pressure switches from pulling (when σ0/σ2 < 1) to compressing (when σ0/σ2 > 1). σ2 = 1.2 S/m in this plot

Full size image

Translational forces produced by the interaction between the induced surface charges and the local electric fields

In order to calculate the forces related to the translational motion of the cell in the electric field, we need to first express the electric field in (x, y, z) directions using a transformation matrix.

$$ \left[\begin{array}{c}\hfill {E}_{o x}\hfill \\ {}\hfill {E}_{o y}\hfill \\ {}\hfill {E}_{o z}\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill \sin \theta \cos \phi \hfill & \hfill \cos \theta \cos \phi \hfill & \hfill -\sin \phi \hfill \\ {}\hfill \sin \theta \sin \phi \hfill & \hfill \cos \theta \sin \phi \hfill & \hfill \cos \phi \hfill \\ {}\hfill \cos \theta \hfill & \hfill -\sin \theta \hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill {E}_{o r}\hfill \\ {}\hfill {E}_{o\theta}\hfill \\ {}\hfill {E}_{o\phi}\hfill \end{array}\right] $$
(17)

Immediately outside the cell vicinity, we obtained (Additional file 5)

$$ {E}_{0x}=-3E\frac{R_{-}^3\left({S}_0+2{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left({S}_0-{S}_1\right)\left(2{S}_1+{S}_2\right)}{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}\sin \theta \cos \theta \cos \varphi $$
(18.1)
$$ {E}_{0y}=-3E\frac{R_{-}^3\left({S}_0+2{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left({S}_0-{S}_1\right)\left(2{S}_1+{S}_2\right)}{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}\sin \theta \cos \theta \sin \varphi $$
(18.2)
$$ {E}_{0z}=3E\frac{-{S}_1\left[2{R}_{-}^3\left({S}_1-{S}_2\right)-{R}_{+}^3\left(2{S}_1+{S}_2\right)\right]{\mathrm{cos}}^2\theta +{S}_0\left[{R}_{-}^3\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_1+{S}_2\right)\right]{\mathrm{sin}}^2\theta }{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)} $$
(18.3)

To test if the induced surface charges contribute to the buildup of the translational force, we integrated the translational pressure (x, y and z directions) on the whole spherical surface.

$$ {F}_{x\_\rho s}=\underset{\theta, \phi }{\iint }{E}_{ox}{q\rho}_{s01} da=0 $$
(19.1)
$$ {F}_{y\_\rho s}=\underset{\theta, \phi }{\iint }{E}_{oy}{q\rho}_{s01} da=0 $$
(19.2)
$$ {F}_{z\_\rho s}=\underset{\theta, \phi }{\iint }{E}_{oz}{q\rho}_{s01} da=0 $$
(19.3)

Here, q is the elementary charge. Interaction between the induced surface charges and the local electric fields generates zero translational force. Therefore, this type of surface charge is not involved in the translational movement of the vesicle/cell inside a strong DC electric field.

Translation forces generated by the interaction between the electric field and the intrinsic charges

Under normal physiological conditions, cell membrane is non-neutral due to the presence of the charged lipid head groups embedded inside the membrane [37]. The accumulation of anionic phospholipids (i.e., phosphatidylserine and phosphatidylinositol) produces an intensive electric field (105 V/cm), which can strongly attract ions, cationic proteins and peptides [38, 39]. This is a biophysics mechanism essential for protein targeting and intracellular signaling. Translation forces (Additional file 6) can be generated for a biological cell when the electric field interacts with the intrinsic surface charges (designated as ρ p ).

$$ {\displaystyle \begin{array}{l}{F}_{x\_{\rho}_p}=\underset{\theta, \varphi }{\iint \limits }{E}_{ox}{\rho}_p qda\\ {}=\underset{\theta, \varphi }{\iint \limits}\left[-3E\frac{R_{-}^3\left({S}_0+2{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left({S}_0-{S}_1\right)\left(2{S}_1+{S}_2\right)}{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}\sin \theta \cos \theta \cos \varphi \right]{\rho}_p{qR}_{+}^2\sin \theta d\theta d\varphi \\ {}=0\end{array}} $$
(20.1)
$$ {\displaystyle \begin{array}{l}{F}_{y\_{\rho}_p}=\underset{\theta, \varphi }{\iint \limits }{E}_{ox}{\rho}_p qda\\ {}=\underset{\theta, \varphi }{\iint \limits}\left[-3E\frac{R_{-}^3\left({S}_0+2{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left({S}_0-{S}_1\right)\left(2{S}_1+{S}_2\right)}{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}\sin \theta \cos \theta \sin \varphi \right]{\rho}_p{qR}_{+}^2\sin \theta d\theta d\varphi \\ {}=0\end{array}} $$
(20.2)
$$ {\displaystyle \begin{array}{l}{F}_{z\_{\rho}_p}=\underset{\theta, \varphi }{\iint \limits }{E}_{oz}{\rho}_p qda\\ {}=\underset{\theta, \varphi }{\iint \limits}\left[3E\frac{-{S}_1\left[2{R}_{-}^3\left({S}_1-{S}_2\right)-{R}_{+}^3\left(2{S}_1+{S}_2\right)\right]{\mathrm{cos}}^2\theta +{S}_0\Big[{R}_{-}^3\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_1+{S}_2\right){\mathrm{sin}}^2\theta }{2{R}_{-}^3\left({S}_0-{S}_1\right)\left({S}_1-{S}_2\right)+{R}_{+}^3\left(2{S}_0+{S}_1\right)\left(2{S}_1+{S}_2\right)}\right]{\rho}_p{qR}_{+}^2\sin \theta d\theta d\varphi \\ {}=4\pi {R}_{+}^2{\rho}_pE={Q}_pE\end{array}} $$
(20.3)

Therefore, translational force generated on a cell is proportional to the net intrinsic charge carried by the cell itself (Q p ), as suggested previously [40]. If we assume the intrinsic charge density to be 3.6 × 104 electronic charges/square micron [8] and cell radius to be 10 μm, we obtain \( {F}_{z\_{\rho}_p}=1.6\times {10}^{-6}N \), a force comparable to that generated by migrating or contracting cells (10−9 N-10−5 N in [6]).

Discussion

Understanding vesicle biomechanics under electric field exposure brings valuable insights into the behavior of biological cells, since both share the same structure components, the enclosing bilipid membrane. However, the overall kinematics of the vesicles and cells are different in a strong DC electric field. Vesicles demonstrate deformation in the strong DC electric field, while cells demonstrate both deformation and migration.

This work provides a three-dimensional modeling of the interaction between a strong DC electric field and the low-conductive, capacitive shell membrane of a cell/vesicle. It provides a set of analytical solutions for the surface charges and electric field distributions. It also provides mechanical analyses on the fixed membrane surface, including the radial pressure for membrane deformation and the translational forces for movement. The distribution of the induced surface charges depends on the orientation of the electric field to the structure. When the membrane becomes significantly conductive in the strong electric field, the directionality of the radial pressure on the membrane can switch between pulling and compressing, depending on the cytoplasm/medium conductivity ratio. Finally, translational force can be built on the structure for migration via its interaction with the intrinsic charges on the membrane, rather than with the induced electric charges. The model thus reconciles the kinematic difference between a cell (deformation and migration) and a vesicle (deformation only) under a strong DC electric field.

Surface charges induced by the externally applied field on the membrane

Analytical expressions were given for the induced surface charges on both sides of the membrane in a DC electric field. On a single interface, the charges are separate by their polarities, making the spherical interface an equivalent electric dipole (Fig. 2, also see [41]). For a 200,000 V/m electric field, the surface charges on the poles can reach 0.025 C/m2, a value that is several folds greater than those charges carried by the cell itself (i.e., 5.76 × 10−3 C/m2 in isolated toad bladder epithelial cells in [8]). The biological effects of such charge accumulation can include an extra voltage to be superimposed on the membrane [25, 26, 42], alteration of meta-stable membrane structure [43], or electroporation of the membrane [44]. More importantly, membrane surface charges are essential in producing electric compressive force for membrane deformation [22]. The static radial pressure on the membrane surface is produced by the interaction between the local electric field and the induced surface charges [45], which can be a complicated function of both the electric/geometrical properties of the shell and the properties of the field (i.e., Eqs. (14.1) and (14.2)).

Impact of conductivity ratio on net radial pressure

Experimentally, it has been shown that vesicle deformation inside an electric field is dependent on the conductivities of both the suspending fluid and the interior cytoplasm [46, 47]. Our model supports this observation, since increasing the medium conductivity could induce the switching of the radial pressure from pulling (Fig. 4a) to compressing (Fig. 4b). Furthermore, this conductivity ratio-dependent switch can only happen when the membrane conductivity is significantly increased (Fig. 5). Considering that the field intensity is 200,000 V/m in this study, a value that is sufficient for vesicle deformation [15] and membrane poration [16], it is likely the membrane conductivity could increase prominently.

Previous works have demonstrated that membrane conductance plays a significant role in inducing transmembrane potential and vesicle shape transition. Using a zero-thickness model of membrane and a hybrid numerical (immersed boundary and immersed interface) method, Hu et al. [22] found that increase in the membrane conductance is required for the vesicle to remain oblate shape in a DC electric field. Using a similar zero-thickness and numerical simulation, McConnell et al. [23] found that the vesicle only experiences oblate steady deformation when σ0/σ2 > 1 and membrane conductance is high. In these zero-thickness membrane model, transmembrane potential is calculated as a “jump” of potential, and the boundary condition of potential continuity across the two media is invalid. Our work uses a more biologically relevant representation of the “shell-like” membrane (approximately 5 nm in thickness), since the physical features (i.e., thickness and radius) of the membrane plays a significant role in electric field distribution, membrane polarization [45], and membrane biomechanics under electromagnetic field [32, 33]. Therefore, the “shell” model not only allows potential continuity across the membrane surface (boundary condition 1), but also allows the calculation of the membrane charges on both side of the membrane. Our analytical solutions support these previous modeling results. When σ0/σ2 < 1, the radial pressure is consistently pulling (prolate), regardless if the membrane conductivity is high. In contrast, when σ0/σ2 > 1, the radial pressure is pulling when the membrane conductance is low, and compressing (oblate) when membrane conductance is high (σ1 > 5 × 10−4 S/m).

Differential migration kinematics between a vesicle and a cell

Our model is successful in reconciling the kinematic difference between a spherical vesicle and a cell with similar shape in a strong DC electric field.

We found that interaction between the induced surface charges and local electric fields produces minimal translational force (Eq. 19.1 to 19.3). Using a method that treated the polarized particle as a dipole, Jones also ound that particles should experience zero net translation force in an even DC field [41] if only the induced electric charges are considered. This could easily be the case for an artificial vesicle, which is made with neutral molecules (L-a-phosphatidylcholine [17]) and its intrinsic surface charges are assumed to be zero. For a biological cell, intrinsic charges is regarded important in its cathodal galvanotaxis [48]. In a surprising simple form, we found the translational force is proportional to the overall net charge carried by the cell (Eq. 20.3). It is reasonable to assume that an evenly distributed intrinsic charge pattern on the cell membrane could produce a zero net radial pressure (Eq. 9). Therefore, the intrinsic charges could contribute to the translational motion of the cell, but not membrane deformation.

The model provides several interesting hypotheses regarding vesicle and cell kinematics. First, since the intrinsic charges are only associated with cell migration (but not membrane deformation) in the strong DC electric field, manipulations of these intrinsic charges should change cell mobility (but not deformation) in the field. Methods includes changing pH value [40] and applying calcium or magnesium to bind the surface charges [8]. Second, partially charged vesicles could be made to mimic cell migrations in the strong DC electric field. These vesicles could be made with lipid mixtures of phosphatidylcholine and phosphatidylglycerol or phosphatidylcholine and phosphatidylserine [15].

It is possible that the distribution of the intrinsic charge will be altered by the electric field [49]. However, if the polarity of the net charge (Q p ) is not affected by their redistribution, direction of the translations force should not be altered (Eq. 20.3). In supporting this model prediction, it was found that the re-distribution of the charged cell surface proteins did not alter the direction of galvanotaxis [49].

It shall be noted that if the intrinsic surface proteins are geometrically inhomogeneous, they may play an important role in cell deformation under a DC field exposure. For example, interactions between the charged protein on the outer hair cells and a transcellular oscillating electric field can cause cell vibration, leading to the deformation of the cell [50]. If one knows the detailed distribution of the charged surface proteins, it is possible to use Eq. (8) to deduce the local pressure generated by the intrinsic charges.

Future directions

Several assumptions have been made to formulate the present model for computational simplicity. First, the model does not represent the geometrical complexity in a real biological cell. Second, the model assumes both the medium and cytoplasmic environment are homogeneous. While this may be the case for vesicles, it could be unrealistic for cells [51, 52]. Third, the model does not consider mechanical factors such as hydrodynamic pressure around the structure [14] and membrane elasticity [4]. Finally, membrane polarization [53] in the strong DC electric field allows for calcium influx, which could alter membrane shape via actin polymerization/depolymerization and actomyosin contractility [54]. Electroporation could also alter local electric fields [55] by allowing ion exchange through the pores, which in turn alter vesicle shapes. Future work should consider multi-compartment modeling or finite element meshes [56,57,58] to represent the detailed anatomic complexity of a biological cell. More complicated simulation should consider numerical methods, whose accuracy is subjected to be validated by analytical works including this one.

Conclusions

The paper studies cellular biomechanics under a strong DC electric field exposure, by simulating the membrane with a “shell-like” structure. It provides the analytical solutions for the pressure and translational force that might contribute to the “shell” deformation and movement, respectively. The model provides a quantitative interpretation for various vesicle deformation scenarios inside the medium with different conductivities. It also explains the kinematic differences between a vesicle and a spherical cell inside the strong DC electric field.