Abstract
The consideration of external costs is becoming more important in supply network design, as companies are under increasing pressure to reduce the environmental and social impacts of their operations. This paper presents a single time period, single-product mixed integer linear programming formulation, which considers such external costs, as well as the impact of waste disposal. The model presented considers a network of suppliers, manufacturing facilities, customers, scrap recyclers, general recycling facilities and landfill sites and makes facility location and allocation decisions so as to minimise both the economic and external costs of all network operations. The model was formulated using the What’s Best Excel add-in and tested on a commercial case study concerning the supply network operations of Hydram, a leading sheet metal fabrication company, considering three different scenarios. Details of how the external and economic costs were determined are included, with reference to the literature. By analysis of the experimental results, commercial recommendations for facility location are made, and the managerial uses of the model for socio-environmentally responsible decision-making are discussed. The benefits and limitations of the proposed model are also discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Background
Introduction
A supply chain, or supply network, may be defined as an integrated process whereby raw materials are acquired, converted into products and delivered to customers [1]. Research attention on the design and analysis of supply networks has increased, and it has become apparent that companies that wish to remain competitive must increasingly pay attention to their supply networks and aim to increase the efficiency of their logistics operations [2]. Furthermore, companies are under increasing pressure to behave in an environmentally and socially responsible manner. By considering sustainability issues, companies can reduce costs whilst enhancing their reputations among customers and investors [3], leading to increased profits and sales revenues. In other words, the consideration of sustainability issues can be an important contributor to successful business performance.
The increasing attention to supply network design and sustainability issues as separate disciplines has naturally led to sustainability considerations becoming more important within the field of supply network design. A 2010 survey [4] in accordance with the UN Global Compact and Accenture found that company CEOs increasingly believe that sustainability issues should be fully integrated into the company supply network, strategy and operations, with 88% of the CEOs interviewed citing that they should be integrating sustainability through their supply chains. The study also finds a ‘significant performance gap’ between the companies who embed sustainability throughout their supply network and those who do not, indicating the importance of such considerations. Whilst these findings highlight the current importance of considering sustainability issues, various factors such as tightening environmental regulation, increasing environmental concern of customers and increasing demand for ‘green’ goods and services mean that sustainability considerations will only become more significant in the future [5].
One method of embedding sustainability into the supply network is through the consideration of the external costs of supply network operations during decision-making. The ExternE Project defines an external cost (also known as an externality) as a cost that ‘arises when the social or economic activities of one group of persons have an impact on another group and when that impact is not fully accounted or compensated for, by the first group’ [6]. Broadly, external costs quantify the effects of a process or action on the environment and society. The most efficient solution to externalities is to require them to be included in the costings of the engaged activity [7]. This method of taking account of external costs is known as ‘internalisation’, whereby policies such as taxation or environmental regulations are employed to incentivise their minimisation. Internalisation of external costs is becoming a common strategy for ensuring sustainable development [6], evidenced by stricter environmental regulations, and rising tariffs for activities that result in external costs such as the landfill tax in the UK.
Supply network operations result in various external costs. Transportation activities cause environmental impacts, accidents and congestion [8], whilst the treatment of waste causes pollution and disamenity effects [9]. Disamenity effects are localised impacts that generate negative local reactions, reflected in reduced house prices in the area surrounding a waste treatment facility.
Although external costs often do not affect companies directly, it is suggested that their consideration during supply network design, in conjunction with traditional economic considerations, would allow the designer to make decisions that are not only cost-effective, but also socially and environmentally responsible. It is argued that this will equip them for the likelihood of stricter regulations and higher environmental taxes in the future and also enhance their customer reputation by projecting an ethos of corporate responsibility.
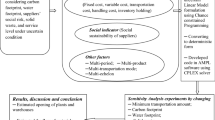
The rest of the paper is structured as follows: the rest of the ‘Background’ section presents a literature review to outline past research in the field of sustainable supply chain design, and the quantification of external costs. In the ‘Methods’ section, the methods employed are presented, including the presentation of a generic model for determining an optimal supply network structure, taking socio-environmental externalities into account, and the application of the model to a case study from the sheet metal industry. The ‘Results and discussion’ section presents and discusses the results of the case study, and the ‘Conclusions and further work’ section presents the conclusions of the report and discusses possible extensions to the model.
Literature review
A great deal of research has already been conducted on the mathematical location modelling for supply network design, and most of the literature focuses on the key questions of location and allocation [10]. Deterministic analytical models are the most common type for supply chain design and analysis, cost minimisation is usually the objective function [1], and most of the past literature fails to consider external costs. However, environmental considerations are incorporated within the objective function in [11], whilst [12] and [13] suggest the use of objective functions in future research that consider factors other than just cost minimisation, such as environmental costs and responsiveness. It is argued that the incorporation of social and environmental impacts in the objective function would give a more comprehensive picture of the total supply chain cost and would be useful to help managers to make more responsible supply chain decisions.
Organizations are facing growing pressure to increase environmental awareness and act in a socially responsible manner. These philosophies are being incorporated throughout all business operations, including their supply chains. As such, interest in reverse logistics is interesting, and the number of publications has been growing steadily. The field of reverse logistics is clearly significant: terms such as recycling, reuse and remanufacture are now known to the general public. As shown by [14], the inclusion of reverse logistics processes in the supply chain can have environmental, economic and social benefits. All of these factors justify reverse logistics as an important and relevant area of research.
One way in which sustainability considerations have been considered within the supply chain design is through the consideration of reverse logistics processes, fitting with the trend that manufacturers are becoming more responsible for the recovery of their products [15]. Mixed integer linear programming (MILP) reverse logistics network models are proposed in [5], [16] and [17], based on traditional warehouse location models. Although reverse flows have been considered in a range of publications for reuse and remanufacture, the consideration of waste disposal appears to be an area that has been neglected in much of the reviewed supply network design literature.
Much of the literature neglects the costs of landfilling, despite the fact that sending waste to a landfill has both economic costs (in the form of tipping fees) and external costs [14]. However, [13] and [15] consider the external costs of landfilling operations, which include impacts to human health, crops, materials and buildings [9]. Landfill sites also cause disamenity costs associated with odour, dust, litter, noise, vermin and visual intrusion [18].
Transport activities also result in significant costs to the environment and society, caused by accidents, congestion, noise and pollution. The contribution of transport to greenhouse gas emissions is widely realised, and transport accounted for 23% of global CO2 emissions in 2007 [19]. The external costs associated with freight transportation are particularly relevant: the total costs caused by goods vehicles in 2000 for the EU15 amounted to EUR 135.85 billion [20]. If ‘real prices’, which incentivise the best choice of mode of transport for sustainable mobility, are to be used in transport, then internalisation must be pursued, and not just at the minimum level for political acceptance [21]. Despite the obvious significance of transportation externalities, at the time of research, their inclusion into supply network models also appears to have been neglected in past research.
Methods
Problem definition and mathematical modelling
In this section, the problem to be solved and the mathematical formulation of the sustainable supply network design model will be presented in detail. The model is inclusive of waste disposal considerations and considers external costs of supply chain operations within the objective function as an attempt to contribute some innovative research to the field of supply network design and management, as these points seem to have been neglected in past research.
The logistics network discussed in this paper is a multi-stage forward logistics network, including customers, potential facilities, raw material suppliers, landfill facilities, recycling facilities for general waste and scrap recyclers who pay for scrap material. As shown in Figure 1, the facilities receive raw material from an allocated supplier. The raw material is converted into a product to satisfy the demand of customers. In producing a unit of product, the facilities also produce a given amount of scrap which is sold to an allocated scrap facility. It is assumed that all of the raw material is either converted into either product or scrap. During operations, the factory also produces a given amount of domestic waste for every amount of produced product. The domestic waste is either recyclable general waste which is sent to an allocated recycling facility or non-recyclable general waste which is sent to an allocated landfill site.
Opening a facility in the network incurs a designated cost. Additionally, all transportation operations have economic and external costs, and the disposal of general waste has differing environmental and economic implications depending upon the method of disposal. The model assumes negligible production costs.
This structure can be translated into a MILP facility location model, as below. The objective of the model is to determine which facilities to open, how much product to produce at the open facilities and how to allocate the product to customers so as to minimise the sum of economic and external costs. The use of a weighting factor on the external cost allows the user to decide the extent to which these economic costs are included.
Index sets
G =: {1,…N G } Set of material suppliers, ∀ g ∈ G; I =: {1,…N I } Set of potential facilities, ∀ i ∈ I; J =: {1,…N J } Set of customers, ∀ j ∈ J; K =: {1,…N K } Set of recycling sites, ∀ k ∈ K; L =: {1,…N L } Set of landfill sites, ∀ l ∈ L; M =: {1,…N M } Set of scrap purchasing centres, ∀ m ∈ M
Costs
Economic costs
fi: Per time-period operating cost of facility i; CTgiv: Transportation cost per unit distance per unit of raw material v from supplier g to facility i; CTijp: Transportation cost per unit distance per unit of product p from facility i to customer j; CTikr: Transportation cost per unit distance per unit of recyclable general waste r from facility i to recycling site k; CTilq: Transportation cost per unit distance per unit of non-recyclable general waste q from facility i to landfill site l; CTimz: Transportation cost per unit distance per unit of scrap waste z from facility i to scrap recycling centre m; CDlq: Unit disposal cost (landfill tax) at landfill site l of non-recyclable general waste q; CDkr: Unit revenue at scrap recycling centre m of scrap waste z
External costs
XTgiv: External cost of transportation per mile per unit of raw material v from supplier g to facility i; XTijp: External cost of transportation per mile per unit of product p from facility i to customer j; XTikr: External cost of transportation per mile per unit of recyclable general waste r from facility i to recycling site k; XTilq: External cost of transportation per mile per unit of non-recyclable general waste q from facility i to landfill site l; XTimz: External cost of transportation per mile per unit of scrap waste z from facility i to scrap recycling centre m; XDlq: External cost of disposing one unit of non-recyclable general waste q at landfill site l; XDkr: External benefit of recycling one unit of recyclable general waste r at recycling site k; XDmz: External benefit of disposing of one unit of scrap z at scrap purchasing centre m
Parameters
Tgi: Distance between supplier g and facility i; Tij: Distance between facility i and customer j ; Tik: Distance between facility i and recycling centre k; Til: Distance between facility i and landfill site l; Zgv: Supply capacity of supplier g for raw material v; Zip: Capacity of potential facility i for product p; Zkr: Capacity of recycling site k for recyclable general waste r; Zlq: Capacity of landfill site l for non-recyclable general waste q; Zmz: Capacity of scrap recycling centre m for scrap waste z; Ymin: Minimum number of facilities to open; Ymax: Maximum number of facilities to open; djp: Demand of customer j for product p; α: Weighting factor for the inclusion of external costs; bpv: Amount of raw material v required per unit of produced product p; bpr: Amount of recyclable general waste r produced per unit of produced product p; bpq: Amount of non-recyclable general waste q produced per unit of produced product p; bpz: Amount of scrap waste z produced per unit of produced product p
Decision variables
Flow variables
sijp: Amount of product p transported from facility i to customer j; sgiv = bpv sijp: Amount of raw material v transported from supplier g to facility i; sikr = bpr sijp: Amount of recyclable general waste r transported from facility i to recycling site k; silq = bpq sijp: Amount of non-recyclable general waste q transported from facility i to landfill site l; simz = bpz sijp: Amount of scrap waste z transported from facility i to scrap recycling centre m
Objective function
The objective function minimises the sum of the economic costs (A 1) and external costs (A 2) by setting the decision variable and flow variables. The weighting factor α allows the user to determine the extent to which external costs are included:
The economic cost formulation (2) includes the cost of opening facilities, the economic cost of all transportation operations, the cost of landfilling non-recyclable waste and the revenue achieved from the sale of scrap (represented as a negative cost). The external cost formulation (3) includes the external cost of all transportation operations and the environmental cost of landfilling waste.
Constraints
Balance of material in the potential facilities is guaranteed by constraint (4), which ensures that all of the raw material going into a potential facility is either converted into a product or scrap. Constraints (5) to (9) are capacity constraints for facilities, suppliers, recycling sites, landfill sites and scrap purchasing centres. Constraint (10) ensures that all customer demand is satisfied. Constraint (11) defines the plant opening decision variable as binary, and constraints (12) to (16) ensure that there are no negative flows of raw material, product, recyclable general waste, non-recyclable general waste or scrap so that all flows follow the arrow directions indicated in Figure 1. Constraint (17) dictates that the number of facilities to open must be between specified bounds.
It was decided that the model should be tested on a case study for validation purposes and to assess its functionalities. The model proposed is highly generic and theoretically widely applicable, as the logistics problem considered is familiar to many companies. However, there were still some challenges to find an appropriate case study to test the model. Firstly, it was decided that the model should be tested on a company which is genuinely looking to solve a facility location problem, to ensure that the results of this paper are useful from a commercial perspective as well as an academic perspective. Secondly, it was realised that in order for the model to be applied properly to a case study, a company should be found with a sufficient amount of data readily available regarding the amount of raw material used, the amount of waste, scrap and product produced, as well as demand data and customer locations for a given time period.
Case study: Hydram
Brief
After analysing various companies according to the aforementioned criteria, Hydram was chosen as a suitable case study upon which the MILP model could be evaluated. Hydram is a subcontract sheet metalwork and fabrication company, based in County Durham, with customers throughout the UK. The sheet metalwork products produced at Hydram are suitable for modelling as a single product, using weight as the demand quantity. The model presented in this paper is a single time period model, and a time period of 1 year was selected as appropriate for analysis of the Hydram problem.
Hydram is looking at the possibility of opening a smaller ‘satellite’ facility, either in Yorkshire or in London. Using commercial property websites, three potential facilities were located for evaluation, in Halifax, Bradford and London.
Data provided
Firstly, sales data were provided for the 12-month period between 1 March 2010 and 1 March 2011. This detailed the total spend during the period for 64 customers. Data were also provided for the amount of metal raw material purchased during this period and the amount of metal that was scrapped. Environmental key performance indicators’ data were also provided, detailing all general waste disposed of by landfill and recycling during the same time period, as well as the total fleet fuel consumption.
The sales data for the period closely follow the Pareto principle, with the top 20.3% of customers accounting for 81.20% of sales. It was decided that it would be sufficient to consider only the top 31 customers in the model, as they account for 88.5% of all demand. As such, all other data were scaled to 88.5% of the original figures to accommodate the neglect of the bottom 33 customers.
Using the data provided, standard units were determined for use in the model. Material flows are in tonnes (t), distances in kilometres (km) and costs in pounds sterling (£). The time period considered is 1 year. The rest of this paper will use these units as standard.
Fitting the data to the model
Assuming that all purchased material is either turned into product or scrapped, the total amount of product produced was calculated as the difference between the amount of raw material purchased and the amount of metal scrapped. Using this calculation, a value was calculated for the amount of product produced per customer £ spent. The results of these calculations, along with some other key input data, are shown in Table 1.
Using the total product produced per customer £ spent value, the customer sales data were next converted to sales in terms of weight for each customer, to be used as d jp inputs for the model. The general waste volumes were also converted to weights, assuming that average general waste has a density of 170 kg/m3 [22]. Finally, using the data in Table 1, the ratios b pv , b pr , b pq and b pz were calculated. These ratios are shown in Table 2.
Using the customer postcodes, the distances between every potential facility and every customer (T ij distances) were calculated. Additionally, each potential facility was allocated a local material supplier, scrap purchasing centre, landfill site and recycling facility. Although it is not necessary in the model to allocate a material supplier, scrap purchasing centre, landfill site and recycling facility to each potential facility, after correspondence with Hydram, it was deemed that this would be the most likely option. Therefore, for the purposes of the case study, G = I = K = L = M.
Using online map tools, the distances between these allocated facilities and the potential facilities were calculated. A network map of the 4 potential facilities, 31 customer locations, chosen material suppliers, recycling sites, landfill sites and scrap purchasing centres as well as all possible product flow routes is shown in Figure 2.
The currently open facility in County Durham has a production capacity of 1,000 tonnes per year, and the potential facilities have initial production capacities of 400 tonnes. For the Hydram problem, it is assumed that the suppliers, recycling sites, landfill sites and scrap recycling centres have capacities that are significantly larger than the flows that they will be required to handle, which means that the constraints (6) to (9) can be ignored.
Allocation of economic costs
The cost of setting up a new satellite facility was estimated to equal £100,000 per year to cover the purchasing of equipment and managerial expenses, assuming a 10-year facility lifetime. Property expenses were also evaluated for each of the potential facilities, using either rent prices or mortgage calculations for the same 10-year period. The sum of the setup cost and property expenses gives a complete yearly operational cost for each facility. As the County Durham facility already owns all equipment and property outright, the operating cost is assumed to be zero which essentially models the facility as an existing facility rather than a potential facility. The yearly operational costs of all facilities are shown in Table 3.
For the Hydram problem, it was established that the suppliers pay the economic cost of transportation. Furthermore, it is assumed that non-recyclable waste, waste and scrap are collected by third parties and transported to their respective facilities. Therefore, Hydram incurs no direct economic cost from any of these transportation activities. As such, for the purposes of the case study,
However, the costs of transportation to customers are directly incurred by Hydram. In order to calculate CT ijp , firstly, the T ij distances were calculated using online mapping tools, and they were used with the scaled sales data to calculate the total number of tonne-kilometres (tkm) travelled during the 12-month period as 74,367.41 tkm.
Using the total fleet fuel consumption value from Table 1 and assuming a diesel cost of £1.4305 per litre, the total expenditure on fuel was calculated as £39,807.03.
Hydram uses 13.5-t trucks, for which fuel costs only amount to 24% of total vehicle operating costs [23]. As such, the total economic cost of transportation for Hydram during the 2010-2011 sales period was calculated as £165,862.63, which gives a CT ijp value of £2.23 per tkm by dividing the total cost by the total number of tkm travelled.
Finally, economic costs and revenues arise out of Hydram’s waste operations. It is assumed that only inactive waste is landfilled, so a rate £2.50 per tonne is used for CD lq [24]. A revenue value of £180 per tonne was allocated for CD kr , using current ferrous metal scrap prices as a guideline.
Allocation of external costs
In order to include external costs into the supply network design model, the external costs must first be quantified. However, the quantification of external costs is a difficult process, and different studies rely on different assumptions to estimate externality costs [25]. Although the estimation of external costs comes with inherent uncertainties, there is a wide consensus on which methods are most appropriate for identifying different types of external cost [8]. This section reviews some of the literature on the external costing of transport operations and landfilling to determine quantitative external costs for use in (3).
Although no economic costs of transportation are incurred between the potential facilities and suppliers, recycling sites, landfill sites or scrap recycling centres, such operations are still within the supply network. As such, their external costs are still included in the model, as the external costs are directly related to decisions made by Hydram. For the purpose of this analysis, it is assumed that all transportation operations within the network use the same type of vehicle and resultantly produce the same external costs per tonne of material per kilometre travelled. As such, for the analysis of the case study problem,
By quantifying the effects of noise, accidents, pollution (and its effects on health, nature and buildings), climate change and effects on the natural landscape, a marginal external cost of 0.3 to 1.2 EUR/tkm for interurban road freight transport and 1.1 to 4.4 EUR/tkm for urban road freight transport is calculated in [26]. Using an intermediate value, but assuming that most transport is interurban, it was decided that an external cost of 1.5 EUR/tkm would be appropriate for application to the model, which translates to £1.25/tkm. The costs in [26] assume heavy goods vehicles with an average load factor of 15 tonnes per vehicle, so are suitable for application to the case study problem, which assumes 13.5-tonne trucks.
For the case study, there are significant revenues to be made from recycling scrap metal. It was decided that the economic benefit achieved is essentially internalisation of the external cost of landfilling metal scrap, as there is a significant direct incentive not to landfill the scrap material. As such, it is argued that the external benefit of recycling the metal scrap is already reflected in the revenue obtained by scrapping the metal and should therefore be ignored to avoid counting it twice.
Similarly, recycling general waste presents an avoided cost of £2.50 per tonne compared to landfilling it, which essentially internalises the external benefit of recycling. As a result of this, as well as a lack of consensus on the literature regarding the environmental benefits of recycling general waste, it was decided that the external benefit of recycling general waste should also be ignored.
Resultantly, for analysis of the case study,
The external costs of landfilling were quantified by [9] and found to range between 10 and 13 EUR/t waste, dominated by the emission of un-captured methane. Using the mid-range value and converting the currency at current rates, this figure translates to £9.74 per tonne of landfilled waste. The external costs associated with transporting waste to a landfill are neglected in [9], so the inclusion of XT ilq is still appropriate in the model.
Disamenity costs were also neglected in [9], but [18] quantified a fixed disamenity cost of between £1.52 and £2.18 per tonne of landfill in 2000. The Nationwide House Price Index (HPI) calculator indicates an increase of 112.08% on the average house price since 2000, so an appropriate current disamenity cost, using the results of [18] adjusted in line with the HPI, is therefore somewhere between £3.22 and £4.62 per tonne of landfill generated. It was decided that the mid-range value of £3.92 per tonne would be appropriate for use in the model. As such, the total cost of XD lq is allocated as £13.66 per tonne, using [9] and [18]. A summary of the economic and external cost inputs is provided in Table 4.
Experimentation
Three key scenarios were analysed using three discrete experiments.
Experiment 1 Experiment 1 was performed to establish the optimum choice of which facilities to open, using the operational costs and capacities as per Table 3. In order to model this open scenario, constraint (17) was effectively neglected by setting Y min to 0 and Y max to 4.
Experiment 2 Experiment 2 was performed to establish which facilities should be open if it is specified that the network should contain at least two facilities, so Y min was set to 2, and Y max was set to 4.
Experiment 3 Experiment 3 was performed to evaluate a different scenario whereby 400 t worth of production capacity from the County Durham facility is moved to a new satellite facility. Through consultation, it was assumed that moving the equipment rather than purchasing new equipment at the new facility would reduce the cost of setting up the new facility to £30,000 per year. However, in order to provide 400 t per year of capacity for a satellite facility, the capacity at the Durham facility would have to reduce by 400 t per year. The new operational costs and capacities due to this proposal are shown in Table 5. Under these conditions, it would only be possible to have a maximum of two facilities in the network, as there is currently only enough equipment to equip two facilities. Resultantly, Y min was set to 0, and Y max was set to 2.
Each of the experiments was modelled using α values between 0 and 1, in increments of 0.2, to evaluate the effects of including external costs during the decision-making process. To solve the problems, the model was formulated using What’sBest, an add-in for Excel, produced by Lindo Systems Incorporated (Chicago, IL, USA), which uses a branch-and-bound algorithm. More information about the allocation of operational costs in Tables 3 and 5 is given in Additional file 1.
Results and discussion
Table 6 shows the Y i outputs of the model, indicating which facilities the model nominates to open, and the total flows from each facility. Figure 3 shows the total cost outputs (the objective value produced by the model) for each of the experiments, using different alpha weightings. A breakdown of the total economic and external costs calculated for each experiment is shown in Figure 4. Figure 5 shows the capacity utilizations of each of the open plants for each of the experiments. The allocation of customers to plants for experiments 2 and 3 is shown in Figure 6.
The major result of the experiments is that external costs are significant in the field of supply network logistics. By analysis of Figure 4, it can be seen for all cases that the external costs form a significant portion of the total cost. In the worst case, experiment 1, the external costs of the Hydram logistics network are more than twice the magnitude of the economic cost.
Initially, it was only intended to model scenario 1 to determine the feasibility of opening a satellite facility for alpha values between 0 and 1. As the alpha value represents the extent to which external costs are factored in, it is suggested that the maximum useful value of alpha to be considered should be 1, as no rational manager would wish to over compensate for the potential of future rising costs brought about by governmental policy which aims to internalise externalities (and no rational government would over-internalise externalities). By analysis of Figure 3 and Table 6, it is clear that the model indicates that it is currently not feasible for Hydram to open up a new facility for all alpha values in this range. However, although the decision not to open a new facility currently has the lowest total cost, it has the greatest external cost and is therefore the most damaging to the environment and society, mainly due to the impact of transport operations. By analysis of the projected flow from the County Durham facility in experiment 1 and the available production capacity, it was calculated that the County Durham facility will run at 78.3% of capacity under this scenario, as shown in Figure 5.
As it was deemed a somewhat trivial result that the model allocated not to open any new facilities when the alpha value is set between 0 and 1, values greater than 1 were considered. The alpha value inputs were varied to determine the extent to which external costs must be considered to make the opening of a facility feasible for the Hydram case, when there is no constraint imposed on the minimum number of facilities to be opened. It can be seen by analysis of the results that the model indicates that it is currently not feasible for Hydram to open up a new facility for all alpha values less than 3.6. At this point, the model indicated that the County Durham and Bradford facilities should be opened. The fact that the facility location decision changes according to the alpha weighting as shown in Table 6 validates the model.
The somewhat trivial initial result in experiment 1 also led to the formulation of experiment 2, which was conducted to determine which facilities should be open when it is specified that there should be at least two facilities in the network, i.e., Y min = 2. The model indicated that the County Durham and Bradford facilities should be open under these circumstances. However, it was noticed that both plants would be running significantly under capacity based on the allocated product flows in Table 6. In experiment 2, the County Durham facility is only operating at 52.4% of capacity, and the Bradford facility also only operates at 64.5% of capacity. Overall, the facilities operate at 55.8% of capacity.
It was this under use of capacity that led to the formulation of experiment 3, which moves 400 t of the Durham production capacity to a new facility, in order to reduce the setup costs of the satellite facility and improve the overall capacity utilisation. Under experiment 3, the model nominates to open the same facilities, Bradford and Durham, and allocate the same production to each facility. Resultantly, the external costs for experiments 2 and 3 are the same, as shown by Figure 4. However, due to reduced operating costs, the economic costs of the proposal are significantly less than those of experiment 2. Furthermore, the projected capacity utilisation figures are better for scenario 3 than for scenario 2: there is an overall 78.3% capacity utilisation as per example 1, as the same amount of product is produced using the same overall capacity.
Therefore, if it is decided by Hydram that a satellite facility is to be opened, it is suggested that the Bradford location should be chosen and that scenario 2 should be employed. By moving 400 t of production capacity in terms of tools and equipment from the County Durham facility to the Bradford facility, Hydram can minimise setup costs and maintain acceptable capacity utilisation, whilst reducing the external costs of the logistics network.
Finally, it is proposed that customer demand is partly affected by the geographical location of facilities. Figure 6 shows that current customers are somewhat clustered geographically around the current County Durham facility. Therefore, it is suggested that if the Bradford satellite facility were to be built, then total demand would likely increase due to the addition of extra customers local to the new satellite facility. If demand in the Bradford area does increase in this manner, then new tools and equipment can be purchased to increase production capacity if necessary.
Conclusions and further work
The concept of green supply chain management is gaining increasing interest among both researchers and practitioners of operations and supply chain management [27], and the consideration of external costs has been steadily growing. The main conclusion from this report is that external costs can form a significant portion of the total cost when considered in a logistics network.
The model presented in this paper incorporates social and environmental impacts of operations through the inclusion of external costs, but allows user discretion on the extent to which external costs are included when making location and allocation decisions. Even if the user chooses to fully ignore the external cost (and set alpha to 0) within their objective function when making their logistics decisions, the spread sheets generated for this paper still give an indication of the external cost that their decisions will make. However, it is suggested that there is a critical need to consider external costs in the supply network design to cope with increasing economic and regulatory pressure and increasing consumer awareness. As legal restrictions tighten and taxes increase to attempt to internalize external costs, it is argued that consideration of the total external cost by the use of a non-zero alpha value would be prudent so as to prepare for the external costs becoming internalized by future governmental policy.
Although there is a wide consensus on which methods are most appropriate for identifying different types of external cost [7], the quantification of external costs is still a difficult process, with inherent uncertainties. For example, even when accredited techniques such as the willingness-to-pay method are used, it is still difficult to put an economic value on something as qualitative as a human life. Therefore, the external costs generated by the model are somewhat uncertain due to the uncertainties in the external costs used as model inputs. It is suggested that more work must be done by the academic community on estimating external costs of logistics operations so that they can be incorporated into future supply network models with more credibility and certainty.
With regard to the Hydram case study, it is concluded that it is currently not feasible to open up a satellite facility, based on the output of the developed model. However, if the managers do wish to open a new facility, it is suggested that the facility should be in the Bradford location suggested and that 400 t of production capacity should be transferred from the County Durham facility, as per experiment 3, in order to maximize capacity utilization and minimise operating costs. Such a decision may also improve customer sales for Hydram, as demand tends to come from customers within a close proximity to the facilities.
This paper presented a single product, single time period model for minimizing both economic and external costs in a logistics network brought about by facility opening, transportation and waste disposal considerations. Real-world supply chains are often more complicated than the one considered in this paper. As such, some extensions to the model have been envisioned, in order to extend the current MILP formulation to more realistic real-world supply network structures, including the following:
The consideration of multiple time periods to analyse dynamic situations
The incorporation of production costs within the model (both economic and external), such as the costs associated with running facilities
Inclusion of reverse logistic options in the model such as reuse and remanufacture to make the model more widely applicable
However, it is recognised that such extensions may prove very difficult to implement. The modelling of more complex supply chains across multiple time periods would lead to much more complicated mathematical models, and it is suggested that the formulation of an MILP that is applicable to a wide range of real-world supply chains would take a great deal of effort to formulate and solve.
References
Beamon BM: Supply chain design and analysis: models and methods. Int. J. Prod. Econ. 1998,2(3):281–294.
Ambrosino D, Scutella M: Distribution network design: new problems and related models. Eur. J. Oper. Res. 2005, 165: 610–624. 10.1016/j.ejor.2003.04.009
Copps A: Emission maps put heat on supply chain. The Times 2012.
Lacy P, Cooper T, Hayward R, Neuberger L: A New Era of Sustainability: UN Global Compact-Accenture CEO Study, 2010. IIinois: Accenture; 2011.
Fleischmann M, Beullens P, Bloemhof-Ruwaard JM, Van Wassenhove L: The impact of product recovery on logistics network design. Prod. Oper. Manage. 2001, 10: 156–173.
European Commission: External costs: research results on socio-environmental damages due to electricity and transport. . Accessed 5 Apr 2011 http://bit.ly/JjYvoL
The Economist: Economics A-Z terms beginning with E. . Accessed 5 Apr 2011 http://www.externe.info/externe_2006/externpr.pdf]
Maibach M, Schreyer C, Sutter D, van Essen HP, Boon BH, Smokers R, Schroten A, Doll C, Pawlowska B, Bak M: Handbook on Estimation of External Costs in the Transport Sector. Internalisation Measures and Policies for All External Cost of Transport (IMPACT). the Netherlands: CE Delft; 2008.
Rabl A, Spadaro S, Zoughaib A: Environmental impacts and costs of solid waste: a comparison of landfill and incineration. Waste Manage. Res. 2008, 26: 147–162. 10.1177/0734242X07080755
Domschke W, Drexl A: Location and Layout Planning. Springer, Berlin: Lecture notes in Economics and Mathematical Systems; 1985.
Pourmohammadi H, Dessouky M, Rahimi M: A reverse logistics model for the distribution of waste/by-products. J. Cleaner Prod 2013. in press
Pishvaee M, Kianfar K, Karimi B: Reverse logistics network design using simulated annealing. Int. J. Adv. Manufact. Technol. 2009, 47: 269–281.
Benaissa M, Benabdelhafid A: A multi-product and multi-period facility location model for reverse logistics. Polish J. Manage. Stud. 2010, 2: 7–19.
Yongsheng Z, Shouyang W: Generic model of reverse logistics network design. Transpn Sys Eng & IT 2008,8(3):71–78.
Krikke H, Kooi E, Schuur P: Network design in reverse logistics: a quantitative model. Lect. Notes Econ. Math. Syst. 1999, 480: 45–62. 10.1007/978-3-642-58568-5_3
Salema M, Pvoa A, Novais A: A warehouse-based design model for reverse logistics. J. Oper. Res. Soc. 2006,57(6):615–629. 10.1057/palgrave.jors.2602035
Locklear EC: Product take-back using geographic information systems. Thesis: University of South Carolina; 2000.
Cambridge Econometrics in association with EFTEC and WRC: A Study to Estimate the Disamenity Costs of Landfill in Great Britain: Final report. Cambridge: Defra; 2003.
Bräuninger M, Schulze S, Leschus L, Perschon J, Hertel C, Field S, Foletta N: Achieving sustainability in urban transport in developing and transition countries (EURIST/HWWI study, 2012). Hamburg: Hamburg Institute of International Economics; 2011.
Persson J, Song D: The Land Transport Sector: Policy and Performance. OECD Economics. Paris: Department Working Papers, No. 817. OECD Publishing; 2010.
International Union of Railways, Greening Transport: reduce external costs. . Accessed 5 Apr 2011 http://www.allianz-pro-schiene.de/presse/pressemitteilungen/2012/013-studie-lkw-maut-pkw-maut/kurzfassung-studie-externe-kosten-verkehr-cer-uic.pdf]
The Environment Protection Agency, Vicoria, Austrailia, Waste materials: density data. . Accessed 5 Apr 2011 http://bit.ly/I6iWp5
The Freight Transport Association, Fuel as a percentage of HGV operating costs. . Accessed 6 Apr 2011 http://www.fta.co.uk/policy_and_compliance/fuel_prices_and_economy/fuel_prices/fuel_fractions.html
HMRC Reference: Notice LFT1 (May 2012): A general guide to landfill tax. . Accessed 6 Apr 2011 http://customs.hmrc.gov.uk/channelsPortalWebApp/channelsPortalWebApp.portal?_nfpb=true%_pageLabel=pageExcise_ShowContent%propertyType=document%id=HMCE_CL_000509#P311_23550
Koomey K, Krause F: Introduction to environmental externality costs. In CRC Handbook on Energy Efficiency: CRC Press, Boca Raton; 1997.
Essen HP, Boon BH, Maibach M, Schreyer C: Methodologies for external cost estimates and internalisation scenarios. Delft: Discussion paper; 2007. . Accessed 6 Apr 2011 http://www.ce.nl/4288_Inputpaper.pdf
Srivastava S: Network design for reverse logistics. Omega 2008, 36: 535–548. 10.1016/j.omega.2006.11.012
Acknowledgements
Special thanks to Andrew Jordan at Hydram for providing the case study data and to Tom Davies for providing technical support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
QW defined the research aim and identified the problem. DA carried out the literature review on external costs, and QW carried out the literature review on logistic network structures. DA carried out mathematical modelling and conceived the case study. QW participated in the experimental design and discussion of the results and corrected the manuscript. Both authors read and approved the final manuscript.
Electronic supplementary material
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ansbro, D., Wang, Q. A facility location model for socio-environmentally responsible decision-making. Jnl Remanufactur 3, 5 (2013). https://doi.org/10.1186/2210-4690-3-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2210-4690-3-5