Abstract
Biometric discretization derives a binary string for each user based on an ordered set of biometric features. This representative string ought to be discriminative, informative, and privacy protective when it is employed as a cryptographic key in various security applications upon error correction. However, it is commonly believed that satisfying the first and the second criteria simultaneously is not feasible, and a tradeoff between them is always definite. In this article, we propose an effective fixed bit allocation-based discretization approach which involves discriminative feature extraction, discriminative feature selection, unsupervised quantization (quantization that does not utilize class information), and linearly separable subcode (LSSC)-based encoding to fulfill all the ideal properties of a binary representation extracted for cryptographic applications. In addition, we examine a number of discriminative feature-selection measures for discretization and identify the proper way of setting an important feature-selection parameter. Encouraging experimental results vindicate the feasibility of our approach.
Similar content being viewed by others
1. Introduction
Binary representation of biometrics has been receiving an increased amount of attention and demand in the last decade, ever since biometric security schemes were widely proposed. Security applications such as biometric-based cryptographic key generation schemes [1–7] and biometric template protection schemes [8–13] require biometric features to be present in binary form before they can be implemented in practice. However, as security is in concern, these applications require binary biometric representation to be
-
Discriminative: Binary representation of each user ought to be highly representative and distinctive so that it can be derived as reliably as possible upon every query request of a genuine user and will neither be misrecognized as others nor extractable by any non-genuine user.
-
Informative: Information or uncertainty contained in the binary representation of each user should be made adequately high. In fact, the use of a huge number of equal-probable binary outputs creates a huge key space which could render an attacker clueless in guessing the correct output during a brute force attack. This is extremely essential in security provision as a malicious impersonation could take place in a straightforward manner if the correct key can be obtained by the adversary with an overwhelming probability. Entropy is a common measure of uncertainty, and it is usually a biometric system specification. By denoting the entropy of a binary representation as L, it can then be related to the N number of outputs with probability p i for i = {1,...,N} by . If the outputs are equal-probable, then the resultant entropy is maximal, that is, L = log2N. Note that the current encryption standard based on the advanced encryption standard (AES) is specified to be 256-bit entropy, signifying that at least 2256 possible outputs are required to withstand a brute force attack at the current state of art. With the consistent technology advancement, adversaries will become more and more powerful, resulting from the growing capability of computers. Hence, it is utmost important to derive highly informative binary strings in coping with the rising encryption standard in the future.
-
Privacy-protective: To avoid devastated consequence upon compromise of the irreplaceable biometric features of every user, the auxiliary information used for bit-string regeneration must not be correlated to the raw or projected features. In the case of system compromise, such non-correlation of the auxiliary information should be guaranteed to impede any adversarial reverse engineering attempt in obtaining the raw features. Otherwise, it has no difference from storing the biometric features in the clear in the system database.
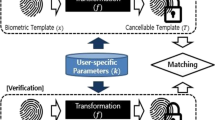
To date, only a handful of biometric modalities such as iris [14] and palm print [15] have their features represented in the binary form upon an initial feature-extraction process. Instead, many remain being represented in the continuous domain upon the feature extraction. Therefore, an additional process in a biometric system is needed to transform these inherently continuous features into a binary string (per user), known as the biometric discretization process. Figure 1 depicts the general block diagram of a biometric discretization-based binary string generator that employs a biometric discretization scheme.
In general, most biometric discretization can be decomposed into two essential components, which can be alternatively described as a two-stage mapping process:
-
Quantization: The first component can be seen as a continuous-to-discrete mapping process. Given a set of feature elements per user, every one-dimensional feature space is initially constructed and segmented into a number of non-overlapping intervals where each of which is associated to a decimal index.
-
Encoding: The second component can be regarded as a discrete-to-binary mapping process, where the resultant index of each dimension is mapped to a unique n-bit binary codeword of an encoding scheme. Next, the codeword output of every feature dimension is concatenated to form the final bit string of a user. The discretization performance is finally evaluated in the Hamming domain.
These two components are governed by a static or a dynamic bit allocation algorithm, determining whether the quantity of binary bits allocated to every dimension is fixed or varied, respectively. Besides, if the (genuine or/and imposter) class information is used in determining the cut points (intervals' boundaries) of the non-overlapping quantization intervals, the discretization is thus known as supervised discretization[1, 3, 16], and otherwise, it is referred to as unsupervised discretization[7, 17–19].
On the other hand, information about the constructed intervals of each dimension is stored as the helper data during enrolment so as to assist reproducing the same binary string of each genuine user during the verification phase. However, similar to the security and the privacy requirements of the binary representation, it is important that such helper data, upon compromise, should neither leak any helpful information about the output binary string (security concern), nor the biometric feature itself (privacy concern).
1.1 Previous works
Over the last decade, numerous biometric discretization techniques for producing a binary string from a given set of features of each user have been reported. These schemes base upon either a fixed-bit allocation principle (assigning a fixed number of bits to each feature dimension) [4–7, 10, 13, 16, 20] or a dynamic-bit allocation principle (assigning a different number of bits to each feature dimension) [1, 3, 17–19, 21].
Monrose et al. [4, 5], Teoh et al. [6], and Verbitsky et al. [13] partition each feature space into two intervals (labeled by '0' and '1') based on a prefix threshold. Tuyls et al. [12] and Kevenaar et al. [9] have used a similar 1-bit discretization technique, but instead of fixing the threshold, the mean of the background probability density function (for modeling inter-class variation) is selected as the threshold in each dimension. Further, reliable components are identified based on either the training bit statistics [12] or a reliability (RL) function [9] so that unreliable dimensions can be eliminated from bits' extraction.
Kelkboom et al. have analytically expressed the genuine and imposter bit error probability [22] and subsequently modeled a discretization framework [23] to analytically estimate the genuine and imposter Hamming distance probability mass functions (pmf) of a biometric system. This model is based upon a static 1-bit equal-probable discretization under the assumption that both intra-class and inter-class variations are Gaussian distributed.
Han et al. [20] proposed a discretization technique to extract a 9-bit pin from each user's fingerprint impressions. The discretization derives the first 6 bits from six pre-identified reliable/stable minutiae: If a minutia belongs to bifurcation, a bit "0" is assigned; otherwise, if it is a ridge ending, a bit "1" is assigned. The derivation of the last 3 bits is constituted by a single-bit discretization on each of three triangular features. If the biometric password/pin is used directly as a cryptographic key in security applications, it will be too short to survive brute force attacks, as an adversary would only require at most 512 attempts to crack the biometric password.
Hao and Chan [3] and Chang et al. [1] employed a multi-bit supervised user-specific biometric discretization scheme, each with a different interval-handling technique. Both schemes initially fix the position of the genuine interval of each dimension dimension around the modeled pdf of the j th user: [μ j -kσ j , μ j +kσ j ] and then construct the remaining intervals based on a constant width of 2kσ j within every feature space. Here, μ j and σ j denote mean and standard deviation (SD) of the user pdf, respectively and k is a free parameter. As for the boundary portions at both ends on each feature space, Hao and Chan unfold every feature space arbitrarily to include all the remaining possible feature values in forming the leftmost and rightmost boundary intervals. Then, all the constructed intervals are labeled with direct binary representation (DBR) encoding elements (i.e. 310 → 0112, 410 → 1002, 510 → 1012). On the other hand, Chang et al. extend each feature space to account for the extra equal-width intervals to form 2 n intervals in accordance to the entire 2 n codeword labels from each n-bit DBR encoding scheme.
Although both these schemes are able to generate binary strings of arbitrary length, they turn out to be greatly inefficient, since the ad-hoc interval handling strategies may probably result in considerable leakage of entropy which will jeopardize the security of the users. In particular, the non-feasible labels of all extra intervals (including the boundary intervals) would allow an adversary to eliminate the corresponding codeword labels from her or his output-guessing range after observing the helper data, or after reliably identifying the "fake" intervals. Apart from this security issue, another critical problem with these two schemes is the potential exposure of the exact location of each genuine user pdf. Based on the knowledge that the user pdf is located at the center of the genuine interval, the constructed intervals thus serve as a clue at which the user pdf could be located to the adversary. As a result, the possible locations of user pdf could be reduced to the amount of quantization intervals in that dimension, thus potentially facilitating malicious privacy violation attempt.
Chen et al. [16] demonstrated a likelihood-ratio-based multi-bit biometric discretization scheme which is likewise to be supervised and user specific. The quantization scheme first constructs the genuine interval to accommodate the likelihood ratio (LR) detected in that dimension and creates the remaining intervals in an equal-probable (EP) manner so that the background probability mass is equally distributed within every interval. The leftmost and rightmost boundary intervals with insufficient background probability mass are wrapped into a single interval that is tagged with a common codeword label from the binary reflected gray code (BRGC)-encoding scheme [24] (i.e., 310 → 0102, 410 → 1102, 510 → 1112). This discretization scheme suffers from the same privacy problem as the previous supervised schemes owing to that the genuine interval is constructed based on the user-specific information.
Yip et al. [7] presented an unsupervised, non-user specific, multi-bit discretization scheme based on equal-width intervals' quantization and BRGC encoding. This scheme adopts the entire BRGC code for labeling, and therefore, it is free from the entropy loss problem. Furthermore, since it does not make use of the user pdf to determine the cut points of the quantization intervals, this scheme does not seem to suffer from the aforementioned privacy problem.
Teoh et al. [18, 19] developed a bit-allocation approach based on an unsupervised equal-width quantization with a BRGC-encoding scheme to compose a long binary string per user by assigning different number of bits to each feature dimension according to the SD of each estimated user pdf. Particularly, the intention is to assign a larger quantity of binary bits to discriminative dimensions and smaller otherwise. In other words, the larger the SD of a user pdf is detected to be, the lesser the quantity of bits will be assigned to that dimension and vice versa. Nevertheless, the length of the binary string is not decided based on the actual position of the pdf itself in the feature space. Although this scheme is invulnerable to the privacy weakness, such a deciding strategy gives a less accurate bit allocation: A user pdf falling across an interval boundary may result in an undesired intra-class variation in the Hamming domain and thus should not be prioritized for bit extraction. Another concern is that pure SD might not be a promising discriminative measure.
Chen et al. [17] introduced another dynamic bit-allocation approach by considering detection rate (DR) (user probability mass captured by the genuine interval) as their bit-allocation measure. The scheme, known as DR-optimized bit-allocation (DROBA), employs an equal-probable quantization intervals construction with BRGC encoding. Similar to Teoh et al.'s dynamic bit allocation scheme, this scheme assigns more bits to more discriminative feature dimensions and vice versa. Recently, Chen et al. [21] developed a similar dynamic bit-allocation algorithm based on optimizing a different bit-allocation measure: area under the FRR curve. Given the bit-error probability, the scheme allocates bits dynamically to every feature component in a similar way as DROBA except that the analytic area under the FRR curve for Hamming distance evaluation is minimized instead of DR maximization.
1.2 Motivation and contributions
It has been recently justified that DBR- and BRGC-encoding-based discretization could not guarantee a discriminative performance when a large per-dimensional entropy requirement is imposed [25]. The reason lies in the underlying indefinite feature mapping of DBR and BRGC codes from a discrete to a Hamming space, causing the actual distance dissimilarity in the Hamming domain unable to be maintained. As a result, feature points from multiple different intervals may be mapped to DBR or BRGC codewords which share a common Hamming distance away from a reference codeword, as illustrated by the 3-bit discretization instance in Figure 2. For this reason, regardless of how discriminative the extracted (real-valued) features could be, deriving discriminative and informative binary strings with DBR or BRGC encoding will not be practically feasible.
Linearly separable Subcode (LSSC) [25] has been put forward to resolve such a performance-entropy tradeoff by introducing bit redundancy to maintain the performance accuracy when a high entropy requirement is imposed. Although the resultant LSSC-extracted binary strings require a larger bit length in addressing an 8-interval discretization problem as exemplified in Figure 3, mapping discrete elements to the Hamming space becomes completely definite.
This article focuses on discretization basing upon the fixed bit-allocation principle. We extend the study of [25] to tackle the open problem of generating desirable binary strings that are simultaneously highly discriminative, informative, and privacy-protective by means of discretization based on LSSC. Specifically, we adopt a discriminative feature extraction with a further feature selection to extract discriminative feature components; an unsupervised quantization approach to offer promising privacy protection; and an LSSC encoding to achieve large entropy without having to sacrifice the actual classification performance accuracy of the discriminative feature components. Note that the preliminary idea of this article has appeared in the context of global discretization [26] for achieving strong security and privacy protection with high training efficiency.
In general, the significance of our contribution is three-fold:
-
a)
We propose a fixed bit-allocation-based discretization approach to extract a binary representation which is able to fulfill all the required criteria from each given set of user-specific features.
-
b)
Required by our approach, we study empirically various discriminative measures that have been put forward for feature selection and identify the reliable ones among them.
-
c)
We identify and analyze factors that influence improvements resulting from the discriminative selection based on the respective measures.
The structure of this article is organized as follows. In the next section, the efficiency of using LSSC over BRGC and DBR for encoding is highlighted. In section 3, detailed descriptions about our approach in generating desirable binary representation will be given and elaborated. In section 4, experimental results justifying the effectiveness of our approach are presented. Finally, concluding remarks are provided in Section 5.
2. The emergence of LSSC
2.1 The security-performance tradeoff of DBR and BRGC
Two common encoding schemes adopted for discretization, before LSSC is introduced, are DBR and BRGC. DBR has each of its decimal indices directly converted into its binary equivalent, while BRGC is a special code that restricts the Hamming distance between every consecutive pair of codewords to unity. Depending on the required size S of a code, the length of both DBR and BRGC are commonly selected to be nDBR = ⌈log2S⌉. Instances of DBR and BRGC with different lengths (nDBR and nBRGC respectively) and sizes S are shown in Table 1. Here, the length of a code refers to the number of bits in which the codewords are represented, while the size of a code refers to the number of elements in a code. The codewords are indexed from 0 to S-1. Note that each codeword index corresponds to the quantization interval index as well.
Conventionally, a tradeoff between discretization performance and entropy length is inevitable when DBR or BRGC is adopted as the encoding scheme. The rationale behind was identified to be the indefinite discrete-to-binary mapping behavior during the discretization process, since the employment of an encoding scheme in general affects only on how each index of the quantization intervals is mapped to a unique binary codeword. More precisely, one may carefully notice that multiple DBR as well as BRGC codewords share a common Hamming distance with respect to any reference codeword in the code for nDBR and nBRGC ≥ 2, mapping possibly most initially well-separated imposter feature elements from a genuine feature element in the index space much nearer than it should be in the Hamming space. Taking 4-bit DBR-based discretization as an example, the interval labelled with "1000", located 8 intervals away from the reference interval "0000", is eventually mapped to one Hamming distance away in the Hamming space. Worse for BRGC, interval "1000" is located even further (15 intervals away) from interval '0000'. As a result, imposter feature components might be misclassified as genuine in the Hamming domain and eventually, the discretization performance would be greatly impeded by such an imprecise discrete-to-binary map. In fact, this defective phenomenon gets more critical as the required entropy increases, or as S increases [25].
2.2 LSSC
Linearly separable subcode (LSSC) [25] was put forward to tackle the aforementioned inabilities of DBR and BRGC effectively in fully preserving the separation of feature points in the index domain when the eventual distance evaluation is performed in the Hamming domain. This code particularly utilizes redundancy to augment the separability in the Hamming space for enabling one-to-one correspondence between every non-reference codeword and the Hamming distance incurred with respect to every possible reference codeword.
Let nLSSC denotes the code length of LSSC. An LSSC contains S = (nLSSC + 1) codewords, that is a subset of codewords (in total). The construction of LSSC can be given as follows: Beginning with an arbitrary nLSSC-bit codeword, say, an all zero codeword, the next nLSSC codewords can be sequentially derived by complementing a bit at a time from the lowest-order (rightmost) to the highest-order (leftmost) bit position. The resultant nLSSC-bit LSSCs in fulfilling S = 4, 8 and 16 are shown in Table 2.
The amount of bit disagreement, or equivalently the Hamming distance between any pair of codewords happens to be the same as the corresponding positive index difference. For a 3-bit LSSC, as an example, the Hamming distance between codewords "111" and "001" is 2, which appears to be equal to the difference between the codeword index "3" and "1". It is in general not difficult to observe that neighbour codewords tend to have a smaller Hamming distance compared to any distant codewords. Thus, unlike DBR and BRGC, LSSC ensures every distance in the index space being thoroughly preserved in the Hamming space, despite the large bit redundancy a system might need to afford. As reported in [25], increasing the entropy per dimension has a trivial effect on discretization performance through the employment of LSSC, with the condition that the quantity of quantization intervals constructed in each dimension is not too few. Instead, the entropy now becomes a function of the bit redundancy incurred.
3. Desirable bit string generation and the appropriate discriminative measures
In the literature review, we have seen that user-specific information (i.e., user pdf) should not be utilized to define cut points of the quantization intervals to avoid reduction of possible locations of user pdf to the quantity of intervals in each dimension. Therefore, strong privacy protection basically limits the choice of quantization to unsupervised techniques. Furthermore, the entropy-performance independence aspect of LSSC encoding allows promising performance to be preserved regardless of how large the entropy is augmented per dimension, and correspondingly how large the quantity of feature-space segmentation in each dimension would be. Therefore, if we are able to extract discriminative feature components for discretization, deriving discriminative, informative, and privacy-protective bit strings can thus be absolutely possible. Our strategy can generally be outlined in the four following fundamental steps:
-
i.
[Feature Extraction]-Employ a discriminative feature extractor ℑ(·) (i.e., Fisher’s linear discriminant analysis (FDA) [27], Eigenfeature regularization and extraction (ERE) [28]) to ensure D quality features being extracted from R raw features;
-
ii.
[Feature Selection]-Select D fs(D fs < D < R) most discriminative feature components from a total of D dimensions according to a discriminative measure χ(·);
-
iii.
[Quantization]-Adopt an unsupervised equal-probable quantization scheme Q(·) to achieve strong privacy protection; and
-
iv.
[Encoding]-Employ LSSC for encoding ℰ LSSC(·) to maintain such discriminative performance, while satisfying arbitrary entropy requirement imposed on the resultant binary string.
This approach initially obtains a set of discriminative feature components in steps (i) and (ii); and produces an informative user-specific binary string (with large entropy) while maintaining the prior discriminative performance in steps (iii) and (iv). The privacy protection is offered by unsupervised quantization in step (iii), where the correlation of helper data with the user-specific data is insignificant. This makes our four-step approach to be capable of producing discriminative, informative, and privacy-protective binary biometric representation.
Among the steps, implementations of (i), (iii), and (iv) are pretty straightforward. The only uncertainty lies in the appropriate discriminative measure and the corresponding parameter Dfs in step (ii) for attaining absolute superiority. Note that step (ii) is embedded particularly to supplement the restrictive performance led by employment of unsupervised quantization. Here, we introduce a couple of discriminative measures that can be adopted for discretization and perform a study on the superiority of such measures in the next section.
3.1 Discriminative measures X(·) for feature selection
The discriminativeness of each feature component is closely related to the well-known Fisher's linear discriminant criterion [27], where the discriminant criterion is defined to be the ratio of between-class variance(inter-class variation) to within-class variance (intra-class variation).
Suppose that we have J users enrolled to a biometric system, where each of them is represented by a total of D-ordered feature elements upon feature extraction from each measurement. In view of potential intra-class variation, the d th feature element of the j th user can be modeled from a set of measurements by a user pdf, denoted by where d ∈ {1, 2,...,D}, j ∈ {1, 2,...,J} and v ∈ feature space . On the other hand, owing to inter-class variation, the d th feature element of the measurements of the entire population can be modeled by a background pdf, denoted by fd (v). Both distributions are assumed to be Gaussian according to the central limit theorem. That is, the d th-dimensional background pdf has mean μd and SD σd while the j th user's d th-dimensional user pdf has mean and variance .
3.1.1. Likelihood ratio (χ= LR)
The idea of using LR to achieve optimal FAR/FRR performance in static discretization was first exploited by Chen et al. [16]. The LR of the j th user in the d th dimensional feature space is generally defined as
with the assumption that the entire population is sufficiently large (excluding a single user should not have any significant effect in changing the background distribution). In their scheme, the cut points of the j-th user's genuine interval in the d th-dimensional feature space are chosen based on a prefix threshold t, such that
The remaining intervals are then constructed equal-probably, that is, with reference to the portion of background distribution captured by the genuine interval. Since different users will have different intervals constructed in each feature dimension, this discretization approach turns out to be user specific.
In fact, the LR could be used to assess discriminativity of each feature component efficiently, since is reversely proportional to because , or equivalently the d th dimensional intra-class variation; and fd (v) is reversely proportional to the d th dimensional inter-class variation, which imply
Therefore, adopting Dfs dimensions with maximum LR would be equivalent to selecting Dfs feature elements with maximum inter- over intra-class variation.
3.1.2. Signal-to-noise ratio (χ= SNR)
Signal-to-noise ratio (SNR) could possibly be another alternative to discriminative measurement, since it is a measure that captures both intra-class and inter-class variations. This measure was first used in feature selection by a user-specific 1-bit RL-based discretization scheme [12] to sort the feature elements which are identified to be reliable. However, instead of using the default average intra-class variance to define SNR, we adopt the user-specific intra-class variance to compute the user-specific SNR for each feature component to obtain an improved precision:
3.1.3. Reliability (χ = RL)
Reliability was employed by Kevenaar et al. [9] to sort the discriminability of the feature components in their user-specific 1-bit-discretization scheme. Thus, it can be implemented in a straightforward manner in our study. The definition of this measure is given by
where erf is the error function. This RL measure would produce a higher value when a feature element has a larger difference between and μd relative to . As a result, a high RL measurement indicates a high discriminating power of a feature component.
3.1.4. Standard deviation (χ = SD)
In dynamic discretization, the amount of bits allocated to a feature dimension indicates how discriminative the user-specific feature component is detected to be. Usually, a more discriminative feature component is assigned with a larger quantity of bits and vice versa. The pure user-specific SD measure signifying intra-class variance, was adopted by Teoh et al. as a bit-allocation measure [18, 19] and hence may serve as a potential discriminative measure.
3.1.5. Detection rate (χ = DR)
Finally, unlike all the above measures that depend solely on the statistical distribution in determining the discrimination of the feature components, DR could be another efficient discriminative measure for discretization that takes into account an additional factor: the position of the user pdf with reference to the constructed genuine interval (the interval that captures the largest portion of the user pdf) in each dimension. This measure, as adopted by Chen et al. in their dynamic bit-allocation scheme [17], is defined as the area under curve of the user pdf enclosed by the genuine interval upon the respective intervals construction in that dimension. It can be described mathematically by
where denotes the j th user's DR in the d th dimension and Sd denotes the number of constructed intervals in the d th dimension.
To select Dfs discriminative feature dimensions properly, schemes employing LR, SNR, RL, and DR measures should take dimensions with the Dfs largest measurements
while schemes employing SD measure should adopt dimensions with the D fs smallest measurements:
We shall empirically identify discriminative measures that can be reliably employed in the next section.
3.2 Discussions and a summary of our approach
In a biometric-based cryptographic key generation application, there is usually an entropy requirement L imposed on the binary output of the discretization scheme. Based on a fixed-bit-allocation principle, L is equally divided by D dimensions for typical equal-probable discretization schemes and by Dfs dimensions for our feature selection approach. Since the entropy per dimension l is logarithmically proportional to the number of equal-probable intervals S (or lfs & Sfs for our approach) constructed in each dimension, this can be written as
or
By denoting n as the bit length of each one-dimensional binary output, the actual bit length N of the final bit string is simply N = Dn; while for LSSC-encoding-based schemes where nLSSC = (2 l - 1) bits, and for our approach where bits, the actual bit length NLSSC and NLSSC(fs) can respectively be described by
and
With the above equations, we illustrate the algorithmic description of our approach in Figure 4. Here, γ and d* are dimensional variables, and || denotes binary concatenation operator.
4. Experiments and analysis
4.1. Experiment set-up
Two popular face datasets are selected to evaluate the experimental discretization performance in this section:
FERET
This employed dataset is a subset of the FERET face dataset [29], in which the images were collected under varying illumination conditions and face expressions. It contains a total of 1800 images with 12 images for each of 150 users.
FRGC
The adopted dataset is a subset of the FRGC dataset (version 2) [30], containing a total of 2124 images with 12 images for each of the 177 identities. The images were taken under controlled illumination condition.
For both datasets, proper alignment is applied to the images based on standard face landmarks. Owing to possible strong variation in hair style, only the face region is extracted for recognition by cropping the images to the size of 30 × 36 for FERET dataset and 61 × 73 for FRGC dataset. Finally, histogram equalization is applied to the cropped images.
Half of each identity's images are used for training, while the remaining half are used for testing. For measuring the system's false acceptance rate (FAR), each image of the corresponding user is matched against that of every other user according to its corresponding image index, while for the False Rejection Rate (FRR) evaluation, each image is matched against every other images of the same user for every user. In the subsequent experiments, the equal error rate (EER) (error rate where FAR = FRR) is used for comparing the discretization performance among different discretization schemes, since it is a quick and convenient way to compare the performance accuracy of the discretizations. Basically, the performance is considered to be better when the EER is lower.
The experiments can be divided into three parts: The first part identifies the reliable discriminative feature selection measures among those listed in the previous section. The second part examines the performance of our approach and illustrates that replacing LSSC with DBR- or BRGC-encoding scheme in our approach would achieve a much poorer performance when high entropy is imposed because of the conventional performance-entropy tradeoff of DBR- and BRGC-encoding-based discretization; The last part scrutinizes and reveals how one could attain reliable parameter estimation, i.e., Dfs, in achieving the highest possible discretization performance.
The experiments were carried out based on two different dimensionality-reduction techniques: ERE [28] and FDA [27], and two different datasets: FRGC and FERET. In the first two parts of the experiments, 4453 raw dimensions of FRGC images and 1080 raw dimensions of FERET images were both reduced to D = 100 dimensions. While for the last part, the raw dimensions of images from both datasets were reduced to D = 50 and 100 dimensions for analytic purpose. Note that EP quantization was employed in all parts of experiment.
4.2. Performance assessment
4.2.1. Experiment Part I: Identification of reliable feature-selection measures
Based on the fixed-bit-allocation principle, n bits are assigned equally to each of the D feature dimensions. A Dn-bit binary string is then extracted for each user through concatenating n-bit binary outputs of the individual dimensions. Since DBR as well as BRGC is a code which comprise the entire 2 n n-bit codewords for labelling S = 2 n intervals in every dimension, the single-dimensional l can be deduced from (9) as
The total entropy L is then equal to the length of the binary string:
Note that L = 100, 200, 300 and 400 correspond to n = 1, 2, 3 and 4, respectively, for each baseline scheme (D = 100). For the feature-selection-based discretization schemes to provide the same amount of entropy (with nfs and lfs denoting the number of bits and the entropy of each selected dimension, respectively), we have
With this, L = 100, 200, 300 and 400 correspond to l fs = n fs = 2, 4, 6 and 8 respectively, for Dfs = 50. This implies that the number of segmentation in each selected feature dimension is now larger than the usual case by a factor of .
For LSSC encoding scheme which utilizes longer codewords than DBR and BRGC in each dimension to fulfil a system-specified entropy requirement, the relation between bit length nLSSC and single-dimensional entropy l can be described by
and for our approach, we have
from (10).
For the baseline discretization scheme of EP + LSSC with D = 100, L = Dl = D log2(n LSSC + 1) = 100log2(n LSSC + 1). Thus, L = {100, 200, 300, 400} corresponds to l = {1, 2, 3, 4}, nLSSC = {1, 3, 7, 15} and the actual length of the extracted bit string is DnLSSC = {100, 300, 700, 1500}. While for the feature-selection schemes with Dfs = 50 where L = D fs l fs = D fs log2(nLSSC(fs)+1) = 50log2(nLSSC(fs)+1), L = {100, 200, 300, 400} corresponds to lfs = {2, 4, 6, 8}, nLSSC(fs) = {3, 15, 63, 255} and the actual length of the extracted bit string becomes DfsnLSSC(fs) = {150, 750, 3150, 12750}. The implication here is that when a particularly large entropy specification is imposed on a feature selection scheme, a much longer LSSC-generated bit string will always be required.
Figure 5 illustrates the EER performance of (I) EP + DBR, (II) EP + BRGC, and (III) EP + LSSC discretization schemes which adopt different discriminative measures-based feature selections with respect to that of the baseline (discretization without feature selection where Dfs = D) based on (a) FERET and (b) FRGC datasets. "Max" and "Min" in each subfigure are referred to as whether Dfs largest or smallest measurements were adopted corresponding to each feature selection method, as illustrated in (7) and (8).
EER performance of EP + DBR, EP + BRGC, and EP + LSSC discretizations with feature selection ( D fs = 50) applied on FDA-extracted features. (a) FERET and (b) FRGC datasets were adopted. The baseline is referred to as the reference scheme without feature-selection capability (discretization of all D = 100 feature dimensions).
A great discretization performance achieved by a feature-selection scheme basically implies a reliable measure for estimating the discriminativity of the features. In all the subfigures, it is noticed that the discretization schemes that select features based on the LR, RL, and DR measures give the best performance among the feature selection schemes. RL seems to be the most reliable discriminative measure, followed by LR and DR. In contrast, SNR and SD turn out to be some poor discriminative measures that could not guarantee any improvement compared to the baseline scheme.
When LSSC encoding in our 4-step approach (see Section 3) is replaced with DBR in Figure 5Ia, Ib; and BRGC in Figure 5IIa, IIb, RL-, LR-, and DR-based feature selection schemes manage to outperform the respective baseline scheme at low L. However, in most cases, these DBR- and BRGC-encoding-based discretization schemes with feature selection are found to underperform their baseline eventually when high entropy requirement is imposed. The reason is that the utilized dimensions in such feature selection schemes are reduced by half, causing the partitioning on each feature space to be augmented more rapidly by a factor of and thus yielding relatively increasing imprecision of discrete-to-binary mapping as the entropy requirement increases. For this reason, significant performance degradation with respect to the baseline can finally be noticed at L = 400 in Figure 5Ia, Ib, IIa. Hence, when entropy increases, the EER performance lines of RL-, LR- and DR-based feature-selection schemes usually have steeper increments (degradation) than that of the baseline.
On the other hand, in Figure 5IIIa, IIIb where LSSC encoding is adopted, it is observed that RL-, LR- and DR-based feature-selection schemes outperform their baseline consistently for all values of L, except for DR-based feature selection scheme, when L ≤ 200 in Figure 5IIIa. This particularly justifies that precise discrete-to-binary mapping of LSSC is essential to enable an effective feature selection-incorporated discretization process when a large entropy requirement is imposed.
4.2.2. Experiment Part II: Performance evaluation of EP + LSSC discretization with RL-, LR- and DR-based feature-selection capabilities
Figure 6 depicts the (a) EER plots and (b) ROC plots of EP + DBR, EP + BRGC, and EP + LSSC discretization schemes with reliable feature-selection schemes (identified in part I) applied to ERE-extracted features from (I) FERET, and (II) FRGC datasets.
EER and ROC performances of EP + DBR, EP + BRGC, and EP + LSSC discretizations with reliable feature selection ( D fs = 50) ERE feature extraction and FERET and FRGC datasets were adopted. The baseline is referred to as the reference scheme without feature-selection capability (discretization of all D = 100 feature dimensions).
From the EER plots in Figure 6Ia, IIa, it is noticed that DBR and BRGC baselines share a common behavior-the deterioration of EER performance as L, or l for every dimension, or proportionally S for every dimension increases. Such an observation justifies the imprecise discrete-to-binary mapping of DBR- and BRGC-encoding-based discretization. Because the fact that the difference between any pair of interval indices is not equal to the Hamming distance incurred between the corresponding DBR and BRGC codeword labels, the separation of feature components in the Hamming domain will eventually become poorer when more and more segmentations are applied to each single-dimensional feature space.
On the other hand, LSSC baseline has its performance stabilized, although with some trivial fluctuations, consistently in Figure 6IIa; and beyond L = 300(l = 3) in Figure 6Ia. Similar performance trend (except with earlier stabilization beyond L = 200 (lfs = 4) can be observed with LSSC encoding-based discretizations with LR-, RL-, and DR-based feature selection in these two subfigures. This observation basically implies that, irrespective of the entropy requirement imposed on the discretization output, the performance led by discriminative feature selection can reliably be preserved. Therefore, along with the employment of an unsupervised quantization approach, binary strings that fulfil all three desired criteria: discriminative, informative, and privacy protective can potentially be derived.
From both EER and ROC plots in Figure 6, the performance curves of LSSC-encoding-based discretizations with LR-, RL-, and DR-based feature selection are very close to one another. It is believed that such a trivial performance discrepancies among them are probably caused by the slight fluctuation inherent to LSSC-based schemes as the entropy requirement is increased. At L = 300, the outperformance of feature-selection schemes to the baseline can averagely be quantified by 2% in Figure 6Ia and 8% in Figure 6IIa. With 0.1% FAR, approximately 5% GAR improvement in Figure 6Ib and 10% GAR improvement in Figure 6IIb are observed.
For LSSC-encoding-based discretization, it is worthy of note that the improvements of RL-, DR-, and LR-discriminative feature selections in FERET dataset is less significant compared to those in FRGC dataset. This could be explained by the fact that decision made by a feature-selecting process on a given set of features may not be ideal due to indefinite pdf estimation from a limited number of training samples. Some indiscriminative feature dimensions may be mistakenly selected. Vice versa, some significantly discriminative dimensions may be excluded by mistake for a similar reason. Therefore, to what extent the influence of a feature selection on a certain baseline performance would greatly depend on the accuracy of the pdf estimation which could range distinctively in accordance with different extracted sets of features. In other words, the quality of the unselected feature dimensions decides the amount of improvement with respect to the baseline. If the excluded feature dimensions are truly the least discriminative dimensions, then the improvement will be the greatest. Otherwise, if the excluded feature dimensions are somehow discriminative, the improvement will be minor; or even worse, performance deterioration could occur. This signifies that the user pdf modelled from as many representative training samples as possible to avoid such trivial improvement or deterioration scenarios. This implies that there is a higher number of less-discriminative ERE-extractable feature components from FRGC dataset than from FERET dataset, where the improvement attained in FRGC-based experiment is generally higher than in FERET-based experiment when the exclusion of those less-discriminative components is precisely made.
4.2.3. Experiment part III: A meticulous analysis on EP + LSSC discretization with LR-, RL- and DR-based feature-selection capability
We have seen in part II that the performance of LSSC-based discretization will be driven into a stable state with a trivial level of fluctuations beyond a certain entropy threshold. On the basis of this observation, it is interesting to find out whether it is possible to estimate a proper range of Dfs values to achieve the lowest possible EER in practice for all kinds of experiment settings; and what are the other aspects that a practitioner should take note when selecting Dfs in the real world implementation. We shall address these issues in the sequel based on LR, RL, and DR discriminative measures that have proven their usefulness in the previous subsections.
In the last part of our experiment, we have varied the number of users (60 and 200 users for FERET dataset; and 75 and 150 users for FRGC dataset) and the number of extracted dimensions (D = 50 for FDA; and D = 100 for ERE) to observe the performance of the discretization schemes in relation to Dfs. The objective for the former parameter variation is to find the minimum Dfs that could possibly represent a large/small number of users globally; however, for the latter variation, our aim is to examine the improvement of the feature-selection schemes with respect to the baseline in accordance with large/small value of D.
Figure 7 depicts the stable-state performance (for lfs = 6) of EP + LSSC feature selection schemes based on two different numbers of (I) FDA- and (II) ERE-extracted features and two different number of users involved in (a) FERET and (b) FRGC datasets. Besides this, a summary of the best Dfs value associated with the lowest EER is provided in Table 3 to identify the minimum number of dimensions to represent each specific number of users efficiently.
In Figure 7, an interesting observation applied to all performance curves is that the EER of each discretization scheme initially decreases until some minimum point(s) before rebounds again, as the number of selected dimensions increases. To explain why this could happen, one needs to first understand that an efficient representation of a given number of users often requires at least a minimal amount of feature dimensions to be utilized to avoid any bit pattern being similarly repeated among other users. Taking performance curves in Figure 7Ia, IIa as an instance, using Dfs = 5 to represent 60 users and 200 users are apparently not as effective as using Dfs = 12, even though Dfs = 12 could have utilized seven additional less-discriminative dimensions which may, in an intuitive sense, give a lower classification performance. Beyond the optimal Dfs value that produces the minimum-EER performance, this is where our prior elucidation holds: the more the less-discriminative dimensions are being utilized, the worse the discretization performance would be.
In Table 3, it is noticed that determining the minimum Dfs which best represent any specific number of users for all kinds of experiment settings is infeasible. This can be seen from the contradiction that FDA-extracted features with D = 50 requires merely 10, 15, and 12 feature dimensions minimally to best represent 200 users from the FERET database for LR-, RL-, and DR-discriminative measures respectively; while ERE extracted features with D = 100 requires at least 20, 25 and 20 features to efficiently represent only 75 users from FRGC database for the three selection measures, respectively. We believe that this could be influenced by different distribution of discriminative measurements for all users according to different feature-extraction methods.
Nonetheless, given a particular quantity of users under an experiment setting, determining the proper value of Dfs should not only rely on the performance aspect. In fact, the amount of bit redundancy should also be taken into consideration. Recall in the previous subsection that the lower the Dfs is set, the higher the bit redundancy per user a system would have to afford in order to fulfill a specified system entropy. Therefore, a practical strategy would be to identify the system capability in processing bit redundancy of all users before setting the exact value of Dfs subject to the condition that the value of Dfs should not be chosen too small to avoid inefficient user-representation problem.
4.3. Summary
In a nutshell, our findings can be summarized in the following aspects:
-
BRGC- and DBR-encoding schemes are not appropriate for being employed to generate highly discriminative, informative, and privacy protective bit strings due to its inability to uphold the perfect discrete-to-binary mapping behavior for performance preservation when high entropy requirement is imposed.
-
Since LSSC-encoding scheme is able to maintain the discriminativity of the (selected) feature components and drive it into a stable state (with insignificant fluctuations) irrespective of how high the entropy requirement could be, this encoding scheme appears to be extremely useful when it comes to discriminative and informative bit-string generations.
-
Our approach integrates high-quality feature extraction, discriminative feature selection, unsupervised quantization and LSSC encoding to address the performance, security, and privacy criteria of a binary representation. Among the five discriminative measures in our evaluation, LR, RL, and DR measures exhibit promising discretization performance when they are adopted in our approach.
-
In general, the improvement amount of our feature-selection-based approach with reference to the baseline can be influenced by the following three factors:
-
› The quality of the discriminative measures - LR, RL, and DR are among the reliable ones.
-
› The accuracy of pdf estimations that could greatly affect the decision of feature selection - it all depends on how reliable and representative the training samples are.
-
› The discriminativity of the unselected feature dimensions - the noisier such feature dimensions are, the higher the improvement would be.
-
-
A tradeoff exists between the redundancy of the bit string and the tunable value of the free parameter Dfs. The lower Dfs is set, the higher the bit redundancy results. Thus, the bit redundancy-processing capability should always be considered before by a system practitioner when setting Dfs, rather than minimizing it arbitrarily with the aim of attaining the minimum-EER performance. Note also that over-minimizing Dfs may lead to inefficient user representation.
5. Conclusion
In this article, we have proposed a four-step approach to generate highly discriminative, informative, and privacy-protective binary representations based on a fixed-bit-allocation principle. The four steps include discriminative feature extraction, discriminative feature selection, equal-probable quantization, and LSSC encoding. Although our binary strings are capable of fulfilling the desired criteria, the binary strings could be significantly longer than any typical static bit-allocation approach due to the employment of LSSC encoding and feature selection, thus requiring advanced storage and processing capabilities of the biometric system. We have investigated a couple of existing measures to identify reliable candidates for discretization. Experimental results showed that LR, RL, and DR are among the best discriminative measures and a discretization scheme that employ any of these feature-selection measures could guarantee a substantial amount of performance improvement compared to the baseline. The free parameter for feature selection, that is, the number of selected dimensions Dfs should be cautiously fixed. This parameter should not be set too small to avoid inefficient user representation problem and enormous bit redundancy overhead. Also, it should not be fixed too large to avoid trivial improvement relative to the baseline.
References
Chang Y, Zhang W, Chen T: Biometric-Based Cryptographic Key Generation. IEEE International Conference on Multimedia and Expo (ICME 2004) 2004, 3: 2203-2206.
Dodis Y, Ostrovsky R, Reyzin L, Smith A, in Fuzzy Extractors: How to Generate Strong Keys from Biometrics and Other Noisy Data. EuroCrypt 2004, LNCS 2004, 3027: 523-540. 10.1007/978-3-540-24676-3_31
Hao F, Chan CW: Private key generation from on-line handwritten signatures. Inf Manag Comput Secur 2002,10(4):159-164. 10.1108/09685220210436949
Monrose F, Reiter MK, Li Q, Wetzel S: Cryptographic Key Generation from Voice. IEEE Symposium on Security and Privacy (S&P 2001) 2001, 202-213.
Monrose F, Reiter MK, Li Q, Wetzel S: Using Voice to Generate Cryptographic Keys. The Speaker Verification Workshop 2001, 237-242.
Teoh ABJ, Ngo DCL, Goh A: Personalised cryptographic key generation based on FaceHashing. Comput Secur 2004,23(7):606-614. 10.1016/j.cose.2004.06.002
Yip WK, Goh A, Ngo DCL, Teoh ABJ: Generation of Replaceable Cryptographic Keys from Dynamic Handwritten Signatures. 1st International Conference on Biometrics, LNCS 2006, 3832: 509-515.
Juels A, Wattenberg M: A Fuzzy Commitment Scheme. The 6th ACM Conference in Computer and Communication Security (CCS'99) 1999, 28-36.
Kevenaar TAM, Schrijen GJ, Van der Veen M, Akkermans AHM, Zuo F: Face Recognition With Renewable and Privacy Preserving Binary Templates. The 4th IEEE Workshop on Automatic Identification Advanced Technologies (AutoID '05) 2005, 21-26.
Linnartz J-P, Tuyls P: New Shielding Functions to Enhance Privacy and Prevent Misuse of Biometric Templates. 4th International Conference on Audio and Video Based Person Authentication (AVBPA 2004), LNCS 2003, 2688: 238-250.
Teoh ABJ, Goh A, Ngo DCL: Random multispace quantisation as an analytic mechanism for Biohashing of biometric and random identity inputs. IEEE Trans Pattern Anal Mach Intell 2006,28(12):1892-1901.
Tuyls P, Akkermans AHM, Kevenaar TAM, Schrijen G-J, Bazen AM, Veldhuis NJ: Practical biometric authentication with template protection. 5th International Conference on Audio- and Video-based Biometric Person Authentication, LNCS 2005, 3546: 436-446. 10.1007/11527923_45
Verbitskiy E, Tuyls P, Denteneer D, Linnartz JP: Reliable biometric authentication with privacy protection. 24th Benelux Symposium on Information Theory 2003, 125-132.
Daugman J: How iris recognition works. IEEE Trans Circuit Syst Video Technol 2004,14(1):21-30. 10.1109/TCSVT.2003.818350
Yue F, Zuo W, Zhang D, Wang K: Orientation selection using modified FCM for competitive code-based palmprint recognition. Pattern Recog 2009,4(11):2841-2849.
Chen C, Veldhuis R, Kevenaar T, Akkermans A: Multi-Bits Biometric String Generation Based on the Likelihood Ratio. IEEE International Conference on Biometrics: Theory, Applications, and System (BTAS 2007) 2007, 1-6.
Chen C, Veldhuis R, Kevenaar T, Akkermans A: Biometric quantization through detection rate optimized bit allocation. EURASIP J Adv Sig Process 2009. Article ID 784834
Teoh ABJ, Toh K-A, Yip WK: 2Ndiscretisation of biophasor in cancellable biometrics. 2nd International Conference on Biometrics (ICB 2007), LNCS 2007, 4642: 435-444.
Teoh ABJ, Yip WK, Toh K-A: Cancellable biometrics and user-dependent multi-state discretization in BioHash. Pattern Anal Appl 2009.
Han F, Hu J, He L, Wang Y: Generation of Reliable PINs from Fingerprints. IEEE International Conference on Communications (ICC '07) 2007, 1191-1196.
Chen C, Veldhuis R: Extracting biometric binary strings with minimal area under the FRR curve for the hamming distance classifier. Sig Process 2011,91(4):906-918. 10.1016/j.sigpro.2010.09.008
Kelkboom EJC, Garcia Molina G, Kevenaar TAM, Veldhuis RNJ, Jonker W: Binary Biometrics: An Analytic Framework to Estimate the Bit Error Probability Under Gaussian Assumption. Biometrics, Theory, Applications and Systems (BTAS '08) 2008, 1-6.
Kelkboom EJC, Garcia Molina G, Breebaart J, Veldhuis RNJ, Kevenaar TAM, Jonker W: Binary biometrics: An analytic framework to estimate the performance curves under Gaussian assumption. IEEE Trans Systems, Man Cybernet 2010, A 40: 555-571.
Gray F: Pulse Code Communications. U.S. Patent 2632058 1953.
Lim M-H, Teoh ABJ: Linearly Separable Subcode: A Novel Output Label With High Separability for Biometric discretization. 5th IEEE Conference on Industrial Electronics and Applications (ICIEA'10) 2010, 290-294.
Lim M-H, Teoh ABJ: Discriminative and non-user-specific binary biometric representation via linearly-separable subCode encoding-based discretization. KSII Trans Inter Inform Sys 2011,5(2):374-389.
Belhumeur PN, Kriegman JP, Kriegman DJ: Eigenfaces vs. fisherfaces: recognition using class specific linear projection. IEEE Trans Pattern Anal Mach Intell 1997,19(7):711-720. 10.1109/34.598228
Jiang XD, Mandal B, Kot A: Eigenfeature regularization and extraction in face recognition. IEEE Trans Pattern Anal Mach Intell 2008,30(3):383-394.
Philips PJ, Moon H, Rauss PJ, Rizvi S: The FERET evaluation methodology for face recognition algorithms. IEEE Trans Pattern Anal Mach Intell 2000.,22(10):
Philips PJ, Flynn PJ, Scruggs T, Bowyer KW, Chang J, Hoffman K, Marques J, Min J, Worek W: Overview of the Face Recognition Grand Challenge. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR "05) 2005, 1: 947-954.
Acknowledgements
This study was supported by the Korea Science and Engineering Foundation (KOSEF) grant funded by the Korean government (MEST) (No. 2011-8-1095).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lim, MH., Teoh, A.B.J. An effective biometric discretization approach to extract highly discriminative, informative, and privacy-protective binary representation. EURASIP J. Adv. Signal Process. 2011, 107 (2011). https://doi.org/10.1186/1687-6180-2011-107
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2011-107