Abstract
In this paper, we propose and analyze a mathematical model for the treatment of chronic myelogenous (myeloid) leukemia (CML), a cancer of the blood. Our main focus is on the combined treatment of CML based on imatinib therapy and immunotherapy. Treatment with imatinib is a molecular targeted therapy that inhibits the cells involved in the chronic CML pathogenesis. Immunotherapy based on interferon alfa-2a (IFN-α) increases cancer cell mortality and leads to improvement of outcomes of the combined therapy. Interaction between CML cancer cells and effector cells of the immune system is modeled by a system of non-linear differential equations, where we introduced biologically motivated time-varying delays in the treatment terms. The analysis of the described system shows the existence of a unique global positive solution and a unique non-trivial equilibrium. We also derive explicit local and global stability conditions for the non-trivial equilibrium.
Similar content being viewed by others
1 Introduction and biological motivation
Chronic myelogenous leukaemia (CML) is a progressive, malignant disease characterized by a large number of abnormal blood cells in the bone marrow and peripheral blood [1, 2]. The schematic progression in time of myelogenous leukemia is shown in Figure 1.
A scheme of myelogenous leukemia progression in time. Myelogenous leukemia progresses through four distinct phases. After an initial period of 3-5 years the abnormal cell counts rise to a relatively steady state, called the chronic phase. At this stage the disease can be diagnosed. Several years of the chronic phase where the abnormal cell count oscillates with a period of the order of months are followed by a phase characterized by oscillatory instability (the acceleration phase). Ultimately, this leads to the usually fatal acute phase with sharp increase in the abnormal cell count. This is known also as the blast crisis [15].
The benefit of the treatment of CML with imatinib (Gleevec (Novartis International AG, Basel, Switzerland)) was first indicated in 2000 [1, 3]. However, the loss of drug effectiveness was observed due to mutations of the target cancer cells, rendering the cells resistant to the drug [4, 5]. About 10 to 20% of patients do not respond to imatinib after prolonged therapy [6, 7].
One of the early mathematical models of CML was a model created by Fokas et al. (1991) [8] which includes hematopoietic process focused on the maturation and proliferation of the T cell precursors in the bone marrow. One of the models of anticancer CML therapy is Moore and Lee’s work [9] based on immune cell interactions with CML. Several recent mathematical models have been developed to study the dynamics of CML under imatinib treatment, including Komarova and Wodarz (2005) [10], Michor et al. (2005) [11], Nanda et al. (2007) [12], Kim et al. (2008) [13], and Paquin et al. (2011) [14]. In all of these studies, the authors conclude that imatinib does not completely eliminate the leukemia cell population and propose that imatinib therapy should be combined with an additional form of treatment.
In this paper, we present a model that combines imatinib with the interferon alfa-2α (IFN-α) immunotherapy. Including IFN-α treatment, we strengthen the immune response. We show that the immune response may play an important role in determining the length of time during treatment with imatinib for CML patients and would allow to keep the patient in the chronic stage for a longer period of time.
Recent data shows that IFN-α activation of immune cells (T killer cells, natural killer cells and others) contributes to the killing of cancer leukemic cells [16, 17]. Moreover, it is already proven that IFN-α may extend imatinib effect by activating immunological effector functions [18]. Therefore, we assume that the combination treatment of imatinib and IFN-α immunotherapy can be a good candidate to improve the current CML therapy.
The mathematical description of the above model is described in Section 2. In Section 3 we discuss the existence of a positive and unique equilibrium and prove local and global stability of this equilibrium. Section 4 validates the model results using published data taken from in vitro, mouse and human studies.
2 Model description
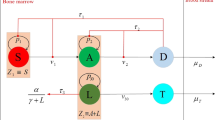
The dynamics of the interaction between the immune system (effector T cells) and CML cancer cells in the body can be described by the following system of two ordinary non-linear differential equations:
where is the CML cells population, is the number of effector T (CTL) cells and , , , , , , is a continuous function such that , , .
We will analyze system (1) behavior under the following initial conditions:
Here, we assume that , where and , where are nonnegative continuous functions where , , , .
The first term on the right-hand side of the first equation of system (1) describes the growth of CML cancer cells population in the form of the Gompertz law with the growth rate . The Gompertz curve provides a significantly better fit for leukemic cancer data than logistic, exponential or polynomial curves [9]. The constant K in the first term represents the maximum carrying capacity of CML cells compartment [19, 20]. The second term of the first equation of system (1) accounts for the loss of CML cancer cells due to their interaction with CTL cells. The third term of this equation describes inhibition of cancer cells by imatinib, where ω is a dose of imatinib given every day and is the time-varying function accounting for the delay of the impact of imatinib treatment on the number of cancer cells in the blood. The presence of such a time lag was shown by Volpe [6], who demonstrated that reduction in the number of cancer cells does not occur immediately after the start of imatinib administration but rather after a certain time period. The maximum delay time (θ) is about three weeks. The influence of drugs tends to zero over time, so a natural candidate for the delay function is . Hence, this function satisfies the condition that in the formulation of the model (1).
The second equation describes the dynamic balance between stimulatory and inhibitory effects of CTL cells. The first term represents the growth of the population of the effector CTL cells due to the influence of CML antigen in the lymph nodes, where is the rate of this growth and is the standard half-saturation concentration in the Michaelis-Menten kinetics. The second term describes the loss of CTL cells due to the interaction between CTL and CML cancer cells with a rate . CTL cells survive many hits by the target CML cells until they are inactivated and die [21]. The third term describes the stimulatory augmentation of the CTL cells due to IFN-α immunotherapy, where is the dose of IFN-α. Interferon-α leads to increased expression of other cytokines, such as interferon-γ that creates the pro-inflammatory environment with delay τ of about seven days [22]. In this term, is the standard half-saturation concentration of CTL immune within the Michaelis-Menten kinetics. Finally, the last term in the second equation describes the loss of CML cells due their natural death at a rate .
It is well known from the medical practice that the value of of the population of CML cells cannot be reduced to zero by treatment of any type, so the therapy can be called successful if the value of does not increase over time. Imatinib has a marked inhibitory effect on the value of , while IFN-α add-on has an additional effect due to the stimulation of CML cell production. From mathematical standpoint, the role of the variable is to decrease the value of .
We used the model developed by Moore and Li [9] to explore treatment combinations. The difference between our model and the model by Moore and Li [9] is that we simplified the model describing the dynamics of their system by removing the third equation accounting for the behavior of the naive effector cells. Also, we added in the first equation the term accounting for the reduction in the number of cancer cells due to drug administration, while in the second equation we added the term describing the rate of increase in the number of immune cells that results from the treatment.
In our mathematical analysis of the above system, we aspire to stabilize the value of in such a way that does not exceed the limit of cancer CML cells in blood, which is characteristic of a chronic phase. The summary of values of the parameters used in the model is presented in Table 1.
3 The local and global stability of combined model for tumor immunotherapy
3.1 Positivity and uniqueness of solution system (1)-(2)
In this section we discuss the positivity and uniqueness of the solution of system (1)-(2).
Lemma 1 [28]
Consider the initial value problem for a scalar linear delay equation
If
then , and for the solution of the inequality
one has .
Theorem 1 Suppose that , . Then system (1)-(2) has the unique global solution such that
Proof System (1) can be presented in the following form:
where , are continuous Lipschitz functions on the domain , , for any positive constants , , , , , . Using Theorem 2.2.1 from [29], we can state that there is a unique local solution of system (1)-(2). Since , , this local solution is positive.
Denote by the maximum existence interval of the system’s solution. For we have from the second equation of system (1)
Hence , .
Suppose , which means that , or there is a such that . Then so , or there is a such that , and . It is clear that , which allows us to obtain that for . Repeating the process of our reasoning, we prove that , .
The case is same as the case (2) if we replace the point .
Now, let us estimate behavior.
Having
we can state that
Denote . Then
From the well-known Gronwall-Bellman inequality, we have
Hence, the inequalities in (3) hold for .
Suppose that . Then there are only two possibilities:
-
(a)
or ;
-
(b)
or .
By inequalities (3), and are bounded on any final interval. Then (a) is impossible.
By (4) relation is also impossible.
Suppose now that . There exists such that , . Hence, the first equation in (1) implies
Consider the following initial value problem:
After substitution , equation (5) has a form
We have . Hence
Lemma 1 and the inequality , imply that , , then also , . Hence, there exists such that , . By Lemma 1 we have , . This is a contradiction to the assumption .
Hence, and the theorem is proven. □
Theorem 2 If
there is the unique equilibrium of system (1) where .
Proof It is obvious that is an equilibrium of system (1). We have to prove the uniqueness only of this equilibrium or, in another words, we have to prove there is no other equilibrium , where , .
Suppose that , where , is the equilibrium of system (1). Then, from the second equation in (1), we have
Hence,
Thus, we have
Then contradicts our assumption and, therefore, system (1) has only one equilibrium . □
In the rest of the paper we assume that the conditions of Theorems 1 and 2 hold.
3.2 Local stability of the equilibrium
To analyze local stability of the equilibrium for system (1), we will use the lemma defined below. Consider the scalar linear equation
where , .
Lemma 2 [30]
If , , then for any solution x of (8), .
Theorem 3 If
then the equilibrium is locally asymptotically stable.
Proof After substitution of , , system (1) can be rewritten in the following form:
The linearized system (10) has a form of
The second inequality (9) implies that the second equation of (11) is exponentially stable. Hence .
The first equation can be rewritten in the form (8), where , , , , , . Since and , then
By Lemma 2 . The theorem is proven. □
3.3 Global stability of the equilibrium
To analyze the global stability of the equilibrium for system (1), we will use the following lemmas.
Lemma 3 [29]
Consider the scalar linear delay differential equation
where a, b are continuous bounded on functions, h, are continuous functions, .
If , , , then the solution of the above equation is asymptotically stable.
Lemma 4 [31]
Consider the following equation and inequalities:



where a, , are continuous bounded on functions, , , are continuous functions, .
Denote by the fundamental function of equation (12). Then , . Moreover, for any , the equality , , implies , , where x, y, z are the solutions of (12), (13), (14) respectively.
Let us formulate one of the classical results by Chaplygin [32] (see also [33]).
Lemma 5 Consider the ODE and corresponding differential inequalities:
where is a continuous function. If , then , .
Theorem 4 If condition (7) holds, then for any solution of system (1), we have , , which means that is a global attractor for all solutions of system (1)-(2).
Proof Suppose is an arbitrary solution of (1). From the second equation (1) we have
By Lemma 3 we have , where u is the solution of the equation
where , . Lemma 4 implies that . Hence . The second part of the theorem is proven.
In order to prove that , at first we will show that is a bounded function. From the first equation (1), we have
Since
then for some , .
Since , then for some . Thus
and for some .
Using all the above, we can rewrite the following:
Since , then for any , there exists such that , .
And therefore,
Consider now an ODE associated with the previous differential inequality
where , and a functional equation , where
We have , . By the implicit function theorem, for small , there exists the unique solution of the equation such that . It is obvious that is a positive equilibrium of ODE (15).
For the solution of equation (15), we have , if and , if . Hence, for any solution of this equation, we have . By Lemma 5 we have , .
We also have
Since
then for any , there exists such that
Consider an ODE
Performing the same calculations as for equation (15), we can show that for small , equation (16) has the unique equilibrium such that . Hence, for any solution of equation (16), we have . By Lemma 5 we obtain , .
Thus, for , we have , . Hence
But
Hence
The theorem is proven. □
By definition, local stability and global attractivity imply global stability. Hence, we have the following result.
Theorem 5 Suppose conditions (7) and (9) hold. Then the equilibrium is globally asymptotically stable.
4 Simulation results
In order to verify the mathematical model of the biological system, it is widely accepted to estimate the conditions defined in the presented theorems based on the parameters set taken from the biological and medical literature (these parameters are taken from Table 1).
System (1) has an equilibrium where . Substituting the relevant parameters from Table 1, we get that , which means that the cancer cells number will not exceed the 23,196 cells at a constant daily dose of 400 mg imatinib.
With increasing the daily dose of imatinib to 600 mg, the amount of cancer cells decreases to almost 10,000. These numerical results are consistent with the data given in [12].
In order to check the local and global stability conditions, we substitute parameters to the expression . The following numerical inequality is received: . The obtained result supports that the model (1)-(2) has a positive stable local and global equilibrium if condition (4) is satisfied.
5 Conclusion
In this work we have proposed a mathematical model for the combination treatment of chronic myelogenous leukemia with imatinib and IFN-α to overcome immune suppressive side effects of imatinib, prolonging the chronic phase of the disease. Our model consists of a system of two non-linear delay differential equations with logarithmic and rational nonlinearities.
In order to describe the influence of two types of the treatment component (imatinib and IFN-α) on the model compartments, we introduced delays and explained a biological motivation for it. The proposed two-compartment model allows to evaluate directly the expected steady states of the system.
In our work we investigate the contribution of IFN-α (immunotherapy) in eliciting strong killer cells (CTL) responses against cancer (CML) cells in addition to imatinib therapy by examination of CTL and CML cells populations only. The dose of IFN-α has an inhibitory effect on the value of , as seen from the formula (4). As a result of calculations shown in Section 4, we observe that inhibits , destroying itself to 0 in spite of constant addition of IFN-α.
The existence of unique global solutions for CML model was defined. Explicit local and global stability conditions for the unique non-trivial equilibrium were obtained by applying the method of delays in differential inequalities and linear stability theory of non-linear delay differential equations. The numerical results show that our model replicates the averaged behavior of the combined treatment.
In the future, in order to avoid resistance to imatinib, it looks reasonable to change the IFN-α to another type of the treatment in combination with imatinib [34]. The best form of combination therapy that leads to improved survival in patients remains to be seen in future by mathematical models and clinical trials.
References
Druker BJ, Talpaz M, et al.: Efficacy and safety of a specific inhibitor of the BCR-ABL tyrosine kinase in chronic myeloid leukemia. N. Engl. J. Med. 2001, 344: 1031–1037. 10.1056/NEJM200104053441401
Faderl S, Talpaz M, Estrov Z, O’Brien S, Kurzrock R, Kantarjian H: The biology of chronic myeloid leukemia. N. Engl. J. Med. 1999, 341(3):164–172. 10.1056/NEJM199907153410306
Deininger MWN, Buchdunger E, Druker BJ: The development of imatinib as a therapeutic agent for chronic myeloid leukemia. Blood 2005, 105: 2640–2653. 10.1182/blood-2004-08-3097
O’Hare T, Eide CA, Deininger MWN: Bcr-Abl kinase domain mutations, drug resistance, and the road to a cure for chronic myeloid leukemia. Blood 2007, 110: 2242–2249. 10.1182/blood-2007-03-066936
Ramirez P, Dipersio JF: Therapy options in imatinib failures. The Oncologist 2008, 13: 424–434. 10.1634/theoncologist.2007-0170
Volpe G, Panuzzo C, Ulisciani S, Cilloni D: Imatinib resistance in CML. Cancer Lett. 2009, 274: 1. 10.1016/j.canlet.2008.06.003
Jabbour E, Fava C, Kantarjian H: Advances in the biology and therapy of patients with chronic myeloid leukaemia. Best. Pract. Res. Clin. Haematol. 2009, 22: 395–407. 10.1016/j.beha.2009.09.002
Fokas AS, Keller JB, Clarkson BD: A mathematical model of granulocytopoiesis and chronic myelogenous leukemia. Cancer 1991, 51: 2084–2091.
Moore H, Li NK: A mathematical model of chronic myelogenous leukemia (CML) and T cell interaction. J. Theor. Biol. 2004, 227: 513. 10.1016/j.jtbi.2003.11.024
Komarova N, Wodarz D: Drug resistance in cancer: principles of emergence and prevention. Proc. Natl. Acad. Sci. USA 2005, 102: 9714–9719. 10.1073/pnas.0501870102
Michor F, Hughes T, Iwasa Y, Branford S, Shah N, Sawyers C, Nowak M: Dynamics of chronic myeloid leukemia. Nature 2005, 435: 1267–1270. 10.1038/nature03669
Nanda S, Moore H, Lenhart S: Optimal control of treatment in a mathematical model of chronic myelogenous leukemia. Math. Biosci. 2007, 210: 143. 10.1016/j.mbs.2007.05.003
Kim P, Lee P, Levy D: Dynamics and potential impact of the immune response to chronic myelogenous leukemia. PLoS Comput. Biol. 2008., 4: Article ID e1000095
Paquin D, Kim PS, Lee PP, Levy D: Strategic treatment interruptions during imatinib treatment of chronic myelogenous leukemia. Bull. Math. Biol. 2011, 73: 1082–1100. 10.1007/s11538-010-9553-0
Guilhot, F, Roy, L, Martineua, G, Guilhot, J, Millot, F: Immunotherapy in chronic myelogenous leukemia. Clin Lymphoma Myeloma 7, Suppl 2:S64–70 (2007)
Montoya M, Schiavoni G, et al.: Tough, type I interferons produced by dendritic cells promote their phenotypic and functional activation. Blood 2002, 99: 3263–3271. 10.1182/blood.V99.9.3263
Burchert A, Neubauer A: Interferon alpha and T-cell responses in chronic myeloid leukemia. Leuk. Lymphoma 2005, 46(2):167–175. 10.1080/10428190400012029
Gao H, Lee BN, Talpaz M, Donato NJ, Cortes JE, Kantarjian HM, Reuben JM: Imatinib mesylate suppresses cytokine synthesis by activated CD4 T cells of patients with chronic myelogenous leukemia. Leukemia 2005, 19: 1905–1911. 10.1038/sj.leu.2403933
Laird AK: Dynamics of tumor growth. Br. J. Cancer 1964, 18: 490–502. 10.1038/bjc.1964.55
Norton L: A Gompertzian model of human breast cancer growth. Cancer Res. 1988, 48: 7067–7071.
Berke G: The binding and lysis of target cells by cytotoxic lymphocytes: molecular and cellular aspects. Annu. Rev. Immunol. 1994, 12: 735–773. 10.1146/annurev.iy.12.040194.003511
Burchert A, Muller MC, et al.: Sustained molecular response with interferon alfa maintenance after induction therapy with imatinib plus interferon alfa in patients with chronic myeloid leukemia. J. Clin. Oncol. 2010, 28: 1429–1435. 10.1200/JCO.2009.25.5075
Duvall CP, Perry S: The use of 51-chromium in the study of leukocyte kinetics in chronic myelocytic leukemia. J. Lab. Clin. Med. 1968, 71: 614–628.
Kuznetsov V, Makalkin I, Taylor M, Perelson A: Nonlinear dynamics of immunogenic tumors: parameter estimation and global bifurcation analysis. Bull. Math. Biol. 1994, 56: 295–321.
Janeway CA, Travers P, Walport M, Shlomchik M: Immunobiology: the Immune System in Health and Disease. Garland Publishing, New York; 2001.
Essunger P, Perelson AS: Modeling HIV infection of CD4+ T-cell subpopulations. J. Theor. Biol. 1994, 170: 367–391. 10.1006/jtbi.1994.1199
Preudhomme C, Guilhot J, Nicolini FE, et al.: Imatinib plus peginterferon alfa-2a in chronic myeloid leukemia. N. Engl. J. Med. 2010, 363(26):2511–2521. 10.1056/NEJMoa1004095
Gyóri I, Ladas G Oxford Mathematical Monographs. In Oscillation Theory of Delay Differential Equations with Applications. Oxford University Press, New York; 1991.
Hale JK: Introduction to Functional Differential Equations. Springer, New York; 1993.
Krisztin T: Global dynamics of delay differential equations. Period. Math. Hung. 2008, 56: 83–95. 10.1007/s10998-008-5083-x
Agarwal R, Berezansky L, Braverman E, Domoshnitsky A: Nonoscillation Theory of Functional Differential Equations and Applications. Springer, New York; 2012.
Chaplygin, SA: Foundations of new method of approximate integration of differential equations. Moscow, 1919. (Collected works 1, GosTechIzdat, 1948) (in Russian)
Lakshmikantham V, Leela S: Differential and Integral Inequalities. Academic Press, New York; 1969.
Deininger MWN, Druker BJ: Specific targeted therapy of chronic myelogenous leukemia with imatinib. Pharmacol. Rev. 2003, 55(3):401–423. 10.1124/pr.55.3.4
Acknowledgements
We thank professor Dina Ben-Yehuda from Hadassah University Hospital (Division of Hematology) for helpful comments and suggestions. The authors are very grateful to the reviewers whose valuable comments greatly contributed to the paper presentation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors contributed equally and significantly in writing this article. The authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Berezansky, L., Bunimovich-Mendrazitsky, S. & Domoshnitsky, A. A mathematical model with time-varying delays in the combined treatment of chronic myeloid leukemia. Adv Differ Equ 2012, 217 (2012). https://doi.org/10.1186/1687-1847-2012-217
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2012-217