Initial functions defining dominant positive solutions of a linear differential equation with delay

Abstract

Linear differential equation

$$\dot{y}(t)=-c(t)y(t-r),$$

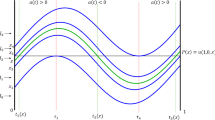
where $c(t)$ is a positive continuous function and delay r is a positive constant, is considered for $t\to \mathrm{\infty }$. It is proved that, under certain assumptions on the function $c(t)$ and delay r, a class of positive linear initial functions defines dominant positive solutions with positive limit for $t\to \mathrm{\infty }$.

MSC:34K15, 34K25.

1 Introduction

This article is devoted to the problem of the asymptotic behavior of solutions of delayed equations of the type

$$\dot{y}(t)=-c(t)y(t-r)$$

(1)

with a positive continuous function $c(t)$ on the set $[t_0-r,\mathrm{\infty })$, $t_0\in \mathbb{R}$, $0<r=\mathrm{const}$ in the non-oscillatory case. The following results on the asymptotic behavior of solutions, needed in the following analysis, are taken from [1] (see [2] as well).

Theorem 1 (Theorem 18 in [1])

Let there exist a positive solution $\tilde{y}$ of (1) on $[t_0-r,\mathrm{\infty })$. Then there are two positive solutions $y_1$ and $y_2$ of (1) on $[t_0-r,\mathrm{\infty })$ satisfying

$$\underset{t\to \mathrm{\infty }}{lim}\frac{y_2(t)}{y_1(t)}=0.$$

(2)

Moreover, every solution y of (1) on $[t_0-r,\mathrm{\infty })$ is represented by the formula

$$y(t)=K{y}_1(t)+O(y_2(t)),$$

(3)

where $t\in [t_0-r,\mathrm{\infty })$ and a coefficient $K\in \mathbb{R}$ depends on y.

In [2] it is shown that in representation (3) an arbitrary couple $y_1$ and $y_2$ of two positive solutions of (1) satisfying (2) can be used, i.e., the following theorem holds.

Theorem 2 Assume that $y_1$ and $y_2$ are two positive solutions of (1) on $[t_0-r,\mathrm{\infty })$ satisfying (2). Then every solution y of (1) on $[t_0-r,\mathrm{\infty })$ is represented by formula (3), where $t\in [t_0-r,\mathrm{\infty })$ and a coefficient $K\in \mathbb{R}$ depends on y.

This is the reason for introducing the following definition.

Definition 1 [2]

Let $y_1$ and $y_2$ be fixed positive solutions of (1) on $[t_0-r,\mathrm{\infty })$ with property (2). Then $(y_1,y_2)$ is called a pair of dominant and subdominant solutions on $[t_0-r,\mathrm{\infty })$.

We note that in the literature one can find numerous criteria of positivity of solutions not only to (1), but more complicated, as well as lots of properties of such solutions and explanation of their importance (see, e.g., books [3–9], papers [1, 2, 10–20], and the references therein). They are formulated as implicit criteria (simultaneously both sufficient and necessary) or as explicit sufficient criteria. In the paper we employ the following explicit criterion (assumptions are slightly modified to restrict the criterion to the considered case).

Theorem 3 [17]

If

$${\int }_{t-r}^{t}c(s)\mathrm{d}s\le \frac{1}{\mathrm{e}}$$

for $t\in [t_0,\mathrm{\infty })$, then (1) has a non-oscillatory solution on $[t_0-r,\mathrm{\infty })$.

In this paper we prove that every positive linear initial function given on the initial interval $[t_0-r,t_0]$ and satisfying certain restrictions, defines a positive solution $y=y(t)$ of (1) on $[t_0-r,\mathrm{\infty })$. Moreover, we show that this positive solution is a dominant solution and its limit $y(\mathrm{\infty })$ is positive.

The paper is organized as follows. The main result (Theorem 5 below) in Section 3 is proved by the sensitive and flexible retract method. It is shortly described in Section 2. Its applicability is performed via Theorem 4, where an important role is played by a system of initial functions (see Definition 3). Proper choice of such a system of initial functions together with the application of Theorem 4 form the mainstay of the proof of Theorem 5.

2 Preliminaries - Ważewski’s retract principle

Let $C([a,b],{\mathbb{R}}^n)$, where $a,b\in \mathbb{R}$, $a<b$, be the Banach space of the continuous mappings from the interval $[a,b]$ into ${\mathbb{R}}^n$ equipped with the supremum norm

$${\parallel \psi \parallel }_C=\underset{\theta \in [a,b]}{sup}\parallel \psi (\theta )\parallel ,\psi \in C([a,b],{\mathbb{R}}^n),$$

where $\parallel \cdot \parallel$ is the maximum norm in ${\mathbb{R}}^n$. In the case $a=-r<0$ and $b=0$, we shall denote this space as ${\mathrm{C}}_r^n$, that is,

$${\mathrm{C}}_r^n:=C([-r,0],{\mathbb{R}}^n).$$

If $\sigma \in \mathbb{R}$, $A\ge 0$, and $y\in C([\sigma -r,\sigma +A],{\mathbb{R}}^n)$, then, for each $t\in [\sigma ,\sigma +A]$, we define $y_t\in {\mathrm{C}}_r^n$ by $y_t(\theta )=y(t+\theta )$, $\theta \in [-r,0]$.

In this section we present Ważewski’s principle for a system of retarded functional differential equations

$$\dot{y}(t)=F(t,y_t),$$

(4)

where is a continuous quasi-bounded map which satisfies a local Lipschitz condition with respect to the second argument and ${\mathrm{\Omega }}^{\ast }$ is an open subset in .

The principle below was for the first time introduced by Ważewski [21] for ordinary differential equations and later extended to retarded functional differential equations by Rybakowski [22].

We recall that the functional F is quasi-bounded if F is bounded on every set of the form $[t_1,t_2]\times {\mathrm{C}}_{r,L}^n\subset {\mathrm{\Omega }}^{\ast }$, where $t_1<t_2$, ${\mathrm{C}}_{r,L}^n:=C([-r,0],L)$ and L is a closed bounded subset of ${\mathbb{R}}^n$ (see [[5], p.305]).

In accordance with [23], a function $y(t)$ is said to be a solution of the system (4) on $[\sigma -r,\sigma +A)$ if there are and $A>0$ such that , $(t,y_t)\in {\mathrm{\Omega }}^{\ast }$ and $y(t)$ satisfies the system (4) for $t\in [\sigma ,\sigma +A)$. For given , $\phi \in {\mathrm{C}}_r^n$, we say $y(\sigma ,\phi )$ is a solution of the system (4) through $(\sigma ,\phi )\in {\mathrm{\Omega }}^{\ast }$ if there is an $A>0$ such that $y(\sigma ,\phi )$ is a solution of the system (4) on $[\sigma -r,\sigma +A)$ and $y_{\sigma }(\sigma ,\phi )=\phi$. In view of the above conditions, each element $(\sigma ,\phi )\in {\mathrm{\Omega }}^{\ast }$ determines a unique solution $y(\sigma ,\phi )$ of the system (4) through $(\sigma ,\phi )\in {\mathrm{\Omega }}^{\ast }$ on its maximal interval of existence $I_{\sigma ,\phi }=[\sigma ,a)$, $\sigma <a\le \mathrm{\infty }$ which depends continuously on initial data [23]. A solution $y(\sigma ,\phi )$ of the system (4) is said to be positive if $y_i(\sigma ,\phi )>0$ on $[\sigma -r,\sigma ]\cup I_{\sigma ,\phi }$ for each $i=1,2,\dots ,n$.

As usual, if a set , then intω and ∂ω denote the interior and the boundary of ω, respectively.

Definition 2 [22]

Let the continuously differentiable functions $l_i(t,y)$, $i=1,2,\dots ,p$ and $m_j(t,y)$, $j=1,2,\dots ,q$, $p^2+q^2>0$ be defined on some open set . The set

$${\omega }^{\ast }=\{(t,y)\in {\omega }_0:l_i(t,y)<0,m_j(t,y)<0,i=1,\dots ,p,j=1,\dots ,q\}$$

(5)

is called a regular polyfacial set with respect to the system (4), provided it is nonempty and the conditions (α) to (γ) below hold:

(α) For such that $(t+\theta ,\pi (\theta ))\in {\omega }^{\ast }$ for $\theta \in [-r,0)$, we have $(t,\pi )\in {\mathrm{\Omega }}^{\ast }$.

(β) For all $i=1,2,\dots ,p$, all $(t,y)\in \partial {\omega }^{\ast }$ for which $l_i(t,y)=0$, and all $\pi \in {\mathrm{C}}_r^n$ for which $\pi (0)=y$ and $(t+\theta ,\pi (\theta ))\in {\omega }^{\ast }$, $\theta \in [-r,0)$, it follows that $D{l}_i(t,y)>0$, where

$$D{l}_i(t,y)\equiv \sum _{k=1}^n\frac{\partial l_i(t,y)}{\partial y_k}{f}_k(t,\pi )+\frac{\partial l_i(t,y)}{\partial t}.$$

(γ) For all $j=1,2,\dots ,q$, all $(t,y)\in \partial {\omega }^{\ast }$ for which $m_j(t,y)=0$, and all $\pi \in {\mathrm{C}}_r^n$ for which $\pi (0)=y$ and $(t+\theta ,\pi (\theta ))\in {\omega }^{\ast }$, $\theta \in [-r,0)$, it follows that $D{m}_j(t,y)<0$, where

$$D{m}_j(t,y)\equiv \sum _{k=1}^n\frac{\partial m_j(t,y)}{\partial y_k}{f}_k(t,\pi )+\frac{\partial m_j(t,y)}{\partial t}.$$

The elements in the sequel are assumed to be such that $(t,\pi )\in {\mathrm{\Omega }}^{\ast }$.

Definition 3 A system of initial functions $p_{A,{\omega }^{\ast }}$ with respect to the nonempty sets A and ${\omega }^{\ast }$, where , is defined as a continuous mapping $p:A\to {\mathrm{C}}_r^n$ such that (i) and (ii) below hold:

• (i) If $z=(t,y)\in A\cap int{\omega }^{\ast }$, then $(t+\theta ,p(z)(\theta ))\in {\omega }^{\ast }$ for $\theta \in [-r,0]$.

• (ii) If $z=(t,y)\in A\cap \partial {\omega }^{\ast }$, then $(t+\theta ,p(z)(\theta ))\in {\omega }^{\ast }$ for $\theta \in [-r,0)$ and $(t,p(z)(0))=z$.

Definition 4 [24]

If $\mathcal{A}\subset \mathcal{B}$ are subsets of a topological space and $\pi :\mathcal{B}\to \mathcal{A}$ is a continuous mapping from ℬ onto $\mathcal{A}$ such that $\pi (p)=p$ for every $p\in \mathcal{A}$, then π is said to be a retraction of ℬ onto $\mathcal{A}$. When a retraction of ℬ onto $\mathcal{A}$ exists, $\mathcal{A}$ is called a retract of ℬ.

The following lemma describes the main result of the paper [22].

Lemma 1 Let ${\omega }^{\ast }\subset {\omega }_0$ be a regular polyfacial set with respect to the system (4), and let W be defined as follows:

$$W=\{(t,y)\in \partial {\omega }^{\ast }:m_j(t,y)<0,j=1,2,\dots ,q\}.$$

Let $Z\subset W\cup {\omega }^{\ast }$ be a given set such that $Z\cap W$ is a retract of W but not a retract of Z. Then, for each fixed system of initial functions $p_{Z,{\omega }^{\ast }}$, there is a point $z_0=({\sigma }_0,y_0)\in Z\cap {\omega }^{\ast }$ such that for the corresponding solution $y({\sigma }_0,p(z_0))(t)$ of (4) we have

$$(t,y({\sigma }_0,p(z_0))(t))\in {\omega }^{\ast }$$

for each $t\in D_{{\sigma }_0,p(z_0)}$.

Remark 1 When Lemma 1 is applied, a lot of technical details should be fulfilled. In order to simplify necessary verifications, it is useful, without loss of generality, to vary the first coordinate t in the definition of the set ${\omega }^{\ast }$ in (5) within a half-open interval open at the right. Then the set ${\omega }^{\ast }$ is not open, but tracing the proof of Lemma 1, it is easy to see that for such sets it remains valid. Such possibility is used below. Similar remark and explanation can be applied to sets of the type Ω, ${\mathrm{\Omega }}^{\ast }$ which serve as domains of definitions of functionals on the right-hand sides of equations considered.

Continuously differentiable functions $l_i(t,y)$, $i=1,2,\dots ,p$ and $m_j(t,y)$, $j=1,2,\dots ,q$, $p^2+q^2>0$ mentioned in Definition 2 are often used in the form:

$$\begin{array}{c}{l}_i(t,y)=(y_i-{\rho }_i(t))(y_i-{\delta }_i(t)),i=1,2,\dots ,p,\hfill \\ m_j(t,y)=(y_j-{\rho }_j(t))(y_j-{\delta }_j(t)),j=p+1,p+2,\dots ,n,\hfill \\ m_{n+1}(t,y)=-t+t_0-r,\hfill \end{array}$$

where ρ, δ are continuous vector functions

$$\rho =({\rho }_1,{\rho }_2,\dots ,{\rho }_n),\delta =({\delta }_1,{\delta }_2,\dots ,{\delta }_n):[t_0-r,\mathrm{\infty })\to {\mathbb{R}}^n,$$

with $\rho (t)\ll \delta (t)$ for $t\in [t_0-r,\mathrm{\infty })$ (the symbol ≪ here and below means ${\rho }_i(t)<{\delta }_i(t)$ for all $i=1,2,\dots ,n$), continuously differentiable on $[t_0,\mathrm{\infty })$. Hence, the shape of the regular polyfacial set ${\omega }^{\ast }$ from Definition 2 can be simplified to

$${\omega }^{\ast }:=\{(t,y):t\in [t_0-r,\mathrm{\infty }),\rho (t)\ll y\ll \delta (t)\}.$$

In the sequel we employ the result from [[11], Theorem 1].

Theorem 4 Let there be a $p\in \{0,\dots ,n\}$ such that:

• (i) If $t\ge t_0$, $\varphi \in {\mathrm{C}}_r^n$ and $(t+\theta ,\varphi (\theta ))\in {\omega }^{\ast }$ for any $\theta \in [-r,0)$, then

  $${\left({\delta }^i\right)}^{\prime }(t)<F^i(t,\varphi )\text{when }{\varphi }^i(0)={\delta }^i(t),$$

  (6)

$${\left({\rho }^i\right)}^{\prime }(t)>F^i(t,\varphi )\text{when }{\varphi }^i(0)={\rho }^i(t)$$

(7)

for any $i=1,2,\dots ,p$. (If $p=0$, this condition is omitted.)

• (ii) If $t\ge t_0$, $\varphi \in {\mathrm{C}}_r^n$ and $(t+\theta ,\varphi (\theta ))\in {\omega }^{\ast }$ for any $\theta \in [-r,0)$, then

  $$\begin{array}{c}{\left({\rho }^i\right)}^{\prime }(t)<F^i(t,\varphi )\mathit{\text{when }}{\varphi }^i(0)={\rho }^i(t),\hfill \\ {\left({\delta }^i\right)}^{\prime }(t)>F^i(t,\varphi )\mathit{\text{when }}{\varphi }^i(0)={\delta }^i(t)\hfill \end{array}$$

for any $i=p+1,p+2,\dots ,n$. (If $p=n$, this condition is omitted.)

Then, for each fixed system of initial functions $p_{Z,{\omega }^{\ast }}$, where the set Z is defined as

$$Z=\{(t_0,y),y\in [\rho (t_0),\delta (t_0)]\},$$

there is a point $z_0=({\sigma }_0,y_0)\in Z\cap {\omega }^{\ast }$ such that for the corresponding solution $y({\sigma }_0,p(z_0))(t)$ of (4) we have

$$(t,y({\sigma }_0,p(z_0))(t))\in {\omega }^{\ast }$$

for each $t\in D_{{\sigma }_0,p(z_0)}$, i.e., then there exists an uncountable set $\mathcal{Y}$ of solutions of (4) on $[t_0-r,\mathrm{\infty })$ such that each $y\in \mathcal{Y}$ satisfies

$$\rho (t)\ll y(t)\ll \delta (t),t\in [t_0-r,\mathrm{\infty }).$$

The original Theorem 1 is in [11] proved using the retract technique combined with Razumikhin-type ideas known in the theory of stability of retarded functional differential equations.

3 Main result

In this section we consider scalar differential equation (1), where $r>0$ and $c:[t_0-r,\mathrm{\infty })\to {\mathbb{R}}^{+}=(0,\mathrm{\infty })$ is a continuous function satisfying

$${\int }_{t-r}^{t}c(s)\mathrm{d}s\le \frac{1}{\mathrm{e}}$$

(8)

for $t\in [t_0-r,\mathrm{\infty })$ and

$${\int }^{\mathrm{\infty }}c(s)\mathrm{d}s<\mathrm{\infty }.$$

(9)

The first condition (8), in accordance with Theorem 3, guarantees the existence of a positive solution $y=y(t)$ on the interval $[t_0-r,\mathrm{\infty })$. Then Theorems 1 and 2 are valid and equation (1) has two different positive solutions (dominant and subdominant) $y=y_1(t)$ and $y=y_2(t)$ on the interval $[t_0-r,\mathrm{\infty })$. Condition (9), as will be seen from the explanation below, implies that the dominant solution has a positive limit for $t\to \mathrm{\infty }$.

We set

$$C:=exp(-\mathrm{e}{\int }_{t_0-r}^{\mathrm{\infty }}c(t)\mathrm{d}t)>0,$$

where the constant C is well defined due to (9), and

$$\phi (t):=exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)-C>0,t\in [t_0-r,\mathrm{\infty }).$$

Obviously, $\phi (\mathrm{\infty })=0$. Denote

$$m=\underset{[t_0-r,t_0]}{min}\left\{|{\phi }^{\prime }(t)|\right\}=\underset{[t_0-r,t_0]}{min}\{\mathrm{e}c(t)exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)\}.$$

Due to positivity of $c(t)$ on $[t_0-r,t_0]$, we have $m>0$.

Let ${\phi }_{K,\mu }\in {\mathrm{C}}_r^1$ be a linear initial function defined on the interval $[t_0-r,t_0]$ as

$${\phi }_{K,\mu }(t_0+\theta ):=K+\mu \theta ,\theta \in [-r,0],$$

(10)

where $K,\mu \in \mathbb{R}$ and $|\mu |\le m$. The following theorem gives sufficient conditions for the property

$$y(t_0,{\phi }_{K,\mu })(t)>0,t\in [t_0-r,\mathrm{\infty })$$

together with

$$\underset{t\to +\mathrm{\infty }}{lim}y(t_0,{\phi }_{K,\mu })(t)=K^{\ast }({\phi }_{K,\mu }),$$

where $K^{\ast }({\phi }_{K,\mu })$ is a positive constant depending on the choice of the initial linear function ${\phi }_{K,\mu }$.

Theorem 5 Let inequalities (8), (9) be valid, a constant $C\ge 3/4$ and ${\phi }_{K,\mu }\in {\mathrm{C}}_r^1$ be defined by (10). Then the solution $y(t_0,{\phi }_{K,\mu })(t)$, where ${\phi }_{K,\mu }$ is defined by (10), $K,\mu \in \mathbb{R}$ and $|\mu |\le m$, is positive including the value $y(t_0,{\phi }_{K,\mu })(\mathrm{\infty })$, i.e.

$$y(t_0,{\phi }_{K,\mu })(t)>0,t\in [t_0-r,\mathrm{\infty })$$

and

$$\underset{t\to +\mathrm{\infty }}{lim}y(t_0,{\phi }_{K,\mu })(t)=K^{\ast }({\phi }_{K,\mu })>0.$$

Proof We will employ Theorem 4 with $p=n=1$, i.e., the case (i) only. Set

$$F(t,\varphi ):=-c(t)\varphi (-r),\rho (t):={\phi }_1(t),\delta (t):={\phi }_2(t),$$

where functions ${\phi }_j:[t_0-r,\mathrm{\infty })\to \mathbb{R}$ are defined as

$$\begin{array}{c}{\phi }_2(t):=C+\phi (t),\hfill \\ {\phi }_1(t):=C-\phi (t).\hfill \end{array}$$

We have

$$\underset{t\to \mathrm{\infty }}{lim}{\phi }_i(t)=C,i=1,2$$

(11)

and since $C\ge 3/4>1/2$ (i.e., $C>\phi (t_0-r)$): ${\phi }_2(t)>{\phi }_1(t)>0$ on $[t_0-r,\mathrm{\infty })$. Now, we define

$${\omega }^{\ast }:=\{(t,y):t\in [t_0-r,\mathrm{\infty }),{\phi }_1(t)<y<{\phi }_2(t)\}$$

and

$$Z:=\{(t_0,y),y\in [{\phi }_1(t_0),{\phi }_2(t_0)]\}.$$

We verify inequality (6). For $t\ge t_0$, $\varphi \in {\mathrm{C}}_r^1$, and $(t+\theta ,\varphi (\theta ))\in {\omega }^{\ast }$, $\theta \in [-r,0)$, with $\varphi (0)=\delta (t)={\phi }_2(t)=C+\phi (t)$, i.e., for

$$\begin{array}{r}{\phi }_1(t+\theta )<\varphi (\theta )<{\phi }_2(t+\theta ),\theta \in [-r,0),\\ \varphi (0)={\phi }_2(t)=C+\phi (t),\end{array}$$

we have

$$\begin{array}{rl}F(t,\varphi )-{\delta }^{\prime }(t)& =-c(t)\varphi (-r)-{\phi }_2^{\prime }(t)\\ =-c(t)\varphi (-r)+\mathrm{e}c(t)exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)\\ >-c(t){\phi }_2(t-r)+\mathrm{e}c(t)exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)\\ =-c(t)[C+\phi (t-r)]+\mathrm{e}c(t)exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)\\ =-c(t)exp(-\mathrm{e}{\int }_{t_0-r}^{t-r}c(s)\mathrm{d}s)+\mathrm{e}c(t)exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)\\ =c(t)exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)[\mathrm{e}-exp(\mathrm{e}{\int }_{t-r}^{t}c(s)\mathrm{d}s)]\\ \ge \left[\text{we use (8)}\right]\\ \ge c(t)exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)[\mathrm{e}-exp(\mathrm{e}\cdot \frac{1}{\mathrm{e}})]=0.\end{array}$$

Therefore, $F(t,\varphi )>{\delta }^{\prime }(t)$ and (6) holds. Inequality (7) holds as well because for $t\ge t_0$, $\varphi \in {\mathrm{C}}_r^1$ and $(t+\theta ,\varphi (\theta ))\in {\omega }^{\ast }$, $\theta \in [-r,0)$, with $\varphi (0)=\rho (t)={\phi }_1(t)=C-\phi (t)$, i.e., for

$$\begin{array}{r}{\phi }_1(t+\theta )<\varphi (\theta )<{\phi }_2(t+\theta ),\theta \in [-r,0),\\ \varphi (0)={\phi }_1(t)=C-\phi (t)\end{array}$$

we have

$$\begin{array}{rl}F(t,\varphi )-{\rho }^{\prime }(t)& =-c(t)\varphi (-r)-{\phi }_1^{\prime }(t)\\ =-c(t)\varphi (-r)+[-\mathrm{e}c(t)exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)]\\ <-c(t){\phi }_1(t-r)-\mathrm{e}c(t)exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)\\ =-c(t)[C-\phi (t-r)]-\mathrm{e}c(t)exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)\\ =-c(t)[2C-exp(-\mathrm{e}{\int }_{t_0-r}^{t-r}c(s)\mathrm{d}s)]-\mathrm{e}c(t)exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)\\ =c(t)[-2C-\mathrm{e}exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)+exp(-\mathrm{e}{\int }_{t_0-r}^{t-r}c(s)\mathrm{d}s)]\\ =c(t)[-2C+exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)(-\mathrm{e}+exp(\mathrm{e}{\int }_{t-r}^{t}c(s)\mathrm{d}s))]\\ \le \left[\text{we use (8)}\right]\\ \le c(t)[-2C+exp(-\mathrm{e}{\int }_{t_0-r}^{t}c(s)\mathrm{d}s)(-\mathrm{e}+exp(\mathrm{e}\cdot \frac{1}{\mathrm{e}}))]\\ =-2c(t)C<0.\end{array}$$

Now, we will specify the system of initial functions $p_{Z,{\omega }^{\ast }}$ mentioned in Theorem 4. For

$$z=(t_0,y^{\ast })\in Z,$$

($y^{\ast }$ varies within the interval $[{\phi }_1(t_0),{\phi }_2(t_0)]$), we define

$$p(z)(\theta ):=y^{\ast }+\mu \theta ,\theta \in [-r,0],|\mu |\le m,$$

i.e., every initial function is a linear function described by formula (10). Since ${\phi }^{\prime }(t)<0$, $t\in [t_0-r,\mathrm{\infty })$, for the system of functions $p_{Z,{\omega }^{\ast }}$, both assumptions (i), (ii) in Definition 3 are valid. Indeed, this property implies

$${\phi }_2^{\prime }(t)={\phi }^{\prime }(t)<0\text{and}{\phi }_1^{\prime }(t)=-{\phi }^{\prime }(t)>0$$

if $t\in [t_0-r,\mathrm{\infty })$,

$$\underset{[t_0-r,t_0]}{min}\left\{|{\phi }_2^{\prime }(t)|\right\}=\underset{[t_0-r,t_0]}{min}\left\{|{\phi }_1^{\prime }(t)|\right\}=m$$

and

$$-m\le {\phi }_i^{\prime }(t)\le m,t\in [t_0-r,t_0],i=1,2.$$

Therefore, every segment

$$y(t)=y^{\ast }+\mu t,|\mu |\le m,t\in [t_0-r,t_0]$$

satisfies inequalities

$${\phi }_2(t)<y(t)<{\phi }_1(t)$$

(12)

if $y^{\ast }\in intZ$, $t\in [t_0-r,t_0]$. Consequently, (i) in Definition 3 holds.

If $y^{\ast }\in \partial Z$, then inequalities (12) hold if $t\in [t_0-r,t_0)$ and (ii) is also valid.

Theorem 4 is also valid for this system. Consequently, there exists a point

$$z_0=(t_0,y_0^{\ast })\in Z\cap {\omega }^{\ast }$$

such that

$$(t,y(t_0,p(z_0))(t))\in {\omega }^{\ast },t\in [t_0-r,\mathrm{\infty }),$$

i.e.,

$${\phi }_1(t)<y(t_0,p(z_0))(t)<{\phi }_2(t),t\in [t_0-r,\mathrm{\infty }).$$

(13)

From inequalities (13) we conclude

$$\underset{t\to +\mathrm{\infty }}{lim}y(t_0,p(z_0))(t)=C$$

because of (11). This solution is positive, i.e.,

$$y(t_0,p(z_0))(t)>0,t\in [t_0-r,\mathrm{\infty })$$

due to positivity of ${\phi }_1(t)$.

Since the statement of the theorem holds for initial functions with $\mu =0$, we can also conclude that due to linearity of equation (1), every constant positive initial function defines a positive solution.

If the solution $y(t_0,p(z_0))(t)$ does not coincide with the solution $y(t_0,{\phi }_{K,\mu })(t)$, i.e., if $y_0^{\ast }\ne K$, then due to linearity, the sum or the difference of $y(t_0,p(z_0))(t)$ and a suitable positive solution generated by a positive constant initial function gives the solution $y(t_0,{\phi }_{K,\mu })(t)$. It is only necessary to show that the solution $y(t_0,{\phi }_{K,\mu })(t)$ will be again positive. The condition for positivity is

$${\phi }_1(t_0-r)>{\phi }_2(t_0)-{\phi }_1(t_0)$$

or, after some computations,

$$4C\ge 1+2exp(-\mathrm{e}{\int }_{t_0-r}^{t_0}c(s)\mathrm{d}s).$$

The last inequality holds since

$$4C\ge 3>1+2exp(-\mathrm{e}{\int }_{t_0-r}^{t_0}c(s)\mathrm{d}s).$$

We finish the proof with the conclusion that the existence of positive limit $K^{\ast }({\phi }_{K,\mu })$ is proved. □

Theorem 6 Let all assumptions of Theorem  5 be valid. Then the solution $y(t_0,{\phi }_{K,\mu })$ of equation (1) is a positive dominant solution.

Proof Every positive solution $y=y(t)$ of equation (1) on $[t_0-r,+\mathrm{\infty })$ is decreasing and therefore its limit ${lim}_{t\to \mathrm{\infty }}y(t)$ exists and is finite. The value of the limit can be either positive or zero. In the case of solution $y(t_0,{\phi }_{K,\mu })$ of equation (1), we have

$$\underset{t\to \mathrm{\infty }}{lim}y(t_0,{\phi }_{K,\mu })(t)=K^{\ast }({\phi }_{K,\mu })>0.$$

By Theorem 1 there must exist another positive solution $y=Y(t)$ of equation (1) on $[t_0-r,+\mathrm{\infty })$ such that either

$$\underset{t\to \mathrm{\infty }}{lim}\frac{y(t_0,{\phi }_{K,\mu })(t)}{Y(t)}=0$$

(14)

or

$$\underset{t\to \mathrm{\infty }}{lim}\frac{Y(t)}{y(t_0,{\phi }_{K,\mu })(t)}=0.$$

(15)

The first possibility (14) is impossible since in such a case there should exist a positive solution $Y(t)$ of equation (1) on $[t_0-r,+\mathrm{\infty })$ with the property

$$\underset{t\to \mathrm{\infty }}{lim}Y(t)=\mathrm{\infty },$$

which is obviously false. The possibility (15) remains. Then, by Definition 1, a solution $y(t_0,{\phi }_{K,\mu })$ of equation (1) is a dominant solution on $[t_0-r,+\mathrm{\infty })$. □

Remark 2 It is well known [[8], Theorem 3.3.1] that every continuous initial function φ, defined on the interval $[t_0-r,t_0]$, such that $\phi (t_0)>0$, $\phi (t_0)\ge \phi (s)$, $s\in [t_0-r,t_0)$, defines a positive solution on $[t_0-r,+\mathrm{\infty })$ if the assumptions of Theorem 5 hold. But it is not known if such a solution is dominant or subdominant or if its limit for $t\to \mathrm{\infty }$ is positive or equals zero. The statements of Theorems 5 and 6 give new results in this direction since, for a class of linear initial positive functions (not fully covered by known results), positivity of generated solutions (including positivity of their limits) is established together with dominant character of their asymptotical behavior. It is a problem for future investigation to find values of positive limits of solutions considered in the paper (e.g., by methods used in [25–27]) or to enlarge the presented method to more general classes of equations and initial functions.

The topic considered in this paper is also connected with problems on the existence of bounded solutions. We refer, e.g., to recent papers [28–30] and to the references therein.