Abstract
In this article, we propose a distributed joint source-channel coding (DJSCC) technique that well exploits source-relay correlation as well as source memory structure simultaneously for transmitting binary Markov sources in a one-way relay system. The relay only extracts and forwards the source message to the destination, which implies imperfect decoding at the relay. The probability of errors occurring in the source-relay link can be regarded as source-relay correlation. The source-relay correlation can be estimated at the destination node and utilized in the iterative processing. In addition, the memory structure of the Markov source is also utilized at the destination. A modified version of the Bahl, Cocke, Jelinek, and Raviv (BCJR) algorithm is derived to exploit the memory structure of the Markov source. Extrinsic information transfer (EXIT) chart analysis is then performed to investigate convergence property of the proposed technique. Results of simulations conducted to evaluate the bit-error-rate (BER) performance and the EXIT chart analysis show that, by exploiting the source-relay correlation and source memory simultaneously, our proposed technique achieves significant performance gain, compared with the case where the correlation knowledge is not fully used.
Similar content being viewed by others
Introduction
Wireless mesh and/or sensor networks having great number of low-power consuming wireless nodes (e.g., small relays and/or micro cameras) have attracted a lot of attention of the society, and a variety of its potential applications has been considered recently[1]. The fundamental challenge of wireless mesh and/or sensor networks is how energy-/spectrum-efficiently as well as reliably the multiple sources can transmit their originating information to the multiple destinations. However, such multi-terminal systems have two practical limitations: (1) wireless channel suffers from various impairments, such as interference, distortions and/or deep fading, (2) signal processing complexity as well as transmitting powers has to be as low as possible due to the power, bandwidth, and/or size restrictions of the wireless nodes.
Cooperative communication techniques provide a potential solution to the problems described above, due to its excellent transmit diversity for fading mitigation[2]. One simple form of cooperative wireless communications is a single relay system, which consists of one source, one relay and one destination. The role of the relay is to provide alternative communication route for transmission, hence improving the probability of successful signal reception of source information sequence at the destination. In this relay system, the information sent from the source and the relay nodes are correlated, which in this article is referred to as source-relay correlation. Furthermore, the information collected at the source node contains memory structure, according to the dynamics that governs the temporal behavior of the originator (or sensing target). The source-relay correlation and the memory structure of the transmitted data can be regarded as redundant information which can be used for source compression and/or error correction in distributed joint source-channel coding (DJSCC).
There are many excellent coding schemes which can achieve efficient node cooperative communications, such as[3, 4], where decode-and-forward (DF) relay strategy is adopted and the source-relay link is assumed to be error free. In practice, when the signal-to-noise ratio (SNR) of the source-relay link falls below certain threshold, successful decoding at relay may become impossible. Besides, to completely correct the errors at the relay, strong codes such as turbo codes or low density parity check (LDPC) codes with iterative decoding are required, which will impose heavy computational burden at the relay. As a result, several coding strategies assuming that the relay cannot always decode correctly the information from the source have been presented in[5–7].
Joint source-channel coding (JSCC) has been widely used to exploit the memory structure inherent within the source information sequence. In the majority of the approaches to JSCC design, variable-length code (VLC) is employed as source encoder and the implicit residual redundancy after source encoding is additionally used for error correction in the decoding process. Some related study can be found in[8–11]. Also, there are some literatures which focus on exploiting the memory structure of the source directly, e.g., some approaches of combining hidden Markov Model (HMM) or Markov chain (MC) with the turbo code design framework are presented in[12–14].
In the schemes mentioned above, the exploitation of the source-relay correlation and the source memory structure have been addressed separately. Not much attention has been paid to relay systems exploiting the source-relay correlation and the source memory simultaneously. A similar study can be found in[15], where the memory structure of the source is represented by a very simple model, bit-flipping between the current information sequence and its previous counterpart, which is not reasonable in many practical scenarios. When the exploitation of the source memory having more generic structures, the problem of code design for relay systems exploiting jointly the source-relay correlation and the source memory structure is still open.
In this article, we propose a new DJSCC scheme for transmitting binary Markov source in a one-way single relay system, based on[7, 14]. The proposed technique makes efficient utilization of the source-relay correlation as well as the source memory structure simultaneously to achieve additional coding gain. The rest of this article is organized as follow. Section ‘System model’ introduces the system model. The proposed decoding algorithm is described in Section ‘Proposed decoding scheme’. Section ‘EXIT chart analysis’ shows the results of extrinsic information transfer (EXIT) chart analysis conducted to evaluate the convergence property of the proposed system. Section ‘Convergence analysis and BER performance evaluation’ shows the bit-error-rate (BER) performance of the system based on EXIT chart analysis. The simulation results for image transmission using the proposed technique is presented in Section ‘Application to image transmission’. Finally, conclusions are drawn in Section ‘Conclusion’ with some remarks.
System model
One-way single relay system
In this article, a single-source single-relay system is considered where all links are assumed to suffer from Additive White Gaussian Noise (AWGN). The relay system operates in a half-duplex mode. During the first time interval, the source node broadcasts the signal to both the relay and destination nodes. After receiving signals from the source, the relay extracts the data even though it may contain some errors, re-encodes, and then transmits the extracted data to the destination node in the second time interval.
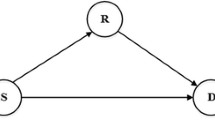
The relay can be located closer to the source or to the destination, or the three nodes keep the same distance with each other. All these three different relay location scenarios are considered in this article, as shown in Figure1. The geometric-gain[4]G xy of the link between the node x and y can be defined as
where d xy denotes the distance of the link between the node x and y. The pass loss exponent l is empirically set at 3.52[4]. Note that the geometric-gain of the source-destination link G sd is normalized to 1 without the loss of generality.
The received signals at the relay and at the destination nodes can be expressed as
where x and x r represent the symbol vectors transmitted from the source and the relay, respectively. Notations n r and n d represent the zero-mean AWGN noise vectors at the relay and the destination with variances and, respectively. The SNR of the source-relay and relay-destination links with the three different relay location scenarios, as shown in Figure1, can be decided as: for location A, SNR sr = SNR rd = SNR sd ; for location B, SNR sr = SNR sd + 21.19 dB and SNR rd = SNR sd + 4.4 dB; for location C, SNR sr = SNR sd + 4.4 dB and SNR rd = SNR sd + 21.19 dB.
Source-relay correlation
The diagram of the proposed relay strategy is illustrated in Figure2. At the source node, the original information bits vector u is first encoded by a recursive systematic convolutional (RSC) code, interleaved by π s , encoded by a doped accumulator (ACC) with a doping rate K s [16] and then modulated using binary-phase shift keying (BPSK) to obtain the coded sequence x. After obtaining the received signal y sr from the source, the relay performs the decoding process only once (i.e., no iterative processing at the relay) to retrieve u r , which is used as an estimate of u. u r is first interleaved by π0 and then encoded following the same encoding process as in the originating node with a doping rate K r to generate the coded sequence x r .
Errors may occur between u and u r , as shown in Figure3, compared to the cases where iterative decoding is performed at the relay node. Apparently, with more iterations better BER performances can be achieved at the relay node. However, this advantage becomes negligible in low SNR sr scenarios. Instead, the estimate of the source information sequence is simply extracted by performing the corresponding channel decoding process just once. Consequently, the relay complexity can be significantly reduced without causing any significant performance degradation by the proposed algorithm, as detailed in Section ‘Proposed decoding scheme’.
The source-relay correlation indicates the correlation between u and u r , which can be represented by a bit-flipping model, as shown in Figure2. u r can be defined as u r = u ⊕ e, where e is an independent binary random variable and ⊕ indicates modulus-2 addition. The correlation between u and u r is characterized by p e , where p e = Pr(e = 1) = Pr(u ≠ u r )[6].
Markov source
In this article, the source we considered is a stationary state emitting binary Markov source u = u1u2…u t …, of which the transition matrix is:
where ai,j is the transition probability defined by
The entropy rate of stationary Markov source[17] is given by
where {μ i } is the stationary state probability.The memory structure of Markov source can be characterized by the state transition probabilities p1 and p2, 0 < p1p2 < 1, with which p1 = p2 = 0.5 indicates the memoryless source, while p1 ≠ 0.5 or p2 ≠ 0.5, and hence H(S) < 1 indicate source with memory.
Proposed decoding scheme
The block diagram of the proposed DJSCC decoder for one-way relay system exploiting the source-relay correlation and the source memory structure is illustrated in Figure4. The maximum a posteriori (MAP) algorithm for the convolutional code proposed by Bahl, Cocke, Jelinek and Raviv (BCJR), is used for MAP-decoding of convolutional code and ACC. Here, D s and D r denote the decoder of C s and C r , respectively. In order to exploit the knowledge of the memory structure of the Markov source, the source and C s are treated as a single constituent code. Hence, it is reasonable to represent the code structure by a super trellis by combining the trellis diagram of the source and C s . A modified version of the BCJR algorithm is derived to jointly perform source and channel decoding over this super trellis at D s . However, D r cannot exploit the source memory due to the additional interleaver π0, as shown in Figure2.
At the destination node, the received signals from the source and the relay are first converted to log-likelihood ratio (LLR) sequences L(y sd ), L(y rd ), respectively, and then decoded via two horizontal iterations (HI), as shown in Figure4. Then the extrinsic LLR s generated from D s and D r in the two HI s are further exchanged by several vertical iterations (VI) through an LLR updating function f c , of which role is detailed in the following section. This process is performed iteratively, until the convergence point is reached. Finally, hard decision is made based on the a posteriori LLR s obtained from D s .
LLR updating function
First of all, the correlation property (error probability occurring in the source-relay link) p e is estimated at the destination using the a posteriori LLR s of the uncoded bits, and from the decoders D s and D r , as
where N indicates the number of the a posteriori LLR pairs from the two decoders with sufficient reliability. Only the LLR s with their absolute values larger than a given threshold can be used in calculating.
After obtaining the estimated error probability using (8), the probability of u can be updated from u r as
where uk and denote the k th elements of u and u r , respectively. This leads to the LLR updating function[6] for u:
Similarly, the LLR updating function for u r can be expressed as:
In summary, the general form of LLR updating function f c , as shown in Figure4, is given as
where x denotes the input LLR s. The output of f c is the updated LLR s by exploiting as the source-relay correlation. The VI operations of the proposed decoder can be expressed as
where π0(·) and denote interleaving and de-interleaving functions corresponding to π0, respectively. and denote the a priori LLR s fed into, and extrinsic LLR s generated by D s , respectively, both for the uncoded bits. Similar definitions should apply to and for D r .
Joint decoding of Markov source and channel encoder C s
Representation of super trellis
Assume that the C s is a memory length v convolutional code. There are 2vstates in the trellis diagram of this code, which are indexed by m,m = 0,1,…,2v−1. The state of C s at the time index t is denoted as. Similarly, there are two states in order-1 binary Markov source, and the state at the time index t is denoted as with. For a binary Markov model described in Section ‘System model’, the source model and its corresponding trellis diagram are illustrated in Figure5a. The output value at a time instant t from the source is the same as the state value of. The trellis branches represent the state transition of which probabilities have been defined by (6). On the other hand, for C s , the branches in its trellis diagram indicate input/output characteristics.
At time instant t, the state of the source and the state of the C s can be regarded as a new state, which leads to the super trellis diagram. A simple example of combining binary Markov source with a recursive convolutional code (RSC) with generator polynominald (G r ,G) = (3,2)8 is depicted in Figure5. At each state, the input to the outer encoder is determined, given the state of the Markov source. Actually, the new trellis branches can be regarded as a combination corresponding to the branches of the Markov source and of the trellis diagram of C s . Hence, the new trellis branches represent both state transition probabilities of the Markov source and input/output characteristics of C s defined in its trellis diagram.
It should be noticed that a drawback of this approach is the exponentially growing number of the states in the super trellis. However, if C s is only a short memory convolutional code, the complexity increase is due mainly to the number of Markov source states. In fact, it is shown in Section ‘Convergence analysis and BER performance evaluation’ that, even with a memory-1 code used as C s can achieve excellent performance. Therefore, the complexity is largely the issue of source modeling depending on applications.
Modified BCJR algorithm for super trellis
In this section, we make modifications of the standard BCJR algorithm[18] for the decoding performed over the super trellis constructed in the previous section. Here, we ignore momentarily the serially concatenated structure, and only focus on the decoding process performed over the super trellis diagram. For a convolutional code with memory length v, there are 2v states in its trellis diagram, which is indexed by m m = 0,1,…,2v−1. The input sequence to the encoder u = u1u2…u t …u L , which is also a series of the states of Markov source, is assumed to have length L. The output of the encoder is denoted as x={xc 1xc 2}. The coded binary sequence is BPSK mapped and then transmitted over AWGN channels. The received signal is a noise-corrupted version of the BPSK mapped sequence, denoted as y={yc 1yc 2}. The received sequence from the time indexes t1 to t2 is denoted as.
The aim of the modified BCJR algorithm is to calculate conditional log-likelihood ratio (LLR) of the coded bits, based on the whole received sequence, which is defined by
where denotes the sets of states yielding the systematic output of the C s being k, k = 0,1.
In order to compute the last term in (16), three parameters indicating the probabilities defined as below have to be introduced:
Now we have
Substituting (20) in (16), we obtain the whole set of equations for the modified BCJR algorithm. α t (i,m), β t (i,m), γ t (y t ,i′,m′,i,m) are found to be functions of both the output of Markov source and the states in the trellis diagram of C s . More specifically, γ t (y t ,i′,m′,i,m) represents information of input/output relationship corresponding to the state transition S t = m′ → S t = m, specified by the trellis diagram of C s , as well as of the state transition probabilities depending on Markov source. Therefore, γ can be decomposed as
where is defined in (6), and is defined as
E t (i,m) is the set of states {(ut−1,St−1)} that have a trellis branch connected with state (u t = i,S t = m) in the super trellis.
After γ is obtained, α and β can also be computed via the following recursive formulae
Since the output encoder always starts from the state zero, while the probabilities for the Markov source starts from state “0” or state “1” is equal. Hence, the appropriate boundary condition for α is α0(0,0) = α0(1,0) = 1/2 and α0(i,m) = 0,i = 0,1;m ≠ 0. Similarly, the boundary conditions for β is β L (i,m) = 1/2v + 1,i = 0,1;m = 0,1,…,2v−1.
Now the whole set of equations for the modified BCJR algorithm can be obtained. Combining all the results described above, we can obtain the conditional LLR s for, as
where
representing the a priori LLR, the channel LLR and the extrinsic LLR, respectively. The same representation should apply to.
EXIT chart analysis
In this section, we present results of three-dimensional (3D) EXIT chart[19–21] analysis conducted to identify the impact of the memory structure of the Markov source and the source-relay correlation on the joint decoder. The analysis focuses on the decoder D s since the main aim is to successfully retrieve the information estimates. As shown in Figure4, the decoder D s exploits two a priori LLR s: and the updated version of,. Therefore, the EXIT function of D s can be characterized as
where denotes the mutual information between the extrinsic LLR s, generated from D s , and the coded bits of D s . can be obtained by the histogram measurement[21]. Similar definitions can be applied to and.
The second parameter of,, represents extrinsic information generated from source-relay correlation. Meanwhile, the modified BCJR algorithm adopted by D s utilizes the memory structure of Markov source. At first, we assume that the source-relay correlation is not exploited and only focus on the exploitation of source memory. In this case, and the EXIT analysis of D s can be simplified to two-dimensional. The EXIT curves with and without the modifications described in the previous section are illustrated in Figure6. The code used in the analysis is a half rate memory-1 RSC with the generator polynomials (G r ,G) = (3,2)8. It can be observed from Figure6 that, compared to the standard BCJR algorithm, the EXIT curves obtained by using the modified BCJR algorithm are lifted up over the whole a priori input region, indicating that larger extrinsic information can be obtained. It is also worth noticing that the contribution of source memory represented by the increase in extrinsic mutual information becomes larger as the entropy of Markov source decreases.
Next we conducted 3D EXIT chart analysis for D s to evaluate the impact of the source-relay correlation, where the source memory is not exploited. The corresponding EXIT planes of D s , shown in gray, are illustrated in Figure7. Two different scenarios, a relatively strong source-relay correlation (corresponding to small p e value) and a relatively weak source-relay correlation (corresponding to large p e value) are considered. It can be seen from Figure7a that with a strong source-relay correlation, the extrinsic information provided by D r , has a significant effect on. On the contrary, when the source-relay correlation is weak, has a negligible influence on, as shown in Figure7b.
The EXIT planes of decoder D s with (a) p e = 0.01 and (b) p e = 0.3. The gray planes indicates the case where only the source-relay correlation is exploited, while the light-blue planes indicates the case where both the source-relay correlation and the source memory structure are exploited. For Markov source, p1 = p2 = 0.8, H(S) = 0.72.
For the proposed DJSCC decoding scheme, both the source memory and the source-relay correlations are exploited in the iterative decoding process. The impact of the source memory and the source-relay correlations on D s , represented by the 3D EXIT planes, shown in light-blue, is presented in Figure7. We can observe that higher extrinsic information can be achieved (EXIT planes are lifted up) by exploiting the source memory and the source-relay correlations simultaneously, which will help decoder D s perfectly retrieve the source information sequence even at a low SNR sd scenario.
Convergence analysis and BER performance evaluation
A series of simulations was conducted to evaluate the convergence property, as well as BER performance of the proposed technique. The information sequences are generated from Markov sources with different state transition probabilities. The block length is 10000 bits, and 1000 different blocks were transmitted for the sake of keeping reasonable accuracy. The encoder used at the source and relay nodes, C s and C r , respectively, are both memory-1 half rate RSC with generator polynomials (G r G) = (3,2)8. Five VI s took place after every HI, with the aim of exchanging extrinsic information to exploit the source-relay correlation. The whole process was repeated 50 times. All the three relay location scenarios were evaluated, with respect to the SNR of the source-destination link. The doping rates are set at K s = K r = 2 for location A, while K s = 1, K r = 16 for both the location B and C. The threshold for estimating[6] is set at 1.
Convergence behavior with the proposed decoder
The convergence behavior with the proposed DJSCC decoder at the relay location A with SNR sd = − 3.5 dB is illustrated in Figure8. As described in Section ‘Proposed decoding scheme’, the decoding algorithms for D s and D r are not the same, and thus the upper and lower HI s are evaluated separately. It can be observed from Figure8b that the EXIT planes of D r and ACC decoder finally intersect with each other at about, which corresponds to. This observation indicates that D r can provide D s with a priori mutual information via the VI. Figure8a shows that when, the convergence tunnel is closed, but it is slightly open when. Therefore, through extrinsic mutual information exchange between D s and D r , the trajectory of the upper HI can sneak through the convergence tunnel and finally reach the convergence point while the trajectory of the lower HI gets stuck. It should be noted here that since is estimated and updated during every iteration, the trajectory of the upper HI does not match exactly with the EXIT planes of D s and the ACC decoder, especially at the first several iterations. Similar phenomena is observed for the trajectory of the lower HI.
Contribution of the source-relay correlation
The performance gains obtained by exploiting only the source-relay correlations largely rely on the quality of the source-relay link (which can be characterized by p e ), as described in the previous section. Figure9 shows the BER performance of the proposed technique when p e is known and unknown at the decoder, while the memory structure of Markov source is not taken into account. It can be observed that for relay location A and C, the BER performance of the proposed decoder is almost the same when p e is known and unknown at the decoder. However, for relay location B, convergence threshold is −7.7 and −7.4 dB when p e is known and unknown at the decoder, respectively, which results in a performance degradation of 0.3 dB. It can also be seen from Figure9 that, the performance gains obtained by exploiting only source-relay correlation (p e is assumed to be unknown at the decoder) for the locations A, B, and C, over the conventional point-to-point (P2P) communication system where relaying is not involved, are 0.6, 5.4, and 2.6 dB, respectively. Among these three different relay location scenarios, the quality of the source-relay link with the location A is the worst and that with the location B is the best, if the SNR sd is the same. This is consistent with the simulation results.
Contribution of the source memory structure
To demonstrate the performance gains obtained by exploiting the memory structure of the Markov source, the BER curves of the proposed DJSCC technique, which only exploits the source memory structure (DJSCC/SM), and hence relaying is not involved in the scenarios assumed in this section, are provided in Figure10, where K s = 1 was assumed. The BER curve of the conventional P2P communication system that does not exploit the memory structure of source is also provided in the same figure. It can be observed that the performance gain of 0.55, 1.5, and 3.6 dB can be obtained by DJSCC/SM exploiting the memory structure of Markov sources with entropy H(S) of 0.88, 0.72, and 0.47, respectively. This is consistent with the fact that as the entropy of the source decreases, the performance gain increases.
For the completeness of the article, performance comparison between the DJSCC/SM and the technique proposed in[14], which is referred to as Joint Source Channel Turbo Coding (JSCTC), is provided in this section. The performance gains of DJSCC/SM over conventional P2P system are summarized in Table1, together with the results of JSCTC as a reference. It can be found from the table that with the both techniques, substantial gains can be achieved by exploiting the knowledge of the state transition probabilities of the Markov sources. This indicates that exploiting the source memory structure provides us with significant advantage. It should be emphasized that JSCTC uses parallel-concatenated codes and employs two memory-4 constituent codes. On the other hand, our proposed system uses serial-concatenated codes and employs two memory-1 constituent codes. Nevertheless, the proposed DJSCC/SM technique outperforms JSCTC, even though the complexity with our proposed DJSCC/SM technique is much smaller than JSCTC.
BER performance of the proposed technique
The proposed DJSCC technique exploits both the source-relay correlation and the memory structure of Markov source simultaneously during the iterative decoding process, thus more performance gains should be achieved. The BER performance of the proposed technique for different Markov sources is shown in Figure11. As a reference, the BER curves of the techniques that only exploit the source-relay correlation are also provided, which are labeled as “w/o Markov source”. The performance gains achieved by the proposed DJSCC technique are summarized in Table2. It can be observed that by exploiting the memory structure of Markov source, considerable gains can be achieved.
Application to image transmission
The proposed technique was applied to image transmission to verify the effectiveness of the proposed DJSCC technique. The results with the conventional P2P, the proposed DJSCC technique that only exploit source-relay correlation (DJSCC/SR) and DJSCC/SM are also provided for comparison. Two cases were tested: (A) binary (black and white) image and (B) Grayscale image with 8-digits pixel representations. In (A), each pixel of the image has only two possible values (0 or 1). Binary images are widely used in simple devices, such as laser printers, fax machines, and bilevel computer displays. It is quite straightforward that the binary image can be modeled as Markov source. A binary image with 256×256 pixels and state transition probabilities p1 = 0.9538 and p2 = 0.9480 is shown in Figure12a as an example. The image data is encoded column-by-column. Figures12b–e show the estimates of the image obtained as the result of decoding at SNR sd = − 10 dB with the conventional P2P technique, DJSCC/SR, DJSCC/SM and DJSCC, respectively. As can be seen from Figure12, with the conventional P2P transmission, the estimated image quality is the worst containing 43.8% pixel errors (see the figure caption), since neither source-relay correlation nor source memory is exploited. With DJSCC/SR and DJSCC/SM, the estimated images contain 19.4% and 8.1% pixel errors, respectively. The proposed DJSCC that exploits both source-relay correlation and source memory achieves perfect recovery of the image, with 0% pixel error.
Grayscale images are widely used in some special applications, such as medical imaging, remote sensing and video monitoring. An example of a grayscale image with 256×256 pixels is shown in Figure13a, which is used in the simulation for (B). There are 8 bit planes in this image: the first bit plane contains the set of the most significant bits of each pixel, and the 8th contains the least significant bits, where each bit plane is a binary image. The image data is encoded plane-by-plane and column-by-column within each plane, the average state transition probabilities are p1 = 0.7167 and p2 = 0.6741. Figures13b–e show the estimates of the image, obtained as the result of decoding, at SNR sd = − 7.5 dB with the conventional P2P, DJSCC/SR, DJSCC/SM, and DJSCC, respectively. It can be observed that the performance with DJSCC/SR (50.27% pixel errors) and DJSCC/SM (96.9% pixel errors) are better than that with conventional P2P (98.1% pixel errors). However, by exploiting source-relay correlation and source memory simultaneously, the proposed DJSCC achieves perfect recovery of the image, with 0% pixel error.
Conclusion
In this article, we have presented a DJSCC scheme for transmitting binary Markov source in a one-way relay system. The relay does not aim to completely eliminate the errors in the source-relay link. Instead, the relay only extracts and forwards the source information sequence to the destination, even though the extracted information sequence may contain some errors. Since the error probability of the source-relay link can be regarded as source-relay correlation, in our proposed technique, the LLR updating function is adopted to estimate and exploit the source-relay correlation. Furthermore, to exploit the memory structure of Markov source, the trellis of Markov source and that of the channel encoder at the source node are combined to construct a super trellis. A modified version of the BCJR algorithm has been derived, based on this super trellis, to perform joint decoding of Markov source and channel code at the destination. By exploiting the source-relay correlation and the memory structure of Markov source simultaneously, the proposed technique can achieve significant gains over the techniques that only exploit the source-relay correlation, which is verified through BER simulations as well as image transmission simulations.
References
Xiong Z, Liveris AD, Cheng S, Distributed source coding for sensor networks: IEEE Signal Process. Mag. 2004, 21(5):80-94. 10.1109/MSP.2004.1328091
Li H, Zhao Q: Distributed modulation for cooperative wireless communications. IEEE Signal Process. Mag 2006, 23(5):30-36.
Zhao B, Valenti MC: Distributed turbo coded diversity for relay channel. Electron Lett 2003, 39(10):786-787. 10.1049/el:20030526
Youssef R, Graell i Amat A: Distributed serially concatenated codes for multi-source cooperative relay networks. IEEE Trans. Wirel. Commun 2011, 10: 253-263.
Si Z, Thobaben R, Skoglund M: On distributed serially concatenated codes. Proc. IEEE 10th Workshop Signal Processing Advances in Wireless Communications SPAWC’09 Perugia, Italy, 2009. 653–657
Garcia-Frias J, Zhao Y: Near-Shannon/Slepian-Wolf performance for unknown correlated sources over AWGN channels. IEEE Trans. Commun 2005, 53(4):555-559. 10.1109/TCOMM.2005.844959
Anwar K, Matsumoto T: Accumulator-assisted distributed Turbo codes for relay system exploiting source-relay correlations. IEEE Commun. Lett 2012, 16(7):1114-1117.
Thobaben R, Kliewer J: Low-complexity iterative joint source-channel decoding for variable-length encoded Markov sources. IEEE Trans. Commun 2005, 53(12):2054-2064. 10.1109/TCOMM.2005.860065
Kliewer J, Thobaben R: Parallel concatenated joint source-channel coding. Electron. Lett 2003, 39(23):1664-1666. 10.1049/el:20031084
Thobaben R, Kliewer J: On iterative source-channel decoding for variable-length encoded Markov sources using a bit-level trellis. Proc. 4th IEEE Workshop Signal Processing Advances in Wireless Communications SPAWC Auckland, New Zealand, 2003. 50–54
Jeanne M, Carlach JC, Siohan P: Joint source-channel decoding of variable-length codes for convolutional codes and turbo codes. IEEE Trans. Commun 2005, 53: 10-15. 10.1109/TCOMM.2004.840664
Garcia-Frias J, Villasenor JD: Combining hidden Markov source models and parallel concatenated codes. IEEE Commun. Lett 1997, 1(4):111-113.
Garcia-Frias J, Villasenor JD: Joint turbo decoding and estimation of hidden Markov sources. IEEE J. Sel. Areas Commun 2001, 9: 1671-1679.
Zhu GC, Alajaji F: Joint source-channel turbo coding for binary Markov sources. IEEE Trans. Wirel. Commun 2006, 5(5):1065-1075.
Kobayashi K, Yamazato T, Okada H, Katayama M: Joint channel decoding of spatially and temporally correlated data in wireless sensor networks. Proc. Int. Symp. Information Theory and Its Applications ISITA Rome, Italy, 2008. 1–5
Anwar K, Matsumoto T: Very simple BICM-ID using repetition code and extended mapping with doped accumulator. Wirel. Personal Commun 2011, 1-12. 10.1007/s11277-011-0397-1
Cover TM, Thomas JA: Elements of Information Theory,. 2006. 2nd edn.(John Wiley & Sons Inc., New York)
Bahl L, Cocke J, Jelinek F, Raviv J: Optimal decoding of linear codes for minimizing symbol error rate (Corresp.). IEEE Trans. Inf. Theory 1974, 20(2):284-287.
Tuchler M: Convergence prediction for iterative decoding of threefold concatenated systems, in. Proc. IEEE Global Telecommunications Conf. GLOBECOM’02 2002, 2: 1358-1362.
ten Brink S: Code characteristic matching for iterative decoding of serially concatenated codes. Ann. Telecommun 2001, 56: 394-408.
ten Brink S: Convergence behavior of iteratively decoded parallel concatenated codes. IEEE Trans. Commun 2001, 49(10):1727-1737. 10.1109/26.957394
Acknowledgements
This research was supported in part by the Japan Society for the Promotion of Science (JSPS) Grant under the Scientific Research KIBAN, (B) No. 2360170, (C) No. 2256037, and in part by Academy of Finland SWOCNET project.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhou, X., Cheng, M., Anwar, K. et al. Distributed joint source-channel coding for relay systems exploiting source-relay correlation and source memory. J Wireless Com Network 2012, 260 (2012). https://doi.org/10.1186/1687-1499-2012-260
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2012-260