Abstract
Based on amplify-and-forward network coding (AFNC) protocol, the outage probability and ergodic capacity of two-way network coding opportunistic relaying (TWOR-AFNC) systems are investigated as well as the corresponding closed-form solutions. For the TWOR-AFNC systems, it is investigated under two scenarios, namely, the TWOR-AFNC systems without direct link (TWOR-AFNC-Nodir) and the TWOR-AFNC systems with direct link (TWOR-AFNC-Dir). First, we investigate TWOR-AFNC-Nodir systems by employing the approximate analysis in high SNR, and obtain closed-form solutions to the cumulative distribution function (CDF) and the probability density function (PDF) of the instantaneous end-to-end signal-to-noise ratio (SNR) with very simple expressions. The derived simple expressions are given by defining an equivalent variable ω eq-k (θ), 2 ≤ θ ≤ 3. When θ = 2, the derived results are the tight lower bounds to CDF and PDF. The sequent simulation demonstrates that the derived tight lower bounds are also very effective over the entire SNR region though which the results are derived in high SNR approximation. Then, with the derived tight closed-form lower bound solutions (θ = 2) in TWOR-AFNC-Nodir systems, we investigate TWOR-AFNC-Dir systems as well as the overall comparison of the outage probability and the ergodic capacity between the two system models. The comparison analysis performed over path loss model basis shows that, in urban environment, due to utilizing the direct link the TWOR-AFNC-Dir outperform considerably the TWOR-AF-Nodir systems. However, when the value of path loss exponent is relatively large, the achievable gain is very small and the direct link can be omitted. In this case, the TWOR-AFNC-Dir model can be displaced by TWOR-AFNC-Nodir model having lower implementation complexity.
Similar content being viewed by others
1. Introduction
Cooperative diversity is an overwhelming research topic in wireless networks [1–6]. The notion of cooperative communications is to enable transmit and receive cooperation at user level by forming virtual multiple-input-multiple-output (MIMO) system, so that the overall performance including power efficiency and communications reliability can be improved greatly. However, due to the half-duplex constraint in practical systems, the advantages of the cooperative diversity come at the expense of both the spectral efficiency and the implementation complexity. Especially, in multi-relay wireless network with K relays, to achieve the full diversity order K + 1 orthogonal wireless channels (slot or frequency) are required, which incurs in the enhancement of implementation complexity as the perfect time synchronization among the relays.
In order to reduce the implementation complexity and to improve the spectrum efficiency but still realize the potential benefits of multi-relay cooperation, based on the network coding (NC) techniques [7] and the opportunistic relaying (OR) techniques [8], the two-way network coding opportunistic relaying (TWOR-NC) has emerged as a promising solution [9], and instantly become one of research hot topics in wireless network fields [10–17]. The basic idea of the TWOR-NC is that, in multi-relay two-way systems, a round of signals exchange between two sources consists of two phases, namely, access phase (AC phase) and broadcast phase (BC phase). Notice that, according to the different transmission protocols employed, time division broadcast (TDBC) and multi-access broadcast (MABC), the AC phase can include one or two sub-slots while the BC phase only does one slot. In AC phase, two sources transmit their signals to relays while the relays are listening state. After receiving the signals from both sources, the best relay selection is performed based on a predefined criterion, which results in that only a best relay is selected for NC-ing the received signals and broadcasting the NC-ed signal in BC phase. Thus, after performing NC on the received signals, the selected best relay simultaneously broadcasts the NC-ed signal to two sources. After receiving the broadcasted signal from the best relay, each source can remove the self-interference from the received signal by taking its own transmitted signal as prior. Thus, the two sources can obtain the wished signal. Obviously, the TWOR-NC perfectly integrates the NC and OR techniques and possesses the advantages of the two techniques. The TWOR-NC systems hold the improvement not only on the spectral efficiency improved by as much as 33 or 50% due to the employing of NC [7], but also on the implementation complexity decreased because the perfect time synchronization among the relays is no longer performed.
Currently, there are a few literatures contributing to TWOR-NC systems [9–17]. In the existing works, based on the fact that whether the direct link between two sources is utilized, the TWOR-NC systems can be grouped into two kinds. The first is the TWOR-NC systems in which there is no direct link, which is referred to as TWOR-NC-Nodir model in the work. On the contrary, in the second TWOR-NC systems where the direct link is utilized perfectly, which is called the TWOR-NC-Dir model. Oechtering and Boche [9] first investigated the TWOR-NC-Nodir systems under the MABC transmission protocol. In the work, the employed NC scheme was superposition network coding [4–6]. For the MABC TWOR-NC-Nodir systems, the updated contribution can be found in [10], where the decode-and-forward NC (DFNC) was employed. By comparing the achievable maximum diversity gains of two TWOR-DFNC-Nodir sytems where the max-min criterion and maxmum sum-rate criterion were adopted, respectively, authors have presented a intelligent switching selection criterion which switches between max-min and maximum sum-rate criterions according to a certain threshold of signal-to-noise ratio (SNR). In [11], with the amplify-and-forward NC (AFNC) protocol, authors first obtained the end-to-end rate expressions, R12 and R21. Then, with the aim of maximizing the sum rate of R12 and R21, i.e., max(R12 and R21), the maximum sum-rate criterion has been proposed. In [12], besides the investigation of the TWOR-NC-Nodir system based on the conventional single best relay selection criterion, authors have studied the TWOR-NC-Nodir system where a double best relay selection criterion was employed. In [13], with the aim of minimzing pairwise error probability, authors have investigated the TWOR-DFNC-Nodir systems.
At the same time, compared with the decode-and-forward TWOR [14], TWOR-AFNC is one of the most attractive protocols due to its operational simplicity. Motivated by its practical implementation potential, the TWOR-AFNC systems have been studied in [15–17] under different channels and assumptions. In these studies, the employed system models are still TWOR-AFNC-Nodir. With the Rayleigh channels, in [16] authors have pointed out that both the instantaneous end-to-end SNRs considered as independence random variables (RVs) in [15] are dependent mutually, and have presented the exact closed-form expression for outage probability in integral form as well as the lower bound. A more overall investigation of the TWOR-AFNC-Nodir has been presented in [17].
Observing the above summarization, we can find that, in existing works, the TWOR-NC-Nodir systems have been investigated widely. For the one with direct link, TWOR-NC-Dir, there is no open report yet. However, in practical implementation systems, such direct link between two sources is always existent. In half-duplex systems, the employed transmission protocol should be TDBC when the direct link is exploited. The reliability of TWOR-NC systems can be further improved when such practical existence direct transmission exploited. For the investigation of TWOR-NC-Dir systems, the canonical argument line [18] is that we must first obtain the statistical description of the instantaneous end-to-end SNRs for the systems without direct link, which includes cumulative distribution function (CDF), probability density function (PDF), moment generating function (MGF), etc. Besides this, the ones of direct link gains are also required. With these obtained statistical results of the system without direct link, we can investigate the TWOR-NC-Dir systems by employing some complicated mathematic manipulations such as (inverse) Laplace transformation, integral, etc. This mathematic manipulation requires that the statistical descriptions of the end-to-end SNRs for the systems without direct link should be given with simple closed-form expressions. However, observing the results given in [16, 17], we find that it is difficult to obtain the simple closed-form expressions of these statistics even if the lower bound expression (4) in [16] is considered. Motivated by these observations, the work contributes to a comprehensive comparison investigation for the TWOR-AFNC. We will first obtain the closed-form tight lower bound statistical descriptions for the TWOR-AFNC-Nodir, and then by using the derived tight lower bound we will study performance of the TWOR-AFNC-Dir systems.
2. TWOR-AFNC system model
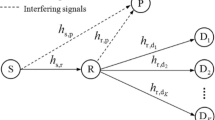
We consider TWOR-AFNC quasi-static reciprocal Rayleigh fading channels consisting of two source nodes, S1 and S2, and K relay nodes, R1,...,R K , where K is the maximum number of the achievable relays. All the nodes are equipped with single antenna and operate in half-duplex mode. The channel coefficient between S i and R k is denoted by h ik , i = 1,2, k = 1,2,...,K, and modeled as zero-mean complex Gaussian RV with variances ω ik . The one of the direct link between the two sources is denoted by βh0, where β = 1 denotes that there is direct link, and β = 0 does that there is no direct link. The variance of the direct link coefficient is ω0. For simplicity, we assume that all the channels' coefficients capture the path loss, shadow fading, and frequency non-selective fading due to the rich scattering environment as well as the transmitting power for signal, and at each node the received signals are affected by symmetric Gaussian additive noise with identical variance σ2 = 1. That is to say, all nodes transmit signals with unit transmitting power P = 1. Thus, the instantaneous squared channel strengths obey exponential distributions with hazard rates 1/ω1k, 1/ω2k, and 1/ω0, respectively, denoted by γ1k= |h1k|2 ~Υ(1/ω1k), γ2k= |h2k|2 ~Υ(1/ω2k), and γ0 = |h0|2 ~Υ(1/ω0). Due to the TDBC transmission protocol employed, the total time of a round for the information exchange between two sources is divided into three slots. In the first two slots, both sources transmit their signals x1 and x2 whereas the relays are in listening state. Thus, the received signal by relay R k is given by y k = h1kx1+h2kx2+n k . In the last slot, based on the AFNC protocol the relay broadcasts y k to both sources. The received signals by sources S1 and S2 are, respectively, given by y1 = G k h1ky k +βh0x2+n1k, y2 = G k h2ky k +βh0x1+n2k, where
Assuming the maximum ratio combining employed, we can obtain the instantaneous equivalent end-to-end SNRs as follows
where γ2k 1and γ1k 2are the receiving SNRs at S1 and S2, respectively, and
where a = 1. Letting γ(k) = min(γ1(k),γ2(k)), we have the best relay selection criterion
This leads to the equivalent instantaneous end-to-end SNR of the best relay for the TWOR-AFNC systems is expressed as
3. PDF and CDF to the equivalent instantaneous end-to-end SNR
In this section, we investigate the statistical characteristic of the TWOR-AFNC scheme. According to the statement in Section 1, the statistical description of the TWOR-AFNC-Nodir systems is required, firstly. Then, one of TWOR-AFNC-Dir systems can be obtained readily. Thus, we first present the statistical description of the TWOR-AFNC-Nodir systems.
3.1. Statistical description for TWOR-AFNC-Nodir systems
For the TWOR-AFNC-Nodir channels, we have β = 0 in (5). With the order statistics [19], the CDF Fγ(k)(γ) of γ(k) = min(γ1(k),γ2(k)) is given by
With the similar approach as the one employed in [17], the difference γ1(k)-γ2(k) is given by
By comparing the values of γ1k, and γ2k, we have
Thus, by substituting (3) into (8), the second part of the right-hand side of (6) can be rewritten into two parts [17]
We first consider the part P1(k). Obviously, to obtain the closed-form solution to P1(k), the condition is required [16]. The condition can be rewritten as (γ1k)2-(3γ)γ1k-γa ≥ 0. With the consideration γ1k≥ 0, we have the condition . This yields that the component P1(k) can be expressed as
where Eγ 1k(.) is the expectation operation with respect to γ1k. Due to γ2k= |h2k|2 ~Υ(1/ω2k), the PDF of γ2kis . This yields that (10) is rewritten as
Similarly, since the PDF ofγ1kis and , we have
In (12), we rewrite the expression of P11(k) as
Letting t = x-y and using some manipulations, this leads to
To obtain the closed-form expression of P11(k), we rewrite Equation (14) as
where and L = 2γ(γ+a/ 2). For the first part A in (15), the closed-form solution can be readily obtained. By using the equation 3.471.9 in [20], we have
where K1(z) is the modified Bessel function. As stated in [21], in high SNR the modified Bessel function can be approximated with K1(z)~1/z. Thus, for (16), with high SNR approximation we have A~1. For the second component B given in (15), using the both approximation e-t~1-t and we have
In high SNR, we have α = σ2/P~0 [17]. This leads to M~3γ, Q~2γ, and L~2γ2~0. Thus, we have
By using the symmetry between γ1(k) and γ2(k) given in (3) and substituting A, B, (15), (12), and (9) into (6), we have the approximate CDF Fγ(k)(γ) of γ(k)
Observing the expression (19) and substituting , , we have
Letting , and , Equation (20) is bounded by
where 2 ≤ θ ≤ 3. By combining (4) and using the order statistics, we have the approximate CDF Fγ(b)(γ, θ) of γ(b).
With the very simple expression for the CDF Fγ(b)(γ, θ) of γ(b), the PDF fγ(b)(γ, θ) of γ(b) can be readily obtained by taking the derivative of Fγ(b)(γ, θ) with respect to γ, and is given approximately by
where b1,...,b k a binary sequence is whose elements assume the value of zero or one.
3.2. Statistical description for TWOR-AFNC-Dir systems
In the above section, the CDF and PDF of γ(b) are achieved with very simple closed-form expressions, which make it is easy to investigate TWOR-AFNC-Dir systems. In (5), since that γ(b) and γ0 are independent, the MGF of γ T (b) = γ(b)+γ0 is given by . Using the definition of MGF given by M γ (s) = E(e-sy ), where E(x) is the expectation operation, we have the MGF of γ0 given by
Similarly, with (23) and the definition of MGF we have the MGF of γ(b) given by
Thus, with (24) and (25) we have the MGF given
To find the PDF of γ T , we use the inverse Laplace transform defined by , where is the inverse Laplace transform operator. This leads to
Taking the integral of (27) with respect to γ, the approximate CDF of γ T is given by
3.3. Ergodic capacity for TWOR-AFNC systems
The capacity of the TWOR-AFNC-Nodir systems is defined as C(γ(b)) = log(1+γ(b)). This leads to the ergodic capacity [22]
Substituting fγ(b)(γ) given in (23) into (29) and following 4.337.1 in [20], we have the ergodic capacity of the considered TWOR-AFNC-Nodir systems as follows
where ε1(m) is the exponential integral function defined by .
Similar to (30), we can obtain the ergodic capacity of TWOR-AFNC-Dir systems.
3.4. Outage probabilities for TWOR-AFNC systems
The outage probability of TWO-AFNC systems is defined as the probability that the instantaneous end-to-end SNR falls bellow a certain predefined threshold μ0. For TWOR-AFNC-Nodir and TWOR-AFNC-Dir systems, the outage probabilities are, respectively, given by
4. Simulation analysis
With the above investigation, the simulations are presented in this section. In the simulation, we employ a path loss model [23], which includes path loss, show fading, and frequency non-selective fading because the rich scattering environment is given by , where h mn and d mn , respectively, denote the link gain and the distance from node m to n, c is attenuation constant, and p is the path loss exponent. In general, in urban or suburban environment, the path loss exponent is a little greater than 3. Without loss of generality, we assume that the distance between two sources is normalized to 1, the normalized distance from S1 to relay R k is d1k, and the one from S2 to R k is d2k. It is also assumed that all the relays are close together and the inter-relay distances are enough small. This assumption is commonly used in the context of cooperative diversity systems and guarantees equivalent average variances: ω1kand ω2kfor links S1 - > R k and S2 - > R k . Thus, we have ω0 = c2, ω1k= ω0(d1k)-p, and ω2k= ω0(1-d1k)-p, where k = 1,...,K, K is the maximum of the achievable relays.
By taking ω0 = 0.33, K = 6, the path loss exponent p = 3, and spectrum efficiency R0 = 1, in Figure 1, we first consider the TWOR-AFNC-Nodir systems (without direct link) and compare the outage performance between the derived results and the one obtained in [16] under symmetric channels (d1k= 0.5). At the same time, we also present the actual accurate simulation results denoted by "o" in Figure 1. From the presented results, we can find clearly that the derived result is the tight lower bound when θ = 2, and is the upper bound when θ = 3. In practice, θ = 3 denotes the high SNR approximate case where the two instantaneous end-to-end SNRs are independent [15]. For the lower bound, in low SNR region, the derived result and the one (4) given in [16] enjoy approximately equal outage probability. In large high SNR region, the derived result is closer to the actual simulation and is tighter lower bound than the one (4) in [16]. Moreover, the gap between the derived result and the actual simulation becomes smaller and smaller with the increasing SNR. However, observing the result presented in [16], we can find that the gap holds a constant, approximately. It is also observed that, for the considered symmetric channels, the result given in [16] have larger error, but the derived result matches with the simulations exactly, especially in high SNR regions. The observation indicates that the derived result is more perfect than the result (4) given in [16] when the channels are symmetric. Thus, by taking θ = 2, we investigate the tight lower bound of the outage probabilities for TWOR-AFNC-Dir systems (with direct link), and the results are denoted by "∇" in Figure 1. The result indicates that when the direct link is utilized the TWOR-AFNC-Dir can obtain approximately 3 dB gain of SNR at 10-10 of outage probability under the symmetric channels.
Figures 2 and 3 are the comparison of the ergodic capacity versus K. Due to the lower bounds of both PDF and CDF employed, the ergodic capacity is the upper bound. From Figure 2, it is observed that when the direct link is exploited the TWOR-AFNC systems obtain obvious improvement on ergodic capacity. The achievable gain of ergodic capacity is decreasing with the number of relays when the number of relays is small. However, when the number of relays is relatively large, the gain of ergodic capacity is constant, approximately. Take the symmetric channels as example, at SNR = 10 dB, the gain of the upper bound of ergodic capacity is 0.6 when the number of relays is 2, but it is 0.3 when the number of relays is greater than 6.
Figure 3 is the comparison of ergodic capacity between the symmetric channels and asymmetric channels for TWOR-AFNC systems with and without direct link cases. It is observed that, in the both TWOR-AFNC systems, the ergodic capacities of symmetric channels are granter than the one of asymmetric channels. When the number of relays is small, the gain of ergodic capacity achieved by symmetric channels over the asymmetric one is increasing with K. However, when K is relatively large (K > 6), it equals to a constant, approximately.
In Figures 4 and 5, we investigate the effect of path loss exponent on the system performance. In the simulation, only the symmetric channels are considered and the values of ω1kand ω2kare constant, i.e., the distance d1k= 0.5, ω1k= ω2k= c2 = 0.33, and ω0 = c2×(0.5) p . This leads to that the corresponding performance of the TWOR-AFNC-Nodir systems should be constant. However, for the systems with direct link, it should be changing with the path loss exponent p. From Figures 4 and 5, we can find that the performance improvement obtained in the systems with direct are considerable when the value of path loss exponent is relatively small. For example, in urban environment (p = 3), the maximum ergodic capacity gain is 0.29 and the SNR gain is 2.5 at 10-10 of outage probability. However, the curves of both outage probability and ergodic capacity are very close to the curves of the systems without direct link when the value of the path loss exponent is grater than 5, which yields that the performance gain obtained in TWOR-AFNC-Dir systems is very small and can be omitted. The observed result indicates that when the value of path loss exponent is relatively large, the direct link can be omitted, which yields that the complexity of systems is degraded greatly. On the contrary, we should consider the direct link. Besides this, in Figure 5(b) it is observed that the gain of ergodic capacity obtained in direct link systems is increasing with SNR when the value of SNR is small (SNR < 20 dB). When it is large (SNR ≥ 20dB), the achieved gain is a constant.
5. Conclusion
Through the high SNR approximation, we first obtain the closed-form analytical solutions to CDF and PDF of the end-to-end SNR for TWOR-AF-Nodir systems, and present the corresponding tight lower bound. Though the tight lower bounds are obtained in high SNR approximation, the sequent simulations demonstrate that the high SNR approximation results are also effective over the entire SNR region. Especially, the results are given with very simple closed-form expressions, which are significant for the investigation of the TWOR-AFNC systems having direct link between two sources. With the approximate lower bounds to PDF and CDF for TWOR-AF-Nodir systems, the outage performance and the ergodic capacity for TWOR-AF-Dir systems are investigated comprehensively. The presented simulation indicates that, in urban environment, by utilizing the direct link the TWOR-AF systems can obtain the considerable improvement on the performance. However, when the value of path loss exponent is large relatively, the TWOR-AF-Dir model can be displaced with the TWOR-AF-Nodir model having lower implementation complexity.
Abbreviations
- AC phase:
-
access phase
- AFNC:
-
amplify-and-forward NC
- BC phase:
-
broadcast phase
- CDF:
-
cumulative distribution function
- DFNC:
-
decode-and-forward NC
- MABC:
-
multi-access broadcast
- MGF:
-
moment generating function
- MIMO:
-
multiple-input-multiple-output
- MRC:
-
maximum ratio combining
- NC:
-
network coding
- OR:
-
opportunistic relaying
- PDF:
-
probability density function
- RV:
-
random variable
- SNR:
-
signal-to-noise ratio
- TDBC:
-
time division broadcast
- TWOR-NC:
-
two-way network coding opportunistic relaying
- TWOR-NC-Dir:
-
TWOR-NC systems where there is direct link between two sources
- TWOR-NC-Nodir:
-
TWOR-NC systems where there is no direct link between two sources.
References
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Trans Inf Theory 2004, 50(11):3062-3080.
Ikki SS, Ahmed MH: On the performance of cooperative-diversity networks with the N th best-relay selection scheme. IEEE Trans Commun 2010, 58(11):3062-3069.
de Oliveira Brante G, Souza D, Pellenz M: Cooperative partial retransmission scheme in incremental decode-and-forward relaying. Eurasip Journal on Wireless Communications and Networking 2011, 2011(1):1-13. 10.1186/1687-1499-2011-1
Jia XD, Fu H, Yang L, Zhao L: Superposition coding cooperative relaying communications: outage performance analysis. Int J Commun Syst 2011, 24(3):384-397. 10.1002/dac.1160
Xiangdong J, Longxiang Y: Diversity-and-multiplexing tradeoff and throughput of superposition coding relaying strategy. J Electron (China) 2010, 27(2):166-175. 10.1007/s11767-010-0316-y
Xiangdong J, Haiyang F: Research on the outage exponent of superposition coding relaying with only relay-to-source channel state feedback. Chin J Electron (CJE) 2011, 20(1):161-164.
Koike-Akino T, Popovski P, Tarokh V: Optimized constellations for two-way wireless relaying with physical network coding. IEEE J Sel Areas Commun 2009, 27(5):773-787.
Bletsas A, Khisti A, Reed DP, Lippman A: A simple cooperative diversity method based on network path selection. IEEE J Sel Areas Commun 2006, 24(3):659-672.
Oechtering TJ, Boche H: Bidirectional regenerative half-duplex relaying using relay selection. IEEE Trans Wirel Commun 2008, 7(5):1879-1888.
Krikidis I: Relay selection for two-way relay channels with MABC DF: a diversity perspective. IEEE Trans Veh Technol 2010, 59(9):4620-4628.
Kyu-Sung H, Young-Chai K, Alouini MS: Performance bounds for two-way amplify-and-forward relaying based on relay path selection. IEEE 69th Proc Vehicular Technology Conference, 2009. VTC Spring 2009 2009, 1-5.
Yonghui L, Louie RHY, Vucetic B: Relay selection with network coding in two-way relay channels. IEEE Trans Veh Technol 59(9):4489-4499.
Zhou QF, Yonghui L, Lau FCM, Vucetic B: Decode-and-forward two-way relaying with network coding and opportunistic relay selection. IEEE Trans Commun 2010, 58(11):3070-3076.
Chen Z, Liu H, Wang W: A novel decoding-and-forward scheme with joint modulation for two-way relay channel. IEEE Commun Lett 2010, 14(12):1149-1151.
Zheng J, Bai B, Li Y: Outage-optimal opportunistic relaying for two-way amplify and forward relay channel. Electron Lett 2010, 46(8):595-597. 10.1049/el.2010.2803
Guo H, Ge JH: Outage probability of two-way opportunistic amplify-and-forward relaying. Electron Lett 2010, 46(13):918-919. 10.1049/el.2010.1315
Ju M, Kim I-M: Relay selection with ANC and TDBC protocols in bidirectional relay networks. IEEE Trans Commun 2010, 58(12):3500-3511.
Torabi M, Haccoun D, Ajib W: Performance analysis of cooperative diversity with relay selection over non-identically distributed links. IET Commun 2010, 4(5):596-605. 10.1049/iet-com.2009.0508
David HA, Nagaraja HN: Order Statistics. 3rd edition. Wiley, New York; 2003.
Gradshteyn IS, Ryzhik IM: Table of Integrals, Series, and Products. 7th edition. Academic, San Diego, CA; 2007.
Xu C, Ting-wai S, Zhou QF, Lau FCM: High-SNR analysis of opportunistic relaying based on the maximum harmonic mean selection criterion. IEEE Signal Process Lett 2010, 17(8):719-722.
Sungeun L, Myeongsu H, Daesik H: Average SNR and ergodic capacity analysis for opportunistic DF relaying with outage over rayleigh fading channels. IEEE Trans Wirel Commun 2009, 8(6):2807-2812.
Zhiguo D, Leung KK, Goeckel DL, Towsley D: On the study of network coding with diversity. IEEE Trans Wirel Commun 2009, 8(3):1247-1259.
Acknowledgements
The study was supported by the Natural Science Foundation of China under Grant 61071090 and 61171093, by the Postgraduate Innovation Program of Scientific Research of Jiangsu Province under Grant CX10B-184Z and CXZZ11_0388, and by the project 11KJA510001 and PAPD.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jia, X., Yang, L. & Fu, H. Tight performance bounds for two-way opportunistic amplify-and-forward wireless relaying networks with TDBC protocols. J Wireless Com Network 2011, 192 (2011). https://doi.org/10.1186/1687-1499-2011-192
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2011-192