Abstract
We discuss several properties of  -functions in the sense of Al-Homidan et al.. In particular, we prove that the partial metric induced by any
-functions in the sense of Al-Homidan et al.. In particular, we prove that the partial metric induced by any  weighted quasipseudometric space is a
weighted quasipseudometric space is a  -function and show that both the Sorgenfrey line and the Kofner plane provide significant examples of quasimetric spaces for which the associated supremum metric is a
-function and show that both the Sorgenfrey line and the Kofner plane provide significant examples of quasimetric spaces for which the associated supremum metric is a  -function. In this context we also obtain some fixed point results for multivalued maps by using Bianchini-Grandolfi gauge functions.
-function. In this context we also obtain some fixed point results for multivalued maps by using Bianchini-Grandolfi gauge functions.
Similar content being viewed by others
1. Introduction and Preliminaries
Kada et al. introduced in [1] the concept of  -distance on a metric space and extended the Caristi-Kirk fixed point theorem [2], the Ekeland variation principle [3] and the nonconvex minimization theorem [4], for
-distance on a metric space and extended the Caristi-Kirk fixed point theorem [2], the Ekeland variation principle [3] and the nonconvex minimization theorem [4], for  -distances. Recently, Al-Homidan et al. introduced in [5] the notion of
-distances. Recently, Al-Homidan et al. introduced in [5] the notion of  -function on a quasimetric space and then successfully obtained a Caristi-Kirk-type fixed point theorem,a Takahashi minimization theorem, an equilibrium version of Ekeland-type variational principle, and a version of Nadler's fixed point theorem for a
-function on a quasimetric space and then successfully obtained a Caristi-Kirk-type fixed point theorem,a Takahashi minimization theorem, an equilibrium version of Ekeland-type variational principle, and a version of Nadler's fixed point theorem for a  - function on a complete quasimetric space, generalizing in this way, among others, the main results of [1] because every
- function on a complete quasimetric space, generalizing in this way, among others, the main results of [1] because every  -distance is, in fact, a
-distance is, in fact, a  -function. This interesting approach has been continued by Hussain et al. [6], and by Latif and Al-Mezel [7], respectively. In particular, the authors of [7] have obtained a nice Rakotch-type theorem for
-function. This interesting approach has been continued by Hussain et al. [6], and by Latif and Al-Mezel [7], respectively. In particular, the authors of [7] have obtained a nice Rakotch-type theorem for  -functions on complete quasimetric spaces.
-functions on complete quasimetric spaces.
In Section 2 of this paper, we generalize the basic theory of  -functions to
-functions to  quasipseudometric spaces. Our approach is motivated, in part, by the fact that in many applications to Domain Theory, Complexity Analysis, Computer Science and Asymmetric Functional Analysis,
quasipseudometric spaces. Our approach is motivated, in part, by the fact that in many applications to Domain Theory, Complexity Analysis, Computer Science and Asymmetric Functional Analysis,  quasipseudometric spaces (in particular, weightable
quasipseudometric spaces (in particular, weightable  quasipseudometric spaces and their equivalent partial metric spaces) rather than quasimetric spaces, play a crucial role (cf. [8–23], etc.). In particular, we prove that for every weighted
quasipseudometric spaces and their equivalent partial metric spaces) rather than quasimetric spaces, play a crucial role (cf. [8–23], etc.). In particular, we prove that for every weighted  quasipseudometric space the induced partial metric is a
quasipseudometric space the induced partial metric is a  -function. We also show that the Sorgenfrey line and the Kofner plane provide interesting examples of quasimetric spaces for which the associated supremum metric is a
-function. We also show that the Sorgenfrey line and the Kofner plane provide interesting examples of quasimetric spaces for which the associated supremum metric is a  -function. Finally, Section 3 is devoted to present a new fixed point theorem for
-function. Finally, Section 3 is devoted to present a new fixed point theorem for  -functions and multivalued maps on
-functions and multivalued maps on  quasipseudometric spaces, by using Bianchini-Grandolfi gauge functions in the sense of [24]. Our result generalizes and improves, in several ways, well-known fixed point theorems.
quasipseudometric spaces, by using Bianchini-Grandolfi gauge functions in the sense of [24]. Our result generalizes and improves, in several ways, well-known fixed point theorems.
Throughout this paper the letter  and
and  will denote the set of positive integer numbers and the set of nonnegative integer numbers, respectively.
will denote the set of positive integer numbers and the set of nonnegative integer numbers, respectively.
Our basic references for quasimetric spaces are [25, 26].
Next we recall several pertinent concepts.
By a  quasipseudometric on a set
quasipseudometric on a set  , we mean a function
, we mean a function  such that for all
such that for all  ,
,
(i) ,
,
(ii) .
.
A  quasipseudometric
quasipseudometric  on
on  that satisfies the stronger condition
that satisfies the stronger condition
(i′)
is called a quasimetric on  .
.
We remark that in the last years several authors used the term "quasimetric" to refer to a  quasipseudometric and the term "
quasipseudometric and the term " quasimetric" to refer to a quasimetric in the above sense.
quasimetric" to refer to a quasimetric in the above sense.
In the following we will simply write  qpm instead of
qpm instead of  quasipseudometric if no confusion arises.
quasipseudometric if no confusion arises.
A  qpm space is a pair
qpm space is a pair  such that
such that  is a set and
is a set and  is a
is a  qpm on
qpm on  . If
. If  is a quasimetric on
is a quasimetric on  , the pair
, the pair  is then called a quasimetric space.
is then called a quasimetric space.
Given a  qpm
qpm  on a set
on a set  , the function
, the function  defined by
defined by  , is also a
, is also a  qpm on
qpm on  , called the conjugate of
, called the conjugate of  , and the function
, and the function  defined by
defined by  is a metric on
is a metric on  , called the supremum metric associated to
, called the supremum metric associated to  .
.
Thus, every  qpm
qpm  on
on  induces, in a natural way, three topologies denoted by
induces, in a natural way, three topologies denoted by  ,
,  and
and  , respectively, and defined as follows.
, respectively, and defined as follows.
(i) is the
is the  topology on
topology on  which has as a base the family of
which has as a base the family of  -open balls
-open balls  , where
, where  , for all
, for all  and
and  .
.
(ii) is the
is the  topology on
topology on  which has as a base the family of
which has as a base the family of  -open balls
-open balls  , where
, where  , for all
, for all  and
and  .
.
(iii) is the topology on
is the topology on  induced by the metric
induced by the metric  .
.
Note that if  is a quasimetric on
is a quasimetric on  , then
, then  is also a quasimetric, and
is also a quasimetric, and  and
and  are
are  topologies on
topologies on  .
.
Note also that a sequence  in a
in a  qpm space
qpm space  is
is  -convergent (resp.,
-convergent (resp.,  -convergent) to
-convergent) to  if and only if
if and only if  (resp.,
(resp.,  .
.
It is well known (see, for instance, [26, 27]) that there exists many different notions of completeness for quasimetric spaces. In our context we will use the following notion.
A  qpm space
qpm space  is said to be complete if every Cauchy sequence is
is said to be complete if every Cauchy sequence is  -convergent, where a sequence
-convergent, where a sequence  is called Cauchy if for each
is called Cauchy if for each  there exists
there exists  such that
such that  whenever
whenever  .
.
In this case, we say that  is a complete
is a complete  qpm on
qpm on  .
.
2.  -Functions on
-Functions on 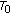 qpm-Spaces
qpm-Spaces
We start this section by giving the main concept of this paper, which was introduced in [5] for quasimetric spaces.
Definition 2.1.
A  -function on a
-function on a  qpm space
qpm space  is a function
is a function  satisfying the following conditions:
satisfying the following conditions:
(Q1) , for all
, for all  ,
,
(Q2) if  , and
, and  is a sequence in
is a sequence in  that
that  -converges to a point
-converges to a point  and satisfies
and satisfies  , for all
, for all  , then
, then  ,
,
(Q3) for each  there exists
there exists  such that
such that  and
and  imply
imply  .
.
If  is a metric space and
is a metric space and  satisfies conditions (Q1) and (Q3) above and the following condition:
satisfies conditions (Q1) and (Q3) above and the following condition:
(Q2′) is lower semicontinuous for all
is lower semicontinuous for all  , then
, then  is called a w-distance on
is called a w-distance on  (cf. [1]).
(cf. [1]).
Clearly  is a
is a  -distance on
-distance on  whenever
whenever  is a metric on
is a metric on  .
.
However, the situation is very different in the quasimetric case. Indeed, it is obvious that if  is a
is a  qpm space, then
qpm space, then  satisfies conditions (Q1) and (Q2), whereas Example 3.2 of [5] shows that there exists a
satisfies conditions (Q1) and (Q2), whereas Example 3.2 of [5] shows that there exists a  qpm space
qpm space  such that
such that  does not satisfy condition (Q3), and hence it is not a Q-function on
does not satisfy condition (Q3), and hence it is not a Q-function on  . In this direction, we next present some positive results.
. In this direction, we next present some positive results.
Lemma 2.2.
Let q be a Q-function on a  qpm space
qpm space  . Then, for each
. Then, for each  , there exists
, there exists  such that
such that  and
and  imply
imply  .
.
Proof.
By condition (Q3),  . Interchanging
. Interchanging  and
and  , it follows that
, it follows that  , so
, so  .
.
Proposition 2.3.
Let  be a
be a  qpm space. If
qpm space. If  is a Q-function on
is a Q-function on  , then
, then  , and hence,
, and hence,  is a metrizable topology on
is a metrizable topology on  .
.
Proof.
Let  be a sequence in
be a sequence in  which is
which is  -convergent to some
-convergent to some  . Then, by Lemma 2.2,
. Then, by Lemma 2.2,  . We conclude that
. We conclude that  .
.
Remark 2.4.
It follows from Proposition 2.3 that many paradigmatic quasimetrizable topological spaces  , as the Sorgenfrey line, the Michael line, the Niemytzki plane and the Kofner plane (see [25]), do not admit any compatible quasimetric
, as the Sorgenfrey line, the Michael line, the Niemytzki plane and the Kofner plane (see [25]), do not admit any compatible quasimetric  which is a
which is a  -function on
-function on  .
.
In the sequel, we show that, nevertheless, it is possible to construct an easy but, in several cases, useful  -function on any quasimetric space, as well as a suitable
-function on any quasimetric space, as well as a suitable  -functions on any weightable
-functions on any weightable  qpm space.
qpm space.
Recall that the discrete metric on a set  is the metric
is the metric  on
on  defined as
defined as  , for all
, for all  , and
, and  , for all
, for all  with
with  .
.
Proposition 2.5.
Let  be a quasimetric space. Then, the discrete metric on
be a quasimetric space. Then, the discrete metric on  is a
is a  -function on
-function on  .
.
Proof.
Since  is a metric it obviously satisfies condition (Q1) of Definition 2.1.
is a metric it obviously satisfies condition (Q1) of Definition 2.1.
Now suppose that  is a sequence in
is a sequence in  that
that  -converges to some
-converges to some  , and let
, and let  and
and  such that
such that  , for all
, for all  . If
. If  , then
, then  . If
. If  , we deduce that
, we deduce that  , for all
, for all  . Since
. Since  , it follows that
, it follows that  , so
, so  ,
, and thus
and thus  . Hence, condition (Q2) is also satisfied.
. Hence, condition (Q2) is also satisfied.
Finally,  satisfies condition (Q3) taking
satisfies condition (Q3) taking  for every
for every 
Example 2.6.
On the set  of real numbers define
of real numbers define  as
as  if
if  , and
, and  if
if  . Then,
. Then,  is a quasimetric on
is a quasimetric on  and the topological space
and the topological space  is the celebrated Sorgenfrey line. Since
is the celebrated Sorgenfrey line. Since  is the discrete metric on
is the discrete metric on  , it follows from Proposition 2.5 that
, it follows from Proposition 2.5 that  is a
is a  -function on
-function on  .
.
Example 2.7.
The quasimetric  on the plane
on the plane  , constructed in Example 7.7 of [25], verifies that
, constructed in Example 7.7 of [25], verifies that  is the so-called Kofner plane and that
is the so-called Kofner plane and that  is the discrete metric on
is the discrete metric on  , so, by Proposition 2.5,
, so, by Proposition 2.5,  is a
is a  -function on
-function on  .
.
Matthews introduced in [14] the notion of a weightable  qpm space (under the name of a "weightable quasimetric space"), and its equivalent partial metric space, as a part of the study of denotational semantics of dataflow networks.
qpm space (under the name of a "weightable quasimetric space"), and its equivalent partial metric space, as a part of the study of denotational semantics of dataflow networks.
A  qpm space
qpm space  is called weightable if there exists a function
is called weightable if there exists a function  such that for all
such that for all  . In this case, we say that
. In this case, we say that  is a weightable
is a weightable  qpm on
qpm on  . The function
. The function  is said to be a weighting function for
is said to be a weighting function for  and the triple
and the triple  is called a weighted
is called a weighted  qpm space.
qpm space.
A partial metric on a set  is a function
is a function  such that, for all
such that, for all  :
:
(i) ,
,
(ii) ,
,
(iii) ,
,
(iv) .
.
A partial metric space is a pair  such that
such that  is a set and
is a set and  is a partial metric on
is a partial metric on  .
.
Each partial metric  on
on  induces a
induces a  topology
topology  on
on  which has as a base the family of open
which has as a base the family of open  -balls
-balls  , where
, where  , for all
, for all  and
and  .
.
The precise relationship between partial metric spaces and weightable  qpm spaces is provided in the next result.
qpm spaces is provided in the next result.
Theorem 2.8 (Matthews [14]).
-
(a)
Let
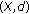 be a weightable
be a weightable 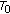 qpm space with weighting function. Then, the function
qpm space with weighting function. Then, the function 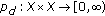 defined by
defined by 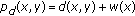 , for all
, for all 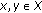 ,
, is a partial metric on
is a partial metric on  . Furthermore
. Furthermore  .
. -
(b)
Conversely, let
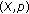 be a partial metric space. Then, the function
be a partial metric space. Then, the function 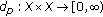 defined by
defined by 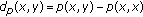 , for all
, for all 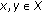 is a weightable
is a weightable 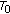 qpm on
qpm on 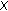 with weighting function
with weighting function  given by
given by 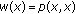 for all
for all  . Furthermore
. Furthermore 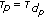 .
.
Remark 2.9.
The domain of words, the interval domain, and the complexity quasimetric space provide distinguished examples of theoretical computer science that admit a structure of a weightable  qpm space and, thus, of a partial metric space (see, e.g., [14, 20, 21]).
qpm space and, thus, of a partial metric space (see, e.g., [14, 20, 21]).
Proposition 2.10.
Let  be a weighted
be a weighted  qpm space. Then, the induced partial metric
qpm space. Then, the induced partial metric  is a Q-function on
is a Q-function on  .
.
Proof.
We will show that  satisfies conditions (Q1), (Q2), and Q(3) of Definition 2.1.
satisfies conditions (Q1), (Q2), and Q(3) of Definition 2.1.
(Q1) Let  , then
, then

(Q2)Let  be a sequence in
be a sequence in  which is
which is  -convergent to some
-convergent to some  . Let
. Let  and
and  such that
such that  , for all
, for all  .
.
Choose  . Then, there exists
. Then, there exists  such that
such that  , for all
, for all  . Therefore,
. Therefore,

Since  is arbitrary, we conclude that
is arbitrary, we conclude that  .
.
(Q3) Given  , put
, put  . If
. If  and
and  , it follows
, it follows

3. Fixed Point Results
Given a  qpm space
qpm space  , we denote by
, we denote by  the collection of all nonempty subsets of
the collection of all nonempty subsets of  , by
, by  the collection of all nonempty
the collection of all nonempty  -closed subsets of
-closed subsets of  , and by
, and by  the collection of all nonempty
the collection of all nonempty  -closed subsets of
-closed subsets of  .
.
Following Al-Homidan et al. [5, Definition 6.1] if  is a quasimetric space, we say that a multivalued map
is a quasimetric space, we say that a multivalued map  is
is  -contractive if there exists a
-contractive if there exists a  -function
-function  on
on  and
and  such that for each
such that for each  and
and  there is
there is  satisfying
satisfying  .
.
Latif and Al-Mezel (see [7]) generalized this notion as follows.
If  is a quasimetric space, we say that a multivalued map
is a quasimetric space, we say that a multivalued map  is generalized
is generalized  -contractive if there exists a
-contractive if there exists a  -function
-function  on
on  such that for each
such that for each  and
and  there is
there is  satisfying
satisfying

where  is a function such that
is a function such that  for all
for all  .
.
Then, they proved the following improvement of the celebrated Rakotch fixed point theorem (see [28]).
Theorem 3.1 (Lafit and Al-Mezel [7, Theorem 2.3]).
Let  be a complete quasimetric space. Then, for each generalized q-contractive multivalued map
be a complete quasimetric space. Then, for each generalized q-contractive multivalued map  there exists
there exists  such that
such that  .
.
On the other hand, Bianchini and Grandolfi proved in [29] the following fixed point theorem.
Theorem 3.2 (Bianchini and Grandolfi [29]).
Let  be a complete metric space and let
be a complete metric space and let  be a map such that for each
be a map such that for each 

where  is a nondecreasing function satisfying
is a nondecreasing function satisfying  , for all
, for all  (
( denotes the nth iterate of
denotes the nth iterate of  ). Then,
). Then,  has a unique fixed point.
has a unique fixed point.
A function  satisfying the conditions of the preceding theorem is called a Bianchini-Grandolfi gauge function (cf [24, 30]).
satisfying the conditions of the preceding theorem is called a Bianchini-Grandolfi gauge function (cf [24, 30]).
It is easy to check (see [30, Page 8]) that if  is a Bianchini-Grandolfi gauge function, then
is a Bianchini-Grandolfi gauge function, then  , for all
, for all  , and hence
, and hence  .
.
Our next result generalizes Bianchini-Grandolfi's theorem for Q-functions on complete  qpm spaces.
qpm spaces.
Theorem 3.3.
Let  be a complete
be a complete  qpm space, q a Q-function on
qpm space, q a Q-function on  , and
, and  a multivalued map such that for each
a multivalued map such that for each  and
and  , there is
, there is  satisfying
satisfying

where  is a Bianchini-Grandolfi gauge function. Then, there exists
is a Bianchini-Grandolfi gauge function. Then, there exists  such that
such that  and
and  .
.
Proof.
Fix  and let
and let  . By hypothesis, there exists
. By hypothesis, there exists  such that
such that  . Following this process, we obtain a sequence
. Following this process, we obtain a sequence  with
with  and
and  , for all
, for all  . Therefore
. Therefore

for all  .
.
Now, choose  . Let
. Let  for which condition (Q3) is satisfied. We will show that there is
for which condition (Q3) is satisfied. We will show that there is  such that
such that  whenever
whenever  .
.
Indeed, if  , then
, then  and thus
and thus  , for all
, for all  , so, by condition (Q1),
, so, by condition (Q1),  whenever
whenever  .
.
If  ,
,  , so there is
, so there is  such that
such that

Then, for  , we have
, we have

In particular,  and
and  whenever
whenever  , so, by Lemma 2.2,
, so, by Lemma 2.2,  whenever
whenever  .
.
We have proved that  is a Cauchy sequence in
is a Cauchy sequence in  (in fact, it is a Cauchy sequence in the metric space
(in fact, it is a Cauchy sequence in the metric space  . Since
. Since  is complete there exists
is complete there exists  such that
such that  .
.
Next, we show that  .
.
To this end, we first prove that  . Indeed, choose
. Indeed, choose  . Fix
. Fix  . Since
. Since  whenever
whenever  , it follows from condition (Q2) that
, it follows from condition (Q2) that  whenever
whenever  .
.
Now for each  take
take  such that
such that

If  , it follows that
, it follows that  . Otherwise we obtain
. Otherwise we obtain  .
.
Hence,  , and by Lemma 2.2,
, and by Lemma 2.2,

Therefore,  .
.
It remains to prove that  .
.
Since  , we can construct a sequence
, we can construct a sequence  in
in  such that
such that  ,
,  and
and


Since  , it follows that
, it follows that  , and thus
, and thus  . So, by Lemma 2.2,
. So, by Lemma 2.2,  is a Cauchy sequence in
is a Cauchy sequence in  (in fact, it is a Cauchy sequence in
(in fact, it is a Cauchy sequence in  . Let
. Let  such that
such that  . Given
. Given  , there is
, there is  such that
such that  , for all
, for all  . By applying condition (Q2), we deduce that
. By applying condition (Q2), we deduce that  , so
, so  . Since
. Since  , it follows from condition (Q1) that
, it follows from condition (Q1) that  . Therefore,
. Therefore,  , for all
, for all  , by condition (Q3). We conclude that
, by condition (Q3). We conclude that  , and thus
, and thus  .
.
The next example illustrates Theorem 3.3.
Example 3.4.
Let  and let
and let  be the
be the  qpm on
qpm on  given by
given by  . It is well known that
. It is well known that  is weightable with weighting function
is weightable with weighting function  given by
given by  , for all
, for all  . Let
. Let  be partial metric induced by
be partial metric induced by  . Then,
. Then,  is a
is a  -function on
-function on  by Proposition 2.10. Note also that, by Theorem 2.8 (a),
by Proposition 2.10. Note also that, by Theorem 2.8 (a),

for all  . Moreover
. Moreover  is clearly complete because
is clearly complete because  is the Euclidean metric on
is the Euclidean metric on  and thus
and thus  is a compact metric space.
is a compact metric space.
Now define  by
by

for all  . Note that
. Note that  because the nonempty
because the nonempty  -closed subsets of
-closed subsets of  are the intervals of the form
are the intervals of the form  ,
,  .
.
Let  be such that
be such that  , for all
, for all  , and
, and  , for all
, for all  . We wish to show that
. We wish to show that  is a Bianchini-Grandolfi gauge function.
is a Bianchini-Grandolfi gauge function.
It is clear that  is nondecreasing.
is nondecreasing.
Moreover,  , for all
, for all  . Indeed, if
. Indeed, if  we have
we have  whenever
whenever  , while for
, while for  , we have
, we have  so,
so,

and following this process we deduce the known fact that  , for all
, for all  . We have shown that
. We have shown that  is a Bianchini-Grandolfi gauge function.
is a Bianchini-Grandolfi gauge function.
Finally, for each  and
and  , there exists
, there exists  such that
such that  . Choose
. Choose  . Then
. Then  and
and

If  , then
, then  , and thus
, and thus  .
.
We have checked that conditions of Theorem 3.3 are fulfilled, and hence, there is  with
with  . In fact
. In fact  is the only point of
is the only point of  satisfying
satisfying  and
and  (actually
(actually  . The following consequence of Theorem 3.3, which is also illustrated by Example 3.4, improves and generalizes in several directions the Banach Contraction Principle for partial metric spaces obtained in Theorem 5.3 of [14].
. The following consequence of Theorem 3.3, which is also illustrated by Example 3.4, improves and generalizes in several directions the Banach Contraction Principle for partial metric spaces obtained in Theorem 5.3 of [14].
Corollary 3.5.
Let  be a partial metric space such that the induced weightable
be a partial metric space such that the induced weightable  qpm
qpm  is complete and let
is complete and let  be a multivalued map such that for each
be a multivalued map such that for each  and
and  , there is
, there is  satisfying
satisfying

where  is a Bianchini-Grandolfi gauge function. Then, there exists
is a Bianchini-Grandolfi gauge function. Then, there exists  such that
such that  and
and  .
.
Proof.
Since  (see Theorem 2.8), we deduce from Proposition 2.10 that
(see Theorem 2.8), we deduce from Proposition 2.10 that  is a
is a  -function for the complete (weightable)
-function for the complete (weightable)  qpm space
qpm space  . The conclusion follows from Theorem 3.3.
. The conclusion follows from Theorem 3.3.
Observe that if  is a nondecreasing function such that
is a nondecreasing function such that  , for all
, for all  , then the function
, then the function  given by
given by  , is a Bianchini-Grandolfi gauge function (compare [31, Proposition 8]). Therefore, the following variant of Theorem 3.1, which improves Corollary 2.4 of [7], is now a consequence of Theorem 3.3.
, is a Bianchini-Grandolfi gauge function (compare [31, Proposition 8]). Therefore, the following variant of Theorem 3.1, which improves Corollary 2.4 of [7], is now a consequence of Theorem 3.3.
Corollary 3.6.
Let  be a complete
be a complete  qpm space. Then, for each generalized q-contractive multivalued map
qpm space. Then, for each generalized q-contractive multivalued map  with q nondecreasing, there exists
with q nondecreasing, there exists  such that
such that  and
and  .
.
Remark 3.7.
The proof of Theorem 3.3 shows that the condition that  is complete can be replaced by the more general condition that every Cauchy sequence in the metric space
is complete can be replaced by the more general condition that every Cauchy sequence in the metric space  is
is  -convergent.
-convergent.
References
Kada O, Suzuki T, Takahashi W: Nonconvex minimization theorems and fixed point theorems in complete metric spaces. Mathematica Japonica 1996,44(2):381–391.
Caristi J, Kirk WA: Geometric fixed point theory and inwardness conditions. In The Geometry of Metric and Linear Spaces, Lecture Notes in Mathematics. Volume 490. Springer, Berlin, Germany; 1975:74–83. 10.1007/BFb0081133
Ekeland I: Nonconvex minimization problems. Bulletin of the American Mathematical Society 1979,1(3):443–474. 10.1090/S0273-0979-1979-14595-6
Takahashi W: Existence theorems generalizing fixed point theorems for multivalued mappings. In Fixed Point Theory and Applications, Pitman Research Notes in Mathematics Series. Volume 252. Edited by: Théra MA, Baillon JB. Longman, Harlow, UK; 1991:397–406.
Al-Homidan S, Ansari QH, Yao J-C: Some generalizations of Ekeland-type variational principle with applications to equilibrium problems and fixed point theory. Nonlinear Analysis: Theory, Methods & Applications 2008,69(1):126–139. 10.1016/j.na.2007.05.004
Hussain N, Shah MH, Kutbi MA: Coupled coincidence point theorems for nonlinear contractions in partially ordered quasi-metric spaces with a -function. Fixed Point Theory and Applications 2011, 2011:-21.
Latif A, Al-Mezel SA: Fixed point results in quasimetric spaces. Fixed Point Theory and Applications 2011, 2011:-8.
Alegre C: Continuous operators on asymmetric normed spaces. Acta Mathematica Hungarica 2009,122(4):357–372. 10.1007/s10474-008-8039-0
Ali-Akbari M, Honari B, Pourmahdian M, Rezaii MM: The space of formal balls and models of quasi-metric spaces. Mathematical Structures in Computer Science 2009,19(2):337–355. 10.1017/S0960129509007439
Cobzaş S: Compact and precompact sets in asymmetric locally convex spaces. Topology and its Applications 2009,156(9):1620–1629. 10.1016/j.topol.2009.01.004
García-Raffi LM, Romaguera S, Sánchez-Pérez EA: The Goldstine theorem for asymmetric normed linear spaces. Topology and its Applications 2009,156(13):2284–2291. 10.1016/j.topol.2009.06.001
García-Raffi LM, Romaguera S, Schellekens MP: Applications of the complexity space to the general probabilistic divide and conquer algorithms. Journal of Mathematical Analysis and Applications 2008,348(1):346–355. 10.1016/j.jmaa.2008.07.026
Heckmann R: Approximation of metric spaces by partial metric spaces. Applied Categorical Structures 1999,7(1–2):71–83.
Matthews SG: Partial metric topology. In Proceedings of the 14th Summer Conference on General Topology and Its Applications, 1994, Annals of the New York Academy of Sciences. Volume 728. The New York Academy of Sciences, New York, NY, USA; 183–197.
Romaguera S: On computational models for the hyperspace. In Advances in Mathematics Research. Vol. 8, Advances in Mathematics. Nova Science, New York, NY, USA; 2009:277–294.
Romaguera S, Schellekens M: Partial metric monoids and semivaluation spaces. Topology and its Applications 2005,153(5–6):948–962. 10.1016/j.topol.2005.01.023
Romaguera S, Tirado P: The complexity probabilistic quasi-metric space. Journal of Mathematical Analysis and Applications 2011,376(2):732–740. 10.1016/j.jmaa.2010.11.056
Romaguera S, Valero O: A quantitative computational model for complete partial metric spaces via formal balls. Mathematical Structures in Computer Science 2009,19(3):541–563. 10.1017/S0960129509007671
Romaguera S, Valero O: Domain theoretic characterisations of quasi-metric completeness in terms of formal balls. Mathematical Structures in Computer Science 2010,20(3):453–472. 10.1017/S0960129510000010
Schellekens M: The Smyth completion: a common foundation for denotational semantics and complexity analysis. In Mathematical Foundations of Programming Semantics (New Orleans, LA, 1995), Electronic Notes in Theoretical Computer Science. Volume 1. Elsevier, Amsterdam, The Netherlands; 1995:535–556.
Schellekens MP: A characterization of partial metrizability: domains are quantifiable. Theoretical Computer Science 2003,305(1–3):409–432.
Waszkiewicz P: Quantitative continuous domains. Applied Categorical Structures 2003,11(1):41–67. 10.1023/A:1023012924892
Waszkiewicz P: Partial metrisability of continuous posets. Mathematical Structures in Computer Science 2006,16(2):359–372. 10.1017/S0960129506005196
Proinov PD: A generalization of the Banach contraction principle with high order of convergence of successive approximations. Nonlinear Analysis: Theory, Methods & Applications 2007,67(8):2361–2369. 10.1016/j.na.2006.09.008
Fletcher P, Lindgren WF: Quasi-Uniform Spaces, Lecture Notes in Pure and Applied Mathematics. Volume 77. Marcel Dekker, New York, NY, USA; 1982:viii+216.
Künzi H-PA: Nonsymmetric distances and their associated topologies: about the origins of basic ideas in the area of asymmetric topology. In Handbook of the History of General Topology, Vol. 3, History of Topology. Volume 3. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001:853–968.
Reilly IL, Subrahmanyam PV, Vamanamurthy MK: Cauchy sequences in quasipseudometric spaces. Monatshefte für Mathematik 1982,93(2):127–140. 10.1007/BF01301400
Rakotch E: A note on contractive mappings. Proceedings of the American Mathematical Society 1962, 13: 459–465. 10.1090/S0002-9939-1962-0148046-1
Bianchini RM, Grandolfi M: Trasformazioni di tipo contrattivo generalizzato in uno spazio metrico. Atti della Accademia Nazionale dei Lincei 1968, 45: 212–216.
Proinov PD: New general convergence theory for iterative processes and its applications to Newton-Kantorovich type theorems. Journal of Complexity 2010,26(1):3–42. 10.1016/j.jco.2009.05.001
Chang TH: Common fixed point theorems for multivalued mappings. Mathematica Japonica 1995,41(2):311–320.
Acknowledgments
The authors thank one of the reviewers for suggesting the inclusion of a concrete example to which Theorem 3.3 applies. They acknowledge the support of the Spanish Ministry of Science and Innovation, Grant no. MTM2009-12872-C02-01.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Marín, J., Romaguera, S. & Tirado, P.  -Functions on Quasimetric Spaces and Fixed Points for Multivalued Maps.
Fixed Point Theory Appl 2011, 603861 (2011). https://doi.org/10.1155/2011/603861
-Functions on Quasimetric Spaces and Fixed Points for Multivalued Maps.
Fixed Point Theory Appl 2011, 603861 (2011). https://doi.org/10.1155/2011/603861
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/603861




 -Functions on
-Functions on  qpm-Spaces
qpm-Spaces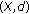 be a weightable
be a weightable 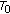 qpm space with weighting function. Then, the function
qpm space with weighting function. Then, the function 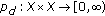 defined by
defined by 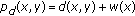 , for all
, for all 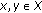 ,
, is a partial metric on
is a partial metric on  . Furthermore
. Furthermore  .
.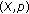 be a partial metric space. Then, the function
be a partial metric space. Then, the function 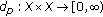 defined by
defined by 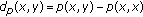 , for all
, for all 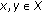 is a weightable
is a weightable 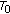 qpm on
qpm on 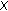 with weighting function
with weighting function  given by
given by 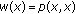 for all
for all  . Furthermore
. Furthermore 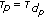 .
.