Abstract
We investigate the asymptotic behavior of solutions of the following higher-order dynamic equation  , on an arbitrary time scale
, on an arbitrary time scale  , where the function
, where the function  is defined on
is defined on  . We give sufficient conditions under which every solution
. We give sufficient conditions under which every solution  of this equation satisfies one of the following conditions: (1)
of this equation satisfies one of the following conditions: (1)  ; (2) there exist constants
; (2) there exist constants  with
with  , such that
, such that  , where
, where 
 are as in Main Results.
are as in Main Results.
Similar content being viewed by others
1. Introduction
In this paper, we investigate the asymptotic behavior of solutions of the following higher-order dynamic equation

on an arbitrary time scale  , where the function
, where the function  is defined on
is defined on  .
.
Since we are interested in the asymptotic and oscillatory behavior of solutions near infinity, we assume that  , and define the time scale interval
, and define the time scale interval  , where
, where  . By a solution of (1.1), we mean a nontrivial real-valued function
. By a solution of (1.1), we mean a nontrivial real-valued function  , which has the property that
, which has the property that  and satisfies (1.1) on
and satisfies (1.1) on  , where
, where  is the space of rd-continuous functions. The solutions vanishing in some neighborhood of infinity will be excluded from our consideration. A solution
is the space of rd-continuous functions. The solutions vanishing in some neighborhood of infinity will be excluded from our consideration. A solution  of (1.1) is said to be oscillatory if it is neither eventually positive nor eventually negative, otherwise it is called nonoscillatory.
of (1.1) is said to be oscillatory if it is neither eventually positive nor eventually negative, otherwise it is called nonoscillatory.
The theory of time scales, which has recently received a lot of attention, was introduced by Hilger's landmark paper [1] in order to create a theory that can unify continuous and discrete analysis. The cases when a time scale is equal to the real numbers or to the integers represent the classical theories of differential and of difference equations. Many other interesting time scales exist, and they give rise to many applications (see [2]). Not only the new theory of the so-called "dynamic equations" unifies the theories of differential equations and difference equations but also extends these classical cases to cases "in between," for example, to the so-called  -difference equations when
-difference equations when  , which has important applications in quantum theory (see [3]).
, which has important applications in quantum theory (see [3]).
On a time scale  , the forward jump operator, the backward jump operator, and the graininess function are defined as
, the forward jump operator, the backward jump operator, and the graininess function are defined as

respectively. We refer the reader to [2, 4] for further results on time scale calculus. Let  with
with  , for all
, for all  , then the delta exponential function
, then the delta exponential function  is defined as the unique solution of the initial value problem
is defined as the unique solution of the initial value problem

In recent years, there has been much research activity concerning the oscillation and nonoscillation of solutions of various equations on time scales, and we refer the reader to [5–18].
Recently, Erbe et al. [19–21] considered the asymptotic behavior of solutions of the third-order dynamic equations

respectively, and established some sufficient conditions for oscillation.
Karpuz [22] studied the asymptotic nature of all bounded solutions of the following higher-order nonlinear forced neutral dynamic equation

Chen [23] derived some sufficient conditions for the oscillation and asymptotic behavior of the  th-order nonlinear neutral delay dynamic equations
th-order nonlinear neutral delay dynamic equations

on an arbitrary time scale T. Motivated by the above studies, in this paper, we study (1.1) and give sufficient conditions under which every solution  of (1.1) satisfies one of the following conditions: (1)
of (1.1) satisfies one of the following conditions: (1)  ; (2) there exist constants
; (2) there exist constants  with
with  , such that
, such that  , where
, where  are as in Section 2.
are as in Section 2.
2. Main Results
Let  be a nonnegative integer and
be a nonnegative integer and  , then we define a sequence of functions
, then we define a sequence of functions  as follows:
as follows:

To obtain our main results, we need the following lemmas.
Lemma 2.1.
Let  be a positive integer, then there exists
be a positive integer, then there exists  , such that
, such that

Proof.
We will prove the above by induction. First, if  , then we take
, then we take  . Thus,
. Thus,

Next, we assume that there exists  , such that
, such that  for
for  and
and  with
with  , then
, then

from which it follows that there exists  , such that
, such that  for
for  and
and  . The proof is completed.
. The proof is completed.
Lemma 2.2 (see [24]).
Let  , then
, then

Lemma 2.3 (see [2]).
Let  and
and  , then
, then

implies

Lemma 2.4 (see [2]).
Let  be a positive integer. Suppose that
be a positive integer. Suppose that  is
is  times differentiable on T. Let
times differentiable on T. Let  and
and  , then
, then

Lemma 2.5 (see [2]).
Assume that  and
and  are differentiable on T with
are differentiable on T with  . If there exists
. If there exists  , such that
, such that

then

Lemma 2.6 (see [23]).
Let  be defined on
be defined on  , and
, and  with
with  for
for  and not eventually zero. If
and not eventually zero. If  is bounded, then
is bounded, then
-
(1)
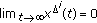 for
for 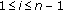 ,
, -
(2)
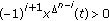 for all
for all  and
and 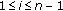 .
.
Now, one states and proves the main results.
Theorem 2.7.
Assume that there exists  , such that the function
, such that the function  satisfies
satisfies

where  are nonnegative functions on
are nonnegative functions on  and
and

with  , then every solution
, then every solution  of (1.1) satisfies one of the following conditions:
of (1.1) satisfies one of the following conditions:
-
(1)
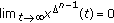 ,
, -
(2)
there exist constants
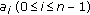 with
with  , such that
, such that (2.13)
(2.13)
Proof.
Let  be a solution of (1.1), then it follows from Lemma 2.4 that for
be a solution of (1.1), then it follows from Lemma 2.4 that for  ,
,

By (2.11) and Lemma 2.1, we see that there exists  , such that for
, such that for  and
and  ,
,

Then we obtain

where

with

Using (2.16) and (2.17), it follows that

By Lemma 2.3, we have

with  . Hence from (2.12), there exists a finite constant
. Hence from (2.12), there exists a finite constant  , such that
, such that  for
for  . Thus, inequality (2.20) implies that
. Thus, inequality (2.20) implies that

By (1.1), we see that if  , then
, then

Since condition (2.12) and Lemma 2.2 implies that

we find from (2.11) and (2.21) that the sum in (2.22) converges as  . Therefore,
. Therefore,  exists and is a finite number. Let
exists and is a finite number. Let  . If
. If  , then it follows from Lemma 2.5 that
, then it follows from Lemma 2.5 that

and  has the desired asymptotic property. The proof is completed.
has the desired asymptotic property. The proof is completed.
Theorem 2.8.
Assume that there exist functions  , and nondecreasing continuous functions
, and nondecreasing continuous functions  , and
, and  such that
such that

with

then every solution  of (1.1) satisfies one of the following conditions:
of (1.1) satisfies one of the following conditions:
-
(1)
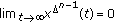 ,
, -
(2)
there exist constants
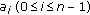 with
with 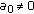 such that
such that

Proof.
Let  be a solution of (1.1), then it follows from Lemma 2.4 that for
be a solution of (1.1), then it follows from Lemma 2.4 that for  ,
,

By Lemma 2.1 and (2.25), we see that there exists  , such that for
, such that for  and
and  ,
,

Then, we obtain

where

with

Using (2.30) and (2.31), it follows that

Write


then

from which it follows that

Since  and
and  is strictly increasing, there exists a constant
is strictly increasing, there exists a constant  , such that
, such that  for
for  . By (2.30), (2.33), and (2.34), we have
. By (2.30), (2.33), and (2.34), we have

It follows from (1.1) that if  , then
, then

Since (2.38) and condition (2.25) implies that

we see that the sum in (2.39) converges as  . Therefore,
. Therefore,  exists and is a finite number. Let
exists and is a finite number. Let  . If
. If  , then it follows from Lemma 2.5 that
, then it follows from Lemma 2.5 that

and  has the desired asymptotic property. The proof is completed.
has the desired asymptotic property. The proof is completed.
Theorem 2.9.
Assume that there exist positive functions  , and nondecreasing continuous functions
, and nondecreasing continuous functions  , and
, and  , such that
, such that

with

then every solution  of (1.1) satisfies one of the following conditions:
of (1.1) satisfies one of the following conditions:
-
(1)
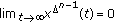 ,
, -
(2)
there exist constants
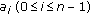 with
with 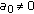 , such that
, such that

Proof.
Arguing as in the proof of Theorem 2.8, we see that there exists  , such that for
, such that for  and
and  ,
,

from which we obtain

where


Using (2.46) and (2.47), it follows that

Write


then

from which it follows that

The rest of the proof is similar to that of Theorem 2.8, and the details are omitted. The proof is completed.
Theorem 2.10.
Assume that the function  satisfies
satisfies
-
(1)
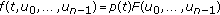 for all
for all 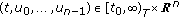 ,
, -
(2)
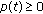 for
for  and
and  ,
, -
(3)
 for
for 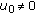 and
and 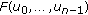 is continuous at
is continuous at  with
with 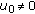 ,
,
then (1) if  is even, then every bounded solution of (1.1) is oscillatory; (2) if
is even, then every bounded solution of (1.1) is oscillatory; (2) if  is odd, then every bounded solution
is odd, then every bounded solution  of (1.1) is either oscillatory or tends monotonically to zero together with
of (1.1) is either oscillatory or tends monotonically to zero together with  .
.
Proof.
Assume that (1.1) has a nonoscillatory solution  on
on  , then, without loss of generality, there is a
, then, without loss of generality, there is a  , sufficiently large, such that
, sufficiently large, such that  for
for  . It follows from (1.1) that
. It follows from (1.1) that  for
for  and not eventually zero. By Lemma 2.6, we have
and not eventually zero. By Lemma 2.6, we have

and  is eventually monotone. Also
is eventually monotone. Also  for
for  if
if  is even and
is even and  for
for  if
if  is odd. Since
is odd. Since  is bounded, we find
is bounded, we find  . Furthermore, if
. Furthermore, if  is even, then
is even, then  .
.
We claim that  . If not, then there exists
. If not, then there exists  , such that
, such that

since  is continuous at
is continuous at  by the condition (3). From (1.1) and (2.55), we have
by the condition (3). From (1.1) and (2.55), we have

Multiplying the above inequality by  , and integrating from
, and integrating from  to
to  , we obtain
, we obtain

Since

we get

where  . Thus,
. Thus,  since
since  is bounded, which gives a contradiction to the condition (2). The proof is completed.
is bounded, which gives a contradiction to the condition (2). The proof is completed.
3. Examples
Example 3.1.
Consider the following higher-order dynamic equation:

where  and
and  . Let
. Let  and
and

then we have

by Example 5.60 in [4]. Thus, it follows from Theorem 2.7 that if  is a solution of (3.1) with
is a solution of (3.1) with  , then there exist constants
, then there exist constants  with
with  , such that
, such that  .
.
Example 3.2.
Consider the following higher-order dynamic equation:

where  ,
,  , and
, and  . Let
. Let  ,
,  , and
, and

It is easy to verify that  satisfies the conditions of Theorem 2.8. Thus, it follows that if
satisfies the conditions of Theorem 2.8. Thus, it follows that if  is a solution of (3.4) with
is a solution of (3.4) with  , then there exist constants
, then there exist constants  with
with  , such that
, such that  .
.
Example 3.3.
Consider the following higher-order dynamic equation:

where  with
with  and
and  . Let
. Let  , and
, and

It is easy to verify that  satisfies the conditions of Theorem 2.9. Thus, it follows that if
satisfies the conditions of Theorem 2.9. Thus, it follows that if  is a solution of (3.6) with
is a solution of (3.6) with  , then there exist constants
, then there exist constants  with
with  , such that
, such that  .
.
References
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1-2):18-56.
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Kac V, Cheung P: Quantum Calculus, Universitext. Springer, New York, NY, USA; 2002:x+112.
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Bohner M, Saker SH: Oscillation of second order nonlinear dynamic equations on time scales. The Rocky Mountain Journal of Mathematics 2004,34(4):1239-1254. 10.1216/rmjm/1181069797
Erbe L: Oscillation results for second-order linear equations on a time scale. Journal of Difference Equations and Applications 2002,8(11):1061-1071. 10.1080/10236190290015317
Hassan TS: Oscillation criteria for half-linear dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2008,345(1):176-185. 10.1016/j.jmaa.2008.04.019
Agarwal RP, Bohner M, Saker SH: Oscillation of second order delay dynamic equations. The Canadian Applied Mathematics Quarterly 2005,13(1):1-17.
Bohner M, Karpuz B, Öcalan Ö: Iterated oscillation criteria for delay dynamic equations of first order. Advances in Difference Equations 2008, 2008:-12.
Erbe L, Peterson A, Saker SH: Oscillation criteria for second-order nonlinear delay dynamic equations. Journal of Mathematical Analysis and Applications 2007,333(1):505-522. 10.1016/j.jmaa.2006.10.055
Han Z, Shi B, Sun S: Oscillation criteria for second-order delay dynamic equations on time scales. Advances in Difference Equations 2007, 2007:-16.
Han Z, Sun S, Shi B: Oscillation criteria for a class of second-order Emden-Fowler delay dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2007,334(2):847-858. 10.1016/j.jmaa.2007.01.004
Şahiner Y: Oscillation of second-order delay differential equations on time scales. Nonlinear Analysis: Theory, Methods and Applications 2005,63(5–7):e1073-e1080.
Akin-Bohner E, Bohner M, Djebali S, Moussaoui T: On the asymptotic integration of nonlinear dynamic equations. Advances in Difference Equations 2008, 2008:-17.
Hassan TS: Oscillation of third order nonlinear delay dynamic equations on time scales. Mathematical and Computer Modelling 2009,49(7-8):1573-1586. 10.1016/j.mcm.2008.12.011
Grace SR, Agarwal RP, Kaymakçalan B, Sae-jie W: On the oscillation of certain second order nonlinear dynamic equations. Mathematical and Computer Modelling 2009,50(1-2):273-286. 10.1016/j.mcm.2008.12.007
Sun T, Xi H, Yu W: Asymptotic behaviors of higher order nonlinear dynamic equations on time scales. Journal of Applied Mathematics and Computing. In press
Sun T, Xi H, Peng X, Yu W: Nonoscillatory solutions for higher-order neutral dynamic equations on time scales. Abstract and Applied Analysis 2010, 2010:-16.
Erbe L, Peterson A, Saker SH: Asymptotic behavior of solutions of a third-order nonlinear dynamic equation on time scales. Journal of Computational and Applied Mathematics 2005,181(1):92-102. 10.1016/j.cam.2004.11.021
Erbe L, Peterson A, Saker SH: Hille and Nehari type criteria for third-order dynamic equations. Journal of Mathematical Analysis and Applications 2007,329(1):112-131. 10.1016/j.jmaa.2006.06.033
Erbe L, Peterson A, Saker SH: Oscillation and asymptotic behavior of a third-order nonlinear dynamic equation. The Canadian Applied Mathematics Quarterly 2006,14(2):129-147.
Karpuz B: Asymptotic behaviour of bounded solutions of a class of higher-order neutral dynamic equations. Applied Mathematics and Computation 2009,215(6):2174-2183. 10.1016/j.amc.2009.08.013
Chen D-X: Oscillation and asymptotic behavior for n th-order nonlinear neutral delay dynamic equations on time scales. Acta Applicandae Mathematicae 2010,109(3):703-719. 10.1007/s10440-008-9341-0
Bohner M: Some oscillation criteria for first order delay dynamic equations. Far East Journal of Applied Mathematics 2005,18(3):289-304.
Acknowledgment
This paper was supported by NSFC (no. 10861002) and NSFG (no. 2010GXNSFA013106, no. 2011GXNSFA018135) and IPGGE (no. 105931003060).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sun, T., Xi, H. & Peng, X. Asymptotic Behavior of Solutions of Higher-Order Dynamic Equations on Time Scales. Adv Differ Equ 2011, 237219 (2011). https://doi.org/10.1155/2011/237219
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/237219




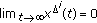 for
for 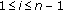 ,
,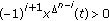 for all
for all  and
and 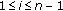 .
.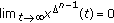 ,
,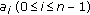 with
with  , such that
, such that
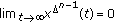 ,
,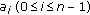 with
with 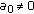 such that
such that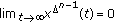 ,
,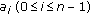 with
with 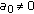 , such that
, such that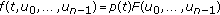 for all
for all 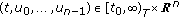 ,
,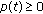 for
for  and
and  ,
, for
for 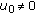 and
and 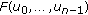 is continuous at
is continuous at  with
with 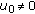 ,
,