Abstract
Using  -strongly accretive and
-strongly accretive and  -strictly pseudocontractive mapping, we introduce a general iterative method for finding a common fixed point of a semigroup of non-expansive mappings in a Hilbert space, with respect to a sequence of left regular means defined on an appropriate space of bounded real-valued functions of the semigroup. We prove the strong convergence of the proposed iterative algorithm to the unique solution of a variational inequality.
-strictly pseudocontractive mapping, we introduce a general iterative method for finding a common fixed point of a semigroup of non-expansive mappings in a Hilbert space, with respect to a sequence of left regular means defined on an appropriate space of bounded real-valued functions of the semigroup. We prove the strong convergence of the proposed iterative algorithm to the unique solution of a variational inequality.
Similar content being viewed by others
1. Introduction
Let  be a real Hilbert space. A mapping
be a real Hilbert space. A mapping  of
of  into itself is called non-expansive if
into itself is called non-expansive if  , for all
, for all  . By
. By  , we denote the set of fixed points of
, we denote the set of fixed points of  (i.e.,
(i.e.,  ).
).
Mann [1] introduced an iteration procedure for approximation of fixed points of a non-expansive mapping  on a Hilbert space as follows. Let
on a Hilbert space as follows. Let  and
and

where  is a sequence in
is a sequence in  . See also [2].
. See also [2].
On the other hand, Moudafi [3] introduced the viscosity approximation method for fixed point of non-expansive mappings (see [4] for further developments in both Hilbert and Banach spaces). Let  be a contraction on a Hilbert space
be a contraction on a Hilbert space  (i.e.,
(i.e.,  for all
for all  and
and  ). Starting with an arbitrary initial
). Starting with an arbitrary initial  , define a sequence
, define a sequence  recursively by
recursively by

where  is sequence in
is sequence in  . It is proved in [3, 4] that, under appropriate condition imposed on
. It is proved in [3, 4] that, under appropriate condition imposed on  , the sequence
, the sequence  generated by (1.2) converges strongly to the unique solution
generated by (1.2) converges strongly to the unique solution  in
in  of the variational inequality:
of the variational inequality:

Assume that  is strongly positive, that is, there is a constant
is strongly positive, that is, there is a constant  with the property
with the property

In [4] (see also [5]), it is proved that the sequence  defined by the iterative method below, with the initial guess
defined by the iterative method below, with the initial guess  chosen arbitrarily,
chosen arbitrarily,

converges strongly to the unique solution of the minimization problem

provided that the sequence  satisfies certain conditions. Marino and Xu [6] combined the iterative (1.5) with the viscosity approximation method (1.2) and considered the following general iterative methods:
satisfies certain conditions. Marino and Xu [6] combined the iterative (1.5) with the viscosity approximation method (1.2) and considered the following general iterative methods:

where  . They proved that if
. They proved that if  is a sequence in
is a sequence in  satisfying the following conditions:
satisfying the following conditions:


either or
or  ,
,
then, the sequence  generated by (1.7) converges strongly, as
generated by (1.7) converges strongly, as  , to the unique solution of the variational inequality:
, to the unique solution of the variational inequality:

which is the optimality condition for minimization problem

where  is a potential function for
is a potential function for  (i.e.,
(i.e.,  , for all
, for all  ).
).
Let  be the topological dual of a Banach space
be the topological dual of a Banach space  . The value of
. The value of  at
at  will be denoted by
will be denoted by  or
or  . With each
. With each  , we associate the set
, we associate the set

Using the Hahn-Banach theorem, it is immediately clear that  for each
for each  . The multivalued mapping
. The multivalued mapping  from
from  into
into  is said to be the (normalized) duality mapping. A Banach space
is said to be the (normalized) duality mapping. A Banach space  is said to be smooth if the duality mapping
is said to be smooth if the duality mapping  is single valued. As it is well known, the duality mapping is the identity when
is single valued. As it is well known, the duality mapping is the identity when  is a Hilbert space; see [7].
is a Hilbert space; see [7].
Let  and
and  be two positive real numbers such that
be two positive real numbers such that  . Recall that a mapping
. Recall that a mapping  with domain
with domain  and range
and range  in
in  is called
is called  -strongly accretive if, for each
-strongly accretive if, for each  , there exists
, there exists  such that
such that

Recall also that a mapping  is called
is called  -strictly pseudo-contractive if, for each
-strictly pseudo-contractive if, for each  , there exists
, there exists  such that
such that

It is easy to see that (1.12) can be rewritten as

see [8].
In this paper, motivated and inspired by Atsushiba and Takahashi [9], Lau et al. [10], Marino and Xu [6] and Xu [4, 11], we introduce the iterative below, with the initial guess  chosen arbitrarily,
chosen arbitrarily,

where  is
is  -strongly accretive and
-strongly accretive and  -strictly pseudo-contractive with
-strictly pseudo-contractive with  ,
,  is a contraction on a Hilbert space
is a contraction on a Hilbert space  with coefficient
with coefficient  ,
,  is a positive real number such that
is a positive real number such that  , and
, and  is a non-expansive semigroup on
is a non-expansive semigroup on  such that the set
such that the set  of common fixed point of
of common fixed point of  is nonempty,
is nonempty,  is a subspace of
is a subspace of  such that
such that  and the mapping
and the mapping  is an element of
is an element of  for each
for each  , and
, and  is a sequence of means on
is a sequence of means on  . Our purpose in this paper is to introduce this general iterative algorithm for approximating a common fixed points of semigroups of non-expansive mappings which solves some variational inequality. We will prove that if
. Our purpose in this paper is to introduce this general iterative algorithm for approximating a common fixed points of semigroups of non-expansive mappings which solves some variational inequality. We will prove that if  is left regular and
is left regular and  is a sequence in
is a sequence in  satisfying the conditions
satisfying the conditions  and
and  , then
, then  converges strongly to
converges strongly to  , which solves the variational inequality:
, which solves the variational inequality:

Various applications to the additive semigroup of nonnegative real numbers and commuting pairs of non-expansive mappings are also presented. It is worth mentioning that we obtain our result without assuming condition  .
.
2. Preliminaries
Let  be a semigroup and let
be a semigroup and let  be the space of all bounded real-valued functions defined on
be the space of all bounded real-valued functions defined on  with supremum norm. For
with supremum norm. For  and
and  , we define elements
, we define elements  and
and  in
in  by
by

Let  be a subspace of
be a subspace of  containing
containing  , and let
, and let  be its dual. An element
be its dual. An element  in
in  is said to be a mean on
is said to be a mean on  if
if  . We often write
. We often write  instead of
instead of  for
for  and
and  . Let
. Let  be left invariant (resp., right invariant), that is,
be left invariant (resp., right invariant), that is,  (resp.,
(resp.,  ) for each
) for each  . A mean
. A mean  on
on  is said to be left invariant (right invariant) if
is said to be left invariant (right invariant) if  (resp.
(resp.  ) for each
) for each  and
and  .
.  is said to be left (resp., right) amenable if
is said to be left (resp., right) amenable if  has a left (resp., right) invariant mean.
has a left (resp., right) invariant mean.  is amenable if
is amenable if  is both left and right amenable. As it is well known,
is both left and right amenable. As it is well known,  is amenable when
is amenable when  is a commutative semigroup; see [12]. A net
is a commutative semigroup; see [12]. A net  of means on
of means on  is said to be left regular if
is said to be left regular if

for each  , where
, where  is the adjoint operator of
is the adjoint operator of  .
.
Let  be a nonempty closed and convex subset of a reflexive Banach space
be a nonempty closed and convex subset of a reflexive Banach space  . A family
. A family  of mapping from
of mapping from  into itself is said to be a non-expansive semigroup on
into itself is said to be a non-expansive semigroup on  if
if  is non-expansive and
is non-expansive and  for each
for each  . We denote by
. We denote by  the set of common fixed points of
the set of common fixed points of  , that is,
, that is,

The open ball of radius  centered at
centered at  is denoted by
is denoted by  . For subset
. For subset  of
of  , by
, by  , we denote the closed convex hull of
, we denote the closed convex hull of  . Weak convergence is denoted by
. Weak convergence is denoted by  , and strong convergence is denoted by
, and strong convergence is denoted by  .
.
Let f be a function of semigroup  into a reflexive Banach space
into a reflexive Banach space  such that the weak closure of
such that the weak closure of  is weakly compact, and let
is weakly compact, and let  be a subspace of
be a subspace of  containing all functions
containing all functions  with
with  . Then, for any
. Then, for any  , there exists a unique element
, there exists a unique element  in
in  such that
such that

for all  . Moreover, if
. Moreover, if  is a mean on
is a mean on  then
then

One can write  by
by 
Lemma 2.2 (see [13]).
Let  be a closed convex subset of a Hilbert space
be a closed convex subset of a Hilbert space  ,
,  a semigroup from
a semigroup from  into
into  such that
such that  , the mapping
, the mapping  an element of
an element of  for each
for each  and
and  , and
, and  a mean on
a mean on  . If one writes
. If one writes  instead of
instead of  , then the following holds.
, then the following holds.
(i) is non-expansive mapping from
is non-expansive mapping from  into
into  .
.
(ii) for each
for each  .
.
(iii) for each
for each  .
.
(iv)If  is left invariant, then
is left invariant, then  is a non-expansive retraction from
is a non-expansive retraction from  onto
onto  .
.
Let  be a nonempty subset of a normed space
be a nonempty subset of a normed space  , and let
, and let  . An element
. An element  is said to be the best approximation to
is said to be the best approximation to  if
if

where  . The number
. The number  is called the distance from
is called the distance from  to
to  or the error in approximating
or the error in approximating  by
by  . The (possibly empty) set of all best approximation from
. The (possibly empty) set of all best approximation from  to
to  is denoted by
is denoted by

This defines a mapping  from
from  into
into  and is called metric (the nearest point) projection onto
and is called metric (the nearest point) projection onto  .
.
Lemma 2.3 (see [7]).
Let  be a nonempty convex subset of a smooth Banach space
be a nonempty convex subset of a smooth Banach space  and let
and let  and
and  . Then, the following is equivalent.
. Then, the following is equivalent.
(i) is the best approximation to
is the best approximation to  .
.
(ii) is a solution of the variational inequality
is a solution of the variational inequality

Let  be a nonempty subset of a Banach space
be a nonempty subset of a Banach space  and
and  a mapping. Then
a mapping. Then  is said to be demiclosed at
is said to be demiclosed at  if, for any sequence
if, for any sequence  in
in  , the following implication holds:
, the following implication holds:

Lemma 2.4 (see [14]).
Let  be a nonempty closed convex subset of a Hilbert space
be a nonempty closed convex subset of a Hilbert space  and suppose that
and suppose that  is non-expansive. Then, the mapping
is non-expansive. Then, the mapping  is demiclosed at zero.
is demiclosed at zero.
The following lemma is well known.
Lemma 2.5.
Let  be a real Hilbert space. Then, for all
be a real Hilbert space. Then, for all 
(i)
(ii)
Lemma 2.6 (see [11]).
Let  be a sequence of nonnegative real numbers such that
be a sequence of nonnegative real numbers such that

where  and
and  are sequences of real numbers satisfying the following conditions:
are sequences of real numbers satisfying the following conditions:
(i)
(ii)either  or
or 
Then, 
The following lemma will be frequently used throughout the paper. For the sake of completeness, we include its proof.
Lemma 2.7.
Let  be a real smooth Banach space and
be a real smooth Banach space and  a mapping.
a mapping.
(i)If  is
is  -strongly accretive and
-strongly accretive and  -strictly pseudo-contractive with
-strictly pseudo-contractive with  , then,
, then,  is contractive with constant
is contractive with constant  .
.
(ii)If  is
is  -strongly accretive and
-strongly accretive and  -strictly pseudo-contractive with
-strictly pseudo-contractive with  , then, for any fixed number
, then, for any fixed number  ,
,  is contractive with constant
is contractive with constant  .
.
Proof.
-
(i)
From (1.11) and (1.13), we obtain
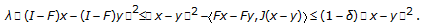 (2.11)
(2.11)Because
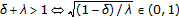 , we have
, we have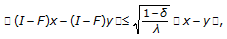 (2.12)
(2.12)and, therefore,
 is contractive with constant
is contractive with constant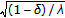 .
. -
(ii)
Because
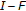 is contractive with constant
is contractive with constant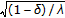 , for each fixed number
, for each fixed number 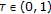 , we have
, we have  (2.13)
(2.13)
This shows that  is contractive with constant
is contractive with constant  .
.
Throughout this paper,  will denote a
will denote a  -strongly accretive and
-strongly accretive and  -strictly pseudo-contractive mapping with
-strictly pseudo-contractive mapping with  , and
, and  is a contraction with coefficient
is a contraction with coefficient  on a Hilbert space
on a Hilbert space  . We will also always use
. We will also always use  to mean a number in
to mean a number in  .
.
3. Strong Convergence Theorem
The following is our main result.
Theorem 3.1.
Let  be a non-expansive semigroup on a real Hilbert space
be a non-expansive semigroup on a real Hilbert space  such that
such that  . Let
. Let  be a left invariant subspace of
be a left invariant subspace of  such that
such that  , and the function
, and the function  is an element of
is an element of  for each
for each  . Let
. Let  be a left regular sequence of means on
be a left regular sequence of means on  , and let
, and let  be a sequence in
be a sequence in  such that
such that  and
and  . Let
. Let  and
and  be generated by the iteration algorithm (1.14). Then,
be generated by the iteration algorithm (1.14). Then,  converges strongly, as
converges strongly, as  , to
, to  , which is a unique solution of the variational inequality (1.15). Equivalently, one has
, which is a unique solution of the variational inequality (1.15). Equivalently, one has

Proof.
First, we claim that  is bounded. Let
is bounded. Let  ; by Lemmas 2.2 and 2.7 we have
; by Lemmas 2.2 and 2.7 we have

By induction,

Therefore,  is bounded and so is
is bounded and so is  .
.
Set  . We remark that
. We remark that  is
is  -invariant bounded closed convex set and
-invariant bounded closed convex set and  . Now we claim that
. Now we claim that

Let  . By [15, Theorem
. By [15, Theorem  ], there exists
], there exists  such that
such that

Also by [15, Corollary  ], there exists a natural number
], there exists a natural number  such that
such that

for all  and
and  . Let
. Let  . Since
. Since  is strongly left regular, there exists
is strongly left regular, there exists  such that
such that  for
for  and
and  . Then we have
. Then we have

By Lemma 2.2 we have

It follows from (3.5), (3.6), (3.7), and (3.8) that

for all  and
and  . Therefore,
. Therefore,

Since  is arbitrary, we get (3.4). In this stage, we will show that
is arbitrary, we get (3.4). In this stage, we will show that

Let  and
and  . Then, there exists
. Then, there exists  , which satisfies (3.5). Take
, which satisfies (3.5). Take

From  and (3.4) there exists
and (3.4) there exists  such that
such that  and
and  , for all
, for all  . By Lemma 2.7, we have
. By Lemma 2.7, we have

for all  . Therefore, we have
. Therefore, we have

for all  . This shows that
. This shows that

Since  is arbitrary, we get (3.11).
is arbitrary, we get (3.11).
Let  . Then
. Then  is a contraction of
is a contraction of  into itself. In fact, we see that
into itself. In fact, we see that

and hence  is a contraction due to
is a contraction due to 
Therefore, by Banach contraction principal,  has a unique fixed point
has a unique fixed point  . Then using Lemma 2.3,
. Then using Lemma 2.3,  is the unique solution of the variational inequality
is the unique solution of the variational inequality

We show that

Indeed, we can choose a subsequence  of
of  such that
such that

Because  is bounded, we may assume that
is bounded, we may assume that  . In terms of Lemma 2.4 and (3.11), we conclude that
. In terms of Lemma 2.4 and (3.11), we conclude that  . Therefore,
. Therefore,

Finally, we prove that  as
as  . By Lemmas 2.5 and 2.7 we have
. By Lemmas 2.5 and 2.7 we have

On the other hand

Since  and
and  are bounded, we can take a constant
are bounded, we can take a constant  such that
such that

So from the above, we reach the following:

Substituting (3.24) in (3.21), we obtain

It follows that

where

Since  is bounded and
is bounded and  , by (3.18), we get
, by (3.18), we get

Consequently, applying Lemma 2.6, to (3.26), we conclude that  .
.
Corollary 3.2.
Let  ,
,  ,
,  , and
, and  be as in Theorem 3.1. Suppose that
be as in Theorem 3.1. Suppose that  a strongly positive bounded linear operator on
a strongly positive bounded linear operator on  with coefficient
with coefficient  and
and  . Let
. Let  be defined by the iterative algorithm
be defined by the iterative algorithm

Then,  converges strongly, as
converges strongly, as  , to
, to  , which is a unique solution of the variational inequality
, which is a unique solution of the variational inequality

Proof.
Because  is strongly positive bounded linear operator on
is strongly positive bounded linear operator on  with coefficient
with coefficient  , we have
, we have

Therefore,  is
is  -strongly accretive. On the other hand,
-strongly accretive. On the other hand,

Since  is strongly positive if and only if
is strongly positive if and only if  is strongly positive, we may assume, with no loss of generality, that
is strongly positive, we may assume, with no loss of generality, that  , so that
, so that

This shows that  is
is  -strictly pseudo-contractive. Now apply Theorem 3.1 to conclude the result.
-strictly pseudo-contractive. Now apply Theorem 3.1 to conclude the result.
Corollary 3.3.
Let  ,
,  ,
,  and
and  be as in Theorem 3.1. Suppose
be as in Theorem 3.1. Suppose  and define a sequence
and define a sequence  by the iterative algorithm
by the iterative algorithm

Then,  converges strongly, as
converges strongly, as  , to a
, to a  , which is a unique solution of the variational inequality
, which is a unique solution of the variational inequality

Proof.
It is sufficient to take  and
and in Theorem 3.1.
in Theorem 3.1.
4. Some Application
Corollary 4.1.
Let  and
and  be non-expansive mappings on a Hilbert space
be non-expansive mappings on a Hilbert space  with
with  such that
such that  . Let
. Let  be a sequence in
be a sequence in  satisfying conditions
satisfying conditions  and
and  . Let
. Let  ,
,  and define a sequence
and define a sequence  by the iterative algorithm:
by the iterative algorithm:

Then,  converges strongly, as
converges strongly, as  , to
, to  which solves the variational inequality:
which solves the variational inequality:

Proof.
Let  for each
for each  . Then
. Then  is a semigroup of non-expansive mappings on
is a semigroup of non-expansive mappings on  . Now, for each
. Now, for each  and
and  , we define
, we define  Then,
Then,  is regular sequence of means [16]. Next, for each
is regular sequence of means [16]. Next, for each  and
and  , we have
, we have

Therefore, applying Theorem 3.1, the result follows.
Corollary 4.2.
Let  be a strongly continuous semigroup of non-expansive mappings on a Hilbert space
be a strongly continuous semigroup of non-expansive mappings on a Hilbert space  such that
such that  . Let
. Let  be a sequence in
be a sequence in  satisfying conditions
satisfying conditions  and
and  . Let
. Let  and
and  . Let
. Let  be a sequence defined by the iterative algorithm:
be a sequence defined by the iterative algorithm:

where  is an increasing sequence in
is an increasing sequence in  such that
such that  and
and  . Then,
. Then,  converges strongly, as
converges strongly, as  , to
, to  , which solves the variational inequality
, which solves the variational inequality

Proof.
For  , we define
, we define  for each
for each  , where
, where  denotes the space of all real-valued bounded continuous functions on
denotes the space of all real-valued bounded continuous functions on  with supremum norm. Then,
with supremum norm. Then,  is regular sequence of means [16]. Furthermore, for each
is regular sequence of means [16]. Furthermore, for each  , we have
, we have  . Now, apply Theorem 3.1 to conclude the result.
. Now, apply Theorem 3.1 to conclude the result.
Corollary 4.3.
Let  be a strongly continuous semigroup of non-expansive mappings on a Hilbert space
be a strongly continuous semigroup of non-expansive mappings on a Hilbert space  such that
such that  . Let
. Let  be a sequence in
be a sequence in  satisfying conditions
satisfying conditions  and
and  . Let
. Let  and
and  . Let
. Let  be a sequence defined by the iterative algorithm
be a sequence defined by the iterative algorithm

where  is an decreasing sequence in
is an decreasing sequence in  such that
such that  . Then
. Then  converges strongly, as
converges strongly, as  , to
, to  , which solves the variational inequality
, which solves the variational inequality

Proof.
For  , we define
, we define  for each
for each  . Then
. Then  is regular sequence of means [16]. Furthermore, for each
is regular sequence of means [16]. Furthermore, for each  , we have
, we have  . Now, apply Theorem 3.1 to conclude the result.
. Now, apply Theorem 3.1 to conclude the result.
Corollary 4.4.
Let  be a non-expansive mapping on a Hilbert space
be a non-expansive mapping on a Hilbert space  such that
such that  . Let
. Let  be a sequence in
be a sequence in  satisfying conditions
satisfying conditions  and
and  and let
and let  be a strongly regular matrix. Let
be a strongly regular matrix. Let  and
and  . Let
. Let  be a sequence defined by the iterative algorithm
be a sequence defined by the iterative algorithm

Then,  converges strongly, as
converges strongly, as  , to
, to  which solves the variational inequality
which solves the variational inequality

Proof.
For each  , we define
, we define

for each  . Since
. Since  is a strongly regular matrix, for each
is a strongly regular matrix, for each  , we have
, we have  , as
, as  ; see [17]. Then, it is easy to see that
; see [17]. Then, it is easy to see that  is regular sequence of means. Furthermore, for each
is regular sequence of means. Furthermore, for each  , we have
, we have  Now, apply Theorem 3.1 to conclude the result.
Now, apply Theorem 3.1 to conclude the result.
References
Mann WR: Mean value methods in iteration. Proceedings of the American Mathematical Society 1953, 4: 506–510. 10.1090/S0002-9939-1953-0054846-3
Halpern B: Fixed points of nonexpanding maps. Bulletin of the American Mathematical Society 1967, 73: 957–961. 10.1090/S0002-9904-1967-11864-0
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000,241(1):46–55. 10.1006/jmaa.1999.6615
Xu HK: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004,298(1):279–291. 10.1016/j.jmaa.2004.04.059
Yamada I: The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings. In Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications, Studies in Computational Mathematics. Volume 8. North-Holland, Amsterdam, The Netherlands; 2001:473–504.
Marino G, Xu HK: A general iterative method for nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2006,318(1):43–52. 10.1016/j.jmaa.2005.05.028
Agarwal RP, O'Regan D, Sahu DR: Fixed Point Theory for Lipschitzian-Type Mappings with Applications, Topological Fixed Point Theory and Its Applications. Springer, New York, NY, USA; 2009:x+368.
Zeidler E: Nonlinear Functional Analysis and Its Applications. III. Springer, New York, NY, USA; 1985:xxii+662.
Atsushiba S, Takahashi W: Approximating common fixed points of nonexpansive semigroups by the Mann iteration process. Annales Universitatis Mariae Curie-Skłodowska A 1997,51(2):1–16.
Lau AT, Miyake H, Takahashi W: Approximation of fixed points for amenable semigroups of nonexpansive mappings in Banach spaces. Nonlinear Analysis. Theory, Methods & Applications 2007,67(4):1211–1225. 10.1016/j.na.2006.07.008
Xu HK: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003,116(3):659–678. 10.1023/A:1023073621589
Lau AT, Shioji N, Takahashi W: Existence of nonexpansive retractions for amenable semigroups of nonexpansive mappings and nonlinear ergodic theorems in Banach spaces. Journal of Functional Analysis 1999,161(1):62–75. 10.1006/jfan.1998.3352
Takahashi W: A nonlinear ergodic theorem for an amenable semigroup of nonexpansive mappings in a Hilbert space. Proceedings of the American Mathematical Society 1981,81(2):253–256. 10.1090/S0002-9939-1981-0593468-X
Jung JS: Iterative approaches to common fixed points of nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 2005,302(2):509–520. 10.1016/j.jmaa.2004.08.022
Bruck RE: On the convex approximation property and the asymptotic behavior of nonlinear contractions in Banach spaces. Israel Journal of Mathematics 1981,38(4):304–314. 10.1007/BF02762776
Takahashi W: Nonlinear Functional Analysis. Yokohama Publishers, Yokohama, Japan; 2000:iv+276. Fixed Point Theory and Its Application
Hirano N, Kido K, Takahashi W: Nonexpansive retractions and nonlinear ergodic theorems in Banach spaces. Nonlinear Analysis. Theory, Methods & Applications 1988,12(11):1269–1281. 10.1016/0362-546X(88)90059-4
Acknowledgments
The authors thank the referee(s) for the helpful comments, which improved the presentation of this paper. This paper is dedicated to Professor Anthony To Ming Lau. This paper is based on final report of the research project of the Ph.D. thesis which is done with financial support of research office of the University of Tabriz.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Piri, H., Vaezi, H. Strong Convergence of a Generalized Iterative Method for Semigroups of Nonexpansive Mappings in Hilbert Spaces. Fixed Point Theory Appl 2010, 907275 (2010). https://doi.org/10.1155/2010/907275
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/907275



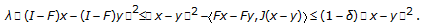
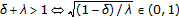 , we have
, we have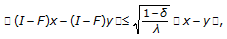
 is contractive with constant
is contractive with constant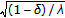 .
.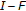 is contractive with constant
is contractive with constant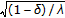 , for each fixed number
, for each fixed number 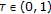 , we have
, we have 