Abstract
We consider the problem of choosing the data flow rate on a wireless link with randomly varying channel gain, to optimally trade off average transmit power and the average utility of the smoothed data flow rate. The smoothing allows us to model the demands of an application that can tolerate variations in flow over a certain time interval; we will see that this smoothing leads to a substantially different optimal data flow rate policy than without smoothing. We pose the problem as a convex stochastic control problem. For the case of a single flow, the optimal data flow rate policy can be numerically computed using stochastic dynamic programming. For the case of multiple flows on a single link, we propose an approximate dynamic programming approach to obtain suboptimal data flow rate policies. We illustrate, through numerical examples, that these approximate policies can perform very well.
Similar content being viewed by others
1. Introduction
We consider the flow rate assignment problem on a wireless link with randomly varying channel gain, to optimally trade off average transmit power and the average utility of the smoothed flow data rate. We pose the multiperiod problem as an infinite-horizon stochastic control problem with linear dynamics and convex objective. For the case of a single flow, the optimal policy is easily found using stochastic dynamic programming (DP) and gridding. For the case of multiple flows, DP becomes intractable, and we propose instead an approximate dynamic programming approach using suboptimal policies developed in the single-flow case. Simulations show that these suboptimal policies perform very well.
In the wireless communications literature, varying a link's transmit rate (and power) depending on channel conditions is called adaptive modulation (AM); see, for example, [1–5]. One drawback of AM is that it is a physical layer optimization technique with no knowledge of upper layer optimization protocols. Maximizing a total utility function is also very common in various communications and networking problem formulations, where it is referred to as network utility maximization (NUM); see, for example, [6–10]. In the NUM framework, performance of an upper layer protocol (e.g., TCP) is determined by utility of flow attributes, for example, utility of link flow rate.
Our setup involves both adaptive modulation and utility maximization but is nonstandard in several respects. We consider the utility of the smoothed flows, and we consider multiple flows over the same wireless link [11].
2. Problem Setup
2.1. Average Smoothed Flow Utility
A wireless communication link supports  data flows in a channel that varies with time, which we model using discrete-time intervals
data flows in a channel that varies with time, which we model using discrete-time intervals  . We let
. We let  be the data flow rate vector on the link, where
be the data flow rate vector on the link, where  ,
,  , is the
, is the  th flow's data rate at time
th flow's data rate at time  and
and  denotes the set of nonnegative numbers. We let
denotes the set of nonnegative numbers. We let  denote the total flow rate over all flows, where
denote the total flow rate over all flows, where  is the vector with all entries one. The flows, and the total flow rate, will depend on the random channel gain (through the flow policy, described below) and so are random variables.
is the vector with all entries one. The flows, and the total flow rate, will depend on the random channel gain (through the flow policy, described below) and so are random variables.
We will work with a smoothed version of the flow rates, which is meant to capture the tolerance of the applications using the data flows to time variations in data rate. This was introduced in [12] using delivery contracts, in which the utility is a function of the total flow over a given time interval; here, we use instead a very simple first-order linear smoothing. At each time  , the smoothed data flow rate vector
, the smoothed data flow rate vector  is given by
is given by

where  ,
,  ,
,  , is the smoothing parameter for the
, is the smoothing parameter for the  th flow, and we take
th flow, and we take  . Thus, we have
. Thus, we have

where at time  , each smoothed flow rate
, each smoothed flow rate  is the exponentially weighted average of previous flow rates.
is the exponentially weighted average of previous flow rates.
The smoothing parameter  determines the level of smoothing on flow
determines the level of smoothing on flow  . Small smoothing parameter values (
. Small smoothing parameter values ( close to zero) correspond to light smoothing; large values (
close to zero) correspond to light smoothing; large values ( close to one) correspond to heavy smoothing. (Note that
close to one) correspond to heavy smoothing. (Note that  means that flow
means that flow  is not smoothed; we have
is not smoothed; we have  .) The level of smoothing can be related to the time scale over which the smoothing occurs. We define
.) The level of smoothing can be related to the time scale over which the smoothing occurs. We define  to be the smoothing time associated with flow
to be the smoothing time associated with flow  . Roughly speaking, the smoothing time is the time interval over which the effect of a flow on the smoothed flow decays by a factor
. Roughly speaking, the smoothing time is the time interval over which the effect of a flow on the smoothed flow decays by a factor  . Light smoothing corresponds to short smoothing times, while heavy smoothing corresponds to longer smoothing times.
. Light smoothing corresponds to short smoothing times, while heavy smoothing corresponds to longer smoothing times.
We associate with each smoothed flow rate  a strictly concave nondecreasing differentiable utility function
a strictly concave nondecreasing differentiable utility function  , where the utility of
, where the utility of  is
is  . The average utility derived over all flows, over all time, is
. The average utility derived over all flows, over all time, is

where  . Here, the expectation is over the smoothed flows
. Here, the expectation is over the smoothed flows  , and we are assuming that the expectations and limit above exist.
, and we are assuming that the expectations and limit above exist.
While most of our results will hold for more general utilities, we will focus on the family of power utility functions, defined for  as
as

parameterized by  and
and  . The parameter
. The parameter  sets the curvature (or risk aversion), while
sets the curvature (or risk aversion), while  sets the overall weight of the utility. (For small values of
sets the overall weight of the utility. (For small values of  ,
,  approaches a log utility.)
approaches a log utility.)
Before proceeding, we make some general comments on our use of smoothed flows. The smoothing can be considered as a type of time averaging; then we apply a concave utility function; finally, we average this utility. The time averaging and utility function operations do not commute, except in the case when the utility is linear (or affine). Jensen's inequality tells us that average smoothed utility is greater than or equal to the average utility applied directly to the flow rates, that is,

So the time smoothing step does affect our average utility; we will see later that it has a dramatic effect on the optimal flow policy.
2.2. Average Power
We model the wireless channel with time-varying positive gain parameters  ,
,  , which we assume are independent identically distributed (IID), with known distribution. At each time
, which we assume are independent identically distributed (IID), with known distribution. At each time  , the gain parameter affects the power
, the gain parameter affects the power  required to support the total data flow rate
required to support the total data flow rate  . The power
. The power  is given by
is given by

where  is increasing and strictly convex in
is increasing and strictly convex in  for each value of
for each value of  (
( is the set of positive numbers).
is the set of positive numbers).
While our results will hold for the more general case, we will focus on the more specific power function described here. We suppose that the signal-to-interference-and-noise ratio (SINR) of the channel is given by  . (Here
. (Here  includes the effect of time-varying channel gain, noise, and interference.) The channel capacity is then
includes the effect of time-varying channel gain, noise, and interference.) The channel capacity is then  , where
, where  is a constant; this must equal at least the total flow rate
is a constant; this must equal at least the total flow rate  , so we obtain
, so we obtain

The total average power is

where, again, we are assuming that the expectations and limit exist.
2.3. Flow Rate Control Problem
The overall objective is to maximize a weighted difference between average utility and average power,

where  is used to trade off average utility and power.
is used to trade off average utility and power.
We require that the flow policy is causal; that is, when  is chosen, we know the previous and current values of the flows, smoothed flows, and channel gains. Standard arguments in stochastic control (see, e.g., [13–17]) can be used to conclude that, without loss of generality, we can assume that the flow control policy has the form
is chosen, we know the previous and current values of the flows, smoothed flows, and channel gains. Standard arguments in stochastic control (see, e.g., [13–17]) can be used to conclude that, without loss of generality, we can assume that the flow control policy has the form

where  . In other words, the policy depends only on the current smoothed flows and the current channel gain value.
. In other words, the policy depends only on the current smoothed flows and the current channel gain value.
The flow rate control problem is to choose the flow rate policy  to maximize the overall objective in (9). This is a standard convex stochastic control problem, with linear dynamics.
to maximize the overall objective in (9). This is a standard convex stochastic control problem, with linear dynamics.
2.4. Our Results
We let  be the optimal overall objective value and let
be the optimal overall objective value and let  be an optimal policy. We will show that in the general (multiple-flow) case, the optimal policy includes a "no-transmit" zone, that is, a region in the
be an optimal policy. We will show that in the general (multiple-flow) case, the optimal policy includes a "no-transmit" zone, that is, a region in the  space in which the optimal flow rate is zero. Not surprisingly, the optimal flow policy can be roughly described as waiting until the channel gain is large, or until the smoothed flow has fallen to a low level, at which point we transmit (i.e., choose nonzero
space in which the optimal flow rate is zero. Not surprisingly, the optimal flow policy can be roughly described as waiting until the channel gain is large, or until the smoothed flow has fallen to a low level, at which point we transmit (i.e., choose nonzero  ). Roughly speaking, the higher the level of smoothing, the longer we can afford to wait for a large channel gain before transmitting. The average power required to support a given utility level decreases, sometimes dramatically, as the level of smoothing increases.
). Roughly speaking, the higher the level of smoothing, the longer we can afford to wait for a large channel gain before transmitting. The average power required to support a given utility level decreases, sometimes dramatically, as the level of smoothing increases.
We show that the optimal policy for the case of a single flow is readily computed numerically, working from Bellman's characterization of the optimal policy, and is not particularly sensitive to the details of the utility functions, smoothing levels, or power functions.
For the case of multiple flows, we cannot easily compute (or even represent) the optimal policy. For this case we propose an approximate policy, based on approximate dynamic programming [18, 19]. By computing an upper bound on  , by allowing the flow control policy to use future values of channel gain (i.e., relaxing the causality requirement [20]), we show in numerical experiments that such policies are nearly optimal.
, by allowing the flow control policy to use future values of channel gain (i.e., relaxing the causality requirement [20]), we show in numerical experiments that such policies are nearly optimal.
3. Optimal Policy Characterization
3.1. No Smoothing
We first consider the special case  , in which there is no smoothing. Then we have
, in which there is no smoothing. Then we have  , so the average smoothed utility is then the same as the average utility, that is,
, so the average smoothed utility is then the same as the average utility, that is,

In this case the optimal policy is trivial, since the stochastic control problem reduces to a simple optimization problem at each time step. At time  , we simply choose
, we simply choose  to maximize
to maximize  . Thus, we have
. Thus, we have

which does not depend on  . A simple and effective approach is to presolve this problem for a suitably large set of values of the channel gain
. A simple and effective approach is to presolve this problem for a suitably large set of values of the channel gain  and store the resulting tables of individual flow rates
and store the resulting tables of individual flow rates  versus
versus  ; online we can interpolate between points in the table to find the (nearly) optimal policy. Another option is to fit a simple function to the optimal flow rate data and use this function as our (nearly) optimal policy.
; online we can interpolate between points in the table to find the (nearly) optimal policy. Another option is to fit a simple function to the optimal flow rate data and use this function as our (nearly) optimal policy.
For future reference, we note that the problem can also be solved using a waterfilling method (see, e.g., [21,Section  ]). Dropping the time index
]). Dropping the time index  and using
and using  to denote the flow index, we must solve the problem
to denote the flow index, we must solve the problem

with variables  and
and  . Introducing a Lagrange multiplier
. Introducing a Lagrange multiplier  for the equality constraint (which we can show must be nonnegative, using monotonicity of
for the equality constraint (which we can show must be nonnegative, using monotonicity of  with
with  ), we are to maximize
), we are to maximize

over  . This problem is separable in
. This problem is separable in  and
and  , so we can maximize over
, so we can maximize over  and
and  separately. We find that
separately. We find that

(Each of these can be expressed in terms of conjugate functions; (see, e.g., [21,Section  ].) We then adjust
].) We then adjust  (say, using bisection) so that
(say, using bisection) so that  . An alternative is to carry out bisection on
. An alternative is to carry out bisection on  , defining
, defining  in terms of
in terms of  as above, until
as above, until  , where
, where  refers to the derivative with respect to
refers to the derivative with respect to  .
.
For our particular power law utility functions (4), we can give an explicit formula for  in terms of
in terms of  :
:

For our particular power function (7), we use bisection to find the value of  that yields
that yields

where the flow values come from the equation above. (The left-hand side is decreasing in  , while the right-hand side is increasing.)
, while the right-hand side is increasing.)
3.2. General Case
We now consider the more general case, with smoothing. We can characterize the optimal flow rate policy  using stochastic dynamic programming [22–25] and a form of Bellman's equation [26]. The optimal flow rate policy has the form
using stochastic dynamic programming [22–25] and a form of Bellman's equation [26]. The optimal flow rate policy has the form

where  is the Bellman (relative) value function. The value function (and optimal value) is characterized via the fixed point equation
is the Bellman (relative) value function. The value function (and optimal value) is characterized via the fixed point equation

where, for any function  , the Bellman operator
, the Bellman operator  is given by
is given by

where the expectation is over  . The fixed point equation and Bellman operator are invariant under adding a constant; that is, we have
. The fixed point equation and Bellman operator are invariant under adding a constant; that is, we have  , for any constant (function)
, for any constant (function)  , and, similarly,
, and, similarly,  satisfies the fixed point equation if and only if
satisfies the fixed point equation if and only if  does. So without loss of generality we can assume that
does. So without loss of generality we can assume that  .
.
The value function can be found (in principle) by value iteration [14, 26]. We take  and repeat the following iteration, for
and repeat the following iteration, for  .
.
-
(1)
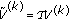 (apply Bellman operator).
(apply Bellman operator). -
(2)
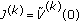 (estimate optimal value).
(estimate optimal value). -
(3)
 (normalize).
(normalize).
For technical conditions under which the value function exists and can be obtained via value iteration, see, for example, [27–29]. We will simply assume here that the value function exists, and  and
and  converge to
converge to  and
and  , respectively.
, respectively.
The iterations above preserve several attributes of the iterates, which we can then conclude holds for  . First of all, concavity of
. First of all, concavity of  is preserved; that is, if
is preserved; that is, if  is concave, so is
is concave, so is  . It is clear that normalization does not affect concavity, since we simply add a constant to the function. The Bellman operator
. It is clear that normalization does not affect concavity, since we simply add a constant to the function. The Bellman operator  preserves concavity since partial maximization of a function concave in two sets of variables results in a concave function (see, i.e.,[21, Section
preserves concavity since partial maximization of a function concave in two sets of variables results in a concave function (see, i.e.,[21, Section  ]) and expectation over a family of concave functions yields a concave function; finally, addition (of
]) and expectation over a family of concave functions yields a concave function; finally, addition (of  ) preserves concavity. So we can conclude that
) preserves concavity. So we can conclude that  is concave.
is concave.
Another attribute that is preserved in value iteration is monotonicity; if  is monotone increasing (in each component of its argument), then so is
is monotone increasing (in each component of its argument), then so is  . We conclude that
. We conclude that  is monotone increasing.
is monotone increasing.
3.3. No-Transmit Region
From the form of the optimal policy, we see that  if and only if
if and only if  is optimal for the (convex) problem
is optimal for the (convex) problem

with variable  . This is the case if and only if
. This is the case if and only if

(see, e.g., [21,page 142]). We can rewrite this as

Using the specific power function (7) associated with the log capacity formula, we obtain

as the necessary and sufficient condition under which  . Since
. Since  is decreasing (by concavity of
is decreasing (by concavity of  ), we can interpret (24) roughly as follows: do not transmit if the channel is bad (
), we can interpret (24) roughly as follows: do not transmit if the channel is bad ( small) or if the smoothed flows are large (
small) or if the smoothed flows are large ( large).
large).
4. Single-Flow Case
4.1. Optimal Policy
In the case of a single flow (i.e.,  ) we can easily carry out value iteration numerically, by discretizing the argument
) we can easily carry out value iteration numerically, by discretizing the argument  and values of
and values of  and computing the expectation and maximization numerically. For the single-flow case, then we can compute the optimal policy and optimal performance (up to small numerical integration errors).
and computing the expectation and maximization numerically. For the single-flow case, then we can compute the optimal policy and optimal performance (up to small numerical integration errors).
4.2. Power Law Suboptimal Policy
We replace the optimal value function (in the above optimal flow policy expression) with a simple analytic approximation of the value function to get the approximate policy

where  is an approximation of the value function.
is an approximation of the value function.
Since  is increasing, concave, and satisfies
is increasing, concave, and satisfies  , it is reasonable to fit it with a power law function as well, say
, it is reasonable to fit it with a power law function as well, say  , with
, with  ,
,  . For example, we can find the minimax (Chebyshev fit) by varying
. For example, we can find the minimax (Chebyshev fit) by varying  ; for each
; for each  we choose
we choose  to minimize
to minimize

where  are the discretized values of
are the discretized values of  , with associated value function values
, with associated value function values  . We do this by bisection on
. We do this by bisection on  .
.
Experiments show that these power law approximate functions are, in general, reasonable approximations for the value function. For our power law utilities, these approximations yield very good matches to the true value function. For other concave utilities, the approximation is not as accurate, but experiments show that the associated approximate policies still yield nearly optimal performance.
We can derive an explicit expression for the approximate policy (25) for our power function:

where

and  is the Lambert function; that is,
is the Lambert function; that is,  is the solution of
is the solution of  [30].
[30].
Note that this suboptimal policy is not needed in the single-flow case since we can obtain the optimal policy numerically. However, we found that the difference between our power law policy and the optimal policy (see the example of value functions below) is small enough that in practice they are virtually the same. This approximate policy is needed in the case of multiple flows.
4.3. Numerical Example
In this section we give simple numerical examples to illustrate the effect of smoothing on the resulting flow rate policy in the single-flow case. We consider two examples, with different levels of smoothing. The first flow is lightly smoothed ( ;
;  ), while the second flow is heavily smoothed (
), while the second flow is heavily smoothed ( ;
;  ). We use utility function
). We use utility function  , that is,
, that is,  ,
,  in our utility (4). The channel gains
in our utility (4). The channel gains  are IID exponential variables with mean
are IID exponential variables with mean  . We use the power function (7), with
. We use the power function (7), with  .
.
We first consider the case  . The value functions are shown in Figure 1, together with the power law approximations, which are
. The value functions are shown in Figure 1, together with the power law approximations, which are  (light smoothing) and
(light smoothing) and  (heavy smoothing). Figure 2 shows the optimal policies for the lightly smoothed flow (
(heavy smoothing). Figure 2 shows the optimal policies for the lightly smoothed flow ( ), and the heavily smoothed flow (
), and the heavily smoothed flow ( ). We can see that the optimal policies are quite different. As expected, the lightly smoothed flow transmits more often, that is, has a smaller no-transmit region.
). We can see that the optimal policies are quite different. As expected, the lightly smoothed flow transmits more often, that is, has a smaller no-transmit region.
Average Power versus Average Utility.
Figure 3 further illustrates the difference between the two flow rate policies. Using values of  , we computed (via simulation) the average power-average utility tradeoff curve for each flow. As expected, we can see that the heavily smoothed flow achieves more average utility, for a given average power, than the lightly smoothed flow. (The heavily smoothed flow requires less average power to achieve a target average utility.)
, we computed (via simulation) the average power-average utility tradeoff curve for each flow. As expected, we can see that the heavily smoothed flow achieves more average utility, for a given average power, than the lightly smoothed flow. (The heavily smoothed flow requires less average power to achieve a target average utility.)
Comparing Average Power.
We compare the average power required by each flow to generate a given average utility. Given a target average utility, we can estimate the average power required roughly from Figure 3, or more precisely via simulation as follows: choose a target average utility, and then run each controller, adjusting  separately, until we reach the target utility. In our example, we chose
separately, until we reach the target utility. In our example, we chose  and found
and found  for the lightly smoothed flow, and
for the lightly smoothed flow, and  for the heavily smoothed flow. Figure 4 shows the associated power trajectories for each flow, along with the corresponding flow and smoothed flow trajectories. The dashed (horizontal) line indicates the average power, average flow, and averaged smoothed flow for each trajectory. Clearly the lightly smoothed flow requires more power than the heavily smoothed flow, by around
for the heavily smoothed flow. Figure 4 shows the associated power trajectories for each flow, along with the corresponding flow and smoothed flow trajectories. The dashed (horizontal) line indicates the average power, average flow, and averaged smoothed flow for each trajectory. Clearly the lightly smoothed flow requires more power than the heavily smoothed flow, by around  : the heavily smoothed flow requires
: the heavily smoothed flow requires  , compared to
, compared to  for the lightly smoothed flow.
for the lightly smoothed flow.
Utility Curvature.
Table 1 shows results from similar experiments using different values of  ,
,  . We see that for each
. We see that for each  value, as expected, the heavily smoothed flow requires less power. Note also that
value, as expected, the heavily smoothed flow requires less power. Note also that  decreases as
decreases as  increases. This is not surprising as lower curvature (higher
increases. This is not surprising as lower curvature (higher  ) corresponds to lower risk aversion.
) corresponds to lower risk aversion.
 , lightly smoothed flow
, lightly smoothed flow  , heavily smoothed flow
, heavily smoothed flow  .
.5. A Suboptimal Policy for the Multiple-Flow Case
5.1. Approximate Dynamic Programming (ADP) Policy
In this section we describe a suboptimal policy that can be used in the multiple-flow case. Our proposed policy has the same form as the optimal policy, with the true value function  replaced with an approximation or surrogate
replaced with an approximation or surrogate  :
:

A policy obtained by replacing  with an approximation is called an approximate dynamic programming (ADP) policy [18, 19, 31]. (Note that by this definition (25) is an ADP policy for
with an approximation is called an approximate dynamic programming (ADP) policy [18, 19, 31]. (Note that by this definition (25) is an ADP policy for  .)
.)
We construct  in a simple way. Let
in a simple way. Let  denote the power law approximate function for the associated single-flow problem with only the
denote the power law approximate function for the associated single-flow problem with only the  th flow. (This can be obtained numerically as described above.) We then take
th flow. (This can be obtained numerically as described above.) We then take

This approximate value function is separable, that is, a sum of functions of the individual flows, whereas the exact value function is (in general) not. The approximate policy, however, is not separable; the optimization problem solving to assign flow rates couples the different flow rates.
In the literature on approximate dynamic programming,  would be considered basis functions [32–34]; however, we fix the coefficients of the basis functions as one. (We have found that very little improvement in the policy is obtained by optimizing over the coefficients.)
would be considered basis functions [32–34]; however, we fix the coefficients of the basis functions as one. (We have found that very little improvement in the policy is obtained by optimizing over the coefficients.)
Evaluating the approximate policy, that is, solving (29), reduces to solving the resource allocation problem

with optimization variables  ,
,  . This is a convex optimization problem; its special structure allows it to be solved extremely efficiently, via waterfilling.
. This is a convex optimization problem; its special structure allows it to be solved extremely efficiently, via waterfilling.
5.2. Solution via Waterfilling
We can solve (31) using the waterfilling method (described earlier). At each time  , we are to maximize
, we are to maximize

over variables  , whereas before,
, whereas before,  is a Lagrange multiplier associated with the equality constraint. For our particular power law approximate functions we can express
is a Lagrange multiplier associated with the equality constraint. For our particular power law approximate functions we can express  in terms of
in terms of  :
:

We then use bisection on  to find the value of
to find the value of  for which
for which

Since our surrogate value function is only approximate, there is no reason to solve this to great accuracy; experiments show that around 5–10 bisection iterations are more than enough.
Each iteration of the waterfilling algorithm has a cost that is  which means that we can solve (31) very fast. An interior point method that exploits the structure would also yield a very efficient method; see, for example, [35].
which means that we can solve (31) very fast. An interior point method that exploits the structure would also yield a very efficient method; see, for example, [35].
5.3. Upper-Bound Policies
In this section we describe two heuristic data flow rate policies: a steady-state flow policy and a prescient flow policy. We show that both policies result in upper bounds on  (the optimal objective value). These upper bounds give us a way to measure the performance of our suboptimal flow policy
(the optimal objective value). These upper bounds give us a way to measure the performance of our suboptimal flow policy  : if we obtain a
: if we obtain a  from
from  that is close to an upper bound, then we know that our suboptimal flow policy is nearly optimal.
that is close to an upper bound, then we know that our suboptimal flow policy is nearly optimal.
5.3.1. Steady-State Policy
The steady-state policy is given by

where  is channel gain at time
is channel gain at time  and
and  is the steady-state flow rate vector (independent of time) obtained by solving the optimization problem
is the steady-state flow rate vector (independent of time) obtained by solving the optimization problem

with optimization variable  , and
, and  being known. Let
being known. Let  be our steady-state upper bound on
be our steady-state upper bound on  obtained using the policy (35) to solve (9). Note that in the above optimization problem, we ignore time (and hence, smoothing) and variations in channel gains, and so, for each
obtained using the policy (35) to solve (9). Note that in the above optimization problem, we ignore time (and hence, smoothing) and variations in channel gains, and so, for each  ,
,  is the optimal (steady-state) flow vector. (This is sometimes called the certainty equivalent problem associated with the stochastic programming problem [36, 37].)
is the optimal (steady-state) flow vector. (This is sometimes called the certainty equivalent problem associated with the stochastic programming problem [36, 37].)
By Jensen's inequality (and convexity of the max) it is easy to see that  is an upper bound on
is an upper bound on  . Note that once
. Note that once  is determined, we can evaluate (35) using the waterfilling algorithm described earlier.
is determined, we can evaluate (35) using the waterfilling algorithm described earlier.
5.3.2. Prescient Policy
To obtain a prescient upper bound on  , we relax the causality requirement imposed earlier on the flow policy in (10) and assume complete knowledge of the channel gains for all
, we relax the causality requirement imposed earlier on the flow policy in (10) and assume complete knowledge of the channel gains for all  . (For more on prescient bounds, see, e.g., [20].) For each realization of channel gains, the flow rate control problem reduces to the optimization problem
. (For more on prescient bounds, see, e.g., [20].) For each realization of channel gains, the flow rate control problem reduces to the optimization problem

where the optimization variables are the flow rates  ,
, ,
, and smoothed flow rates
and smoothed flow rates  ,
, ,
, . (The problem data are
. (The problem data are  and
and  ,
, ,
, .) The optimal value of (37) is a random variable parameterized by
.) The optimal value of (37) is a random variable parameterized by  . Let
. Let  denote our prescient upper bound on
denote our prescient upper bound on  . We obtain
. We obtain  by using Monte Carlo simulation: we take
by using Monte Carlo simulation: we take  large and solve (37) for independent realizations of the channel gains. The mean is our prescient upper bound.
large and solve (37) for independent realizations of the channel gains. The mean is our prescient upper bound.
5.4. Numerical Example
In this section we compare the performance of our ADP policy to the above prescient policy using a numerical example.
We construct a simple two-flow problem using the previous problem instance from Section 4.3 with  , where, now, both flows share the single link, that is,
, where, now, both flows share the single link, that is,  . Our approximate value function is
. Our approximate value function is

(Note that this is easily extended to a problem with more than two flows.)
Let  denote the objective obtained using our ADP policy. Each
denote the objective obtained using our ADP policy. Each  obtains an ADP controller, a point
obtains an ADP controller, a point  in the
in the  plane. Using the same
plane. Using the same  , we can compute the corresponding prescient bound giving the point
, we can compute the corresponding prescient bound giving the point  . (Every feasible controller must lie on or below the line, with slope
. (Every feasible controller must lie on or below the line, with slope  , that passes through
, that passes through  .)
.)
We carried out Monte Carlo simulation (100 realizations, each with  time steps) for several values of
time steps) for several values of  , computing
, computing  as described in Section 5.2 and our prescient upper bound as described above.
as described in Section 5.2 and our prescient upper bound as described above.
Figure 5 shows our ADP controllers and the associated upper bounds. We can see that the ADP controllers are clearly feasible and perform very well depending on  . For example, for
. For example, for  ,
, 
 and
and 
 , so we know that
, so we know that  . So in this example, for
. So in this example, for  ,
,  is not more than
is not more than  suboptimal.
suboptimal.
6. Conclusion
In this paper we present a variation on a multiperiod stochastic network utility maximization problem as a constrained convex stochastic control problem. We show that judging flow utilities dynamically, that is, with a utility function and a smoothing time scale, is a good way to account for network applications with heterogenous rate demands.
For the case of a single flow, our numerically computed value functions obtain flow policies that optimally trad off average utility and average power. We show that simple power law functions are reasonable approximations of the optimal value functions and that these simple functions obtain near optimal performance.
For the case of multiple flows on a single link (where the value function is not practically computable using dynamic programming), we approximate the value function with a combination of the simple one-dimensional power law functions. Simulations, and comparison with upper bounds on the optimal value, show that the resulting ADP policy can obtain very good performance.
References
Hayes J: Adaptive feedback communications. IEEE Transactions on Communication Technology 1968, 16(1):29-34. 10.1109/TCOM.1968.1089811
Cavers J: Variable-rate transmission for Rayleigh fading channels. IEEE Transactions on Communications 1972, 20(1):15-22. 10.1109/TCOM.1972.1091106
Hentinen VO: Error performance for adaptive transmission on fading channels. IEEE Transactions on Communications 1974, 22(9):1331-1337. 10.1109/TCOM.1974.1092383
Webb WT, Steele R: Variable rate QAM for mobile radio. IEEE Transactions on Communications 1995, 43(7):2223-2230. 10.1109/26.392965
Soon-Ghee C, Goldsmith AJ: Variable-rate variable-power MQAM for fading channels. IEEE Transactions on Communications 1997, 45(10):1218-1230. 10.1109/26.634685
Kelly FP, Maulloo AK, Tan D: Rate control for communication networks: shadow prices, proportional fairness and stability. Journal of the Operational Research Society 1997, 49(3):237-252.
Low SH, Lapsley DE: Optimization flow control—I: basic algorithm and convergence. IEEE/ACM Transactions on Networking 1999, 7(6):861-874. 10.1109/90.811451
Chiang M, Low SH, Calderbank AR, Doyle JC: Layering as optimization decomposition: a mathematical theory of network architectures. Proceedings of the IEEE 2007, 95(1):255-312.
Neely MJ, Modiano E, Li C-P: Fairness and optimal stochastic control for heterogeneous networks. IEEE/ACM Transactions on Networking 2008, 16(2):396-409.
Chen J, Xu W, He S, Sun Y, Thulasiraman P, Shen X: Utility-based asynchronous flow control algorithm for wireless sensor networks. IEEE Journal on Selected Areas in Communications 2010, 28(7):1116-1126.
O'Neill D, Akuiyibo E, Boyd S, Goldsmith AJ: Optimizing adaptive modulation in wireless networks via multi-period network utility maximization. Proceedings of the IEEE International Conference on Communications, 2010
Trichakis N, Zymnis A, Boyd S: Dynamic network utility maximization with delivery contracts. Proceedings of the IFAC World Congress, 2008 2907-2912.
Bertsekas D: Dynamic Programming and Optimal Control: Volume 1. Athena Scientific; 2005.
Bertsekas D: Dynamic Programming and Optimal Control: Volume 2. Athena Scientific; 2007.
Åström K: Introduction to Stochastic Control Theory. Dover, New York, NY, USA; 1970.
Whittle P: Optimization Over Time: Dynamic Programming and Stochastic Control. John Wiley & Sons, New York, NY, USA; 1982.
Bertsekas D, Shreve S: Stochastic Optimal Control: The Discrete-Time Case. Athena Scientific; 1996.
Bertsekas D, Tsitsiklis J: Neuro-Dynamic Programming. Athena Scientific; 1996.
Powell W: Approximate Dynamic Programming: Solving the Curses of Dimensionality. John Wiley & Sons, New York, NY, USA; 2007.
Brown DB, Smith JE, Sun P: Information relaxations and duality in stochastic dynamic programs. Operations Research 2010, 58(4):785-801. 10.1287/opre.1090.0796
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, Cambridge, UK; 2004.
Puterman M: Markov Decision Processes: Discrete Stochastic Dynamic Programming. John Wiley & Sons, New York, NY, USA; 1994.
Ross S: Introduction to Stochastic Dynamic Programming: Probability and Mathematical. Academic Press; 1983.
Denardo E: Dynamic Programming: Models and Applications. Prentice-Hall, New York, NY, USA; 1982.
Wang Y, Boyd S: Performance bounds for linear stochastic control. Systems and Control Letters 2009, 58(3):178-182. 10.1016/j.sysconle.2008.10.004
Bellman R: Dynamic Programming. Courier Dover, New York, NY, USA; 1957.
Derman C: Finite State Markovian Decision Processes. Academic Press; 1970.
Blackwell D: Discrete dynamic programming. The Annals of Mathematical Statistics 1962, 33: 719-726. 10.1214/aoms/1177704593
Arapostathis A, Borkar V, Fernández-Gaucherand E, Ghosh MK, Marcus SI: Discrete-time controlled Markov processes with average cost criterion: a survey. SIAM Journal on Control and Optimization 1993, 31(2):282-344. 10.1137/0331018
Corless RM, Gonnet GH, Hare DEG, Jeffrey DJ, Knuth DE: On the Lambert W function. Advances in Computational Mathematics 1996, 5(4):329-359.
Manne A: Linear programming and sequential decisions. Management Science 1960, 6(3):259-267. 10.1287/mnsc.6.3.259
Schweitzer PJ, Seidmann A: Generalized polynomial approximations in Markovian decision processes. Journal of Mathematical Analysis and Applications 1985, 110(2):568-582. 10.1016/0022-247X(85)90317-8
Trick MA, Zin SE: Spline approximations to value functions: linear programming approach. Macroeconomic Dynamics 1997, 1(1):255-277.
De Farias DP, Van Roy B: The linear programming approach to approximate dynamic programming. Operations Research 2003, 51(6):850-865. 10.1287/opre.51.6.850.24925
Madan R, Boyd SP, Lall S: Fast algorithms for resource allocation in wireless cellular networks. IEEE/ACM Transactions on Networking 2010, 18(3):973-984.
Birge J, Louveaux F: Introduction to Stochastic Programming. Springer, New York, NY, USA; 1997.
Prekopa A: Stochastic Programming. Kluwer Academic Publishers, New York, NY, USA; 1995.
Acknowledgments
This material is based upon work supported by AFOSR Grant FA9550-09-0130 and by Army contract W911NF-07-1-0029. The authors thank Yang Wang and Dan O'Neill for helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Akuiyibo, E., Boyd, S. Adaptive Modulation with Smoothed Flow Utility. J Wireless Com Network 2010, 815213 (2010). https://doi.org/10.1155/2010/815213
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/815213





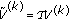 (apply Bellman operator).
(apply Bellman operator).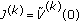 (estimate optimal value).
(estimate optimal value). (normalize).
(normalize).
 (blue) with
(blue) with  (red, dashed) for the lightly smoothed flow. (b) Comparing
(red, dashed) for the lightly smoothed flow. (b) Comparing  (blue) with
(blue) with  (red, dashed) for the heavily smoothed flow.
(red, dashed) for the heavily smoothed flow.
 for smoothing time
for smoothing time  (
( ). (b) Optimal policy for
). (b) Optimal policy for  (
(


