Abstract
Some sufficient conditions are established for the oscillation of second-order neutral differential equation  ,
,  , where
, where  . The results complement and improve those of Grammatikopoulos et al. Ladas, A. Meimaridou, Oscillation of second-order neutral delay differential equations, Rat. Mat. 1 (1985), Grace and Lalli (1987), Ruan (1993), H. J. Li (1996), H. J. Li (1997), Xu and Xia (2008).
. The results complement and improve those of Grammatikopoulos et al. Ladas, A. Meimaridou, Oscillation of second-order neutral delay differential equations, Rat. Mat. 1 (1985), Grace and Lalli (1987), Ruan (1993), H. J. Li (1996), H. J. Li (1997), Xu and Xia (2008).
Similar content being viewed by others
1. Introduction
In recent years, the oscillatory behavior of differential equations has been the subject of intensive study; we refer to the articles [1–13]; Especially, the study of the oscillation of neutral delay differential equations is of great interest in the last three decades; see for example [14–38] and references cited therein. Second-order neutral delay differential equations have applications in problems dealing with vibrating masses attached to an elastic bar and in some variational problems (see [39]).
This paper is concerned with the oscillatory behavior of the second-order neutral delay differential equation

where 
 Throughout this paper, we assume that
Throughout this paper, we assume that
-
(a)
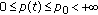 ,
,  and
and 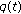 is not identically zero on any ray of the form
is not identically zero on any ray of the form 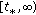 for any
for any  where
where  is a constant;
is a constant; -
(b)
 for
for 
 is a constant;
is a constant; -
(c)
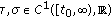 ,
,  ,
,  ,
, 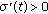 ,
,  ,
, 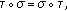 where
where  is a constant.
is a constant.
In the study of oscillation of differential equations, there are two techniques which are used to reduce the higher-order equations to the first-order Riccati equation (or inequality). One of them is the Riccati transformation technique. The other one is called the generalized Riccati technique. This technique can introduce some new sufficient conditions for oscillation and can be applied to different equations which cannot be covered by the results established by the Riccati technique.
Philos [7] examined the oscillation of the second-order linear ordinary differential equation

and used the class of functions as follows. Suppose there exist continuous functions  such that
such that  ,
,  ,
,  and
and  has a continuous and nonpositive partial derivative on
has a continuous and nonpositive partial derivative on  with respect to the second variable. Moreover, let
with respect to the second variable. Moreover, let  be a continuous function with
be a continuous function with

The author obtained that if

then every solution of (1.2) oscillates. Li [4] studied the equation

used the generalized Riccati substitution, and established some new sufficient conditions for oscillation. Li utilized the class of functions as in [7] and proved that if there exists a positive function  such that
such that

where  and
and  then every solution of (1.5) oscillates. Yan [13] used Riccati technique to obtain necessary and sufficient conditions for nonoscillation of (1.5). Applying the results given in [4, 13], every solution of the equation
then every solution of (1.5) oscillates. Yan [13] used Riccati technique to obtain necessary and sufficient conditions for nonoscillation of (1.5). Applying the results given in [4, 13], every solution of the equation

is oscillatory.
An important tool in the study of oscillation is the integral averaging technique. Just as we can see, most oscillation results in [1, 3, 5, 7, 11, 12] involved the function class  Say a function
Say a function  belongs to a function class
belongs to a function class  denoted by
denoted by  if
if  where
where  and
and  which satisfies
which satisfies

and has partial derivatives  and
and  on
on  such that
such that

In [10], Sun defined another type of function class  and considered the oscillation of the second-order nonlinear damped differential equation
and considered the oscillation of the second-order nonlinear damped differential equation

Say a function  is said to belong to
is said to belong to  denoted by
denoted by  if
if  where
where  which satisfies
which satisfies  for
for  and has the partial derivative
and has the partial derivative  on
on  such that
such that  is locally integrable with respect to
is locally integrable with respect to  in
in 
In [8], by employing a class of function  and a generalized Riccati transformation technique, Rogovchenko and Tuncay studied the oscillation of (1.10). Let
and a generalized Riccati transformation technique, Rogovchenko and Tuncay studied the oscillation of (1.10). Let  Say a continuous function
Say a continuous function  belongs to the class
belongs to the class  if:
if:
-
(i)
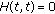 and
and  for
for 
-
(ii)
 has a continuous and nonpositive partial derivative
has a continuous and nonpositive partial derivative 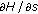 satisfying, for some
satisfying, for some  ,
,  where
where 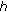 is nonnegative.
is nonnegative.
Meng and Xu [22] considered the even-order neutral differential equations with deviating arguments

where  ,
,  The authors introduced a class of functions
The authors introduced a class of functions  Let
Let  and
and  The function
The function  is said to belong to the class
is said to belong to the class  (defined by
(defined by  for short) if
for short) if
 ,
,  ,
,  for
for 
 has a continuous and nonpositive partial derivative on
has a continuous and nonpositive partial derivative on  with respect to the second variable;
with respect to the second variable;
there exists a nondecreasing function  such that
such that

Xu and Meng [31] studied the oscillation of the second-order neutral delay differential equation

where  by using the function class
by using the function class  an operator
an operator  and a Riccati transformation of the form
and a Riccati transformation of the form

the authors established some oscillation criteria for (1.13). In [31], the operator  is defined by
is defined by

for  and
and  The function
The function  is defined by
is defined by

It is easy to verify that  is a linear operator and that it satisfies
is a linear operator and that it satisfies

In 2009, by using the function class  and defining a new operator
and defining a new operator  , Liu and Bai [21] considered the oscillation of the second-order neutral delay differential equation
, Liu and Bai [21] considered the oscillation of the second-order neutral delay differential equation

where  The authors defined the operator
The authors defined the operator  by
by

for  and
and  The function
The function  is defined by
is defined by

It is easy to see that  is a linear operator and that it satisfies
is a linear operator and that it satisfies

Wang [11] established some results for the oscillation of the second-order differential equation

by using the function class  and a generalized Riccati transformation of the form
and a generalized Riccati transformation of the form

Long and Wang [6] considered (1.22); by using the function class  and the operator
and the operator  which is defined in [31], the authors established some oscillation results for (1.22).
which is defined in [31], the authors established some oscillation results for (1.22).
In 1985, Grammatikopoulos et al. [16] obtained that if  and
and  then equation
then equation

is oscillatory. Li [18] studied (1.1) when  and established some oscillation criteria for (1.1). In [15, 19, 25], the authors established some general oscillation criteria for second-order neutral delay differential equation
and established some oscillation criteria for (1.1). In [15, 19, 25], the authors established some general oscillation criteria for second-order neutral delay differential equation

where  In 2002, Tanaka [27] studied the even-order neutral delay differential equation
In 2002, Tanaka [27] studied the even-order neutral delay differential equation

where  or
or  The author established some comparison theorems for the oscillation of (1.26). Xu and Xia [28] investigated the second-order neutral differential equation
The author established some comparison theorems for the oscillation of (1.26). Xu and Xia [28] investigated the second-order neutral differential equation

and obtained that if  for
for  and
and  then (1.27) is oscillatory. We note that the result given in [28] fails to apply the cases
then (1.27) is oscillatory. We note that the result given in [28] fails to apply the cases  or
or  for
for  To the best of our knowledge nothing is known regarding the qualitative behavior of (1.1) when
To the best of our knowledge nothing is known regarding the qualitative behavior of (1.1) when 

Motivated by [10, 21], for the sake of convenience, we give the following definitions.
Definition 1.1.
Assume that  . The operator is defined by
. The operator is defined by  by
by

for  and
and 
Definition 1.2.
The function  is defined by
is defined by

It is easy to verify that  is a linear operator and that it satisfies
is a linear operator and that it satisfies

In this paper, we obtain some new oscillation criteria for (1.1). The paper is organized as follows. In the next section, we will use the generalized Riccati transformation technique to give some sufficient conditions for the oscillation of (1.1), and we will give two examples to illustrate the main results. The key idea in the proofs makes use of the idea used in [23]. The method used in this paper is different from that of [27].
2. Main Results
In this section, we give some new oscillation criteria for (1.1). We start with the following oscillation result.
Theorem 2.1.
Assume that  for
for  Further, suppose that there exists a function
Further, suppose that there exists a function  such that for some
such that for some  and some
and some  one has
one has

where 

 Then every solution of (1.1) is oscillatory.
Then every solution of (1.1) is oscillatory.
Proof.
Let  be a nonoscillatory solution of (1.1). Without loss of generality, we assume that there exists
be a nonoscillatory solution of (1.1). Without loss of generality, we assume that there exists  such that
such that  ,
,  ,
,  , for all
, for all  Define
Define  for
for  then
then  for
for  From (1.1), we have
From (1.1), we have

It is obvious that  and
and  for
for  imply
imply  for
for  Using (2.2) and condition
Using (2.2) and condition  there exists
there exists  such that for
such that for  we get
we get

We introduce a generalized Riccati transformation

Differentiating (2.4) from (2.2), we have  Thus, there exists
Thus, there exists  such that for all
such that for all  ,
,

Similarly, we introduce another generalized Riccati transformation

Differentiating (2.6), note that  by (2.2), we have
by (2.2), we have  then for all sufficiently large
then for all sufficiently large  one has
one has

From (2.5) and (2.7), we have

By (2.3) and the above inequality, we obtain

Multiplying (2.9) by  and integrating from
and integrating from  to
to  we have, for any
we have, for any  and for all
and for all 

From the above inequality and using monotonicity of  for all
for all  we obtain
we obtain

and, for all 

By (2.12),

which contradicts (2.1). This completes the proof.
Remark 2.2.
We note that it suffices to satisfy (2.1) in Theorem 2.1 for any  which ensures a certain flexibility in applications. Obviously, if (2.1) is satisfied for some
which ensures a certain flexibility in applications. Obviously, if (2.1) is satisfied for some  it well also hold for any
it well also hold for any  Parameter
Parameter  introduced in Theorem 2.1 plays an important role in the results that follow, and it is particularly important in the sequel that
introduced in Theorem 2.1 plays an important role in the results that follow, and it is particularly important in the sequel that 
With an appropriate choice of the functions  and
and  one can derive from Theorem 2.1 a number of oscillation criteria for (1.1). For example, consider a Kamenev-type function
one can derive from Theorem 2.1 a number of oscillation criteria for (1.1). For example, consider a Kamenev-type function  defined by
defined by

where  is an integer. It is easy to see that
is an integer. It is easy to see that  and
and

As a consequence of Theorem 2.1, we have the following result.
Corollary 2.3.
Suppose that  for
for  Furthermore, assume that there exists a function
Furthermore, assume that there exists a function  such that for some integer
such that for some integer  and some
and some 

where  and
and  are as in Theorem 2.1. Then every solution of (1.1) is oscillatory.
are as in Theorem 2.1. Then every solution of (1.1) is oscillatory.
For an application of Corollary 2.3, we give the following example.
Example 2.4.
Consider the second-order neutral differential equation

where  ,
,  Let
Let  ,
, 
 , and
, and  Then
Then  ,
,  Take
Take  Applying Corollary 2.3 with
Applying Corollary 2.3 with  for any
for any 

for  Hence, (2.17) is oscillatory for
Hence, (2.17) is oscillatory for 
Remark 2.5.
Corollary 2.3 can be applied to the second-order Euler differential equation

where  Let
Let 
 , and
, and  Then
Then  ,
,  Take
Take  ,
,  Applying Corollary 2.3 with
Applying Corollary 2.3 with  for any
for any 

for  Hence, (2.19) is oscillatory for
Hence, (2.19) is oscillatory for 
It may happen that assumption (2.1) is not satisfied, or it is not easy to verify, consequently, that Theorem 2.1 does not apply or is difficult to apply. The following results provide some essentially new oscillation criteria for (1.1).
Theorem 2.6.
Assume that  for
for  and for some
and for some 

Further, suppose that there exist functions  and
and  such that for all
such that for all  and for some
and for some 

where  ,
,  are as in Theorem 2.1. Suppose further that
are as in Theorem 2.1. Suppose further that

where  Then every solution of (1.1) is oscillatory.
Then every solution of (1.1) is oscillatory.
Proof.
We proceed as in the proof of Theorem 2.1, assuming, without loss of generality, that there exists a solution  of (1.1) such that
of (1.1) such that  , and
, and  for all
for all  We define the functions
We define the functions  and
and  as in Theorem 2.1; we arrive at inequality (2.10), which yields for
as in Theorem 2.1; we arrive at inequality (2.10), which yields for  sufficiently large
sufficiently large

Therefore, for  sufficiently large
sufficiently large

It follows from (2.22) that

for all  and for any
and for any  Consequently, for all
Consequently, for all  we obtain
we obtain

In order to prove that

suppose the contrary, that is,

Assumption (2.21) implies the existence of a  such that
such that

By (2.30), we have

and there exists a  such that
such that  for all
for all  On the other hand, by virtue of (2.29), for any positive number
On the other hand, by virtue of (2.29), for any positive number  there exists a
there exists a  such that, for all
such that, for all 

Using integration by parts, we conclude that, for all 

It follows from (2.33) that, for all 

Since  is an arbitrary positive constant, we get
is an arbitrary positive constant, we get

which contradicts (2.17). Consequently, (2.28) holds, so

and, by virtue of (2.27),

which contradicts (2.23). This completes the proof.
Choosing  as in Corollary 2.3, it is easy to verify that condition (2.21) is satisfied because, for any
as in Corollary 2.3, it is easy to verify that condition (2.21) is satisfied because, for any 

Consequently, we have the following result.
Corollary 2.7.
Suppose that  for
for  Furthermore, assume that there exist functions
Furthermore, assume that there exist functions  and
and  such that for all
such that for all  for some integer
for some integer  and some
and some 

where  and
and  are as in Theorem 2.1. Suppose further that (2.23) holds, where
are as in Theorem 2.1. Suppose further that (2.23) holds, where  is as in Theorem 2.6. Then every solution of (1.1) is oscillatory.
is as in Theorem 2.6. Then every solution of (1.1) is oscillatory.
From Theorem 2.6, we have the following result.
Theorem 2.8.
Assume that  for
for  Further, suppose that
Further, suppose that  such that (2.21) holds, there exist functions
such that (2.21) holds, there exist functions  and
and  such that for all
such that for all  and for some
and for some 

where  and
and  are as in Theorem 2.1. Suppose further that (2.23) holds, where
are as in Theorem 2.1. Suppose further that (2.23) holds, where  is as in Theorem 2.6. Then every solution of (1.1) is oscillatory.
is as in Theorem 2.6. Then every solution of (1.1) is oscillatory.
Theorem 2.9.
Assume that  for
for  Further, assume that there exists a function
Further, assume that there exists a function  such that for each
such that for each  for some
for some 

where  ,
,  are defined as in Theorem 2.1, the operator
are defined as in Theorem 2.1, the operator  is defined by (1.28), and
is defined by (1.28), and  is defined by (1.29). Then every solution of (1.1) is oscillatory.
is defined by (1.29). Then every solution of (1.1) is oscillatory.
Proof.
We proceed as in the proof of Theorem 2.1, assuming, without loss of generality, that there exists a solution  of (1.1) such that
of (1.1) such that  ,
,  , and
, and  for all
for all  We define the functions
We define the functions  and
and  as in Theorem 2.1; we arrive at inequality (2.9). Applying
as in Theorem 2.1; we arrive at inequality (2.9). Applying  to (2.9), we get
to (2.9), we get

By (1.30) and the above inequality, we obtain

Hence, from (2.43) we have

that is,

Taking the super limit in the above inequality, we get

which contradicts (2.41). This completes the proof.
If we choose

for  and
and  then we have
then we have

Thus by Theorem 2.9, we have the following oscillation result.
Corollary 2.10.
Suppose that  for
for  Further, assume that for each
Further, assume that for each  there exist a function
there exist a function  and two constants
and two constants  such that for some
such that for some 

where  ,
,  are as in Theorem 2.1. Then every solution of (1.1) is oscillatory.
are as in Theorem 2.1. Then every solution of (1.1) is oscillatory.
If we choose

where  then we have
then we have

where  ,
,  are defined as the following:
are defined as the following:

According to Theorem 2.9, we have the following oscillation result.
Corollary 2.11.
Suppose that  for
for  Further, assume that for each
Further, assume that for each  there exist two functions
there exist two functions  such that for some
such that for some 

where  ,
,  are as in Theorem 2.1. Then every solution of (1.1) is oscillatory.
are as in Theorem 2.1. Then every solution of (1.1) is oscillatory.
In the following, we give some new oscillation results for (1.1) when  for
for 
Theorem 2.12.
Assume that  for
for  Suppose that there exists a function
Suppose that there exists a function  such that for some
such that for some  and for some
and for some  one has
one has

where 
 and
and  is as in Theorem 2.1. Then every solution of (1.1) is oscillatory.
is as in Theorem 2.1. Then every solution of (1.1) is oscillatory.
Proof.
Let  be a nonoscillatory solution of (1.1). Without loss of generality, we assume that there exists a solution
be a nonoscillatory solution of (1.1). Without loss of generality, we assume that there exists a solution  of (1.1) such that
of (1.1) such that  ,
,  , and
, and  for all
for all  Proceeding as in the proof of Theorem 2.1, we obtain (2.2) and (2.3). In view of (2.2), we have
Proceeding as in the proof of Theorem 2.1, we obtain (2.2) and (2.3). In view of (2.2), we have  for
for  We introduce a generalized Riccati transformation
We introduce a generalized Riccati transformation

Differentiating (2.55) from (2.2), we have  Thus, there exists
Thus, there exists  such that for all
such that for all  ,
,

Similarly, we introduce another generalized Riccati transformation

Differentiating (2.57), then for all sufficiently large  one has
one has

From (2.56) and (2.58), we have

Note that  then we have
then we have  By (2.3) and the above inequality, we obtain
By (2.3) and the above inequality, we obtain

Multiplying (2.60) by  and integrating from
and integrating from  to
to  we have, for any
we have, for any  and for all
and for all 

The rest of the proof is similar to that of Theorem 2.1, we omit the details. This completes the proof.
Take  where
where  is an integer. As a consequence of Theorem 2.12, we have the following result.
is an integer. As a consequence of Theorem 2.12, we have the following result.
Corollary 2.13.
Suppose that  for
for  Furthermore, assume that there exists a function
Furthermore, assume that there exists a function  such that for some integer
such that for some integer  and some
and some 

where  and
and  are as in Theorem 2.12. Then every solution of (1.1) is oscillatory.
are as in Theorem 2.12. Then every solution of (1.1) is oscillatory.
For an application of Corollary 2.13, we give the following example.
Example 2.14.
Consider the second-order neutral differential equation

where  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  , for
, for  Let
Let  ,
,  , and
, and  . Then
. Then  ,
,  Applying Corollary 2.13 with
Applying Corollary 2.13 with  for any
for any 

for  Hence, (2.63) is oscillatory for
Hence, (2.63) is oscillatory for 
By (2.61), similar to the proof of Theorem 2.6, we have the following result.
Theorem 2.15.
Assume that  for
for  Assume also that
Assume also that  such that (2.21) holds. Moreover, suppose that there exist functions
such that (2.21) holds. Moreover, suppose that there exist functions  and
and  such that for all
such that for all  and for some
and for some 

where  and
and  are as in Theorem 2.12. Suppose further that
are as in Theorem 2.12. Suppose further that

where  is defined as in Theorem 2.6. Then every solution of (1.1) is oscillatory.
is defined as in Theorem 2.6. Then every solution of (1.1) is oscillatory.
Choosing  ,
,  where
where  is an integer. By Theorem 2.15, we have the following result.
is an integer. By Theorem 2.15, we have the following result.
Corollary 2.16.
Suppose that  for
for  Furthermore, assume that there exist functions
Furthermore, assume that there exist functions  and
and  such that for all
such that for all  some integer
some integer  and some
and some 

where  and
and  are as in Theorem 2.12. Suppose further that (2.66) holds, where
are as in Theorem 2.12. Suppose further that (2.66) holds, where  is defined as in Theorem 2.6. Then every solution of (1.1) is oscillatory.
is defined as in Theorem 2.6. Then every solution of (1.1) is oscillatory.
From Theorem 2.15, we have the following result.
Theorem 2.17.
Assume that  for
for  Assume also that
Assume also that  such that (2.21) holds. Moreover, suppose that there exist functions
such that (2.21) holds. Moreover, suppose that there exist functions  and
and  such that for all
such that for all  and for some
and for some 

where  and
and  are as in Theorem 2.12. Suppose further that (2.66) holds, where
are as in Theorem 2.12. Suppose further that (2.66) holds, where  is as in Theorem 2.6. Then every solution of (1.1) is oscillatory.
is as in Theorem 2.6. Then every solution of (1.1) is oscillatory.
Next, by (2.60), similar to the proof of Theorem 2.9, we have the following result.
Theorem 2.18.
Assume that  for
for  Further, assume that there exists a function
Further, assume that there exists a function  such that for each
such that for each  for some
for some 

where  are defined as in Theorem 2.12, the operator
are defined as in Theorem 2.12, the operator  is defined by (1.28), and
is defined by (1.28), and  is defined by (1.29). Then every solution of (1.1) is oscillatory.
is defined by (1.29). Then every solution of (1.1) is oscillatory.
If we choose  as (2.47), then from Theorem 2.18, we have the following oscillation result.
as (2.47), then from Theorem 2.18, we have the following oscillation result.
Corollary 2.19.
Suppose that  for
for  Further, assume that for each
Further, assume that for each  there exist a function
there exist a function  and two constants
and two constants  such that for some
such that for some 

where  ,
,  are as in Theorem 2.12. Then every solution of (1.1) is oscillatory.
are as in Theorem 2.12. Then every solution of (1.1) is oscillatory.
If we choose  as (2.50), then from Theorem 2.18, we have the following oscillation result.
as (2.50), then from Theorem 2.18, we have the following oscillation result.
Corollary 2.20.
Suppose that  for
for  Further, assume that for each
Further, assume that for each  there exist two functions
there exist two functions  such that for some
such that for some 

where  ,
,  are as in Theorem 2.12. Then every solution of (1.1) is oscillatory.
are as in Theorem 2.12. Then every solution of (1.1) is oscillatory.
Remark 2.21.
The results of this paper can be extended to the more general equation of the form

The statement and the formulation of the results are left to the interested reader.
Remark 2.22.
One can easily see that the results obtained in [15, 16, 18, 19, 25, 28] cannot be applied to (2.17), (2.63), so our results are new.
References
Agarwal RP, Wang Q-R: Oscillation and asymptotic behavior for second-order nonlinear perturbed differential equations. Mathematical and Computer Modelling 2004,39(13):1477-1490. 10.1016/j.mcm.2004.07.007
Džurina J, Stavroulakis IP: Oscillation criteria for second-order delay differential equations. Applied Mathematics and Computation 2003,140(2-3):445-453. 10.1016/S0096-3003(02)00243-6
Kamenev IV: An integral test for conjugacy for second order linear differential equations. Matematicheskie Zametki 1978,23(2):249-251.
Li H: Oscillation criteria for second order linear differential equations. Journal of Mathematical Analysis and Applications 1995,194(1):217-234. 10.1006/jmaa.1995.1295
Li W-T, Agarwal RP: Interval oscillation criteria related to integral averaging technique for certain nonlinear differential equations. Journal of Mathematical Analysis and Applications 2000,245(1):171-188. 10.1006/jmaa.2000.6749
Long Q, Wang Q-R: New oscillation criteria of second-order nonlinear differential equations. Applied Mathematics and Computation 2009,212(2):357-365. 10.1016/j.amc.2009.02.040
Philos ChG: Oscillation theorems for linear differential equations of second order. Archiv der Mathematik 1989,53(5):482-492. 10.1007/BF01324723
Rogovchenko YV, Tuncay F: Oscillation criteria for second-order nonlinear differential equations with damping. Nonlinear Analysis: Theory, Methods & Applications 2008,69(1):208-221. 10.1016/j.na.2007.05.012
Sun YG, Meng FW: Note on the paper of Džurina and Stavroulakis. Applied Mathematics and Computation 2006,174(2):1634-1641. 10.1016/j.amc.2005.07.008
Sun YG: New Kamenev-type oscillation criteria for second-order nonlinear differential equations with damping. Journal of Mathematical Analysis and Applications 2004,291(1):341-351. 10.1016/j.jmaa.2003.11.008
Wang Q-R: Interval criteria for oscillation of certain second order nonlinear differential equations. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2005,12(6):769-781.
Wang Q-R: Oscillation criteria for nonlinear second order damped differential equations. Acta Mathematica Hungarica 2004,102(1-2):117-139. 10.1023/B:AMHU.0000023211.53752.03
Yan JR: Oscillatory properties of second-order differential equations with an "integralwise small" coefficient. Acta Mathematica Sinica 1987,30(2):206-215.
Agarwal RP, Grace SR: Oscillation theorems for certain neutral functional-differential equations. Computers & Mathematics with Applications 1999,38(11-12):1-11. 10.1016/S0898-1221(99)00280-1
Grace SR, Lalli BS: Oscillation of nonlinear second order neutral differential equations. Radovi Matematički 1987, 3: 77-84.
Grammatikopoulos MK, Ladas G, Meimaridou A: Oscillations of second order neutral delay differential equations. Radovi Matematički 1985,1(2):267-274.
Karpuz B, Manojlović JV, Öcalan Ö, Shoukaku Y: Oscillation criteria for a class of second-order neutral delay differential equations. Applied Mathematics and Computation 2009,210(2):303-312. 10.1016/j.amc.2008.12.075
Li H: Oscillatory theorems for second-order neutral delay differential equations. Nonlinear Analysis: Theory, Methods & Applications 1996,26(8):1397-1409. 10.1016/0362-546X(94)00346-J
Li H: Oscillation of solutions of second-order neutral delay differential equations with integrable coefficients. Mathematical and Computer Modelling 1997,25(3):69-79. 10.1016/S0895-7177(97)00016-2
Lin X, Tang XH: Oscillation of solutions of neutral differential equations with a superlinear neutral term. Applied Mathematics Letters 2007,20(9):1016-1022. 10.1016/j.aml.2006.11.006
Liu L, Bai Y: New oscillation criteria for second-order nonlinear neutral delay differential equations. Journal of Computational and Applied Mathematics 2009,231(2):657-663. 10.1016/j.cam.2009.04.009
Meng F, Xu R: Kamenev-type oscillation criteria for even order neutral differential equations with deviating arguments. Applied Mathematics and Computation 2007,190(2):1402-1408. 10.1016/j.amc.2007.02.017
Parhi N, Rath RN: On oscillation of solutions of forced nonlinear neutral differential equations of higher order. Czechoslovak Mathematical Journal 2003,53(128)(4):805-825. 10.1007/s10587-004-0805-8
Rath RN, Misra N, Padhy LN: Oscillatory and asymptotic behaviour of a nonlinear second order neutral differential equation. Mathematica Slovaca 2007,57(2):157-170. 10.2478/s12175-007-0006-7
Ruan SG: Oscillations of second order neutral differential equations. Canadian Mathematical Bulletin 1993,36(4):485-496. 10.4153/CMB-1993-064-4
Şahiner Y: On oscillation of second order neutral type delay differential equations. Applied Mathematics and Computation 2004,150(3):697-706. 10.1016/S0096-3003(03)00300-X
Tanaka S: A oscillation theorem for a class of even order neutral differential equations. Journal of Mathematical Analysis and Applications 2002,273(1):172-189. 10.1016/S0022-247X(02)00235-4
Xu R, Xia Y: A note on the oscillation of second-order nonlinear neutral functional differential equations. International Journal of Contemporary Mathematical Sciences 2008,3(29–32):1441-1450.
Xu R, Meng F: Some new oscillation criteria for second order quasi-linear neutral delay differential equations. Applied Mathematics and Computation 2006,182(1):797-803. 10.1016/j.amc.2006.04.042
Xu R, Meng F: Oscillation criteria for second order quasi-linear neutral delay differential equations. Applied Mathematics and Computation 2007,192(1):216-222. 10.1016/j.amc.2007.01.108
Xu R, Meng F: New Kamenev-type oscillation criteria for second order neutral nonlinear differential equations. Applied Mathematics and Computation 2007,188(2):1364-1370. 10.1016/j.amc.2006.11.004
Xu Z, Liu X: Philos-type oscillation criteria for Emden-Fowler neutral delay differential equations. Journal of Computational and Applied Mathematics 2007,206(2):1116-1126. 10.1016/j.cam.2006.09.012
Ye L, Xu Z: Oscillation criteria for second order quasilinear neutral delay differential equations. Applied Mathematics and Computation 2009,207(2):388-396. 10.1016/j.amc.2008.10.051
Zafer A: Oscillation criteria for even order neutral differential equations. Applied Mathematics Letters 1998,11(3):21-25. 10.1016/S0893-9659(98)00028-7
Zhang Q, Yan J, Gao L: Oscillation behavior of even-order nonlinear neutral differential equations with variable coefficients. Computers & Mathematics with Applications 2010,59(1):426-430. 10.1016/j.camwa.2009.06.027
Han Z, Li T, Sun S, Sun Y: Remarks on the paper [Appl. Math. Comput. 207 (2009) 388–396]. Applied Mathematics and Computation 2010,215(11):3998-4007. 10.1016/j.amc.2009.12.006
Han Z, Li T, Sun S, Chen W: On the oscillation of second-order neutral delay differential equations. Advances in Difference Equations 2010, 2010:-8.
Li T, Han Z, Zhao P, Sun S: Oscillation of even-order neutral delay differential equations. Advances in Difference Equations 2010, 2010:-7.
Hale J: Theory of Functional Differential Equations, Applied Mathematical Sciences. 2nd edition. Springer, New York, NY, USA; 1977:x+365.
Acknowledgment
The authors sincerely thank the reviewers for their valuable suggestions and useful comments that have led to the present improved version of the original manuscript. This research is supported by the Natural Science Foundation of China (60774004, 60904024), China Postdoctoral Science Foundation Funded Project (20080441126, 200902564), Shandong Postdoctoral Funded Project (200802018) and supported by the Natural Science Foundation of Shandong (Y2008A28, ZR2009AL003), also supported by University of Jinan Research Funds for Doctors (XBS0843).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Han, Z., Li, T., Sun, S. et al. Oscillation Criteria for Second-Order Nonlinear Neutral Delay Differential Equations. Adv Differ Equ 2010, 763278 (2010). https://doi.org/10.1155/2010/763278
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/763278



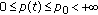 ,
,  and
and 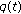 is not identically zero on any ray of the form
is not identically zero on any ray of the form 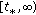 for any
for any  where
where  is a constant;
is a constant; for
for 
 is a constant;
is a constant;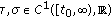 ,
,  ,
,  ,
, 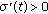 ,
,  ,
, 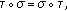 where
where  is a constant.
is a constant.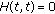 and
and  for
for 
 has a continuous and nonpositive partial derivative
has a continuous and nonpositive partial derivative 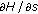 satisfying, for some
satisfying, for some  ,
,  where
where 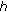 is nonnegative.
is nonnegative.