1. Introduction

The use of multiple antennas at both ends of a communication link, commonly referred to as a multiple-input multiple-output (MIMO) system, has been widely studied and is considered as one of the prospective technologies to provide high data rate transmission and good performance for the dramatically growing wireless communications demands nowadays. Many studies have confirmed that, without additional power and spectrum compared with conventional single-input single-output (SISO) systems, channel capacity of MIMO systems can increase in proportion to the number of antennas in Rayleigh fading environments [1–3]. Moreover, when channel state information (CSI) is available at a transmitter (TX), the performance of the MIMO system can be improved further by applying an eigenbeam-space division multiplexing (E-SDM) technique, which is also called eigenmode transmission or singular value decomposition- (SVD-) based technique [1–6]. In the E-SDM technique, orthogonal transmit beams are formed based on the eigenvectors obtained from singular value decomposition of a MIMO channel matrix, and transmit data resources can be allocated adaptively. In the ideal case, in which the transmit weight matrix completely matches an instantaneous MIMO channel response, spatially orthogonal substreams with the optimal resource allocation can be achieved. As a result, a simple maximum ratio combining (MRC) detector or a spatial filter such as a minimum mean square error (MMSE) filter or zero-forcing (ZF) filter can detect the substreams without inter-substream interference, and the maximum channel capacity is obtained.

In realistic environments, however, due to dynamic nature of the channel and processing delay at both the TX and the receiver (RX), a channel transition may cause a severe loss of subchannel orthogonality, which results in large inter-substream interference. In addition, the channel change prevents optimal resource allocation from being achieved. Consequently, based on computer-generated channels assuming the Jakes model [7], we have confirmed that the performance of MIMO E-SDM systems is degraded in time-varying fading environments with rich scatterers [8, 9]. The Jakes model is very simple because required parameters are very few, and it is easy as regards simulations. However, actual MIMO systems may be used in line-of-sight (LOS) environments, and even in a non-LOS (NLOS) case, scatterers may not be uniformly distributed around an RX and/or a TX. The geometry-based stochastic channel model (GSCM) has been proposed for multiple antenna systems [10–13]. The model includes also the LOS component and is more comprehensive than the Jakes model. It is expected that GSCM can explain phenomena in real-life fading environments. In order to apply GSCM, however, we need to determine several parameters, and we need three-dimensional ray tracing or extensive measurement campaigns [12, 13]. This is much more difficult to apply than the Jakes model. On the other hand, when using multiple antennas at both the TX and the RX, mutual coupling among antenna elements cannot be ignored because it affects the system performance in practical implementation [14–16]. Therefore, investigations into the systems in actual communications are necessary.

MIMO measurement campaigns have already been extensively conducted as reported in papers such as [6, 15–18]. However, most of MIMO measurement campaigns have not explicitly considered the effect of time-varying fading on the performance of MIMO systems. In [19], measurements were carried out in a case where a mobile station was moving. The objective of the study was not to examine the effect of time-varying channels but to introduce a stochastic MIMO radio channel model. In [20], the performance of closed-loop MIMO (i.e., MIMO E-SDM) systems was investigated in the fading environment where both TX and RX were fixed, and scatterers were moving during the experiment. It is said that the effects of moving scatterers in the environment were relatively unimportant.

In time-varying wireless communications, Doppler spectrum is a useful measure to evaluate the mobility of terminals [21]. Then, the Doppler spectrum may affect the performance of MIMO E-SDM systems in dynamic channels. Due to various distributions of scatterers, LOS wave existence, and mutual coupling effect among antennas, the Doppler spectrum of SISO and MIMO channels in actual environments are, in general, different from the theoretical analyses. To the best of our knowledge, such work has rarely been considered [22, 23]. In [22], Doppler spectrum of a SISO channel was investigated where the base and user were both stationary, but scatterers in the environment were moving, causing time variations in the channel response. In [23], Doppler spectrum of a MIMO channel was examined in both indoor and outdoor environments. The results in [22, 23] revealed that the effects of moving scatterers in the environment were relatively unimportant. Both of [22, 23] did not consider the Doppler spectrum in the case of the LOS condition and the effect of the spectrum on the performance of MIMO systems. Also, array configurations have been considered based on measurement campaigns to clarify the channel capacity [24, 25]. The studies did not consider the effect of the array configuration to the MIMO E-SDM performance in time-varying environments.

We conducted SISO and MIMO measurement campaigns at a 5.2 GHz frequency band in an indoor time-varying fading environment. In our measurement campaigns, the RX was moved while the TX and scatterers were fixed. We evaluated the MIMO system performance partially using the HIPERLAN/2 standard [26]. Based on the measured channel data, in this paper, we examined some channel properties such as antenna pattern, received power, channel autocorrelation, and Doppler spectrum of both SISO and MIMO cases. Then, we evaluated the bit-error rate (BER) performance of MIMO E-SDM systems in the environment.

The main contributions of the paper are the following.

  1. (i)

    The radiation patterns of the antenna elements in MIMO case are examined. It can be seen that the patterns change from the SISO case due to mutual coupling. This has an effect on the received power.

  2. (ii)

    The received power, channel autocorrelation, and Doppler spectrum in actual fading LOS and obstructed LOS (OLOS) environments are considered. The results show that they are dependent on the direction of the RX motion, the antenna array configuration, and the propagation environments.

  3. (iii)

    The performance of the E-SDM system is investigated in actual time-varying fading environments. It is shown that the performance can be degraded by the channel change during the time interval between the transmit weight matrix determination and the actual data transmission.

The paper is organized as follows. In the next section, a detailed measurement setup for our experiment is presented. In Section 3, the antenna pattern of a two-element array is considered. Based on the measured channel data, we examine received power in Section 4 and channel autocorrelation and Doppler spectrum in Section 5 for both SISO and MIMO cases. To investigate the performance of MIMO E-SDM systems in actual environments, we first describe the systems in Section 6. Then, a procedure of applying measured data for evaluation of the system performance in an indoor time-varying fading environment is given in Section 7. Based on the measured data, the performance of MIMO E-SDM systems in the environment is evaluated in Section 8. The conclusions are provided in Section 9.

2. Channel Measurement Setup

The measurement campaigns were carried out in a meeting room in a building of the Graduate School of Information Science and Technology, Hokkaido University, as shown in Figure 1. The room has an area of about 95 . The walls of the room consist of plasterboard around reinforced concrete pillars and metal doors. The metal whiteboard behind the TX was fixed on the wall, and the bottom of the whiteboard was 1 m above the floor, whereas the TX and RX were placed 0.9 m above the floor. In the room, TX and RX antennas, omnidirectional colinear antennas AT-CL010 (TSS JAPAN), were placed on two tables separated by 4 m. The nominal gain of these antennas on the horizontal plane was about 4 dBi.

Figure 1
figure 1

Measurement site (top view).

Full size image

On the RX side, a stepping motor was used to move the RX array along the - or -axis during the experiments. Each step of the motor was 0.0088 cm. This motor was exactly controlled by a personal computer. The RX array was stopped at every 10 steps (equal to 0.088 cm) of the motor. Channels were measured at intervals of 0.088 cm, and we had a total of 500 spatial measurement points. Therefore, the length of the measurement route was  cm = 44 cm. Here, we chose the length of 44 cm because it covered several wavelengths of signal and the difference of pathloss measured at the first point and the last point was less than 1 dB.

Channels were measured for all the TX and the RX antenna pairs through a vector network analyzer (VNA), as shown in Figure 2. RF switches at both the TX and the RX sides were controlled by a personal computer and selected a TX antenna and an RX antenna, respectively. Measured data were then saved in the computer. The unselected antennas were automatically connected to 50  dummy loads. The measurement band was from 5.15 GHz to 5.40 GHz (bandwidth = 250 MHz), and we obtained 1601 frequency domain data with 156.25 kHz interval. Each channel was averaged over 10 snapshots in order to reduce thermal noise included in the raw measurements. We examined both SISO and real MIMO systems. For the MIMO case, the antenna spacing was 3 and 6 cm (half- and one wavelength at 5 GHz), and two array orientations (TX-/RX- (endfire) and TX-/RX- (broadside)) along the - and the -axes, respectively, were examined, as shown in Figure 3. When there was a metal partition between the TX and RX antennas, we had an OLOS environment, as shown in Figure 4(a). In the absence of the partition, we had a LOS environment, as shown in Figure 4(b).

Figure 2
figure 2

Channel measurement system.

Full size image
Figure 3
figure 3

Antenna array orientations. TX-/RX-TX-/RX-

Full size image
Figure 4
figure 4

Measurement environments. OLOS environment (TX antennas are behind the partition)LOS environment

Full size image

The total of channel response matrix data was obtained for each case of the direction of the RX antenna motion, the array orientation, the antenna spacing, and the LOS/OLOS condition. It should be noted that the measurement campaigns were conducted while no one was in the room, to ensure statistical stationarity of propagation.

3. Antenna Patterns

It is well known that when antenna spacing (AS) among elements is not large enough, there exists mutual coupling among the elements and their patterns are changed. In MIMO systems, due to the limitation of space, especially at mobile stations, the antenna spacing may be small. As a result, mutual coupling among antennas may be large, and this would affect the system performance. Thus, in this section, we consider the antenna pattern for a two-element linear array.

The patterns for the two-element array with AS of and used in our measurement campaigns are shown in Figure 5 (solid curves). The dashed curve corresponding to the pattern of a single antenna is also included for comparison. The patterns were obtained by conducting measurement of the antennas in an anechoic chamber. It is seen that the single antenna has an almost omnidirectional pattern because it does not have the mutual coupling effect. However, in the multiple antenna case, the patterns are very different from an omnidirectional one. The antenna gain seems to decrease as the AS becomes smaller. On the other hand, the patterns tend to become similar to the omnidirectional one as the AS becomes larger. The numbers under each pattern correspond to the ones in Figure 3.

Figure 5
figure 5

Antenna patterns for a two-element array with mutual coupling (solid curves) and single isolated antenna pattern (dashed curve). AS = 0.5 AS = 1.0 

Full size image

Given the TX-/RX- orientation, the RX end is located in the direction with respect to the TX end, and the TX end is located in the direction with respect to the RX end. Thus, the direct wave departs from the TX end in the direction and arrives at the RX end in the direction. On the other hand, given the TX-/RX- orientation, the RX end is located in the direction with respect to the TX end, and the TX end is also located in the direction with respect to the RX end. Thus, the direct wave departs from the TX end and arrives at the RX end in the direction. The gains at the and directions tend to be smaller than those at the direction, especially in the case of AS = . These phenomena are shown in Figure 6.

Figure 6
figure 6

Antenna gain toward the direct wave for the case of AS = 0. 5 .Lower gain for TX-/RX-Higher gain for TX-/RX-

Full size image

4. Received Power

In this section, based on the measured channel data, we examine received power of both SISO and MIMO channels.

Received power of the SISO channel in the frequency domain at the first spatial measurement position is shown in Figure 7. It should be noted that the first spatial measurement position when the RX array moves along the -axis is different from the one when the array moves along the -axis, as shown in Figure 8. It is seen from Figure 7 that the received power for the LOS condition is generally larger than the power for the OLOS condition due to the direct wave.

Figure 7
figure 7

Received power of SISO channel in the frequency domain at the first spatial measurement position. RX motion along the -axisRX motion along the -axis

Full size image
Figure 8
figure 8

The first spatial measurement position.

Full size image

Received power of the SISO channel in the spatial domain at the frequency of 5.15 GHz is shown in Figure 9. It can be seen that the power fluctuation is much dependent on the direction of the RX array motion. In the LOS environment, the power fluctuates more rapidly when the array moves along the -axis than when it moves along the -axis. The interval of the ripples of the power, when the RX motion is along the -axis, is about 3 cm (half-wavelength at 5 GHz). This can be explained as follows. The most dominant wave was the direct wave (to direction) from the TX to the RX. It is conjectured that other dominant waves were the reflected wave (to direction) from the wall behind the TX array and the reflected wave (to direction) from the wall behind the RX array. These three waves caused a standing wave along the -axis.

Figure 9
figure 9

Received power of SISO channel in the spatial domain at the frequency of 5. 15 GHz.RX motion along the -axisRX motion along the -axis

Full size image

Received power of the SISO channel averaged over the 1601 frequency domain data at each spatial measurement position is shown in Figure 10. It is confirmed that the power for the LOS condition is higher than that for the OLOS condition due to the direct wave. It can also be seen that in the OLOS case, the power is almost the same in both cases of the RX array motion; meanwhile in the LOS case, the power when the array motion is along the -axis is more variable than when the motion is along the -axis.

Figure 10
figure 10

Received power of SISO channel averaged over the frequency domain data at each spatial measurement position.

Full size image

Received power of 2 2 MIMO channels averaged over the four channels and 1601 frequency domain data at each spatial measurement position is shown in Figure 11. As in the SISO case, the power for the LOS condition is higher than that for the OLOS condition due to the direct wave. Here, we can see that in the LOS case, the power for the TX-/RX- orientation is considerably larger than that for the TX-/RX- one when the antenna spacing is . However, the power is almost the same for both of the TX-/RX- orientation and TX-/RX- one when the antenna spacing is . This is due to the effect of mutual coupling between antenna elements. When AS = , the antenna gain toward the direct wave for the TX-/RX- orientation is much higher than that for the TX-/RX- orientation, as seen from Figures 5(a) and 6. However, when AS = , the antenna gain toward the direct wave for the TX-/RX- orientation is almost the same as that for the TX-/RX- orientation, as seen from Figure 5(b).

Figure 11
figure 11

Received power of 2 2 MIMO channels averaged over the four channels and frequency domain data at each spatial measurement position. AS = AS =

Full size image

5. Channel Autocorrelation and Doppler Spectrum in the Indoor Fading Environment

In this section, based on our measured channel data, we examine channel autocorrelation and Doppler spectrum of both SISO and MIMO cases.

We assume that a mobile terminal is moving at a constant velocity . With a time interval , the distance that the mobile terminal has moved is given by

(1)

It is well known that the maximum Doppler frequency occurring during the mobile terminal's motion is as follows:

(2)

where is the speed of light ( m/s) and is the carrier frequency of the mobile terminal.

Combining (1) and (2), we have

(3)

where is the wavelength of the carrier frequency.

Assuming that the time interval between the adjacent measurement points ( cm) is 0.5  milliseconds (  milliseconds), then is calculated from (3) as follows:

(4)

where the carrier frequency was assumed to be the center of the measurement band .

The channel autocorrelation and Doppler spectrum for = 31Hz of the SISO case when the RX moves along the - and -axes are shown in Figure 12. The channel autocorrelation was estimated by averaging over the spatial domain data and the 1601 frequency domain data. If we divide the measurement distance (abscissa) in Figure 12 by the velocity , we have the channel autocorrelation versus time. The Doppler spectra of both the measured data and the Jakes model were calculated by applying the 450-point DFT process to the time domain channel autocorrelation after multiplying it by the Hamming window. It can be seen that the channel autocorrelation and Doppler spectrum are much dependent on the direction of the RX motion. The channel autocorrelation in the LOS environment fluctuates much more when the RX moves along the -axis than when it moves along the -axis. In the LOS case, the power spectrum density (PSD) is mainly concentrated around of Hz when the RX moves along the -axis. This is because most of dominant incoming waves were the direct wave ( direction) from the TX to the RX, the reflected wave (+ direction) from the wall behind the TX, and the reflected wave ( direction) from the wall behind the RX. It should be noted that the interval of the ripples of the channel autocorrelation is about 3cm (the half wavelength at 5GHz). When the RX moves along the -axis, on the other hand, the PSD is mainly distributed around the Doppler frequency of 0Hz. The reason is that the direction of RX motion is approximately perpendicular to most of the dominant incoming waves. In the OLOS case, the PSD was expected to be the U-shaped Jakes spectrum. However, as seen from Figure 12, the observed PSD is quite different from the one in the Jakes model. The reason for this is considered to be that scatterers in the indoor environment are not uniformly distributed around an RX as well as those that are assumed in the Jakes model.

Figure 12
figure 12

Channel autocorrelation and Doppler spectrum for = 31 Hz of SISO channel. RX motion along the -axisRX motion along the -axis

Full size image

The channel autocorrelation and Doppler spectrum for = 31Hz of MIMO channels are shown in Figure 13. Here, the channel autocorrelation was estimated by averaging over the four channels as well as the spatial domain and frequency domain data. The Doppler spectrum, as in the SISO case, was calculated by applying the 450-point DFT process to the time domain channel autocorrelation after multiplying it by the Hamming window. It is observed that the channel autocorrelation and Doppler spectrum of the MIMO case are quite similar to those of the SISO case. In addition, from Figure 13, it can also be observed that the channel autocorrelation and Doppler spectrum are dependent not only on the direction of the RX motion but also on the array orientation and the antenna spacing. This is due to the effect of the mutual coupling between antenna elements at both the TX and the RX, as shown in Figure 5. Even in the OLOS case, the Doppler spectrum of MIMO channels is different from the U-shaped Jakes one.

Figure 13
figure 13

Channel autocorrelation and Doppler spectrum for = 31 Hz of 22 MIMO channels. RX array motion along the -axis and AS = 0.5 RX array motion along the -axis and AS = 0.5 RX array motion along the -axis and AS = 1.0 RX array motion along the -axis and AS = 1.0 

Full size image

6. MIMO E-SDM Systems

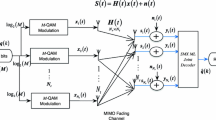
Before investigating the performance of MIMO E-SDM systems in actual time-varying fading environments, the concept of a MIMO E-SDM system is briefly described in the section. For more details on the system, refer to [4].

A block diagram of a MIMO E-SDM system with antennas at a TX and antennas at an RX is shown in Figure 14. When MIMO CSI is available at the TX, orthogonal transmit beams can be formed by eigenvalue decomposition of the matrix HHH where H denotes the MIMO channel matrix, and denotes Hermitian transpose. The E-SDM technique is assumed to be used for downlink (DL) transmission. This study also assumes that the channel is narrow enough so that no frequency selective fading occurs, and that the average power of each substream prior to power control is identical.

Figure 14
figure 14

Block diagram of a MIMO E-SDM system.

Full size image

At the TX side, an input stream is divided into substreams . Then, signals before transmission are driven by a TX weight matrix to form orthogonal eigenbeams and control power allocation. At the RX side, received signals are detected by an RX weight matrix.

The TX weight matrix is determined as

(5)

where is the MIMO channel matrix obtained by the eigenvalue decomposition as

(6)

Here, are positive eigenvalues of HHH The columns of are the eigenvectors corresponding to those positive eigenvalues, and is the diagonal transmit power matrix. It should be noted that holds.

In an ideal MIMO E-SDM system, in which the TX weight matrix completely matches an instantaneous MIMO channel response, spatially orthogonal substreams with optimal resource allocation can be achieved. Under the circumstance, received signals can easily be demultiplexed by using a maximal ratio combining (MRC) or spatial filtering weight. However, in time-varying fading environments spatial filtering weight is a better choice to mitigate the degradation of system performance [5].

The signal-to-noise power ratio of the th detected substream is given by

(7)

where , and is noise power. This indicates that the quality of each detected substream is different. Therefore, the channel capacity and performance of MIMO E-SDM systems can be improved by adapting the TX data resource and power allocation [4].

7. A Procedure of Adapting Measured Data for Performance Evaluation in Dynamic Channels

The E-SDM technique is assumed to be used in a time division duplexing (TDD) system (Although a TDD system is considered in the paper, the obtained results are equivalently applied to a frequency division duplex system in which CSI is estimated at the RX and then fed back to the TX.), such as HIPERLAN/2 [26]. The TX weights are determined by the channel responses estimated by the uplink acknowledgment (ACK) packet periodically transmitted at times (), and DL packet transmission is done at times , as shown in Figure 15. The terminal was assumed to be moving at the constant velocity yielding  Hz, as stated in Section 5. Here, we assumed that the frame duration of the TDD system was 2.0 milliseconds, as in the HIPERLAN/2 standard [26], and the time delay for the actual DL data transmission from ACK was 1.5  milliseconds. Also, as mentioned earlier, in the experiments, we measured MIMO channels at 500 spatially different points along the - or the -axis. If the MIMO channels at measurement points () were those for the uplink ACK packets, then the MIMO channels at the measurement points were those for the DL packets, as shown in Figure 16(a). This is because the ratio was .

Figure 15
figure 15

TDD transmission frame format.

Full size image
Figure 16
figure 16

Uplink and downlink MIMO positions for the different . Hz Hz

Full size image

If the terminal's velocity increased up to , then also rose to  Hz. In this case, the MIMO channel responses for the uplink ACK and DL packets were given by the measurement points and , respectively, as shown in Figure 16(b).

8. Performance Analyses of MIMO E-SDM Systems in the Time-Varying Fading Enviroment

8.1. Simulation Parameters

As mentioned earlier, we obtained 800 500 measured MIMO channel matrices in each case of the array orientation, the direction of the RX array motion, the antenna spacing, and the LOS/OLOS condition. In this section, we used them to evaluate the BER performance of MIMO E-SDM systems in the indoor time-varying fading environment. The BER performance was obtained under simulation parameters shown in Table 1. All the channel data were regarded as frequency flat fading channels. The validity of this assumption is as follows.

Table 1 Simulation Parameters of MIMO E-SDM System.
Full size table

We assumed the DL packet duration of 0.12  milliseconds. This value is not shown in Table 1 because it does not explicitly affect the results. Because we have 48 symbols in the DL packet, the symbol duration is 0.0025  milliseconds. Then, the bandwidth is 400 kHz when the roll-off parameter is 0. On the other hand, as examined in [15], the time delay spread in the measurement site was less than 40 ns; thus the channel coherence bandwidth was considered to be wider than 2.5 MHz. The transmission bandwidth is much narrower than the coherence bandwidth, and we can assume the frequency flat fading.

The data rate was set to 2 bps/Hz (2 bits per symbol duration) per TX antenna; therefore, the total data rate was fixed constantly at 4 bps/Hz (4 bits per symbol duration) for the 22 MIMO system. The number of substreams was dependent on the resource adaptation, specifically the modulation scheme and the transmit power. We had two cases of the resource selection, namely, 16QAM1 (1 stream) and QPSK2 (2 streams). The reason why we need resource selection is because we should send more bits over a substream with higher SNR and fewer bits over a substream with lower SNR to obtain better BER under the fixed data rate requirement. Thus, we need to determine the modulation schemes for each substream considering the SNR that was stated in Section 6. Also, we need to allocate transmit power to each substream properly. The modulation and power allocation are determined in such a way that the upper bound of BER has the lowest value [4].

The HIPERLAN/2 system may be used in some different scenarios as described in [26], and depending on the scenarios, the mobility of mobile terminals may be fixed, walking speed, or slow vehicles limited within 10 m/s. In this paper, two values of of 31 and 93 Hz, which correspond to two terminal's velocities of 1.8 and 5.4 m/s for the carrier frequency of 5.2 GHz, were considered. The mobility can be considered as walking speed or slow vehicles. For those terminal velocities, we can assume that both of the uplink and the downlink packet duration were so short that the channel change during the duration was negligible.

8.2. Simulation Results

The average BER performance of MIMO E-SDM system versus normalized total TX power for = 31 and 93 Hz is shown in Figure 17. Many conventional studies have evaluated the performance of MIMO systems as a function of average SNR. However, in NLOS or OLOS environments, the transmit power must be higher than in LOS environments in order to obtain the same average SNR. Therefore, for fair comparison, the performance evaluation of MIMO systems should be done under the same transmit power condition as in [15]. In this study, the BER performance of MIMO E-SDM systems in LOS and OLOS environments was examined as a function of the normalized total transmit power. The normalized total TX power is the total TX power that is normalized by the value yielding  dB when we have only the direct wave in the SISO-LOS transmission environment. This value was measured in an anechoic chamber with the same measurement setup mentioned in Section 2. Here, is received signal energy per symbol and is the noise power density. The ideal case in Figure 17 is that where the time delay from ACK to actual DL data transmission is equal to zero (i.e., ); that is, the channel for the E-SDM transmission is exactly the same as the estimated one for the weight matrix determination and resource allocation.

Figure 17
figure 17

BER performance of MIMO E-SDM system. RX array motion along the -axisRX array motion along the -axis

Full size image

BER performance in the LOS environment is better than that in the OLOS one due to the higher received power, as shown in Figure 11. The BER performance is related to the direction of the RX motion. Better performance can be obtained in the LOS environment when the motion is along the -axis than when it is along the -axis. This is due to the effect of Dopper spectrum. As seen from Figure 13, the Doppler spectrum is distributed around 0 Hz in the LOS case for the RX motion along the -axis, whereas it is concentrated around for the RX motion along the -axis. It can be easily seen that the more distributed around 0 Hz the Doppler spectrum is, the better BER performance is obtained because of the less channel transition. In addition, the BER performance is also related to the antenna orientation. Better BER performance is obtained for the TX-/RX- orientation than for the TX-/RX- orientation in the case of the LOS environment and AS = 0.5 . This is because the antenna gain for the opposite end in the MIMO system was higher for the TX-/RX- orientation than for the TX-/RX- orientation due to the effect of mutual coupling among antenna elements, as shown in Figure 6. As a result, higher received power was obtained for the TX-/RX- orientation than for the TX-/RX- orientation in both cases of the RX array motion along the - and the -axes in the LOS environment and AS = 0.5 , as shown in Figure 11.

Furthermore, as in simulation results based on computer generated channels assuming the Jakes model [8, 9], the higher was, the more the BER performance was degraded in the indoor fading environment. This is because greater channel change during the time interval caused larger inter-substream interference and prevented optimal resource allocation from being achieved. Therefore, a countermeasure such as a channel prediction scheme [8, 9] may be necessary for MIMO E-SDM transmission in fast time-varying fading environments.

9. Conclusions

In this paper, we have presented an experiment for measuring SISO and MIMO channel responses at the 5.2 GHz frequency band in an indoor time-varying fading environment. In the environment, not only OLOS condition but also LOS condition was considered; scatterers were located at both the TX and the RX, and were not necessarily distributed uniformly; the effect of mutual coupling among antennas was also taken into account.

We first considered the antenna patterns of SISO and MIMO systems. Different from the SISO case where the antenna has an omnidirectional pattern, in the MIMO case, the patterns of antenna elements are changed due to the mutual coupling among antennas, and the antenna gain seems to decrease as the AS becomes smaller.

Based on the measured data, we second examined received power, channel autocorrelation, and Doppler spectrum. The results showed that these fading properties are dependent not only on the direction of the RX motion but also on the array configuration and propagation environments. These are due to the effects of various distributions of scatterers, multipath signals, LOS wave existence, and mutual coupling among antenna elements. Unlike theoretical analysis, Doppler spectrum in the indoor fading environment is different from the U-shaped Jakes one.

Finally, based on the measured data, the performance of MIMO E-SDM systems was evaluated. Simulation results showed that a channel change during the time interval between the transmit weight matrix determination and the actual data transmission could degrade the system performance in indoor communications. It was shown that the performance relates to the Doppler spectrum. Therefore, a channel prediction scheme may be necessary for the systems in indoor fast time-varying fading environments.