Abstract
We propose a new time-varying maximum transition run (TMTR) code for DVD recording systems, which has a rate  higher than the EFMPlus code and a lower power spectral density (PSD) at low frequencies. An enumeration method for constructing the new TMTR code is presented. Computer simulations indicate that the proposed TMTR code outperforms the EFMPlus code in error performance when applied to partial response optical recording channels.
higher than the EFMPlus code and a lower power spectral density (PSD) at low frequencies. An enumeration method for constructing the new TMTR code is presented. Computer simulations indicate that the proposed TMTR code outperforms the EFMPlus code in error performance when applied to partial response optical recording channels.
Similar content being viewed by others
1. Introduction
In data storage systems, a modulation code is known as  -constrained code, where
-constrained code, where  and
and  represent the maximal and minimal number of zeros between two consecutive ones. The main function of a
represent the maximal and minimal number of zeros between two consecutive ones. The main function of a  modulation code is to improve the recording density and increase the storage capacity. The timing information could also be controlled using a
modulation code is to improve the recording density and increase the storage capacity. The timing information could also be controlled using a  modulation code. For example, magnetic tape and disk systems often adopt
modulation code. For example, magnetic tape and disk systems often adopt  or
or  codes, while optical systems such as CD and DVD usually employ
codes, while optical systems such as CD and DVD usually employ  EFM (Eight-to-Fourteen Modulation) or
EFM (Eight-to-Fourteen Modulation) or  EFMPlus [1] modulation codes.
EFMPlus [1] modulation codes.
Recent research on the  modulation code has focused on the time-varying maximum transition run (TMTR) code [2–9], which can be treated as a
modulation code has focused on the time-varying maximum transition run (TMTR) code [2–9], which can be treated as a  modulation code. The TMTR code matched to the partial response channel can delete some dominant error events and enhance the Euclidian distance of the partial response channel to the matched filter bound. As a result, a coding gain over the conventional scheme can be obtained when the time-varying Viterbi detector is applied to the TMTR-coded partial response channel. In a previous work [10], we proposed a new time-varying maximum transition run (TMTR) code with
modulation code. The TMTR code matched to the partial response channel can delete some dominant error events and enhance the Euclidian distance of the partial response channel to the matched filter bound. As a result, a coding gain over the conventional scheme can be obtained when the time-varying Viterbi detector is applied to the TMTR-coded partial response channel. In a previous work [10], we proposed a new time-varying maximum transition run (TMTR) code with  constraint for DVD recording systems, which has rate
constraint for DVD recording systems, which has rate  higher than the EFMPlus code and a lower power spectral density (PSD) at low frequencies. The
higher than the EFMPlus code and a lower power spectral density (PSD) at low frequencies. The  TMTR code was realized with a look-up table, and the k-constraint was not considered during construction. In this paper, instead of a look-up table we present an enumeration method for constructing the
TMTR code was realized with a look-up table, and the k-constraint was not considered during construction. In this paper, instead of a look-up table we present an enumeration method for constructing the  codes. Based on this construction, a rate
codes. Based on this construction, a rate  code with
code with  is found. The proposed code can achieve better timing recovery performance. We show that 387 surviving words exist with length 11 from the construction technique. This new method needs one bit of memory for encoding, but no memory is required for decoding. An enumerating algorithm is used for encoding/decoding, and a look-up table is not required.
is found. The proposed code can achieve better timing recovery performance. We show that 387 surviving words exist with length 11 from the construction technique. This new method needs one bit of memory for encoding, but no memory is required for decoding. An enumerating algorithm is used for encoding/decoding, and a look-up table is not required.
The rest of this paper is organized as follows. In Section 2, we briefly describe the  TMTR codes for partial response (PR) optical recording channels. In Section 3, an outline of the design methodology for constructing a high-rate TMTR code is presented. We illustrate concatenation problem between codewords and provide a solution. Section 4 introduces an enumerative coding method for TMTR codes. In Section 5, the power spectral density (PSD) of the rate
TMTR codes for partial response (PR) optical recording channels. In Section 3, an outline of the design methodology for constructing a high-rate TMTR code is presented. We illustrate concatenation problem between codewords and provide a solution. Section 4 introduces an enumerative coding method for TMTR codes. In Section 5, the power spectral density (PSD) of the rate  code is evaluated and compared with the EFMPlus code. An error performance comparison between uncoded, TMTR-coded, and EFMPlus-coded EPRII optical recording channel is presented in Section 6. The conclusion is provided in Section 7.
code is evaluated and compared with the EFMPlus code. An error performance comparison between uncoded, TMTR-coded, and EFMPlus-coded EPRII optical recording channel is presented in Section 6. The conclusion is provided in Section 7.
2. TMTR Codes for Partial Response Optical Recording Channels
The maximum transition run (MTR) method is a coding method, which limits the number of consecutive potential variations being not greater than  . The time-varying maximum transition run (TMTR) is a further modification of the MTR, which sets different constraints for the number of consecutive variations depending upon whether it starts at an odd or even position. For example,
. The time-varying maximum transition run (TMTR) is a further modification of the MTR, which sets different constraints for the number of consecutive variations depending upon whether it starts at an odd or even position. For example,  TMTR constraints mean that the number of consecutive 1s starting at an even position is not greater than
TMTR constraints mean that the number of consecutive 1s starting at an even position is not greater than  and the number of consecutive 1s starting at an odd position is not greater than
and the number of consecutive 1s starting at an odd position is not greater than  . The method can increase the minimum distance of the encoded system to an upper matched filter bound (MFB); therefore, it has the distance enhancing property. The TMTR constraint can be described using a finite state transition diagram (FSTD), given in Figure 1. The vertices at the top of the diagram represent even positions, and the number of 1s starting at the even positions can be
. The method can increase the minimum distance of the encoded system to an upper matched filter bound (MFB); therefore, it has the distance enhancing property. The TMTR constraint can be described using a finite state transition diagram (FSTD), given in Figure 1. The vertices at the top of the diagram represent even positions, and the number of 1s starting at the even positions can be  only, satisfying the constraint of
only, satisfying the constraint of  . The vertex at the bottom of the diagram represents odd positions, and the number of 1s starting at the odd positions can be
. The vertex at the bottom of the diagram represents odd positions, and the number of 1s starting at the odd positions can be  or
or  , satisfying the constraint of
, satisfying the constraint of  . Figure 2 shows a simplified FSTD with the
. Figure 2 shows a simplified FSTD with the  TMTR constraints.
TMTR constraints.
Cideciyan et al. [11] suggested an advanced signal processing technique, the partial response and maximal likelihood (PRML) channel, to further increase the recording densities and reliability over that achieved by the conventional peak detector. The signal processing technique employing the PRML channel has become a standard widely used in most of today's data storage systems. The most popular partial response system for optical recording has the form  , where
, where  is a nonnegative integer. The PR systems with
is a nonnegative integer. The PR systems with  and
and  are referred to as the PRII and EPRII systems, respectively. Karabed and Siegel [12] proposed a class of modulation codes that take advantage of the well-defined spectral nulls presented in partial response channels. The time-varying maximum transition run (TMTR) code [2–9], which can be treated as a
are referred to as the PRII and EPRII systems, respectively. Karabed and Siegel [12] proposed a class of modulation codes that take advantage of the well-defined spectral nulls presented in partial response channels. The time-varying maximum transition run (TMTR) code [2–9], which can be treated as a  modulation code, has recently been studied for partial response channels. The TMTR code matched to the partial response channel can delete some dominant error events and enhance the Euclidian distance of the partial response channel.
modulation code, has recently been studied for partial response channels. The TMTR code matched to the partial response channel can delete some dominant error events and enhance the Euclidian distance of the partial response channel.
Vannucci and Foschini [13] described a powerful algorithm to search for the minimum Euclidean distance  for
for  partial response channels. They found that the shortest error event achieving
partial response channels. They found that the shortest error event achieving  has the type of
has the type of  for most of
for most of  partial response channels. As a matter of fact they found that those error events of the form
partial response channels. As a matter of fact they found that those error events of the form  always have a distance less than the matched filter bound
always have a distance less than the matched filter bound  which is defined as the distance corresponding to the one-bit error event.
which is defined as the distance corresponding to the one-bit error event.
If the error event  can be forbidden to occur in coded sequences for
can be forbidden to occur in coded sequences for  partial response channels, the minimum distance of the channels can be increased to
partial response channels, the minimum distance of the channels can be increased to  resulting in a coding gain of
resulting in a coding gain of  dB. With NRZI modulation there are four pairs of binary coded sequences, which could generate the error event
dB. With NRZI modulation there are four pairs of binary coded sequences, which could generate the error event  shown as follows:
shown as follows:

The TMTR modulation code with constraint  can be used to forbid the occurrence of sequences 111 and 011, and as a result error event
can be used to forbid the occurrence of sequences 111 and 011, and as a result error event  would not occur in the detection of
would not occur in the detection of  channels, and a coding gain of 3 dB can be obtained. The channel capacity of the
channels, and a coding gain of 3 dB can be obtained. The channel capacity of the  TMTR code is equal to
TMTR code is equal to  , which indicates that a codeword with length 11 bits at least is required to encode or represent a byte (8-bit) message.
, which indicates that a codeword with length 11 bits at least is required to encode or represent a byte (8-bit) message.
3. Construction for 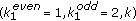 TMTR Codes
TMTR Codes
A TMTR code is specified as  constraint, where k is the maximum number of consecutive zeros,
constraint, where k is the maximum number of consecutive zeros,  and
and  constraints represent the maximum numbers of consecutive ones starting from an even position and an odd position, respectively. This construction is based upon
constraints represent the maximum numbers of consecutive ones starting from an even position and an odd position, respectively. This construction is based upon  constraint. Both
constraint. Both  and
and  represent the maximum number of ones after the last zero and the maximum number of zeros after the last one, respectively. In similar, parameters
represent the maximum number of ones after the last zero and the maximum number of zeros after the last one, respectively. In similar, parameters  and
and  represent the maximum number of ones before the first zero and the maximum number of zeros before the first one. Any two sequences satisfying
represent the maximum number of ones before the first zero and the maximum number of zeros before the first one. Any two sequences satisfying  constraint can be freely concatenated without violating the
constraint can be freely concatenated without violating the  constraint. In order to reduce the consecutive zero length in the sequences after concatenation, the following substitution rule is applied: assume that a sequence
constraint. In order to reduce the consecutive zero length in the sequences after concatenation, the following substitution rule is applied: assume that a sequence  is followed by a sequence
is followed by a sequence  , then
, then
if  has more than
has more than  zeros before the first one, and the last bit of
zeros before the first one, and the last bit of  is a zero, then flip the first 2 bits of
is a zero, then flip the first 2 bits of  into two ones, for example,
into two ones, for example,  ;
;
otherwise, use  as the encoder output.
as the encoder output.
In the case of  , a long sequence of consecutive zeros is spread into two parts by "11" in the beginning of the 2nd sequence. Because
, a long sequence of consecutive zeros is spread into two parts by "11" in the beginning of the 2nd sequence. Because  , a sequence beginning with "11" is not an original code.
, a sequence beginning with "11" is not an original code.
Rates of some constructed codes using this method are listed in Table 1. As displayed, a rate  code with
code with  and
and  constraints is found, and this code has the
constraints is found, and this code has the  constraint. Sequences of even lengths satisfying the
constraint. Sequences of even lengths satisfying the  constraint can be freely concatenated without violating the
constraint can be freely concatenated without violating the  constraint. Odd lengths sequences, however, cannot be freely concatenated without violating the
constraint. Odd lengths sequences, however, cannot be freely concatenated without violating the  constraint. To solve this problem, assuming that there is a modulo-
constraint. To solve this problem, assuming that there is a modulo- counter synchronized to the data, the two transitions in arrow can end at times
counter synchronized to the data, the two transitions in arrow can end at times  and
and  relative to counter. The even and odd positions in a codeword of 11 bits are given as (e o e o e o e o e o e). For example, a sequence of 3 codewords will be
relative to counter. The even and odd positions in a codeword of 11 bits are given as (e o e o e o e o e o e). For example, a sequence of 3 codewords will be

 codes.
codes.where the 1st line expresses the positions of the code bits. The 2nd line expresses the even/odd code bit positions. The 3rd line expresses the maximum number of consecutive "1" starting at the position. There is no two consecutive "2" in the 3rd line. It means that no dominant error event  will occur. To obtain the coding gain of this encoder, a time-varying Viterbi detector is required. The trellis diagrams of the Viterbi detector for even and odd times are shown in Figure 7(c). The Viterbi detector for code bit stream positions will be the same as shifting the 2nd line to right by 1 position. The result is shown in the 4th line. The even or odd Viterbi detector properties must match the bit position shown in the 4th line.
will occur. To obtain the coding gain of this encoder, a time-varying Viterbi detector is required. The trellis diagrams of the Viterbi detector for even and odd times are shown in Figure 7(c). The Viterbi detector for code bit stream positions will be the same as shifting the 2nd line to right by 1 position. The result is shown in the 4th line. The even or odd Viterbi detector properties must match the bit position shown in the 4th line.
4. Enumerative Encoding 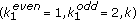 TMTR Codes
TMTR Codes
Let us lexicographically order the binary sequences of length  by
by

An enumerating encoder maps a set of consecutive integers onto a lexicographically ordered set of sequences. In order to describe the enumerating encoder/decoder, some notations will be defined as follows.
-
(D.1)
 is the lexicographically ordered set of
is the lexicographically ordered set of 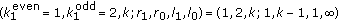 sequences of length
sequences of length  .
. -
(D.2)
R(
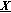 ) is the number of sequences
) is the number of sequences  such that
such that 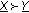 .
. -
(D.3)
R(
 )
)  0, where
0, where  is the all zero sequence.
is the all zero sequence. -
(D.4)
res(
 ) is the sequence obtained by modifying the first nonzero bit of
) is the sequence obtained by modifying the first nonzero bit of 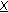 to zero.
to zero. -
(D.5)
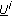 is the minimum sequence among sequences in
is the minimum sequence among sequences in 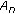 and having the first symbol one at position
and having the first symbol one at position  .
. -
(D.6)
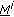 is the maximum sequence among sequences in
is the maximum sequence among sequences in 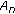 and having the first symbol one at position
and having the first symbol one at position  .
. -
(D.7)
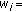 ? R(
? R(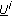 )
) R(res(
R(res(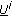 )), then we have
)), then we have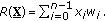 (4)
(4) -
(D.8)
We have
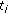 = R(
= R( ).
).
By definitions (D.5) and (D.6), it is easy to see that

The  's and
's and  's can be obtained by the following recursive relation with initial values
's can be obtained by the following recursive relation with initial values  :
:

For illustration, consider  sequences with length
sequences with length  ; one has
; one has

where

Similarly, when using a codeword of length  and code rate of
and code rate of  , the enumerating encoding method is as follows:
, the enumerating encoding method is as follows:

where

Let  be a subset of
be a subset of  consisting of sequences with no more than
consisting of sequences with no more than  leading zeros. Then the number of elements of
leading zeros. Then the number of elements of  is given as
is given as

We can then encode an integer  to a sequence
to a sequence  using the enumerative algorithm given in Figure 3 (assuming the previous block is
using the enumerative algorithm given in Figure 3 (assuming the previous block is  ). The decoding is simply done by
). The decoding is simply done by

where  is the value of first codeword,
is the value of first codeword,  and
and  for
for  .
.
For illustration, the mapping relationship between data and codewords of a rate  code satisfying
code satisfying  constraint is given in Table 2. The data to codeword mapping for a rate
constraint is given in Table 2. The data to codeword mapping for a rate  code satisfying
code satisfying  constraint is listed in Table 3.
constraint is listed in Table 3.
 code.
code. code.
code.5. Power Spectral Density
In DVD systems the power spectral density at low frequency, referred to as the low-frequency content, of the encoded data sequences should normally be maintained as low as possible to alleviate interference with pilot and focus servo signals. For example, in addition to satisfying the  constraint, the
constraint, the  EFMPlus code employed in the DVD system is also designed to achieve very low low-frequency content to reduce the interference between the written signal and the servo signal. Efficient low-frequency component suppression is a crucial criterion for the
EFMPlus code employed in the DVD system is also designed to achieve very low low-frequency content to reduce the interference between the written signal and the servo signal. Efficient low-frequency component suppression is a crucial criterion for the 
 TMTR code rate. The low-frequency content is based upon the running digital sum (RDS)
TMTR code rate. The low-frequency content is based upon the running digital sum (RDS)  given by
given by

where  represents the writing sequences. A lower RDS results in lower low-frequency content. The power spectral density of a sequence can be expressed as
represents the writing sequences. A lower RDS results in lower low-frequency content. The power spectral density of a sequence can be expressed as

For a bounded RDS, that is,  , C is a constant, and the DC content is then given as
, C is a constant, and the DC content is then given as

that indicates a DC-free content. As shown in (11), the number of sequences with length 11 satisfying  is
is  , but it only requires
, but it only requires  codewords in the rate
codewords in the rate  TMTR code. The surplus
TMTR code. The surplus  code sequences can be exploited for minimizing both
code sequences can be exploited for minimizing both  -constraint and low-frequency content. The
-constraint and low-frequency content. The  surplus code sequences are then used to suppress the low-frequency content by reducing the running digital sum (RDS). There are two tables (a main table and a substitute table) used in the encoder, as shown in Figure 4. The main table consists of 256 codewords (i.e., sequences
surplus code sequences are then used to suppress the low-frequency content by reducing the running digital sum (RDS). There are two tables (a main table and a substitute table) used in the encoder, as shown in Figure 4. The main table consists of 256 codewords (i.e., sequences  corresponding to
corresponding to  in the enumerating algorithm), and the substitute table with
in the enumerating algorithm), and the substitute table with  codewords (i.e., sequences
codewords (i.e., sequences  corresponding to
corresponding to  ) is used to minimize the power spectral density at low frequencies.
) is used to minimize the power spectral density at low frequencies.
The PSD of both EFMPlus code and  TMTR code can be computed using the fast Fourier transform (FFT)
TMTR code can be computed using the fast Fourier transform (FFT)

where
Figure 5 depicts the power spectral density (PSD) versus the normalized frequency for the  EFMPlus code, the rate
EFMPlus code, the rate 
 TMTR code, and the
TMTR code, and the 
 TMTR code with method of enumerative, respectively. As shown, at frequency of
TMTR code with method of enumerative, respectively. As shown, at frequency of  , the PSDs for both EFMPlus and TMTR codes are
, the PSDs for both EFMPlus and TMTR codes are  dB,
dB,  dB and
dB and dB, respectively. The result indicates that the
dB, respectively. The result indicates that the 
 TMTR code achieves a lower low-frequency content (with 5 dB lower) than the EFMPlus code. In Figure 5, we notice that the rate
TMTR code achieves a lower low-frequency content (with 5 dB lower) than the EFMPlus code. In Figure 5, we notice that the rate 
 TMTR code has only
TMTR code has only  dB at frequency of
dB at frequency of  and it is not suitable for optical recording systems, although it has a higher code rate compared to the
and it is not suitable for optical recording systems, although it has a higher code rate compared to the 
 TMTR code.
TMTR code.
6. Simulation Results
The superiority of the rate 
 TMTR code over the EFMPlus code is also demonstrated on error performance through a computer simulation on the EPRII optical channel of the form
TMTR code over the EFMPlus code is also demonstrated on error performance through a computer simulation on the EPRII optical channel of the form  . Figure 6 depicts the optical recording system for simulation. An 8-state transition diagram, as depicted in Figure 7(a), can describe the EPRII optical channel. During simulation, a Gaussian optical recording channel was assumed with impulse response
. Figure 6 depicts the optical recording system for simulation. An 8-state transition diagram, as depicted in Figure 7(a), can describe the EPRII optical channel. During simulation, a Gaussian optical recording channel was assumed with impulse response  given by
given by

where  represents the user information density.
represents the user information density.  is the channel bit period assumed to be one (
is the channel bit period assumed to be one ( ) for uncoded systems in simulation. The optical recording channel is then corrupted with the additive white Gaussian noise (AWGN), and at receiver an ideal EPRII equalizer is employed to equalize the optical channel in the form of
) for uncoded systems in simulation. The optical recording channel is then corrupted with the additive white Gaussian noise (AWGN), and at receiver an ideal EPRII equalizer is employed to equalize the optical channel in the form of  .
.
The Viterbi detector is then employed on the 8-state trellis diagram of the EPRII optical channel, to recover binary-recorded data from the equalized and sampled output. Note that for the EFMPlus-coded EPRII channel the 8-state trellis diagram can be reduced to a 6-state trellis diagram due to the  constraint, as shown in Figure 7(b), while for the TMTR-coded EPRII channel the 8-state trellis diagram is still required with some branches deleted as depicted in Figure 7(c). Figure 8 demonstrates the bit error rate versus the signal to noise ratio (SNR) for TMTR-coded, EFMPlus-coded and uncoded EPRII optical recording channels at user density
constraint, as shown in Figure 7(b), while for the TMTR-coded EPRII channel the 8-state trellis diagram is still required with some branches deleted as depicted in Figure 7(c). Figure 8 demonstrates the bit error rate versus the signal to noise ratio (SNR) for TMTR-coded, EFMPlus-coded and uncoded EPRII optical recording channels at user density  . The SNR in dB is defined in this paper as the ratio of the input complex waveform signal energy generated by a 127-bit pseudorandom binary sequence to the channel noise energy of the same duration. As shown both the TMTR-coded and EFMPlus-coded EPRII systems achieve better performance than the uncoded EPRII system. This is because both coded EPRII systems have a coding gain of 3 dB when these modulation codes are considered in the 8-state trellis diagram of the EPRII system during detection. This leads to a coding gain of 3 dB. As also can be seen in this figure, the TMTR-coded EPRII system improves the EFMPlus-coded EPRII system by approximately 1 dB in bit error rate. The coding loss of the EFMPlus-coded EPRII system is due to the bit rate loss. Figure 9 shows the signal to noise (SNR) required to achieve a bit rate error of
. The SNR in dB is defined in this paper as the ratio of the input complex waveform signal energy generated by a 127-bit pseudorandom binary sequence to the channel noise energy of the same duration. As shown both the TMTR-coded and EFMPlus-coded EPRII systems achieve better performance than the uncoded EPRII system. This is because both coded EPRII systems have a coding gain of 3 dB when these modulation codes are considered in the 8-state trellis diagram of the EPRII system during detection. This leads to a coding gain of 3 dB. As also can be seen in this figure, the TMTR-coded EPRII system improves the EFMPlus-coded EPRII system by approximately 1 dB in bit error rate. The coding loss of the EFMPlus-coded EPRII system is due to the bit rate loss. Figure 9 shows the signal to noise (SNR) required to achieve a bit rate error of  , as a function of user density, at a rate of
, as a function of user density, at a rate of 
 TMTR code and a rate of
TMTR code and a rate of  EFMPlus code, applied to an EPRII optical channel. Figure 9 shows how the TMTR code provides little coding gain at user densities below 1.2 but increases coding gain at higher densities. At a user density of
EFMPlus code, applied to an EPRII optical channel. Figure 9 shows how the TMTR code provides little coding gain at user densities below 1.2 but increases coding gain at higher densities. At a user density of  , the TMTR code on the EPRII optical channel provides nearly 2.7 dB of coding gain above the rate of
, the TMTR code on the EPRII optical channel provides nearly 2.7 dB of coding gain above the rate of  EFMPlus code on the EPRII optical channel. Therefore, from the performance comparison made in Figure 9, it can be seen that even a greater improvement in coding gain could be achieved for TMTR-coded EPRII system at higher user densities.
EFMPlus code on the EPRII optical channel. Therefore, from the performance comparison made in Figure 9, it can be seen that even a greater improvement in coding gain could be achieved for TMTR-coded EPRII system at higher user densities.
7. Conclusion
In this paper, we present an enumeration method for constructing  codes, and the look-up table described in a previous work is not required for the encoder/decoder. Based on the construction, a rate
codes, and the look-up table described in a previous work is not required for the encoder/decoder. Based on the construction, a rate 
 TMTR code is found. This code can achieve lower power spectral density at low frequencies compared to the EFMPlus code. In addition, computer simulations reveal that the rate
TMTR code is found. This code can achieve lower power spectral density at low frequencies compared to the EFMPlus code. In addition, computer simulations reveal that the rate  TMTR code outperforms the EFMPlus code in error performance when applied to partial response optical recording channels.
TMTR code outperforms the EFMPlus code in error performance when applied to partial response optical recording channels.
References
Immink KAS: EFMPlus: the coding format of the multimedia compact disc. IEEE Transactions on Consumer Electronics 1995, 41(3):491-497. 10.1109/30.468040
Moon J, Brickner B: Maximum transition run codes for data storage systems. IEEE Transactions on Magnetics 1996, 32(5):3992-3994. 10.1109/20.539241
Moision BE, Siegel PH, Soljanin E: Distance-enhancing codes for digital recording. IEEE Transactions on Magnetics 1998, 34(1):69-74. 10.1109/20.663448
Bliss WG: An 8/9 rate time-varying trellis code for high density magnetic recording. IEEE Transactions on Magnetics 1997, 33(5):2746-2748. 10.1109/20.617717
Fitzpatrick KK, Modlin CS: Time-varying MTR codes for high density magnetic recording. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '97), November 1997, Phoenix, Ariz, USA 1250-1253.
Nikolić B, Leung MM-T, Fu LK-C: Rate 8/9 sliding block distance-enhancing code with stationary detector. IEEE Transactions on Magnetics 2001, 37(3):1168-1174. 10.1109/20.920493
Cideciyan RD, Eleftheriou E: Codes satisfying maximum transition run and parity-check constraints. Proceedings of the IEEE International Conference on Communications, June 2004 635-639.
Demirkan I, Lee YX: The combined constraints for perpendicular recording channels. IEEE Transactions on Magnetics 2006, 42(2):220-225.
Poo TL, Marcus BH: Time-varying maximum transition run constraints. IEEE Transactions on Information Theory 2006, 52(10):4464-4480.
Tsai H-F, Lin Y: Turbo decoding for a new DVD recording system. IEEE Transactions on Consumer Electronics 2005, 51(3):864-871. 10.1109/TCE.2005.1510496
Cideciyan RD, Dolivo F, Hermann R, Hirt W, Schott W: A PRML system for digital magnetic recording. IEEE Journal on Selected Areas in Communications 1992, 10(1):38-56. 10.1109/49.124468
Karabed R, Siegel PH: Matched spectral-null codes for partial-response channels. IEEE Transactions on Information Theory 1991, 37(3):818-855.
Vannucci G, Foschini GJ: The minimum distance for digital magnetic recording partial responses. IEEE Transactions on Information Theory 1991, 37(3):955-960.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tsai, HF. Enumerative Encoding of TMTR Codes for Optical Recording Channel. EURASIP J. Adv. Signal Process. 2010, 695237 (2010). https://doi.org/10.1155/2010/695237
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/695237






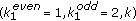 TMTR Codes
TMTR Codes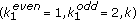 TMTR Codes
TMTR Codes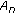 is the lexicographically ordered set of
is the lexicographically ordered set of 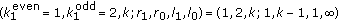 sequences of length
sequences of length  .
.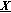 ) is the number of sequences
) is the number of sequences  such that
such that 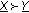 .
. )
)  0, where
0, where  is the all zero sequence.
is the all zero sequence. ) is the sequence obtained by modifying the first nonzero bit of
) is the sequence obtained by modifying the first nonzero bit of 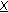 to zero.
to zero.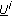 is the minimum sequence among sequences in
is the minimum sequence among sequences in 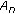 and having the first symbol one at position
and having the first symbol one at position  .
.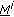 is the maximum sequence among sequences in
is the maximum sequence among sequences in 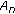 and having the first symbol one at position
and having the first symbol one at position  .
.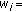 ? R(
? R(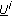 )
) R(res(
R(res(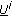 )), then we have
)), then we have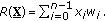
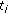 = R(
= R( ).
).
 codes.
codes.

 TMTR code.
TMTR code.




