Abstract
In the previous paper by the first and the third authors, we present six algorithms for determining whether a given symmetric matrix is strictly copositive, copositive (but not strictly), or not copositive. The algorithms for matrices of order  are not guaranteed to produce an answer. It also shows that for 1000 symmetric random matrices of order 8, 9, and 10 with unit diagonal and with positive entries all being less than or equal to 1 and negative entries all being greater than or equal to
are not guaranteed to produce an answer. It also shows that for 1000 symmetric random matrices of order 8, 9, and 10 with unit diagonal and with positive entries all being less than or equal to 1 and negative entries all being greater than or equal to  , there are 8, 6, and 2 matrices remaing undetermined, respectively. In this paper we give two more algorithms for
, there are 8, 6, and 2 matrices remaing undetermined, respectively. In this paper we give two more algorithms for  and our experiment shows that no such matrix of order 8 or 9 remains undetermined; and almost always no such matrix of order 10 remains undetermined. We also do some discussion based on our experimental results.
and our experiment shows that no such matrix of order 8 or 9 remains undetermined; and almost always no such matrix of order 10 remains undetermined. We also do some discussion based on our experimental results.
Similar content being viewed by others
1. Introduction
Reference [1] gives six algorithms for determining whether a given symmetric matrix is strictly copositive, copositive (but not strictly), or not copositive. The algorithms for matrices of order 3, 4, 5, 6 or 7 are efficient. But for matrices of order  , it cannot guarantee to produce an answer. Table
, it cannot guarantee to produce an answer. Table  of [1] shows that for 1000 symmetric random matrices of order
of [1] shows that for 1000 symmetric random matrices of order  with unit diagonal and with positive entries all being less than or equal to 1 and negative entries all being greater than or equal to
with unit diagonal and with positive entries all being less than or equal to 1 and negative entries all being greater than or equal to  , there are 8, 6, and 2 matrices remaining undetermined when
, there are 8, 6, and 2 matrices remaining undetermined when  , respectively. In this paper we continue our study as in [1] and give two algorithms for
, respectively. In this paper we continue our study as in [1] and give two algorithms for  and our experiment shows that no such matrix of order 8 or 9 remains undetermined; and almost always no such matrix of order 10 remains undetermined. We also do some discussion based on our experimental results.
and our experiment shows that no such matrix of order 8 or 9 remains undetermined; and almost always no such matrix of order 10 remains undetermined. We also do some discussion based on our experimental results. 
In this paper we use all the concepts and notations of [1, 2] without explanation. Our main theorems will give the necessary and sufficient conditions for symmetric matrices of order 8 or 9 to be (strictly) copositive.
Let  be symmetric and be partitioned into
be symmetric and be partitioned into

with  ,
,  . As in [2], let
. As in [2], let

be the simplex of order  ; and let
; and let

be the standard simplex of order  whose vertices are all vertices of
whose vertices are all vertices of  . It is proved in [2] that an
. It is proved in [2] that an  symmetric matrix
symmetric matrix  is copositive if and only if
is copositive if and only if  for all
for all  . Consider the polyhedron in
. Consider the polyhedron in  is the given vector of dimension
is the given vector of dimension  in (1.1)) which has some vertices being vertices of
in (1.1)) which has some vertices being vertices of  , and all the other vertices being in the hyperplane
, and all the other vertices being in the hyperplane  . It is known (see [2, Section
. It is known (see [2, Section  and Lemma
and Lemma  ]) that the polyhedron
]) that the polyhedron  can be subdivided into
can be subdivided into  simplices
simplices  in
in  such that
such that  ,
,  is a subsimplex of
is a subsimplex of  and
and  if
if  , and the vertices of
, and the vertices of  are all vertices of
are all vertices of  . We mention this fact since that
. We mention this fact since that  is subdivided into simplices
is subdivided into simplices  .
.
Denote the vertices of  by
by  , then
, then  is a vertex of
is a vertex of  , or a common point of the line connecting two vertices of
, or a common point of the line connecting two vertices of  and the hyperplane
and the hyperplane  and should be presented in the barycenter coordinates of
and should be presented in the barycenter coordinates of  . If
. If  is the
is the  th vertex of
th vertex of  , then it is represented by the coordinate vector
, then it is represented by the coordinate vector  with a 1 in the
with a 1 in the  th position and all 0's elsewhere; otherwise write
th position and all 0's elsewhere; otherwise write  to denote that it is the common point of line
to denote that it is the common point of line  and the hyperplane
and the hyperplane  . Each
. Each  determines a matrix
determines a matrix  (see [2, Lemma
(see [2, Lemma  ]), to simplify the notation we still write
]), to simplify the notation we still write  with
with  or
or  . For example, if
. For example, if  share only one vertex
share only one vertex  with
with  and the other vertices are
and the other vertices are  , then
, then

Lemma 1.1 (see [2]).
Let  be symmetric and partitioned as in (1.1) with
be symmetric and partitioned as in (1.1) with  ,
,  being copositive and
being copositive and  is subdivided into simplices
is subdivided into simplices  which determine matrices
which determine matrices  . Then
. Then  is copositive if and only if
is copositive if and only if  ,
,  are all copositive (see [2, Lemma 3.1]);
are all copositive (see [2, Lemma 3.1]);  is strictly copositive if and only if
is strictly copositive if and only if  ,
,  are all strictly copositive and
are all strictly copositive and  and
and  is strictly copositive (see [1]).
is strictly copositive (see [1]).
It is noticed from [2] that if the polyhedron  contains
contains  vertices (coordinate vectors of the standard simplex
vertices (coordinate vectors of the standard simplex  not in the hyperplane
not in the hyperplane  , then
, then  contains exact
contains exact  vertices in the hyperplane
vertices in the hyperplane  , and that
, and that  can be subdivided into
can be subdivided into  simplices
simplices  of dimension
of dimension  such that
such that  is a simplex of dimension
is a simplex of dimension  for
for  and
and  is a simplex of dimension
is a simplex of dimension  when
when  .
.
Lemma 1.2 (see [1]).
Let  . If there are
. If there are 
 -triples of pairwise different vertices of
-triples of pairwise different vertices of  satisfying the following two conditions:
satisfying the following two conditions:
(i)each  contains at least one coordinate vector vertex;
contains at least one coordinate vector vertex;
(ii) has exactly
has exactly  vertices for
vertices for  , and
, and  has less than
has less than  vertices when
vertices when  ,
,
then  can be subdivided into
can be subdivided into  simplices
simplices  , where
, where  is the simplex whose vertices are the elements of
is the simplex whose vertices are the elements of  .
.
These two lemmas are basic for proving Theorems  , 2.6, 2.7, and 2.8 in [1]; they are also basic for proving Theorems 2.1 and 2.2 of this paper.
, 2.6, 2.7, and 2.8 in [1]; they are also basic for proving Theorems 2.1 and 2.2 of this paper.
2. Main Theorems and Algorithms
The following two theorems give two algorithms for determining the copositivity of a given symmetric matrix of order 8 or 9. These two theorems can be proved by Lemma 1.1 and Lemma 1.2 following the same pattern as in [1]. 
Theorem 2.1.
Let  be symmetric and be partitioned as in (1.1) and
be symmetric and be partitioned as in (1.1) and  , then at least one of the following cases must happen:
, then at least one of the following cases must happen:
-
(a)
If one
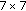 principal submatrix of
principal submatrix of  is not copositive, then
is not copositive, then 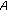 is not copositive. Otherwise it holds that
is not copositive. Otherwise it holds that 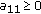 and
and 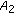 is copositive.
is copositive. -
(b)
If
 then
then 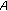 is copositive; if
is copositive; if 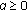 with
with 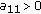 and
and  is strictly copositive, then
is strictly copositive, then  is strictly copositive.
is strictly copositive. -
(c)
If
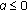 , then
, then 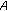 is copositive if and only if
is copositive if and only if 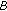 is copositive;
is copositive; 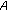 is strictly copositive if and only if
is strictly copositive if and only if 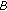 is strictly copositive and
is strictly copositive and 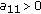 and
and  is strictly copositive.
is strictly copositive. -
(d)
If
 has exactly one negative entry:
has exactly one negative entry: 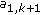 , then
, then 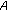 is copositive if and only if
is copositive if and only if  is copositive;
is copositive; 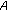 is strictly copositive if and only if
is strictly copositive if and only if 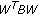 is strictly copositive, and
is strictly copositive, and 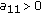 and
and 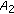 is strictly copositive, where
is strictly copositive, where

(e) If  has exactly two negative entries:
has exactly two negative entries: , and
, and  , then
, then  is copositive if and only if
is copositive if and only if  and
and  are all copositive;
are all copositive;  is strictly copositive if and only if
is strictly copositive if and only if  are all strictly copositive and
are all strictly copositive and  and
and  is strictly copositive, where
is strictly copositive, where

(f) If  has exactly three negative entries:
has exactly three negative entries:  and
and  , then
, then  is copositive if and only if
is copositive if and only if  are all copositive;
are all copositive;  is strictly copositive if and only if
is strictly copositive if and only if  are all strictly copositive and
are all strictly copositive and  and
and  is strictly copositive, where
is strictly copositive, where

(g) If  has exactly four negative entries:
has exactly four negative entries:  and
and  , then
, then  is copositive if and only if
is copositive if and only if  are all copositive;
are all copositive;  is strictly copositive if and only if
is strictly copositive if and only if  are all strictly copositive and
are all strictly copositive and  and
and  is strictly copositive, where
is strictly copositive, where

(h) If  has exactly five negative entries:
has exactly five negative entries:  and
and  , then
, then  is copositive if and only if
is copositive if and only if  are all copositive;
are all copositive;  is strictly copositive if and only if
is strictly copositive if and only if  are all strictly copositive and
are all strictly copositive and  and
and  is strictly copositive, where
is strictly copositive, where

(i) If  has exactly six negative entries:
has exactly six negative entries:  and
and  , then
, then  is copositive if and only if
is copositive if and only if  are all copositive;
are all copositive;  is strictly copositive if and only if
is strictly copositive if and only if  are all strictly copositive and
are all strictly copositive and  and
and  is strictly copositive, where
is strictly copositive, where


It is clear (see [1, Remark  ]) that if
]) that if  is odd, then a copositive matrix
is odd, then a copositive matrix  must have a row with an even number of negative entries. In other words, if a symmetric matrix of odd order has row with an even number of negative entries, then some
must have a row with an even number of negative entries. In other words, if a symmetric matrix of odd order has row with an even number of negative entries, then some  principal submatrices of it are not copositive. This fact will be used in Theorem 2.2.
principal submatrices of it are not copositive. This fact will be used in Theorem 2.2. 
Theorem 2.2.
If  is symmetric, then at least one of the following cases must happen:
is symmetric, then at least one of the following cases must happen:
-
(a)
If one
 principal submatrix of
principal submatrix of 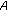 is not copositive, then
is not copositive, then  is not copositive.
is not copositive.
Otherwise ( must have a row with an even number of negative entries and
must have a row with an even number of negative entries and  is copositive) find a row of
is copositive) find a row of  which has exactly
which has exactly  negative entries. If the
negative entries. If the  th row does, then interchange the
th row does, then interchange the  th row and column with the first row and column, and partition
th row and column with the first row and column, and partition  into (1.1) as in Theorem 2.1.
into (1.1) as in Theorem 2.1.
-
(b)
If
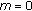 , then
, then 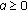 and
and  is copositive; if
is copositive; if 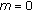 with
with  and
and  is strictly copositive, then
is strictly copositive, then 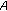 is strictly copositive.
is strictly copositive. -
(c)
If
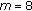 , then
, then 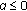 , then
, then 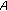 is copositive if and only if
is copositive if and only if  is copositive;
is copositive; 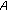 is strictly copositive if and only if
is strictly copositive if and only if 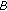 is strictly copositive and
is strictly copositive and 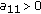 and
and 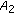 is strictly copositive.
is strictly copositive. -
(d)
If
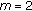 , then
, then  has exactly two negative entries:
has exactly two negative entries:  , and
, and  , then
, then 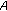 is copositive if and only if
is copositive if and only if 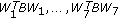 are all copositive;
are all copositive; 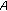 is strictly copositive if and only if
is strictly copositive if and only if 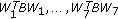 are all strictly copositive and
are all strictly copositive and 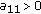 and
and 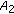 is strictly copositive, where
is strictly copositive, where

(e) If  , then
, then  has exactly four negative entries:
has exactly four negative entries:  and
and  , then
, then  is copositive if and only if
is copositive if and only if  are all copositive;
are all copositive;  is strictly copositive if and only if
is strictly copositive if and only if  are all strictly copositive and
are all strictly copositive and  and
and  is strictly copositive, where
is strictly copositive, where

(f) If  , then
, then  has exactly six negative entries:
has exactly six negative entries:  and
and  , then
, then  is copositive if and only if
is copositive if and only if  are all copositive;
are all copositive;  is strictly copositive if and only if
is strictly copositive if and only if  are all strictly copositive and
are all strictly copositive and  and
and  is strictly copositive, where
is strictly copositive, where


As mentioned in [1], we have made six MATLAB functions: Cha3( ), Cha4(
), Cha4( ), Cha5(
), Cha5( ), Cha6(
), Cha6( ), Cha7(
), Cha7( ) and Cha(
) and Cha( ), for determining the copositivity of symmetric matrices. Now we have made two more MATLAB functions of these type: Cha8(
), for determining the copositivity of symmetric matrices. Now we have made two more MATLAB functions of these type: Cha8( ) and Cha9(
) and Cha9( ) based on the two algorithms given by Theorems 2.1 and 2.2. The input of the functions is any
) based on the two algorithms given by Theorems 2.1 and 2.2. The input of the functions is any  or
or  symmetric matrix
symmetric matrix  and there are four possible return values:
and there are four possible return values:  meaning "not copositive", "copositive (not strictly)" and "strictly copositive", "cannot determined," respectively.
meaning "not copositive", "copositive (not strictly)" and "strictly copositive", "cannot determined," respectively. 
Main steps of Function 
( ) Find out if
) Find out if  has any
has any  principal submatrix which is not copositive. If so, then return with "
principal submatrix which is not copositive. If so, then return with " " (Theorem 2.1(a)). Otherwise go to next step.
" (Theorem 2.1(a)). Otherwise go to next step.
( ) Calculate the number
) Calculate the number  of the negative entries of the first row of
of the negative entries of the first row of  .
.
When  use Theorem 2.1(b) to determine copositivity of
use Theorem 2.1(b) to determine copositivity of  and return.
and return.
When  use Theorem 2.1(c) to determine copositivity of
use Theorem 2.1(c) to determine copositivity of  and return.
and return.
When  use Theorem 2.1(d) to determine copositivity of
use Theorem 2.1(d) to determine copositivity of  and return.
and return.
When  use Theorem 2.1(e) to determine copositivity of
use Theorem 2.1(e) to determine copositivity of  and return.
and return.
When  use Theorem 2.1(f) to determine copositivity of
use Theorem 2.1(f) to determine copositivity of  and return.
and return.
When  use Theorem 2.1(g) to determine copositivity of
use Theorem 2.1(g) to determine copositivity of  and return.
and return.
When  use Theorem 2.1(h) to determine copositivity of
use Theorem 2.1(h) to determine copositivity of  and return.
and return.
When  use Theorem 2.1(i) to determine copositivity of
use Theorem 2.1(i) to determine copositivity of  and return.
and return.
Main steps of Function 
( ) Find out if
) Find out if  has any
has any  principal submatrix which is not copositive. If so, then return with "
principal submatrix which is not copositive. If so, then return with " " (Theorem 2.2(a)). Otherwise
" (Theorem 2.2(a)). Otherwise  must have some row containing exactly
must have some row containing exactly  negative entries and go to the next step.
negative entries and go to the next step.
( ) Find out if
) Find out if  has any row which has exactly
has any row which has exactly  negative entries. If the
negative entries. If the  th row does, then interchange the
th row does, then interchange the  th row and column of
th row and column of  with the first row and column.
with the first row and column.
When  use Theorem 2.2(b) to determine copositivity of
use Theorem 2.2(b) to determine copositivity of  and return.
and return.
When  use Theorem 2.2(c) to determine copositivity of
use Theorem 2.2(c) to determine copositivity of  and return.
and return.
When  use Theorem 2.2(d) to determine copositivity of
use Theorem 2.2(d) to determine copositivity of  and return.
and return.
When  use Theorem 2.2(e) to determine copositivity of
use Theorem 2.2(e) to determine copositivity of  and return.
and return.
When  use Theorem 2.2(f) to determine copositivity of
use Theorem 2.2(f) to determine copositivity of  and return.
and return.
3. Numerical Experiments and Discussion
Having all these eight functions: Cha3( ), Cha4(
), Cha4( ),
),  Cha8(
Cha8( ), Cha9(
), Cha9( ), and Cha(
), and Cha( ) we have performed the following experiments. Firstly, we use these functions to determine the copositivity of the
) we have performed the following experiments. Firstly, we use these functions to determine the copositivity of the  symmetric matrix
symmetric matrix  studied in [3], where
studied in [3], where  satisfies
satisfies  ;
;  only if
only if  and
and  . When
. When  the experimental results obtained by old Cha(
the experimental results obtained by old Cha( ) together with Cha3(
) together with Cha3( ), Cha4(
), Cha4( ),
),  Cha7(
Cha7( ) are "
) are " " meaning "cannot be determined" and the experimental results by Cha9(
" meaning "cannot be determined" and the experimental results by Cha9( ) are "
) are " " meaning "copositive but not strictly", which are the same results as obtained in [3]. Secondly we generate 1000 symmetric random matrices of order
" meaning "copositive but not strictly", which are the same results as obtained in [3]. Secondly we generate 1000 symmetric random matrices of order  with unit diagonal and with positive entries all being less than or equal to 1 and negative entries all being greater than or equal to
with unit diagonal and with positive entries all being less than or equal to 1 and negative entries all being greater than or equal to  , and then use our MATLAB functions to determine the copositivity of these matrices. The main numerical result of the experiments is given in Table 1, where
, and then use our MATLAB functions to determine the copositivity of these matrices. The main numerical result of the experiments is given in Table 1, where  ,
,  ,
,  ,
,  undeter denote the number of strictly copositive matrices, the number of copositive (but not strictly) matrices, the number of noncopositive matrices, and the number of the remained matrices whose copositivity could not be determined by our algorithms, respectively.
undeter denote the number of strictly copositive matrices, the number of copositive (but not strictly) matrices, the number of noncopositive matrices, and the number of the remained matrices whose copositivity could not be determined by our algorithms, respectively.
Kaplan [4, Theorem  ] proved that a symmetric matrix
] proved that a symmetric matrix  is copositive if and only if the minimum principal submatrix
is copositive if and only if the minimum principal submatrix  of
of  which shares the maximum positive diagonal entries with
which shares the maximum positive diagonal entries with  is copositive and the matrix which is constructed from
is copositive and the matrix which is constructed from  by replacing each entry of
by replacing each entry of  by 0 is nonnegative. To answer the third open problem of [4, 5], we proved that a symmetric matrix
by 0 is nonnegative. To answer the third open problem of [4, 5], we proved that a symmetric matrix  with unit diagonal is copositive if and only if the matrix constructed from
with unit diagonal is copositive if and only if the matrix constructed from  by replacing each off-diagonal entry
by replacing each off-diagonal entry  by
by  is copositive. These two results make it reasonable that for determining copositivity we can restrict our attention only to symmetric matrices with unit diagonal and with positive entries all being less than or equal to 1, and our experimental matrices are all of this type. Furthermore, each of the test matrices is required that every of its principal
is copositive. These two results make it reasonable that for determining copositivity we can restrict our attention only to symmetric matrices with unit diagonal and with positive entries all being less than or equal to 1, and our experimental matrices are all of this type. Furthermore, each of the test matrices is required that every of its principal  submatrix is copositive (Note that for a matrix with
submatrix is copositive (Note that for a matrix with  the chance that every principal
the chance that every principal  submatrix is copositive is much less). In addition, the last line of Table 1 also holds for
submatrix is copositive is much less). In addition, the last line of Table 1 also holds for  because of the fact that a symmetric matrix is not copositive if any of its principal submatrix is not copositive. Table 1 does give us some noticeable information as follows.
because of the fact that a symmetric matrix is not copositive if any of its principal submatrix is not copositive. Table 1 does give us some noticeable information as follows.
Remark 3.1.
For  almost always no random matrix is copositive, in other words, there is almost always no matrix remaining undetermined by our algorithms including the new ones developed in this paper. Therefore, the algorithms for
almost always no random matrix is copositive, in other words, there is almost always no matrix remaining undetermined by our algorithms including the new ones developed in this paper. Therefore, the algorithms for  and so forth. which might be established by our method are not practically needed.
and so forth. which might be established by our method are not practically needed.

We surely believe that algorithm for  will be tedious to describe and take more time to run because of its recurrent property.
will be tedious to describe and take more time to run because of its recurrent property.
Since there is almost always no symmetric copositive matrix of order larger than 9, the interest of researchers may concentrate on sufficient conditions for copositive matrices of larger orders, or of general order  . For instance, [3] proved the matrix
. For instance, [3] proved the matrix  mentioned at the beginning of this section is copositive (but not strictly) for any
mentioned at the beginning of this section is copositive (but not strictly) for any  . Here we give another interesting example as follows.
. Here we give another interesting example as follows.
Proposition 3.2.
Let  be a symmetric matrix of any order,
be a symmetric matrix of any order,  ;
;  be the sum of all the negative entries of the
be the sum of all the negative entries of the  th row of
th row of  . Then
. Then  is copositive if
is copositive if  ;
;  is strictly copositive if
is strictly copositive if  ;
;  is irreducible and
is irreducible and  .
.
Proof.
Write  , where
, where  and
and  is the
is the  nonnegative matrix which shares all the negative (nonnegative) entries with
nonnegative matrix which shares all the negative (nonnegative) entries with  and has the remained entries all being zero. Then
and has the remained entries all being zero. Then  , where
, where  and
and  is a nonnegative matrix whose spectral radius
is a nonnegative matrix whose spectral radius  if
if  . Therefore,
. Therefore,  is an M-matrix if
is an M-matrix if  ; a nonsingular M-matrix if
; a nonsingular M-matrix if  or
or  is irreducible and
is irreducible and  , whence it is copositive, strictly copositive, respectively by [1, Theorem
, whence it is copositive, strictly copositive, respectively by [1, Theorem  ]. Finally
]. Finally  (as the sum of two copositive matrices) is copositive.
(as the sum of two copositive matrices) is copositive.
References
Yang S-J, Li X-X: Algorithms for determining the copositivity of a given symmetric matrix. Linear Algebra and Its Applications 2009, 430(2–3):609–618. 10.1016/j.laa.2008.07.028
Andersson L-E, Chang G, Elfving T: Criteria for copositive matrices using simplices and barycentric coordinates. Linear Algebra and Its Applications 1995, 220: 9–30.
Johnson CR, Reams R: Constructing copositive matrices from interior matrices. Electronic Journal of Linear Algebra 2008, 17: 9–20.
Kaplan W: A copositivity probe. Linear Algebra and Its Applications 2001, 337: 237–251. 10.1016/S0024-3795(01)00351-2
Hogben L, Johnson CR, Reams R: The copositive completion problem. Linear Algebra and Its Applications 2005, 408: 207–211.
Acknowledgments
This work was supported by the NNSF China no. 10871230, NSF Zhejiang no. y607480, and Innovation Group Foundation of Anhui University
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Shang-jun, Y., Chang-qing, X. & Xiao-xin, L. A Note on Algorithms for Determining the Copositivity of a Given Symmetric Matrix. J Inequal Appl 2010, 498631 (2009). https://doi.org/10.1155/2010/498631
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/498631



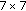 principal submatrix of
principal submatrix of  is not copositive, then
is not copositive, then 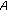 is not copositive. Otherwise it holds that
is not copositive. Otherwise it holds that 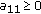 and
and 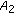 is copositive.
is copositive. then
then 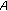 is copositive; if
is copositive; if 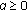 with
with 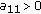 and
and  is strictly copositive, then
is strictly copositive, then  is strictly copositive.
is strictly copositive.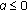 , then
, then 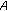 is copositive if and only if
is copositive if and only if 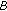 is copositive;
is copositive; 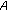 is strictly copositive if and only if
is strictly copositive if and only if 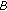 is strictly copositive and
is strictly copositive and 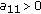 and
and  is strictly copositive.
is strictly copositive. has exactly one negative entry:
has exactly one negative entry: 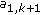 , then
, then 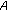 is copositive if and only if
is copositive if and only if  is copositive;
is copositive; 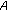 is strictly copositive if and only if
is strictly copositive if and only if 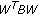 is strictly copositive, and
is strictly copositive, and 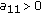 and
and 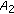 is strictly copositive, where
is strictly copositive, where principal submatrix of
principal submatrix of 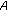 is not copositive, then
is not copositive, then  is not copositive.
is not copositive.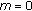 , then
, then 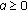 and
and  is copositive; if
is copositive; if 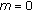 with
with  and
and  is strictly copositive, then
is strictly copositive, then 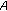 is strictly copositive.
is strictly copositive.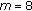 , then
, then 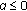 , then
, then 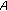 is copositive if and only if
is copositive if and only if  is copositive;
is copositive; 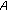 is strictly copositive if and only if
is strictly copositive if and only if 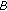 is strictly copositive and
is strictly copositive and 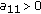 and
and 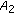 is strictly copositive.
is strictly copositive.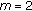 , then
, then  has exactly two negative entries:
has exactly two negative entries:  , and
, and  , then
, then 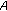 is copositive if and only if
is copositive if and only if 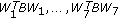 are all copositive;
are all copositive; 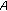 is strictly copositive if and only if
is strictly copositive if and only if 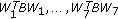 are all strictly copositive and
are all strictly copositive and 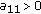 and
and 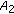 is strictly copositive, where
is strictly copositive, where