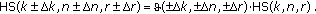1. Introduction

The hypersphere function is a hypothetical function connected to multidimensional space. It belongs to the group of special functions, so its testing is performed on the basis of known functions such as the -gamma, -psi, - beta, anderf- error function. The most significant value is in its generalization from discrete to continuous. In addition, we can move from the scope of natural integers to the set of real and noninteger values. Therefore, there exist conditions both for its graphical interpretation and a more concise analysis. For the development of the hypersphere function theory see Bishop and Whitlock [1], Collins [2], Conway and Sloane [3], Dodd and Coll [4], Hinton [5], Hocking and Young [6], Manning [7], Maunder [8], Neville [9], Rohrmann and Santos [10], Rucker [11], Maeda et al. [12], Sloane [13], Sommerville [14], Wells et al. [15] Nowadays, the research of hyperspherical functions is given both in Euclid's and Riemann's geometry and topology (Riemann's and Poincare's sphere) multidimensional potentials, theory of fluids, nuclear physics, hyperspherical black holes, and so forth.

2. Hypersphere Function with Two Degrees of Freedom

The former results (see [4–30]) as it is known present two-dimensional (surface-surfs ), respectively, three-dimensional (volume-solids) geometrical entities. In addition to certain generalizations [27], there exists a family of hyperspherical functions that can be presented in the simplest way through the hyperspherical matrix , with two degrees of freedom and (), instead of the former presentation based only on vector approach (on the degree of freedom k). This function is based on the general value of integrals, and so we obtain it's generalized form.

Definition 2.1.

The generalized hyperspherical function is defined by

(2.1)

where is the gamma function.

On this function, we can also perform "motions'' to the lower degrees of freedom by differentiating with respect to the radius , starting from the th, on the basis of recurrence

(2.2)

The example of the spherical functions derivation is shown in Figure 1. The second () degree of freedom is achieved, and it is one level lower than the volume level (). Several fundamental characteristics are connected to the sphere. With its mathematically geometrical description, the greatest number of information is necessary for a solid sphere as a full spherical body. Then we have the surface sphere or surf-sphere, and so forth.

Figure 1
figure 1

Moving through the vector of real surfaces (left column), deducting one degree of freedom k of the surface sphere we obtain the circumference, and for two (degrees) we get the point 2. Moving through the vector of real solids (right column), that is, by deduction of one degree of freedom k from the solid sphere, we obtain a circle (disc), and for two (degrees of freedom), we obtain a line segment or diameter.

Full size image

The appropriate matrix () is formed on the basis of the general hyperspherical function, and here it gives the concrete values for the selected submatrix () as shown in Figure 2.

Figure 2
figure 2

The submatrix of the function that covers one area of real degrees of freedom ( ) . Also noticeable are the coordinates of six sphere functions (undef. are nondefined, predominantly of singular value, and 0 are zeros of this function).

Full size image

3. Translators in the Matrix Conversion of Functions

A more generalized relation which would connect every element in the matrix, (Figures 3 and 4) both discrete and/or continual ones, can be defined on the basis of relation (quotient) of two hyperspherical functions, one with increment of arguments dimensions—degrees of freedom (), that is, the assigned one—while the other would be the starting one (the referred one). On the basis of the previous definition, the translator is

(3.1)
Figure 3
figure 3

The position of the reference element and its surrounding in the hypersphere matrix when

Full size image
Figure 4
figure 4

The example of the position of the referent and assigned element (of the nested HS function in the block-matrix) in the space of the selected hyperspheric block-matrix.

Full size image

Note.

In the previous expression we do not take into consideration the radius increase as a degree of freedom, so . The defining function thus equals

(3.2)

This equation can be expressed in the form

(3.3)

Every matrix element as a referring one can have in total eight elements in its neighbourhood, and it makes nine types of connections (one with itself) in the matrix plane (Figure 3). Considering that two degrees of freedom have a positive or negative increment (in this case integer), the selected submatrix is representative enough from the aspect of the functions conversion in plane with the help of the translator .

Since the accepted increments are threefold , and connections are established only between the two elements, the number of total connections in the representative submatrix is . All relations of this submatrix and the translators that enable those connections can now be summarised in Table 1.

Table 1
Full size table

4. Generalized Translators of the Hyperspherical Matrix

In this section the extended recurrent operators include one more dimension as a degree of freedom, which is the radius r. If the increment and/or reduction is applied on this argument as well, the translator will get the extended form

Definition 4.1.

The translator is defined with

(4.1)

Since all the three increments can be positive or in symmetrical case negative (in reduction), expression (3.1) is extended and is reduced to relation (4.1), where the differences are the increment values or reduction of the variables and in relation to the referent coordinate (-function) in the matrix. All three variables can be real numbers (). The obtained expression is a more generalized translator, a more generalized functional operator, and in that sense it will be defined as the generalized translator. When, besides the unitary increments of the degree of freedom and , we introduce the radius increment the number of combinations becomes exponential (Table 2), and it is .

Table 2
Full size table

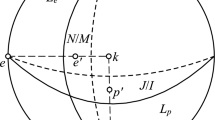
The schematic presentation of "3D motions'' through the space of block-submatrix and locating the assigned HS function on the basis of translators and the starting hyperspherical function is given in Figure 4.

According to the translator that includes three arguments, and in view of it "covering the field'' of the block-submatrix according to Figure 4, we have the following function:

(4.2)

Examples 4.2.

Depending on which level we observe, the translator can be applied on block-matrix, matrix, or vector relations. The most common is the recurrent operator for the elements of columns' vector. Then, it is usually reduced onto one variable and that is the degree of freedom . If the increment is an integer and , the recurrent relation for any element of the n th column is defined as

(4.3)

If the relation is restricted to , that is, on the vector particular to this degree of freedom and on the increment , the translator can be simplified as

(4.4)

For the unit radius this expression can be reduced to the relation

(4.5)

If we analyze the relation for the vector with the degree of freedom and the increment , the translator now becomes

(4.6)

On the basis of the previous positions and results, we define two recurrent operators for defining the assigned functions

  1. (1)

    for the matrix

    (4.7)
  2. (2)

    and for the block-matrix (Figure 3)

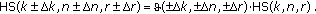    (4.8)

As the recurrent operator is generalized, the increments can also be negative (ones) and noninteger; so, for example, for the block matrix recursion, with the selected increments , and , the operator has a more complex structure

(4.9)

5. Conversion of the Basic Spheric Entities

Example 5.1.

All relations among the six real geometrical sphere entities are presented on the basis of the translator . These entities are P-point, D-diameter, C-circumference, A-circle, S-surface, and V-sphere volume, given in Figure 5. In addition to the graph presentation, the relation among these entities can also be a graphical one, as shown in Figure 5.

Figure 5
figure 5

The selected entities (left) and the oriented graph of their mutual connections (right).

Full size image

6. The Relation of a Point and Real Spherical Entities

A point is a mathematical notion that from the epistemological standpoint has great theoretical and practical meaning. Here, a point is a solid-sphere of which two degrees of freedom of type and one of type are reduced. Of course, a point can be also defined in a different way, which has not been analyzed in the previous procedures. Here these relations are considered separately, and therefore we develop specific translators of the type. On the basis of the established graph, all option relations are shaped. There are in total thirty of them (), and they are presented in Table 3.

Table 3
Full size table

The conversion solution of the selected entities is given in Table 4.

Table 4
Full size table

The previous operators can form a relation among six real spherical entities. From a formal standpoint some of them can be shaped as well on the basis of the beta function, if we include the following relation originating from Legendre

(61)

The position of the six analyzed coordinates of the real spherical functions can be presented on the surface hyperspherical function 3D (Figure 6, using the software Mathematica).

Figure 6
figure 6

The positions of spherical entities on 3D graphic of the HS function of unit radius.

Full size image

7. Conclusion

The hyperspherical translators have a specific role in establishing relations among functions of some spherical entities. Meanwhile, their role is also enlarged, because this relation can be analytically expanded to the complex part of the hyperspherical function (matrix). In addition, there can be increments of degrees of freedom with noninteger values. The previous function properties of translator functions are provided thanks to the interpolating and other properties of the gamma function. Functional operators defined in the previously described way can be applied in defining the total dimensional potential of the hyperspherical function in the field of natural numbers (degrees of freedom ). Namely, this potential (dimensional flux) can be defined with the double series:

(71)

Here, the translators are applied taking into consideration that every defining function can be presented on the basis of the reference HS function, if we correctly define the recurrent relations both for the series and for the columns of the hyperspherical matrix [27].