Abstract
We shall introduce and construct explicitly the complementary Lidstone interpolating polynomial  of degree
of degree  , which involves interpolating data at the odd-order derivatives. For
, which involves interpolating data at the odd-order derivatives. For  we will provide explicit representation of the error function, best possible error inequalities, best possible criterion for the convergence of complementary Lidstone series, and a quadrature formula with best possible error bound. Then, these results will be used to establish existence and uniqueness criteria, and the convergence of Picard's, approximate Picard's, quasilinearization, and approximate quasilinearization iterative methods for the complementary Lidstone boundary value problems which consist of a
we will provide explicit representation of the error function, best possible error inequalities, best possible criterion for the convergence of complementary Lidstone series, and a quadrature formula with best possible error bound. Then, these results will be used to establish existence and uniqueness criteria, and the convergence of Picard's, approximate Picard's, quasilinearization, and approximate quasilinearization iterative methods for the complementary Lidstone boundary value problems which consist of a  th order differential equation and the complementary Lidstone boundary conditions.
th order differential equation and the complementary Lidstone boundary conditions.
Similar content being viewed by others
1. Introduction
In our earlier work [1, 2] we have shown that the interpolating polynomial theory and the qualitative as well as quantitative study of boundary value problems such as existence and uniqueness of solutions, and convergence of various iterative methods are directly connected. In this paper we will extend this technique to the following complementary Lidstone boundary value problem involving an odd order differential equation

and the boundary data at the odd order derivatives

Here  ,
,  but fixed, and
but fixed, and  is continuous at least in the interior of the domain of interest. Problem (1.1), (1.2) complements Lidstone boundary value problem (nomenclature comes from the expansion introduced by Lidstone [3] in 1929, and thoroughly characterized in terms of completely continuous functions in the works of Boas [4], Poritsky [5], Schoenberg [6–8], Whittaker [9, 10], Widder [11, 12], and others) which consists of an even-order differential equation and the boundary data at the even-order derivatives
is continuous at least in the interior of the domain of interest. Problem (1.1), (1.2) complements Lidstone boundary value problem (nomenclature comes from the expansion introduced by Lidstone [3] in 1929, and thoroughly characterized in terms of completely continuous functions in the works of Boas [4], Poritsky [5], Schoenberg [6–8], Whittaker [9, 10], Widder [11, 12], and others) which consists of an even-order differential equation and the boundary data at the even-order derivatives

Problem (1.3) has been a subject matter of numerous studies in the recent years [13–45], and others.
In Section 2, we will show that for a given function  explicit representations of the interpolation polynomial
explicit representations of the interpolation polynomial  of degree
of degree  satisfying the conditions
satisfying the conditions

and the corresponding residue term  can be deduced rather easily from our earlier work on Lidstone polynomials [46–48]. Our method will avoid unnecessarily long procedure followed in [49] to obtain the same representations of
can be deduced rather easily from our earlier work on Lidstone polynomials [46–48]. Our method will avoid unnecessarily long procedure followed in [49] to obtain the same representations of  and
and  We will also obtain error inequalities
We will also obtain error inequalities

where the constants  are the best possible in the sense that in (1.5) equalities hold if and only if
are the best possible in the sense that in (1.5) equalities hold if and only if  is a certain polynomial. The best possible constant
is a certain polynomial. The best possible constant  was also obtained in [49]; whereas they left the cases
was also obtained in [49]; whereas they left the cases  without any mention. In Section 2, we will also provide best possible criterion for the convergence of complementary Lidstone series, and a quadrature formula with best possible error bound.
without any mention. In Section 2, we will also provide best possible criterion for the convergence of complementary Lidstone series, and a quadrature formula with best possible error bound.
If  then the complementary Lidstone boundary value problem (1.1), (1.2) obviously has a unique solution
then the complementary Lidstone boundary value problem (1.1), (1.2) obviously has a unique solution  if
if  is linear, that is,
is linear, that is,  then (1.1), (1.2) gives the possibility of interpolation by the solutions of the differential equation (1.1). In Sections 3–5, we will use inequalities (1.5) to establish existence and uniqueness criteria, and the convergence of Picard's, approximate Picard's, quasilinearization, and approximate quasilinearization iterative methods for the complementary Lidstone boundary value problem (1.1), (1.2). In Section 6, we will show the monotone convergence of Picard's iterative method. Since the proofs of most of the results in Sections 3–6 are similar to those of our previous work [1, 2] the details are omitted; however, through some simple examples it is shown how easily these results can be applied in practice.
then (1.1), (1.2) gives the possibility of interpolation by the solutions of the differential equation (1.1). In Sections 3–5, we will use inequalities (1.5) to establish existence and uniqueness criteria, and the convergence of Picard's, approximate Picard's, quasilinearization, and approximate quasilinearization iterative methods for the complementary Lidstone boundary value problem (1.1), (1.2). In Section 6, we will show the monotone convergence of Picard's iterative method. Since the proofs of most of the results in Sections 3–6 are similar to those of our previous work [1, 2] the details are omitted; however, through some simple examples it is shown how easily these results can be applied in practice.
2. Interpolating Polynomial
We begin with the following well-known results.
Lemma 2.1 (see [47]).
Let  Then,
Then,

where  is the Lidstone interpolating polynomial of degree
is the Lidstone interpolating polynomial of degree 

and  is the residue term
is the residue term

here


Recursively, it follows that

( is the Bernoulli polynomial of degree
is the Bernoulli polynomial of degree  and
and  is the
is the  th Bernoulli number
th Bernoulli number  ,
,  ;
;  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ).
).
Lemma 2.2 (see [47]).
The following hold:



( is the Euler polynomial of degree
is the Euler polynomial of degree  and
and  is the
is the  th Euler number
th Euler number  ,
,  ;
;  ,
,  ,
,  ,
,  )
)

Theorem 2.3.
Let  Then,
Then,

where  is the complementary Lidstone interpolating polynomial of degree
is the complementary Lidstone interpolating polynomial of degree 

and  is the residue term
is the residue term

here


Remark 2.4.
From (2.4) and (2.15) it is clear that  ;
;  ,
,  ;
; 
 ,
,  ;
;  ,
,  ;
;  ,
,  ;
;  ,
, 

Proof.
In (2.1), we let  and integrate both sides from
and integrate both sides from  to
to  to obtain
to obtain

Now, since

and, similarly

it follows that

Next since

for  from (2.7), we get
from (2.7), we get

and similarly, for  we have
we have

Finally, since (2.12) is exact for any polynomial of degree up to  we find
we find

and hence, for  it follows that
it follows that

Combining (2.23) and (2.25), we obtain

Theorem 2.5.
Let  Then, inequalities (1.5) hold with
Then, inequalities (1.5) hold with


.
Proof.
From (2.14) and (2.8) it follows that

Now, from (2.11) and (2.13), we find

However, from (2.9), we have

Thus, from  ,
,  ,
,  and
and  we obtain
we obtain

Using the above estimate in (2.29), the inequality (1.5) for  follows.
follows.
Next, from (2.11), (2.13) and (2.14), we have

and hence in view of (2.5) and (2.9) it follows that

and similarly, by (2.5) and (2.10), we get

Remark 2.6.
From (2.13), (2.28), and the above considerations it is clear that

Remark 2.7.
Inequality (1.5) with the constants  given in (2.27) is the best possible, as equalities hold for the function
given in (2.27) is the best possible, as equalities hold for the function  (polynomial of degree
(polynomial of degree  ) whose complementary Lidstone interpolating polynomial
) whose complementary Lidstone interpolating polynomial  and only for this function up to a constant factor.
and only for this function up to a constant factor.
Remark 2.8.
From the identity (see [47, equation (1.2.21)])

we have

and hence

We also have the estimate (see [47, equation (1.2.41)])

Thus, from (2.27), (2.38), and (2.39), we obtain

Therefore, it follows that

Combining (1.5) and (2.41), we get

Hence, if  for a fixed
for a fixed  as
as  ,
,  converges absolutely and uniformly to
converges absolutely and uniformly to  in
in  provided that there exists a constant
provided that there exists a constant  and an integer
and an integer  such that
such that  for all
for all  ,
, 
In particular, the function  ,
,  satisfies the above conditions. Thus, for each fixed
satisfies the above conditions. Thus, for each fixed  expansions
expansions


converge absolutely and uniformly in  provided
provided  For
For  (2.43) and (2.44), respectively, reduce to absurdities,
(2.43) and (2.44), respectively, reduce to absurdities,  and
and  Thus, the condition
Thus, the condition  is the best possible.
is the best possible.
Remark 2.9.
If  then
then


Thus, in view of  ,
,  we have
we have

Now, since  ,
,  ,
,  from (2.6), we find
from (2.6), we find

and hence by (2.15) it follows that

Using these relations in (2.47), we obtain an approximate quadrature formula

It is to be remarked that (2.50) is different from the Euler-MacLaurin formula, but the same as in [49] obtained by using different arguments. To find the error  in (2.50), from (2.28) and (2.46) we have
in (2.50), from (2.28) and (2.46) we have

Thus, it immediately follows that

From (2.52) it is clear that (2.50) is exact for any polynomial of degree at most  Further, in (2.52) equality holds for the function
Further, in (2.52) equality holds for the function  and only for this function up to a constant factor.
and only for this function up to a constant factor.
We will now present two examples to illustrate the importance of (2.50) and (2.52).
Example 2.10.
Consider integrating  over
over  Here,
Here,  ,
,  and
and  The exact value of the integral is
The exact value of the integral is

In Table 1, we list the approximates of the integral using (2.50) with different values of  the actual errors incurred, and the error bounds deduced from (2.52).
the actual errors incurred, and the error bounds deduced from (2.52).
Note that  hence the error
hence the error  when
when  or
or  Although the errors for other values of
Although the errors for other values of  are large, ultimately the approximates tend to the exact value as
are large, ultimately the approximates tend to the exact value as 
Example 2.11.
Consider integrating  over
over  Here,
Here,  ,
,  and
and  The exact value of the integral is
The exact value of the integral is

In Table 2, we list the approximates of the integral using (2.50) with different values of  the actual errors incurred, and the error bounds deduced from (2.52).
the actual errors incurred, and the error bounds deduced from (2.52).
Unlike Example 2.10, here the error decreases as  increases. In both examples, the approximates tend to the exact value as
increases. In both examples, the approximates tend to the exact value as  Of course, for increasing accuracy, instead of taking large values of
Of course, for increasing accuracy, instead of taking large values of  one must use composite form of formula (2.50).
one must use composite form of formula (2.50).
3. Existence and Uniqueness
The equalities and inequalities established in Section 2 will be used here to provide necessary and sufficient conditions for the existence and uniqueness of solutions of the complementary Lidstone boundary value problem (1.1), (1.2).
Theorem 3.1.
Suppose that  ,
,  are given real numbers and let
are given real numbers and let  be the maximum of
be the maximum of  on the compact set
on the compact set  where
where

Further, suppose that

then, the boundary value problem (1.1), (1.2) has a solution in 
Proof.
The set

is a closed convex subset of the Banach space  We define an operator
We define an operator  as follows:
as follows:

In view of Theorem 2.3 and (2.28) it is clear that any fixed point of (3.4) is a solution of the boundary value problem (1.1), (1.2). Let  Then, from (1.5), (3.2), and (3.4), we find
Then, from (1.5), (3.2), and (3.4), we find

Thus,  Inequalities (3.5) imply that the sets
Inequalities (3.5) imply that the sets  ,
,  are uniformly bounded and equicontinuous in
are uniformly bounded and equicontinuous in  Hence,
Hence,  that is compact follows from the Ascoli-Arzela theorem. The Schauder fixed point theorem is applicable and a fixed point of
that is compact follows from the Ascoli-Arzela theorem. The Schauder fixed point theorem is applicable and a fixed point of  in
in  exists.
exists.
Corollary 3.2.
Assume that the function  on
on  satisfies the following condition:
satisfies the following condition:

where  ,
,  are nonnegative constants, and
are nonnegative constants, and  ,
,  then, the boundary value problem (1.1), (1.2) has a solution.
then, the boundary value problem (1.1), (1.2) has a solution.
Theorem 3.3.
Suppose that the function  on
on  satisfies the following condition:
satisfies the following condition:

where



then, the boundary value problem (1.1), (1.2) has a solution in 
Theorem 3.4.
Suppose that the differential equation (1.1) together with the homogeneous boundary conditions

has a nontrivial solution  and the condition (3.7) with
and the condition (3.7) with  is satisfied on
is satisfied on  where
where

and  then, it is necessary that
then, it is necessary that 
Remark 3.5.
Conditions of Theorem 3.4 ensure that in (3.7) at least one of the  ,
,  will not be zero; otherwise the solution
will not be zero; otherwise the solution  will be a polynomial of degree at most
will be a polynomial of degree at most  and will not be a nontrivial solution of (1.1), (1.2). Further,
and will not be a nontrivial solution of (1.1), (1.2). Further,  is obviously a solution of (1.1), (1.2), and if
is obviously a solution of (1.1), (1.2), and if  then it is also unique.
then it is also unique.
Theorem 3.6.
Suppose that for all  the function
the function  satisfies the Lipschitz condition
satisfies the Lipschitz condition

where  then, the boundary value problem (1.1), (1.2) has a unique solution in
then, the boundary value problem (1.1), (1.2) has a unique solution in 
Example 3.7.
Consider the complementary Lidstone boundary value problem


where  is fixed. Here,
is fixed. Here,  and the interpolating polynomial satisfying (1.4) is computed as
and the interpolating polynomial satisfying (1.4) is computed as  with
with

We illustrate Theorem 3.1 by the following two cases.
Case 1.
Suppose  and
and  then, Theorem 3.1 states that (3.14), (3.15) has a solution in the set
then, Theorem 3.1 states that (3.14), (3.15) has a solution in the set  provided
provided

We will look for a constant  that satisfies (3.17). Since
that satisfies (3.17). Since

the condition  simplifies to
simplifies to  Coupled with another condition
Coupled with another condition  we see that
we see that  fulfills (3.17). Therefore, we conclude that the differential equation
fulfills (3.17). Therefore, we conclude that the differential equation

with the boundary conditions (3.15) has a solution in  where
where 
Case 2.
Suppose  and
and  then, Theorem 3.1 states that (3.14), (3.15) has a solution in the set
then, Theorem 3.1 states that (3.14), (3.15) has a solution in the set  ,
,  ,
,  provided
provided

Here

and the conditions  ,
,  reduce to
reduce to

Pick  ,
,  ,
,  which satisfy (3.22) and also
which satisfy (3.22) and also  ,
,  It follows from Theorem 3.1 that the differential equation
It follows from Theorem 3.1 that the differential equation

with the boundary conditions (3.15) has a solution in  ,
,  ,
, 
Example 3.8.
Consider the complementary Lidstone boundary value problem

with the boundary conditions (3.15). Here,  ,
,  and the interpolating polynomial
and the interpolating polynomial  satisfying (1.4) is given in Example 3.7. To illustrate Theorem 3.3, we note that for
satisfying (1.4) is given in Example 3.7. To illustrate Theorem 3.3, we note that for  and any
and any 

Thus, condition (3.7) is satisfied with  ,
,  ,
,  ,
,  The constants
The constants  and
and  are then computed as
are then computed as

By Theorem 3.3, problem (3.24), (3.15) has a solution in

4. Picard's and Approximate Picard's Methods
Picard's method of successive approximations has an important characteristic, namely, it is constructive; moreover, bounds of the difference between iterates and the solution are easily available. In this section, we will provide a priori as well as posteriori estimates on the Lipschitz constants so that Picard's iterative sequence  converges to the unique solution
converges to the unique solution  of the problem (1.1), (1.2).
of the problem (1.1), (1.2).
Definition 4.1.
A function  is called an approximate solution of (1.1), (1.2) if there exist nonnegative constants
is called an approximate solution of (1.1), (1.2) if there exist nonnegative constants  and
and  such that
such that


where  and
and  are polynomials of degree
are polynomials of degree  satisfying (1.2), and
satisfying (1.2), and

respectively.
Inequality (4.1) means that there exists a continuous function  such that
such that

Thus, from Theorem 2.3 the approximate solution  can be expressed as
can be expressed as

In what follows, we will consider the Banach space  and for
and for 

Theorem 4.2.
With respect to the boundary value problem (1.1), (1.2) one assumes that there exists an approximate solution  and
and
(i)the function  satisfies the Lipschitz condition (3.13) on
satisfies the Lipschitz condition (3.13) on  where
where

(ii)
Then, the following hold:
(1)there exists a solution  of (1.1), (1.2) in
of (1.1), (1.2) in 
(2) is the unique solution of (1.1), (1.2) in
is the unique solution of (1.1), (1.2) in 
(3)the Picard iterative sequence  defined by
defined by

where  converges to
converges to  with
with  and
and

-
(4)
for any
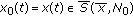 ,
, 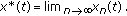
In Theorem 4.2 conclusion (3) ensures that the sequence  obtained from (4.8) converges to the solution
obtained from (4.8) converges to the solution  of the boundary value problem (1.1), (1.2). However, in practical evaluation this sequence is approximated by the computed sequence, say,
of the boundary value problem (1.1), (1.2). However, in practical evaluation this sequence is approximated by the computed sequence, say,  To find
To find  the function
the function  is approximated by
is approximated by  Therefore, the computed sequence
Therefore, the computed sequence  satisfies the recurrence relation
satisfies the recurrence relation

where 
With respect to  we will assume the following condition.
we will assume the following condition.
Condition C1.
For  obtained from (4.10), the following inequality holds:
obtained from (4.10), the following inequality holds:

where  is a nonnegative constant.
is a nonnegative constant.
Inequality (4.11) corresponds to the relative error in approximating the function  by
by  for the
for the  th iteration.
th iteration.
Theorem 4.3.
With respect to the boundary value problem (1.1), (1.2) one assumes that there exists an approximate solution  and Condition C1 is satisfied. Further, one assumes that
and Condition C1 is satisfied. Further, one assumes that
(i)condition (i) of Theorem 4.2,
(ii)
(iii) where
where 
then,
(1)all the conclusions (1)–(4) of Theorem 4.2 hold,
(2)the sequence  obtained from (4.10) remains in
obtained from (4.10) remains in 
(3)the sequence  converges to
converges to  the solution of (1.1), (1.2) if and only if
the solution of (1.1), (1.2) if and only if  where
where

and the following error estimate holds

In our next result we will assume the following.
Condition C2.
For  obtained from (4.10), the following inequality is satisfied:
obtained from (4.10), the following inequality is satisfied:

where  is a nonnegative constant.
is a nonnegative constant.
Inequality (4.14) corresponds to the absolute error in approximating the function  by
by  for the
for the  th iteration.
th iteration.
Theorem 4.4.
With respect to the boundary value problem (1.1), (1.2) one assumes that there exists an approximate solution  and Condition C2 is satisfied. Further, one assumes that
and Condition C2 is satisfied. Further, one assumes that
(i)condition (i) of Theorem 4.2,
(ii)
then,
(1)all the conclusions (1)–(4) of Theorem 4.2 hold,
(2)the sequence  obtained from (4.10) remains in
obtained from (4.10) remains in 
(3)the sequence  converges to
converges to  the solution of (1.1), (1.2) if and only if
the solution of (1.1), (1.2) if and only if  and the following error estimate holds:
and the following error estimate holds:

Example 4.5.
Consider the complementary Lidstone boundary value problem

with the boundary conditions (3.15). Pick  to be an approximate solution of (4.16), (3.15), that is, let
to be an approximate solution of (4.16), (3.15), that is, let  Then, from (4.2) we get
Then, from (4.2) we get  Further, from (4.1) we have
Further, from (4.1) we have

To illustrate Theorem 4.2, we note that the Lipschitz condition (3.13) is satisfied globally with  ,
,  ,
,  and the constants
and the constants  and
and  are computed directly as
are computed directly as

By Theorem 4.2, it follows that
(1)there exists a solution  of (4.16), (3.15) in
of (4.16), (3.15) in 
(2) is the unique solution of (4.16), (3.15) in
is the unique solution of (4.16), (3.15) in 
(3)the Picard iterative sequence  defined by
defined by

where  converges to
converges to  with
with

Suppose that we require the accuracy  then from above we just set
then from above we just set

to get  Thus,
Thus,  will fulfill the required accuracy.
will fulfill the required accuracy.
Finally, we will illustrate how to obtain  from (4.19). First, we integrate
from (4.19). First, we integrate

from  to
to  to get
to get

Next, integrating (4.23) from  to
to  as well as from
as well as from  to
to  respectively, gives
respectively, gives


Adding (4.24) and (4.25) yields  Now, integrate (4.24) (or (4.25)) from
Now, integrate (4.24) (or (4.25)) from  to
to  gives
gives

A similar method can be used to obtain  ,
, 
5. Quasilinearization and Approximate Quasilinearization
Newton's method when applied to differential equations has been labeled as quasilinearization. This quasilinear iterative scheme for (1.1), (1.2) is defined as


where  is an approximate solution of (1.1), (1.2).
is an approximate solution of (1.1), (1.2).
In the following results once again we will consider the Banach space  and for
and for  the norm
the norm  is as in (4.6).
is as in (4.6).
Theorem 5.1.
With respect to the boundary value problem (1.1), (1.2) one assumes that there exists an approximate solution  and
and
(i)the function  is continuously differentiable with respect to all
is continuously differentiable with respect to all  ,
,  on
on 
(ii)there exist nonnegative constants  ,
,  such that for all
such that for all 

(iii)the function  is continuous on
is continuous on  ,
,  and
and 
(iv)
Then, the following hold:
(1)the sequence  generated by the iterative scheme (5.1), (5.2) remains in
generated by the iterative scheme (5.1), (5.2) remains in 
(2)the sequence  converges to the unique solution
converges to the unique solution  of the boundary value problem (1.1), (1.2),
of the boundary value problem (1.1), (1.2),
(3)a bound on the error is given by

Theorem 5.2.
Let in Theorem 5.1 the function  Further, let
Further, let  be twice continuously differentiable with respect to all
be twice continuously differentiable with respect to all  ,
,  on
on  and
and

Then,

where  Thus, the convergence is quadratic if
Thus, the convergence is quadratic if

Conclusion (3) of Theorem 5.1 ensures that the sequence  generated from the scheme (5.1), (5.2) converges linearly to the unique solution
generated from the scheme (5.1), (5.2) converges linearly to the unique solution  of the boundary value problem (1.1), (1.2). Theorem 5.2 provides sufficient conditions for its quadratic convergence. However, in practical evaluation this sequence is approximated by the computed sequence, say,
of the boundary value problem (1.1), (1.2). Theorem 5.2 provides sufficient conditions for its quadratic convergence. However, in practical evaluation this sequence is approximated by the computed sequence, say,  which satisfies the recurrence relation
which satisfies the recurrence relation

where 
With respect to  we will assume the following condition.
we will assume the following condition.
Condition C3.

is continuously differentiable with respect to all  ,
,  on
on  with
with

and Condition C1 is satisfied.
Theorem 5.3.
With respect to the boundary value problem (1.1), (1.2) one assumes that there exists an approximate solution  and the Condition C3 is satisfied. Further, one assumes
and the Condition C3 is satisfied. Further, one assumes
(i)conditions (i) and (ii) of Theorem 5.1,
(ii)
(iii)
then,
(1)all conclusions (1)–(3) of Theorem 5.1 hold,
(2)the sequence  generated by the iterative scheme (5.8), remains in
generated by the iterative scheme (5.8), remains in 
(3)the sequence  converges to
converges to  the unique solution of (1.1), (1.2) if and only if
the unique solution of (1.1), (1.2) if and only if  and the following error estimate holds:
and the following error estimate holds:

Theorem 5.4.
Let the conditions of Theorem 5.3 be satisfied. Further, let  for all
for all  and
and  be twice continuously differentiable with respect to all
be twice continuously differentiable with respect to all  ,
,  on
on  and
and

Then,

where  is the same as in Theorem 5.2.
is the same as in Theorem 5.2.
Example 5.5.
Consider the complementary Lidstone boundary value problem

again with the boundary conditions (3.15). First, we will illustrate Theorem 5.1. Pick  and
and  (so
(so  ). Clearly,
). Clearly,  is continuously differentiable with respect to
is continuously differentiable with respect to  for all
for all  For
For  we have
we have

Thus,

Let  so that
so that  Next, from (4.1) we have
Next, from (4.1) we have  Also, from (4.2) we find
Also, from (4.2) we find

and so we take  Now,
Now,

yields  Coupled with
Coupled with  (so that
(so that  ), we should impose
), we should impose

The corresponding range of  will then be
will then be

The conditions of Theorem 5.1 are satisfied and so
(1)the sequence  generated by
generated by

where  remains in
remains in  that is,
that is, 
the sequence  converges to the unique solution
converges to the unique solution  of (5.13), (3.15) with
of (5.13), (3.15) with

Next, we will illustrate Theorem 5.2. For  we have
we have

Hence, we may take  From Theorem 5.2, we have
From Theorem 5.2, we have

The convergence is quadratic if

which is the same as

and is satisfied if  or
or  Combining with (5.18), we conclude that the convergence of the scheme (5.20) is quadratic if
Combining with (5.18), we conclude that the convergence of the scheme (5.20) is quadratic if

6. Monotone Convergence
It is well recognized that the method of upper and lower solutions, together with uniformly monotone convergent technique offers effective tools in proving and constructing multiple solutions of nonlinear problems. The upper and lower solutions generate an interval in a suitable partially ordered space, and serve as upper and lower bounds for solutions which can be improved by uniformly monotone convergent iterative procedures. Obviously, from the computational point of view monotone convergence has superiority over ordinary convergence. We will discuss this fruitful technique for the boundary value problem (1.1), (1.2) with 
Definition 6.1.
A function  is said to be a lower solution of (1.1), (1.2) with
is said to be a lower solution of (1.1), (1.2) with  provided
provided

Similarly, a function  is said to be an upper solution of (1.1), (1.2) with
is said to be an upper solution of (1.1), (1.2) with  if
if

Lemma 6.2.
Let  and
and  be lower and upper solutions of (1.1), (1.2) with
be lower and upper solutions of (1.1), (1.2) with  and let
and let  and
and  be the polynomials of degree
be the polynomials of degree  satisfying
satisfying

and

respectively. Then, for all  ,
,  ,
, 
Proof.
From (2.5), (2.6), and (2.8) it is clear that  ,
,  ,
,  and this in turn from (2.18) and (2.19) implies that
and this in turn from (2.18) and (2.19) implies that  ,
,  ,
,  ,
,  ,
,  Now, since
Now, since

it follows that

Similarly, we have  The proof of
The proof of  ,
,  is similar.
is similar.
In the following result for  we will consider the norm
we will consider the norm 
 and introduce a partial ordering
and introduce a partial ordering  as follows. For
as follows. For  we say that
we say that  if and only if
if and only if  and
and  for all
for all 
Theorem 6.3.
With respect to the boundary value problem (1.1), (1.2) with  one assumes that
one assumes that  is nondecreasing in
is nondecreasing in  and
and  Further, let there exist lower and upper solutions
Further, let there exist lower and upper solutions  such that
such that  Then, the sequences
Then, the sequences  where
where  and
and  are defined by the iterative schemes
are defined by the iterative schemes

are well defined, and  converges to an element
converges to an element  converges to an element
converges to an element  (with the convergence being in the norm of
(with the convergence being in the norm of  ). Further,
). Further,  ,
,  are solutions of (1.1), (1.2) with
are solutions of (1.1), (1.2) with  and each solution
and each solution  of this problem which is such that
of this problem which is such that  satisfies
satisfies 
Example 6.4.
Consider the complementary Lidstone boundary value problem

Here,  and the function
and the function  is nondecreasing in
is nondecreasing in  and
and  We find that (6.8) has a lower solution
We find that (6.8) has a lower solution

and an upper solution

such that

Hence,  and the conditions of Theorem 6.3 are satisfied. The iterative schemes
and the conditions of Theorem 6.3 are satisfied. The iterative schemes


will converge respectively to some  and
and  Moreover,
Moreover,

and  are solutions of (6.8). Any solution
are solutions of (6.8). Any solution  of (6.8) which is such that
of (6.8) which is such that  fulfills
fulfills  As an illustration, by direct computation (as in Example 4.5), we find
As an illustration, by direct computation (as in Example 4.5), we find

References
Agarwal RP: Boundary Value Problems for Higher Order Differential Equations. World Scientific, Teaneck, NJ, USA; 1986:xii+307.
Agarwal RP: Focal Boundary Value Problems for Differential and Difference Equations, Mathematics and Its Applications. Volume 436. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1998:x+289.
Lidstone GJ: Notes on the extension of Aitken's theorem (for polynomial interpolation) to the Everett types. Proceedings of the Edinburgh Mathematical Society 1929, 2: 16–19.
Boas RP Jr.: Representation of functions by Lidstone series. Duke Mathematical Journal 1943, 10: 239–245. 10.1215/S0012-7094-43-01021-X
Poritsky H: On certain polynomial and other approximations to analytic functions. Transactions of the American Mathematical Society 1932,34(2):274–331. 10.1090/S0002-9947-1932-1501639-4
Schoenberg IJ: On certain two-point expansions of integral functions of exponential type. Bulletin of the American Mathematical Society 1936,42(4):284–288. 10.1090/S0002-9904-1936-06293-2
Schoenberg IJ: Contributions to the problem of approximation of equidistant data by analytic functions—part A. Quarterly of Applied Mathematics 1946, 4: 45–99.
Schoenberg IJ: Contributions to the problem of approximation of equidistant data by analytic functions—part B. Quarterly of Applied Mathematics 1946, 4: 112–141.
Whittaker JM: On Lidstone's series and two-point expansions of analytic functions. Proceedings of the London Mathematical Society 1934,36(1):451–469. 10.1112/plms/s2-36.1.451
Whittaker JM: Interpolatory Function Theory. Cambridge University Press, Cambridge, UK; 1935.
Widder DV: Functions whose even derivatives have a prescribed sign. Proceedings of the National Academy of Sciences of the United States of America 1940, 26: 657–659. 10.1073/pnas.26.11.657
Widder DV: Completely convex functions and Lidstone series. Transactions of the American Mathematical Society 1942, 51: 387–398.
Agarwal RP, Akrivis G: Boundary value problems occurring in plate deflection theory. Journal of Computational and Applied Mathematics 1982,8(3):145–154. 10.1016/0771-050X(82)90035-3
Agarwal RP, Wong PJY: Lidstone polynomials and boundary value problems. Computers & Mathematics with Applications 1989,17(10):1397–1421. 10.1016/0898-1221(89)90023-0
Agarwal RP, Wong PJY: Quasilinearization and approximate quasilinearization for Lidstone boundary value problems. International Journal of Computer Mathematics 1992,42(1–2):99–116. 10.1080/00207169208804054
Agarwal RP, O'Regan D, Wong PJY: Positive Solutions of Differential, Difference and Integral Equations. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1999:xii+417.
Agarwal RP, O'Regan D: Lidstone continuous and discrete boundary value problems. Memoirs on Differential Equations and Mathematical Physics 2000, 19: 107–125.
Agarwal RP, O'Regan D, Staněk S: Singular Lidstone boundary value problem with given maximal values for solutions. Nonlinear Analysis: Theory, Methods & Applications 2003,55(7–8):859–881. 10.1016/j.na.2003.06.001
Avery RI, Davis JM, Henderson J: Three symmetric positive solutions for Lidstone problems by a generalization of the Leggett-Williams theorem. Electronic Journal of Differential Equations 2000,2000(40):1–15.
Bai Z, Ge W: Solutions of 2
 th Lidstone boundary value problems and dependence on higher order derivatives. Journal of Mathematical Analysis and Applications 2003,279(2):442–450. 10.1016/S0022-247X(03)00011-8
th Lidstone boundary value problems and dependence on higher order derivatives. Journal of Mathematical Analysis and Applications 2003,279(2):442–450. 10.1016/S0022-247X(03)00011-8Baldwin P: Asymptotic estimates of the eigenvalues of a sixth-order boundary-value problem obtained by using global phase-integral methods. Philosophical Transactions of the Royal Society of London. Series A 1987,322(1566):281–305. 10.1098/rsta.1987.0051
Baldwin P: Localised instability in a Bénard layer. Applicable Analysis 1987,24(1–2):117–156. 10.1080/00036818708839658
Boutayeb A, Twizell EH: Finite-difference methods for twelfth-order boundary-value problems. Journal of Computational and Applied Mathematics 1991,35(1–3):133–138.
Chyan CJ, Henderson J: Positive solutions of 2
 th-order boundary value problems. Applied Mathematics Letters 2002,15(6):767–774. 10.1016/S0893-9659(02)00040-X
th-order boundary value problems. Applied Mathematics Letters 2002,15(6):767–774. 10.1016/S0893-9659(02)00040-XDavis JM, Eloe PW, Henderson J: Triple positive solutions and dependence on higher order derivatives. Journal of Mathematical Analysis and Applications 1999,237(2):710–720. 10.1006/jmaa.1999.6500
Davis JM, Henderson J, Wong PJY: General Lidstone problems: multiplicity and symmetry of solutions. Journal of Mathematical Analysis and Applications 2000,251(2):527–548. 10.1006/jmaa.2000.7028
Eloe PW, Henderson J, Thompson HB: Extremal points for impulsive Lidstone boundary value problems. Mathematical and Computer Modelling 2000,32(5–6):687–698. 10.1016/S0895-7177(00)00165-5
Eloe PW, Islam MN: Monotone methods and fourth order Lidstone boundary value problems with impulse effects. Communications in Applied Analysis 2001,5(1):113–120.
Forster P: Existenzaussagen und Fehlerabschätzungen bei gewissen nichtlinearen Randwertaufgaben mit gewöhnlichen Differentialgleichungen. Numerische Mathematik 1967, 10: 410–422. 10.1007/BF02162874
Graef JR, Qian C, Yang B: Multiple symmetric positive solutions of a class of boundary value problems for higher order ordinary differential equations. Proceedings of the American Mathematical Society 2003,131(2):577–585. 10.1090/S0002-9939-02-06579-6
Guo Y, Ge W: Twin positive symmetric solutions for Lidstone boundary value problems. Taiwanese Journal of Mathematics 2004,8(2):271–283.
Guo Y, Gao Y: The method of upper and lower solutions for a Lidstone boundary value problem. Czechoslovak Mathematical Journal 2005,55(3):639–652. 10.1007/s10587-005-0051-8
Kiguradze T: On Lidstone boundary value problem for higher order nonlinear hyperbolic equations with two independent variables. Memoirs on Differential Equations and Mathematical Physics 2005, 36: 153–156.
Liu Y, Ge W: Positive solutions of boundary-value problems for 2
 -order differential equations. Electronic Journal of Differential Equations 2003,2003(89):1–12.
-order differential equations. Electronic Journal of Differential Equations 2003,2003(89):1–12.Liu Y, Ge W: Solutions of Lidstone BVPs for higher-order impulsive differential equations. Nonlinear Analysis: Theory, Methods & Applications 2005,61(1–2):191–209. 10.1016/j.na.2004.12.004
Ma Y: Existence of positive solutions of Lidstone boundary value problems. Journal of Mathematical Analysis and Applications 2006,314(1):97–108. 10.1016/j.jmaa.2005.03.059
Palamides PK: Positive solutions for higher-order Lidstone boundary value problems. A new approach via Sperner's lemma. Computers & Mathematics with Applications 2001,42(1–2):75–89. 10.1016/S0898-1221(01)00132-8
Twizell EH, Boutayeb A: Numerical methods for the solution of special and general sixth-order boundary value problems, with applications to Bénard layer eigenvalue problems. Proceedings of the Royal Society of London. Series A 1990,431(1883):433–450. 10.1098/rspa.1990.0142
Wang Y-M: Higher-order Lidstone boundary value problems for elliptic partial differential equations. Journal of Mathematical Analysis and Applications 2005,308(1):314–333. 10.1016/j.jmaa.2005.01.019
Wang Y-M: On 2
 th-order Lidstone boundary value problems. Journal of Mathematical Analysis and Applications 2005,312(2):383–400. 10.1016/j.jmaa.2005.03.039
th-order Lidstone boundary value problems. Journal of Mathematical Analysis and Applications 2005,312(2):383–400. 10.1016/j.jmaa.2005.03.039Wang Y-M, Jiang H-Y, Agarwal RP: A fourth-order compact finite difference method for higher-order Lidstone boundary value problems. Computers and Mathematics with Applications 2008,56(2):499–521. 10.1016/j.camwa.2007.04.051
Wei Z: Existence of positive solutions for 2
 th-order singular sublinear boundary value problems. Journal of Mathematical Analysis and Applications 2005,306(2):619–636. 10.1016/j.jmaa.2004.10.037
th-order singular sublinear boundary value problems. Journal of Mathematical Analysis and Applications 2005,306(2):619–636. 10.1016/j.jmaa.2004.10.037Yao Q: Monotone iterative technique and positive solutions of Lidstone boundary value problems. Applied Mathematics and Computation 2003,138(1):1–9. 10.1016/S0096-3003(01)00316-2
Zhang B, Liu X: Existence of multiple symmetric positive solutions of higher order Lidstone problems. Journal of Mathematical Analysis and Applications 2003,284(2):672–689. 10.1016/S0022-247X(03)00386-X
Zhao Z: On the existence of positive solutions for 2
 -order singular boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2006,64(11):2553–2561. 10.1016/j.na.2005.09.003
-order singular boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2006,64(11):2553–2561. 10.1016/j.na.2005.09.003Agarwal RP: Sharp inequalities in polynomial interpolation. In General Inequalities 6, International Series of Numerical Mathematics. Volume 103. Edited by: Walter W. Birkhäuser, Basel, Switzerland; 1992:73–92.
Agarwal RP, Wong PJY: Error Inequalities in Polynomial Interpolation and Their Applications. Kluwer Academic Publishers, Dodrecht, The Netherlands; 1993.
Agarwal RP, Wong PJY: Error bounds for the derivatives of Lidstone interpolation and applications. In Approximation Theory. In memory of A. K. Varma, Monogr. Textbooks Pure Appl. Math.. Volume 212. Edited by: Govil NKet al.. Marcel Dekker, New York, NY, USA; 1998:1–41.
Costabile FA, Dell'Accio F, Luceri R: Explicit polynomial expansions of regular real functions by means of even order Bernoulli polynomials and boundary values. Journal of Computational and Applied Mathematics 2005,176(1):77–90. 10.1016/j.cam.2004.07.004
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Agarwal, R.P., Pinelas, S. & Wong, P.J.Y. Complementary Lidstone Interpolation and Boundary Value Problems. J Inequal Appl 2009, 624631 (2009). https://doi.org/10.1155/2009/624631
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/624631





 ,
, 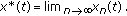
 th Lidstone boundary value problems and dependence on higher order derivatives. Journal of Mathematical Analysis and Applications 2003,279(2):442–450. 10.1016/S0022-247X(03)00011-8
th Lidstone boundary value problems and dependence on higher order derivatives. Journal of Mathematical Analysis and Applications 2003,279(2):442–450. 10.1016/S0022-247X(03)00011-8 th-order boundary value problems. Applied Mathematics Letters 2002,15(6):767–774. 10.1016/S0893-9659(02)00040-X
th-order boundary value problems. Applied Mathematics Letters 2002,15(6):767–774. 10.1016/S0893-9659(02)00040-X -order differential equations. Electronic Journal of Differential Equations 2003,2003(89):1–12.
-order differential equations. Electronic Journal of Differential Equations 2003,2003(89):1–12. th-order Lidstone boundary value problems. Journal of Mathematical Analysis and Applications 2005,312(2):383–400. 10.1016/j.jmaa.2005.03.039
th-order Lidstone boundary value problems. Journal of Mathematical Analysis and Applications 2005,312(2):383–400. 10.1016/j.jmaa.2005.03.039 th-order singular sublinear boundary value problems. Journal of Mathematical Analysis and Applications 2005,306(2):619–636. 10.1016/j.jmaa.2004.10.037
th-order singular sublinear boundary value problems. Journal of Mathematical Analysis and Applications 2005,306(2):619–636. 10.1016/j.jmaa.2004.10.037 -order singular boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2006,64(11):2553–2561. 10.1016/j.na.2005.09.003
-order singular boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2006,64(11):2553–2561. 10.1016/j.na.2005.09.003