Abstract
This paper considers a broadcast system in which a single transmitter sends a common message and (independent) particular messages to  receivers over
receivers over  unmatched parallel scalar Gaussian subchannels. For this system the set of all rate tuples that can be achieved via superposition coding and Gaussian signalling (SPCGS) can be parameterized by a set of power loads and partitions, and the boundary of this set can be expressed as the solution of an optimization problem. Although that problem is not convex in the general case, it will be shown that it can be used to obtain tight and efficiently computable inner and outer bounds on the SPCGS rate region. The development of these bounds relies on approximating the original optimization problem by a (convex) Geometric Program (GP), and in addition to generating the bounds, the GP also generates the corresponding power loads and partitions. There are special cases of the general problem that can be precisely formulated in a convex form. In this paper, explicit convex formulations are given for three such cases, namely, the case of 2 users, the case in which only particular messages are transmitted (in both of which the SPCGS rate region is the capacity region), and the case in which only the SPCGS sum rate is to be maximized.
unmatched parallel scalar Gaussian subchannels. For this system the set of all rate tuples that can be achieved via superposition coding and Gaussian signalling (SPCGS) can be parameterized by a set of power loads and partitions, and the boundary of this set can be expressed as the solution of an optimization problem. Although that problem is not convex in the general case, it will be shown that it can be used to obtain tight and efficiently computable inner and outer bounds on the SPCGS rate region. The development of these bounds relies on approximating the original optimization problem by a (convex) Geometric Program (GP), and in addition to generating the bounds, the GP also generates the corresponding power loads and partitions. There are special cases of the general problem that can be precisely formulated in a convex form. In this paper, explicit convex formulations are given for three such cases, namely, the case of 2 users, the case in which only particular messages are transmitted (in both of which the SPCGS rate region is the capacity region), and the case in which only the SPCGS sum rate is to be maximized.
Similar content being viewed by others
1. Introduction
Consider a broadcast communication scenario in which a single transmitter wishes to send a combination of (independent) particular messages that are intended for individual users and a common message that is intended for all users [1]. Such broadcast systems can be classified according to the probabilistic model that describes the communication channels between the transmitter and the receivers. A special class of broadcast channels is the class of degraded channels, in which the probabilistic model is such that the signals received by the users form a Markov chain. Using this Markovian property, a coding scheme that can attain every point in the capacity region for this class of channels was developed in [2]. If, however, the received signals do not form a Markov chain, the broadcast channel is said to be nondegraded, and the coding scheme developed in [2] does not apply directly to this case. Although degraded channels are useful in modelling single-input single-output broadcast systems, many practical systems give rise to nondegraded channels, including those that employ multicarrier transmission [3], and the class of multiple-input multiple-output (MIMO) systems [4].
Most of the studies on nondegraded broadcast channels have focused on scenarios in which only particular messages are sent to the users [5, 6], and, of late, particular emphasis has been placed on Gaussian MIMO broadcast channels [4, 7–12]. For that class of channels, it has been shown that dirty paper coding [13] with Gaussian signalling can achieve every point in the capacity region [4]. For general nondegraded systems with common information, single-letter characterizations of achievable inner bounds were obtained in [14, 15], and a single-letter characterization of an outer bound was obtained in [16].
In this paper, we will focus on a class of nondegraded broadcast channels that arises in multicarrier transmission schemes; for example, [3, 17]. In particular, we consider systems in which a common message and particular messages are to be broadcast to  users over
users over  parallel scalar Gaussian subchannels. In such a system, each component subchannel is a degraded broadcast channel, but the overall broadcast channel is not degraded in the general case, because the ordering of the users in the Markov chain on each subchannel may be different. When that is the case, the subchannels are said to be unmatched [17]. As discussed below, the development of coding schemes for some related multicarrier broadcast systems has exploited the degraded nature of each subchannel, and we will do so in the proposed scheme.
parallel scalar Gaussian subchannels. In such a system, each component subchannel is a degraded broadcast channel, but the overall broadcast channel is not degraded in the general case, because the ordering of the users in the Markov chain on each subchannel may be different. When that is the case, the subchannels are said to be unmatched [17]. As discussed below, the development of coding schemes for some related multicarrier broadcast systems has exploited the degraded nature of each subchannel, and we will do so in the proposed scheme.
For degraded broadcast channels superposition coding is an optimal coding scheme [18, 19], and, in fact, superposition coding can be shown to be equivalent to dirty paper coding for degraded broadcast channels [10]. The superposition coding scheme divides the transmission power into partitions, and each partition is used to encode an incremental message that can be decoded by any user that observes the signal at, or above, a certain level of degradation, but cannot be decoded by weaker users. Since each component subchannel of the parallel scalar Gaussian channel model is degraded, superposition coding is optimal for each subchannel, and this observation was used in [17] to characterize the capacity region of the unmatched 2-user 2-subchannel scenario with both particular messages and a common message. For that case, a rather complicated method for obtaining optimal power allocations was provided in [20]. For the case in which only particular messages are transmitted to the users, the capacity region for the unmatched  -user
-user  -subchannel case was characterized in [21], and methods for obtaining the optimal power allocations for that case were provided in [21–23].
-subchannel case was characterized in [21], and methods for obtaining the optimal power allocations for that case were provided in [21–23].
In this paper, we consider a broadcast system with  (unmatched) Gaussian subchannels and
(unmatched) Gaussian subchannels and  users in which both a common message and particular messages are transmitted to the users. For this system we provide a characterization of the rate region that can be achieved using superposition coding and Gaussian signalling. For convenience, this region will be referred to as the SPCGS rate region. This characterization encompasses as special cases the characterization of the capacity region of the 2-user 2-subchannel scenario [17], and the characterization of the capacity region of the
users in which both a common message and particular messages are transmitted to the users. For this system we provide a characterization of the rate region that can be achieved using superposition coding and Gaussian signalling. For convenience, this region will be referred to as the SPCGS rate region. This characterization encompasses as special cases the characterization of the capacity region of the 2-user 2-subchannel scenario [17], and the characterization of the capacity region of the  -user
-user  -subchannel scenario with particular messaging only [21].
-subchannel scenario with particular messaging only [21].
Using the characterization developed herein, we express the boundary points of the SPCGS rate region as the solution of an optimization problem. Although that optimization problem is not convex in the general case, we use convex optimization tools to provide efficiently computable inner and outer bounds on the SPCGS region. In particular, we employ (convex) Geometric Programming (GP) techniques [24, 25] to efficiently compute these bounds, and to generate the corresponding power loads and partitions. In addition to the inner and outer bounds for the general case, we will develop (precise) convex formulations for the optimal power allocations in two special cases for which the capacity region is known; namely, the 2-user case with common information [17], and the case in which only particular messages are broadcast to  users [21]. (Concurrent with our early work on this topic [26], geometric programming was used in [23] to find the optimal power allocation for the case of particular messaging.) In contrast to the methods proposed in [20, 21], which are based on a search for Lagrange multipliers, our formulations for the optimal power allocation for these two problems are in the form of a geometric program, and hence are amenable to efficient numerical optimization techniques. In addition, we will provide a (precise) convex formulation for the problem of maximizing the SPCGS sum rate in the general
users [21]. (Concurrent with our early work on this topic [26], geometric programming was used in [23] to find the optimal power allocation for the case of particular messaging.) In contrast to the methods proposed in [20, 21], which are based on a search for Lagrange multipliers, our formulations for the optimal power allocation for these two problems are in the form of a geometric program, and hence are amenable to efficient numerical optimization techniques. In addition, we will provide a (precise) convex formulation for the problem of maximizing the SPCGS sum rate in the general  -user
-user  -subchannel case.
-subchannel case.
2. The Superposition Coding and Gaussian Signalling (SPCGS) Rate Region
We consider a broadcast channel with  users and
users and  unmatched parallel degraded Gaussian subchannels, which is a common model for multicarrier transmission schemes; for example, [3]. We will find it convenient to parameterize this model by normalizing the subchannel gains for each user to 1, and scaling the corresponding noise power by the inverse of the squared modulus of the gain. (The scaled noise power will be referred to as the "equivalent noise variance''.) Since the ordering of the users' noise powers is not necessarily the same on each subchannel, the overall broadcast channel is not degraded in the general case. This situation is depicted in Figure 1, in which the signal transmitted on the
unmatched parallel degraded Gaussian subchannels, which is a common model for multicarrier transmission schemes; for example, [3]. We will find it convenient to parameterize this model by normalizing the subchannel gains for each user to 1, and scaling the corresponding noise power by the inverse of the squared modulus of the gain. (The scaled noise power will be referred to as the "equivalent noise variance''.) Since the ordering of the users' noise powers is not necessarily the same on each subchannel, the overall broadcast channel is not degraded in the general case. This situation is depicted in Figure 1, in which the signal transmitted on the  th subchannel is denoted by
th subchannel is denoted by  , the signal received by User
, the signal received by User  on the
on the  th subchannel is denoted by
th subchannel is denoted by  , and the (equivalent) noise variance on the
, and the (equivalent) noise variance on the  th subchannel at the
th subchannel at the  th degradation level by
th degradation level by  . The signal
. The signal  is the auxiliary signal on the
is the auxiliary signal on the  th subchannel that corresponds to the
th subchannel that corresponds to the  th degradation level. The role of these auxiliary signals will become clear as we discuss the achievability of the superposition coding rate region.
th degradation level. The role of these auxiliary signals will become clear as we discuss the achievability of the superposition coding rate region.
To simplify the description of that characterization, we first establish some notation. Let  denote the level of degradation of User
denote the level of degradation of User  on the
on the  th subchannel. Using this notation, if the received signal of User
th subchannel. Using this notation, if the received signal of User  ,
,  , is the strongest signal on the
, is the strongest signal on the  th subchannel then
th subchannel then  , and if the received signal of User
, and if the received signal of User  ,
,  , is the weakest signal on this subchannel, then
, is the weakest signal on this subchannel, then  . Let the power assigned to the
. Let the power assigned to the  th subchannel be denoted by
th subchannel be denoted by  , where
, where  , and
, and  is the total power budget. Furthermore, denote the power partitions on the
is the total power budget. Furthermore, denote the power partitions on the  th subchannel by
th subchannel by  , where
, where  . Using these partitions, the power assigned to each auxiliary signal
. Using these partitions, the power assigned to each auxiliary signal  in Figure 1 is given by
in Figure 1 is given by  , where
, where  corresponds to the partition on the
corresponds to the partition on the  th subchannel at the
th subchannel at the  th degradation level. As mentioned above, we will denote the equivalent noise variance on the
th degradation level. As mentioned above, we will denote the equivalent noise variance on the  th subchannel at the
th subchannel at the  th level of degradation by
th level of degradation by  , and hence
, and hence  . We will also use the standard notation
. We will also use the standard notation  to denote
to denote  .
.
We will use  to denote the rate of the common message to all users, and
to denote the rate of the common message to all users, and  to denote the rate of the particular message to User
to denote the rate of the particular message to User  . (For simplicity, we will use the natural logarithm throughout this paper, and hence rates are measured in nats per (real) channel use.) Using these notations, we can now express the rate that is achievable via superposition coding and Gaussian signalling (SPCGS) for a broadcast system with
. (For simplicity, we will use the natural logarithm throughout this paper, and hence rates are measured in nats per (real) channel use.) Using these notations, we can now express the rate that is achievable via superposition coding and Gaussian signalling (SPCGS) for a broadcast system with  users and
users and  parallel Gaussian subchannels. This is a generalization of the characterization in [17] for the system with
parallel Gaussian subchannels. This is a generalization of the characterization in [17] for the system with  .
.
Proposition 1.
Let  denote a power allocation, and let
denote a power allocation, and let  denote a set of power partitions. Let
denote a set of power partitions. Let  be the set of rate vectors that satisfy
be the set of rate vectors that satisfy



Then the set of all rate vectors  that are achievable using superposition coding and Gaussian signalling over the
that are achievable using superposition coding and Gaussian signalling over the  parallel scalar Gaussian subchannels depicted in Figure 1 is given by
parallel scalar Gaussian subchannels depicted in Figure 1 is given by

where


Proof.
For a given power allocation  and a given set of power partitions
and a given set of power partitions  the region bounded by the constraints in (1a)–(1c) is the region of rates achievable by superposition coding and Gaussian signalling (SPCGS). To show that, we first observe that each subchannel is a degraded broadcast channel. On subchannel
the region bounded by the constraints in (1a)–(1c) is the region of rates achievable by superposition coding and Gaussian signalling (SPCGS). To show that, we first observe that each subchannel is a degraded broadcast channel. On subchannel  , a composite signal of power
, a composite signal of power  is transmitted, and this signal is synthesized from Gaussian component signals that are superimposed on each other using the power partitions
is transmitted, and this signal is synthesized from Gaussian component signals that are superimposed on each other using the power partitions  . The rates that can be achieved by that scheme on subchanel
. The rates that can be achieved by that scheme on subchanel  are well known; see, for example, [27]. The rate region in (1a)–(1c) is then obtained by using the
are well known; see, for example, [27]. The rate region in (1a)–(1c) is then obtained by using the  th power partitions to (jointly) encode the common message across the
th power partitions to (jointly) encode the common message across the  subchannels, and the other partitions to encode the particular messages. The SPCGS achievable region is then the union of all such regions over all power allocations satisfying the power constraint and all valid power partitions.
subchannels, and the other partitions to encode the particular messages. The SPCGS achievable region is then the union of all such regions over all power allocations satisfying the power constraint and all valid power partitions.
More details regarding the way in which the Gaussian signals are constructed are provided in the following remark.
Remark 1.
Assume that the values of  and
and  are fixed and that these values satisfy (3) and (4), respectively. In the following remarks, we refer to the signals illustrated in Figure 1.
are fixed and that these values satisfy (3) and (4), respectively. In the following remarks, we refer to the signals illustrated in Figure 1.
-
(i)
For subchannel
 , and degradation level
, and degradation level 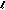 ,
, 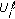 is an auxiliary Gaussian signal that is constructed by superimposing an incremental Gaussian signal on
is an auxiliary Gaussian signal that is constructed by superimposing an incremental Gaussian signal on 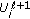 . Being Gaussian and independent of the noise, this incremental signal contributes additively to the total noise plus interference power observed by any user attempting to decode the signal
. Being Gaussian and independent of the noise, this incremental signal contributes additively to the total noise plus interference power observed by any user attempting to decode the signal 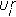 with
with  [2].
[2]. -
(ii)
The common message to all users is encoded using a single Gaussian codebook, and this message is embedded in the signals
 . The power assigned to these signals is
. The power assigned to these signals is 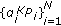 , and the aggregate mutual information that User
, and the aggregate mutual information that User  gathers about these signals is
gathers about these signals is  . For User
. For User  to be able to decode the common message, the rate of this message must be less than the aggregate mutual information, and conversely, all users whose aggregate mutual information is greater than this rate will be able to be reliably decodable the common message. Hence, for the common message to reliably decodable by all users, the rate at which this message is transmitted must be less than the aggregate information of the weakest user. Therefore, the rate of the common message is limited by the constraint in (1a).
to be able to decode the common message, the rate of this message must be less than the aggregate mutual information, and conversely, all users whose aggregate mutual information is greater than this rate will be able to be reliably decodable the common message. Hence, for the common message to reliably decodable by all users, the rate at which this message is transmitted must be less than the aggregate information of the weakest user. Therefore, the rate of the common message is limited by the constraint in (1a). -
(iii)
The particular and common messages that are intended for any User
 are embedded in the signals
are embedded in the signals  . The respective powers of these signals are
. The respective powers of these signals are 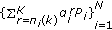 . For these messages to be reliably decodable, the sum of the rates of these messages must be less than the aggregate mutual information that this user gathers about
. For these messages to be reliably decodable, the sum of the rates of these messages must be less than the aggregate mutual information that this user gathers about  . This leads to the set of constraints in (1b).
. This leads to the set of constraints in (1b). -
(iv)
Consider a specific user, say User
 , in the subset of
, in the subset of 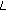 users
users  . As in (1b), the sum of the rates of the messages that are intended for User
. As in (1b), the sum of the rates of the messages that are intended for User  is bounded by
is bounded by 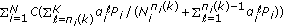 ; compare with the first term in (1c). On the
; compare with the first term in (1c). On the  th subchannel, the degradation level of User
th subchannel, the degradation level of User 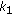 is
is 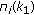 . Now if the sum of the rates intended for User
. Now if the sum of the rates intended for User  is such that the
is such that the  th term in the summation in (1b) is satisfied with equality, the other users in the subset
th term in the summation in (1b) is satisfied with equality, the other users in the subset  whose degradation level is above that of User
whose degradation level is above that of User  (i.e., their degradation level is less than
(i.e., their degradation level is less than 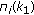 ) can still reliably decode messages that are embedded in
) can still reliably decode messages that are embedded in 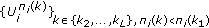 . Hence, the sum of the rates of these messages that can be achieved by superposition coding and Gaussian signalling is bounded by the second term in (1c). This holds for all permutations of users, that is, for all choices of
. Hence, the sum of the rates of these messages that can be achieved by superposition coding and Gaussian signalling is bounded by the second term in (1c). This holds for all permutations of users, that is, for all choices of  in
in  .
.
Before proceeding to particular instances of Proposition 1, we make the following remark regarding the number of inequalities required to characterize the SPCGS rate region of a general broadcast channel with  parallel Gaussian scalar subchannels and
parallel Gaussian scalar subchannels and  users.
users.
Remark 2.
In the general case, the number of inequalities that are required to characterize the  -dimensional SPCGS rate region in Proposition 1 is independent of the number of subchannels and is given by
-dimensional SPCGS rate region in Proposition 1 is independent of the number of subchannels and is given by

where the first term is the number of inequalities that are required to account for the achievable rate of the common message, and the second and third terms are the maximum number of inequalities that are required toaccount for partial sums of the achievable rates of the particular messages in the presence of a common message.
In contrast with the exponential number of inequalities in (5), the number of inequalities that are required to characterize the capacity region when no common message is transmitted is equal to  [21].
[21].
Although Proposition 1 provides a unified framework that allows us to describe the set of rates that can be achieved by superposition coding and Gaussian signalling for an arbitrary set of degradation orderings of the users on each subchannel, for some orderings some of the bounds given in Proposition 1 will be redundant, and significantly simpler expressions can be obtained by removing this redundancy. For example, for the 2-user 2-subchannel case, for which the SPCGS rate region is the capacity region [17, 28], direct substitution in Proposition 1 and simple manipulation of the resulting inequalities shows that for matched subchannels, the description of the region in Proposition 1 can be reduced to the two inequalities in [28]. For unmatched subchannels, the description in Proposition 1 yields the six inequalities in [17, Theorem 2].
That Proposition 1 coincides with [17, Theorem 2] in the special case of 2 subchannels and 2 users is not surprising because the underlying principles used in the derivation of these results are similar. However, in order to demonstrate some of the difficulties that arise in generalizing from 2-user to  -user scenarios, we now discuss a slightly more complicated example than the 2-user 2-subchannel one, namely, the 3-user 2-subchannel scenario depicted in Figure 2. For this situation we have
-user scenarios, we now discuss a slightly more complicated example than the 2-user 2-subchannel one, namely, the 3-user 2-subchannel scenario depicted in Figure 2. For this situation we have  and
and  . By substituting these values of
. By substituting these values of  and
and  into Proposition 1, we obtain the following corollary.
into Proposition 1, we obtain the following corollary.
Corollary 1 ( ).
).
Let  denote a power allocation, and let
denote a power allocation, and let  denote a set of power partitions. Let
denote a set of power partitions. Let  be the set of rate vectors that satisfy
be the set of rate vectors that satisfy













Then the set of all rate vectors  that are achievable using superposition coding and Gaussian signalling over the
that are achievable using superposition coding and Gaussian signalling over the  parallel scalar Gaussian subchannels depicted in Figure 2 is given by
parallel scalar Gaussian subchannels depicted in Figure 2 is given by

where

By examining the constraints in Corollary 1, it can be seen that for the scenario in Figure 2, the constraints in (6g) and (6h) are redundant. In order to see that, we note that because  , the right-hand side (RHS) of (6l) is less than or equal to the RHS of (6g), and for any
, the right-hand side (RHS) of (6l) is less than or equal to the RHS of (6g), and for any  , the left-hand side (LHS) of (6l) is greater than the LHS of (6g). Hence, the constraint in (6l) is tighter than that in (6g). In a similar way, one can show that (6n) is tighter than the constraint in (6h), whence the redundancy of (6h).
, the left-hand side (LHS) of (6l) is greater than the LHS of (6g). Hence, the constraint in (6l) is tighter than that in (6g). In a similar way, one can show that (6n) is tighter than the constraint in (6h), whence the redundancy of (6h).
Remark 3.
In order to assist in the interpretation of Corollary 1, we now identify the role of each signal.
-
(i)
The signal
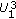 contains common information for all users, and particular information for User 3.
contains common information for all users, and particular information for User 3. -
(ii)
For a fixed value of
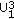 , the signal
, the signal  contains particular information for User 2.
contains particular information for User 2. -
(iii)
For a fixed value of
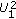 , the signal
, the signal 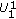 contains particular information for User 1.
contains particular information for User 1. -
(iv)
The signal
 contains common information for all users, and particular information for User 1.
contains common information for all users, and particular information for User 1. -
(v)
For a fixed value of
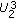 , the signal
, the signal  contains particular information for User 2.
contains particular information for User 2. -
(vi)
For a fixed value of
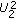 , the signal
, the signal  contains particular information for User 3.
contains particular information for User 3.Note that, as pointed out in Remark 1, to achieve an arbitrary rate vector within the SPCGS region, the common message must be encoded and decoded jointly across the subchannels, whereas the particular messages may be encoded using independent codebooks on each subchanne.
3. Power Loads and Partitions via Geometric Programming
In Proposition 1 we have provided a set of inequalities that characterize the SPCGS region. These inequalities are expressed in terms of the power loads  and the power partitions
and the power partitions  . In order to achieve particular points on the boundary of this region, one can determine the power loads and partitions that maximize the weighted sum rate for any given weight vector. However, as shown in (5) and the discussion thereafter, the number of constraints that characterize the rate region of multicarrier broadcast channels with common information grows very rapidly with the number of users. Since it appears to be unlikely that a closed-form solution for the power allocation problem can be obtained, it is desirable to develop an efficient numerical technique to determine the optimal power loads and partitions. Towards that end, in this section, we formulate the problem of finding the SPCGS rate region as an optimization problem. Unfortunately, this formulation is not convex. However, we will provide two alternative formulations that will be used in Section 4 to obtain convex formulations for tight inner and outer bounds on the SPCGS region along with the corresponding power allocations. In addition, in Section 5, we will use these formulations to provide precise convex formulations for three important special cases of the optimal power allocation problem.
. In order to achieve particular points on the boundary of this region, one can determine the power loads and partitions that maximize the weighted sum rate for any given weight vector. However, as shown in (5) and the discussion thereafter, the number of constraints that characterize the rate region of multicarrier broadcast channels with common information grows very rapidly with the number of users. Since it appears to be unlikely that a closed-form solution for the power allocation problem can be obtained, it is desirable to develop an efficient numerical technique to determine the optimal power loads and partitions. Towards that end, in this section, we formulate the problem of finding the SPCGS rate region as an optimization problem. Unfortunately, this formulation is not convex. However, we will provide two alternative formulations that will be used in Section 4 to obtain convex formulations for tight inner and outer bounds on the SPCGS region along with the corresponding power allocations. In addition, in Section 5, we will use these formulations to provide precise convex formulations for three important special cases of the optimal power allocation problem.
Let  be the weight associated with the rate
be the weight associated with the rate  ,
,  , where
, where  . Our goal is to maximize
. Our goal is to maximize  subject to the constraints of Proposition 1 being satisfied. That is, we would like to solve
subject to the constraints of Proposition 1 being satisfied. That is, we would like to solve

In order to transform the optimization problem in (9) into a more convenient form, we introduce the change of variables  ,
,  Furthermore, we will denote
Furthermore, we will denote  by
by  . By observing that the logarithm is a monotonically increasing function, we can recast (9) as
. By observing that the logarithm is a monotonically increasing function, we can recast (9) as






The power loads and partitions that correspond to every point on the boundary of the SPCGS region can be obtained by varying the weights in (9), which appear as the exponents in (10a). For instance, the loads and partitions that correspond to a "fair'' rate tuple can be obtained by maximizing  for an appropriately chosen set of weights, subject to the constraints in (10a)–(10f) and, possibly, a lower bound constraint on
for an appropriately chosen set of weights, subject to the constraints in (10a)–(10f) and, possibly, a lower bound constraint on  . A more direct technique for obtaining "fair'' loads and partitions is to draw insight from [29] and maximize the harmonic mean of
. A more direct technique for obtaining "fair'' loads and partitions is to draw insight from [29] and maximize the harmonic mean of  , namely,
, namely,  subject to the constraints in (10a)–(10f) and the lower bound constraint on
subject to the constraints in (10a)–(10f) and the lower bound constraint on  (if it is imposed). Although we will not pursue that problem in this paper, its objective, and the additional constraint, can be written as posynomials (in the sense of [24, 25]), and the techniques that we will apply to the weighted sum rate problem can also be applied to the problem of maximizing the harmonic mean of the rates.
(if it is imposed). Although we will not pursue that problem in this paper, its objective, and the additional constraint, can be written as posynomials (in the sense of [24, 25]), and the techniques that we will apply to the weighted sum rate problem can also be applied to the problem of maximizing the harmonic mean of the rates.
A key step in providing a convenient reformulation of (10a)–(10f) is the following sequence of substitutions. Let  . Because each subchannel is degraded,
. Because each subchannel is degraded,  for all
for all  and
and  . Let
. Let

Using these new variables we can eliminate  and write the constraints in (10a)–(10f) as follows
and write the constraints in (10a)–(10f) as follows



Using (12a)–(12c), we will develop, below, two alternative formulations of (10a)–(10f), each of which will be used in Section 4 to develop a certain outer bound. Before we do so, let us bound the terms of the form  by new variables
by new variables  . Hence, the constraints of the form
. Hence, the constraints of the form

where  is a posynomial (cf. [24, 25]), can be equivalently expressed as
is a posynomial (cf. [24, 25]), can be equivalently expressed as

Both parts of (14) are in the form of posynomial constraints, and hence can be easily incorporated into a Geometric Program (GP) [24, 25].
3.1. Formulation 1
In order to develop a more convenient formulation, we note that in (12a)–(12c) the only constraint in which the variables  appear is (12c). Hence, the set of constraints in (12c) can be written in a GP compatible form as
appear is (12c). Hence, the set of constraints in (12c) can be written in a GP compatible form as

We can now recast the constraints in (12a)–(12c) as






The feasible set for the constraints in (16a)–(16f) is not convex because of the nonposynomial terms generated by the inverse of the sum of optimization variables in the right-hand side of (16c). However, in Section 4, we will show how the reformulation in (16a)–(16f) can be used to develop an efficiently computable outer bound on the capacity region.
3.2. Formulation 2
We now provide a different formulation that will be used to develop another useful outer bound and an inner bound on the achievable rate region. Consider the formulation in (12a)–(12c), and let us bound the terms of the form  by new variables
by new variables  . Using these bounds, the constraints of the form
. Using these bounds, the constraints of the form

where  is a posynomial can be equivalently expressed as
is a posynomial can be equivalently expressed as

However,

Therefore, one can write the constraints on the right of (18) as

This constraint now is in the form of posynomial, and hence can be incorporated into a GP. Therefore, we can rewrite the constraints in (12a)–(12c) as




By examining the constraints in (21a)–(21d), it can be seen that all the constraints are in the form of posynomial inequalities except for the constraint in (21d). Because of this posynomial equality constraint, the formulation in (21a)–(21d) is not a geometric program. However, there are important instances in which the boundary of the rate region and the corresponding power loads and partitions can be formulated in the form of a geometric program; namely, the unmatched two user case and the case in which only independent information is transmitted to the  users. In Section 5 we will provide convex formulations for these cases. In Section 5 we will also provide a convex formulation for obtaining the power loads and partitions that maximize the SPCGS sum rate. In the next section we will develop inner and outer bounds for the rate region that can be achieved by superposition coding and Gaussian signalling.
users. In Section 5 we will provide convex formulations for these cases. In Section 5 we will also provide a convex formulation for obtaining the power loads and partitions that maximize the SPCGS sum rate. In the next section we will develop inner and outer bounds for the rate region that can be achieved by superposition coding and Gaussian signalling.
4. Outer and Inner Bounds on the SPCGS Region
In this section, we use the formulations in (16a)–(16f) and (21a)–(21d) to develop tight inner and outer bounds on the SPCGS rate region.
4.1. Outer Bounds
4.1.1. An Outer Bound Based on Formulation 1
The formulation in (16a)–(16f) is not convex due to the terms of the form  in (16c). In order to derive an outer bound on the rate region, we use the transformation
in (16c). In order to derive an outer bound on the rate region, we use the transformation  . By invoking this transformation in the formulation in (16a)–(16f), one can verify that for each constraint of the nonposynomial form in (16c), an inverse term appears in one of the constraints in (16a). We can multiply each constraint that contains an offending term in the denominator by the corresponding constraints that contain the same term but in the numerator. By doing so we develop new constraints that do not contain offending terms. These new constraints are obviously a relaxation of the original constraints and hence lead to an outer bound on the SPCGS rate region. Indeed, the rates yielded by the relaxed constraints are not necessarily decodable by the users, even though the power allocations and partitions satisfy their respective constraints. However, these new constraints are posynomial constraints that can be used to replace the nonposynomial ones. As a result, the outer bound can be efficiently computed via geometric programming techniques. If any constraint that contains the offending term in the numerator is active, the relaxed constraint will (precisely) enforce the original nonposynomial constraint.
. By invoking this transformation in the formulation in (16a)–(16f), one can verify that for each constraint of the nonposynomial form in (16c), an inverse term appears in one of the constraints in (16a). We can multiply each constraint that contains an offending term in the denominator by the corresponding constraints that contain the same term but in the numerator. By doing so we develop new constraints that do not contain offending terms. These new constraints are obviously a relaxation of the original constraints and hence lead to an outer bound on the SPCGS rate region. Indeed, the rates yielded by the relaxed constraints are not necessarily decodable by the users, even though the power allocations and partitions satisfy their respective constraints. However, these new constraints are posynomial constraints that can be used to replace the nonposynomial ones. As a result, the outer bound can be efficiently computed via geometric programming techniques. If any constraint that contains the offending term in the numerator is active, the relaxed constraint will (precisely) enforce the original nonposynomial constraint.
4.1.2. An Outer Bound Based on Formulation 2
In order to develop an alternative outer bound, we recall that the nonconvexity of the formulation in (21a)–(21d) arises from the posynomial equality constraint in (21d). An outer bound can therefore be obtained by relaxing this constraint. In particular, for all  we replace the
we replace the  th constraint in (21d) by
th constraint in (21d) by

This relaxation may yield power partitions that do not add up to unity, and hence the generated rates are not necessarily decodable by the users. However, this constraint is in a GP-compatible posynomial inequality form and therefore can be used to develop an efficiently computable outer bound on the SPCGS region.
4.2. An Inner Bound
The fact that the relaxation in Section 4.1.2 leads to an outer bound can be verified by observing that if (22) is satisfied with strict inequality, the corresponding rate tuple might not be achievable because the set  does not necessarily represent a set of feasible power partitions. On the other hand, any rate tuple for which the corresponding set
does not necessarily represent a set of feasible power partitions. On the other hand, any rate tuple for which the corresponding set  satisfies
satisfies  is achievable, and the set of such rate tuples forms an inner bound on the SPCGS rate region. In order to efficiently determine valid power partitions (that satisfy
is achievable, and the set of such rate tuples forms an inner bound on the SPCGS rate region. In order to efficiently determine valid power partitions (that satisfy  ) that yield (achievable) rates that are close to the boundary of the SPCGS region, we will consider an auxiliary problem in which we fix the value of the weighted sum rate and search for a valid power partitioning that achieves this weighted sum rate. One formulation of the auxiliary problem is as follows. Let
) that yield (achievable) rates that are close to the boundary of the SPCGS region, we will consider an auxiliary problem in which we fix the value of the weighted sum rate and search for a valid power partitioning that achieves this weighted sum rate. One formulation of the auxiliary problem is as follows. Let  denote twice the weighted sum rate. For a fixed value of
denote twice the weighted sum rate. For a fixed value of  , solve
, solve




For the given value of  , if the solution of (23a)–(23d) satisfies (23c) with equality, the corresponding solution represents a valid power partitioning and this value of
, if the solution of (23a)–(23d) satisfies (23c) with equality, the corresponding solution represents a valid power partitioning and this value of  corresponds to twice a weighted sum of achievable rates. However, if the solution does not satisfy (23c) with equality, this value of
corresponds to twice a weighted sum of achievable rates. However, if the solution does not satisfy (23c) with equality, this value of  corresponds to rates outside the SPCGS rate region. Hence, our goal is to find the maximum value of
corresponds to rates outside the SPCGS rate region. Hence, our goal is to find the maximum value of  for which the solution of (23a)–(23d) satisfies (23c) with equality. In order to do that, we require a method for choosing the value of
for which the solution of (23a)–(23d) satisfies (23c) with equality. In order to do that, we require a method for choosing the value of  and a technique for solving (23a)–(23d) in an efficient manner.
and a technique for solving (23a)–(23d) in an efficient manner.
In order to select appropriate values for  we observe that the optimal value of
we observe that the optimal value of  is a monotonically increasing function of the total power budget,
is a monotonically increasing function of the total power budget,  . In order to show that, we note that
. In order to show that, we note that  is a monotonically increasing function of each of the rates
is a monotonically increasing function of each of the rates  . For any valid power partition, each rate
. For any valid power partition, each rate  is the sum of terms of the form
is the sum of terms of the form  , where
, where  . Now,
. Now,  , which implies that the each rate is monotonically increasing in the total power budget,
, which implies that the each rate is monotonically increasing in the total power budget,  . Now for any valid power allocation that corresponds to a point on the boundary of the SPCGS rate region we have
. Now for any valid power allocation that corresponds to a point on the boundary of the SPCGS rate region we have  . Hence, if we assume that the optimization in (23a)–(23d) can be solved exactly, one can perform bisection search over
. Hence, if we assume that the optimization in (23a)–(23d) can be solved exactly, one can perform bisection search over  to find the largest value of
to find the largest value of  for which the power partitions that maximize the objective in (23a)–(23d) satisfy
for which the power partitions that maximize the objective in (23a)–(23d) satisfy  . Note that in order to determine a search interval for the bisection technique, one may solve the relaxed problem in Section 3.2. Now, if
. Note that in order to determine a search interval for the bisection technique, one may solve the relaxed problem in Section 3.2. Now, if  is the optimum value of the relaxed problem, then the optimal feasible value of
is the optimum value of the relaxed problem, then the optimal feasible value of  for (23a)–(23d) must lie in the interval
for (23a)–(23d) must lie in the interval  .
.
We now consider solving (23a)–(23d). Observe that although all the constraints in (23a)–(23d) are GP compatible, the objective is not GP compatible. One way to find an inner bound is to use a monomial to approximate the objective in (23a)–(23d). This approximation results in a geometric program that can be efficiently solved. An inner bound can then be found by using the bisection technique described above to find the largest value of  for which maximizing the approximated objective yields a valid power allocation. By varying the monomial used to approximate the objective, one obtains a family of inner bounds. Of course, it is desirable to find the outermost inner bound. An efficient technique for doing so is to employ Signomial Programming (SP) [25]. In this technique, the objective is iteratively approximated by the best fitting monomial in the neighbourhood of the current iterate. Since all the constraints in (23a)–(23d) are GP compatible, each iteration in the signomial programming technique involves the solution of a geometric program, and because the objective is the only expression in (23a)–(23d) that is not GP compatible, signomial programming is likely to provide solutions that are close to optimal [24, 25]. In fact, our numerical experiments show that for the scenarios in which the capacity region can be computed exactly, the region generated by the proposed algorithm almost coincides with the capacity region; see Figure 5.
for which maximizing the approximated objective yields a valid power allocation. By varying the monomial used to approximate the objective, one obtains a family of inner bounds. Of course, it is desirable to find the outermost inner bound. An efficient technique for doing so is to employ Signomial Programming (SP) [25]. In this technique, the objective is iteratively approximated by the best fitting monomial in the neighbourhood of the current iterate. Since all the constraints in (23a)–(23d) are GP compatible, each iteration in the signomial programming technique involves the solution of a geometric program, and because the objective is the only expression in (23a)–(23d) that is not GP compatible, signomial programming is likely to provide solutions that are close to optimal [24, 25]. In fact, our numerical experiments show that for the scenarios in which the capacity region can be computed exactly, the region generated by the proposed algorithm almost coincides with the capacity region; see Figure 5.
For completeness, we now describe the proposed algorithm in more detail. In signomial programming, the set  is initialized by arbitrary values that satisfy the constraints in (23a)–(23d). We then find the best fitting monomial for
is initialized by arbitrary values that satisfy the constraints in (23a)–(23d). We then find the best fitting monomial for  in the neighbourhood of the initial values of
in the neighbourhood of the initial values of  using the Taylor expansion in the logarithmic domain. This monomial takes the form
using the Taylor expansion in the logarithmic domain. This monomial takes the form  . Using this approximation, we solve the following geometric program:
. Using this approximation, we solve the following geometric program:

By solving this geometric program, we obtain a new set  . This set is used to generate a new set of exponents
. This set is used to generate a new set of exponents  . (For the current objective, the exponents that correspond to the best fitting monomial at the
. (For the current objective, the exponents that correspond to the best fitting monomial at the  th iteration are given by
th iteration are given by  where
where  is a positive scalar that is a function of all
is a positive scalar that is a function of all  . Being positive and common to all exponents,
. Being positive and common to all exponents,  can be dropped from the formulation of the optimization program in (24).) We continue to iterate in this manner until either the inequality constraint in (23c) is satisfied with equality or the sequence of sets
can be dropped from the formulation of the optimization program in (24).) We continue to iterate in this manner until either the inequality constraint in (23c) is satisfied with equality or the sequence of sets  converges without (23c) being satisfied with equality. In the former case, the SP approach has generated a solution to (23a)–(23d) that satisfies (23c) with equality. Hence, the current value of
converges without (23c) being satisfied with equality. In the former case, the SP approach has generated a solution to (23a)–(23d) that satisfies (23c) with equality. Hence, the current value of  corresponds to twice the weighted sum rate of an achievable rate tuple, and the next step is to use the bisection rule to increase the value of
corresponds to twice the weighted sum rate of an achievable rate tuple, and the next step is to use the bisection rule to increase the value of  and solve (23a)–(23d) again. In the latter case, the SP approach has been unable to find a solution to (9) that satisfies (23c) with equality. While this does not necessarily mean that such a solution does not exist, we adopt the conservative approach and use the bisection rule to reduce
and solve (23a)–(23d) again. In the latter case, the SP approach has been unable to find a solution to (9) that satisfies (23c) with equality. While this does not necessarily mean that such a solution does not exist, we adopt the conservative approach and use the bisection rule to reduce  and solve (23a)–(23d) again. This conservative approach is the reason why our approach generates an inner bound on the SPCGS rate region rather than the SPCGS rate region itself, but it is also the key to the computational efficiency of the algorithm.
and solve (23a)–(23d) again. This conservative approach is the reason why our approach generates an inner bound on the SPCGS rate region rather than the SPCGS rate region itself, but it is also the key to the computational efficiency of the algorithm.
5. Exact Convex Formulations—Special Cases
In the previous section we considered a general Gaussian broadcast channel with  parallel subchannels and
parallel subchannels and  users, and we showed how to derive convex formulations for inner and outer bounds on the SPCGS rate region. In this section we provide exact convex formulations for three particular instances of the general problem, namely, the 2-user case and the case of
users, and we showed how to derive convex formulations for inner and outer bounds on the SPCGS rate region. In this section we provide exact convex formulations for three particular instances of the general problem, namely, the 2-user case and the case of  users with (independent) particular messages only, and the SPCGS sum rate point of the general
users with (independent) particular messages only, and the SPCGS sum rate point of the general  -user
-user  -subchannel case. (For the first two cases, the SPCGS rate region is known to be the capacity region [17, 21].) Using these convex formulations, optimal power loads and partitions for these three cases can be obtained using efficient interior point techniques.
-subchannel case. (For the first two cases, the SPCGS rate region is known to be the capacity region [17, 21].) Using these convex formulations, optimal power loads and partitions for these three cases can be obtained using efficient interior point techniques.
5.1. Optimal Power Allocation for the 2-User Case
For this case, the capacity region was shown in [17] to be the same as the SPCGS rate region. Similar to the general case considered in Proposition 1, the boundary of the 2-user SPCGS rate region is parameterized by power loads and partitions. Although the optimal values of these parameters can be determined using the indirect Lagrange multiplier search technique provided in [20], in this section we provide a (precise) convex formulation that enables us to determine those loads and partitions directly, and in a computationally efficient manner.
Recall that in our notation the degradedness condition on each subchannel implies that  . Let
. Let  ,
,  , be the set of subchannels on which User
, be the set of subchannels on which User  is the stronger user. Using Proposition 1 and the logarithmic substitutions:
is the stronger user. Using Proposition 1 and the logarithmic substitutions:  and
and  , we formulate the weighted sum rate optimization problem as
, we formulate the weighted sum rate optimization problem as

where  , and
, and  is the power partition associated with the stronger user on the
is the power partition associated with the stronger user on the  th subchannel. In order to transform this optimization problem into a convex form, we perform the variable substitutions
th subchannel. In order to transform this optimization problem into a convex form, we perform the variable substitutions

and  . Using these variable substitutions, and the equivalent constraints in (14), the optimization problem in (25) can be reformulated as
. Using these variable substitutions, and the equivalent constraints in (14), the optimization problem in (25) can be reformulated as

The formulation in (27) is in the form of a convex geometric program and the optimal values of  and
and  ,
,  , can be efficiently found. Once
, can be efficiently found. Once  and
and  have been computed, one can use (26) to find the power loads
have been computed, one can use (26) to find the power loads  and the power partitions
and the power partitions  .
.
5.2. Optimal Power Allocation for the Broadcast of Particular Information to 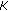 users
users
The capacity region for the case in which only particular information is to be transmitted to  users over
users over  parallel channels was considered in [21–23]. In [21] the concept of utility functions was introduced. Using the properties of these functions and a search for a Lagrange multiplier, optimal power loads and power partitions were determined algebraically. In this section we will present an alternative efficient numerical technique for determining these loads and partitions through the solution of a convex optimization problem. (This technique is similar to that presented in [23] and was developed independently.) Using our notation for the rate of particular information of User
parallel channels was considered in [21–23]. In [21] the concept of utility functions was introduced. Using the properties of these functions and a search for a Lagrange multiplier, optimal power loads and power partitions were determined algebraically. In this section we will present an alternative efficient numerical technique for determining these loads and partitions through the solution of a convex optimization problem. (This technique is similar to that presented in [23] and was developed independently.) Using our notation for the rate of particular information of User  ,
,  , the capacity region is the closure of all points of the form [21]
, the capacity region is the closure of all points of the form [21]

where  , and
, and  . In order to simplify the notation, we will use
. In order to simplify the notation, we will use  to denote
to denote  and
and  to denote
to denote  . Finding each point on the boundary of the capacity region and the corresponding power loads and partitions is equivalent to solving the following optimization problem for a given set of weights
. Finding each point on the boundary of the capacity region and the corresponding power loads and partitions is equivalent to solving the following optimization problem for a given set of weights  that satisfy
that satisfy  :
:





In its current form, the formulation in (29a)–(29e) is not convex. The key to casting (29a)–(29e) in a convex form is the change of variables

To begin with, we note that this substitution is one-to-one. That is, once the problem is solved in terms of the variables  , one can readily obtain the required power partitions
, one can readily obtain the required power partitions  . We now examine the constraints in (29a)–(29e). The set of constraints in (29b) can be rewritten as
. We now examine the constraints in (29a)–(29e). The set of constraints in (29b) can be rewritten as

Observe that because each subchannel is degraded, the constant  is greater than or equal to zero. Hence, (31) is in the form of a posynomial constraint, and can be easily incorporated in a geometric program. In order to account for the constraints (29c), (29d), and (29e), we observe that from (30) we have
is greater than or equal to zero. Hence, (31) is in the form of a posynomial constraint, and can be easily incorporated in a geometric program. In order to account for the constraints (29c), (29d), and (29e), we observe that from (30) we have

where we will use the convention that  . The set of constraints in (29e) can now be expressed as
. The set of constraints in (29e) can now be expressed as

This constraint is also in a posynomial format. Finally, we observe that the constraints in (29c) and (29d) can be merged together. In particular, the variables  can be eliminated. Using (30), this will lead to the following constraint:
can be eliminated. Using (30), this will lead to the following constraint:

Using these transformations, the weighted sum rate optimization problem in (29a)–(29e) can be recast in the following convex format:

Once (35) has been solved, one can use (32) and (29c) to obtain the required power loads and partitions.
5.3. Optimal Power Allocation for SPCGS Sum Rate Maximization
In Section 3.1 we expressed the points on the boundary of the SPCGS rate region of a  -user
-user  -subchannel broadcast channel as the solution of the optimization problem in (16a)–(16f). As discussed in Section 3.1, that problem is not convex for general values of the weights
-subchannel broadcast channel as the solution of the optimization problem in (16a)–(16f). As discussed in Section 3.1, that problem is not convex for general values of the weights  . However, for the case in which all the weights are equal, the objective in (16a)–(16f) corresponds to the sum of the common and particular SPCGS rates. We will now show that finding the power loads and partitions that maximize this sum rate can be cast a (convex) geometric program. In order to do that, we observe that the constraints in (16a)–(16f) that bound the sum rate can be extracted from (16c) by setting
. However, for the case in which all the weights are equal, the objective in (16a)–(16f) corresponds to the sum of the common and particular SPCGS rates. We will now show that finding the power loads and partitions that maximize this sum rate can be cast a (convex) geometric program. In order to do that, we observe that the constraints in (16a)–(16f) that bound the sum rate can be extracted from (16c) by setting  equal to
equal to  . It can be shown that in the problem of maximizing the sum rate only these constraints and the constraints in (16d)–(16f) can be active. That is, the constraints in (16a) and (16b) and the constraints in (16c) that correspond to
. It can be shown that in the problem of maximizing the sum rate only these constraints and the constraints in (16d)–(16f) can be active. That is, the constraints in (16a) and (16b) and the constraints in (16c) that correspond to  do not constrain the optimal solution to the sum rate optimization problem. In order to see that, we observe that solving (16a)–(16f) with these constraints removed results in a relaxation of the optimization problem. This relaxation yields an upper bound on the maximum sum rate. However, the solution of the relaxed problem provides power allocations that satisfy the power constraints in (16d)–(16f) and achieve this upper bound on the maximum sum rate. Hence, the maximum sum rate that can be achieved by superposition coding and Gaussian signalling, and the corresponding power allocations, can be obtained by solving the relaxed problem.
do not constrain the optimal solution to the sum rate optimization problem. In order to see that, we observe that solving (16a)–(16f) with these constraints removed results in a relaxation of the optimization problem. This relaxation yields an upper bound on the maximum sum rate. However, the solution of the relaxed problem provides power allocations that satisfy the power constraints in (16d)–(16f) and achieve this upper bound on the maximum sum rate. Hence, the maximum sum rate that can be achieved by superposition coding and Gaussian signalling, and the corresponding power allocations, can be obtained by solving the relaxed problem.
We now provide an explicit formulation of the relaxed problem in a convex form. In order to do that, let the sum rate  be equal to
be equal to  , and note that by setting
, and note that by setting  to be equal to
to be equal to  in (16c), we have
in (16c), we have  . Hence, the relaxed problem can be expressed as
. Hence, the relaxed problem can be expressed as





In order to cast the optimization problem in (36a)–(36e) in a convex form, we use the transformation in (30) to write the constraints in (36b) in a posynomial form as

Noting from (11) and (30) that  is equal to
is equal to  , the constraints in (36c)–(36e) can be easily transformed into posynomial inequality constraints using the same technique that was used to formulate (35).
, the constraints in (36c)–(36e) can be easily transformed into posynomial inequality constraints using the same technique that was used to formulate (35).
Remark 4.
In addition to casting the SPCGS sum rate in a convex form, it is also possible to show that by setting all the particular rates equal to zero, one can cast the problem of maximizing the common SPCGS rate as a GP. This can be done by removing the constraints in (16b) and (16c) and solving the resulting GP directly.
6. Numerical Example
In this section we will provide a numerical example based on the 3-user 2-subchannel scenario depicted in Figure 2. Although it is straightforward to particularize the general formulation in (12a)–(12c) for this scenario, for completeness we have provided an explicit formulation in the appendix. Using this formulation, we obtain formulations for the outer and inner bounds on the SPCGS rate region using the approaches described in Section 4.
The rate region for this scenario lies in a 4-dimensional space  , which can be rather difficult to visualize. Therefore, in Figures 3, 4, and 5 we will provide exemplary cross-sections of the rate region for different values of the common information rate,
, which can be rather difficult to visualize. Therefore, in Figures 3, 4, and 5 we will provide exemplary cross-sections of the rate region for different values of the common information rate,  . The parameters of the system model in Figure 2 were chosen by setting the transmitted power,
. The parameters of the system model in Figure 2 were chosen by setting the transmitted power,  , to be equal to 1, and picking the values for the equivalent noise variances at random, such that
, to be equal to 1, and picking the values for the equivalent noise variances at random, such that  . In these figures we will show the rate regions for a system with
. In these figures we will show the rate regions for a system with  ,
,  ,
,  ,
,  ,
,  , and
, and  . (Other results for this scenario are available in [26].) Using the observation in Remark 4, the maximum common information rate
. (Other results for this scenario are available in [26].) Using the observation in Remark 4, the maximum common information rate  , can be efficiently computed, and in this setting it is equal to
, can be efficiently computed, and in this setting it is equal to  nats per channel use.
nats per channel use.
A comparison between the inner and outer bounds on the SPCGS rate region at  . Inner (marked "
. Inner (marked " '') and outer (marked "o'') bounds on SPCGS rate regionIntensity illustration of the difference between the values of
'') and outer (marked "o'') bounds on SPCGS rate regionIntensity illustration of the difference between the values of  given by the outer and inner bounds. The boundary of the SPCGS rate region with
given by the outer and inner bounds. The boundary of the SPCGS rate region with  is marked by "
is marked by " ''
''
As an initial illustration of the proposed approach, in Figure 3 we show the regions of SPCGS achievable rate triples  that are obtained via the signomial programming technique described in Section 4.2 for different values of the common information rate:
that are obtained via the signomial programming technique described in Section 4.2 for different values of the common information rate:  and
and  . As can be seen from this figure, increasing the rate of the common message simultaneously reduces the maximum achievable rates for all particular messages; a result that conforms with natural intuition.
. As can be seen from this figure, increasing the rate of the common message simultaneously reduces the maximum achievable rates for all particular messages; a result that conforms with natural intuition.
In order to investigate the tightness of the proposed inner and outer bounds on the set of SPCGS achievable rates, in Figure 4 we provide a comparison between the inner bound proposed in Section 4.2, which is obtained via signomial programming and bisection search, and the outer bound proposed in Section 4.1.1, which is obtained via a geometric program. In particular, Figure 4(a) shows a 3-dimensional plot of the inner and outer bounds on the rate triples  when the common information rate is set at
when the common information rate is set at  . For fixed values of
. For fixed values of  and
and  , the difference between the inner and the outer bounds on
, the difference between the inner and the outer bounds on  in Figure 4(a) is illustrated in Figure 4(b) using a 2-dimensional intensity plot, with black and white colours corresponding to the maximum and minimum differences, respectively. From this figure, it can be seen that the maximum difference is about
in Figure 4(a) is illustrated in Figure 4(b) using a 2-dimensional intensity plot, with black and white colours corresponding to the maximum and minimum differences, respectively. From this figure, it can be seen that the maximum difference is about  , corresponding to a relative difference of approximately
, corresponding to a relative difference of approximately  . It can also be seen from this Figure that although the bounds do not agree on the entire rate region, they almost coincide over a significant portion of it.
. It can also be seen from this Figure that although the bounds do not agree on the entire rate region, they almost coincide over a significant portion of it.
Finally, we investigate the tightness of the inner bound when the rate of the common message is set to zero; that is,  . In that case, the SPCGS region coincides with the capacity region, and can be precisely (and efficiently) computed using the formulation in Section 5.2. In Figure 5, the difference between the SPCGS rate region and the proposed inner bound is illustrated using an intensity plot. It can be seen from this plot that the maximum difference is about
. In that case, the SPCGS region coincides with the capacity region, and can be precisely (and efficiently) computed using the formulation in Section 5.2. In Figure 5, the difference between the SPCGS rate region and the proposed inner bound is illustrated using an intensity plot. It can be seen from this plot that the maximum difference is about  , which demonstrates the utility of the proposed inner bound.
, which demonstrates the utility of the proposed inner bound.
7. Conclusion
In this paper we have provided a general characterization of the rate region that can be achieved by superposition coding and Gaussian signalling (SPCGS) on a  -user
-user  -subchannel Gaussian broadcast system in which a common message and particular messages are transmitted to the users. We have also expressed the boundary points of this region as the solution of an optimization problem. Although that problem is not convex in the general case, it was used to obtain efficiently computable inner and outer bounds on the SPCGS rate region. In addition, we have provided precise convex formulations for some important special cases of the general problem, including two cases in which the SPCGS rate region is known to be the capacity region (the 2-user case and the
-subchannel Gaussian broadcast system in which a common message and particular messages are transmitted to the users. We have also expressed the boundary points of this region as the solution of an optimization problem. Although that problem is not convex in the general case, it was used to obtain efficiently computable inner and outer bounds on the SPCGS rate region. In addition, we have provided precise convex formulations for some important special cases of the general problem, including two cases in which the SPCGS rate region is known to be the capacity region (the 2-user case and the  -user case with particular messages only), and the
-user case with particular messages only), and the  -user
-user  -subchannel case in which only the SPCGS sum rate is maximized.
-subchannel case in which only the SPCGS sum rate is maximized.
References
Cover T: Broadcast channels. IEEE Transactions on Information Theory 1972, 18(1):2-14. 10.1109/TIT.1972.1054727
Bergmans P: Random coding theorem for broadcast channels with degraded components. IEEE Transactions on Information Theory 1973, 19(2):197-207. 10.1109/TIT.1973.1054980
Goldsmith AJ, Effros M: The capacity region of broadcast channels with intersymbol interference and colored Gaussian noise. IEEE Transactions on Information Theory 2001, 47(1):219-240. 10.1109/18.904524
Weingarten H, Steinberg Y, Shamai S: The capacity region of the Gaussian multiple-input multiple-output broadcast channel. IEEE Transactions on Information Theory 2006, 52(9):3936-3964.
Marton K: A coding theorem for the discrete memoryless broadcast channel. IEEE Transactions on Information Theory 1979, 25(3):306-311. 10.1109/TIT.1979.1056046
Sato H: An outer bound to the capacity region of broadcast channels. IEEE Transactions on Information Theory 1978, 24(3):374-377. 10.1109/TIT.1978.1055883
Caire G, Shamai S: On the achievable throughput of a multiantenna Gaussian broadcast channel. IEEE Transactions on Information Theory 2003, 49(7):1691-1706. 10.1109/TIT.2003.813523
Yu W, Cioffi JM: Sum capacity of Gaussian vector broadcast channels. IEEE Transactions on Information Theory 2004, 50(9):1875-1892. 10.1109/TIT.2004.833336
Vishwanath S, Jindal N, Goldsmith A: Duality, achievable rates, and sum-rate capacity of Gaussian MIMO broadcast channels. IEEE Transactions on Information Theory 2003, 49(10):2658-2668. 10.1109/TIT.2003.817421
Yu W: Uplink-downlink duality via minimax duality. IEEE Transactions on Information Theory 2006, 52(2):361-374.
Vishwanath S, Kramer G, Shamai S, Jafar S, Goldsmith A: Capacity bounds for Gaussian vector broadcast channels. In Proceedings of DIMACS workshop on Signal Processing for Wireless Transmissions, October 2002, Rutgers, NJ, USA Edited by: Foschini GJ, Verdú S. 71-80.
Viswanath P, Tse DNC: Sum capacity of the vector Gaussian broadcast channel and uplink-downlink duality. IEEE Transactions on Information Theory 2003, 49(8):1912-1921. 10.1109/TIT.2003.814483
Costa M: Writing on dirty paper. IEEE Transactions on Information Theory 1983, 29(3):439-441. 10.1109/TIT.1983.1056659
Cover TM: An achievable rate region for the broadcast channel. IEEE Transactions on Information Theory 1975, 21(4):399-404. 10.1109/TIT.1975.1055418
van der Meulen EC: Random coding theorems for the general discrete memoryless broadcast channel. IEEE Transactions on Information Theory 1975, 21(2):180-190. 10.1109/TIT.1975.1055347
Nair C, El Gamal A: An outer bound to the capacity region of the broadcast channel. IEEE Transactions on Information Theory 2007, 53(1):350-355.
El Gamal AA: Capacity of the product and sum of two unmatched broadcast channels. Problems of Information Transmission 1980, 16(1):3-23.
Bergmans P: A simple converse for broadcast channels with additive white Gaussian noise. IEEE Transactions on Information Theory 1974, 20(2):279-280. 10.1109/TIT.1974.1055184
Gallager RG: Capacity and coding for degraded broadcast channels. Problemy Peredachi Informatsii 1974, 10(3):185-193.
Jindal N, Goldsmith A: Capacity and dirty paper coding for Gaussian broadcast channels with common information. Proceedings of the IEEE International Symposium on Information Theory (ISIT '04), June-July 2004, Chicago, Ill, USA 215.
Tse DNC: Optimal power allocation over parallel Gaussian broadcast channels. Proceedings of IEEE International Symposium on Information Theory (ISIT '97), June-July 1997, Ulm, Germany 27.
Wunder G, Michel T: Optimal resource allocation for OFDM multiuser channels. submitted to IEEE Transactions on Information Theory
Seong K, Yu DD, Kim Y, Cioffi JM: CTH03-5: optimal resource allocation via geometric programming for OFDM broadcast and multiple access channels. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '06), November 2006, San Francisco, Calif, USA 1-5.
Chiang M: Geometric programming for communication systems. Foundations and Trends in Communications and Information Theory 2005, 2(1-2):1-154. 10.1561/0100000005
Boyd S, Kim S-J, Vandenberghe L, Hassibi A: A tutorial on geometric programming. Optimization and Engineering 2007, 8(1):67-127. 10.1007/s11081-007-9001-7
Gohary RH, Davidson TN: On the capacity region of parallel Gaussian broadcast channels with common information. Proceedings of the IEEE International Symposium on Information Theory (ISIT '07), June 2007, Nice, France 1146-1150.
Cover TM, Thomas JA: Elements of Information Theory. Wiley-Interscience, New York, NY, USA; 1991.
Hughes-Hartogs D: The capacity of a degraded spectral Gaussian broadcast channel, Ph.D. thesis. Stanford University, Stanford, Calif, USA; July 1975.
Luo Z-Q, Zhang S: Dynamic spectrum management: complexity and duality. IEEE Journal on Selected Topics in Signal Processing 2008, 2(1):57-73.
Acknowledgments
This work was supported, in part, by a Premier's Research Excellence Award from the Government of Ontario. The work of the second author is also supported by the Canada Research Chairs program.
Author information
Authors and Affiliations
Corresponding author
Appendix
Equivalent Optimization Problem for the 3-User 2-Subchannel Case
Using the transformation in (11), the rate region described in (6a)–(6n) can be cast as


Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gohary, R.H., Davidson, T.N. On Power Allocation for Parallel Gaussian Broadcast Channels with Common Information. J Wireless Com Network 2009, 482520 (2009). https://doi.org/10.1155/2009/482520
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/482520






 unmatched parallel degraded broadcast subchannels with
unmatched parallel degraded broadcast subchannels with
 users.
users.
 , and degradation level
, and degradation level 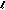 ,
, 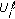 is an auxiliary Gaussian signal that is constructed by superimposing an incremental Gaussian signal on
is an auxiliary Gaussian signal that is constructed by superimposing an incremental Gaussian signal on 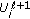 . Being Gaussian and independent of the noise, this incremental signal contributes additively to the total noise plus interference power observed by any user attempting to decode the signal
. Being Gaussian and independent of the noise, this incremental signal contributes additively to the total noise plus interference power observed by any user attempting to decode the signal 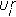 with
with  [
[ . The power assigned to these signals is
. The power assigned to these signals is 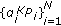 , and the aggregate mutual information that User
, and the aggregate mutual information that User  gathers about these signals is
gathers about these signals is  . For User
. For User  to be able to decode the common message, the rate of this message must be less than the aggregate mutual information, and conversely, all users whose aggregate mutual information is greater than this rate will be able to be reliably decodable the common message. Hence, for the common message to reliably decodable by all users, the rate at which this message is transmitted must be less than the aggregate information of the weakest user. Therefore, the rate of the common message is limited by the constraint in (1a).
to be able to decode the common message, the rate of this message must be less than the aggregate mutual information, and conversely, all users whose aggregate mutual information is greater than this rate will be able to be reliably decodable the common message. Hence, for the common message to reliably decodable by all users, the rate at which this message is transmitted must be less than the aggregate information of the weakest user. Therefore, the rate of the common message is limited by the constraint in (1a). are embedded in the signals
are embedded in the signals  . The respective powers of these signals are
. The respective powers of these signals are 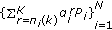 . For these messages to be reliably decodable, the sum of the rates of these messages must be less than the aggregate mutual information that this user gathers about
. For these messages to be reliably decodable, the sum of the rates of these messages must be less than the aggregate mutual information that this user gathers about  . This leads to the set of constraints in (1b).
. This leads to the set of constraints in (1b). , in the subset of
, in the subset of 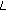 users
users  . As in (1b), the sum of the rates of the messages that are intended for User
. As in (1b), the sum of the rates of the messages that are intended for User  is bounded by
is bounded by  ; compare with the first term in (1c). On the
; compare with the first term in (1c). On the  th subchannel, the degradation level of User
th subchannel, the degradation level of User  is
is 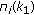 . Now if the sum of the rates intended for User
. Now if the sum of the rates intended for User  is such that the
is such that the  th term in the summation in (1b) is satisfied with equality, the other users in the subset
th term in the summation in (1b) is satisfied with equality, the other users in the subset  whose degradation level is above that of User
whose degradation level is above that of User  (i.e., their degradation level is less than
(i.e., their degradation level is less than 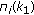 ) can still reliably decode messages that are embedded in
) can still reliably decode messages that are embedded in 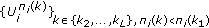 . Hence, the sum of the rates of these messages that can be achieved by superposition coding and Gaussian signalling is bounded by the second term in (1c). This holds for all permutations of users, that is, for all choices of
. Hence, the sum of the rates of these messages that can be achieved by superposition coding and Gaussian signalling is bounded by the second term in (1c). This holds for all permutations of users, that is, for all choices of  in
in  .
.
 unmatched degraded broadcast channels with
unmatched degraded broadcast channels with
 users.
users.
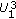 contains common information for all users, and particular information for User 3.
contains common information for all users, and particular information for User 3.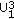 , the signal
, the signal  contains particular information for User 2.
contains particular information for User 2.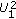 , the signal
, the signal 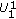 contains particular information for User 1.
contains particular information for User 1. contains common information for all users, and particular information for User 1.
contains common information for all users, and particular information for User 1.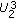 , the signal
, the signal  contains particular information for User 2.
contains particular information for User 2.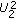 , the signal
, the signal  contains particular information for User 3.
contains particular information for User 3. users
users
 ,
,  and
and  .
.

 on the boundary of the capacity region for particular messaging (
on the boundary of the capacity region for particular messaging ( ) and the values of
) and the values of  generated by the proposed inner bound (for
generated by the proposed inner bound (for  ). The boundary of the capacity region is marked by "
). The boundary of the capacity region is marked by " ''.
''.