Abstract
We link some equivalent forms of the arithmetic-geometric mean inequality in probability and mathematical statistics.
Similar content being viewed by others
1. Introduction
The arithmetic-geometric mean inequality (in short, AG inequality) has been widely used in mathematics and in its applications. A large number of its equivalent forms have also been developed in several areas of mathematics. For probability and mathematical statistics, the equivalent forms of the AG inequality have not been linked together in a formal way. The purpose of this paper is to prove that the AG inequality is equivalent to some other renowned inequalities by using probabilistic arguments. Among such inequalities are those of Jensen, Hölder, Cauchy, Minkowski, and Lyapunov, to name just a few.
2. The Equivalent Forms
Let  be a random variable, we define
be a random variable, we define

where  denotes the expected value of
denotes the expected value of  .
.
Throughout this paper, let  be a positive integer and we consider only the random variables which have finite expected values.
be a positive integer and we consider only the random variables which have finite expected values.
In order to establish our main results, we need the following lemma which is due to Infantozzi [1, 2], Marshall and Olkin [3, Page 457], and Maligranda [4, 5]. For other related results, we refer to [6–19].
Lemma 2.1.
The following inequalities are equivalent.

AG inequality:  , where
, where  is a nonnegative random variable.
is a nonnegative random variable.

if  and
and  for
for  with
with  . The arithmetic-geometric mean inequality is usually applied in a simple version of
. The arithmetic-geometric mean inequality is usually applied in a simple version of  with
with  for each
for each  .
.

if  and
and  , and the opposite inequality holds if
, and the opposite inequality holds if  or
or  .
.

if  and
and  , and the opposite inequality holds if
, and the opposite inequality holds if  or
or  and
and  .
.

for  if
if  with
with  , and the opposite inequality holds if
, and the opposite inequality holds if  with
with  .
.

if  and
and  for
for  , and the opposite inequality holds if
, and the opposite inequality holds if  .
.

if  for
for  and
and  .
.

Let  be a measure space. If
be a measure space. If  is finitely
is finitely  ,
, and let
and let  . Then
. Then  is finitely integrable and
is finitely integrable and  .
.

If  and
and  is
is  -integrable, where
-integrable, where  is a probability space, then
is a probability space, then  .
.

Artin's theorem. Let  be an open convex subset of
be an open convex subset of  and
and  satisfy
satisfy
(a) is Borel-measurable in
is Borel-measurable in  for each fixed
for each fixed 
(b) is convex in
is convex in  for each fixed
for each fixed  .
.
If  is a measure on the Borel subsets of
is a measure on the Borel subsets of  such that
such that  is
is  integrable for each
integrable for each  then
then  is a convex function on
is a convex function on  .
.

Jensen's inequality. Let  be a probability space and
be a probability space and  be a random variable taking values in the open convex set
be a random variable taking values in the open convex set  with finite expectation
with finite expectation  . If
. If  is convex, then
is convex, then  .
.
Proof.
The proof of the equivalent relations of  can be found in [1, 2, 4, 5].
can be found in [1, 2, 4, 5].
The proof of the equivalent relations of  , and
, and  can be found in [3].
can be found in [3].
Theorem 2.2.
The following inequalities are equivalent.

if  are random variables and
are random variables and  with
with  and
and  .
.

if  are random variables and
are random variables and  with
with  and
and  .
.

if  are random variables and
are random variables and  with
with  .
.

if  are random variables and
are random variables and  with
with  , that is,
, that is,  if
if  with
with  .
.

if  are random variables and
are random variables and  with
with  and
and  .
.

if  are random variables and
are random variables and  with
with  .
.

if  are random variables and
are random variables and  .
.

if  are random variables and
are random variables and  .
.

if  is a random variable and
is a random variable and  , that is,
, that is,  is nondecreasing on
is nondecreasing on  .
.

(see [10, 18])  , where
, where  is a random variable if
is a random variable if  or
or  , and the opposite inequality holds if
, and the opposite inequality holds if  .
.

if  are random variables and
are random variables and  with
with  .
.

if  are random variables and
are random variables and  with
with  .
.

if  are random variables and
are random variables and  with
with  .
.

if  are random variables and
are random variables and  .
.

if  are random variables and
are random variables and  .
.

if  are random variables and
are random variables and  .
.

Cauchy-Bunyakovski and Schwarz's (CBS) inequality:  if
if  are random variables.
are random variables.

if  are random variables.
are random variables.

if  are random variables and
are random variables and  (the inequality is reversed if
(the inequality is reversed if  or
or  ).
).

 for any
for any  if
if  are random variables and
are random variables and  .
.

if  are random variables and either
are random variables and either  or
or  .
.

if  are random variables and
are random variables and  .
.

if  are random variables and either
are random variables and either  or
or  .
.

if  are random variables and either
are random variables and either  or
or  .
.

increases with  if
if  are random variables and
are random variables and  .
.

Minkowski's inequality:  if
if  are random variables,
are random variables,  , and the opposite inequality holds if
, and the opposite inequality holds if  .
.

Triangle inequality:  if
if  are random variables,
are random variables,  and the opposite inequality holds if
and the opposite inequality holds if  .
.

if  is a random variable,
is a random variable,  and
and  are two continuous and strictly increasing functions such that
are two continuous and strictly increasing functions such that  is convex.
is convex.

for any  if
if  is a random variable.
is a random variable.
The above listed inequalities are also equivalent to the inequalities in Lemma 2.1.
Proof.
The sketch of the proof of this theorem is illustrated by the following maps of equivalent circles:
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5) ;
;
(6) ;
;
(7) ;
;
(8) ;
;
(9) .
.
Now, we are in a position to give the proof of this theorem as follows.

, see Casella and Berger [7, page 187].

is clear.

: If  and
and  , then
, then  and
and  . This and
. This and  imply
imply

Replacing  by
by  in the above inequality, we obtain
in the above inequality, we obtain  .
.
Similarly, we can prove the case that  and
and  .
.

is proved similarly.

is clear.

. Letting  , and
, and  be replaced by
be replaced by  and
and  in
in  , respectively, we obtain
, respectively, we obtain  .
.

is similarly proved.

: Let  . Then
. Then  . It follows from
. It follows from  that
that

That is,  holds.
holds.

is similarly proved.

. Taking  in
in  , we see that
, we see that

which implies

Replacing  by
by  ,
,

Thus

This proves  .
.
Next, let  . Then
. Then  and
and  . This and
. This and  imply
imply

Replacing  and
and  by
by  and
and  in the above inequality, respectively, and using
in the above inequality, respectively, and using  , we obtain
, we obtain

This proves  holds.
holds.

is proved similarly.

. (a) Taking  and
and  in
in  ,
,

which implies

-
(b)
Taking
 and
and 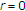 in
in 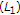 ,
, 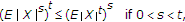 (2.12)
(2.12)
which implies

-
(c)
Taking
 and
and 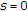 in
in 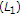 ,
,  (2.14)
(2.14)
which implies

-
(d)
It follows from (a), (b), and (c) that
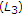 holds.
holds.
Thus, we complete the proof.

is similarly proved.

is clear.

by using the technique of  .
.

. Letting  and
and  in
in  , we obtain
, we obtain  .
.

. It follows from  and
and  that
that  . This and
. This and  imply
imply

Replacing  and
and  by
by  and
and  in the above inequality, respectively, we obtain
in the above inequality, respectively, we obtain  .
.

and  are similarly proved.
are similarly proved.

and  follow by taking
follow by taking  and
and  .
.

and  follow by taking
follow by taking  in
in  and
and  , respectively.
, respectively.

Casella and Berger [7, page 188].

(see [5]): Let  with
with  and
and  . It follows from Benoulli's inequality
. It follows from Benoulli's inequality  that
that

This and  imply
imply

Hence

This proves  holds.
holds.

follows by replacing  and
and  by
by  and
and  in
in  , respectively.
, respectively.

follows by replacing  and
and  in
in  with
with  and
and  , respectively.
, respectively.

. Let  for
for  . Then, it follows from
. Then, it follows from  that
that

Thus,  is midconvex on
is midconvex on  , and hence
, and hence  is convex on
is convex on  . Hence
. Hence

Therefore,

Letting  in the both sides of the above inequality,
in the both sides of the above inequality,

This shows  (see [13]).
(see [13]).

. First note that, as shown above,  and
and  are equivalent. It follows from
are equivalent. It follows from  that, for
that, for  ,
,

These imply  for the case
for the case  .
.
Similarly, we can prove the case for  or
or  by using
by using  .
.

follows by replacing  in
in  by
by  if
if  or
or  if
if 
 , respectively.
, respectively.

follows by replacing  in
in  by
by  , respectively.
, respectively.

follows by replacing  by
by  or
or  in
in  , respectively.
, respectively.

follows by taking  with
with  in
in  .
.

follows by taking  and
and  in
in  .
.

is clear.

follows by letting  and
and  in
in  .
.

follows by replacing  and
and  in
in  by
by  and
and  , respectively.
, respectively.

. Replacing  by
by  and
and  by
by  in
in  and changing appropriately the notation for the exponents, we obtain
and changing appropriately the notation for the exponents, we obtain  .
.

is clear.
To complete our proof of equivalence of all inequalities in this theorem and in Lemma 2.1, it suffices to show further the following implications.

follows by taking  in
in  .
.

: Let  , where
, where  (hence
(hence  or
or  ). Then it follows from
). Then it follows from  that
that  . Setting
. Setting  , we obtain
, we obtain  , see [14, page 162].
, see [14, page 162].

follows by taking  in
in  .
.

follows by taking  and replacing
and replacing  by
by  in
in  .
.
Remark 2.3.
Letting  and
and  with
with  and
and  in
in  , we obtain the inequality (5) of [18]:
, we obtain the inequality (5) of [18]:

That is,

is a decreasing function of Sclove et al. [18] proved this property by means of the convexity of  , see [14]. Clearly, our method is simpler than theirs.
, see [14]. Clearly, our method is simpler than theirs.
Remark 2.4.
Each  (or
(or  ) is called Hölder's inequality, each
) is called Hölder's inequality, each  (or
(or  ) is called CBS inequality, each
) is called CBS inequality, each  is called Lyapunov's inequality, each
is called Lyapunov's inequality, each  is called Radon's inequality, each
is called Radon's inequality, each  is related to Jensen's inequality.
is related to Jensen's inequality.
References
Infantozzi CA: An introduction to relations among inequalities. Proceedings of the American Mathematical Society Meeting 700, 1979, Cleveland, Ohio, USA
Infantozzi CA: An introduction to relations among inequalities. Notices of the American Mathematical Society 1972, 141: A918-A820.
Marshall AW, Olkin I: Inequalities: Theory of Majorization and Its Applications, Mathematics in Science and Engineering. Volume 143. Academic Press, New York, NY, USA; 1979:xx+569.
Maligranda L: Why Hölder's inequality should be called Rogers' inequality. Mathematical Inequalities & Applications 1998,1(1):69–83.
Maligranda L: Equivalence of the Hölder-Rogers and Minkowski inequalities. Mathematical Inequalities & Applications 2001,4(2):203–207.
Beckenbach EF, Bellman R: Inequality. 4th edition. Springer, Berlin, Germany; 1984.
Casella G, Berger RL: Statistical Inference, Duxbury Advanced Series. Thomson Learning, Duxbury, Mass, USA; 2002.
Callebaut DK: Generalization of the Cauchy-Schwarz inequality. Journal of Mathematical Analysis and Applications 1965,12(3):491–494. 10.1016/0022-247X(65)90016-8
Chung KL: A Course in Probability Theory, Probability and Mathematical Statistics. Volume 2. 2nd edition. Academic Press, New York, NY, USA; 1974:xii+365.
Gurland J: Inequalities of expectations of random variables derived by monotonicity or convexity. The American Statistician 1968,22(2):26–27. 10.2307/2681985
Hardy GH, Littlewood JE, Pólya G: Inequalities. 2nd edition. Cambridge University Press, Cambridge, UK; 1952:xii+324.
Kendall M, Stuart A: The Advanced Theory of Statistics Vol 1. 4th edition. Macmillan, New York, NY, USA; 1977.
Li Y-C, Shaw S-Y: A proof of Hölder's inequality using the Cauchy-Schwarz inequality. Journal of Inequalities in Pure and Applied Mathematics 2006,7(2):-3.
Loève M: Probability Theory. 3rd edition. Springer, New York, NY, USA; 1998.
McLaughlin HW, Metcalf FT: Remark on a recent generalization of the Cauchy-Schwarz inequality. Journal of Mathematical Analysis and Applications 1967,18(3):522–523. 10.1016/0022-247X(67)90043-1
Mitrinović DS: Analytic Inequalities. Springer, New York, NY, USA; 1970:xii+400.
Mullen K: A note on the ratio of two independent random variables. The American Statistician 1967,21(3):30–31.
Sclove SL, Simons G, Ryzin JV: Further remarks on the expectation of the reciprocal of a positive random variable. The Americam Statistician 1967,21(4):33–34.
Zong XF: A further generalization of the Cauchy inequality. Journal of Qufu Normal University 2000,26(4):32–34.
Acknowledgments
The authors wish to thank three reviewers for their valuable suggestions that lead to substantial improvement of this paper. This work is dedicated to Professor Haruo Murakami on his 80th birthday.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yeh, CC., Yeh, HW. & Chan, W. Some Equivalent Forms of the Arithematic-Geometric Mean Inequality in Probability: A Survey. J Inequal Appl 2008, 386715 (2008). https://doi.org/10.1155/2008/386715
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/386715




 and
and 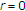 in
in 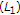 ,
, 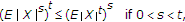
 and
and 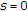 in
in 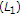 ,
, 
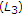 holds.
holds.