Abstract
Most of digital signal processing applications are specified and designed with floatingpoint arithmetic but are finally implemented using fixed-point architectures. Thus, the design flow requires a floating-point to fixed-point conversion stage which optimizes the implementation cost under execution time and accuracy constraints. This accuracy constraint is linked to the application performances and the determination of this constraint is one of the key issues of the conversion process. In this paper, a method is proposed to determine the accuracy constraint from the application performance. The fixed-point system is modeled with an infinite precision version of the system and a single noise source located at the system output. Then, an iterative approach for optimizing the fixed-point specification under the application performance constraint is defined and detailed. Finally the efficiency of our approach is demonstrated by experiments on an MP3 encoder.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.1. Introduction
In digital image and signal processing domains, computing oriented applications are widespread in embedded systems. To satisfy cost and power consumption challenges, fixed-point arithmetic is favored compared to floating-point arithmetic. In fixed-point architectures, memory and bus widths are smaller, leading to a definitively lower cost and power consumption. Moreover, floating-point operators are more complex, having to deal with the exponent and the mantissa, and hence, their area and latency are greater than those of fixed-point operators. Nevertheless, digital signal processing (DSP) algorithms are usually specified and designed with floating-point data types. Therefore, prior to the implementation, a fixed-point conversion is required.
Finite precision computation modifies the application functionalities and degrades the desired performances. Fixed-point conversion must, however, maintain a sufficient level of accuracy. The unavoidable error due to fixed-point arithmetic can be evaluated through analytical- or simulation-based approaches. In our case, the analytical approach has been favored to obtain reasonable optimization times for fixed-point design space exploration. In an analytical approach, the performance degradations are not analyzed directly in the conversion process. An intermediate metric is used to measure the computational accuracy. Thus, the global conversion method is split into two main steps. Firstly, a computational accuracy constraint is determined according to the application performances, and secondly the fixed-point conversion is carried out. The implementation cost is minimized under this accuracy constraint during the fixed-point conversion process. The determination of the computational accuracy constraint is a difficult and open problem and this value cannot be defined directly. This accuracy constraint has to be linked to the quality evaluation and to the performance of the application.
A fixed-point conversion method has been developed for software implementation in [1] and for hardware implementation in [2]. This method is based on an analytical approach to evaluate the fixed-point accuracy. The implementation cost is optimized under an accuracy constraint. In this paper, an approach to determine this accuracy constraint from the application performance requirements is proposed. This module for accuracy constraint determination allows the achieving of a complete fixed-point design flow for which the user only specifies the application performance requirements and not an intermediate metric. The approach proposed in this paper is based on an iterative process to adjust the accuracy constraint. The first value of the accuracy constraint is determined through simulations and depends on the application performance requirements. The fixed-point system behavior is modeled with an infinite precision version of the system and a single noise source located at the system output. The accuracy constraint is thus determined as the maximal value of the noise source power which maintains the desired application quality. Our noise model is valid for rounding quantization law and for systems based on arithmetic operations (addition, subtraction, multiplication, division). This includes LTI and non-LTI systems with or without feedbacks. In summary, the contributions of this paper are (i) a technique to determine the accuracy constraint according to the application performance requirements, (ii) a noise model to estimate the application performances according to the quantization noise level, (iii) an iterative process to adjust the accuracy constraint.
The paper is organized as follows. After the description of the problem and the related works in Section 2, our proposed fixed-point design flow is presented in Section 3. The noise model used to determine the fixed-point accuracy is detailed in Section 4. The case study of an MP3 coder is presented in Section 5. Different experiments and simulations have been conducted to illustrate our approach ability to model quantization effect and to predict performance degradations due to fixed-point arithmetic.
2. Problem Description and Related Works
The aim of fixed-point design is to optimize the fixed-point specification by minimizing the implementation cost. Nevertheless, fixed-point arithmetic introduces an unalterable quantization error which modifies the application functionalities and degrades the desired performance. A minimum computational accuracy must be guaranteed to maintain the application performance. Thus, in the fixed-point conversion process, the fixed-point specification is optimized. The implementation cost is minimized as long as the application performances are fulfilled. In the case of software implementations, the cost corresponds to the execution time, the memory size, or the energy consumption. In the case of hardware implementations, the cost corresponds to the chip area, the critical path delay, or the power consumption.
One of the most critical parts of the conversion process is the evaluation of the degradation of the application performance due to fixed-point arithmetic. This degradation can be evaluated with two kinds of methods corresponding to analytical- and simulation-based approaches. In the simulation-based method, fixed-point simulations are carried out to analyze the application performances [3]. This simulation can be done with system-level design tools such as CoCentric (Synopsys) [4] or Matlab-Simulink (Mathworks) [5]. Also, C++ classes to emulate the fixed-point mechanisms have been developed as in SystemC [4] or Algorithmic C data types [6]. These techniques suffer from a major drawback which is the time required for the simulation [7]. It becomes a severe limitation when these methods are used in the fixed-point specification optimization process where multiple simulations are needed. This optimization process needs to explore the design-space of different data word-lengths. A new fixed-point simulation is required when a fixed-point format is modified. The simulations are made on floating-point machines and the extra-code used to emulate fixed-point mechanisms increases the execution time to between one and two orders of magnitude compared to traditional simulations with floating-point data types [8]. Different techniques [7, 9, 10] have been investigated to reduce this emulation extra-cost. To obtain an accurate estimation of the application performance, a great number of samples must be taken for the simulation. For example, in the digital communication domain, to measure a bit error rate of  , at least
, at least  samples are required. This large number of samples combined with the fixed-point mechanism emulation leads to very long simulation times. For example, in our case, one fixed-point C code simulation of an MP3 coder required 480 seconds. Thus, fixed-point optimization based on simulation leads to too long execution times.
samples are required. This large number of samples combined with the fixed-point mechanism emulation leads to very long simulation times. For example, in our case, one fixed-point C code simulation of an MP3 coder required 480 seconds. Thus, fixed-point optimization based on simulation leads to too long execution times.
In the case of analytical approaches, a mathematical expression of a metric is determined. Determining an expression of the performance for every kind of application is generally an issue. Thus, the performance degradations are not analyzed directly in the conversion process and an intermediate metric which measures the fixed-point accuracy must be used. This computational accuracy metric can be the quantization error bounds [11], the mean square error [12], or the quantization noise power [10, 13]. In the conversion process, the implementation cost is minimized as long as the fixed-point accuracy metric is greater than the accuracy constraint. The analytical expression of the fixed-point accuracy metric is first determined. Then, in the optimization process, this mathematical expression is evaluated to obtain the accuracy value for a given fixed-point specification. This evaluation is much more rapid than in the case of a simulation-based approach. The determination of the accuracy constraint is a difficult problem and this value cannot be defined directly. This accuracy constraint has to be linked to the quality evaluation and performances of the application.
Most of the existing fixed-point conversion methods based on an analytical approach [1, 11, 13–15] evaluate the output noise level, but they do not predict the application performance degradations due to fixed-point arithmetic. In [12], an analytical expression is proposed to link the bit error rate and the mean square error. Nevertheless, to our knowledge, no general method was proposed to link computational accuracy constraint with any application performance metric. In this paper, a global fixed-point design flow is presented to optimize the fixed-point specification under application performance requirements. A technique to determine the fixed-point accuracy constraint is proposed and the associated noise model is detailed.
3. Proposed Fixed-Point Design Process
3.1. Global Process
A fixed-point datum  of
of  bits is made up of an integer part and a fractional part. The number of bits associated with each part does not change during the processing leading to a fixed binary position. Let
bits is made up of an integer part and a fractional part. The number of bits associated with each part does not change during the processing leading to a fixed binary position. Let  and
and  be the binary-point position referenced, respectively, from the most significant bit (MSB) and the least significant bit (LSB). The terms
be the binary-point position referenced, respectively, from the most significant bit (MSB) and the least significant bit (LSB). The terms  and
and  correspond, respectively, to the integer and fractional part word-length. The word-length
correspond, respectively, to the integer and fractional part word-length. The word-length  is equal to the sum of
is equal to the sum of  and
and  . The aim of the fixed-point conversion is to determine the number of bits for each part and for each datum.
. The aim of the fixed-point conversion is to determine the number of bits for each part and for each datum.
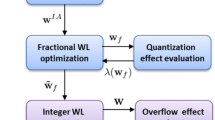
The global process proposed for designing fixed-point systems under application performance constraints is presented in Figure 1 and detailed in the next sections. The metric used to evaluate the fixed-point accuracy is the output quantization noise power. Let  be the system output quantization noise. The noise power is also called in this paper noise level and is represented by the term
be the system output quantization noise. The noise power is also called in this paper noise level and is represented by the term  . The accuracy constraint
. The accuracy constraint  used for the fixed-point conversion process corresponds to the maximal noise level under which the application performance is maintained. The challenge is to establish a link between the accuracy constraint
used for the fixed-point conversion process corresponds to the maximal noise level under which the application performance is maintained. The challenge is to establish a link between the accuracy constraint  and the desired application performances
and the desired application performances  . These application performances must be predicted according to the noise level
. These application performances must be predicted according to the noise level  . The global fixed-point design flow is made-up of three stages and an iterative process is used to adjust the accuracy constraint used for the fixed-point conversion. These three stages are detailed in the following sections.
. The global fixed-point design flow is made-up of three stages and an iterative process is used to adjust the accuracy constraint used for the fixed-point conversion. These three stages are detailed in the following sections.
3.2. Accuracy Constraint Determination
The first step corresponds to the initial accuracy constraint determination  which is the maximal value of the noise level satisfying the performance objective
which is the maximal value of the noise level satisfying the performance objective  . For example, in a digital communication receiver, the maximal quantization noise level is determined according to the desired bit error rate.
. For example, in a digital communication receiver, the maximal quantization noise level is determined according to the desired bit error rate.
First, a prediction of the application performance is performed with the technique presented below. Let  be the function representing the predicted performances according to the noise level
be the function representing the predicted performances according to the noise level  . To determine the initial accuracy constraint value (
. To determine the initial accuracy constraint value ( ), equation
), equation  is solved graphically, and
is solved graphically, and  is the solution of this equation.
is the solution of this equation.
3.2.1. Performance Prediction
To define the initial value of the accuracy constraint ( ), the application performance is predicted according to the noise level
), the application performance is predicted according to the noise level  . The fixed-point system is modeled by the infinite precision version of the system and a single noise source
. The fixed-point system is modeled by the infinite precision version of the system and a single noise source  located at the system output as shown in Figure 2. This noise source models all the quantization noise sources inside the fixed-point system. The system floating-point version is used and the noise
located at the system output as shown in Figure 2. This noise source models all the quantization noise sources inside the fixed-point system. The system floating-point version is used and the noise  is added to the output. The noise model used for
is added to the output. The noise model used for  is presented in Section 4. Different noise levels
is presented in Section 4. Different noise levels  for the noise source
for the noise source  are tested to measure the application performance and to obtain the predicted performance
are tested to measure the application performance and to obtain the predicted performance  function according to the noise level
function according to the noise level  . The accuracy constraint
. The accuracy constraint  corresponds to the maximal value of the noise level which allows the maintenance of the desired application performance.
corresponds to the maximal value of the noise level which allows the maintenance of the desired application performance.
Most of the time, the floating-point simulation has already been developed during the application design step, and the application output samples can be used directly. Therefore, the time required for exploring the noise power values is significantly reduced and becomes negligible with regard to the global implementation flow. Nevertheless, this technique cannot be applied for systems where the decision on the output is used inside the system like, for example, decision-feedback equalization. In this case, a new floating-point simulation is required for each noise level which is tested.
3.3. Fixed-Point Conversion Process
The second step corresponds to the fixed-point conversion. The goal is to optimize the application fixed-point specification under the accuracy constraint  . The approaches presented in [1] for software implementation and in [2] for hardware implementation are used. This fixed-point conversion can be divided into two main modules. The flow diagram used for this conversion is shown in Figure 3.
. The approaches presented in [1] for software implementation and in [2] for hardware implementation are used. This fixed-point conversion can be divided into two main modules. The flow diagram used for this conversion is shown in Figure 3.
The first part corresponds to the determination of the integer part word-length of each datum. The number of bits  for this integer part must allow the representation of all the values taken by the data and is obtained from the data bound values. Thus, firstly the dynamic range is evaluated for each datum. Then, these results are used to determine, for each data, the binary-point position which minimizes the integer part word-length and which avoids overflow. Moreover, scaling operations are inserted in the application to adapt the fixed-point format of a datum to its dynamic range or to align the binary-point of the addition inputs.
for this integer part must allow the representation of all the values taken by the data and is obtained from the data bound values. Thus, firstly the dynamic range is evaluated for each datum. Then, these results are used to determine, for each data, the binary-point position which minimizes the integer part word-length and which avoids overflow. Moreover, scaling operations are inserted in the application to adapt the fixed-point format of a datum to its dynamic range or to align the binary-point of the addition inputs.
The second part corresponds to the determination of the fractional part word-length. The number of bits  for this fractional part defines the computational accuracy. Thus, the data word-lengths are optimized. The implementation cost is minimized under the accuracy constraint. Let
for this fractional part defines the computational accuracy. Thus, the data word-lengths are optimized. The implementation cost is minimized under the accuracy constraint. Let  be an
be an  -size vector including the word-length of the
-size vector including the word-length of the  application data. Let
application data. Let  be the implementation cost and let
be the implementation cost and let  be the computational accuracy obtained for the word-length vector
be the computational accuracy obtained for the word-length vector  . The implementation cost
. The implementation cost  is minimized under the accuracy constraint
is minimized under the accuracy constraint  :
:

The vector  is the optimized fixed-point specification obtained for the constraint value
is the optimized fixed-point specification obtained for the constraint value  at iteration
at iteration  of the process.
of the process.
The data word-length determination corresponds to an optimization problem where the implementation cost and the application accuracy must be evaluated. The major challenge is to evaluate the fixed-point accuracy. To obtain reasonable optimization times, analytical approaches to evaluate the accuracy have been favored. The computational accuracy is evaluated using the quantization noise power. The mathematical expression of this noise power is computed for systems based on arithmetic operations with the technique presented in [16]. This mathematical expression is determined only once and is used for the different iterations of the fixed-point conversion process and for the different iterations of the global design flow.
3.4. Performance Evaluation and Accuracy Constraint Adjustment
The third step corresponds to the evaluation of the real application performance. The optimized fixed-point specification  is simulated and the application performance is measured. The measured performances
is simulated and the application performance is measured. The measured performances  and the objective value
and the objective value  are compared and, if (2) is not satisfied, the accuracy constraint is adjusted and a new iteration is performed:
are compared and, if (2) is not satisfied, the accuracy constraint is adjusted and a new iteration is performed:

where the term  is the tolerance on the objective value.
is the tolerance on the objective value.
To modify the accuracy constraint value, two measurements are used. Nevertheless, in the first iteration, only the point  is available. To obtain a second point, all the data word-lengths are increased (or decreased) by
is available. To obtain a second point, all the data word-lengths are increased (or decreased) by  bits. In this case, as demonstrated in appendix the noise level is increased (or decreased) by
bits. In this case, as demonstrated in appendix the noise level is increased (or decreased) by  dB. The number of bits
dB. The number of bits  is chosen as the minimal value respecting the following inequality:
is chosen as the minimal value respecting the following inequality:

The choice to increment or decrement depends on the slope sign of  and the sign of the difference between
and the sign of the difference between  and
and  . For the next iterations, two or more measured points are available. The two consecutive points of abscissa
. For the next iterations, two or more measured points are available. The two consecutive points of abscissa  and
and  such as
such as  are selected and let
are selected and let  be the linear equation linking the two points
be the linear equation linking the two points  and
and  . The adjusted accuracy constraint used for the next iteration
. The adjusted accuracy constraint used for the next iteration  is
is  defined such as
defined such as  . The adjustment process is illustrated in Section 5.3 through an example.
. The adjustment process is illustrated in Section 5.3 through an example.
4. Noise Model
4.1. Noise Model Description
4.1.1. Quantization Noise Model
The use of fixed-point arithmetic introduces an unavoidable quantization error when a signal is quantified. A common model for signal quantization has been proposed by Widrow in [17] and refined in [18]. The quantization of a signal is modeled by the sum of this signal and a random variable  , which represents the quantization noise. This additive noise
, which represents the quantization noise. This additive noise  is a uniformly distributed white noise that is uncorrelated with the signal, and independent from the other quantization noises. In this study, the round-off method is used rather than truncation. For convergent rounding, the quantization leads to an error with a zero mean. For classical rounding, the mean can be assumed to be null as soon as several bits (more than 3 bits) are eliminated in the quantization process. The expression of the statistical parameters of the noise sources can be found in [16]. If
is a uniformly distributed white noise that is uncorrelated with the signal, and independent from the other quantization noises. In this study, the round-off method is used rather than truncation. For convergent rounding, the quantization leads to an error with a zero mean. For classical rounding, the mean can be assumed to be null as soon as several bits (more than 3 bits) are eliminated in the quantization process. The expression of the statistical parameters of the noise sources can be found in [16]. If  is the quantization step (accuracy), the noise values are in the interval
is the quantization step (accuracy), the noise values are in the interval  .
.
4.1.2. Noise Model for Fixed-Point System
The noise model for fixed-point systems presented in [16] is used. The output quantization noise  is the contribution of the different noise sources. Each noise source
is the contribution of the different noise sources. Each noise source  is due to the elimination of some bits during a cast operation. From the propagation model presented in [16], for each arithmetic operation it can be shown that the operation output noise is a weighted sum of the input noises associated with each operation input. The weights of the sum do not include noise terms, because the product of the noise terms can be neglected. Thus, in the case of systems based on arithmetic operations, the expression of the output quantization noise
is due to the elimination of some bits during a cast operation. From the propagation model presented in [16], for each arithmetic operation it can be shown that the operation output noise is a weighted sum of the input noises associated with each operation input. The weights of the sum do not include noise terms, because the product of the noise terms can be neglected. Thus, in the case of systems based on arithmetic operations, the expression of the output quantization noise  is as follows:
is as follows:

where the term  represents the impulse response of the system having
represents the impulse response of the system having  as output and
as output and  as input. In the case of linear time invariant (LTI) systems, the different terms
as input. In the case of linear time invariant (LTI) systems, the different terms  are constant. In the case of non-LTI systems the terms
are constant. In the case of non-LTI systems the terms  are time varying. In this context, two extreme cases can be distinguished. In the first case, a quantization noise
are time varying. In this context, two extreme cases can be distinguished. In the first case, a quantization noise  predominates in terms of variance compared to the other noise sources. A typical example is an extensive reduction of the number of bits at the system output compared to the other fixed-point formats. In this case, the level of this output quantization noise exceeds the other noise source levels. Thus, the probability density function of the output quantization noise is very close to that of the predominant noise source and can be assimilated to a uniform distribution. In the second case, an important number of independent noise sources have similar statistical parameters and no noise source predominates. All the noise sources are uniformly distributed and independent of each other. By using the central limit theorem, the sum of the different noise sources can be modeled by a centered normally distributed noise.
predominates in terms of variance compared to the other noise sources. A typical example is an extensive reduction of the number of bits at the system output compared to the other fixed-point formats. In this case, the level of this output quantization noise exceeds the other noise source levels. Thus, the probability density function of the output quantization noise is very close to that of the predominant noise source and can be assimilated to a uniform distribution. In the second case, an important number of independent noise sources have similar statistical parameters and no noise source predominates. All the noise sources are uniformly distributed and independent of each other. By using the central limit theorem, the sum of the different noise sources can be modeled by a centered normally distributed noise.
From these two extreme cases, an intuitive way to model the output quantization noises of a complex system is to use a noise  which is the weighted sum of a Gaussian and a uniform noise. Let
which is the weighted sum of a Gaussian and a uniform noise. Let  be the probability density function of the noise
be the probability density function of the noise  . Let
. Let  be a normally distributed noise with a mean and variance equal, respectively, to 0 and 1. Let
be a normally distributed noise with a mean and variance equal, respectively, to 0 and 1. Let  be a uniformly distributed noise in the interval
be a uniformly distributed noise in the interval  . The noise
. The noise  is defined with the following expression:
is defined with the following expression:

The weight  is set in the interval
is set in the interval  and allows the representation of the different intermediate cases between the two extreme cases presented above. The weight
and allows the representation of the different intermediate cases between the two extreme cases presented above. The weight  fixes the global noise variance.
fixes the global noise variance.
4.1.3. Choice of Noise Model Parameters
The noise  is assumed to be white noise. Nevertheless, the spectral density function of the real quantization noise depends on the system and most of the time is not white. If the application performance is sensitive to the noise spectral characteristic, this assumption will degrade the performance prediction. Nevertheless, the imperfections of the noise model are compensated by the iteration process which adapts the accuracy constraint. The effects of the noise model imperfections increase in the number of iterations required to converge to the optimized solution.
is assumed to be white noise. Nevertheless, the spectral density function of the real quantization noise depends on the system and most of the time is not white. If the application performance is sensitive to the noise spectral characteristic, this assumption will degrade the performance prediction. Nevertheless, the imperfections of the noise model are compensated by the iteration process which adapts the accuracy constraint. The effects of the noise model imperfections increase in the number of iterations required to converge to the optimized solution.
To take account of the noise spectral characteristics, the initial accuracy constraint  can be adjusted and determined in a two-step process. The accuracy constraint
can be adjusted and determined in a two-step process. The accuracy constraint  is determined firstly assuming that the noise
is determined firstly assuming that the noise  is white. Then, the fixed-point conversion is carried out and the fixed-point specification
is white. Then, the fixed-point conversion is carried out and the fixed-point specification  is simulated. The spectral characteristics of the real output quantization noise
is simulated. The spectral characteristics of the real output quantization noise  are measured. Afterwards, the accuracy constraint
are measured. Afterwards, the accuracy constraint  is adjusted and determined a second time assuming that the noise
is adjusted and determined a second time assuming that the noise  has the same spectral characteristics as the real quantization noise
has the same spectral characteristics as the real quantization noise  .
.
Like for the spectral characteristics, the weight  is set to an arbitrary value depending of the kind of implementation. Then, after the first iteration, the
is set to an arbitrary value depending of the kind of implementation. Then, after the first iteration, the  value is adjusted by using the measured
value is adjusted by using the measured  value obtained from the real output quantization noise
value obtained from the real output quantization noise  .
.
In most of the processors the architecture is based on a double precision computation. Inside the processing unit, most of the computations are carried out without loss of information and truncation occurs when the data are stored in memory. This approach tends to obtain a predominant noise source at the system output. Thus, for software implementation the weight  is fixed to 1. For hardware implementation the optimization of the operator word-length leads to a fixed-point system where no noise source is predominant. The optimization distributes the noise to each operation. Thus, for hardware implementation the weight
is fixed to 1. For hardware implementation the optimization of the operator word-length leads to a fixed-point system where no noise source is predominant. The optimization distributes the noise to each operation. Thus, for hardware implementation the weight  is fixed to 0.
is fixed to 0.
4.2. Validation of the Proposed Model
4.2.1. Validation Methodology
The aim of this section is to analyze the accuracy of our model with real quantization noises. The real noises are obtained through simulations. The output quantization noise is the difference between the system outputs obtained with a fixed-point and a floating-point simulation. The floating-point simulation which uses double-precision types is considered to be the reference. Indeed, in this case, the error due to the floating-point arithmetic is definitely less than the error due to the fixed-point arithmetic. Thus, the floating-point arithmetic errors can be neglected.
Our model is valid if a balance weight  can be found to model the real noise probability density function with (5). The accuracy of our model with real noises is analyzed with the
can be found to model the real noise probability density function with (5). The accuracy of our model with real noises is analyzed with the  goodness-of-fit test. This test is a statistical tool which can be used to determine if a real quantization noise
goodness-of-fit test. This test is a statistical tool which can be used to determine if a real quantization noise  follows a chosen probability density function
follows a chosen probability density function  [19]. Let
[19]. Let  be the hypothesis that
be the hypothesis that  follows the probability density function
follows the probability density function  . The test is based on the distance between the two probability density functions. If
. The test is based on the distance between the two probability density functions. If  is the observed frequency for interval
is the observed frequency for interval  ,
,  is the expected frequency for
is the expected frequency for  and
and  the number of interval
the number of interval  , the statistical test is:
, the statistical test is:

This statistical test follows the  distribution with
distribution with  degrees of freedom. Therefore, if the distance is higher than the threshold
degrees of freedom. Therefore, if the distance is higher than the threshold  , then the hypothesis
, then the hypothesis  (
( follows the probability density function
follows the probability density function  ) is rejected. The significance level of the test is the probability of rejecting
) is rejected. The significance level of the test is the probability of rejecting  when the hypothesis is true. Choosing a certain value for this level will set the threshold distance for the test. According to [20], the significance level
when the hypothesis is true. Choosing a certain value for this level will set the threshold distance for the test. According to [20], the significance level  should be in
should be in  .
.
Concerning the observed noise, there is no a priori knowledge of the balance coefficient  . Thus, the
. Thus, the  test has to be used collectively with a searching algorithm. This algorithm finds the
test has to be used collectively with a searching algorithm. This algorithm finds the  weight for which the
weight for which the  fits the best to the noise. Let
fits the best to the noise. Let  be the optimized value which minimizes the term
be the optimized value which minimizes the term  from (6), then:
from (6), then:

The real quantization noise can be modeled with (5) if the optimized value  is lower than the threshold
is lower than the threshold  .
.
4.2.2. FIR Filter Example
The first system on which the before-mentioned test has been performed is a 32-tap FIR filter. The filter output  is obtained from the following expression:
is obtained from the following expression:

where  is the filter input and
is the filter input and  the filter coefficients.
the filter coefficients.
The signal flow graph of one cell  is presented in Figure 4. To simplify the presentation, the integer part word-length for the multiplication output and the input and output of the addition are set to be equal. Thus, no scaling operation is necessary to align the binary point positions at the adder input. This simplification has no influence on the generality of the results.
is presented in Figure 4. To simplify the presentation, the integer part word-length for the multiplication output and the input and output of the addition are set to be equal. Thus, no scaling operation is necessary to align the binary point positions at the adder input. This simplification has no influence on the generality of the results.
The word-lengths of the input signal ( ) and of the coefficient (
) and of the coefficient ( ) are equal to 16 bits. If no bit is eliminated during the multiplication, the multiplier output word-length
) are equal to 16 bits. If no bit is eliminated during the multiplication, the multiplier output word-length  is equal to 32 bits. The adder input and output word-length are equal to
is equal to 32 bits. The adder input and output word-length are equal to  . At the filter output, the data is stored in memory with a word-length
. At the filter output, the data is stored in memory with a word-length  equal to 16 bits.
equal to 16 bits.
Two kinds of quantization noise sources can be located in the filter. A noise source  can be located at each multiplier output if bits are eliminated between the multiplication and the addition. The number of eliminated bits
can be located at each multiplier output if bits are eliminated between the multiplication and the addition. The number of eliminated bits  is obtained with the following expression:
is obtained with the following expression:

A noise source  is located at the filter output if bits are eliminated when the addition output is stored in memory. The number of eliminated bits
is located at the filter output if bits are eliminated when the addition output is stored in memory. The number of eliminated bits  is obtained with the following expression:
is obtained with the following expression:

The adder word-length  is varying between 16 and 32 bits, while the output of the system is always quantized on 16 bits.
is varying between 16 and 32 bits, while the output of the system is always quantized on 16 bits.
The probability density function of the filter output quantization noise is shown in Figure 5 for different values of  . The noise is uniform when one source is prevailing (the adder is on 32 bits). As long as the influence of the sources at the output of the multiplier is increasing (the length is decreasing), the distribution of the output noise tends to become Gaussian. These simple visual observations can be confirmed using the
. The noise is uniform when one source is prevailing (the adder is on 32 bits). As long as the influence of the sources at the output of the multiplier is increasing (the length is decreasing), the distribution of the output noise tends to become Gaussian. These simple visual observations can be confirmed using the  -searching algorithm. The change of the optimized value
-searching algorithm. The change of the optimized value  for different adder word-lengths, varying from 16 to 32 bits, is shown in Figure 6. When the output of the multiplier is 16 or 17 bits,
for different adder word-lengths, varying from 16 to 32 bits, is shown in Figure 6. When the output of the multiplier is 16 or 17 bits,  , the sources are numerous. Their influence on the system output leads to a Gaussian noise. As the length of the multiplier increases,
, the sources are numerous. Their influence on the system output leads to a Gaussian noise. As the length of the multiplier increases,  also grows and eventually tends to 1. When
also grows and eventually tends to 1. When  is greater than 26 bits, the variance of the noise sources
is greater than 26 bits, the variance of the noise sources  located at each multiplier output is insignificant compared to the variance of the noise source
located at each multiplier output is insignificant compared to the variance of the noise source  located at the filter output. Thus, this latter is prevailing and its influence on the output signal is a uniform white noise. In this case, the boundary values of the noise are
located at the filter output. Thus, this latter is prevailing and its influence on the output signal is a uniform white noise. In this case, the boundary values of the noise are  .
.
4.2.3. Benchmarks
To validate our noise model, different DSP application benchmarks have been tested and the adequacy between our model and real noises has been measured. For each application, different output noises have been obtained by evaluating several fixed-point specifications and different application parameters. The number of output noises analyzed for one application is defined through the term  . For these different applications based on arithmetic operations, the input and the output word-length are fixed to 16 bits. The different fixed-point specifications are obtained by modifying the adder input and output word-lengths. Eight values are tested for the adder:
. For these different applications based on arithmetic operations, the input and the output word-length are fixed to 16 bits. The different fixed-point specifications are obtained by modifying the adder input and output word-lengths. Eight values are tested for the adder:  .
.
The results are shown in Table 1 for two significance levels  corresponding to the boundary values (0.05 and 0.001). For each application, the number
corresponding to the boundary values (0.05 and 0.001). For each application, the number  of real noise which can be modeled with our noise model is measured. The adequacy between our model and real noises is measured with the metric
of real noise which can be modeled with our noise model is measured. The adequacy between our model and real noises is measured with the metric  defined with the following expression:
defined with the following expression:

This metric corresponds to the ratio of output noises for which a weight  can be found to model the noise probability density function with (5).
can be found to model the noise probability density function with (5).
The different applications used to test our approach are presented in this paragraph. A fast Fourier transform (FFT) has been performed on vectors made-up of 16 or 32 samples. Linear time-invariant (LTI) recursive systems have been tested through an eight-order infinite impulse filter (IIR). This filter is implemented with a cascaded form based on four second order cells. For this cascaded eight-order IIR filter, 24 permutations of the second-order cells can be tested leading to very different output noise characteristics [21]. Three forms have been tested corresponding to Direct-form I, Direct-Form II and Transposed-Form. An adaptive filter based on the affine projection algorithm (APA) structure [22] has been tested. This filter is made-up of eight taps and the observation vector length is equal to five. A nonlinear nonrecursive filter has been tested using a second-order Volterra filter. Our benchmarks do not include non linear systems with memory and thus do not validate this specific class of algorithms.
More complex applications have been studied through a WCDMA receiver and an MP3 coder. The MP3 coder is presented in Section 5.1. For the third generation mobile communication systems based on the WCDMA technique, the receiver is mainly made up of an FIR receiving filter and a rake receiver including synchronization mechanisms [23]. The rake receiver is made-up of three parts corresponding to the transmission channel estimation, synchronization and symbol decoding. The synchronization of the code and the received signal is realized with a delay-locked loop (DLL). The noises are observed at the output of the symbol decoding part.
The results from Table 1 show that our noise model can be applied to most of the real noises obtained for different applications. For some applications, like FFT, FIR, WCDMA receiver and the Volterra filter, a balance coefficient  can always be found. These four applications are nonrecursive and the FFT, FIR, WCDMA receiver are LTI systems.
can always be found. These four applications are nonrecursive and the FFT, FIR, WCDMA receiver are LTI systems.
For the eight-order infinite impulse filter, almost all the noises (97%–100%) can be modeled with our approach. For these filters, 90% of the output quantization noise are modeled with a balance coefficient  equal to 0. Thus, the output noise is a purely normally distributed noise. In LTI system, the output noise
equal to 0. Thus, the output noise is a purely normally distributed noise. In LTI system, the output noise  due to the noise
due to the noise  corresponds to the convolution of the noise
corresponds to the convolution of the noise  with
with  . This term
. This term  is the impulse response of the transfer function between the noise source and the output. Thus, the output noise is the weighted sum of the delayed version of the noise
is the impulse response of the transfer function between the noise source and the output. Thus, the output noise is the weighted sum of the delayed version of the noise  . The noise
. The noise  is a uniformly distributed white noise, thus the delayed versions of the noise
is a uniformly distributed white noise, thus the delayed versions of the noise  are uncorrelated. The samples are uncorrelated but are not independent and thus the central limit theorem cannot be applied directly. Even if only one noise source is located in the filter, the output noise is a sum of noncorrelated noises and this output noise tends to have a Gaussian distribution. For the MP3 coder, when the level is 0.001 the test is successful about 87% of the time (78% when
are uncorrelated. The samples are uncorrelated but are not independent and thus the central limit theorem cannot be applied directly. Even if only one noise source is located in the filter, the output noise is a sum of noncorrelated noises and this output noise tends to have a Gaussian distribution. For the MP3 coder, when the level is 0.001 the test is successful about 87% of the time (78% when  is 0.05).
is 0.05).
For the different applications, the metric  is close to 100%. These results show that our model is suitable to model the output quantization noise of fixed-point systems.
is close to 100%. These results show that our model is suitable to model the output quantization noise of fixed-point systems.
5. Case Study: MP3 Coder
The application used to illustrate our approach and to underline its efficiency comes from audio compression and corresponds to an MP3 coder. First, the application and the associated quality criteria are briefly described. Then, the ability of our noise model to predict application performance is evaluated. Finally, a case study to obtain an optimized fixed-point specification which ensures the desired performances is detailed.
5.1. Application Presentation
5.1.1. MP3 Coder Description
The MP3 compression, corresponding to MPEG-1 Audio Layer 3, is a popular digital audio encoding which allows efficient audio data compression. It must maintain a reproduction quality close to the original uncompressed audio. This compression technique relies on a psychoacoustic model which analyzes the audio signal according to how human beings perceive a sound. This step allows the formation of some signal to noise masks which indicate where noise can be added without being heard. The MP3 encoder structure is shown in Figure 7. The signal to be compressed is analyzed using a polyphase filter which divides the signal into 32 equal-width frequency bands. The modified discrete cosine transform (MDCT) further decomposes the signal into 576 subbands to produce the signal which will actually be quantized. Then, the quantization loop allocates different accuracies to the frequency bands according to the signal to noise mask. The processed signal is coded using Huffman code [24]. The MP3 coder can be divided into two signal flows. The one composed from the polyphase filter and the MCDT and the one composed from the FFT and the psychoacoustic model. The fixed-point conversion of the second signal flow has low influence on compression quality and thus, in this paper, the results are presented only for the first signal flow.
The BLADE [25] coder has been used with a 192 Kbits/s constant bit rate. This coder leads to a good quality compression with floating-point data types. A sample group of audio data has been defined for the experiments. This group contains various kinds of sounds, where each can lead to different problems during encoding (harmonic purity, high or low dynamic range,  ). Ten different input tracks have been selected and tested.
). Ten different input tracks have been selected and tested.
5.1.2. Quality Criteria
In the case of an MP3 coder, the output noise power metric cannot be used directly as a compression quality criterion. The compression is indeed based on adding quantization noises where it is imperceptible, or at least barely audible. The compression quality has been tested using EAQUAL [26] which stands for evaluation of audio quality. It is an objective measurement tool very similar to the ITU-R recommendation BS.1387 based on PEAQ technique. This has to be used because listening tests are impossible to formalize. In EAQUAL, the degradations due to compression are measured with the objective degradation grade (ODG) metric. This metric varies from 0 (no degradation) to −4 (inaudible). The level of −1 is the threshold beyond the degradation becomes annoying for ears. This ODG is used to measure the degradation due to fixed-point computation. Thus for the fixed-point design, the aim is to obtain the fixed-point specification of the coder which minimizes the implementation cost and maintains an ODG lower or equal to −1 for the different audio tracks of the sample group.
5.2. Performance Prediction
The efficiency of our approach depends on the quality of the noise model used to determine the accuracy constraint. To validate this latter, its ability to model real quantization noises and its capability to predict the application performance according to the quantization noise level are analyzed through experiments.
Our model capability to predict application performance according to the quantization noise level has been analyzed. The real and the predicted performances are compared for different noise levels  . The application performance prediction is obtained with our model as described in Figure 2. The random signal modeling the output quantization noise with a noise level of
. The application performance prediction is obtained with our model as described in Figure 2. The random signal modeling the output quantization noise with a noise level of  is added to the infinite precision system output. The real performances are measured with a fixed-point simulation of the application. This fixed-point specification is obtained with a fixed-point conversion having
is added to the infinite precision system output. The real performances are measured with a fixed-point simulation of the application. This fixed-point specification is obtained with a fixed-point conversion having  as an accuracy constraint. For this audio compression application, the evolution of the predicted (
as an accuracy constraint. For this audio compression application, the evolution of the predicted ( ) and the real (
) and the real ( ) objective degradation grade (ODG) is given in Figure 8(a). These performances have been measured for different quantization noise levels
) objective degradation grade (ODG) is given in Figure 8(a). These performances have been measured for different quantization noise levels  included in the range [−108 dB; −88 dB].
included in the range [−108 dB; −88 dB].
The predicted and real performances are very close except for two noise levels equal to −98.5 dB and −88 dB. In these cases, the difference between the two functions  and
and  is, respectively, equal to 0.2 and 0.4. In the other cases, the difference is less than 0.1. It must be underlined that when the ODG is lower than −1.5, the ODG evolution slope is higher, and a slight difference in the noise level leads to a great difference on the ODG. The case where only the polyphase filter is considered to use fixed-point data type (the MDCT is computed with floating-point data-types) has been tested. The difference between the two functions
is, respectively, equal to 0.2 and 0.4. In the other cases, the difference is less than 0.1. It must be underlined that when the ODG is lower than −1.5, the ODG evolution slope is higher, and a slight difference in the noise level leads to a great difference on the ODG. The case where only the polyphase filter is considered to use fixed-point data type (the MDCT is computed with floating-point data-types) has been tested. The difference between the two functions  and
and  is less than 0.13. Thus, our approach allows the accurate prediction of the application performance.
is less than 0.13. Thus, our approach allows the accurate prediction of the application performance.
5.3. Fixed-Point Optimization under Performance Constraint
In this section, the design process to obtain an optimized fixed-point specification which guarantees a given level of performances is detailed. The ODG objective  is fixed to −1 corresponding to the acceptable degradation limit.
is fixed to −1 corresponding to the acceptable degradation limit.
First, to determine the initial value of the accuracy constraint, a prediction of the application performance is made. This initial value determination corresponds to the first stage of the design flow presented in Figure 1. The function  is determined for different noise levels with a balance coefficient varying from 0 to 1. Two results can be underlined. Firstly, the influence of the balance coefficient
is determined for different noise levels with a balance coefficient varying from 0 to 1. Two results can be underlined. Firstly, the influence of the balance coefficient  has been tested and is relatively low. Between the extreme values of
has been tested and is relatively low. Between the extreme values of  , the ODG variation is on average less than 0.1. In these experiments, a hardware implementation is under consideration, thus the balance coefficient
, the ODG variation is on average less than 0.1. In these experiments, a hardware implementation is under consideration, thus the balance coefficient  is fixed to 0.
is fixed to 0.
Secondly, the ODG change is strongly linked to the kind of input tracks used for the compression.
In these experiments, 10 different input tracks have been tested. To obtain an ODG equal to −1, a difference of 33 dB is obtained between the minimal and the maximal ODG. These results underline the necessity to have inputs which are representative of the different audio tracks encountered in the real world. In the rest of the study, the audio sample which leads to the minimal ODG is used as a reference. The results obtained in this case are shown in Figure 8(a) and a zoom is given in Figure 8(b).
To determine the initial value of the accuracy constraint, equation  is graphically solved. The noise level
is graphically solved. The noise level  is equal to −99.35 dB.
is equal to −99.35 dB.  is used as an accuracy constraint for the fixed-point conversion. This conversion is the second stage of the design flow (see Figure 1). The aim is to find the fixed-point specification which minimizes the implementation cost and maintains a noise level lower than
is used as an accuracy constraint for the fixed-point conversion. This conversion is the second stage of the design flow (see Figure 1). The aim is to find the fixed-point specification which minimizes the implementation cost and maintains a noise level lower than  . After the conversion, the fixed-point specification is simulated to measure the performance. It corresponds to the third stage of the design flow (see Figure 1). The measured performance
. After the conversion, the fixed-point specification is simulated to measure the performance. It corresponds to the third stage of the design flow (see Figure 1). The measured performance  is equal to −1.2. To obtain the second point of
is equal to −1.2. To obtain the second point of  abscissa, all the data word-lengths are increased by one bit and the measured performance
abscissa, all the data word-lengths are increased by one bit and the measured performance  is equal to −0.77. The accuracy constraint
is equal to −0.77. The accuracy constraint  for the next iteration is obtained by solving
for the next iteration is obtained by solving  . The function
. The function  is the linear equation linking the points
is the linear equation linking the points  and
and  . The obtained value is equal to −102.2 dB. The process is iterated and the following accuracy constraints are equal to −101 dB and −100,7 dB. The values obtained for the different iterations are presented in Table 2. For this example, six iterations are needed to obtain an optimized fixed-point specification which leads to an ODG equal to −0.99. Only, three iterations are needed to obtain an ODG of −0.95.
. The obtained value is equal to −102.2 dB. The process is iterated and the following accuracy constraints are equal to −101 dB and −100,7 dB. The values obtained for the different iterations are presented in Table 2. For this example, six iterations are needed to obtain an optimized fixed-point specification which leads to an ODG equal to −0.99. Only, three iterations are needed to obtain an ODG of −0.95.
 . The term
. The term  corresponds to the accuracy constraint for the fixed-point conversion. The term
corresponds to the accuracy constraint for the fixed-point conversion. The term  is the measured performance obtained after the fixed-point conversion.
is the measured performance obtained after the fixed-point conversion.5.3.1. Execution Time
For our approach, the execution time of the iterative process has been measured. First, the initial accuracy constraint is determined. The floating-point simulations have already been carried out in the algorithm design process and this floating-point simulation time is not considered. For each tested noise level, the noise is added to the MDCT output and then the ODG is computed. The global execution time  of this first stage is equal to 420 seconds. This stage is carried out only once.
of this first stage is equal to 420 seconds. This stage is carried out only once.
For the fixed-point conversion, the analytical model for noise level estimation is determined at the first iteration. This execution time  of this process is equal to 120 seconds. It takes a small amount of time but it is done only once. Then, this model is used in the process of fixed-point optimization and the fixed-point accuracy is computed instantaneously by evaluating a mathematical expression. For this example, each fixed-point conversion
of this process is equal to 120 seconds. It takes a small amount of time but it is done only once. Then, this model is used in the process of fixed-point optimization and the fixed-point accuracy is computed instantaneously by evaluating a mathematical expression. For this example, each fixed-point conversion  takes only 0.7 seconds due to the analytical approach.
takes only 0.7 seconds due to the analytical approach.
In this fixed-point design process, most of the time is spent in the fixed-point simulation (stage 3). This simulation is carried out with C++ code with optimized fixed-point data types. For this example, the execution time  of each fixed-point simulation is equal to 480 seconds. But, only one fixed-point simulation is required by iteration and a small number of iterations are needed.
of each fixed-point simulation is equal to 480 seconds. But, only one fixed-point simulation is required by iteration and a small number of iterations are needed.
The expression of the global execution time  for our approach based on analytical approach for fixed-point conversion is as follows:
for our approach based on analytical approach for fixed-point conversion is as follows:

where  represents the number of iterations required to obtain the optimized fixed-point specification for a given ODG constraint. In this example, six iterations are needed to obtain an optimized fixed-point specification which leads to an ODG equal to −0.99 and three iterations are needed to obtain an ODG of −0.95. Thus, the global execution time is equal to 49 minutes for an ODG of −0.99 and 33 minutes for an ODG of −0.95.
represents the number of iterations required to obtain the optimized fixed-point specification for a given ODG constraint. In this example, six iterations are needed to obtain an optimized fixed-point specification which leads to an ODG equal to −0.99 and three iterations are needed to obtain an ODG of −0.95. Thus, the global execution time is equal to 49 minutes for an ODG of −0.99 and 33 minutes for an ODG of −0.95.
A classical fixed-point conversion approach based on simulations has also been tested to compare with our approach. The same code as in our proposed approach is used to simulate the application. For this approach most of the time is consumed by the fixed-point simulation used to evaluate the application performances. Thus, the expression of the global execution time  for this approach based on simulation is as follows:
for this approach based on simulation is as follows:

where  is the number of iterations of the optimization process based on simulation.
is the number of iterations of the optimization process based on simulation.
An optimization algorithm based on  bits procedure [27] is used. This algorithm allows the limitation of the iteration number in the optimization process. The number of variables in the optimization process has been restricted to 9 to limit the fixed-point design search space. In this case, the number of iterations
bits procedure [27] is used. This algorithm allows the limitation of the iteration number in the optimization process. The number of variables in the optimization process has been restricted to 9 to limit the fixed-point design search space. In this case, the number of iterations  is equal to 388. Given that each fixed-point simulation requires 480 seconds, the global execution becomes huge and is equal to 51 hours.
is equal to 388. Given that each fixed-point simulation requires 480 seconds, the global execution becomes huge and is equal to 51 hours.
In our case, the optimization time is definitively lower. For this real application, a fixed-point simulation requires several minutes. For this example, the analytical approach reduces the execution time by a factor 63. Moreover, the fixed-point design space is very large and it cannot be explored with classical techniques based on fixed-point simulations.
6. Conclusion
In embedded systems, fixed-point arithmetic is favored but the application performances are reduced due to finite precision computation. During the fixed-point optimization process, the performance degradations are not analyzed directly during the conversion. An intermediate metric is used to measure the computational accuracy. In this paper, a technique to determine the accuracy constraint associated with a global noise model has been proposed. The probability density function of the noise model has been detailed and the choice of the parameters has been discussed. The different experiments show that our model predicts sufficiently accurately the application performances according to the noise level. The technique proposed to determine the accuracy constraint and the iterative process used to adjust this constraint allow the obtention of an optimized fixed-point specification guaranteeing minimum performance. The optimization time is definitively lower and has been divided by factor of 63 compared to the simulation based approach. Our future work is focused on the case of quantization by truncation.
References
Menard D, Chillet D, Sentieys O: Floating-to-fixed-point conversion for digital signal processors. EURASIP Journal on Applied Signal Processing 2006, 2006:-19.
Herve N, Menard D, Sentieys O: Data wordlength optimization for FPGA synthesis. Proceedings of the IEEE Workshop on Signal Processing Systems (SIPS '05), November 2005, Athens, Grece 623-628.
Belanovic P, Rupp M: Automated floating-point to fixed-point conversion with the fixify environment. Proceedings of the 16th IEEE International Workshop on Rapid System Prototyping (RSP '05), June 2005, Montreal, Canada 172-178.
Berens F, Naser N: Algorithm to System-on-Chip Design Flow that Leverages System Studio and SystemC 2.0.1. Synopsys Inc., March 2004
Mathworks : Fixed-Point Blockset User's Guide (ver. 2.0). 2001.
Mentor Graphics : Algorithmic C Data Types. Mentor Graphics, version 1.2 edition, May 2007
De Coster L, Adé M, Lauwereins R, Peperstraete J: Code generation for compiled bit-true simulation of DSP applications. Proceedings of the 11th IEEE International Symposium on System Synthesis (ISSS '98), December 1998, Hsinchu, Taiwan 9-14.
Keding H, Willems M, Coors M, Meyr H: FRIDGE: a fixed-point design and simulation environment. Proceedings of the Conference on Design, Automation and Test in Europe (DATE '98), February 1998, Paris, France 429-435.
Keding H, Coors M, Luthje O, Meyr H: Fast bit-true simulation. Proceedings of the 38th Design Automation Conference (DAC '01), June 2001, Las Vegas, Nev, USA 708-713.
Kim S, Kum K-I, Sung W: Fixed-point optimization utility for C and C++ based digital signal processing programs. IEEE Transactions on Circuits and Systems II 1998,45(11):1455-1464. 10.1109/82.735357
Özer E, Nisbet AP, Gregg D: Stochastic bit-width approximation using extreme value theory for customizable processors. Trinity College, Dublin, Ireland; October 2003.
Shi C, Brodersen RW: Floating-point to fixed-point conversion with decision errors due to quantization. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '04), May 2004, Montreal, Canada 5: 41-44.
Keding H, Hurtgen F, Willems M, Coors M: Transformation of floating-point into fixed-point algorithms by interpolation applying a statistical approach. Proceeding of the 9th International Conference on Signal Processing Applications and Technology (ICSPAT '98), September 1998, Toronto, Canada
Constantinides GA: Perturbation analysis for word-length optimization. Proceedings of the 11th Annual IEEE Symposium on Field-Programmable Custom Computing Machines (FCCM '03), April 2003, Napa, Calif, USA 81-90.
Lopez JA, Caffarena G, Carreras C, Nieto-Taladriz O: Fast and accurate computation of the roundoff noise of linear time-invariant systems. IET Circuits, Devices & Systems 2008,2(4):393-408. 10.1049/iet-cds:20070198
Rocher R, Menard D, Sentieys O, Scalart P: Analytical accuracy evaluation of fixed-point systems. Proceedings of the 15th European Signal Processing Conference (EUSIPCO '07), September 2007, Poznań, Poland
Widrow B: Statistical analysis of amplitude quantized sampled-data systems. Transactions of the American Institute of Electrical Engineers–Part II 1960, 79: 555-568.
Sripad A, Snyder D: A necessary and sufficient condition for quantization errors to be uniform and white. IEEE Transactions on Acoustics, Speech and Signal Processing 1977,25(5):442-448. 10.1109/TASSP.1977.1162977
Knuth DE: The Art of Computer Programming, Addison-Wesley Series in Computer Science and Information. 2nd edition. Addison-Wesley, Boston, Mass, USA; 1978.
Menezes AJ, van Oorschot PC, Vanstone SA: Handbook of Applied Cryptography. CRC Press, Boca Raton, Fla, USA; 1996.
Rocher R, Menard D, Herve N, Sentieys O: Fixed-point configurable hardware components. EURASIP Journal on Embedded Systems 2006, 2006:-13.
Ozeki K, Umeda T: An adaptive filtering algorithm using an orthogonal projection to an affine subspace and its properties. Electronics and Communications in Japan 1984,67(5):19-27.
Ojanperä T, Prasad R: WCDMA: Towards IP Mobility and Mobile Internet, Artech House Universal Personal Communications Series. Artech House, Boston, Mass, USA; 2002.
Pan D: A tutorial on MPEG/audio compression. IEEE MultiMedia 1995,2(2):60-74. 10.1109/93.388209
Jansson T: BladeEnc MP3 encoder. 2002
Lerch A: EAQUAL–Evaluation of Audio QUALity. Software repository: January 2002, http://sourceforge.net/projects/eaqual
Cantin M-A, Savaria Y, Lavoie P: A comparison of automatic word length optimization procedures. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS '02), May 2002, Scottsdale, Ariz, USA 2: 612-615.
Author information
Authors and Affiliations
Corresponding author
Appendix
This section demonstrates the increase of  of the noise power when all fixed-point data formats are increased of
of the noise power when all fixed-point data formats are increased of  bits. The output noise is given by the expression (4).The output noise power
bits. The output noise is given by the expression (4).The output noise power  is presented in [16]. In our case, the rounding quantization mode is considered. Thus, noise means are equal to zero and the output noise power is given by the following relation:
is presented in [16]. In our case, the rounding quantization mode is considered. Thus, noise means are equal to zero and the output noise power is given by the following relation:

 the variance of the noise source
the variance of the noise source  . The terms
. The terms  are constants computed with impulse response terms
are constants computed with impulse response terms  and independent of the fixed-point formats [16]:
and independent of the fixed-point formats [16]:

 the quantization step of the data after the quantization process which generates the noise
the quantization step of the data after the quantization process which generates the noise  . The term
. The term  is the number of bits that have been eliminated by the quantization process.Let us consider that
is the number of bits that have been eliminated by the quantization process.Let us consider that  bits are added to each fixed-point data format. In that case, the new quantization step
bits are added to each fixed-point data format. In that case, the new quantization step  is equal to:
is equal to:

 is given by:
is given by:

 are constant and independent from fixed-point data formats, the new output noise power
are constant and independent from fixed-point data formats, the new output noise power  becomes:
becomes:


 bits of all fixed-point data formats increases the noise level of
bits of all fixed-point data formats increases the noise level of  .
.





Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Menard, D., Serizel, R., Rocher, R. et al. Accuracy Constraint Determination in Fixed-Point System Design. J Embedded Systems 2008, 242584 (2008). https://doi.org/10.1155/2008/242584
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/242584





 for the fixed-point conversion.
for the fixed-point conversion.
 located at the system output.
located at the system output.


 .
.

 found for different adder word-lengths
found for different adder word-lengths 

 and the real
and the real  objective degradation grade (ODG) for the MP3 coder. (b) Zoom on the range [−105 dB, −99 dB], the point
objective degradation grade (ODG) for the MP3 coder. (b) Zoom on the range [−105 dB, −99 dB], the point  involved in each iteration
involved in each iteration  are given.
are given.