Instabilities and pattern formation in viscoelastic fluids

Abstract

Instabilities and pattern formation in viscous fluids have been a major topic of non-linear fluid dynamics for several decades. The study of pattern formation in viscoelastic thin films offers the opportunity to find new fascinating structures that cannot be observed in viscous fluids. Rayleigh–Taylor and Faraday instabilities, such as the resulting patterns in thin films of viscoelastic fluids, are investigated. We use the long-wave approximation and a Karman–Pohlhausen approach to simplify the mass and momentum equations. The viscoelastic stress tensor is calculated applying the linear Maxwell model. Conditions for the Faraday instability have been found using Floquet’s theorem. It is shown that viscoelastic films can exhibit harmonic resonance under external vibration. Moreover, a simulation of the non-linear problem in 2D and 3D is conducted with a finite difference method. Unstable oscillating Rayleigh–Taylor modes occur in the 2D numerical solution. Furthermore, we find that the wavenumber changes with the relaxation time of the fluid. Faraday patterns in viscous films emerge as regular structures of the surface, like squares or hexagons. Numerical simulations of the viscoelastic fluid also show regular structures. However, they collapse into a chaotic stripe-like pattern after a certain time.

1 Introduction

This paper discusses instabilities in the case of a viscoelastic fluid. A pure viscous (Newtonian) fluid exposed to external stress converts all the stress energy into heat. A viscoelastic fluid on the other hand is able to store a part of the energy. To model this behavior, we choose the linear Maxwell fluid.

One of the instabilities we want to discuss is the Rayleigh–Taylor instability (RTI). RTI appears if a more dense liquid is located above (below) a less dense one and a volume force pointing downward (upward) exists. Such a constellation is unstable and any small disturbance of the flat interface between the two liquids will grow exponentially in time. The instability is named after Taylor [1] and Strutt, 3rd Baron Rayleigh [2]. The Rayleigh–Taylor instability appears quite often, from the structures which are formed by a collapsing star to the patterns in the billows of cigarette smoke. RTI of a Newtonian two-layer system is studied in [3].

RTI of viscoelastic drops is examined in [4] using the Oldroyd-B fluid model. Reference [5] discusses gravity and Rayleigh–Taylor waves with a Jeffrey fluid model. In Ref. [6], the linear stability analysis is applied on a Maxwell fluid. Two Maxwell fluid layers are investigated in Ref. [7] in context of tectonics in the upper mantel, while Ref. [8] assumes a Maxwell fluid over a Newtonian fluid to describe large-scale processes in the lithosphere. RTI of linear viscoelastic fluids is investigated by Ref. [9] through a displacement field which is applied to the stress tensor. Linear and weakly non-linear results are presented.

We shall also consider the Faraday instability, first studied by and named after Faraday [10]. The Faraday instability is caused by an external vertical vibration. The surface of the fluid starts oscillating after some time if a critical amplitude is exceeded. Depending on the vibration amplitude and frequencies, the surface of a vibrating fluid is organized in regular structures like triangles, rectangles, or hexagons. Stability analysis of Faraday waves on viscoelastic fluids is discussed in Ref. [11]. Experimental results of vibrating viscoelastic fluids are shown in Ref. [12, 13]. Numerical investigations of Newtonian Faraday instability using a phase field model one can find in [14]. Reference [15] studies the stability of a viscous fluid layer covered with an elastic polymer film under external vibration by usage of Floquet’s theorem.

A combination of Faraday and Rayleigh–Taylor instability is studied in [16]. The falling of viscoelastic films down an inclined plane is investigated through long-wave approximation, linear stability analysis, and weakly non-linear approaches by [17].

2 Governing equations

Fig. 1

A linear Maxwell Fluid film of mean depth d. The fluid has a viscosity $\eta$, a density $\rho$, and a relaxation time $\Lambda$. The boundary between the environment and the fluid is located at $z=h(x,y,t)$. The surface tension of the interface is $\gamma$

Using the linear Maxwell fluid, we have two parameters for the description of the viscoelastic behavior. The relation between the stress tensor $\bar{\sigma }$ and the shear rate tensor $\bar{D}$ is given by [18]

$$\begin{aligned} \Lambda \partial _t \bar{\sigma } + \bar{\sigma } = 2 \eta \bar{D} \, \end{aligned}$$

(1)

where $\eta$ and $\Lambda$ are the dynamic viscosity and the relaxation time of the fluid. If $\Lambda = 0$, Eq. (1) constitutes the inner stress of the Newtonian fluid. The ratio $\eta /\Lambda$ is equal to Young’s modulus E, so we can find another special case. For $\eta \rightarrow \infty$ and $\Lambda \rightarrow \infty$, but $\eta /\Lambda$ = const., the linear Maxwell fluid is equivalent to the elastic solid. We describe conservation of mass and momentum with the incompressible Navier–Stokes equations

$$\begin{aligned} \partial _t \vec {v} + \left( \vec {v}\cdot \nabla \right) \vec {v}= \, & \frac{1}{\rho _0} \nabla \cdot \bar{\sigma } - \frac{1}{\rho _0} \nabla p + \vec {g} \end{aligned}$$

(2)

$$\begin{aligned} \nabla \cdot \vec {v}\,= \, & 0. \end{aligned}$$

(3)

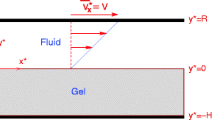
A two-dimensional sketch of our system is shown in Fig. 1. At $z = 0$, the fluid is in contact with the solid substrate and no fluid movement is possible

$$\begin{aligned} \vec {v}=0. \end{aligned}$$

(4)

On the other hand, the boundary at $z= h(x,y,t)$ is assumed to be a free surface and the tangential stress must disappear. Thus

$$\begin{aligned} \hat{t}\cdot \bar{\sigma }\cdot \hat{n} = 0. \end{aligned}$$

(5)

The normal stress balance on the free surface reads

$$\begin{aligned} \hat{n}\cdot \bar{\sigma } \cdot \hat{n} = p_0 - p-\gamma K. \end{aligned}$$

(6)

Here, $p_0$ is the pressure of the environment, p the fluid pressure under the surface, $\gamma$ the surface tension, and K the curvature. The free surface is defined by a function h(x, y, t). This function gives the fluid depth at every location and time and its temporal evolution is ruled by the kinematic condition

$$\begin{aligned} \partial _t h = v_{z} - v_{x} \partial _x h - v_{y} \partial _y h. \end{aligned}$$

(7)

In lateral directions, we assume periodic boundaries with $x\in \left[ 0,L\right]$ and $y\in \left[ 0,L\right]$.

Equation (1) can be simplified by assuming a viscoelastic force field

$$\begin{aligned} \vec {F} = \nabla \cdot \bar{\sigma }, \end{aligned}$$

(8)

which leads with the use of Eq. (3) to

$$\begin{aligned} \Lambda \partial _t \vec {F} + \vec {F} = \eta \Delta \vec {v}. \end{aligned}$$

(9)

One characteristic time scale of the system is the diffusion time

$$\begin{aligned} \tau = \frac{d^2\rho }{\eta } = \frac{d^2}{\nu }, \end{aligned}$$

(10)

where $\nu$ is the kinematic viscosity. We introduce the dimensionless quantities (bearing tildes)

$$\begin{aligned} \tilde{p} = \frac{d^2}{\nu ^2 \rho _0} p,\ \ \tilde{\vec {v}} = \frac{\tau }{\textrm{d}} \vec {v},\ \ \tilde{\Lambda } = \frac{\Lambda }{\tau },\ \ \tilde{\vec {F}} = \eta \tau \textrm{d} \vec {F}. \end{aligned}$$

(11)

Applying long-wave approximation [19] and the Karman–Pohlhausen method [20], our system (leaving all tildes) simplifies to (see Appendix A)

$$\begin{aligned} \frac{6}{5}\Big [ \frac{\partial \vec {q}}{\partial t} + \nabla _2\cdot \bar{Q} - \frac{1}{7}\frac{\vec {q}\left( \nabla _2\cdot \vec {q}\right) }{h}\Big ]&= \vec {F} h + G h \nabla _2h + \Gamma h \nabla _2(\Delta _2 h) \end{aligned}$$

(12a)

$$\begin{aligned} \partial _{t} h(x,y,t)&= -\nabla _2\cdot \vec {q} \end{aligned}$$

(12b)

$$\begin{aligned} \Lambda \partial _{t}\vec {F} + \vec {F}&= \frac{-3 \vec {q}}{h^3} \end{aligned}$$

(12c)

with $Q_{ij} = \frac{9}{7} \frac{q_iq_j}{h}$. A similar approximation of a thin film is also applied by Ref. [21].

The system variables are the flow rate $\vec {q} = \left( q_x,\ q_y\right) ^T$, force $\vec {F} = \left( F_x,\ F_y\right) ^T$ and the height h(x, y, t). Here, the operator $\nabla _2 = \left( \partial _x, \partial _y\right) ^T$. Note that all dependent variables are now 2D instead of the original 3D fields. In addition to $\Lambda$, two new parameters appear, the dimensionless surface tension

$$\begin{aligned} \Gamma = \frac{\gamma \textrm{d}}{\nu ^2 \rho _0} \end{aligned}$$

(13)

and the Galileo number G:

$$\begin{aligned} G = \frac{gd^3}{\nu ^2}. \end{aligned}$$

(14)

When we apply harmonic oscillations, the Galileo number becomes time-dependent and reads

$$\begin{aligned} G(t)= \frac{gd^3}{\nu ^2} ( 1 + a \cos (\omega t)). \end{aligned}$$

(15)

Oscillations are characterized by their frequency $\omega$ and amplitude a. Their dimensional counterparts are notated with $\Omega =\omega /\tau$ and $A=ga/\Omega ^2$.

3 Linear stability analysis

3.1 Rayleigh–Taylor instability

First, we investigate the instability of Rayleigh–Taylor waves. Due to isotropy in the horizontal plane, it is sufficient to examine the 2D case

$$\begin{aligned} q(x,t)=\, & ue^{\lambda t + ikx},\quad F_x(x,t)= \, f e^{\lambda t + ikx},\nonumber \\ h(x,t)= \, & 1 + \eta e^{\lambda t + ikx}. \end{aligned}$$

(16)

After linearizing with respect to the small amplitudes u, f, and $\eta$, the resulting eigenvalue problem yields the characteristic equation

$$\begin{aligned} \Lambda \lambda ^3 + \lambda ^2 +\frac{5}{6}\left[ 3 + \Lambda k^2 \left( G + \Gamma k^2 \right) \right] \lambda + \frac{5}{6}k^2\left[ G+\Gamma k^2\right] = 0. \end{aligned}$$

(17)

The most dangerous mode has the growth rate $\max \left( \Re (\lambda )\right)$. The system is unstable if $\max \left( \Re (\lambda )\right) >0$. Only with a negative Galileo number, an instability can be observed. The dependency of $\max \left( \Re (\lambda )\right)$ from k can be understand as dispersion relation. We notice that the growth rate has a maximum in k, which is independent of $\Lambda$. With increasing $\Lambda$, the maximum growth rate increases stagnating. A destabilizing effect of relaxation time was also found by Ref. [22, 23].

An increase of the surface tension $\Gamma$ leads to a decrease of the fastest growing wavenumber in the unstable RTI domain. A decrease of G shifts the unstable domain to the short-wave region of the dispersion spectrum. In Fig. 2, we show dispersion relations for varying values of $\Lambda$. The scaling parameters are chosen $\Gamma = -G = 1$, therefore equal forces from surface tension and gravity. They are equivalent to a fluid with $\rho _0 = 999\ kg/m^3$, $\gamma = 0.07\ N/m$, $\nu = 4.4 \cdot 10 ^{-4}\ m^2/s$ and $d = 2.6\ mm$. These parameters can be achieved, e.g., by a viscous water-based polymer solution. It should be mentioned that viscoelastic solutions have higher viscosities than their solvents; therefore, it is acceptable to assume a viscosity 440 times higher than for water.

Fig. 2

Dispersion relation of Rayleigh–Taylor waves for different $\Lambda$ with $\Gamma =1$ and $G = -1$

3.2 Faraday instability

Under harmonic external excitations, we utilize Floquet’s theorem to estimate the stability condition of the system. We take

$$\begin{aligned} h(x,t)=\, & e^{ikx} \eta (t),\quad q(x,t) = \, e^{ikx} u (t),\nonumber \\ F_x(x,t)=\, & e^{ikx} f (t). \end{aligned}$$

(18)

The time-dependent components build a vector $\vec {\xi }(t) = \, \left( \eta (t),\ u(t),\ f(t)\right) ^T$, which fulfils the linear system

$$\begin{aligned} \partial _{t}\vec {\xi }(t) = \bar{A}(t) \vec {\xi }(t). \end{aligned}$$

(19)

Here, $\bar{A}$ denotes the Jacobian where $\bar{A}(t) = \bar{A}(t+T)$ with $T=2\pi /\omega$ due to Eq. (15). A matrix $\bar{M}$ which transform the system one period ahead is introduced. Therefore

$$\begin{aligned} \vec {\xi }(t+nT) = \bar{M}^n \vec {\xi }(t). \end{aligned}$$

(20)

We determine the columns of the monodromy matrix $\bar{M}$ by integrating

$$\begin{aligned} \vec {M}_i = \int \limits _{0}^{T} dt\bar{A}(t)\vec {\xi }_i(t) \end{aligned}$$

(21)

for three linearly independent initial conditions $i=1,2,3$. The vector $\vec {\xi }$ can be decomposed into

$$\begin{aligned} \vec {\xi }(t) = \sum _{i=1}^3 \vec {w}_i(t) \exp (\lambda _it), \end{aligned}$$

(22)

where $w_i(t) = w_i(t+T)$. The $\lambda _i$ are the Floquet exponents. According to Floquet’s theorem, it applies

$$\begin{aligned} \lambda _i = \frac{1}{T} \ln (\sigma _i), \end{aligned}$$

(23)

where $\sigma _i$ are the eigenvalues of $\bar{M}$. Due to Eqs. (22, 23), $\max |\sigma |$ determines the system stability. We compute $\sigma _i$ by solving Eq. (21) applying a fourth-order Runge–Kutta method. As initial condition, we take an Euclidean base. Figure 3 shows lines of marginal stability (Arnold tongues), $\max |\sigma |\,= \, 1$. We observe successive subharmonic and harmonic unstable solutions. A change of relaxation time causes also a change of the position of the marginal lines in amplitude and wavenumber.

There is a critical amplitude where the system becomes unstable. This amplitude decreases with increasing frequency. The decrease in frequency is faster for higher relaxation times. The wavenumber of this amplitude is denoted with $k_{crit}$. In Fig. 4, the critical wavenumber is plotted over the frequency. The $k_{crit}(\omega )$—curves show a discontinuity, when an Arnold tongue replaces another one as the most dominant in the system. In the region where $\Lambda \omega \approx 1$, we observe a harmonic tongue as critical. Also, the size of the appointed frequency window (H2 in (a) and H1 in (b)) increases compared to the Newtonian fluid (c) in Fig. 4. Reference [11] also found a harmonic resonance in that region and a minimum for the critical amplitude.

Fig. 3

The lines of marginal stability in space of a and k. Parameters are chosen with $\Gamma = G = 40$. Above: $\Lambda =0$. Below: $\Lambda = 0.5$. Black solid: $\omega =2\pi$. Red dashed: $\omega =\pi$. The unstable regions are separated in harmonic (H) and subharmonic (S) ones, which are numbered with increasing wave number. The horizontal blue lines correspond to the numerical solution as shown in Figs. 7 and 8

Fig. 4

The critical wave number $k_{crit}(\omega )$. For various frequencies, different subharmonical (S) and harmonical(H) Arnold tongues take the critical position. Parameters are $G = 40$, $\Gamma = 40$, and $\Lambda =$ 0 (a), 0.159 (b), and 0.5 (c)

4 Numerical results

Applying a standard finite difference method [24], solutions in two (2D) and in three dimensions (3D) have been determined. The code has been developed in C++. In Fig. 5, a 2D Rayleigh–Taylor wave is shown for different time steps. There are two resonances, one at $x\approx 27$ and one at $x\approx 66$. Two perturbations with nearly the same amplitudes merge at $t=40$ and form a new bigger RT wave crest at $t = 50$. After its formation, it begins to shrink as quickly as it has been formed, and at $t=54$, the drop is not much bigger than the others. This swapping back behavior is a hint to the elastic property of the film. The second resonance, at $x \approx 66$, grows to such an extent that it finally causes rupture. Figure 6 shows an RTI in 3D. Surface perturbations grow over time. The flow field has sinks where the surface height increases and sources where it decreases. Average flow rates and surface perturbations increase in time.

Fig. 5

Rayleigh–Taylor patterns in 2D. Parameters are $\Gamma =1$, $G = -1$, and $\Lambda = 10$

Fig. 6

Rayleigh–Taylor patterns in 3D. Contour of h(x, y, t) and flow rate $\vec {q}(x,y,t)$ with $\Lambda = 10$, $\Gamma =1$, and $G =-1$

The 2D Faraday waves of a Newtonian fluid are shown in Fig. 7. There is a $\pi$-phase shift after one period; the structures are subharmonic. The wavenumber fits to the results from Floquet analysis, where we expect to be in the $1\,S$ and $1\,H$ Arnold tongue region. Therefore, the harmonic solution is not visible in the numerics.

In Fig. 8, the height for a viscoelastic fluid with $\Lambda =0.5$ is illustrated. We observe a fundamental difference between the patterns of the Newtonian fluid and the linear Maxwell fluid. In the beginning, the Maxwell fluid acts quite similar to the Newtonian fluid. It takes some time before the structures of the surface appear, and then, they look quite similar to their viscous equivalent. After some time, the repeating structures begin to change. The surface oscillates almost chaotically, a full phase repeats only almost the same pattern. The explanation to this can be that the linear Maxwell fluid has a memory of every stress to which it was exposed. This phenomenon is called stress relaxation, it is the major difference between the Newtonian fluid and the linear Maxwell fluid and the best explanation for the appearance of these strange surface patterns. A more detailed presentation of stress relaxation can be found in [18].

The Faraday instability of Newtonian fluids in 3D produces surface patterns like squares or hexagons [21, 25]. In Fig. 9, we can see how the 3D viscoelastic film develops from the random perturbation in the beginning to a subharmonic stripe structure. At $t=10$, we see a random surface, which becomes a subharmonic square structure at $t=124$. The squares repeat periodically for some time with small changes. At $t= 208$, we observe that some of the former squares have developed into diamonds and connect with their neighbors. Then, at $t= 228$, the regular structure begins to collapse. It follows a kind of transition phase where irregularly changing structures occur, similar to the almost chaotic surface patterns we also observe in the 2D calculation ($t = 252$). After the transition phase ($t= 320$), the surface ends up in a stripe pattern. This is a similar behavior as the corresponding 2D solution. The applied scaling is $G=\Gamma = 40$. This can be associated with $\rho _0=789\ kg/m^3$, $\gamma = 0.022\ N/m$, $\nu =3.4\cdot 10^{-5}\ m^2/s$ and $d =1.67\ mm$ (e.g., ethanol-based polymer solution). Vibrating with $12\ Hz$ ($\omega = \pi$) or $24\ Hz$ ($\omega = 2 \pi$).

Reference [13] studied Faraday waves of viscoelastic fluids experimentally. The authors use a $1.5\%$ polyacrylamid-co-acid solvent. A similar transition of hexagonal patterns to a stripe-like structure is observed.

Fig. 7

Faraday patterns in 2D. Parameters $\Gamma = G = 40$, $a=2.5$, $\omega = 2\pi$, and $\Lambda = 0$

Fig. 8

Faraday patterns in 2D. Parameters are $\Gamma = 40$, $G = 40$, $a=0.99$, $\omega = 2\pi$, and $\Lambda = 0.5$

Fig. 9

Faraday patterns in 3D. Contour of h(x, y, t) with $\Lambda = 0.5$, $a=0.99$, $\omega = 2\pi$, $\Gamma =40$, and $G = 40$. Solid lines are height at 0.9 (violet), 1.0 (turquoise), and 1.1 (yellow)

5 Conclusions

The Rayleigh–Taylor and the Faraday instability for a viscoelastic Maxwell fluid are examined applying a linear stability analysis as well as direct numerical simulations of a recently derived long-wave model. The results of the numerical solution and the linear analysis confirm each other. The wave numbers and frequencies predicted by the linear model are reproduced by the numerical approach.

The linear stability analysis has shown that the highest growth rate $\lambda _{max}$ of RTI increases with $\Lambda$. For high values of $\Lambda$, the increase stagnates. Here, it should be mentioned that in practice, it is very difficult to increase a fluids’ relaxation time without increasing its viscosity too. The corresponding $k_{max}$ is not influenced by the relaxation time. Numerical solutions of 2D RTI waves show elastic behavior and resonance.

The Faraday instability in 2D and 3D creates erratic surface patterns. The 3D simulation shows a subharmonic stripe structure which does not occur in Newtonian fluids.

Further research can focus on the implementation of various viscoelastic models and can clarify how pattern formation in these materials distinguish from each other. Also, the Faraday instability of viscoelastics offers many possibilities for further research. For example, the characterization of the patterns which are not observable in Newtonian fluids or a detailed study of the resonance behavior is conceivable. High-frequency regions are not considered by our model due to their short-wave nature.

The long-wave model we developed here can be extended in several directions. One can add horizontal vibrations, resulting in another kind of Faraday instability [27].

Certain combinations of instabilities are possible too. One can combine RTI and Faraday instability or consider the Faraday instability on an inclined surface.

The study of instabilities and pattern formation in viscoelastic fluids is a complex topic which offers many possibilities for future research.

Appendix A: Deviation of Eqs. 12a–12c

The derivation of the y-components look analogous to the x-components, so only the x-components are presented in detail. Long-wave approximation is based on the assumption that the considered system is much less prominent in one direction of space (z-direction) than in the others. Rescaling with long-wave approximation leads to $F_z = O(\delta )$, $v_z= O(\delta )$, $\partial _y = O(\delta )$ and $\partial _x = O(\delta )$, with scaling factor $\delta = \frac{d}{l}<< 1$. Here, l represents the characteristic length in x- and y-direction. Neglecting all terms of $O(\delta ^2)$ in Eqs. (2) and (9) leads to

$$\begin{aligned} \partial _t v_x + \left( \vec {v}\nabla \right) v_x\,= \, & F_x +\partial _x p, \end{aligned}$$

(A1)

$$\begin{aligned} 0=\, & -\partial _z p - G \end{aligned}$$

(A2)

and

$$\begin{aligned} \Lambda \partial _t F_x +- F_x = \partial ^2_{zz} v_x. \end{aligned}$$

(A3)

Under application of Eq. (3) to the kinematic boundary condition (7), it follows:

$$\begin{aligned} \partial _{t} h(x,y,t) = -\partial _x\left( \int \limits _{0}^{h(x,y,t)} \textrm{d}z v_x\right) -\partial _y\left( \int \limits _{0}^{h(x,y,t)} \textrm{d}z v_y\right) . \end{aligned}$$

(A4)

The pressure gradient can be found by the boundary condition (6) and Eq. (A2), which yields to

$$\begin{aligned} \partial _xp = -G\partial _xh(x,y,t) + \Gamma \left( \partial ^3_{xxx} h(x,y,t) + \partial ^3_{yyx} h(x,y,t)\right) . \end{aligned}$$

(A5)

Karman–Pohlhausen method assumes a flow rate

$$\begin{aligned} q(x,y,t)= \int \limits _{0}^{h} \textrm{d}z v_x(x,y,z,t) \end{aligned}$$

(A6)

and separates the velocity in x-according to

$$\begin{aligned} v_x(x,y,z,t) = q_x(x,y,t)f(z), \end{aligned}$$

with

$$\begin{aligned} f(z) = \frac{3\left( zh-\frac{z^2}{2}\right) }{h^3}. \end{aligned}$$

(A7)

Using this assumption, the z-coordinate can be eliminated in Eqs. (A1, A3) and (A4) by integrating over a weight function

$$\begin{aligned} w(z) = hz-\frac{z^2}{2}. \end{aligned}$$

(A8)

The right-hand side of Eq. (A1) is

$$\begin{aligned} \begin{aligned}&\int \limits _{0}^{h}\textrm{d}z w(z)\left[ F_x -G\partial _xh + \Gamma \left( \partial ^3_{xxx} h + \partial ^3_{yyx} h\right) \right] \\&\quad=\frac{h^3}{3} \left[ F_x -G\partial _xh + \Gamma \left( \partial ^3_{xxx} h + \partial ^3_{yyx} h\right) \right] . \end{aligned} \end{aligned}$$

The left-hand side is¹

$$\begin{aligned} \int\limits_{0}^{h} {\text{d}} zw(z)\left[ {\partial _{t} v_{x} + v_{x} \partial _{x} v_{x} + v_{y} \partial _{y} v_{x} + v_{z} \partial _{z} v_{x} } \right] = \frac{6}{5}\left[ {\partial _{t} q_{x} + \frac{9}{7}\left( {\partial _{x} \frac{{q_{x}^{2} }}{h} + \partial _{y} \frac{{q_{x} q_{y} }}{h}} \right) - \frac{1}{7}\frac{{q_{x} \left( {\partial _{x} q_{x} + \partial _{y} q_{y} } \right)}}{h}} \right]. \end{aligned}$$

(A9)

Integrating Eq. (A3) gives

$$\begin{aligned} \begin{aligned}&\int \limits _{0}^{h} \textrm{d}z w(z)\left( \Lambda \partial _t F_x + F_x\right) = -\frac{h^3}{3}\left( \Lambda \partial _t F_x + F_x\right) \\&\quad=\int \limits _{0}^{h} \textrm{d}z w(z)\partial ^2_{zz} v_x = q_x. \end{aligned} \end{aligned}$$

(A10)

Equation (A4) is already

$$\begin{aligned} \begin{aligned} \partial _{t} h=-\left( \partial _{x} q_x + \partial _{y}q_y\right) . \end{aligned} \end{aligned}$$

(A11)

The result of this calculation is the system shown in 12a–12c.