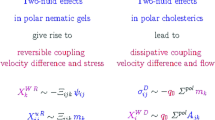Abstract.
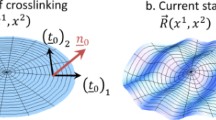
We present the derivation of the macroscopic equations for uniaxial polar nematic gels and elastomers. We include the strain field as well as relative rotations as independent dynamic macroscopic degrees of freedom. As a consequence, special emphasis is laid on possible static and dynamic cross-couplings between these macroscopic degrees of freedom associated with the network, and the other macroscopic degrees of freedom including reorientations of the macroscopic polarization. In particular, we find static and dissipative dynamic cross-couplings between strain fields and relative rotations on one hand and the macroscopic polarization on the other that allow for new possibilities to manipulate polar nematics. To give one example each for the effects of a static and a dissipative cross-coupling: we find that a static electric field applied perpendicularly to the polar preferred direction leads to relative rotations while dynamically relative rotations can lead to transverse electric currents. In addition to a permanent network, we also consider the effect of a transient network, which is particularly important for the case of gels, melts and concentrated polymer solutions. A section on the influence of macroscopic chirality is included as well.
Graphical abstract

Article PDF
Similar content being viewed by others
References
H. Hsiung, Th. Rasing, Y.R. Shen, F.P. Shvartsman, I.R. Cabrera, V.A. Krongauz, J. Chem. Phys. 87, 3127 (1987)
H. Zimmermann, R. Poupko, Z. Luz, J. Billard, Z. Naturforsch. A 40, 149 (1985)
H. Pleiner, H.R. Brand, Europhys. Lett. 9, 243 (1989)
H.R. Brand, P.E. Cladis, H. Pleiner, Macromolecules 25, 7223 (1992)
T. Niori, T. Sekine, J. Watanabe, T. Furukawa, H. Takezoe, J. Mater. Chem. 6, 1231 (1996)
D.R. Link, G. Natale, R. Shao, J.E. McLennan, N.A. Clark, E. Körblova, D.M. Walba, Science 278, 1924 (1997)
H.R. Brand, P.E. Cladis, H. Pleiner, Eur. Phys. J. B 6, 347 (1998)
H.R. Brand, P.E. Cladis, H. Pleiner, Eur. Phys. J. B 31, 147 (2003)
G. Pelzl, S. Diele, W. Weissflog, Adv. Mater. 11, 707 (1999)
T. Niori, J. Yamamoto, H. Yokoyama, Mol. Cryst. Liq. Cryst. 409, 475 (2004)
D. Shen, S. Diele, G. Pelzl, I. Wirth, C. Tschierske, J. Mater. Chem. 9, 661 (1999)
W. Weissflog, H. Nadasi, U. Dunemann, G. Pelzl, S. Diele, A. Eremin, H. Kresse, J. Mater. Chem. 11, 2748 (2001)
G. Pelzl, A. Eremin, S. Diele, H. Kresse, W. Weissflog, J. Mater. Chem. 12, 2591 (2002)
M. Hird, Y. Raoul, J.W. Goodby, H.F. Gleeson, Ferroelectrics 309, 95 (2004)
H.R. Brand, P.E. Cladis, H. Pleiner, Int. J. Eng. Sci. 38, 1099 (2000)
C.-C. Yen, M. Tokita, B. Park, H. Takezoe, J. Watanabe, Macromolecules 39, 1313 (2006)
M. Koike, C.-C. Yen, L. Yuqing, H. Tsuchiya, M. Tokita, S. Kawauchi, H. Takezoe, J. Watanabe, Macromolecules 40, 2524 (2007)
Y. Taguchi, C.-C. Yen, S. Kang, M. Tokita, J. Watanabe, J. Phys. Chem. B 113, 5341 (2009)
P. Martin, O. Parodi, P.S. Pershan, Phys. Rev. A 6, 2401 (1972)
D. Forster, Hydrodynamic Fluctuations, Broken Symmetry and Correlation Functions (Benjamin, Reading, MA, 1975)
H. Pleiner, H.R. Brand, in Pattern Formation in Liquid Crystals, edited by A. Buka, L. Kramer (Springer, New York, 1996) p. 15
I.M. Khalatnikov, Introduction to the Theory of Superfluidity (Benjamin, New York, 1965)
M. Liu, Phys. Rev. Lett. 35, 1577 (1975)
H. Brand, M. Dorfle, R. Graham, Ann. Phys. (N.Y.) 119, 434 (1979)
M. Liu, Phys. Rev. A 19, 2090 (1979)
H.R. Brand, Phys. Rev. A 33, 643 (1986)
H.R. Brand, H. Pleiner, F. Ziebert, Phys. Rev. E 74, 021713 (2006)
H.R. Brand, H. Pleiner, Physica A 208, 359 (1994)
P.G. de Gennes, in Liquid Crystals of One- and Two-Dimensional Order, edited by W. Helfrich, G. Heppke (Springer, New York, 1980) p. 231
M.S. Green, A.V. Tobolsky, J. Chem. Phys. 14, 80 (1946)
R.G. Larson, Constitutive Equations for Polymer Melts and Solutions (Butterworths, Boston, 1988)
H.R. Brand, H. Pleiner, W. Renz, J. Phys. (Paris) 51, 1065 (1990)
H. Pleiner, H.R. Brand, Mol. Cryst. Liq. Cryst. 199, 407 (1991)
H. Temmen, H. Pleiner, M. Liu, H.R. Brand, Phys. Rev. Lett. 84, 3228 (2000)
H. Pleiner, M. Liu, H.R. Brand, Rheol. Acta 39, 560 (2000)
H. Temmen, H. Pleiner, M. Liu, H.R. Brand, Phys. Rev. Lett. 86, 745 (2001)
M. Grmela, Phys. Lett. A 296, 97 (2002)
H. Pleiner, M. Liu, H.R. Brand, Rheol. Acta 41, 375 (2002)
H. Pleiner, M. Liu, H.R. Brand, Rheol. Acta 43, 502 (2004)
H. Pleiner, M. Liu, H.R. Brand, in IMA Volume in Mathematics and its Applications 141, edited by M.-C.T. Calderer, E.M. Terentjev (Springer, Berlin, 2005) p. 99
H.R. Brand, H. Pleiner, Phys. Rev. A 35, 3122 (1987)
J.L. Ericksen, Arch. Rat. Mech. Anal. 113, 97 (1991)
S.R. de Groot, P. Mazur, Nonequilibrium Thermodynamics (North Holland, Amsterdam, 1962)
P.G. de Gennes, J. Prost, The Physics of Liquid Crystals (Oxford University Press, Oxford, 1995)
H.R. Brand, K. Kawasaki, J. Phys. C 19, 937 (1986)
W.P. Mason, Physical Acoustics and the Properties of Solids (D. Van Nostrand, New York, 1958)
H.R. Brand, H. Pleiner, Macromol. Rapid Commun. 11, 607 (1990)
H.R. Brand, P.E. Cladis, H. Pleiner, Phys. Rev. E 79, 032701 (2009)
M. Liu, Phys. Rev. Lett. 43, 1740 (1979)
S. Bohlius, H.R. Brand, H. Pleiner, Phys. Rev. E 70, 061411 (2004)
P.G. de Gennes, The Physics of Liquid Crystals (Clarendon Press, Oxford, 1975)
H.R. Brand, H. Pleiner, Phys. Rev. A 37, 2736 (1988)
H.R. Brand, H. Pleiner, in Encyclopedia of Materials: Science and Technology (Elsevier) 5, 1214 (2001) and Cholesteric Liquid Crystals: Flow Properties, Thermo- and Electromechanical Coupling, in Reference Module in Materials Science and Materials Engineering, edited by Saleem Hashmi (Elsevier, Oxford, 2016) pp. 1--8
D. Svenšek, H. Pleiner, H.R. Brand, Phys. Rev. E 78, 021703 (2008)
H.R. Brand, H. Pleiner, D. Svenšek, Phys. Rev. E 88, 024501 (2013)
H. Pleiner, H.R. Brand, EPL 89, 26003 (2010)
F.C. Frank, Disc. Faraday Soc. 25, 19 (1958)
H.R. Brand, A. Fink, H. Pleiner, Eur. Phys. J. E 38, 65 (2015)
S.T. Kim, H. Finkelmann, Makromol. Chem. Rapid Commun. 22, 429 (2001)
A. Komp, J. Rühe, H. Finkelmann, Makromol. Chem. Rapid Commun. 26, 813 (2005)
H.R. Brand, Makromol. Chem. Rapid Commun. 10, 441 (1989)
A.M. Menzel, H.R. Brand, J. Chem. Phys. 125, 194704 (2006)
P.G. de Gennes, C.R. Acad. Sci. (Paris) B 281, 101 (1975)
H.R. Brand, Makromol. Chem. Rapid Commun. 10, 57, 317 (1989)
H.R. Brand, H. Pleiner, Eur. Phys. J. E 31, 37 (2010)
H. Pleiner, H.R. Brand, Eur. Phys. J. E 37, 11 (2014)
H. Pleiner, P.E. Cladis, H.R. Brand, Eur. Phys. J. E 20, 257 (2006)
H.R. Brand, H. Pleiner, P.E. Cladis, Physica A 351, 189 (2005)
H. Pleiner, H.R. Brand, Braz. J. Phys. 46, 565 (2016)
J.W. Felix, D. Mukamel, R.M. Hornreich, Phys. Rev. Lett. 57, 2180 (1986)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Brand, H., Pleiner, H. & Svenšek, D. Macroscopic behavior of polar nematic gels and elastomers. Eur. Phys. J. E 39, 105 (2016). https://doi.org/10.1140/epje/i2016-16105-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epje/i2016-16105-7