Abstract
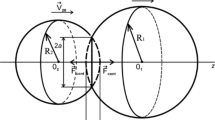
We report a new theory of dissipative forces acting between colliding viscoelastic bodies. The impact velocity is assumed not to be large to neglect plastic deformations in the material and propagation of sound waves. We consider the general case of bodies of an arbitrary convex shape and of different materials. We develop a mathematically rigorous perturbation scheme to solve the continuum mechanics equations that deal with both displacement and displacement rate fields and accounts for the dissipation in the bulk of the material. The perturbative solution of these equations allows to go beyond the previously used quasi-static approximation and obtain the dissipative force. The derived force does not suffer from the inconsistencies of the quasi-static approximation, like the violation of the third Newton’s law for the case of different materials, and depends on particle deformation and deformation rate.
Graphical abstract
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
H.J. Herrmann, J.-P. Hovi, S. Luding (Editors), Physics of Dry Granular Media NATO ASI Series (Kluwer, Dordrecht, 1998).
H. Jaeger, S. Nagel, R. Behringer, Rev. Mod. Phys. 68, 1259 (1996).
H. Hinrichsen, D.E. Wolf, The Physics of Granular Media (Wiley, Berlin, 2004).
J. Duran, Sands, Powders and Grains (Springer-Verlag, Berlin, 2000).
R. Greenberg, A. Brahic, Planetary Rings (The University of Arizona Press, Tucson, 1984).
N.V. Brilliantov, T. Pöschel, Kinetic theory of Granular Gases (Oxford University Press, Oxford, 2004).
T. Pöschel, S. Luding, Granular Gases, Vol. 564 of Lecture Notes in Physics (Springer, Berlin, 2001).
T. Pöschel, N.V. Brilliantov, Granular Gas Dynamics, Vol. 624 of Lecture Notes in Physics (Springer, Berlin, 2003).
A. Barrat, E. Trizac, M.H. Ernst, J. Phys.: Condens. Matter 17, 2429 (2005).
R.D. Wildman, D.J. Parker, Phys. Rev. Lett. 88, 064301 (2002).
K. Feitosa, N. Menon, Phys. Rev. Lett. 88, 198301 (2002).
O. Zik, D. Levine, S. Lipson, S. Shtrikman, J. Stavans, Phys. Rev. Lett. 73, 644 (1994).
H. Hertz, J. f. reine u. angewandte Math. 92, 156 (1882).
T. Poeschel, T. Schwager, Computational Granular Dynamics (Springer, Berlin, 2005).
S. Luding, Nonlinearity 22, R101 (2009).
T. Poeschl, Z. Phys. 46, 142 (1928).
M. Montaine, M. Heckel, C. Kruelle, T. Schwager, T. Poeschel, Phys. Rev. E 84, 041306 (2011).
Y.-H. Pao, J. Appl. Phys. 26, 1083 (1955).
N. Brilliantov, F. Spahn, J. Hertzsch, T. Pöschel, Phys. Rev. E 53, 5382 (1996).
G. Kuwabara, K. Kono, J. Appl. Phys. Part 1 26, 1230 (1987).
Q.J. Zheng, H.P. Zhu, A.B. Yu, Powder Technol. 226, 130 (2012).
Q.J. Zheng, Z.Y. Zhou, A.B. Yu, Powder Technol. 248, 25 (2013).
N.V. Brilliantov, A.V. Pimenova, D.S. Goldobin, EPL 109, 14005 (2015).
L.D. Landau, E.M. Lifshitz, Theory of Elasticity (Oxford University Press, Oxford, 1965).
A.N. Tikhonov, A.A. Samarskii, Equations of Mathematical Physics (Dover Publications Inc., New York, 1963).
M. Abramowitz, A. Stegun, Handbook of Mathematical Functions (Dover Publications, 1965).
N.V. Brilliantov, T. Poeschel, Collision of adhesive viscoelastic particles, in The Physics of Granular Media edited by H. Hinrichsen, D. Wolf, (Wiley-VCH, Berlin, 2004).
N.V. Brilliantov, N. Albers, F. Spahn, T. Pöschel, Phys. Rev. E 76, 051302 (2007).
E. Dintwa, M. van Zeebroeck, H. Ramon, Eur. Phys. J. B 39, 77 (2004).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Goldobin, D.S., Susloparov, E.A., Pimenova, A.V. et al. Collision of viscoelastic bodies: Rigorous derivation of dissipative force. Eur. Phys. J. E 38, 55 (2015). https://doi.org/10.1140/epje/i2015-15055-x
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1140/epje/i2015-15055-x