1 Introduction

Current observational and experimental data is consistent with the General Relativity by the latter is considered as the standard theory of gravity. However, the general theory of relativity breaks down on a quantum scale. One may consider alternative or modified theories of gravity to resolve this problem. The new modified theory of gravity proposed in [1] is one of the most promising models for the extension of general relativity. It may be considered as the next step in approaching the quantum gravity model. Since the new theory contains the scalar and massive vector field one may call it scalar-tensor-vector gravity (STVG) [1]. The massive vector field in the theory at the quantum scale creates a repulsive force by the charge \(Q=\sqrt{\alpha G}M\), where G is the gravitational constant, M is the mass of the central object, and \(\alpha \) is the new coupling parameter.

The proposed new theory has a solution describing the non-rotating and rotating black holes [2]. The test particle motion and stability of their orbits around the so-called Schwarzschild-MOG black hole have been studied in [3]. Since it was proposed the MOG theory has been tested through solar system tests [1], galaxy rotation curve [4, 5], through X-ray observations [6], black hole shadow [2, 7], the study of thermodynamics [8], supernovae [9], gravitational lensing [10], quasinormal modes [11]. Authors of [12] have studied the thermodynamic properties of MOG theory. The Ref [13] has been devoted to study the epicyclic frequencies in Kerr-MOG black hole. Quasi-periodic oscillations around Kerr-MOG black holes have been considered in [14]. Authors of [15] have studied the test particle dynamics near Kerr-MOG black hole. The gravitational instability in the Newtonian limit of MOG has been discussed in [16]. Our recent paper has been devoted to study the magnetized particle motion around MOG black hole in the presence of magnetic field [17].

Gravitational lensing is considered as one of the fundamental properties of the metric theories of gravity which is based on the light deflection effect due to gravitational interaction. Gravitational lensing has been started to be considered as a useful tool to study either source or lens system after first discovery by Einstein within the General Relativity. The review of the effect of gravitational lensing can be found in Refs. [18,19,20,21]. Recently, the strong gravitational lensing properties of gravitational field of MOG has been studied analysing the Einstein ring at the core of the galaxy cluster Abell 3827 and the constrain on the MOG parameter in the galaxy claster has been found about \(\alpha \simeq 10\) in Ref. [22]. The propagation of electromagnetic waves around a black hole in the presence of MOG field have been investigated in Ref. [23] and it was shown that the null-geodesics of photons in MOG is not the same as it is in general relativity and the effects of MOG becomes more sufficient in large scale structures. Moreover, weak gravitational lensing around Kerr-MOG black holes have been studied in Ref. [24] and it was concluded that an increase in the MOG parameter, the deflection angle becomes significantly larger than that the increase of the spin of rotating Kerr black hole. On the other hand, the plasma near the compact object may also effect on the photon trajectory. The study of plasma effect on photon motion in different spacetime for the different plasma configurations can be found in Refs. [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. The obtained first-ever image of a supermassive black hole in the center of galaxy M87 [46, 47] accelerated the investigations of optical properties of black holes. The image of the supermassive black hole is obtained using the Event Horizon Telescope (EHT) based on the very large interferometry (VLBI) technique. This discovery opens a new window to study gravity in a strong field regime near the compact object and to test the theories of gravity. The image of the supermassive black hole or so-called shadow of the black hole theoretically studied in Refs. [32, 48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75]. In this paper, we plan to study the effect of MOG corrections on the gravitational lensing near the compact object in the presence of plasma.

Particularly we consider the deflection angle of the light near the MOG black hole in the presence of the plasma medium. The paper is organized as follows: in Sect. 2 we study the photon motion and gravitational lensing in the gravitational field of Schwarzschild-MOG black hole. The Sect. 3 is devoted to studying the effect of plasma with the different configurations on the gravitational lensing effect. The brightness of the image source due to gravitational lensing around MOG black hole in the presence of plasma is considered in Sect. 4. We conclude our results in Sect. 5. Throughout the paper, we use the system of unit where \(G=1=c\), Greek indices run from 0 to 1, while Latin indices run from 1 to 3.

2 Light propagation around a black hole immersed in plasma

In this section we will review the effects of plasma medium around a black hole on light propagation formulated by Synge [18] and developed by the authors of Refs. [36, 39]. One can explore the gravitational effects in the weak field approximation using the following decomposition of the spacetime around a compact object:

$$\begin{aligned} g_{\alpha \beta } = \eta _{\alpha \beta } + h_{\alpha \beta }, \end{aligned}$$
(1)

where \(\eta _{\alpha \beta }\) is the metric tensor of the flat spacetime known as Minkowski and \(h_{\alpha \beta }\) is a small perturbation to the flat spacetime with the following properties:

$$\begin{aligned}&\eta _{\alpha \beta } = \mathrm{diag} (-1, 1, 1, 1),\nonumber \\&h_{\alpha \beta } \ll 1, \quad h_{\alpha \beta } \rightarrow 0 \quad \mathrm{under } \quad x^i\rightarrow \infty , \nonumber \\&g^{\alpha \beta }=\eta ^{\alpha \beta }-h^{\alpha \beta },\ \ \ h^{\alpha \beta }=h_{\alpha \beta }. \end{aligned}$$
(2)

Taking into account the Fermat’s principle - the least action principle for light propagation in a medium in the presence of gravitational field one may write the following condition for the 4-momenta of the photon \(p^\alpha \):

$$\begin{aligned} \delta \left( \int p_\alpha d x^\alpha \right) =0. \end{aligned}$$
(3)

Consequently, the motion of photons in a medium can be described by the following set of equations

$$\begin{aligned} \frac{dx^\alpha }{d\lambda } = \frac{\partial H}{\partial p_\alpha }, \quad \frac{dp_\alpha }{d\lambda } = - \frac{\partial H}{\partial x^\alpha }, \end{aligned}$$
(4)

where the Hamiltonian for the light rays H including the interaction between the electromagnetic wave and the plasma medium has the following form for the spherical symmetric spacetime [18]

$$\begin{aligned}&H(x^\alpha , p^\alpha ) = \frac{1}{2} \left[ g^{\alpha \beta }p_\alpha p_\beta -(n^2 - 1)(p_\alpha V^\alpha )^2\right] \nonumber \\&\quad = \frac{1}{2} \left[ g^{00}p_0 p_0 + g^{ik}p_i p_k -(n^2 - 1)\frac{\hbar ^2\omega ^2(x^i)}{c^2}\right] , \ \ \ \end{aligned}$$
(5)

where \(p^\alpha \) is the photon four-momentum, \(V^\alpha \) is the observer’s four-velocity, n is the refractive index of the plasma medium around the black hole, and \(\lambda \) is the affine parameter along the light ray, \(\hbar \) is the Planck constant, \(\omega (x^i)\) is the coordinate dependent frequency of photons, which includes the gravitational red-shift effect, c is the speed of light propagation in vacuum and

$$\begin{aligned} p_\alpha V^\alpha = -\frac{\hbar \omega (x^i)}{c} . \end{aligned}$$
(6)

The refraction index of inhomogeneous plasma depending on the photon and plasma frequencies has the following form

$$\begin{aligned} n^2=1-\frac{\omega _e^2}{\omega ^2(x^i)}, \quad \omega _e^2=\frac{4\pi e^2N(x^i)}{m}=K_e N(x^i), \end{aligned}$$
(7)

where \(N=N(x^i)\) is the density of electrons in plasma and the electron’s mass and electric charges are denoted by m and e, respectively. The phase speed of the electromagnetic wave in a plasma is given by \(v=c/n\). One can see from Eq. (7) that when \(\omega _e>\omega \) the plasma medium plays a role of a refractive medium, in the other words in that condition electromagnetic waves can not propagate in a such dense plasma. Only in the case when \(\omega _e<\omega \) the plasma medium illustrates reflective medium effects and in the limit \(\omega _e\ll \omega \) (\(n\rightarrow 1\)) Eq. (7) reduces to the vacuum case. For simplicity we will use the following notations in our further calculations:

$$\begin{aligned} \omega= & {} \omega (x^i\rightarrow \infty ),\nonumber \\ n_0= & {} n(x^i\rightarrow \infty ). \end{aligned}$$
(8)

Now, one can easily find the equations of motion of photons using Eqs. (4) and (7) in the following for

$$\begin{aligned} \frac{dx^i}{d\lambda }= & {} g^{ik} p_k = p^i, \end{aligned}$$
(9)
$$\begin{aligned} \frac{dp_i}{d\lambda }= & {} -\frac{1}{2} g^{kl}_{,i} p_k p_l -\frac{1}{2} g^{00}_{,i} p_0^2-\frac{1}{2} \frac{\hbar ^2 K_e N(x^i){,i}}{c^2}, \end{aligned}$$
(10)

where notation , i implies the partial derivation with respect to spatial coordinates. The weak gravitational field and plasma approximations allow the components of the four-momentum of the photon propagating along z direction to be in the following form

$$\begin{aligned} p^\alpha =\frac{\hbar \omega }{c}\left( 1, 0, 0,n_0\right) , \ \ p_\alpha =\frac{\hbar \omega }{c}\left( -1, 0, 0, n_0\right) . \end{aligned}$$
(11)

The deflection angle of the light ray coming from infinity and goes to infinity passing through the gravitating object in the plane perpendicular to the z axis can be expressed by the following form:

$$\begin{aligned} {\hat{\alpha }}_k= & {} [p_k(\infty )-p_k(-\infty )]/p\ ,\nonumber \\ p= & {} \sqrt{p_1^2+p_2^2+p_3^2}=|p_3|=\frac{n_0\hbar \omega }{c}, \ \ k=1,2. \end{aligned}$$
(12)

Finally, one can eaily find the equation for the deflection angle taking into account Eqs. (9) and (12) in the form

$$\begin{aligned} {\hat{\alpha }}_k= & {} \frac{1}{2} \int _{-\infty }^\infty \left( h_{33} +\frac{h_{00} \omega ^2-K_e N(x^i)}{\omega ^2-\omega _e^2}\right) _{,k} dz \nonumber \\= & {} \frac{1}{2} \int _{-\infty }^\infty \frac{b}{r}\Bigg (\frac{dh_{33}}{dr}+\frac{1}{1-\omega _e^2/\omega ^2}\frac{dh_{00}}{dr}\nonumber \\&- \frac{K_{e}}{\omega ^2-\omega _e^2}\frac{dN}{dr}\Bigg ) dz , \end{aligned}$$
(13)

where b is the impact parameter, which characterized by the radius-vector \(r^2 =b^2 + z^2\).

Note, that negative values of \({\hat{\alpha }}_b\) correspond to the bending of the light ray towards the central object and vice versa.

Now we will investigate the effects of plasma medium together with gravitational field of the Schwarschild-MOG black hole as an applications of above-described formalism. The geometry around the static and spherically symmetric black hole in MOG is described by the following form of spacetime metric [2]

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{1}{f(r)}dr^2+r^2(d\theta ^2+\sin ^2\theta d\phi ^2), \end{aligned}$$
(14)

where

$$\begin{aligned} f(r)= 1-\frac{2(1+\alpha ) M}{r}-\frac{\alpha (1+\alpha ) M^2}{r^2}, \end{aligned}$$
(15)

and \(\alpha \) is the coupling parameter of the modified gravity (hereafter we call it as MOG parameter). One can see that the spacetime metric (14) turns to flat-Minkowski one when \(\alpha =-1\) and the case when \(\alpha =0\) corresponds to the Schwarzschild solution.

In the weak gravitational field limit (\(M/r\ll 1\)) one may rewrite the spacetime metric (14) around the MOG black hole as

$$\begin{aligned} ds^2= & {} ds^2_{0} + \frac{(1+\alpha )R_{s}}{r} \left( 1+\frac{\alpha R_{s}}{4r} \right) dt^2\nonumber \\&+\frac{(1+\alpha )R_{s}}{r}\left( 1+\frac{(4+9\alpha +5\alpha ^2)R_{s}}{4(1+\alpha )r} \right) dr^2, \end{aligned}$$
(16)

where \(R_s=2M\) and \(ds^2_{0}=-dt^2+dr^2+r^2(d\theta ^2+\sin ^2\theta d\phi ^2)\) is the line element in Minkowski spacetime.

In the Cartesian coordinates the components \(h_{\alpha \beta }\) can be written as

$$\begin{aligned} h_{00}= & {} \frac{(1+\alpha )R_{s}}{r}\left( 1+\frac{\alpha R_{s}}{4r} \right) , \nonumber \\ h_{ik}= & {} h_{00}n_{i}n_{k},\nonumber \\ h_{33}= & {} h_{00}\cos ^2\chi . \end{aligned}$$
(17)

3 Deflection angle in the presence of plasma

In this section, we will calculate the deflection angle of light ray passing through Schwarzschild-MOG black hole immersed in plasma medium with various configurations of plasma and analyse the effects of MOG and plasma parameters. The terms in expression under the integral (13) can be expressed as

$$\begin{aligned} \frac{b}{r}\frac{dh_{33}}{dr}= & {} -\frac{(1+\alpha )R_{s}}{r}\frac{b}{r} \frac{z^2}{r^2}\left( 3+(4+5\alpha )\frac{R_s}{r}\right) , \end{aligned}$$
(18)
$$\begin{aligned} \frac{b}{r}\frac{dh_{00}}{dr}= & {} -\frac{R_{s} b }{2r^4} (1+\alpha )\left( 2r+\alpha R_{s}\right) . \end{aligned}$$
(19)

One can see from Eq. (13) that the expression includes the effects of gravity and plasma. Here we rewrite the integral form of deflection angle by separating the effects as:

$$\begin{aligned} {\hat{\alpha }}_1= & {} \frac{1}{2} \int _{-\infty }^\infty \frac{b}{r}\Bigg (\frac{dh_{33}}{dr}\Bigg ) dz, \end{aligned}$$
(20)
$$\begin{aligned} {\hat{\alpha }}_2= & {} \frac{1}{2} \int _{-\infty }^\infty \frac{b}{r}\Bigg (\frac{1}{1-\omega _e^2/\omega ^2}\frac{dh_{00}}{dr}\Bigg ) dz, \end{aligned}$$
(21)
$$\begin{aligned} \ {\hat{\alpha }}_3= & {} -\frac{1}{2} \int _{-\infty }^\infty \frac{b}{r}\Bigg (\frac{K_{e}}{\omega ^2-\omega _e^2}\ \frac{dN}{dr}\Bigg ) dz. \end{aligned}$$
(22)

Now, we calculate the integrals for the deflection angle for the different configurations of the plasma distribution. Below we consider several configuration of plasma surrounding the MOG compact object.

3.1 Uniform plasma

First we explore the effects of uniform plasma together with MOG parameter on deflection angle. We start with calculating the terms related to only effects of spacetime curvature:

$$\begin{aligned} {\hat{\alpha }}_1= & {} \frac{1}{2} \int _{-\infty }^\infty \frac{b}{r}\left( \frac{dh_{33}}{dr}\right) dz\nonumber \\= & {} -\frac{R_{s}(1+\alpha )}{b}-\frac{R_{s}^2 \pi \alpha (9+5\alpha )}{16b^2}. \end{aligned}$$
(23)

One can see from Eq. (23) that when \(\alpha =0\) we will get \({\hat{\alpha }}_1=R_s/b\). The second one is mixed term reflecting the spacetime and plasma effects which has the following form:

$$\begin{aligned} {\hat{\alpha }}_2= & {} \frac{1}{2} \int _{-\infty }^\infty \frac{b}{r}\left( \frac{1}{1-\omega _e^2/\omega ^2}\frac{dh_{00}}{dr}\right) dz\nonumber \\= & {} -\frac{R_{s}(1+\alpha )}{b}-\frac{\pi \alpha R_{s}^2 (1+\alpha )}{8b^2} \frac{1}{1-\omega _e^2/\omega ^2}. \end{aligned}$$
(24)

The Eq. (24) also turns to \({\hat{\alpha }}_2=R_s/b\) at \(\alpha =0\). Thus one may get the expression for the deflection angle for Schwarschild case \({\hat{\alpha }}_{b}=2R_s/b\) when \(\alpha =0\). In the case of the uniform plasma distribution the third term of the deflection angle given by Eq. (22) turns to zero. Finally, one can express the deflection angle of light in the case of uniform plasma around MOG compact object as

$$\begin{aligned} -{\hat{\alpha }}_b= & {} \frac{(1+\alpha )R_{s}}{b}\left( 1+\frac{1}{1-\omega _e^2/\omega ^2}\right) \nonumber \\&+\frac{\pi \alpha R_{s}^2 (9+5 \alpha )}{16b^2}+\frac{\pi \alpha R_{s}^2(1+\alpha )}{8b^2 (1-\omega _e^2/\omega ^2)}. \end{aligned}$$
(25)
Fig. 1
figure 1

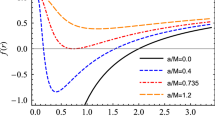
Deflection angle \({\hat{\alpha }}_{b}\) as a function of the impact parameter b for different values of MOG and plasma parameters. The Left panel corresponds to the value of the plasma frequency \(\omega _{e}/\omega =0.5\), in the middle one is for the Schwarzschild case and the right panel is for the fixed value of the MOG parameter \(\alpha =0.2\), respectively

Full size image

Figure 1 illustrates the dependence of deflection angle from the impact parameter for the different values of the plasma frequency and MOG parameter. One can see from the figure that the increase of both plasma frequency and MOG parameter causes to increase of the deflection angle, with compare to Schwarzschild black hole in a vacuum.

3.2 Singular isothermal sphere medium

In this subsection, we will study effects of MOG field on the gravitational lensing of the gravitating object immersed in a singular isothermal sphere (SIS). The model is best suits to lensing systems like galaxies and galaxy clusters. Plasma density distribution for the SIS has the following form [36, 76]

$$\begin{aligned} \rho (r)=\frac{\sigma ^2_v}{2\pi } r^{-2}, \end{aligned}$$
(26)

where \(\sigma ^2_v\) is a one dimensional velocity dispersion. One can find the plasma concentration using the plasma density (26) and the relation

$$\begin{aligned} N(r)=\frac{\rho (r)}{\kappa m_p} \end{aligned}$$
(27)

where \(m_p\) is proton mass, \(\kappa \) is a coefficient which reflects the dark matter effects called one-dimensional coefficient. Finally, the plasma frequency takes the form [36]

$$\begin{aligned} \omega _e^2=K_eN(r)=\frac{K_e\sigma _v^2}{2\pi \kappa m_p}r^{-2}. \end{aligned}$$
(28)

Now one can calculate deflection angle in the presence of the plasma with the SIS distribution around MOG object using Eq. (20). Here, we have separated the deflection angle as Eqs. (20)–(22) and express as

$$\begin{aligned}&{\hat{\alpha }}_{\mathrm{SIS}}={\hat{\alpha }}_{\mathrm{SIS}}^{(1)}+{\hat{\alpha }}_{\mathrm{SIS}}^{(2)}+{\hat{\alpha }}_{\mathrm{SIS}}^{(3)}. \end{aligned}$$
(29)

Since the first term does not include the plasma effects it takes the same form as Eq. (23)

$$\begin{aligned}&{\hat{\alpha }}_{\mathrm{SIS}}^{(1)}={\hat{\alpha }}_1. \end{aligned}$$
(30)

One can now easily calculate the other terms of the deflection angle and obtain the following expressions

$$\begin{aligned} {\hat{\alpha }}_{\mathrm{SIS}}^{(2)}= & {} \frac{1}{2} \int _{-\infty }^\infty \frac{b}{r}\left( \frac{1}{1-\omega _e^2/\omega ^2}\frac{dh_{00}}{dr}\right) dz\nonumber \\= & {} -\frac{(1+\alpha )R_{s}^3}{96 b^4 \pi }\frac{\omega _{c}^2}{\omega ^2} \left( 64b+9 \pi \alpha R_{s}\right) , \end{aligned}$$
(31)
$$\begin{aligned} {\hat{\alpha }}_{SIS}^{(3)}= & {} \frac{K_{e} b}{\omega ^2}\frac{1}{2} \int _{-\infty }^\infty \frac{\omega _{e}^2}{r} \frac{dN(r)}{dr} dz \nonumber \\= & {} -\frac{K_{e} b}{\omega ^2}\frac{1}{2} \int _{-\infty }^\infty \frac{\sigma ^2}{k m_{p} \pi (b^2+z^2)^2}dz \nonumber \\= & {} -\frac{\omega _{c}^2 R_{s}^2}{2 \omega ^2 b^2}, \end{aligned}$$
(32)

where

$$\begin{aligned} \omega _{c}^2=\frac{K_{e}\sigma ^2}{2km_{p}R_{s}^2}. \end{aligned}$$

Collecting all the integrals we can get

$$\begin{aligned} -{\hat{\alpha }}_{\mathrm{SIS}}= & {} \frac{2R_{s}(1+\alpha )}{b}+\frac{\alpha R_{s}^2 \pi (11+7\alpha )}{16 b^2}+\frac{R_{s}^2 \omega _{c}^2}{2b^2 \omega ^2}\nonumber \\&\times \left\{ 1+\frac{4(1+\alpha )R_{s}}{3b \pi }+\frac{3\alpha (1+\alpha ) R_{s}^2 }{16 b^2 }\right\} . \end{aligned}$$
(33)
Fig. 2
figure 2

Deflection angle \({\hat{\alpha }}_{b}\) as a function of the impact parameter b for MOG compact object surrounded SIS plasma. In the left panel we have fixed the plasma frequency as \(\omega _{c}/\omega =0.5\), the middle one corresponds to the Schwrazschild case and right panel corresponds to the fixed values of the MOG parameter \(\alpha =0.2\)

Full size image

Figure 2 shows the dependence of the deflection angle of the light ray passing through the lensing object in the plasma with the SIS model from the impact parameter. One can see from the figure that in the SIS model the deflection angle smaller with compare to the uniform plasma and the effects of the plasma frequency is not significantly as the uniform case.Moreover, positive (negative) values of the MOG parameter forces to bind the light rays greater (smaller) than the Schwarzschild case.

3.3 Non-singular isothermal gas sphere medium

In this subsection we study the deflection angle of photons by Schwarzschild-MOG black hole in the presence of the plasma with the electron density distributed as non-isothermal gas sphere (NSIS) model in the following form [36]:

$$\begin{aligned} N(r)=\frac{\sigma ^2}{2\pi k m_{p} (r^2+r_c^2)}, \end{aligned}$$
(34)

and corresponding plasma frequency

$$\begin{aligned} \omega _e^2=K_{e} N(r)=\frac{K_{e} \sigma ^2}{2\pi k m_{p} (r^2+r_c^2)}. \end{aligned}$$
(35)

The deflection angle in this case can be calculated using decomposition (20)–(22) in the following form:

$$\begin{aligned} {\hat{\alpha }}_{\mathrm{NSIS}}={\hat{\alpha }}^{\mathrm{nsis}}_{1}+{\hat{\alpha }}^{\mathrm{nsis}}_{2}+{\hat{\alpha }}^{\mathrm{nsis}}_{3} , \end{aligned}$$
(36)

where the first term is automatically can be expressed as

$$\begin{aligned}&{\hat{\alpha }}_1^{\mathrm{nsis}}={\hat{\alpha }}_1. \end{aligned}$$
(37)

Other terms of the Eq. (36) will take the following form

$$\begin{aligned} {\hat{\alpha }}^{\mathrm{nsis}}_2= & {} \frac{1}{2} \int _{-\infty }^\infty \frac{b}{r}\left( \frac{1}{1-\omega _e^2/\omega ^2}\frac{dh_{00}}{dr}\right) dz\nonumber \\= & {} \frac{R_{s}^3 \omega _{c}^2}{\pi r_c^2\omega ^2}(1+\alpha )\left\{ \frac{b}{r_{c} }\frac{\mathrm{arctanh}[\frac{r_c}{\sqrt{b^2+r_c^2}}] }{\sqrt{b^2+r_{c}^2}}-\frac{1}{b} \right. \nonumber \\&\left. + \frac{\pi \alpha R_{s}}{4 r_c^2}\Bigg (1-\frac{r_c^2 }{2 b^2}-\frac{b}{\sqrt{b^2+r_c^2}}\Bigg )\right\} , \end{aligned}$$
(38)
$$\begin{aligned} {\hat{\alpha }}^{\mathrm{nsis}}_{3}= & {} \frac{K_{e} b}{\omega ^2}\frac{1}{2} \int _{-\infty }^\infty \frac{\omega _{e}^2}{r} \frac{dN(r)}{dr} dz\nonumber \\ {}= & {} - \frac{K_{e} b}{\omega ^2}\frac{1}{2} \int _{-\infty }^\infty \frac{\sigma ^2}{k m_{p} \pi (b^2+z^2+r_c^2)^2}dz \nonumber \\= & {} -\frac{\omega _c^2}{\omega ^2}\frac{b R_{s}^2}{2 (b^2+r_c^2)^{3/2}}. \end{aligned}$$
(39)

Summarizing all terms one may obtain the expression for the deflection angle in the form

$$\begin{aligned} -{\hat{\alpha }}_{\mathrm{NSIS}}= & {} \frac{2R_{s}(1+\alpha )}{b}+\frac{\alpha R_{s}^2 \pi (11+7\alpha )}{16 b^2}\nonumber \\&+\frac{\omega _c^2}{\omega ^2}\frac{b R_{s}^2}{2 (b^2+r_c^2)^{3/2}} \nonumber \\&- \frac{R_{s}^3 \omega _{c}^2}{\pi r_c^2\omega ^2}(1+\alpha )\left\{ \frac{b}{r_{c} }\frac{\mathrm{arctanh}[\frac{r_c}{\sqrt{b^2+r_c^2}}] }{\sqrt{b^2+r_{c}^2}}-\frac{1}{b}\right. \nonumber \\&\left. + \frac{\pi \alpha R_{s}}{4 r_c^2}\Bigg (1-\frac{r_c^2 }{2 b^2}-\frac{b}{\sqrt{b^2+r_c^2}}\Bigg )\right\} . \end{aligned}$$
(40)
Fig. 3
figure 3

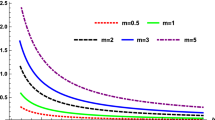
Deflection angle \({\hat{\alpha }}_{b}\) as a function of the impact parameter b around MOG black hole surrounded NSIS plasma. In the left panel we have fixed the plasma frequency as \(\omega _{c}/\omega =0.5\) by varying the MOG parameter with the comparison the Schwarzschild case, the middle panel is devoted to the pure Schwarzschild case for the different values of the plasma frequency with the comparison of the vacuum case, and the right panel corresponds to the values of the MOG parameter \(\alpha =0.2\). In all cases we take \(r_c=3M\)

Full size image

Figure 3 demonstrates the dependence deflection angle from the impact parameter for the different values of the MOG and plasma parameters. One can see from the left panel that the existence of the MOG field with the positive parameter cause to the increase of the deflection angle due to the increase of the gravitational properties of the central object while the negative value of the MOG parameter decreases it. Moreover, the deflection angle is slightly increases due to the effect of plasma medium with the NSIS distribution.

Now, in order to compare the effects of the plasma with different distribution we will study the deflection angle for the fixed values of the MOG parameter and plasma frequency.

Fig. 4
figure 4

Deflection angle \({\hat{\alpha }}_{b}\) as a function of the a impact parameter b, b MOG parameter and c plasma frequency for different type of plasma distributions. In the left panel we have used \(\alpha = 0.2\), in the middle one \(b = r_c = 3M\), \(\omega _c/\omega =0.5\) and the right one \(b=r_c=3M\), \(\alpha =0.2\). In these plots we have compared the effects of uniform, the SIS and NSIS models for the fixed value of plasma density

Full size image

The comparison of effects of plasma with uniform distribution, singular-isothermal gas and non-singular isothermal gas around Shwarzschild-MOG black hole is shown in Fig. 4. Here, in the right and middle panels, we have chosen \(\omega _{c}/\omega =\omega _{e}/\omega =0.5\) for plasma and \(\alpha =0.2\) for MOG parameter. The value of the impact parameter is taken to be \(b=3M\) and for the NSIS model the core radius is also chosen to be \(r_c=3M\). One can easily see that the refracting properties of the uniform density plasma is stronger than the plasma in the models SIS and NSIS, and the strength of the effects increases with the increase of the MOG parameter and this analysis also show that the deflection of the light rays is bigger in the case of existence of positive MOG parameter than the Schwarzschild case.

4 Image source brightness

Now we will explore the magnification of image source using the expression for the deflection angle in the presence of plasma around MOG black hole. The gravitational lens equation reads as [77, 78]

$$\begin{aligned} \theta D_s=\beta D_s +{\hat{\alpha }}_{b} D_{ls}, \end{aligned}$$
(41)

where \(\beta \) is the angle of the real source from the observer-lens axis, \(\theta \) is the angle of source’s apparent image, \(\alpha \) is the deflection angle of the light ray coming from the distant source to the observer passing through the gravitating objects, the geometrical distance between the observer and the source object is denoted by \(D_s\) and \(D_{ls}\) is the distances from the lens to the source. Since impact parameter is \(b=D_l\theta \), where \(D_l\) is the distance from the observer to the lens, we obtain the relation in the form [39, 40]

$$\begin{aligned} \beta = \theta - \frac{D_{ls}}{D_s}\frac{F(\theta )}{D_l} \frac{1}{\theta } \end{aligned}$$
(42)

where \(F(\theta )=|\alpha _b| b=|\alpha _b (\theta )| D_l \theta \). Solutions of Eq. (42) with respect to the apparent image angle \(\theta \) give the positions \(\theta _k\) of the images of the source object.

In the special case when the source, lensing object and observer lie in a straight line the solution of the Eq. (42) is called Einstein angle \(\theta _0\) and the image takes a ring shape which is called the Einstein’s ring. Radius of the Einstein’s ring is \(R_0=D_l \theta _0\), where \(\theta _0\) is the solution of Eq. (42) when \(\beta =0\). In fact that the Einstein angle is an infinite small angle which have to be resolved by modern telescopes. However, the lensing by a gravitating astrophysical object like a massive star or stellar black hole is detectable due to the changes of the apparent brightness of the source, in other words, the magnification of the image brightness can help to get information from the lensing object properties. The expression of the magnification of image brightness is

$$\begin{aligned} \mu _\Sigma =\frac{I_{\mathrm{tot}}}{I_{*}}=\sum _k \left| \left( \frac{\theta _k}{\beta }\right) \left( \frac{d\theta _k}{d\beta }\right) \right| , \quad k=1,2,\ldots , s,\nonumber \\ \end{aligned}$$
(43)

where s is the total number of images, \(I_{\mathrm{tot}}\) is the total brightness of the images and \(I_{*}\) is the brightness of the pure source without the lensing effect and k is the number of an image.

The Einstein angle \(\theta _{\mathrm{E}}\) in the Schwarzschild spacetime has the following form

$$\begin{aligned} \theta _{\mathrm{E}}=\sqrt{2R_{s}\frac{D_{ds}}{D_s D_d}} . \end{aligned}$$
(44)

Below we will investigate effects of plasma medium together with MOG field around Schwarzschild black hole on the magnification of the images for the different configurations of plasma concentration.

4.1 Uniform plasma

In this subsection, we will investigate modified expression for the Einstein angle \((\theta _0^{pl})_{\mathrm{MOG}}\) in the presence of uniform plasma medium around the MOG-black hole. Using Eqs. (25) and (42) one may get

$$\begin{aligned} (\theta _0^{pl})_{\mathrm{uni}}= & {} {\theta _{\mathrm{E}}}\Bigg \{\frac{1+\alpha }{2}\left( 1+\frac{1}{1-\omega _e^2/\omega ^2}\right) \nonumber \\&+\frac{\pi \alpha R_{s}}{16b}\left[ \frac{9+5 \alpha }{2}+\frac{1+\alpha }{1-\omega _e^2/\omega ^2}\right] \Bigg \}^{1/2}. \end{aligned}$$
(45)

The total magnification of image source can be found using Eq. (43) together with the following expression:

$$\begin{aligned} \mu _{tot}^{pl}=\mu _{+}^{pl}+\mu _{-}^{pl}=\frac{x^2+2}{x\sqrt{x^2+4}} \end{aligned}$$
(46)

where the quantity x in the presence of uniform plasma takes the following form:

$$\begin{aligned} x_{un}= & {} \frac{\beta }{(\theta _0^{pl})_{\mathrm{uni}}}=x_{0}\Bigg \{\frac{1+\alpha }{2}\left( 1+\frac{1}{1-\omega _e^2/\omega ^2}\right) \nonumber \\&+\frac{\pi \alpha R_{s}}{16b}\left[ \frac{9+5 \alpha }{2}+\frac{1+\alpha }{1-\omega _e^2/\omega ^2}\right] \Bigg \}^{-\frac{1}{2}} , \end{aligned}$$
(47)

where the notation \(x_{0} = \beta / \theta _0 \) and the magnifications of the image source read as

$$\begin{aligned} \left( \mu _{+}^{pl}\right) _{\mathrm{un}}= & {} \frac{1}{4}\Bigg (\frac{x_{un}}{\sqrt{x_{un}^2+4}}+\frac{\sqrt{x_{un}^2+4}}{x_{un}}+2\Bigg ), \end{aligned}$$
(48)
$$\begin{aligned} \left( \mu _{-}^{pl}\right) _{\mathrm{un}}= & {} \frac{1}{4}\Bigg (\frac{x_{un}}{\sqrt{x_{un}^2+4}}+\frac{\sqrt{x_{un}^2+4}}{x_{un}}-2\Bigg ). \end{aligned}$$
(49)
Fig. 5
figure 5

The dependence of the total magnification \(\mu _{tot}\) on the MOG parameter for the different values of the plasma frequency at \(b=3M\)

Full size image

Figure 5 illustrates the effect of the MOG parameter on the total magnification with the comparison of the absence and presence of the uniform plasma medium cases with the parameter \(\omega _c/\omega =0.3, 0.5\). One can see that the magnification increases (quasi)linearly with the increase of the MOG parameter and plasma frequency.

4.2 Singular isothermal sphere medium

This subsection devoted the study of the magnification of images in the presence of plasma medium with SIS distribution around Schwarschild-MOG black hole. In this model the generalized expression for the Einstein ring \((\theta _0^{pl})\) takes the following form

$$\begin{aligned} (\theta _0^{pl})_{\mathrm{{SIS}}}= & {} {\theta _{\mathrm{E}}}\Bigg \{1+\alpha +\frac{\alpha R_{s} \pi }{32 b}(11+7\alpha )+\frac{R_{s} \omega _{c}^2}{4b \omega ^2}\nonumber \\&\times \left[ 1+\frac{ 4R_{s}}{3b \pi }(1+\alpha )\left( 1+\frac{9\alpha \pi R_{s} }{64 b }\right) \right] \Bigg \}^{\frac{1}{2}}.\quad \end{aligned}$$
(50)

Using (43) one can write magnification of the image source for MOG-black hole :

$$\begin{aligned} \left( \mu _{tot}^{pl}\right) _{\mathrm{SIS}}=\left( \mu _{+}^{pl}\right) _{\mathrm{SIS}}+\left( \mu _{-}^{pl}\right) _{\mathrm{SIS}}=\frac{x^2+2}{x\sqrt{x^2+4}}, \end{aligned}$$
(51)

where

$$\begin{aligned} \left( \mu _{+}^{pl}\right) _{\mathrm{SIS}}= & {} \frac{1}{4}\left( \frac{x_{\mathrm{SIS}}}{\sqrt{x_{\mathrm{SIS}}^2+4}}+\frac{\sqrt{x_{\mathrm{SIS}}^2+4}}{x_{\mathrm{SIS}}}+2\right) , \end{aligned}$$
(52)
$$\begin{aligned} \left( \mu _{-}^{pl}\right) _{\mathrm{SIS}}= & {} \frac{1}{4}\left( \frac{x_{\mathrm{SIS}}}{\sqrt{x_{\mathrm{SIS}}^2+4}}+\frac{\sqrt{x_{\mathrm{SIS}}^2+4}}{x_{\mathrm{SIS}}}-2\right) , \end{aligned}$$
(53)

and

$$\begin{aligned} x_{\mathrm{SIS}}= & {} \frac{\beta }{(\theta _0^{pl})_{\mathrm{SIS}}}=x_{0}\Bigg \{1+\alpha +\frac{\alpha R_{s} \pi }{32 b}(11+7\alpha ) \nonumber \\&+\frac{R_{s} \omega _{c}^2}{4b \omega ^2} \left[ 1+\frac{ 4R_{s}}{3b \pi }(1+\alpha )\left( 1+\frac{9\alpha \pi R_{s} }{64 b }\right) \right] \Bigg \}^{-\frac{1}{2}}.\nonumber \\ \end{aligned}$$
(54)
Fig. 6
figure 6

The total magnification of the images as a function of the MOG parameter. Here, plasma is distributed as SIS medium with the frequency \(\omega _{c}^2/\omega ^2=0.5\) at \(b=3M\)

Full size image

Figure 6 demonstrates the dependence of total magnification of images of the source on the MOG parameter for the SIS plasma model. In Fig. 6 we have chosen the value for the plasma frequency as \(\omega _c/\omega =0.5\) at the distance from the central black hole \(b=3M\). One can see that in the SIS model the magnification also increases with the increase of the MOG parameter as it obtained in the uniformly distributed plasma medium. However, in the SIS model the value of the magnification is smaller than the uniform case for the same plasma frequency.

Fig. 7
figure 7

Relations between degeneracy values of plasma frequency and the MOG parameter for the same total magnification value for uniform plasma model and SIS one

Full size image

Figure 7 demonstrates relations between degeneracy values of the MOG parameter and the plasma frequency for the fixed values of the total magnification of images for the both uniformly distributed plasma and the plasma in SIS model. One can see that it is impossible to distinguish the effects of the plasma medium and MOG field on the magnification of images. From the Fig. 7 we may conclude that the growing of the plasma frequency leads to the decrease of the MOG parameter and it is more rapidly decreasing in the SIS model than the uniformly distributed plasma.

5 Conclusion

In this paper, we have investigated weak gravitational lensing properties of Schwarzcshild-MOG black holes immersed in a plasma medium. The obtained results can be summarized as follows:

  • In this paper we have focused on study the effects of MOG model together with the plasma medium on the photon deflection angle.

  • Particularly, we have considered uniform distributed plasma, singular isothermal sphere medium and non-isothermal sphere medium.

  • We have obtained that the effect of negative values of the MOG parameter to the weak gravitational lensing is weaker than the effect of positive MOG parameter.

  • We have also shown that the deflection angle increases with the increase of the plasma frequency due to refractive effect of the medium.

  • The analysis of the deflection angle of the light ray around the MOG-black hole in the plasma medium in SIS and NSIS models show that the effect of plasma environment is much stronger in the case of SIS model than NSIS one for the same values of the plasma frequency.

  • Moreover, in SIS model the deflection angle more sensitive to the plasma frequency near the central black hole, while in NSIS model it is almost the same everywhere.

  • We have also studied the total magnifications of images of the source due to gravitational lensing around MOG-black hole surrounded by plasma. The analysis of the total magnification of images of the source show that the magnification increases linearly with the increase of the MOG parameter and plasma frequency in the case of uniform distribution.

  • In the case of SIS model the magnification also increases with the increase of the MOG parameter. However, in the SIS model the value of the magnification is smaller than the uniform distribution case for the same plasma frequency.

  • Comparisons of deflection angle of light rays passing through the Schwarzschild and Schwarzschild-MOG black holes in Figs. 2, 3 and 4 show that the MOG field with the positive (negative) MOG parameter makes much stronger (weaker) the gravitational field and it causes the deflection angle and the total magnifications of images to increase (decrease) with compare to the Schwarzschild case.